Comparison of Machine Learning Approaches for Reconstructing Sea Subsurface Salinity Using Synthetic Data
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.1.1. Coupled Model Intercomparison Project Phase 6 (CMIP6) Model Data
2.1.2. Synthetic Data
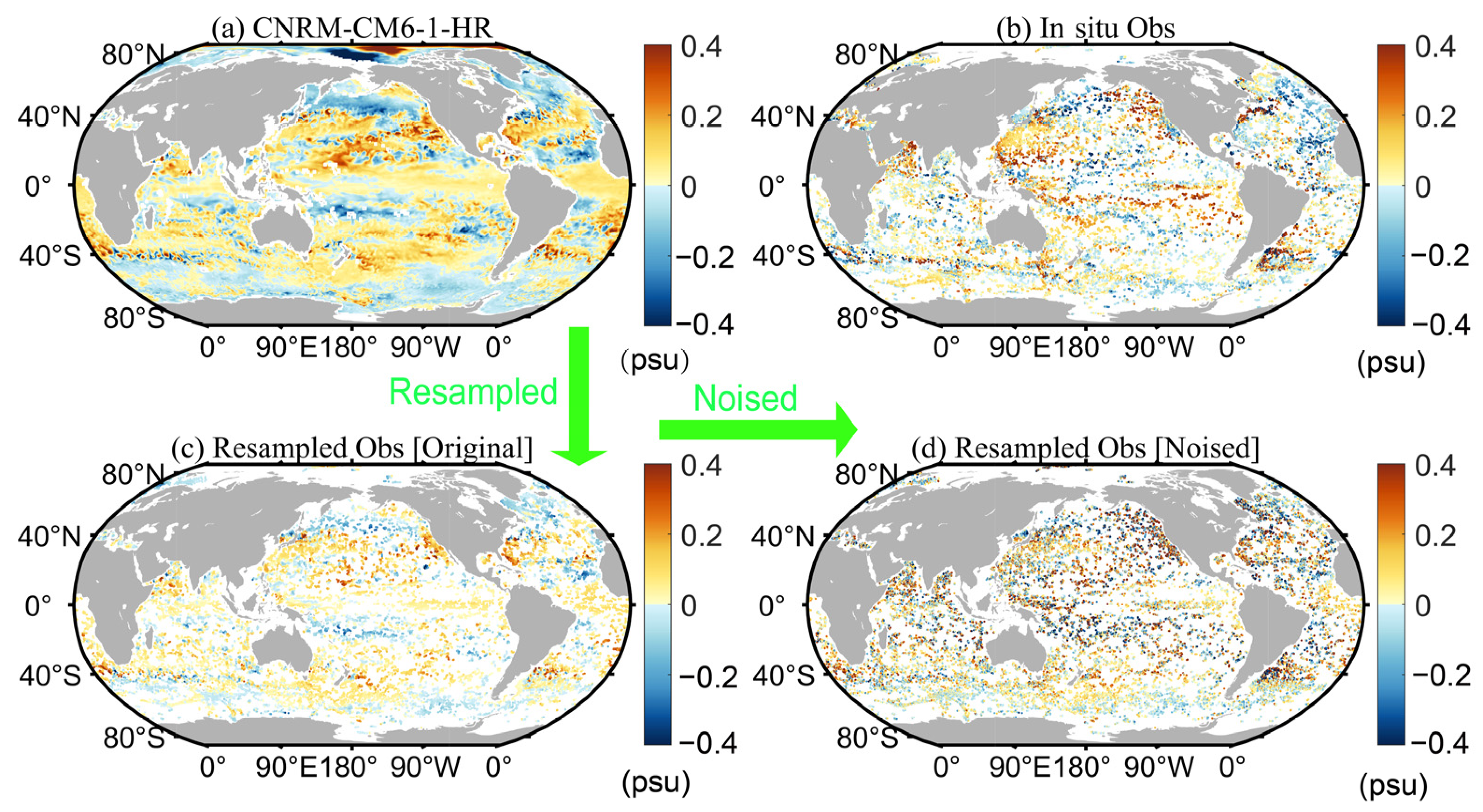
Resampling
Noising of the Truth Value
Equivalence between the CNRM-CM6-1-HR and IAP1° Salinity Data
2.2. Method
2.2.1. FFNN
2.2.2. LightGBM
2.2.3. Design of the Data Reconstruction Experiments
3. Reconstruction Results
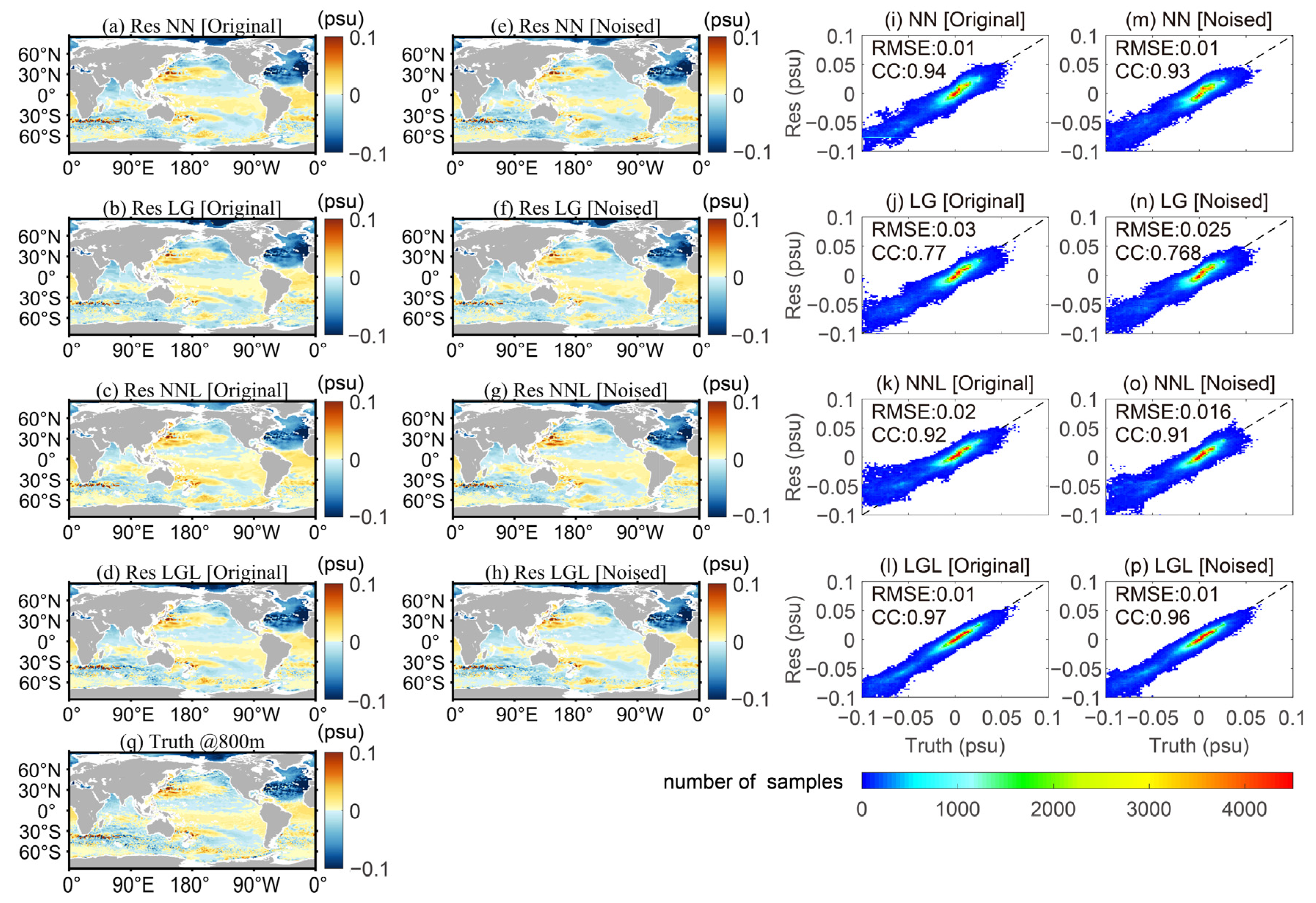
3.1. Reconstruction of Geographical Pattern
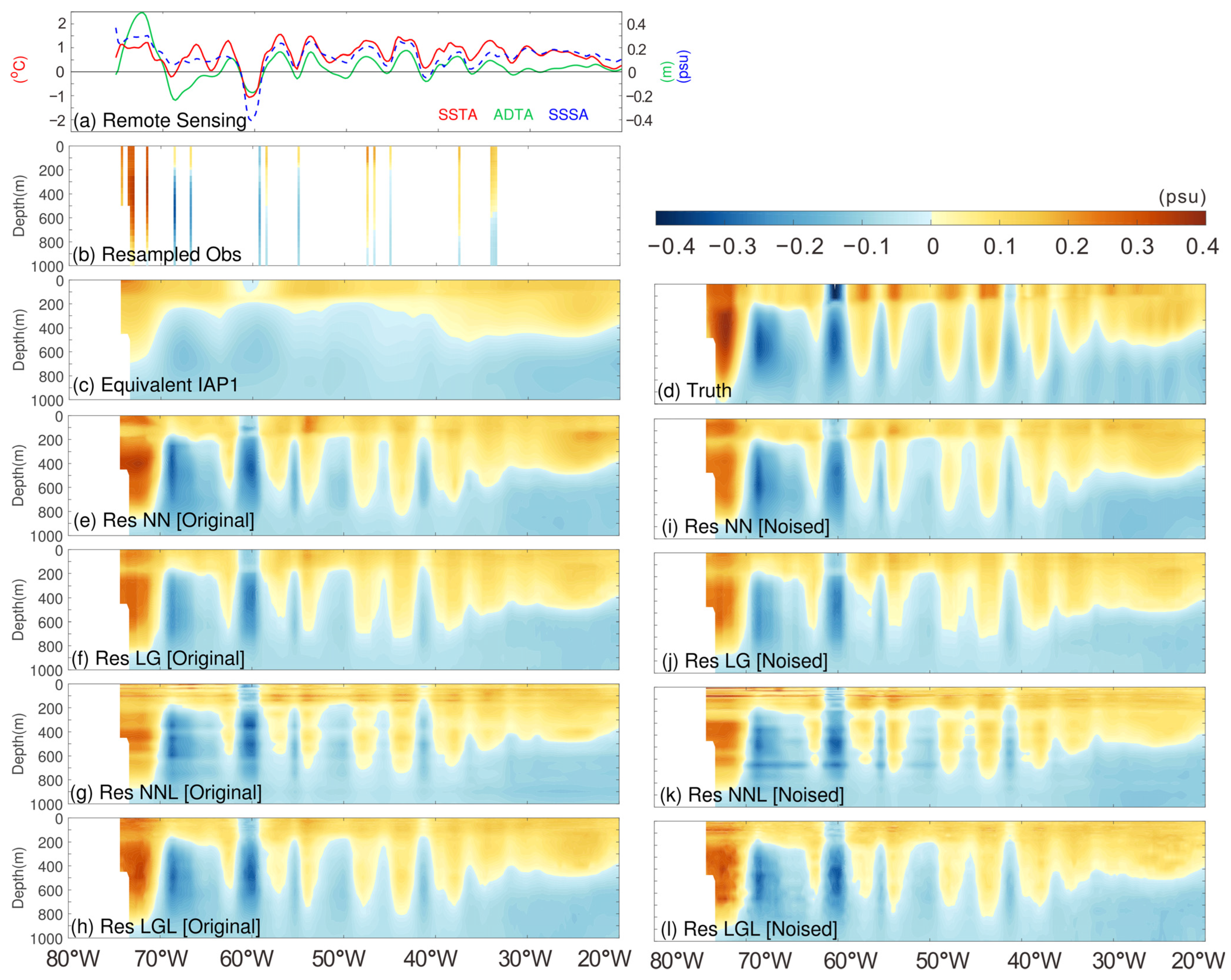
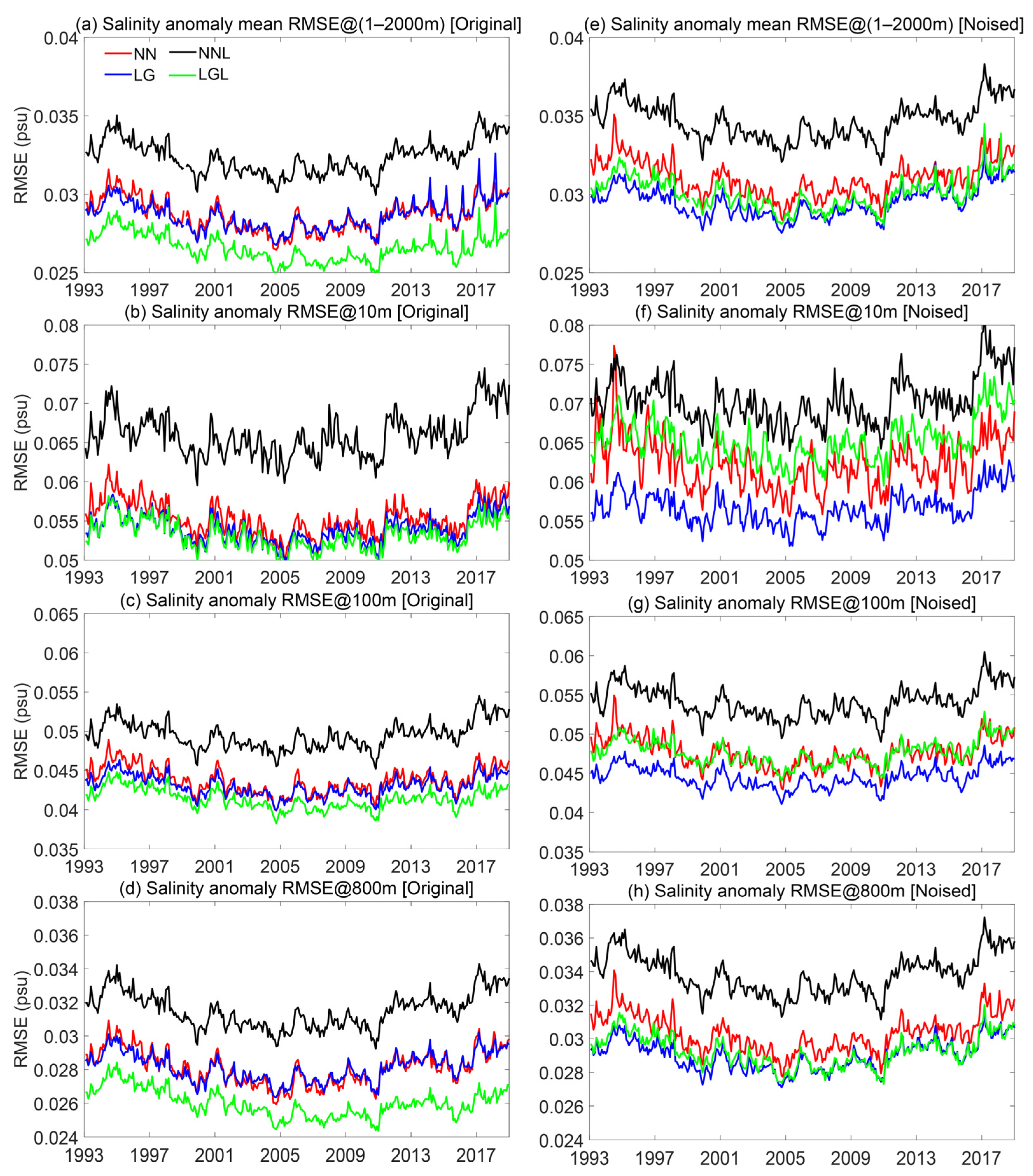
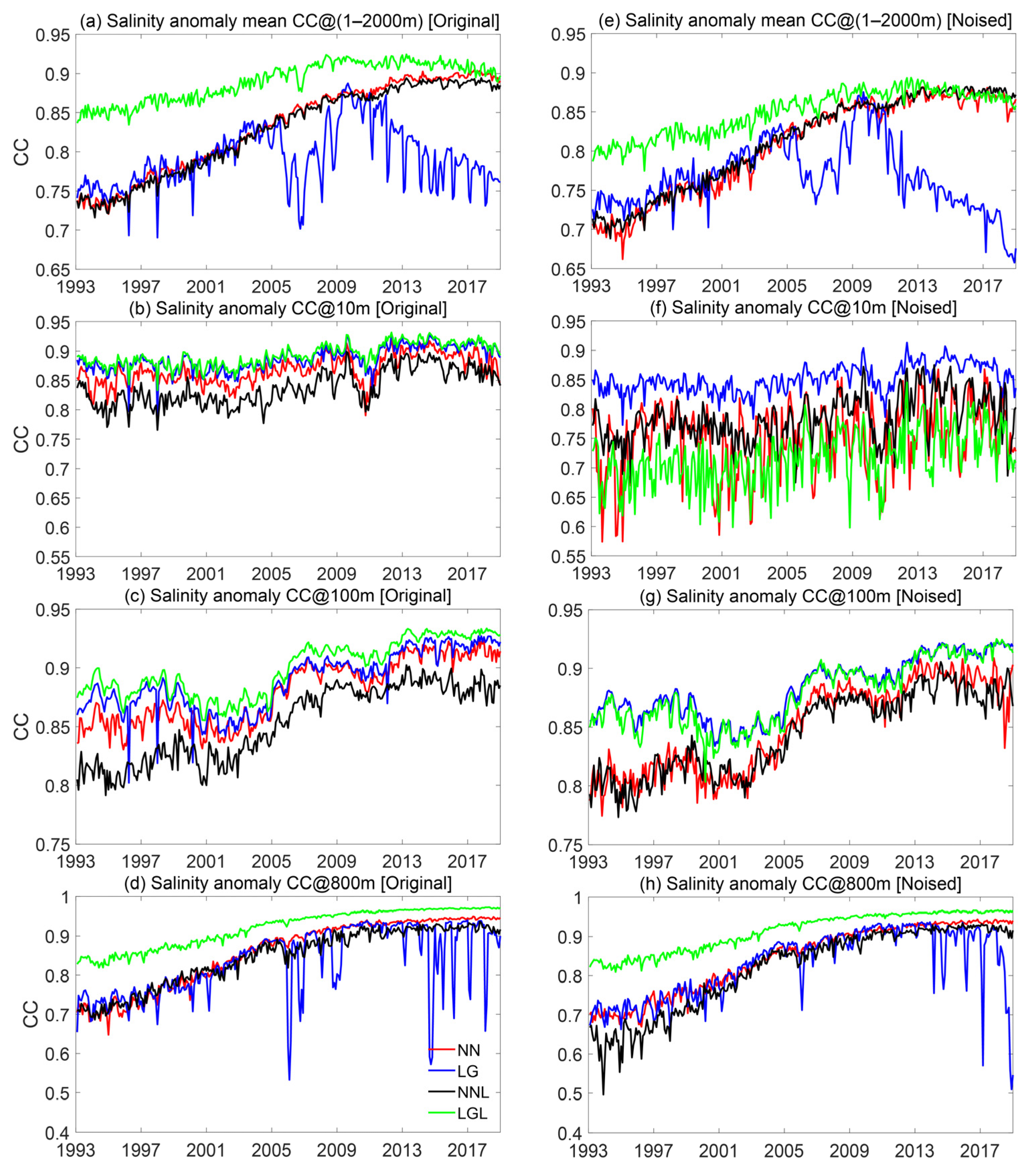
3.2. Reconstruction of Vertical Structure
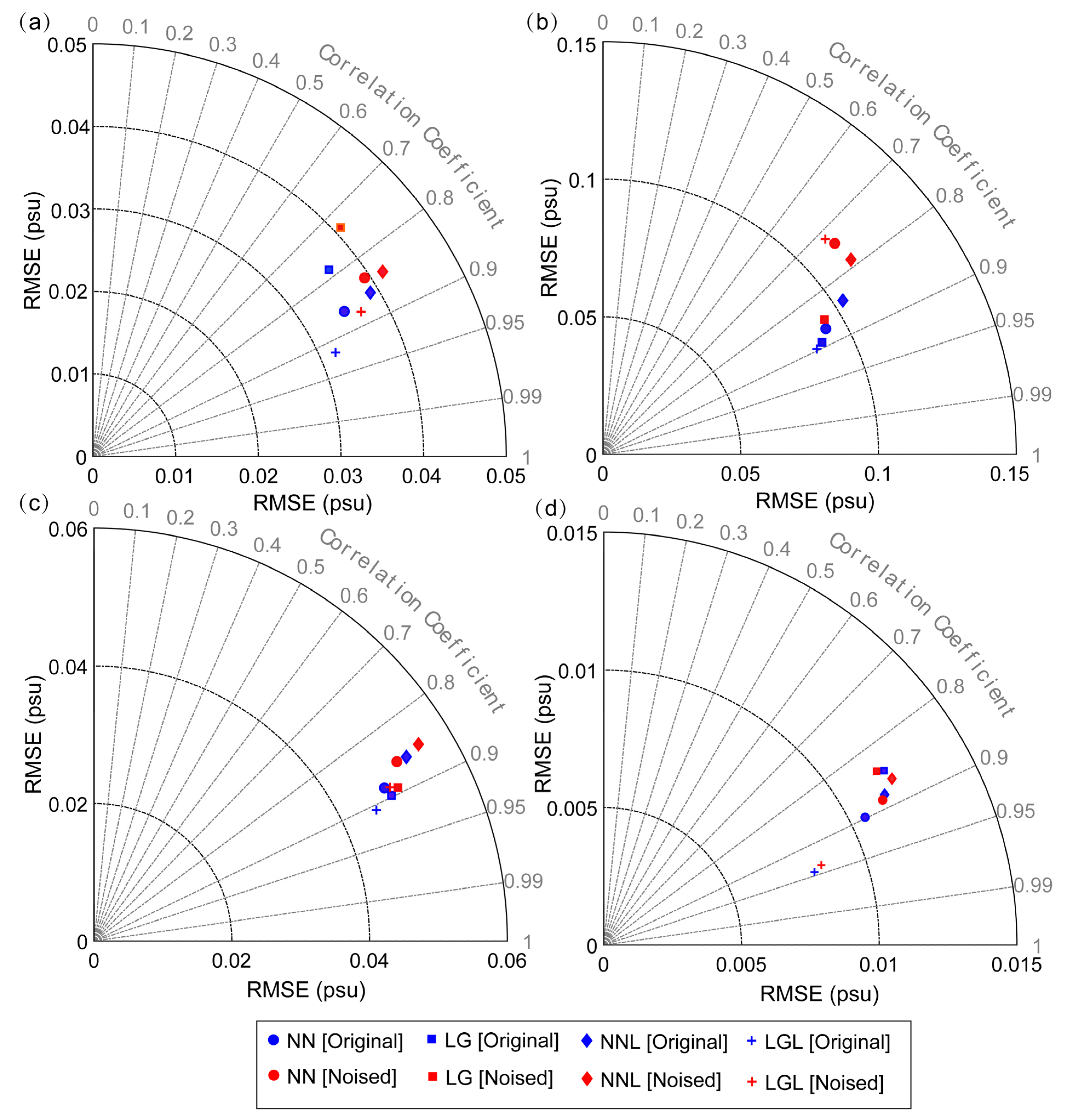
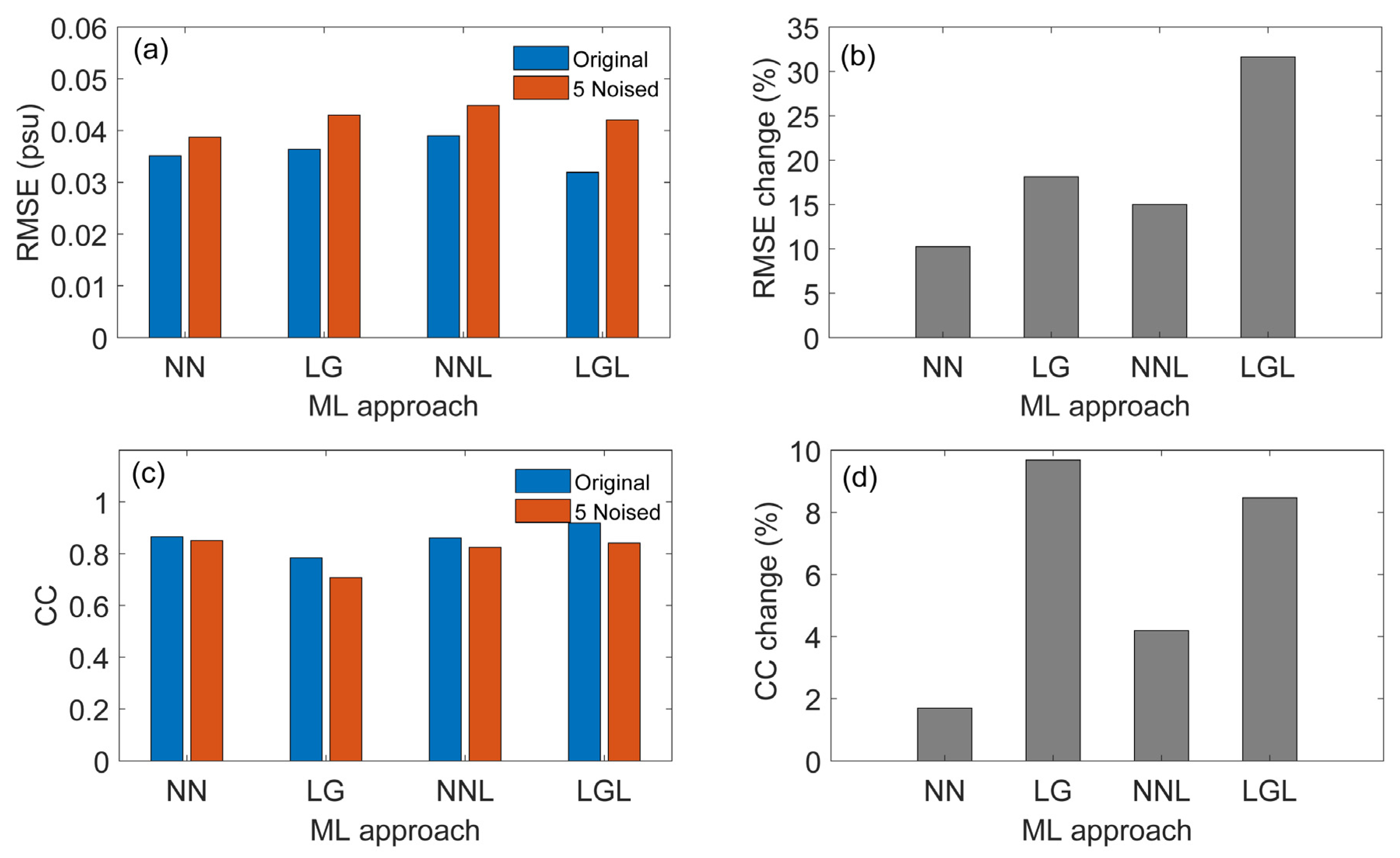
3.3. Overall Reconstruction Performance
3.4. Evaluation of Spatial Patterns of Long-Term Salinity Changes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lyman, J.M.; Johnson, G.C. Estimating Global Ocean Heat Content Changes in the Upper 1800 m since 1950 and the Influence of Climatology Choice. J. Clim. 2014, 27, 1945–1957. [Google Scholar] [CrossRef]
- Durack, P.J.; Gleckler, P.J.; Landerer, F.W.; Taylor, K.E. Quantifying Underestimates of Long-Term Upper-Ocean Warming. Nat. Clim. Chang. 2014, 4, 999–1005. [Google Scholar] [CrossRef]
- Ciais, P.; Sabine, C.; Bala, G.; Bopp, L.; Brovkin, V.; Canadell, J.; Chhabra, A.; DeFries, R.; Galloway, J.; Heimann, M.; et al. Climate Change 2013—The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Domingues, C.M.; Church, J.A.; White, N.J.; Gleckler, P.J.; Wijffels, S.E.; Barker, P.M.; Dunn, J.R. Improved Estimates of Upper-Ocean Warming and Multi-Decadal Sea-Level Rise. Nature 2008, 453, 1090–1093. [Google Scholar] [CrossRef] [PubMed]
- Bagnell, A.; DeVries, T. 20th Century Cooling of the Deep Ocean Contributed to Delayed Acceleration of Earth’s Energy Imbalance. Nat. Commun. 2021, 12, 4604. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zhang, Y.; Xiao, J.; Song, X.; Abraham, J.; Cheng, L.; Zhu, J. Examining the Salinity Change in the Upper Pacific Ocean during the Argo Period. Clim. Dyn. 2019, 53, 6055–6074. [Google Scholar] [CrossRef]
- Durack, P.J. Ocean Salinity and the Global Water Cycle. Oceanography 2015, 28, 20–31. [Google Scholar] [CrossRef]
- Guinehut, S.; Dhomps, A.L.; Larnicol, G.; Le Traon, P.Y. High Resolution 3-D Temperature and Salinity Fields Derived from in Situ and Satellite Observations. Ocean Sci. 2012, 8, 845–857. [Google Scholar] [CrossRef]
- Johnson, G.C.; Hosoda, S.; Jayne, S.R.; Oke, P.R.; Riser, S.C.; Roemmich, D.; Suga, T.; Thierry, V.; Wijffels, S.E.; Xu, J. Argo-Two Decades: Global Oceanography, Revolutionized. Ann. Rev. Mar. Sci. 2022, 14, 379–403. [Google Scholar] [CrossRef]
- Cheng, L.; Zhu, J. Benefits of CMIP5 Multimodel Ensemble in Reconstructing Historical Ocean Subsurface Temperature Variations. J. Clim. 2016, 29, 5393–5416. [Google Scholar] [CrossRef]
- Ishii, M.; Kimoto, M.; Kachi, M. Historical Ocean Subsurfaces Temperature Analysis with Error Estimates. Mon. Weather Rev. 2003, 131, 51–73. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.; Boyer, T. Warming of the World Ocean, 1955–2003. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Lyman, J.M.; Johnson, G.C. Estimating Annual Global Upper-Ocean Heat Content Anomalies despite Irregular In Situ Ocean Sampling. J. Clim. 2008, 21, 5629–5641. [Google Scholar] [CrossRef]
- Willis, J.K.; Roemmich, D.; Cornuelle, B. Interannual Variability in Upper Ocean Heat Content, Temperature, and Thermosteric Expansion on Global Scales. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef]
- Good, S.A.; Martin, M.J.; Rayner, N.A. EN4: Quality Controlled Ocean Temperature and Salinity Profiles and Monthly Objective Analyses with Uncertainty Estimates. J. Geophys. Res. Ocean. 2013, 118, 6704–6716. [Google Scholar] [CrossRef]
- Levitus, S.; Antonov, J.I.; Boyer, T.P.; Baranova, O.K.; Garcia, H.E.; Locarnini, R.A.; Mishonov, A.V.; Reagan, J.R.; Seidov, D.; Yarosh, E.S.; et al. World Ocean Heat Content and Thermosteric Sea Level Change (0–2000 m), 1955–2010. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Ishii, M.; Kimoto, M. Reevaluation of Historical Ocean Heat Content Variations with Time-Varying XBT and MBT Depth Bias Corrections. J. Oceanogr. 2009, 65, 287–299. [Google Scholar] [CrossRef]
- Cheng, L.; Trenberth, K.E.; Fasullo, J.; Boyer, T.; Abraham, J.; Zhu, J. Improved Estimates of Ocean Heat Content from 1960 to 2015. Sci. Adv. 2017, 3, e1601545. [Google Scholar] [CrossRef]
- Jiang, M.; Zhu, Z. The Role of Artificial Intelligence Algorithms in Marine Scientific Research. Front. Mar. Sci. 2022, 9, 781. [Google Scholar] [CrossRef]
- Lou, R.; Lv, Z.; Dang, S.; Su, T.; Li, X. Application of Machine Learning in Ocean Data. Multimed. Syst. 2021. [Google Scholar] [CrossRef]
- Radin, C.; Nieves, V. Machine-Learning Based Reconstructions of Past Regional Sea Level Variability from Proxy Data. Geophys. Res. Lett. 2021, 48, e2021GL095382. [Google Scholar] [CrossRef]
- Gan, M.; Pan, S.; Chen, Y.; Cheng, C.; Pan, H.; Zhu, X. Application of the Machine Learning LightGBM Model to the Prediction of the Water Levels of the Lower Columbia River. J. Mar. Sci. Eng. 2021, 9, 496. [Google Scholar] [CrossRef]
- Foster, D.; Gagne II, D.J.; Whitt, D.B. Probabilistic Machine Learning Estimation of Ocean Mixed Layer Depth from Dense Satellite and Sparse In Situ Observations. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002474. [Google Scholar] [CrossRef] [PubMed]
- Stamell, J.; Rustagi, R.; Gloege, L.; McKinley, G. Strengths and weaknesses of three Machine Learning methods for pCO2 interpolation. Geosci. Model Dev. Discuss. 2020, 2020, 1–25. [Google Scholar] [CrossRef]
- Hu, S.; Liu, H.; Zhao, W.; Shi, T.; Hu, Z.; Li, Q.; Wu, G. Comparison of Machine Learning Techniques in Inferring Phytoplankton Size Classes. Remote Sens. 2018, 10, 191. [Google Scholar] [CrossRef]
- Hu, S.; Zhou, W.; Wang, G.; Cao, W.; Xu, Z.; Liu, H.; Wu, G.; Zhao, W. Comparison of Satellite-Derived Phytoplankton Size Classes Using In-Situ Measurements in the South China Sea. Remote Sens. 2018, 10, 526. [Google Scholar] [CrossRef]
- Chen, S.; Hu, C.; Barnes, B.B.; Wanninkhof, R.; Cai, W.-J.; Barbero, L.; Pierrot, D. A Machine Learning Approach to Estimate Surface Ocean PCO2 from Satellite Measurements. Remote Sens. Environ. 2019, 228, 203–226. [Google Scholar] [CrossRef]
- Wang, H.; Song, T.; Zhu, S.; Yang, S.; Feng, L. Subsurface Temperature Estimation from Sea Surface Data Using Neural Network Models in the Western Pacific Ocean. Mathematics 2021, 9, 852. [Google Scholar] [CrossRef]
- Lu, W.; Su, H.; Yang, X.; Yan, X.H. Subsurface Temperature Estimation from Remote Sensing Data Using a Clustering-Neural Network Method. Remote Sens. Environ. 2019, 229, 213–222. [Google Scholar] [CrossRef]
- Voldoire, A. CNRM-CERFACS CNRM-CM6-1-HR Model Output Prepared for CMIP6 ScenarioMIP. Earth Syst. Grid Fed. 2019. [Google Scholar] [CrossRef]
- Boyer, T.P.; Baranova, O.K.; Coleman, C.; Garcia, H.E.; Grodsky, A.; Locarnini, R.A.; Mishonov, A.V.; Paver, C.R.; Reagan, J.R.; Seidov, D.; et al. World Ocean Database 2018. Mishonov, A.V., Technical Editor, NOAA Atlas NESDIS 87. 2018; pp. 1–207. Available online: https://www.ncei.noaa.gov/sites/default/files/2020-04/wod_intro_0.pdf (accessed on 15 May 2022).
- Gouretski, V.; Cheng, L. Correction for Systematic Errors in the Global Dataset of Temperature Profiles from Mechanical Bathythermographs. J. Atmos. Ocean. Technol. 2020, 37, 841–855. [Google Scholar] [CrossRef]
- Abraham, J.P.; Cowley, R.; Cheng, L. Quantification of the Effect of Water Temperature on the Fall Rate of Expendable Bathythermographs. J. Atmos. Ocean. Technol. 2016, 33, 1271–1284. [Google Scholar] [CrossRef]
- Klemas, V.; Yan, X.H. Subsurface and Deeper Ocean Remote Sensing from Satellites: An Overview and New Results. Prog. Oceanogr. 2014, 122, 1–9. [Google Scholar] [CrossRef]
- Cheng, L.; Trenberth, K.E.; Gruber, N.; Abraham, J.P.; Fasullo, J.T.; Li, G.; Mann, M.E.; Zhao, X.; Zhu, J. Improved Estimates of Changes in Upper Ocean Salinity and the Hydrological Cycle. J. Clim. 2020, 33, 10357–10381. [Google Scholar] [CrossRef]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A Review of Uncertainty Quantification in Deep Learning: Techniques, Applications and Challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Contractor, S.; Roughan, M. Efficacy of Feedforward and LSTM Neural Networks at Predicting and Gap Filling Coastal Ocean Timeseries: Oxygen, Nutrients, and Temperature. Front. Mar. Sci. 2021, 8, 368. [Google Scholar] [CrossRef]
- Gabella, M. Topology of Learning in Feedforward Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3588–3592. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.A.; Bottou, L.; Orr, G.B.; Müller, K.R. Efficient Backprop. In Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Montavon, G., Orr, G.B., Müller, K.-R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7700, ISBN 9783642352881. [Google Scholar]
- Moussa, H.; Benallal, M.A.; Goyet, C.; Lefèvre, N. Satellite-Derived CO2 Fugacity in Surface Seawater of the Tropical Atlantic Ocean Using a Feedforward Neural Network. Int. J. Remote Sens. 2016, 37, 580–598. [Google Scholar] [CrossRef]
- Vikas Gupta. Understanding Feedforward Neural Networks. Learn Open CV 2017, 1. Available online: https://learnopencv.com/understanding-feedforward-neural-networks/ (accessed on 15 June 2022).
- Keras: Deep Learning Library for Theano and TensorFlow. Available online: https://faroit.com/keras-docs/1.1.1/ (accessed on 20 June 2022).
- Liashchynskyi, P.; Liashchynskyi, P. Grid Search, Random Search, Genetic Algorithm: A Big Comparison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
- Dan Foresee, F.; Hagan, M.T. Gauss-Newton Approximation to Bayesian Learning. In Proceedings of the IEEE International Conference on Neural Networks—Conference Proceedings, Houston, TX, USA, 12 June 1997; Volume 3, pp. 1930–1935. [Google Scholar]
- Su, H.; Lu, X.; Chen, Z.; Zhang, H.; Lu, W.; Wu, W. Estimating Coastal Chlorophyll-A Concentration from Time-Series OLCI Data Based on Machine Learning. Remote Sens. 2021, 13, 576. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U., Von Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- He, Z.; Wang, X.; Wu, X.; Chen, Z.; Chen, J. Projecting Three-Dimensional Ocean Thermohaline Structure in the North Indian Ocean from the Satellite Sea Surface Data Based on a Variational Method. J. Geophys. Res. Ocean. 2021, 126, e2020JC016759. [Google Scholar] [CrossRef]
- Su, H.; Zhang, T.; Lin, M.; Lu, W.; Yan, X.-H. Predicting Subsurface Thermohaline Structure from Remote Sensing Data Based on Long Short-Term Memory Neural Networks. Remote Sens. Environ. 2021, 260, 112465. [Google Scholar] [CrossRef]
- Meng, L.; Yan, C.; Zhuang, W.; Zhang, W.; Yan, X.H. Reconstruction of Three-Dimensional Temperature and Salinity Fields From Satellite Observations. J. Geophys. Res. Ocean. 2021, 126, e2021JC017605. [Google Scholar] [CrossRef]
- Denvil-Sommer, A.; Gehlen, M.; Vrac, M.; Mejia, C. LSCE-FFNN-v1: A Two-Step Neural Network Model for the Reconstruction of Surface Ocean PCO2 over the Global Ocean. Geosci. Model Dev. 2019, 12, 2091–2105. [Google Scholar] [CrossRef]
- Su, H.; Wang, A.; Zhang, T.; Qin, T.; Du, X.; Yan, X.H. Super-Resolution of Subsurface Temperature Field from Remote Sensing Observations Based on Machine Learning. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102440. [Google Scholar] [CrossRef]
- Su, H.; Zhang, H.; Geng, X.; Qin, T.; Lu, W.; Yan, X.H. OPEN: A New Estimation of Global Ocean Heat Content for Upper 2000 Meters from Remote Sensing Data. Remote Sens. 2020, 12, 2294. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of Sample Size, Data Type and Prediction Method for Remote Sensing-Based Estimations of Aboveground Forest Biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Chen, G.; Peng, L.; Ma, C. Climatology and Seasonality of Upper Ocean Salinity: A Three-Dimensional View from Argo Floats. Clim. Dyn. 2018, 50, 2169–2182. [Google Scholar] [CrossRef]
- Yan, H.; Wang, H.; Zhang, R.; Bao, S.; Chen, J.; Wang, G. The Inconsistent Pairs Between In Situ Observations of Near Surface Salinity and Multiple Remotely Sensed Salinity Data. Earth Space Sci. 2021, 8, e2020EA001355. [Google Scholar] [CrossRef]
- Wong, A.P.S.; Wijffels, S.E.; Riser, S.C.; Pouliquen, S.; Hosoda, S.; Roemmich, D.; Gilson, J.; Johnson, G.C.; Martini, K.; Murphy, D.J.; et al. Argo Data 1999–2019: Two Million Temperature-Salinity Profiles and Subsurface Velocity Observations from a Global Array of Profiling Floats. Front. Mar. Sci. 2020, 7, 700. [Google Scholar] [CrossRef]
- Roemmich, D.; Alford, M.H.; Claustre, H.; Johnson, K.; King, B.; Moum, J.; Oke, P.; Owens, W.B.; Pouliquen, S.; Purkey, S.; et al. On the Future of Argo: A Global, Full-Depth, Multi-Disciplinary Array. Front. Mar. Sci. 2019, 6. [Google Scholar] [CrossRef]
- Frenger, I.; Münnich, M.; Gruber, N.; Knutti, R. Southern Ocean Eddy Phenomenology. J. Geophys. Res. Ocean. 2015, 120, 7413–7449. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Fox-Kemper, B.; Yeager, S.G.; Bozec, A. Sources and Sinks of Ocean Mesoscale Eddy Energy. CLIVAR Exch. CLIVAR Var. 2020, 18, 3–8. [Google Scholar]
- Rhines, P.B. Mesoscale Eddies. In Encyclopedia of Ocean Sciences, 3rd ed.; Cochran, J.K., Bokuniewicz, H.J., Yager, P.L., Eds.; Academic Press: Oxford, UK, 2019; pp. 115–127. ISBN 9780128130810. [Google Scholar]
- Skliris, N.; Marsh, R.; Josey, S.A.; Good, S.A.; Liu, C.; Allan, R.P. Salinity Changes in the World Ocean since 1950 in Relation to Changing Surface Freshwater Fluxes. Clim. Dyn. 2014, 43, 709–736. [Google Scholar] [CrossRef]
- Llovel, W.; Lee, T. Importance and Origin of Halosteric Contribution to Sea Level Change in the Southeast Indian Ocean during 2005–2013. Geophys. Res. Lett. 2015, 42, 1148–1157. [Google Scholar] [CrossRef]
- Adler, R.F.; Sapiano, M.R.P.; Huffman, G.J.; Wang, J.J.; Gu, G.; Bolvin, D.; Chiu, L.; Schneider, U.; Becker, A.; Nelkin, E.; et al. The Global Precipitation Climatology Project (GPCP) Monthly Analysis (New Version 2.3) and a Review of 2017 Global Precipitation. Atmosphere 2018, 9, 138. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, L.; Pan, Y.; Abraham, J.; Zhang, B.; Zhu, J.; Song, J. Climatological Seasonal Variation of the Upper Ocean Salinity. Int. J. Climatol. 2022, 42, 3477–3498. [Google Scholar] [CrossRef]
- Durack, P.J.; Wijffels, S.E. Fifty-Year Trends in Global Ocean Salinities and Their Relationship to Broad-Scale Warming. J. Clim. 2010, 23, 4342–4362. [Google Scholar] [CrossRef]
- Boyer, T.P.; Levitus, S.; Antonov, J.I.; Locarnini, R.A.; Garcia, H.E. Linear Trends in Salinity for the World Ocean, 1955–1998. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Gregor, L.; Lebehot, A.D.; Kok, S.; Scheel Monteiro, P.M. A comparative assessment of the uncertainties of global surface ocean CO2 estimates using a machine-learning ensemble (CSIR-ML6 version 2019a)-Have we hit the wall? Geosci. Model Dev. 2019, 12, 5113–5136. [Google Scholar] [CrossRef]
- Gloege, L.; McKinley, G.A.; Landschützer, P.; Fay, A.R.; Frölicher, T.L.; Fyfe, J.C.; Ilyina, T.; Jones, S.; Lovenduski, N.S.; Rodgers, K.B.; et al. Quantifying Errors in Observationally Based Estimates of Ocean Carbon Sink Variability. Glob. Biogeochem. Cycles 2021, 35, e2020GB006788. [Google Scholar] [CrossRef]






| Experiment | Input | Truth Value | Vertical Layering Scheme | ML Approach |
|---|---|---|---|---|
| Case NN | time, longitude, latitude, depth, equ-IAP1SA, ADTA, SSTA, USSWA, VSSWA | Original/Noised | Non-layered, one model | FFNN |
| Case LG | Original/Noised | Non-layered, one model | LightGBM | |
| Case NNL | Original/Noised | Divided into 41 layers, with one model for each layer | FFNN | |
| Case LGL | Original/Noised | Divided into 41 layers, with one model for each layer | LightGBM |
| Original Synthetic Dataset | Noised Synthetic Dataset | Degradation Rate (%) | ||||
|---|---|---|---|---|---|---|
| RMSE (psu) | CC | RMSE (psu) | CC | RMSE | CC | |
| Case NN | 0.035 | 0.866 | 0.039 | 0.835 | 12.0 | 3.5 |
| Case LG | 0.036 | 0.784 | 0.041 | 0.734 | 12.2 | 6.4 |
| Case NNL | 0.039 | 0.861 | 0.042 | 0.843 | 6.7 | 2.1 |
| Case LGL | 0.032 | 0.919 | 0.037 | 0.880 | 15.5 | 4.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, T.; Leng, H.; Wang, G.; Li, G.; Song, J.; Zhu, J.; An, Y. Comparison of Machine Learning Approaches for Reconstructing Sea Subsurface Salinity Using Synthetic Data. Remote Sens. 2022, 14, 5650. https://doi.org/10.3390/rs14225650
Tian T, Leng H, Wang G, Li G, Song J, Zhu J, An Y. Comparison of Machine Learning Approaches for Reconstructing Sea Subsurface Salinity Using Synthetic Data. Remote Sensing. 2022; 14(22):5650. https://doi.org/10.3390/rs14225650
Chicago/Turabian StyleTian, Tian, Hongze Leng, Gongjie Wang, Guancheng Li, Junqiang Song, Jiang Zhu, and Yuzhu An. 2022. "Comparison of Machine Learning Approaches for Reconstructing Sea Subsurface Salinity Using Synthetic Data" Remote Sensing 14, no. 22: 5650. https://doi.org/10.3390/rs14225650
APA StyleTian, T., Leng, H., Wang, G., Li, G., Song, J., Zhu, J., & An, Y. (2022). Comparison of Machine Learning Approaches for Reconstructing Sea Subsurface Salinity Using Synthetic Data. Remote Sensing, 14(22), 5650. https://doi.org/10.3390/rs14225650






