Abstract
During emergency events, we could significantly depend on the stable operation of radio communication, navigation, and radars. The ionosphere, especially its auroral regions, significantly influences radio systems, which is why scientists and engineers create systems to monitor these regions. Using data from the global GNSS network, we analyzed the 10 strongest magnetic storms of solar cycle 24: five coronal mass ejection-driven (CME-driven) and five high-speed stream-driven (HSS-driven) storms. The analysis was based on the calculation of the standard deviation of the total electron content (TEC) derivative (rate of TEC index, ROTI). Under all the storms, the ROTI featured similar dynamics: the average ROTI reaches the highest values during the main phase, and the higher the intensity is, the more intense and equatorward the average ROTI registered. The highest cross-correlations are observed with a lag of 1 h, between the IMF z-component Bz and the magnetic latitude where the highest ROTI values appear. The auroral electrojet (SME index) shows the highest impact on the ROTI dynamics. An increase in the space weather indices (in absolute value) is accompanied by a decrease in the latitude where the maximal ROTI occurs. We found that the peculiarities of a storm affect the ROTI dynamics: all the CME-driven storms feature a high cross-correlation (>0.75) between the IMF z-component Bz and the magnetic latitude where the highest ROTI appears, while the HSS-driven storms feature a lower cross-correlation (<0.75) between them. The difference in duration of similar (by maximal values of geomagnetic indices) HSS- and CME-driven storms could produce differences in the highest ROTI values. Correlations show that compared to HSS-driven storms, CME-driven ones more directly impact the ROTI values and locations of regions with a high ROTI.
1. Introduction
The auroral ovals are high-latitude regions in the southern and northern hemispheres where energetic particles from the solar wind penetrate into the Earth’s atmosphere and cause multiple different effects including auroras, irregularities’ generation, atmosphere heating, etc. Additional ionization in the ionospheric D region and small-scale irregularities in the E and F regions worsen the operation of radio technical systems using ionospheric radio channels. Besides, plasma dynamics and magnetic field peculiarities influence (and reflect) the whole magnetospheric system coupled with the Earth’s atmosphere. So, scientists and engineers strive to monitor and predict the ovals.
The SuperDARN network is a collaborative project to monitor the northern and southern ovals [1]. The network recovers global magnetospheric convection and estimates the boundary of the oval (as a boundary of the magnetospheric convection [2]). The global navigation satellite system (GNSS) provides another way to monitor the oval through total electron content data: Pi et al. [3] suggested the ROTI index to estimate the small-scale irregularities’ location, while the ovals feature increased ROTI values (ROTI oval) compared to the mid-latitudes. Different instruments catch the ovals’ boundary in a similar way [4].
Projects to treat GNSS data (such as DRAWING-TEC [5], SIMuRG [6], or IGS daily ROTI maps [7]) help scientists to study physical processes.
The current article raises the question: How does the ROTI oval shift during a magnetic storm? To answer, we considered the impact of 10 magnetic storms that occurred between 2017–2021, analyzing the GNSS data, geomagnetic indices, and solar wind parameters.
2. Data and Methods
Global and regional GNSS networks allow us to investigate the ionosphere with good temporal and spatial (in the case of dense networks) resolution. Most of the networks freely provide GNSS data in RINEX format, allowing for the calculation of total electron content (TEC). Raw TEC data are usually distorted, contain some errors introduced by different sources (e.g., phase ambiguity, loss-of-lock, etc.), and need to be properly prepared before usage. Yasyukevich et al. [6] developed a service, SIMuRG (the System of Ionosphere Monitoring and Research from GNSS, http://simurg.space accessed on 1 September 2022), to process GNSS data. The system provides TEC variations within three bands (2–10 min, 10–20 min, and 20–60 min), absolute TEC, Rate of TEC Index (ROTI), and ROTI-like indexes with 30 sec time resolution. All the values can be obtained for a given time and region, by request in the form of a map or individual series. The present research is based on data provided by the SIMuRG.
ROTI is widely used for investigation of thin structure and small-scale irregularities in the ionosphere [7,8,9,10,11]. This index is useful to study the storm effects in the equatorial [9,12], mid-latitude [13], and auroral regions [4,11,14]. Global distribution of the GNSS network reveals the irregularities’ dynamics on a planetary scale [4,9]. Figure 1a shows a map of ROTI values during the 25–26 August 2018 magnetic storm at 06:00 UT. Each point in the map depicts the ROTI value (calculated for the previous 5 min data set) at the corresponding line-of-sight to a GNSS satellite at the given moment. This map is produced by SIMuRG. Figure 1 points out that small-scale ionospheric irregularities are more intense at high latitudes than at middle ones. According to [8], boundaries of an oval of high ROTI values correspond with the boundaries of an auroral oval. Therefore, the polar region distribution of ROTI can be used for the investigation of auroral oval dynamics. The advantage of the ROTI-based method in comparison with optical (mainly satellite-based) instruments is the independence from weather and continuous observation mode.
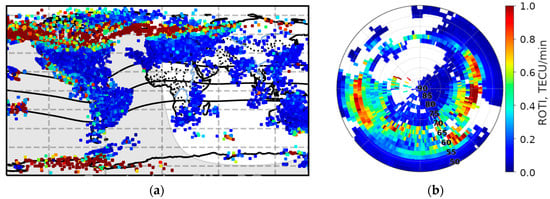
Figure 1.
Dynamic ROTI maps in different frames on 26 August 2018: (a) 30-s map of ROTI at 06:00 UT from SIMuRG service; (b) map of ROTI averaged for Northern Hemisphere in MLAT × MLT reference frame over 1 h (5:30–6:30 UT).
International GNSS service (IGS) provides diurnal maps of ROTI. These maps are calculated on a fixed grid in a system of magnetic latitude (MLAT) and magnetic local time (MLT) with a 2 × 2° resolution [7]. Such a long accumulation shows a global distribution of small-scale irregularities but makes it impossible to distinguish any short-term (several hours) details on the map.
The global network of GNSS receivers provides sufficient coverage by measurements, at least in the Northern Hemisphere, to map ROTI continuously over a shorter period. Using the same MLAT × MLT grid of 2 × 2°, and hourly (1 h) averaging gives us a series of maps that allow us to watch some of short-term dynamics of corresponding duration. Figure 1b shows the averaged ROTI map calculated with data over a period of 5:30–6:30 UT on 26 August 2018. Each cell shows a mean ROTI value, within all those observed in the cell during the mentioned period.
The blank spots on the map correspond to the areas lacking measurement. Future GNSS receivers could cover some regions, but some of them (e.g., over the oceans) will remain. The increment of averaging time to 2 h provides 70–85% coverage of the Northern Hemisphere’s surface, while 3 h averaging provides 82–90%, 4 h provides 88–92%, 6 h provides 92–96%, and 8 h provides 100% (Figure 2). In this article, we used 1 h averaging because it was enough to observe dynamics in the auroral oval boundary (although it is insufficient to provide total coverage of the hemisphere).
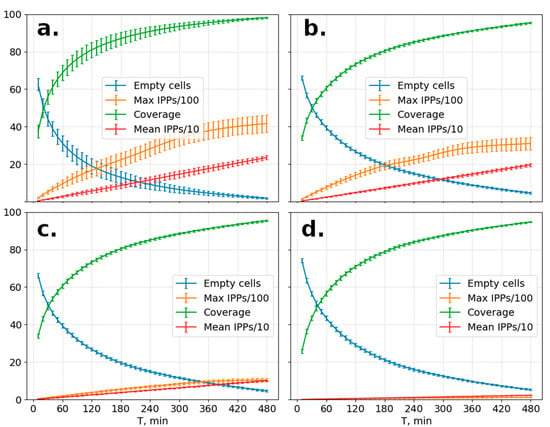
Figure 2.
Percentage of filled (green) and empty cells (blue) and max/average (orange/red) amount of ROTI measurements used to calculate a single cell value versus duration of the averaging period. The calculation was performed on (a) all the available data and data with a spatial step of (b) 70 km, (c) 150 km, and (d) 700 km.
Geomagnetic storms impact both the oval position and small-scale irregularity intensity within the oval. That allow us to observe an increase in ROTI values and an equatorward shift in the oval boundary position during a magnetic storm. Using OMNI [15] and SuperMAG project [16] data we can compare the shift value with the main indices of geomagnetic weather and parameters of solar wind.
Dynamics of the oval boundaries are convenient to observe by keograms: 3D-distributions of time-latitudinal (UT-MLat) dependence of ROTI. In a keogram, values from all the MLT sectors are averaged (or medianized) to reflect the general condition of the polar ionosphere. Assuming an auroral oval is a proper circle in magnetic coordinates, we can evaluate the position of the oval boundaries from a keogram and compare it with parameters of space weather. Figure 3 shows the keogram for the magnetic storm of 26 August 2018. Color reflects the median ROTI value for a given MLAT and UT.
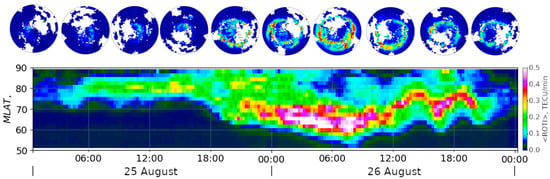
Figure 3.
ROTI keogram during a magnetic storm of 25–26 August 2018 (bottom), with several corresponding maps (top).
3. Variations in ROTI during Magnetic Storms of 2017–2021 Solar Minimum
To analyze the ROTI dynamics, we selected the most powerful magnetic storms (Kp ≥ 6) of the period 2017–2021. The peak values of the SYM-H, IMF Bz (negative), Kp, and SME parameters for each of the selected storms are presented in Table 1. The moment of the minimum SYM-H and the type of process responsible for the storm are given as well.

Table 1.
The peak values of space weather indices during the strongest storms of 2017–2021.
Half of the events are storms caused by coronal mass ejections (CME-storms), and half are storms caused by high-speed streams (CIR-storms). CME-storms produce a stronger impact on the ring current, so they produce a higher Kp and SYM-H (Table 1). However, the 28 September 2017 CIR-storm induced a comparable (according to the Kp index) geomagnetic field disturbance. Below, we analyze all the storms and ROTI dynamics.
3.1. 12 May 2021 G3 Storm
Coronal mass ejection occurred 9 May 2021 in Region 2822 [17], reached the Earth on 12 May, and caused a strong (G3) magnetic storm (Kpmax = 7). At ~6:40, the proton density increased almost five times from 7.5 to 35 n/cc (number of protons per cubic centimeter), the wind bulk speed jumped from 320 to 440 km/s, and the SYM-H index sharply increased from 0 to 44 nT, indicating sudden storm commencement (SSC) (Figure 4). The high density lasted until ~8:30 and then showed an increment thrice: up to 30 n/cc (10:20–11:10), up to 35 n/cc (11:55–12:25), and to ~25–30 n/cc (15:10–15:45). After the last increment, the speed sharply increased to 485 km/s and then gradually increased to 520 km/s within 2 h. The speed started to decrease at ~2 h on 13 May and reached a minimum value of ~360 km/s at 15:00 on 14 May. Along with the decay of the second peak in the density, the Bz component of the IMF started to decrease, became negative at 11:30 on 12 May, and reached its minimum of −20 nT at 13:30. The SYM-H index started to fall at 12:20, crossed the zero mark twice (12:30 and 13:04), and then was monotonically decreasing to its minimum of −59 nT (14:49), staying below −20 nT until the middle of the next day. The Kp index was exceeding level 6 for 12–17 h, with a maximum of 7 at 12–14 h.
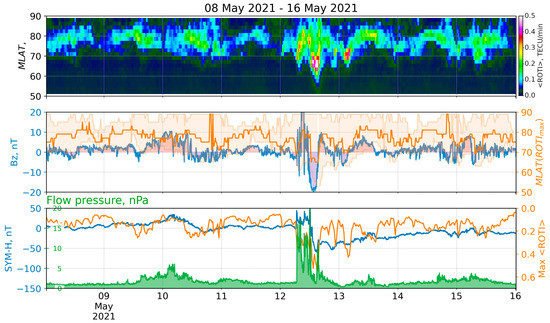
Figure 4.
ROTI keogram and space weather parameters for the storm of 12 May 2021: (top) keogram of average ROTI (<ROTI> versus MLAT versus time); (middle) IMF Bz (blue), MLAT positions of maximum <ROTI> (orange), and values exceeding median ROTI at the moment (orange filling); (bottom) SYM-H index (blue), <ROTI> max (orange), and flow pressure (green).
The top panel in Figure 4 shows average ROTI (<ROTI>) versus magnetic latitude (MLAT) and time – ROTI keogram. The middle panel shows variations in IMF Bz (blue) and the magnetic latitude of the maximal <ROTI> at the moment (orange, Y-axis at right). The area filled by pale orange (Figure 4, middle) reflects magnetic latitudes of all the <ROTI> values exceeding the entire map median (Y-axis at right). The bottom panel shows solar wind flow pressure (green), SYM-H (blue) and the maximal <ROTI> value (orange, Y-axis at right).
3.2. 24 September 2020 G2 Storm
A moderate geomagnetic storm (Kpmax = 6−, G2) of 24 September 2020 was produced by a positive polarity coronal hole/high speed stream [18]. The wind bulk speed started to increase at 6:00 on 23 September, from 360 km/s to the maximum value of 680 km/s, which was observed at 02:53 on 28 September. The flow pressure showed several increments over a period of 23–30 September. The first one started at 5:00 on 23 September, when the pressure sharply increased from 1 to 2.5 nPa, reaching the maximum of 7 nPa at 5:00 on 24 September. The storm started after half an hour, at 6:30, when the wind bulk speed reached the local maximum of 500 km/s and the Bz component of the IMF fell from 5.7 to −7.6 nT within 10 minutes. The IMF was remaining southward until 9:30 UTC. The SYM-H index started to significantly decrease at 6:40 and reached its minimum of −31 nT at 8:50. During the entire period of increased pressure, high values of proton density (>5 n/cc) were observed, and the maximum density of 18.5 n/cc was registered at 3 UTC. Figure 5 shows the ROTI keogram (top) during 23–25 September 2020 with some keogram derivatives and the corresponding space weather indices (middle, bottom).
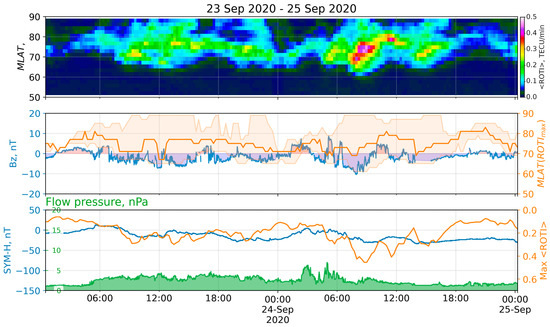
Figure 5.
ROTI keogram and space weather parameters for the storm of 24 September 2020: (top) keogram of average ROTI (<ROTI> versus MLAT versus time); (middle) IMF Bz (blue), MLAT positions of maximum <ROTI> (orange), and values exceeding median ROTI at the moment (orange filling); (bottom) SYM-H index (blue), <ROTI> max (orange), and flow pressure (green).
3.3. 14 May 2019 G3 Storm
Coronal mass ejection erupted on 11 May, reached the Earth on 14 May, and produced a strong magnetic storm (Kpmax = 6+, G3) [19]. The storm started at 3:50 on 14 May, when the IMF Bz component fell from 5 nT to −10 nT within 5 minutes. Its value was negative until 7:19, with the minimal value of −15 nT at 6:18 observed after a short period (4 min) of near-zero values. The SYM-H index was decreasing monotonically from 4:04 (0 nT) until 7:10 (−78 nT), indicating the storm’s main phase [20]. At 7:13, the proton density jumped from about 7.9 to 23 n/cc within 4 min and reached the maximum of 26.6 at 7:30. The recovery phase continued from 07:00 UT on 14 May 2019 to 08:00 UT on 15 May 2019. The index remained below −20 nT until 3:28 on 15 May. The solar wind speed was about 320 km/s at the beginning of 13 May and started to grow at 14:20. At 23:40, the growth intensified, and the speed reached a maximum of about 580 km/s at 5:00 on 14 May. Figure 6 shows the ROTI keogram (top) during 14–16 May 2019 with some keogram derivatives and the corresponding space weather indices (middle, bottom).
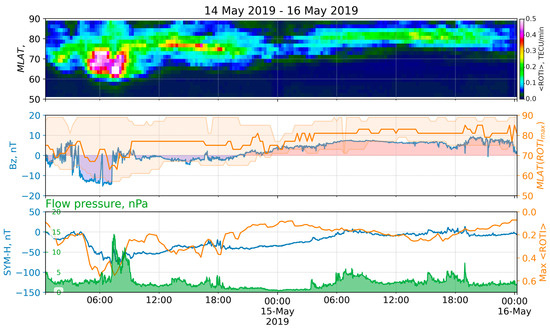
Figure 6.
ROTI keogram and space weather parameters for the storm of 14 May 2019: (top) keogram of average ROTI (<ROTI> versus MLAT versus time); (middle) IMF Bz (blue), MLAT positions of maximum <ROTI> (orange), and values exceeding median ROTI at the moment (orange filling); (bottom) SYM-H index (blue), <ROTI> max (orange), and flow pressure (green).
3.4. G2 Storm on 31 August –2 September 2019
At midday on 30 August, the Earth came under the influence of a large, recurrent positive polarity CH HSS [21,22], and the geomagnetic activity level was consequently increased from quiet to minor and moderate. At 13:22 on 30 August, the wind bulk speed exceeded 400 km/s and was growing until an average level of 750 km/s (1 September, 2:02), with the peak higher than 810 km/s (1 September, 6:02). The storm commencement was observed to occur from 10 to 14 August 30. The SYM-H index started decreasing at 22:09 on August 30 and reached its minimum of −43 nT at 2:52 on August 31. The index value was below −20 nT for several days until 6:23 on September 3, and the minimum was observed at 6:00 on 1 September. This period, of the decreasing SYM-H, corresponds to the main phase of the storm. After 06:00 on 1 September, the storm transitioned to the recovery phase, which lasted for a few days. During all of that period, the Bz component of the IMF was oscillating around zero, with an amplitude of less than 10 nT. The value of the Kp index was around 5 during the period from 8:00 on 31 August utnil 1:00 on 2 September, with the maximum of 6− at 13:00 on 31 August. Figure 7 shows the ROTI keogram (top) during 30 August–3 September 2019 with some keogram derivatives and the corresponding space weather indices (middle, bottom).
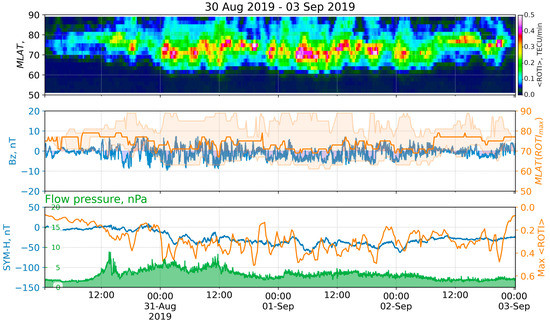
Figure 7.
ROTI keogram and space weather parameters for the storm of 31 August–2 September 2019: (top) keogram of average ROTI (<ROTI> versus MLAT versus time); (middle) IMF Bz (blue), MLAT positions of maximum <ROTI> (orange), and values exceeding median ROTI at the moment (orange filling); (bottom) SYM-H index (blue), <ROTI> max (orange), and flow pressure (green).
3.5. 20 April 2018 G2 Storm
This unpredicted magnetic storm was caused by a transequatorial coronal hole CH861 [23]. The hole took a frontal position on the solar disk on 17 April, and its influence caused a moderate (G2) geomagnetic storm on 20 April. The storm commenced at 00:27 on 20 April, when the SYM-H index rose from 7 to 37 nT within 7 min, and the flow pressure consequently jumped from 2.4 to 6.7 nPa (00:24), then from 2.4 to 10.4 nPa (00:35), and finally started to grow monotonically to 16.5 nPa at 4:20. At 00:27, the SYM-H index jumped and started to decrease, became negative at 4:11 (when the Bz fell from 4.4 to −12 nT), and reached several local minima: −56 nT at 6:06, −67 at 7:42, and −86 nT at 9:35. The solar wind bulk speed jumped from ~290 to ~335 km/s at 00:34 and started to grow, reaching the maximum of ~657 km/s at 00:24 on 21 April. The recovery phase started at ~00 h on 21 April and lasted approximately until 16:30 on 24 April, when the speed decreased to ~350 km/s and the SYM-H index increased to ~−10 nT. On 20 April, the Kp index was 4 and was higher during 3–20 h, with its maximum of 6 between 6–8 h. Figure 8 shows the ROTI keogram (top) during 20–22 April 2018 with some keogram derivatives and the corresponding space weather indices (middle, bottom).
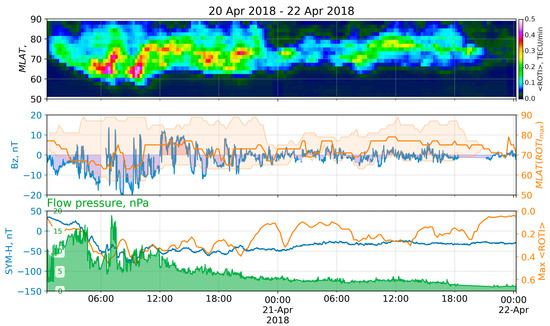
Figure 8.
ROTI keogram and space weather parameters for the storm of 20 April 2018: (top) keogram of average ROTI (<ROTI> versus MLAT versus time); (middle) IMF Bz (blue), MLAT positions of maximum <ROTI> (orange), and values exceeding median ROTI at the moment (orange filling); (bottom) SYM-H index (blue), <ROTI> max (orange), and flow pressure (green).
3.6. 25–26 August 2018 G3 Storm
The storm was caused by a Coronal Mass Ejection (CME) that occurred on 20 August and reached the Earth at 2:45 UT on 25 August [24,25]. The storm commenced around 8:00 of 25 August 2018, when flow pressure jumped from 3.9 to 9.9 nPa. The Bz component became negative at 17:03 and was monotonically decreasing until 5:07 of the next day, when it reached its minimum of −18 nT. The SYM-H index started to decrease at 17:30 of 25 August and, consequently, reached its minimum of −205 nT at 7:10 on the next day. Its value stayed below the mark of −20 nT until 4:00 of 31 August. From the point of view of the minimum SYM-H excursion, this storm has become the third-strongest in solar cycle 24 [26]. The maximal Kp index of 7+ was observed between 6–8 on 26 August, and its values exceeding 5 were registered thrice: between 2:00–8:00, from 15 to 18, and between 15–17 on 27 August. Intensive small-scale irregularities and a high ROTI appeared at high latitudes in both hemispheres [4]. Figure 9 shows the ROTI keogram (top) during 25–27 August 2018 with some keogram derivatives and the corresponding space weather indices (middle, bottom).
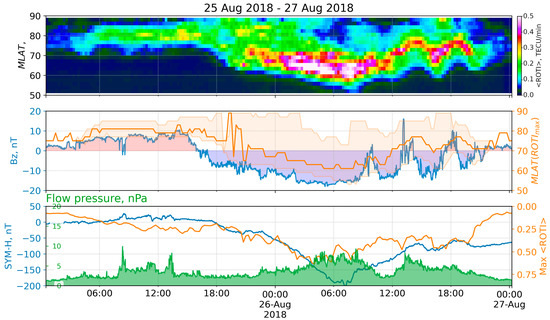
Figure 9.
ROTI keogram and space weather parameters for the storm of 25–26 August 2018: (top) keogram of average ROTI (<ROTI> versus MLAT versus time); (middle) IMF Bz (blue), MLAT positions of maximum <ROTI> (orange), and values exceeding median ROTI at the moment (orange filling); (bottom) SYM-H index (blue), <ROTI> max (orange), and flow pressure (green).
3.7. 11 September 2018 G2 Storm
The onset of a CIR ahead of a positive polarity CH HSS on 10 September increased the geomagnetic activity from quiet to the G1 level. A bulk wind speed increased to around 550 km/s on 11 September, increasing the geomagnetic activity to the G2 (moderate) level [27]. At ~9:00 on 10 September, the wind speed was ~350 km/s and started to increase until ~22:10, when it jumped from ~430 to 515 km/s, and then, for about 4 h, it smoothly increased to ~550 km/s. The SYM-H index started to grow at ~9:00 on 10 September, reached the mark of 10 nT at ~10:40, and started to fall. It reached the first minimum of −57 nT at ~23:00 and the second minimum of −63 nT at ~10:10 on 11 September. The Kp index values during the period 15:00 10 September–12:00 11 September were in the range of 4–6, with the maximum value between 6:00–8:00. Figure 10 shows the ROTI keogram (top) during 11–13 September 2018 with some keogram derivatives and the corresponding space weather indices (middle, bottom).
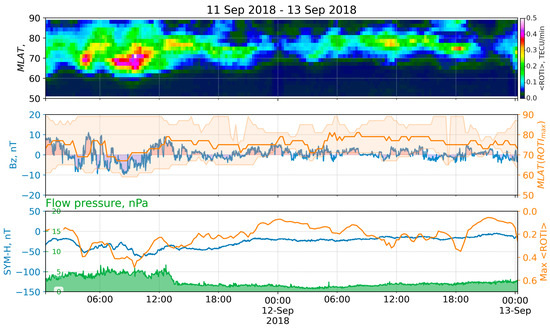
Figure 10.
ROTI keogram and space weather parameters for the storm of 11 September 2018: (top) keogram of average ROTI (<ROTI> versus MLAT versus time); (middle) IMF Bz (blue), MLAT positions of maximum <ROTI> (orange), and values exceeding median ROTI at the moment (orange filling); (bottom) SYM-H index (blue), <ROTI> max (orange), and flow pressure (green).
3.8. 27 May 2017 G3 Storm
A geomagnetic sudden impulse was observed on 27 May at 15:36 (19 nT at the Boulder magnetometer), indicating the arrival of the CME that occurred on 23 May [28]. A sharp increment of plasma flow pressure from 1.2 to 7.9 nPa forced the SYM-H to grow from 15:30 until 21:30 on 27 May. The IMF Bz component became negative at 21:35 and fell to −17.7 nT within 20 minutes. Its value was under −10 nT until 9:45 on 28 May. The main phase developed from 22:05 on 27 May until 7:13 on 27 May, when the SYM-H index reached its minimum of −141 nT [29]. The index values exceeded the mark of −20 nT only at the beginning (1:00) of the next day. From 21:00 on 27 May to 8:00 on 28 May, the Kp index was more than or equal to 6-, with the maximum value of 7 observed between 3:00–5:00 on 28 May. Figure 11 shows the ROTI keogram (top) during 27–29 May 2017 with some keogram derivatives and the corresponding space weather indices (middle, bottom).
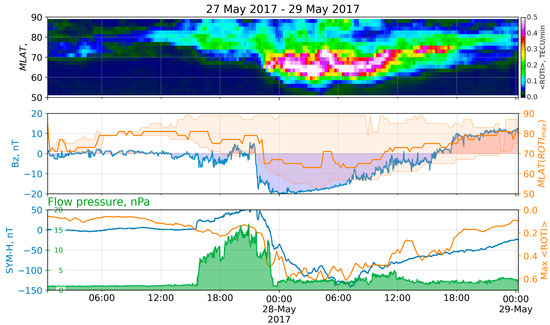
Figure 11.
ROTI keogram and space weather parameters for the storm of 27 May 2017: (top) keogram of average ROTI (<ROTI> versus MLAT versus time); (middle) IMF Bz (blue), MLAT positions of maximum <ROTI> (orange), and values exceeding median ROTI at the moment (orange filling); (bottom) SYM-H index (blue), <ROTI> max (orange), and flow pressure (green).
3.9. 7–8 September 2017 G4 Storm
The SSC occurred on 6 September 2017 at 23:43 UT, when the SYM-H reached about 50 nT [30]. Although it caused a small disturbance in the SYM-H index, it impacted the following magnetospheric state. The CME arrival dropped the Bz component from 6 to −7.5 nT within 7 minutes on 7 September at 20:37 UT, stayed at ~−10 nT until 23:10, then sharply fell to −20 nT, and after 17 minutes fell again to −30 nT. The Bz drop at 23:10 UT corresponded to a sharp increase in solar wind proton density, pressure, and velocity: from 4 to 14 cm−3, from 2 to 9 nPa, and from 391 to 591 km/s, respectively [31]. The change in the Bz component resulted in a severe storm, with two SYM-H minima on September 08: at 01:08 UT, the SYM-H reached −146 nT, and, after some recovery at 13:56 UT, the SYM-H reached −115 nT. The storm was classified as a severe one (G4), and during three periods the Kp exceeded 7+: 7 September 21–24 UT, 8 September 00–03 UT, and 8 September 12–15 UT. Both SYM-H and SME showed an intense first response and a weaker second one: peak values of −146 nT and 4455 nT versus −112 nT and 3503 nT, respectively. At the same time, the AE index showed a more intense disturbance during the second SYM-H minimum: 1300 nT versus 2000 nT [25]. Figure 12 shows the ROTI keogram (top) during 7–8 September 2017 with some keogram derivatives and the corresponding space weather indices (middle, bottom).
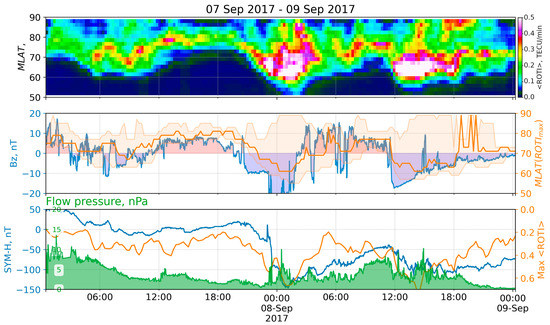
Figure 12.
ROTI keogram and space weather parameters for the storm of 7–8 September 2017: (top) keogram of average ROTI (<ROTI> versus MLAT versus time); (middle) IMF Bz (blue), MLAT positions of maximum <ROTI> (orange), and values exceeding median ROTI at the moment (orange filling); (bottom) SYM-H index (blue), <ROTI> max (orange), and flow pressure (green).
3.10. 27 September 2017 Storm
The Earth was affected by a corotating interaction region (CIR) during the period from 00:15 UT of 27 September to 08:38 UT of 28 September. The solar wind proton density rapidly increased from 10 to 55 n/cc during the first 6–7 h of the period [32]. After the proton density decreased to less than 10 n/cc, the solar wind flow speed started to increase from 350 to 720 km/s. The observed CIR is bounded by a fast forward shock at the leading edge and a reverse wave at the trailing edge [31]. Sudden commencement occurred on 26 September at ~23:55, when the SYM-H grew from 25 to 40 nT within 9 min. The index gradually decreased to 13 nT (1:30 27 September), increased to 40 nT two more times (at ~5:30 and ~6:30), and became negative at ~7:40. It reached several local minima: at 8:46 (−27 nT), ~13:40 (−38 nT), ~22:17 (−52 nT), and ~3:40 on 28 September (−60 nT); the absolute minimum was −74 nT at 5:57 on 28 September. The IMF Bz component was oscillating during the entire period. The longest continuous interval of the negative Bz was on 27 September from ~10:40 to ~13:55, and the minimum value of −15 nT was at ~7:30. The Kp index from 27 September at 18:00 to 28 September at 8:00 was in the range of 5+ to 6+, with the maximum value between 6–8 h on 28 September. Figure 13 shows the ROTI keogram (top) during 27–29 September with some keogram derivatives and the corresponding space weather indices (middle, bottom).
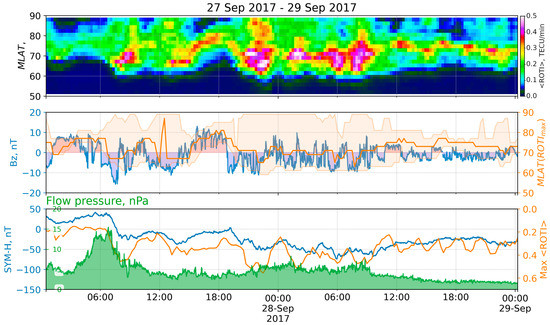
Figure 13.
ROTI keogram and space weather parameters for the storm of 27 September 2017: (top) keogram of average ROTI (<ROTI> versus MLAT versus time); (middle) IMF Bz (blue), MLAT positions of maximum <ROTI> (orange), and values exceeding median ROTI at the moment (orange filling); (bottom) SYM-H index (blue), <ROTI> max (orange), and flow pressure (green).
4. Results
Despite all the presented storms being of different natures, we find common features in the ROTI keograms. The main phase of the storm is always indicated by the maximum values of <ROTI> over a given period. The magnetic latitude of the highest <ROTI> tends to decrease with a magnetic storm development.
The blue line in the middle panel of Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 shows the IMF Bz variations. The orange line and the Y-axis on the right of the panel reflect the location of the <ROTI> maximum (MLATmax) for a given moment. The orange area confines the values of the <ROTI> that are higher than the median value for the map. Mostly, the variations in the Bz agree with the variations in the MLATmax: both the falls and rises of the Bz are accompanied by the falls and rises of the MLATmax.
The best correspondence is observed during the periods of long-term variations in the Bz: 12 May 2021, 14 May 2019, 26 August 2018, 11 May, and 8 September 2017 (Figure 4, Figure 6, Figure 9, Figure 11, Figure 12, respectively). All the listed storms were caused by CME. Cross-correlation between the Bz and MLATmax is shown in Figure 14 by a solid blue line (mlat.Bz): all the CME-driven storms (Figure 14, top) are indicated by high (0.7–0.85) correlation values, when HSS-driven values are mostly below 0.5 (except for the storm of 28 September 2018). Note that in all of the cases, the highest correlation values are observed with a lag of 1 h. Similarly, the Bz correlates with an equatorial boundary of high ROTI values (a lower latitude of the ROTI values exceeding a median, orange line): the correlation is observed with a lag of 1–2 h and is significantly higher for CME-storms.
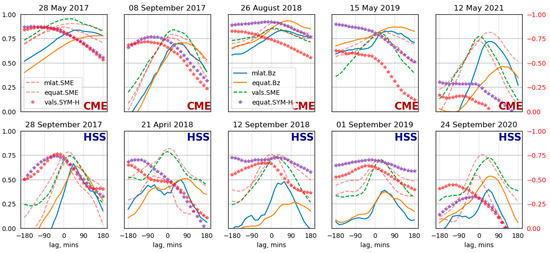
Figure 14.
Cross-correlation between keogram derivatives and SW indices: Bz versus MLAT_max (blue), Bz versus equatorial boundary (orange), SYM-H versus equatorial boundary (purple stars), SYM-H versus max <ROTI> (red starts, reversed Y-axis at right), SME index versus max <ROTI> (green dashed), and SME versus MLAT_max and equatorial boundary (red and dark red dashed line; reversed Y-axis at right).
The bottom panel in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 shows variations in the SYM-H index (blue) and the maximum value of the average ROTI (orange). The Y-axis for the <ROTI> is reversed and given on the right side (orange labels). The green area depicts the flow pressure. Variations in the <ROTI> maximum follow the SYM-H; to be precise, they are antiphase: a decrease in the SYM-H corresponds to the growth of the <ROTI>max. The red stars in Figure 14 represent an anticorrelation between the maximum <ROTI> and the SYM-H index (vals. SYM-H) the red-labeled Y-axis at right is inverted). During CME-storms, the highest anticorrelation was observed with an advance of several hours without any clear peak.
Purple stars show the SYM-H correlation with an equatorial boundary (equat.SYM-H). Correlation is observed for the CME-driven storms on 8 September 2017 (0.77), 28 May 2017 (0.87), and 26 August 2018 (0.92) and the HSS-driven storm on 28 September 2017 (0.74) (Table 2).

Table 2.
Cross-correlation maxima.
The best correlation of the Bz and the latitude of the maximal ROTI is observed during the storms of 12 May 2021 and 26 August 2018 and all the storms in 2017 (Figure 4, Figure 9, and Figure 11, Figure 12, Figure 13). These storms were the strongest, and the maximum Kp index was equal to or exceeded 7. Some correlation is seen during the initial and the main phases of the storms for the events on 14 May 2019 and 20 April 2018 (Figure 6 and Figure 8). The maximal Kp index for these storms was 6+ and 60, respectively.
The values of the maximal ROTI, its latitudinal location, and an equatorial boundary are in correspondence with the auroral electrojet index SME, for both types of magnetic storms. CME-storms show a higher correlation (Table 2): 0.81–0.95 (maximum ROTI), 0.76–0.87 (maximum ROTI latitude), and 0.82–0.91 (equatorial boundary). For the HSS-storms, the correlation is pretty high as well: 0.70–0.79 (maximum ROTI), 0.54–0.76 (maximum ROTI latitude) and 0.70–0.82 (equatorial boundary). The lag of the correlation varies within 1 h for all the storms (Figure 14, dashed lines).
5. Discussion
The paper considers ROTI maps’ dynamics during magnetic storms and searches for how the auroral oval shifts under different solar wind/geomagnetic parameters. We found similarities and differences in the auroral oval dynamics.
The importance of the study is due to the auroral oval influence, significantly on radio technical systems [33,34], including GNSS [35,36,37,38]. The high-frequency over-the-horizon radars suffer from the aurora: the aurora reduces the available range and coverage area twice [34]. The auroral phenomenon causes GNSS scintillations and decreases the GNSS positioning [35,38]. Engineers know about the auroral radio absorption, when working with high-frequency radio wave propagation [33].
Since the process in the auroral oval could significantly influence manmade technical systems, the scientific community studies how to monitor and forecast the oval location [39,40,41]. In particular, the community needs oval boundary dynamics detection.
Scientists developed models of the auroral region. Hardy et al. [39] suggested a Kp-based model of the auroral precipitations. Newell et al. [42] created an auroral precipitation model based on DMSP satellite data—OVATION Prime. OVATION Prime-2013 [40] involved UV image data from the GUVI instrument on the satellite TIMED. Vorobev et al. [41] created a web server to visualize the OVATION forecast for users.
Different ways appear to estimate auroral oval position. Huge systems are developed to monitor the auroral region, such as the SuperDARN network [1]. The global magnetic network suggests a way to estimate auroral currents and zones [43]. GNSS-based data, including ROTI data, suggest an alternative way to monitor the auroral oval [11,44,45]. The correspondence between auroral and ROTI ovals was shown in [8]. The ROTI maps become reliable GNSS products for ionospheric small-scale structures [6,7].
To automatic detection, auroral oval scientists have made significant efforts. Han et al. [46] suggested machine learning for Ultraviolet Imager data. Vasiliev et al. [47] involved computer vision to estimate oval locations from ROTI maps. We believe the presented results will help to advance the problem of auroral oval monitoring and prediction.
We considered two storm drivers: CME and HSS. CME-driven storms differ from CIR/SSH-driven storms [48]:
- CME-driven storms are brief, have denser plasma sheets, have stronger ring currents and Dst perturbation, have solar energetic particle events, and can produce new radiation belts, great auroras, and dangerous geomagnetically induced currents. One might identify CME-driven storms by the stronger magnetic field, enhanced solar wind speed, and low proton temperature [12].
- CIR-driven storms are of longer duration, have hotter plasma sheets and, hence, stronger spacecraft charging, and produce higher fluxes of relativistic electrons. Long-lasting Joule heating during HSS increases the temperature in the ionosphere, changes the recombination coefficient, and speeds up the formation of ionosphere irregularities in the auroral region [49]. This produces long-lasting high ROTI values during HSS, which can be observed in Figure 5, Figure 7, Figure 8, Figure 10, and Figure 13.
There is a difference is between dayside and nightside auroral oval behavior [50,51]. To analyze the local time differences, we calculated the distributions of the median ROTI separately for dayside (7–16 MLT) and nightside (18–6 MLT) and for CME- and HSS-driven storms (Figure 15 and Figure 16).
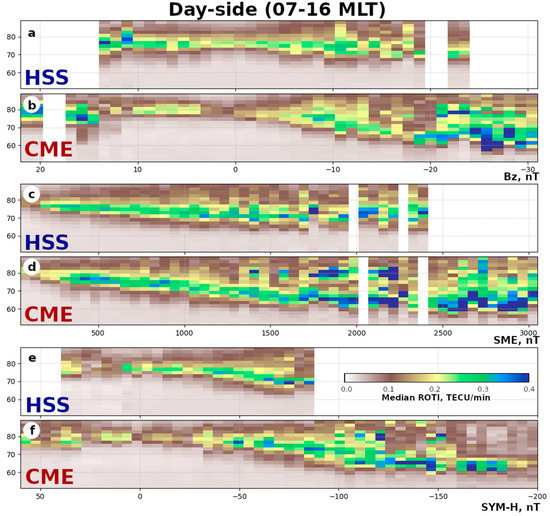
Figure 15.
Median ROTI versus magnetic latitude MLAT and IMF Bz (a,b), SME (c,d), and SYM-H indices (e,f) during magnetic local day (7–16 MLT) of HSS- and CME-driven storms.
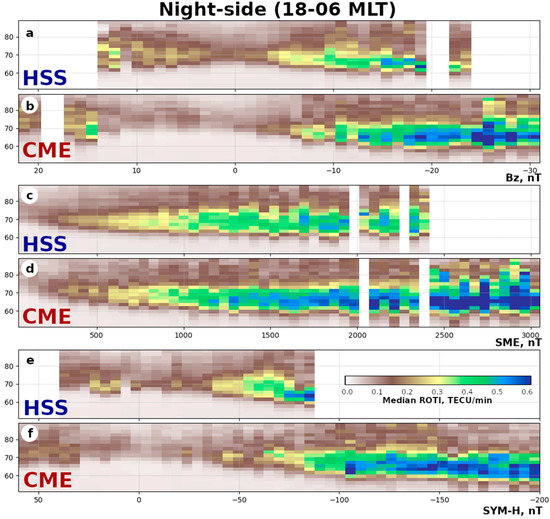
Figure 16.
Median ROTI versus magnetic latitude MLAT and IMF Bz (a,b), SME (c,d), and SYM-H indices (e,f) during magnetic local night (18–6 MLT) of HSS- and CME-driven storms.
Figure 15 presents the latitudinal distributions of the median ROTI versus the Bz (Figure 15a,b), SME (Figure 15c,d), and SYM-H indices (Figure 15e,f) during the MLT day (7–16 MLT) of HSS- and CME-driven storms. We define the ROTI oval boundaries by the values of the yellow level (>0.15 (day) and >0.2 TECU/min (night)). For both the HSS- and CME-driven storms, the magnetic latitude decreases with a fall in the Bz and SYM-H and growth in the SME: the equatorial boundary shifts equatorward while a storm develops. The distributions of the SME (Figure 15c,d) seem to be the best to compare. The polar oval boundary during HSS does not depend on the index, e.g., high values are near 78–80° of the magnetic latitude with SME growth (Figure 15c). For the CME-driven storm, both of the dayside boundaries (polar and equatorial) shift equatorward. The polar boundary shifted from 80° to 70° MLAT, with growth of the SME from 0 to 1500 nT, and remained near this latitude with further SME growth. Generally, the dayside median ROTI during CME-driven storms is higher for both the quiet and disturbed conditions.
Similarly, the combined median ROTI distributions for the nighttime (18–6 MLT) are shown in Figure 16. Unlike the dayside, the initial (quiet conditions) location of the boundaries is about 70° MLAT. With the development of a storm, both the boundaries shift in opposite directions (Figure 16c,d): the equatorial boundary equatorward and the polar one poleward. For both types of storms, the oval widens with an SME increment. During a CME-driven storm, the nighttime median ROTI shows higher values with the same index values, and, at the high values of SME (>2400 nT), the polar boundary exceeds 80° MLAT.
The width increment of the ROTI oval agrees with the location of the auroras [52]: the equatorial boundary of the aurora shifts equatorward with an increase in magnetic activity, while their polar boundary shifts equatorward at dayside and poleward at nightside. At the same time, the polar boundary of the ROTI oval at dayside shifts poleward. So, during strong storms (SME > 2500 nT), the ROTI seems to be intensified not only at the oval boundary but also in the polar cap as well.
The median ROTI distribution depends in the same way on SYM-H during CME-drive storm development in both dayside and nightside (Figure 16e,f panels): the more negative the SYM-H index is, the higher the median ROTI. The SYM-H correlates with the latitudinal location of both the equatorial and polar boundaries. This corresponds with the correlation presented in Figure 14 (the purple and red stars).
That agrees with the results of observing the aurora [48]: “Since the aurora do not progress as far equatorward for CIR-driven storms, it may also follow that the polar-cap area does not get as large for CIR-driven storms as it can during CME-driven storms.” The HSS events are known to last longer, so the overall energy input during HSS-driven storms could exceed those of CME-driven storms [48]. Milan et al. [51] showed that the auroral oval increases (increasing open magnetic flux in the magnetosphere) when the SYM-H decreases. Our results show that higher ROTI values still correspond to CME-driven storms, and we do not see integrated effects of the lasting energy on the ROTI.
The observed dependence of boundaries on the SYM-H (Figure 15 and Figure 16) corresponds with the SYM-H dependence of the auroral oval radius offered by [51].
Although the ROTI values are available only for the ionosphere pierce points (IPPs) and cannot give us total coverage of the polar region, this oval observation has some benefits. All the optical methods (both ground- and satellite-based) are strongly dependent on weather and time of the day, whereas transionospheric methods (e.g., GNSS-based) are not affected by these factors. According to [8], both the noticeable ROTI and auroral oval boundary variations demonstrate similar behavior with the seasonal and solar cycle variations. Speaking of the coverage, the auroral oval boundaries mainly do not involve the polar cap itself. That means that full coverage is not necessary, and a latitudinal area of 70–85° is sufficient to investigate the oval dynamics.
Despite all the presented data being taken from receivers in the Northern Hemisphere, we believe the results apply to the Southern Hemisphere as well. According to [53], near the equinox, the effects of ionospheric storms are symmetrical for the polar regions in both hemispheres. Shen et al. [54] point out that during summer in the Northern Hemisphere, the hemispheric symmetry should be observed as well. All the presented HSS-driven storms occurred in autumn (4/5) and spring (1/5), and the CME-driven ones mostly occurred in summer. With all the above in mind, we believe the results can be extrapolated to the Southern Hemisphere.
6. Conclusions
The article analyzed 10 magnetic storms of the solar cycle 24: 5 CME-driven and 5 HSS-driven storms. Under all the storms, the ROTI featured similar dynamics.
- (1)
- The main phase of the storm is always accompanied by maximal <ROTI> values.
- (2)
- The magnetic latitude of the highest ROTI decreases with a magnetic storm development.
- (3)
- Mostly, the variations in the Bz agree with the variations in the magnetic latitude of the maximal ROTI values.
- (4)
- The highest cross-correlations are observed with a lag of 1 h, between the IMF z-component Bz and the magnetic latitude where the highest ROTI values appear.
- (5)
- The auroral electrojet (SME index) shows the highest impact on the ROTI dynamics.
- (6)
- An increase in the space weather indices (in absolute value) is accompanied by a decrease in the latitude where the maximal ROTI occurs (except for proton-density effects).
- (7)
- Even at a small negative Bz, we observe accumulating energy and an increase in the ROTI values.
We found that the peculiarities of a storm affect the ROTI dynamics.
- (1)
- All the CME-driven storms feature high cross-correlation (>0.75) between the IMF z-component Bz and the magnetic latitude where the highest ROTI appears, while the HSS-driven storms feature a lower cross-correlation (<0.75) between them.
- (2)
- The difference in the duration of similar (by maximal values of geomagnetic indices) HSS- and CME-driven storms could produce differences in the highest ROTI values.
- (3)
- Correlations show that CME-driven storms impact the ROTI values and locations of regions with a high ROTI more directly compared with HSS-driven storms.
- (4)
- CME-driven storms feature higher ROTI values compared with HSS-driven ones at the same level of geomagnetic activity.
Author Contributions
Conceptualization, I.K.E. and Y.V.Y.; methodology, I.K.E.; visualization, I.K.E.; software, I.K.E.; validation, I.K.E. and Y.V.Y.; formal analysis, I.K.E.; investigation, I.K.E. and Y.V.Y.; resources, I.K.E.; writing—original draft preparation, I.K.E. and Y.V.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The work was financially supported by the Ministry of Science and Higher Education of the Russian Federation (Subsidy No. 075-GZ/C3569/278).
Data Availability Statement
All the treated data are available through SIMuRG (https://simurg.space accessed on 29 September 2022). The space weather indices are provided by the OMNI database (https://omniweb.gsfc.nasa.gov/ accessed on 29 September 2022) [15] and the SuperMag project (https://supermag.jhuapl.edu/info/ accessed on 29 September 2022) [16].
Acknowledgments
We acknowledge the OMNI database and SuperMag project for the geomagnetic indices data and the SIMuRG project [6] for treating the GNSS data. We acknowledge the providers for the GNSS data in the RINEX format: the Continuously Operating Reference Station, Instituto Brasileiro de Geografia e Estatística, Instituto Geográfico Nacional, UNAVCO Facility (supported by the National Science Foundation (NSF) and National Aeronautics and Space Administration (NASA) under NSF Cooperative Agreement No. EAR-0735156), Bundesamt für Kartographie und Geodäsie (BKG) Data Center, Institut Geographique National, Crustal Dynamics Data Information System (CDDIS), Institute of solar-terrestrial physics SB RAS and Center for Common Use «Angara» (http://ckp-rf.ru/ckp/3056/), Système d’Observation du Niveau des Eaux Littorales (SONEL), Northern California Earthquake Data Center, the New Zealand GeoNet project (supported by EQC, GNS Science, and LINZ), TLALOCNET GSAC data center, Geoscience Australia, Instituto Tecnológico Agrario de Castilla y León, Canadian High Arctic Ionospheric Network, Wuhan University, Rete Integrata Nazionale GPS (INGV), Geodetic Data Archiving Facility, Korea Astronomy and Space Institute, Institute of Geodynamics, National Observatory of Athens, Bundesamt für Kartographie und Geodäsie (BKG) Data Center, Pacific Northwest Geodetic Array (PANGA), Royal Observatory of Belgium, REseau NAtional GPS permanent (RENAG), Austrian data center (BEV), Dutch Permanent GNSS Array (DPGA), Western Canada Deformation Array (WCDA), Scripps Orbit and Permanent Array Center, UCSD, and Information and Analysis Center for Positioning, Navigation and Timing [55,56,57,58].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chisham, G.; Lester, M.; Milan, S.E.; Freeman, M.P.; Bristow, W.A.; Grocott, A.; McWilliams, K.A.; Ruohoniemi, J.M.; Yeoman, T.K.; Dyson, P.L.; et al. A decade of the Super Dual Auroral Radar Network (SuperDARN): Scientific achievements, new techniques and future directions. Surv. Geophys. 2007, 28, 33–109. [Google Scholar] [CrossRef]
- Imber, S.M.; Milan, S.E.; Lester, M. The Heppner-Maynard Boundary measured by SuperDARN as a proxy for the latitude of the auroral oval. J. Geophys. Res. Space Phys. 2013, 118, 685–697. [Google Scholar] [CrossRef]
- Pi, X.; Mannucci, A.J.; Lindqwister, U.J.; Ho, C.M. Monitoring of global ionospheric irregularities using the Worldwide GPS Network. Geophys. Res. Lett. 1997, 24, 2283–2286. [Google Scholar] [CrossRef]
- Astafyeva, E.; Yasyukevich, Y.V.; Maletckii, B.; Oinats, A.; Vesnin, A.; Yasyukevich, A.S.; Syrovatskii, S.; Guendouz, N. Ionospheric disturbances and irregularities during the 25–26 August 2018 geomagnetic storm. J. Geophys. Res. Space Phys. 2022, 127, e2021JA029843. [Google Scholar] [CrossRef]
- Tsugawa, T.; Nishioka, M.; Ishii, M.; Hozumi, K.; Saito, S.; Shinbori, A.; Otsuka, Y.; Saito, A.; Buhari, S.M.; Abdullah, M. Total Electron Content Observations by Dense Regional and Worldwide International Networks of GNSS. J. Disaster Res. 2018, 13, 535–545. [Google Scholar] [CrossRef]
- Yasyukevich, Y.; Kiselev, A.V.; Zhivetiev, I.V.; Edemskiy, I.K.; Syrovatskii, S.V.; Maletckii, B.M.; Vesnin, A.M. SIMuRG: System for Ionosphere Monitoring and Research from GNSS. GPS Solut. 2020, 24, 69. [Google Scholar] [CrossRef]
- Cherniak, I.; Krankowski, A.; Zakharenkova, I. ROTI Maps: A new IGS ionospheric product characterizing the ionospheric irregularities occurrence. GPS Solut. 2018, 22, 69. [Google Scholar] [CrossRef]
- Kotulak, K.; Zakharenkova, I.; Krankowski, A.; Cherniak, I.; Wang, N.; Fron, A. Climatology Characteristics of Ionospheric Irregularities Described with GNSS ROTI. Remote Sens. 2020, 12, 2634. [Google Scholar] [CrossRef]
- Sori, T.; Shinbori, A.; Otsuka, Y.; Tsugawa, T.; Nishioka, M. The occurrence feature of plasma bubbles in the equatorial to midlatitude ionosphere during geomagnetic storms using long-term GNSS-TEC data. J. Geophys. Res. Space Phys. 2021, 126, e2020JA029010. [Google Scholar] [CrossRef]
- Li, W.; Song, S.; Jin, X. Ionospheric scintillation monitoring with ROTI from geodetic receiver: Limitations and performance evaluation. Radio Sci. 2022, 57, 1–15. [Google Scholar] [CrossRef]
- Sieradzki, R.; Paziewski, J. GNSS-based analysis of high latitude ionospheric response on a sequence of geomagnetic storms performed with ROTI and a new relative STEC indicator. J. Space Weather Space Clim. 2019, 9, A5. [Google Scholar] [CrossRef]
- Dugassa, T.; Habarulema, J.B.; Nigussie, M. Equatorial and low-latitude ionospheric TEC response to CIR-driven geomagnetic storms at different longitude sectors. Adv. Space Res. 2020, 66, 1947–1966. [Google Scholar] [CrossRef]
- Maruyama, T.; Ma, G.; Tsugawa, T. Storm-induced plasma stream in the low-latitude to midlatitude ionosphere. J. Geophys. Res. Space Phys. 2013, 118, 5931–5941. [Google Scholar] [CrossRef]
- Beeck, S.S.; Jensen, A.B.O. ROTI maps of Greenland using kriging. J. Geod. Sci. 2021, 11, 83–94. [Google Scholar] [CrossRef]
- King, J.H.; Papitashvili, N.E. Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. J. Geophys. Res. Space Phys. 2005, 110, A02209. [Google Scholar] [CrossRef]
- Gjerloev, J.W. The SuperMAG data processing technique. J. Geophys. Res. Space Phys. 2012, 117, A09213. [Google Scholar] [CrossRef]
- Space Weather Highlights by SWPC for Week 2385 (10–16 May 2021). Available online: ftp://ftp.swpc.noaa.gov/pub/warehouse/2021/WeeklyPDF/prf3285.pdf (accessed on 29 September 2022).
- Space Weather Highlights by SWPC for Week 2352 (21–27 September 2020). Available online: Ftp://ftp.swpc.noaa.gov/pub/warehouse/2020/2020_WeeklyPDF.tar.gz/prf2352.pdf (accessed on 29 September 2022).
- Space Weather Highlights by SWPC for Week 2281 (13–19 May 2019). Available online: Ftp://ftp.swpc.noaa.gov/pub/warehouse/2019/2019_WeeklyPDF.tar.gz/prf2281.pdf (accessed on 29 September 2022).
- Chernogor, L.F.; Garmash, K.P.; Guo, Q.; Luo, Y.; Rozumenko, V.T.; Zheng, Y. Ionospheric storm effects over the People’s Republic of China on 14 May 2019: Results from multipath multi-frequency oblique radio sounding. Adv. Space Res. 2020, 66, 226–242. [Google Scholar] [CrossRef]
- Luo, Y.; Chernogor, L.; Garmash, K.; Guo, Q.; Rozumenko, V.; Zheng, Y. Dynamic processes in the magnetic field and in the ionosphere during the 30 August–2 September 2019 geospace storm: Influence on high frequency radio wave characteristics. Ann. Geophys. 2021, 39, 657–685. [Google Scholar] [CrossRef]
- Space Weather Highlights by SWPC for Week (26 August–1 September 2019). Available online: Ftp://ftp.swpc.noaa.gov/pub/warehouse/2019/2019_WeeklyPDF.tar.gz/prf2296.pdf (accessed on 29 September 2022).
- Velinov, P.I.Y.; Tassev, Y.; Tomova, D.; Mateev, L. Analysis and characteristics of unpredictable G2—Moderate geomagnetic storm on 20 April 2018 in solar cycle 24 minimum. C. R. Acad. Bulg. Sci. 2018, 71, 1357–1365. [Google Scholar] [CrossRef]
- Piersanti, M.; De Michelis, P.; Del Moro, D.; Tozzi, R.; Pezzopane, M.; Consolini, G.; Marcucci, M.F.; Laurenza, M.; Di Matteo, S.; Pignalberi, A.; et al. From the Sun to Earth: Effects of the 25 August 2018 geomagnetic storm. Ann. Geophys. 2020, 38, 703–724. [Google Scholar] [CrossRef]
- Blagoveshchensky, D.V.; Sergeeva, M.A. Impact of geomagnetic storm of 7–8 September 2017 on ionosphere and HF propagation: A multi-instrument study. Adv. Space Res. 2019, 63, 239–256. [Google Scholar] [CrossRef]
- Astafyeva, E.; Bagiya, M.S.; Förster, M.; Nishitani, N. Unprecedented Hemispheric Asymmetries During a Surprise Ionospheric Storm: A Game of Drivers. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027261. [Google Scholar] [CrossRef]
- Space Weather Highlights by SWPC for Week 2246 (10–16 September 2018). Available online: Ftp://ftp.swpc.noaa.gov/pub/warehouse/2018/2018_WeeklyPDF.tar.gz/prf2246.pdf (accessed on 29 September 2022).
- Space Weather Highlights by SWPC for Week 2178 (22–28 May 2017). Available online: Ftp://ftp.swpc.noaa.gov/pub/warehouse/2017/2017_WeeklyPDF.tar.gz/prf2178.pdf (accessed on 29 September 2022).
- Ovodenko, V.B.; Klimenko, M.V.; Zakharenkova, I.E.; Oinats, A.V.; Kotova, D.S.; Nikolaev, A.V.; Chernyshov, A.A. Spatial and temporal evolution of different-scale ionospheric irregularities in Central and East Siberia during the 27–28 May 2017 geomagnetic storm. Space Weather 2020, 18, e2019SW002378. [Google Scholar] [CrossRef]
- De Paula, E.R.; de Oliveira, C.M.; Caton, R.G.; Negreti, P.M.; Batista, I.S.; Martinon, A.R.F.; Neto, A.C.; Abdu, M.A.; Monico, J.F.G.; Sousasantos, J.; et al. Ionospheric irregularity behavior during the 6–10 September 2017 magnetic storm over Brazilian equatorial–low latitudes. Earth Planets Space 2019, 71, 42. [Google Scholar] [CrossRef]
- Hajra, R. September 2017 Space-Weather Events: A Study on Magnetic Reconnection and Geoeffectiveness. Sol. Phys. 2021, 296, 50. [Google Scholar] [CrossRef]
- Shinbori, A.; Otsuka, Y.; Sori, T.; Tsugawa, T.; Nishioka, M. Temporal and spatial variations of total electron content enhancements during a geomagnetic storm on 27 and 28 September 2017. J. Geophys. Res. Space Phys. 2020, 125, e2019JA026873. [Google Scholar] [CrossRef]
- Hargreaves, J.K. Auroral radio absorption: The prediction question. Adv. Space Res. 2010, 45, 1075–1092. [Google Scholar] [CrossRef]
- Ruck, J.J.; Themens, D.R. Impacts of auroral precipitation on HF propagation: A hypothetical over-the-horizon radar case study. Space Weather 2021, 19, e2021SW002901. [Google Scholar] [CrossRef]
- Smith, A.M.; Mitchell, C.N.; Watson, R.J.; Meggs, R.W.; Kintner, P.M.; Kauristie, K.; Honary, F. GPS scintillation in the high Arctic associated with an auroral arc. Space Weather 2008, 6, 1–7. [Google Scholar] [CrossRef]
- van der Meeren, C.; Oksavik, K.; Lorentzen, D.A.; Rietveld, M.T.; Clausen, L.B.N. Severe and localized GNSS scintillation at the poleward edge of the nightsideauroral oval during intense substorm aurora. J. Geophys. Res. Space Phys. 2015, 120, 10607–10621. [Google Scholar] [CrossRef]
- Prikryl, P.; Ghoddousi-Fard, R.; Thomas, E.G.; Ruohoniemi, J.M.; Shepherd, S.G.; Jayachandran, P.T.; Danskin, D.W.; Spanswick, E.; Zhang, Y.; Jiao, Y. GPS phase scintillation at high latitudes during geomagnetic storms of 7–17 March 2012—Part 1: The North American sector. Ann. Geophys. 2015, 33, 637–656. [Google Scholar] [CrossRef]
- Demyanov, V.V.; Yasyukevich, Y.V. Space weather: Risk factors for global navigation satellite systems. Sol. -Terr. Phys. 2021, 7, 28–47. [Google Scholar] [CrossRef]
- Hardy, D.A.; Gussenhoven, M.S.; Holeman, E. A statistical model of auroral electron precipitation. J. Geophys. Res. Space Phys. 1985, 90, 4229–4248. [Google Scholar] [CrossRef]
- Newell, P.T.; Liou, K.; Zhang, Y.; Sotirelis, T.; Paxton, L.J.; Mitchell, E.J. OVATION Prime-2013: Extension of auroral precipitation model to higher disturbance levels. Space Weather 2014, 12, 368–379. [Google Scholar] [CrossRef]
- Vorobev, A.V.; Pilipenko, V.A.; Krasnoperov, R.I.; Vorobeva, G.R.; Lorentzen, D.A. Short-term forecast of the auroral oval position on the basis of the “virtual globe” technology. Russ. J. Earth Sci. 2020, 20, ES6001. [Google Scholar] [CrossRef]
- Newell, P.T.; Sotirelis, T.; Wing, S. Seasonal variations in diffuse, monoenergetic, and broadband aurora. J. Geophys. Res. Space Phys. 2010, 115, A03216. [Google Scholar] [CrossRef]
- Lunyushkin, S.B.; Penskikh, Y.V. Diagnostics of the auroral oval boundaries on the basis of the magnetogram inversion technique. Sol. -Terr. Phys. 2019, 5, 88–100. [Google Scholar] [CrossRef]
- Perevalova, N.P.; Romanova, E.B.; Tashchilin, A.V. Detection of high-latitude ionospheric structures using GNSS. J. Atmos. Sol. -Terr. Phys. 2020, 207, 105335. [Google Scholar] [CrossRef]
- Yasyukevich, Y.; Vasilyev, R.; Ratovsky, K.; Setov, A.; Globa, M.; Syrovatskii, S.; Yasyukevich, A.; Kiselev, A.; Vesnin, A. Small-Scale Ionospheric Irregularities of Auroral Origin at Mid-latitudes during the 22 June 2015 Magnetic Storm and Their Effect on GPS Positioning. Remote Sens. 2020, 12, 1579. [Google Scholar] [CrossRef]
- Han, Y.; Han, B.; Hu, Z.; Gao, X.; Zhang, L.; Yang, H.; Li, B. Prediction and variation of the auroral oval boundary based on a deep learning model and space physical parameters. Nonlin. Process. Geophys. 2020, 27, 11–22. [Google Scholar] [CrossRef]
- Vasiliev, A.; Yasyukevich, Y.; Garashchenko, A.; Edemskiy, I.; Vesnin, A.; Sidorov, D. Computer Vision for GNSS-based Detection of the Auroral Oval Boundary. Int. J. Artif. Intell. 2021, 19, 132–151. [Google Scholar]
- Borovsky, J.E.; Denton, M.H. Differences between CME-driven storms and CIR-driven storms. J. Geophys. Res. Space Phys. 2006, 111, A07S08. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Fu, L.; Wang, J.; Radicella, S.M.; Zhang, C. Analyzing Ionosphere TEC and ROTI Responses on 2010 August High Speed Solar Winds. IEEE Access 2019, 7, 29788–29804. [Google Scholar] [CrossRef]
- Gustafsson, G.; Feldstein, Y.I.; Shevnina, N.F. The auroral orientation curves for the IQSY. Planet. Space Sci. 1969, 17, 1657–1666. [Google Scholar] [CrossRef]
- Milan, S.E.; Hutchinson, J.; Boakes, P.D.; Hubert, B. Influences on the radius of the auroral oval. Ann. Geophys. 2009, 27, 2913–2924. [Google Scholar] [CrossRef]
- Starkov, G.V.; Feldshtein, Y.I. Orientation of extended auroral forms. Geomagn. Aeron. 1967, 7, 72–77. [Google Scholar]
- Jin, S.; Jin, R.; Kutoglu, H. Positive and negative ionospheric responses to the March 2015 geomagnetic storm from BDS observations. J. Geod. 2017, 91, 613–626. [Google Scholar] [CrossRef]
- Shen, C.-S.; Zi, M.-Y.; Wang, J.-S.; Xu, J.-Y.; Liu, S.-L. On the Asymmetry of the Storm-Time Current System in the Ionosphere Between Southern and Northern Hemispheres. Chin. J. Geophys. 2006, 49, 1425–1435. [Google Scholar] [CrossRef]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The International GNSS Service in a changing landscape of Global Navigation Satellite Systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Yasyukevich, Y.V.; Vesnin, A.M.; Perevalova, N.P. SibNet–Siberian Global Navigation Satellite System Network: Current state. Sol. -Terr. Phys. 2018, 4, 63–72. [Google Scholar] [CrossRef]
- Jayachandran, P.T.; Langley, R.; Macdougall, J.; Mushini, S.; Hamza, A.; Mann, I.; Milling, D.; Kale, Z.; Chadwick, R.; Kelly, T.; et al. Canadian High Arctic Ionospheric Network (CHAIN). Radio Sci. 2009, 44, RS0A03. [Google Scholar] [CrossRef]
- Bruyninx, C.; Habrich, H.; Kenyeres, A.W.; Söhne, W.; Stangl, G.; Völksen, C. Enhancement of the EUREF Permanent Network Services and Products. Geod. Planet Earth IAG Symp. 2012, 136, 27–35. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).