Abstract
The evaporation duct height (EDH) can reflect the main characteristics of the near-surface meteorological environment, which is essential for designing a communication system under this propagation mechanism. This study proposes an EDH prediction network with multi-layer perception (MLP). Further, we construct a multi-dimensional EDH prediction model (multilayer-MLP-EDH) for the first time by adding spatial and temporal “extra data” derived from the meteorological measurements. The experimental results show that: (1) compared with the naval-postgraduate-school (NPS) model, the root-mean-square error (RMSE) of the meteorological-MLP-EDH model is reduced to 2.15 m, and the percentage improvement reached 54.00%; (2) spatial and temporal parameters can reduce the RMSE to 1.54 m with an improvement of 66.96%; (3) the multilayer-MLP- EDH model can match measurements well at both large and small scales by attaching meteorological parameters at extra height, the error is further reduced to 1.05 m, with 77.51% improvement compared with the NPS model. The proposed model can significantly improve the prediction accuracy of the EDH and has great potential to improve the communication quality, reliability, and efficiency of ducting in evaporation ducts.
1. Introduction
An atmospheric duct is a unique phenomenon in the lower atmosphere, and electromagnetic waves can experience less attenuation in the trapped layer by limiting the spread of the wavefront from spherical to cylindrical expansion, where the waves are bent by atmospheric refraction [,]. A long-range transmission in microwave bands can also be realized. Namely, microwave radio signals may refract in the lower layers of Earth’s atmosphere and propagate far beyond the line of sight []. This feature may be appropriate for communications at sea [], while the public land mobile network (PLMN) [,] is limited due to the special meteorological conditions and terrain features [,]. Moreover, communication systems using evaporation ducts are expected to become an important means of the sixth-generation communication system until we further understand its distribution characteristics.
As a strong negative vertical humidity gradient near the sea surface, the evaporation duct exists due to the moisture content rapidly decreasing with increasing altitude [,]. Dramatic effects may be applied to the microwave communication system while transmitting in the ducting layer, especially for frequencies above 1 GHz [], which may meet the demand for large-bandwidth, high-speed, and long-range applications []. The evaporation duct frequently occurs over the ocean and the occurrence in the South China Sea (SCS) exceeds 75% []. However, the spatial and temporal refractivity variations significantly affect shipboard communication performances at sea and near shore [,,]. As a result, communication effects may experience several disadvantages, including a specific time loss (about 25% in the SCS based on the above statistical characteristic of the evaporation duct) and an available low antenna height with minimal effects on any land–land or ship-based system, etc., constraining it from becoming a convenient and widely used maritime communication. Therefore, the prerequisite for communication using evaporation ducts is the accurate prediction of transmission effects, which relies on two critical components: the atmospheric refractive condition and the prediction in the given environment []. The evaporation duct height (EDH) is the characteristic parameter of the refractivity profile. The accurate prediction of the EDH has special significance in the practical design of the evaporation duct communication system and the instrument parameters. The EDH can be directly measured [,] and evaluated by numerous methods [,,] and theoretical models [,,,,,]. The directly measured method may take lots of time and effort, and the latter two methods can calculate from meteorological detection at a certain height, but the accuracy needs further improvement. Therefore, a focus topic in the present and the future is to maximize the use of measurement datasets and to improve the prediction accuracy of EDH.
Presently, “artificial intelligent (AI) enhanced operation” has become one of the hotspot directions [,,,,]. The combination of AI and the analysis of evaporation ducts has also boosted the accuracy of EDH prediction. In modeling construction, Yan et al., propose a numerical profiling method that adopts the artificial neural network and training data from the remote sensing data and the naval postgraduate school (NPS) model []. Zhao et al., propose a method based on a multi-layer perception (MLP) of five hidden layers to predict the EDH, and the applicability in different areas is analyzed []. In short-term prediction, Zhao et al., constructed an EDH prediction model based on a long short-term memory network []. In addition, Mai et al., introduced the Darwinian evolutionary algorithm and compared the accuracy with the neural network in EDH prediction [].
In this paper, deep learning methods are utilized to improve the prediction accuracy of the EDH so that the communication system can be better designed and operated. Furthermore, we construct a multi-dimensional EDH prediction model for the first time by blending with spatial and temporal “extra data” during meteorological detection []. Section II describes the background and previous EDH prediction method and Section III describes the modeling process of the proposed model. Finally, predictions of the proposed model and the theoretical method are compared with the measurements; the effectiveness has also been verified.
2. Background and Methods
2.1. Evaporation duct Diagnosis
The refraction in the atmosphere refers to the bending characteristics while the electromagnetic wave propagates in the medium, and the degree can be measured by the refraction index n
where c and v are the propagation speed of the electromagnetic wave in free space and the medium, respectively.
Radio refractivity N (N-unit) is usually used in the troposphere to reflect the corresponding spatial structure characteristics. According to the ITU-R Recommendation P.453-14 []
where P is the atmospheric pressure (hPa), T is the absolute temperature (K), and e is the water vapor pressure (hPa).
For the convenience of considering the curvature of the Earth, the modified refractivity M (M-unit) is often utilized as [,]
where z is the height above the ground (m) and re is Earth’s radius (the average Earth radius is 6371 km).
Electromagnetic waves are bent towards the ground by atmospheric refraction, while the vertical gradient of modified refractivity becomes negative (dM/dz < 0). Signals can refract and propagate over the horizon with matching frequencies and angles.
2.2. Theoretical Models of EDH
Based on the Monin–Obukhov similarity theory [,], the vertical profile of mean wind speed U(m/s), potential temperature θ (K), and specific humidity q (kg/kg) in the surface layer can be calculated. At present, the extensively utilized numerical methods in the evaporation duct prediction include the Paulus–Jeske (PJ) model [], the Musson–Gauthier–Bruth (MGB) model [], the Babin–Young–Carton (BYC) model [], the NPS model [], and the surface heat budget of the arctic ocean experiment (SHEBA) model [] are extensively utilized at present. An evaporation duct’s modified refractivity (M-profile) can be defined by a limited number of meteorological factors, such as pressure and temperature at the sea surface, relative humidity, temperature, and wind speed at a certain altitude.
The comparison between the BYC model, the NPS model, and the SHEBA model are listed in Table 1. During the calculation, the scale parameters and the thermodynamically roughness height of the sea surface are defined by the COARE algorithm [], and the profile stability functions calculate the wind speed and temperature under stable conditions.

Table 1.
The prediction methods of evaporation ducts.
Taking the NPS model as an example, the advanced air–sea flux algorithm COARE 3.0 is adopted, keeping good consistency with the measured results []. The input parameters are used to determine the modified refractivity profile, and the altitude with minimum value is the EDH. The vertical profile of air temperature T and specific humidity q at altitude z can be calculated as []:
where and are the characteristic scales of potential temperature and specific humidity, respectively; is stability functions; is thermodynamic roughness height; Γd is the dry adiabatic decline rate; κ is Karman constant; L is the Monin–Obukhov length.
According to theoretical models, the EDH can be calculated with meteorological parameters at the sea surface and at a certain height. The calculation function can be expressed as
where and are the pressure and temperature at the sea surface h0, respectively, , , and are the relative humidity, temperature, and wind speed at the altitude h1, respectively.
2.3. Analysis of Transmission Effects
For long distance transmission in the microwave band, the main transmission mechanisms are normal propagation close to the Earth’s surface and troposcatter propagation [,]. Anomalous propagation of transmission in the ducting layer may apply to communication systems over the ocean, signals may experience less attenuation under appropriate conditions.
The spatial and temporal distribution of meteorological parameters is uneven, leading to the changes of transmission effect changes with the variation of the evaporation duct. As a result, extra propagation loss among the designed communication system may be incurred. To analyze the influence of the variation of evaporation ducts quantitatively, a communication link was designed with the antenna heights fixed at 10 m. A specific position in the Pacific Ocean (30.0°N, 130.0°W) was selected, where the annual refractivity was 346.68 N-units []. The transmission loss diagram at 12 GHz with a distance of 0–500 km is shown in Figure 1. To perform the propagation curves corresponding to the typical EDH varied from 6 m to 18 m, the parabolic equation toolbox (PETOOL) [,] with the parabolic equation (PE) method [,] has been applied.
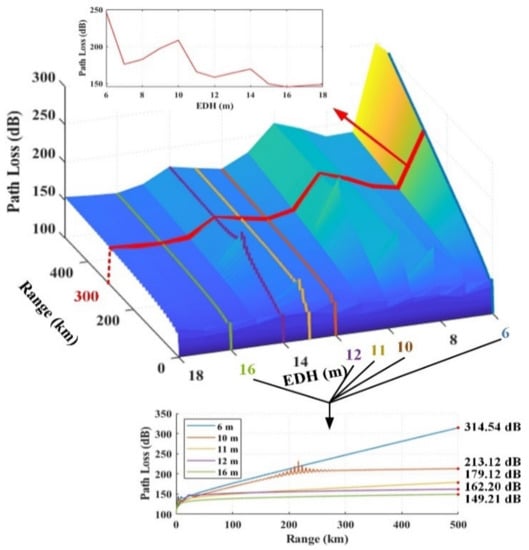
Figure 1.
The transmission loss diagram at 12 GHz with a distance of 0–500 km.
In Figure 1, the path loss curves varied considerably with different EDH. Path losses increase with the EDH fixed at 6 m and lower than the antenna height, resulting in a poor communication effect. Significant improvement of channel conditions arises when the EDH is between 16 m and 18 m and the path loss fluctuates around 150 dB. Overall, the transmission loss fluctuates with the increase of the EDH. Especially in the range of 10–12 m, a 1 m variation in the height may lead to an increase in the path loss at 500 km of 16.92 dB to 34.00 dB, which brings much uncertainty to the operation of the communication system. This is roughly the same as the results of [,].
3. Datasets and Methodology
3.1. Modeling Data
3.1.1. MAGIC Datasets
To verify the prediction accuracy of existing models and to explore a better method, we use measured meteorological data from the ship-based marine ARM GCSS Pacific cross-section intercomparison (GPCI) investigation of clouds (MAGIC) field campaign. The ship-based MAGIC field campaign, with the marine-capable second ARM mobile facility (AMF2) deployed, lasted for nearly 200 days between Los Angeles, California and Honolulu, Hawaii, which provided high-resolution measured datasets of clouds, precipitation, and marine boundary layer (MBL) [,]. The ship completed 20 round trips from October 2012 to September 2013. Lots of instruments were deployed to measure meteorological parameters aboard the ship throughout the campaign: a Vaisala weather station, an inertial navigational location and attitude system, an infrared SST autonomous radiometer (ISAR), radiosondes, etc. [].
The meteorological parameters of the MAGIC datasets collected in this paper mainly include temperature, pressure, relative humidity, wind speed, and direction measured by the marine meteorological system (MARMET) at approximately 27 m above sea level; the sea surface skin temperature (SSST) measured by the ISAR; the ship location by a navigation system. The time resolution of the MARMET and the ISAR devices is 1 min. The time distribution of the sounding data collected from MAGIC datasets is shown in Figure 2.
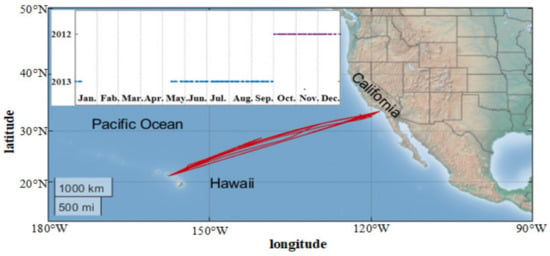
Figure 2.
The spatial and temporal distribution of MAGIC measurements.
In addition, standard radiosondes (Vaisala model MW-31, SN E50401) were launched at 1 m to measure the vertical profiles of temperature, pressure, relative humidity, and wind speed and direction. Meteorological data at different altitudes were also collected using the Vaisala radiosonde (MW-31), with 0.5 Hz vertical resolution at fixed times []. As a result, 571 sets of radiosonde data were formed.
3.1.2. Data Processing
Using the boat measurements of the MARMET and ISAR devices at the sea surface and 27 m above sea level and the radiosonde-collected data during their ascent, we can obtain meteorological parameters for at least seven altitudes at each geographic location. The sea surface relative humidity (RH) was set at 98% []. As shown in Table 2, the measured datasets are preprocessed before modeling, with invalid datasets removed.

Table 2.
The dataset preprocessing process.
In addition, we selected 476 effective datasets from 571 collections of radiosonde sounding data. Then, the modified refractivity index at seven layers can be obtained based on the effective meteorological datasets. A least-squares curve fit was applied to each of the 476 measurements. Furthermore, we got the M-refractivity profile by a log-linear function [,,].
where M is the modified refractivity (M-units) and h is the altitude (m). f0, f1, and f2 are coefficients that can be calculated for a least-squares best fit. The constant 0.001 was used to prevent the curve from blowing up at zero altitudes [,].
Figure 3 shows the calculating process of the EDH, modified refractivity M for every 0.1 m between the surface and 40 m altitude based on MAGIC datasets, and the height at which the minimum M is achieved is the EDH.
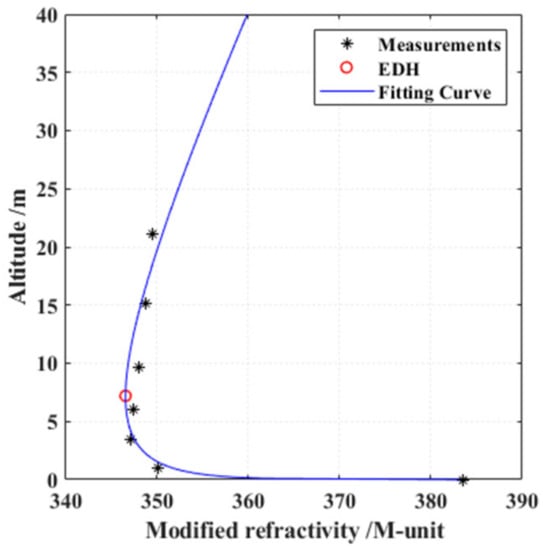
Figure 3.
The calculating method of the EDH.
3.1.3. Reliability Assessment of Theoretical Models
Meteorological parameters, including the pressure and temperature at the surface, the relative humidity, the temperature, the wind speed in the air, and the altitude, will be considered in the calculation of the evaporation duct characteristics using theoretical models []. The statistical root-mean-square error (RMSE) of the EDH predictions of the BYC model, the NPS model, and the SHEBA model based on the MAGIC datasets are described in Table 3. The minimum RMSE is 4.52 m by the NPS model. Let x and y represent measured EDH and predicted EDH of the NPS model, and the fitting line is y = 0.42x + 5.52, far from the evaluation criteria y = x, as shown in Figure 4.

Table 3.
The statistical RMSEs of three theoretical methods.
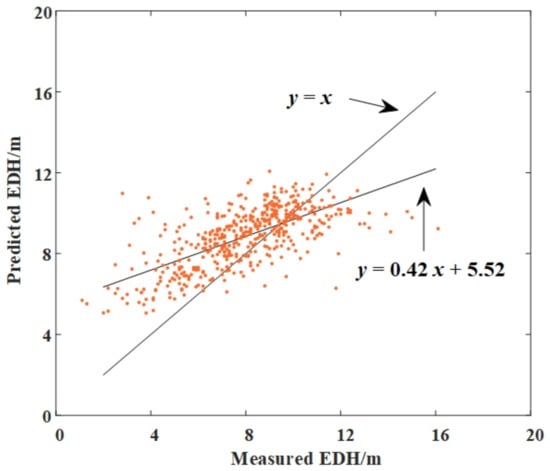
Figure 4.
The EDH fitting line by the MAGIC datasets and inverted by the NPS model.
The EDH calculated by the NPS model does not match the measured data well. According to Figure 1, the RMSE exceeds 4 m, which may lead to a transmission loss error of more than 100 dB, which may bring significant deviation to the receiving effect of the transmission system.
3.2. Modeling Method
Theoretical models are generally based on the Monin–Obukhov similarity theory and are constrained by some basic physical boundary layer assumptions []. On the contrary, the neural network training prediction method can be derived entirely from original data. Therefore, it is more suitable for the natural atmospheric environment and will not be constrained by theoretical assumptions.
Considering that MAGIC has special characteristics from other similar experiments: (1) the experimental positions were spatially repeatable (the ship completed 20 round trips); (2) the radiosonde data were concentrated at several hours (it launched every 6 h); (3) the experiment instruments were set at multilayers, which have great data background both in time and space. Therefore, combine the experimental data with the neural network by adding the spatial data, such as latitude, longitude, and meteorological parameters in multilayers, and the temporal data, such as experiment time, to construct new datasets as training input for the prediction model.
Artificial intelligence originated in the 20th century and has been used in various industries, but it is seldom used in EDH prediction [,,,]. MLP is a kind of artificial neural network (ANN) with a forward structure [,,] that maps a group of input vectors to a group of output vectors. The MLP consists of multiple layers and their neurons are fully connected to the next layer. It has a high nonlinear global function and powerful adaptive and self-learning ability, which is suitable for finding the characteristics of EDH prediction data in multi-dimensions. Here, the MLP model is considered to implement the construction of the training network.
3.2.1. Principle of the MLP
The MLP has universal approximation property []. Theoretically, an MLP network composed of a linear output layer and at least one hidden layer with activation functions can describe any function from a finite dimensional space to another with arbitrarily high precision with sufficient hidden neurons supplied. Each node in the MLP is the neuron with a nonlinear activation function, except the input node. MLP is an extension of perceptron, which overcomes the weakness of not recognizing linear non-fractional data.
Compared with the single-layer perceptron, the hidden layer of MLP changes from one to multiple. The training purpose of MLP is to make the network approximate the function that needs to be fitted. During the training process, the information is carried out from the input layer to the hidden layers and then to the output layer. The input layer is responsible for receiving the characteristics of the training data and is connected to the hidden layer with weight parameters. In contrast, the output layer is the target value that the training is expected to achieve through the hidden layers to realize the nonlinear mapping of the input space.
A typical MLP training process is as follows: (1) the weights are randomly allocated; (2) the neural network is activated by using all features of the training datasets from the input layer and then the output value is obtained through forwarding propagation; (3) the error is calculated between the output and the target value and the weight is updated by backpropagation; (4) the training is repeated until the output error is lower than the established standard. The trained MLP network can accept new input datasets at the end of this process.
3.2.2. Modeling
The essence of prediction is complex regression function construction and a multi-dimensional EDH prediction model can be constructed with the “extra data” in the experiment. The essence of MLP is also a nonlinear function mapping from input vector to output, similar to the model we tried to train. The advantages of MLP in learning and in processing nonlinear global data may solve the regression problem of meteorological characteristics. With a reasonable network structure and hyperparameters combined with enough training data, the performance of MLP can be excellent compared with the theoretical model.
While constructing the complete dataset of the MLP model, spatial data, temporal data, and meteorological data at multiple altitudes, including temperature, pressure, wind speed, and RH at the data measurement location of the MAGIC field campaign, were collected as a set of modeling data. To complete a comprehensively trained network for the validation of testing datasets and the generality of the method, we should select the training dataset that would cover the main features of the total dataset. A commonly accepted hold-out approach [] is a 7:3 ratio between the training and the testing set. Namely, the training and the testing set proportion is 70% and 30% of the total dataset. Therefore, the first 334 groups of data in about 12 round trips were selected and randomly reordered as training datasets. The remaining 142 groups of data were used as a testing dataset.
By classifying and selecting the corresponding parameter information with the training datasets, meteorological-MLP-EDH, spatial-MLP-EDH, temporal-MLP-EDH, spatial–temporal-MLP-EDH, and multilayer-MLP-EDH models were constructed. The modeling process is shown in Figure 5.
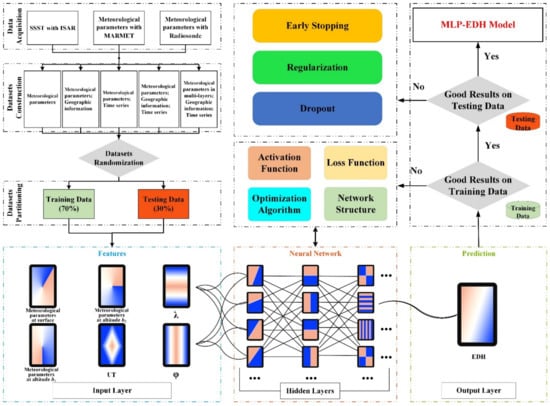
Figure 5.
The modeling processes.
- (1)
- Meteorological-MLP-EDH
As a comparison with the theoretical models, the meteorological-MLP-EDH model takes the temperature (T) and the pressure (P) at the sea surface (h0); temperature, wind speed (U), and RH in the air (h1); measured altitudes in each training dataset as the input parameters. The mapping output is the corresponding EDH and the calculation function can be expressed as
- (2)
- Spatial-MLP-EDH
The spatial data such as latitude and longitude may positively affect the prediction results of the experiment ship completing 20 round trips. The input vector of the spatial-MLP-EDH model takes the same parameters as the meteorological-MLP-EDH model. Furthermore, the spatial parameters of the experimental positions with latitude (λ) and longitude (φ) in the MAGIC campaign are also used as additional information to supply the feature of the selected meteorological parameters on a complete path.
- (3)
- Temporal-MLP-EDH
The radiosonde data were collected every 6 h in the MAGIC campaign. The temporal information may have a positive effect on prediction accuracy. With the measured time (UT), new datasets can be collected to construct the temporal-MLP-EDH model, implying the feature of the selected meteorological parameters at the specific time.
- (4)
- Spatial–Temporal-MLP-EDH
The spatial–temporal-MLP-EDH model is a three-dimensional regression function consisting of spatial–temporal information and meteorological parameters at a single layer at sea surface and air. The input values supply the feature of selected meteorological parameters at a specific time on a complete path.
- (5)
- Multilayer-MLP-EDH
In addition, we constructed a four-dimensional regression function multilayer-MLP-EDH with meteorological parameters located on another layer. The sensitivity and accuracy of predicted results have been explored. The input vector mainly consists of spatial–temporal information and meteorological parameters at multiple layers with the altitudes of h0, h1, and h2, which implies the feature of selected meteorological parameters over a wide vertical range at a specific time on a complete path.
During the modeling process, the design of MLP and the selection of corresponding parameters will also greatly influence the prediction accuracy of the training data, so the related parameters need to be adjusted systematically. The section for MLP design mainly includes the activation function, loss function, optimization algorithm, and network structure [].
- (1)
- Activation Function
In the hidden layer of MLP, the activation function is to introduce nonlinear changes to enhance the approximation ability of the neural network []. It uses differentiable functions and a back-propagation algorithm for effective learning. The most commonly used activation functions include rectified linear unit (ReLU), logistic sigmoid function, radial basis function (RBF), etc. In this paper, ReLU was used so that it can be tuned in a biomimetic way. The problem of gradient explosion and gradient disappearance is avoided by more efficient gradient descent and backpropagation []. ReLU function can be expressed as
where x is the input data that the neuron received.
- (2)
- Loss Function
In addition to the activation function, the loss function also needs to be defined to evaluate the difference between the output of the current network and the expected result. The network will update the weight parameter automatically according to the difference so that the whole network can fit the nonlinear mapping relationship as much as possible.
The general loss function mainly includes mean squared error (MSE), cross-entropy (CE), etc. The CE function is usually chosen when facing the problem of image classification and recognition. MSE is mainly used to deal with data prediction and inversion, as in this paper, and its calculation function is
where n is the dataset number, is the measured EDH, and is the predicted EDH.
- (3)
- Optimization Algorithm
The original intention of the optimization algorithm is to define the parameters to be optimized, to create the objective function, to set the learning rate, etc. Then, the descent gradient is calculated and iterated according to the gradient.
Stochastic gradient descent with momentum (SGDM) and adaptive moment estimation (Adam) are the most commonly used optimization algorithms []. SGDM can reach the optimal global solution, but it has strict requirements on the learning rate and is easy to stop at the saddle point, which is suitable for reliable initialization parameters. Meanwhile, with the progress of training, the speed of the SGDM method will slow down and the learning rate needs to be manually adjusted. Sometimes, it will converge to the optimal local value and the training results will also be affected. Adam has the advantages of fast speed, small memory requirements, and adaptive learning rates for different parameters. It is good at handling sparse gradients and non-stationary objects and is more suitable for large datasets and high-dimensional spaces to be processed in this paper. Using the Adam function will eventually converge to the optimal global value by automatically adjusting the learning rate. Therefore, the Adam function is finally selected as the optimization algorithm given the inversion problem to be solved in this paper. The initial learning rate is set as 0.0001.
- (4)
- Network Structure
MLP introduces one-to-multiple hidden layers based on the single-layer neural network; the appropriate hidden layers can be selected according to the original intention.
For the data input module, the hold-out method [] was used to randomly divide the 476 sets of measurements into fixed mutually exclusive datasets; the proportion is 70% in the training set and 30% in the testing set. To avoid the impact of deviations introduced in the partitioning process, we tried to maintain the spatial and temporal consistency of the training and the testing set. The first 334 groups of data in about 12 round trips were selected and randomly reordered as training datasets and the remaining 142 groups of data were used as a testing dataset.
The selection of hyperparameters is complicated and engineering work and network hyperparameters, including the hidden layers, the number of neurons in each layer, the batch size, and the number of training epochs, are introduced during the modeling process. The number of hidden layers is essential to the hyperparameter in the MLP design, which is directly related to the function approximation capability of the network. However, excessive hidden layers may lead to overfitting by learning extra characteristics of the training datasets. Therefore, in the parameter adjustment experiment, we explored the parameter ranges during the parameter selection: the number of hidden layers (1-8) and the number of neurons per hidden layer (1-300). In the end, we selected an MLP with four hidden layers by a large number of computer experiments; the neurons in each layer were 100, 50, 20, and 5, respectively.
When constructing the EDH prediction model, it is necessary to consider that its design performs well on training data and can generalize on new input datasets. A deep learning model with too many parameters and few training datasets is easily overfitting during the training progress. The specific performance of overfitting is as follows: the loss function of the model is small in the training data and the prediction accuracy is high; however, the loss function of the testing data is relatively large and the prediction accuracy is low. In deep learning, regularization strategies are designed to reduce test errors, which may come at the expense of increasing training errors.
- (1)
- Early stopping
The regularization strategy most commonly used in deep learning is called early stopping. When the training has sufficient representation ability and even overfits the model, the training error will gradually decrease with time, but the verification error will rise as a consequence. The early stopping strategy means storing a copy of the model parameters after each validation error improvement. The algorithm terminates when the validation error does not improve further within a predetermined number of cycles.
- (2)
- L2 regularization
L2 regularization is one of the means to prevent overfitting. The model complexity is controlled by limiting the parameter range space, thus overfitting can be avoided. In this paper, L2 regularization is adopted for the convenience of derivation and optimization.
- (3)
- Dropout
Dropout can be a choice for training deep neural networks. The concept of dropout makes the model more generalized by stopping the activation of a particular neuron with a certain probability, thus it will not fully connect to local features. In addition, the interaction between neurons in the hidden layer can be reduced.
4. Results and Discussion
To evaluate the accuracy and improvement of the prediction model, we introduced three evaluating standards as follows: (1) bias, which reflects the deviation from the measurements; (2) variance, which reflects the stability and robustness of the prediction model; (3) improvement, which reflects the enhancement compared with the original model. Meanwhile, three performance indexes were also introduced to measure better the bias of multi-dimensional EDH prediction models: the RMSE, the mean absolute error (MAE), and the coefficient of determination (R2). In addition, the variance of prediction error (Var) and the improvement (σ) are also used to assess the accuracy of predictions. The definitions and characteristics of these indexes are listed in Table 4.

Table 4.
Equation and characteristics of the performance criteria.
4.1. Generalization Performance of Spatial–Temporal Models Based on MLP
In order to better analyze the robustness of the trained model, testing datasets were used for prediction accuracy analysis. Meanwhile, the number of floating-point operations (FLOPs) is utilized to compare the computational load of the algorithm, considering that the number of input parameters used for models (9)–(13) is different []. The analysis results are shown in Figure 6 and Figure 7 and Table 5.
where I and O are the input and output neuron numbers.
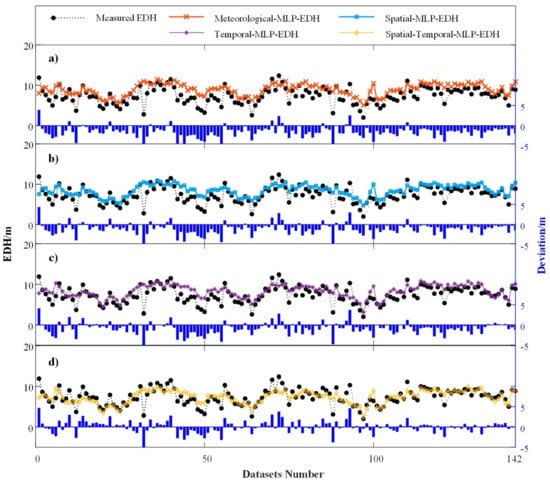
Figure 6.
Generalization performance of the EDH prediction models based on MLP.
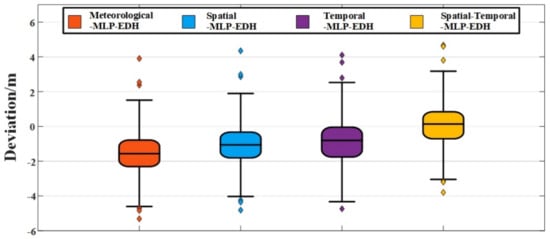
Figure 7.
Statistical results of EDH prediction models based on MLP.

Table 5.
Equation and characteristics of the performance criteria.
It can be seen that:
- (1)
- In Figure 6a, the trained meteorological-MLP-EDH model with the same input parameters as the NPS model has a better-matched degree with the measured data. The RMSE decreases from 4.67 m to 2.15 m and the percentage improvement reaches 54.00%. In addition, the MAE and variance all improve, while the coefficient of determination R2 remains at a low level with the promotion of the MLP. The RMSE of the meteorological-MLP-EDH model exceeds 2 m so that the maximum variation of transmission loss at 500 km could exceed 120 dB, according to Figure 1.
- (2)
- The prediction curve of the model fits much closer to the measurements by continuously adding spatial information (such as latitude and longitude) and temporal information (such as UT). The blue bar in the diagram, which symbolizes absolute deviation, gradually decreases. While the RMSE in Figure 6d has been greatly improved, the RMSE of the spatial-MLP-EDH, the temporal-MLP-EDH, and the spatial–temporal-MLP-EDH is 1.84 m, 1.75 m, and 1.54 m, and the coefficient R2 has also made furtherly progress. The corresponding percentage improvement reached 60.53%, 62.53%, and 66.96%, respectively. Notably, introducing spatial and temporal parameters has little effect on the variation results. In Figure 6 and Table 5, the spatial–temporal-MLP-EDH essentially agrees with the measured EDH, but it still fails to match the local maximum.
- (3)
- The statistical results in Figure 7 show the deviation variation of the abovementioned models. The box of each frequency represents the upper and the lower quartiles of the deviations and the horizontal line in the middle of the box is the median of deviations. The black line connected with the colored box shows the confidence interval of the deviations. Diamond symbols of corresponding colors represent outliers that deviate from the confidence range. The variation range of each model changes on a small scale, but the median value of deviation changes from -1.57 m of the meteorological-MLP-EDH model to 0.13 m of the spatial–temporal-MLP-EDH model, which is essentially in agreement with the measurements on a large scale.
Overall, the model has excellent generalization ability after training 70% of the original datasets and maintains good consistency in the testing datasets. Overall, the EDH prediction model based on MLP can maintain good consistency with the measurements at a large scale. However, a significant difference exists when predicting small-scale fluctuations, such as local maximum and minimum. Moreover, an optimization model with low bias and variance is always preferable based on MLP.
The training and testing datasets were collected from 20 repeated trips along one path and the experiment time was covered diurnal cycles. With the spatial parameters of the experimental positions with latitude and longitude and temporal parameters every 6 h in the MAGIC campaign introduced, the prediction accuracy of the model is gradually improved, indicating that the spatial and temporal variability is significant. By extracting much more “hidden information” from “extra data” in the training process, the spatial variability of the three-dimensional geographic information and the temporal variability of the diurnal cycles are repeatedly learned and memorized based on the MLP method. With the constructed multi-dimensional deep learning model, the geographic and time domain feature can be extracted, which supplies an improvement in EDH prediction.
4.2. Generalization Performance of Multilayer Model Based on MLP
The RMSE of the spatial–temporal-MLP-EDH model has improved to 1.54 m and the parameters as a coefficient of determination and variance of prediction error still have room for improvement. Adding the temperature, RH, and wind speed at an additional height, new datasets with the original parameters may improve prediction accuracy. The comparison results with measured data, EDH predicted by the NPS model, and the multilayer-MLP-EDH model are shown in Figure 8.
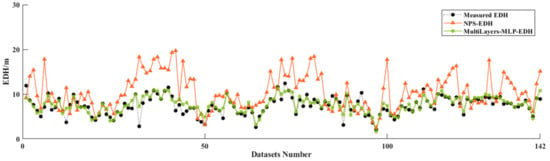
Figure 8.
Generalization performance of the multilayer-MLP-EDH model.
The variance achieves another reduction with meteorological parameters in multilayers and decreases to 1.02 m. The trained model can match the trend of measurements at a large scale; meanwhile, the maximum and minimum values of the measurements at a small scale can also become significantly matched. According to statistical analysis, the RMSE of the multilayer-MLP-EDH method reached 1.05 m and the improvement percentage reached 77.51%, compared with the NPS model. Furthermore, the computational load of this algorithm (FLOPs) is 2.27 times as much as the meteorological-MLP-EDH model, which reached 8.64 × 1013.
The overall trend of predicted EDH by NPS differs significantly from the measurements, mainly because air–sea coupling conditions limit the NPS model. The prediction accuracy is hard to maintain when the air–sea temperature difference (ASTD) is greater than 0 []. Table 6 shows the statistical RMSEs in stable and unstable conditions, and the prediction error of the NPS model increases when ASTD > 0. The multilayer-MLP-EDH method is maintained in RMSE, which reflects the consistency of the proposed method in dealing with different conditions.

Table 6.
The statistical RMSEs in different conditions.
As shown in Figure 9, the fitting line between the predicted and the measured data changes from y = 0.42 x + 5.52 of the NPS model to y = 0.93 x + 0.99, close to y =x. Therefore, this method has better operability by setting meteorological instruments at two different heights (the cabin and the deck, for instance). The EDH predicted error could reach nearly 1 m combined with the sea surface meteorological parameters.
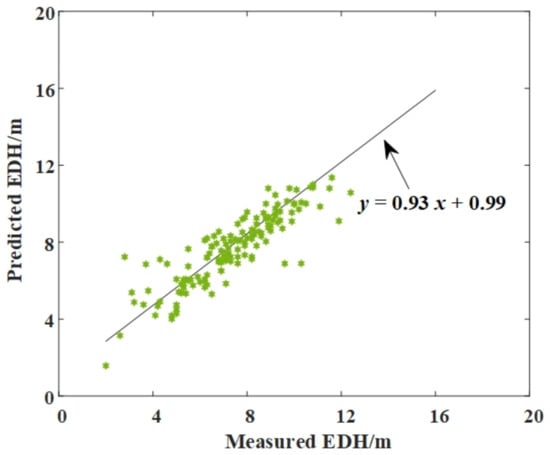
Figure 9.
Scatter plot of measured EDH against modeled EDH using the multilayer-MLP-EDH model.
The predicted RMSE of EDH of the theoretical method is 4.67 m, which may lead to the uncertainty range of path loss exceeding 120 dB at the 500 km transmission range. For instance, as shown in Figure 1, the path loss can increase from the original design of 179.12 dB at a predicted EDH of 11 m to exceed 300 dB at a true EDH of nearly 6 m. This state will leave the transmission system in an unstable situation. However, a significant improvement arises when single-layer models based on MLP become involved. The predicted deviation of EDH decreases to 1.54–2.15 m, corresponding to a path loss variation from 162.20 to 213.12dB. The prediction accuracy of the evaporation duct channel continues to improve with multilayers. Furthermore, the uncertainty of path loss is reduced by 16.92 dB on the single-layer models. Therefore, the multilayer-MLP-EDH model can be essential in designing a communication system using the evaporation duct.
Table 7 provides a summary and comparison of the performance of EDH prediction, with the AI method introduced. From the comparison results, the four-dimensional regression function multilayer-MLP-EDH with meteorological parameters located on another layer proposed in this paper has the advantage of extracting the spatial–temporal information and the meteorological parameters at multiple altitudes in the training process. At the same time, a wider application range, higher precision, and model generalization are also achieved. Furthermore, the proposed model has great potential for enhancing the communication quality, reliability, and efficiency of ducting in evaporation ducts.

Table 7.
Comparison of different models in EDH prediction.
5. Conclusions
Low altitude atmospheric refractive conditions significantly affect the performance of shipboard communications at sea and near shore []. The accurate prediction of the EDH is thus crucial in the demonstration, design, development, operation, and maintenance management of the communication system under this mechanism. Based on the MLP deep-learning method, the multidimensional deep-learning model was proposed to improve the prediction accuracy of EDH. First, the meteorological-MLP-EDH model was designed, which improved the prediction accuracy by 54.00%, with the same input parameters as the NPS model. The spatial–temporal-MLP-EDH model has gone one step further by superimposing the spatial–temporal “extra data” in the experiment. As a result, it can be essentially in agreement with measurements at large scales and the predicted RMSE is 1.54 m, with a 66.96% percentage improvement compared with the NPS model. Lastly, the multilayer-MLP-EDH model with the temperature, RH, and wind speed at an additional height was trained, significantly matching measurements at large and small scales. According to statistical results, the predicted RMSE can reach 1.05 m and the percentage improvement reached 77.51%.
The proposed model in this paper can break through the limitations of theoretical models by extracting much more “hidden information” from “extra data” in the training process, significantly improving EDH prediction accuracy. As a result, the proposed model has great potential for enhancing the communication quality, reliability, and efficiency of ducting in evaporation ducts.
The models constructed in this paper are based on 476 sets of MAGIC data in the Pacific Ocean; the training and testing datasets are limited to a sea area of 21.2197°N, 33.6001°N, 118.3299°W, 157.7416°W at specific experimental time intervals. Future experiments should be performed to more completely validate the models. In addition, measurements should be made at comprehensive coverage, massive data acquisition, and high spatial and temporal resolution to improve the constructed model. Furthermore, the distribution of EDH in high precision, detailed resolution, and broad coverage with the improved proposed model would be valuable to the communication system using evaporation ducts over the ocean.
Author Contributions
C.Y.: conceptualization (equal); data curation (equal); investigation (equal); methodology (equal); software (equal); validation (equal); visualization (equal); writing—original draft (equal); writing—review and editing (equal). J.W.: conceptualization (equal); data curation (equal); investigation (equal); methodology (equal); software (equal); validation (equal); visualization (equal); writing—original draft (equal); writing—review and editing (equal). Y.S.: data curation (equal); investigation (equal); software (equal); validation (equal); visualization (equal); writing—initial draft (supporting). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 62031008) and the State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information Systems (No. CEMEE2022G0201, CEMEE-002-20220224).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The MAGIC data used for the analyses were obtained from the Atmospheric Radiation Measurement (ARM) Program (https://www.arm.gov/research/campaigns/amf2012magic (accessed on 18 February 2022)).
Acknowledgments
The authors would like to acknowledge the reviewers for their constructive comments and suggestions to improve this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Danklmayer, A.; Förster, J.; Fabbro, V.; Biegel, G.; Brehm, T.; Colditz, P.; Castanet, L.; Hurtaud, Y. Radar Propagation Experiment in the North Sea: The Sylt Campaign. IEEE Trans. Geosci. Remote Sens. 2018, 56, 835–846. [Google Scholar] [CrossRef]
- Huang, L.F.; Liu, C.G.; Wang, H.G.; Zhu, Q.L.; Zhang, L.J.; Han, J.; Zhang, Y.S.; Wang, Q.N. Experimental Analysis of Atmospheric Ducts and Navigation Radar Over-the-Horizon Detection. Remote Sens. 2022, 14, 2588. [Google Scholar] [CrossRef]
- Gilles, M.A.; Earls, S.; Bindel, D. A Subspace Pursuit Method to Infer Refractivity in the Marine Atmospheric Boundary Layer. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5606–5617. [Google Scholar] [CrossRef]
- Woods, G.S.; Ruxton, A.; Huddlestone-Holmes, C.; Gigan, G. High-Capacity, Long-Range, Over Ocean Microwave Link Using the Evaporation Duct. IEEE J. Ocean. Eng. 2009, 34, 323–330. [Google Scholar] [CrossRef]
- Wang, J.; Yang, C.; Yan, N.N. Study on digital twin channel for the B5G and 6G communication. Chin. J. Radio Sci. 2021, 36, 340–348. [Google Scholar]
- Kim, S.M.; Kim, J.; Han, C.; Min, S.S.; Kim, S.L. Opportunism in Spectrum Sharing for Beyond 5G With Sub-6 GHz: A Concept and Its Application to Duplexing. IEEE Access 2020, 8, 148877–148891. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, H.; Ye, L.; Qiang, S.; Chen, X. Wireless Channel Models for Maritime Communications. IEEE Access 2018, 6, 68070–68088. [Google Scholar] [CrossRef]
- Zaidi, K.S.; Jeoti, V.; Awang, A. Wireless backhaul for broadband communication over Sea. In Proceedings of the 2013 IEEE 11th Malaysia International Conference on Communications (MICC), Kuala Lumpur, Malaysia, 26–28 November 2013; pp. 298–303. [Google Scholar]
- Babin, S.M.; Young, G.S.; Carton, J.A. A new model of the oceanic evaporation duct. J. Appl. Meteorol. Climatol. 1997, 36, 193–204. [Google Scholar] [CrossRef]
- Babin, S.M.; Dockery, G.D. LKB-Based Evaporation Duct Model Comparison with Buoy Data. J. Appl. Meteorol. Climatol. 2002, 41, 434–446. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, K.; Yang, Y.; Ma, Y. A new evaporation duct climatology over the South China Sea. J. Meteorol. Res. 2015, 41, 764–778. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J.; Ma, J.G. Exploration of X-band Communication for Maritime Applications in the South China Sea. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 481–485. [Google Scholar] [CrossRef]
- Zhao, X.F.; Wang, D.X.; Huang, S.X.; Huang, K.; Chen, J. Statistical estimations of atmospheric duct over the South China Sea and the Tropical Eastern Indian Ocean. Chin. Sci. Bull. 2013, 58, 2794–2797. [Google Scholar] [CrossRef]
- Yan, X.; Yang, K.; Ma, Y. Calculation Method for Evaporation Duct Profiles Based on Artificial Neural Network. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2274–2278. [Google Scholar] [CrossRef]
- Fountoulakis, V.; Earls, C. Inverting for Maritime Environments Using Proper Orthogonal Bases From Sparsely Sampled Electromagnetic Propagation Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7166–7176. [Google Scholar] [CrossRef]
- Wang, Q.; Burkholder, R.J.; Yardim, C.; Xu, L.Y.; Pozderac, J.; Fernando, H.J.S.; Alappattu, D.P.; Wang, Q. Range and Height Measurement of X-Band EM Propagation in the Marine Atmospheric Boundary Layer. IEEE Trans. Antennas Propag. 2019, 67, 2063–2073. [Google Scholar] [CrossRef]
- Tian, B.; Han, L.; Kong, D.W.; Liu, C.G.; Zhou, M.; Yu, M.H. Study on Wireless Detection Using the Pseudo-Refractivity Model. In Proceedings of the 2012 8th International Conference on Wireless Communications, Networking and Mobile Computing, Shanghai, China, 21–23 September 2012; pp. 1–4. [Google Scholar]
- Wang, H.; Wu, Z.; Kang, S.; Zhao, Z. Monitoring the Marine Atmospheric Refractivity Profiles by Ground-Based GPS Occultation. IEEE Geosci. Remote Sens. Lett. 2013, 10, 962–965. [Google Scholar] [CrossRef]
- Karimian, A.; Yardim, C.; Gerstoft, P.; Hodgkiss, W.S.; Barrios, A.E. Refractivity estimation from sea clutter: An invited review. Radio Sci. 2011, 46, 1–16. [Google Scholar] [CrossRef]
- Bussey, H.E.; Birnbaum, G. Measurement of variations in atmospheric refractive index with an airborne microwave refractometer. J. Res. Nat. Bur. Stand. 1953, 51, 171–178. [Google Scholar] [CrossRef]
- Rowland, J.R.; Babin, S.M. Fine-scale measurements of microwave refractivity profiles with helicopter and low-cost rocket probes. Johns Hopkins APL Tech. Dig 1987, 8, 413–417. [Google Scholar]
- Paulus, R.A. Practical application of an evaporation duct model. Radio Sci. 1985, 20, 887–896. [Google Scholar] [CrossRef]
- Musson-Genon, L.; Gauthier, S.; Bruth, E. A simple method to determine evaporation duct height in the sea surface boundary layer. Radio Sci. 1992, 27, 635–644. [Google Scholar] [CrossRef]
- Frederickson, P.A.; Davidson, K.L.; Goroch, A.K. Operational Bulk Evaporation Duct Model for MORIAH Version 1.2; Naval Postgraduate School: Monterey, CA, USA, 2000. [Google Scholar]
- Beljaars, A.C.M.; Holtslag, A.A.M. Flux parameterization over land surfaces for atmospheric models. J. App. Meteorol. 1991, 30, 327–341. [Google Scholar] [CrossRef]
- Grachev, A.A.; Andreas, E.L.; Fairall, C.W.; Guest, P.S.; Persson, P.O.G. SHEBA flux–profile relationships in the stable atmospheric boundary layer. Bound.-Layer Meteor. 2007, 124, 315–333. [Google Scholar] [CrossRef]
- Han, J.; Wu, J.; Zhu, Q.; Wang, H.; Zhou, Y.; Jiang, M.; Zhang, S.; Wang, B. Evaporation Duct Height Nowcasting in China’s Yellow Sea Based on Deep Learning. Remote Sens. 2021, 13, 1577. [Google Scholar] [CrossRef]
- Zhu, X.; Li, J.; Zhu, M.; Jiang, Z.; Li, Y. An Evaporation Duct Height Prediction Method Based on Deep Learning. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1307–1311. [Google Scholar] [CrossRef]
- Zhao, W.; Zhao, J.; Li, J.; Zhao, D.; Huang, L.; Zhu, J.; Lu, J.; Wang, X. An evaporation duct height prediction model based on a Long Short-Term Memory Neural Network. IEEE Trans. Antennas Propag. 2021, 69, 7795–7804. [Google Scholar] [CrossRef]
- Mai, Y.; Sheng, Z.; Shi, H.; Li, C.; Liao, Q.; Bao, J. A New Short-Term Prediction Method for Estimation of the Evaporation Duct Height. IEEE Access 2020, 8, 136036–136045. [Google Scholar] [CrossRef]
- Vaisala MARWIN Sounding System MW32 Features. Available online: https://www.vaisala.com/en/products/weather-environmental-sensors/marwin-sounding-system-mw32 (accessed on 1 May 2021).
- Recommendation ITU-R P.453-14 The Radio Refractive Index: Its Formula and Refractivity Data. Available online: https://www.itu.int/rec/R-REC-P.453-14-201908-I/en (accessed on 8 March 2020).
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Grachev, A.A.; Fairall, C.W. Dependence of the Monin–Obukhov Stability Parameter on the Bulk Richardson Number over the Ocean. J. Appl. Meteorol. Climatol. 1997, 36, 406–415. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Q.; Wang, S.; Yang, K.; Ma, Y. Impact of Typhoon on Evaporation Duct in the Northwest Pacific Ocean. IEEE Access 2019, 7, 109111–109119. [Google Scholar] [CrossRef]
- Recommendation ITU-R P.525-4 Calculation of Free-Space Attenuation. Available online: https://www.itu.int/dms_pubrec/itu-r/rec/p/R-REC-P.525-4-201908-I!!PDF-E.pdf (accessed on 17 October 2020).
- Recommendation ITU-R P.2001-4 A General Purpose Wide-Range Terrestrial Propagation Model in the Frequency Range 30 MHz to 50 GHz. Available online: https://www.itu.int/rec/R-REC-P.2001-4-202109-I/en (accessed on 4 January 2022).
- Ozgun, O.; Apaydin, G.; Kuzuoglu, M.; Sevgi, L. PETOOL: MATLAB-Based One-Way and Two-Way Split-Step Parabolic Equation Tool for Radiowave Propagation over Variable Terrain. Comput. Phys. Commun. 2011, 182, 2638–2654. [Google Scholar] [CrossRef]
- Ozgun, O.; Sahin, V.; Erguden, M.E.; Apaydin, G.; Yilmaz, A.E.; Kuzuoglu, M.; Sevgi, L. PETOOL v2.0: Parabolic Equation Toolbox with evaporation duct models and real environment data. Comput. Phys. Commun. 2020, 256, 107454. [Google Scholar] [CrossRef]
- Dockery, G.D.; Kuttler, J.R. An improved impedance-boundary algorithm for Fourier split-step solutions of the parabolic wave equation. IEEE Trans. Antennas Propag. 1996, 44, 1592–1599. [Google Scholar] [CrossRef]
- Hardin, R.; Tappert, F. Applications of the Split-Step Fourier Method to the Numerical Solution of Nonlinear and Variable Coefficient Wave Equations. SIAM Rev. 1973, 15, 423. [Google Scholar]
- Shi, Y.; Zhang, Q.; Wang, S.W.; Yang, K.D.; Yang, Y.X.; Yan, X.D.; Ma, Y.L. A Comprehensive Study on Maximum Wavelength of Electromagnetic Propagation in Different Evaporation Ducts. IEEE Access 2019, 7, 82308–82319. [Google Scholar] [CrossRef]
- Alappattu, D.P.; Wang, Q.; Kalogiros, J. Anomalous propagation conditions over eastern Pacific Ocean derived from MAGIC data. Radio Sci. 2016, 51, 1142–1156. [Google Scholar] [CrossRef]
- Zhou, X.; Kollias, P.; Lewis, E.R. Clouds, Precipitation, and Marine Boundary Layer Structure during the MAGIC Field Campaign. J. Climate. 2015, 28, 2420–2442. [Google Scholar] [CrossRef]
- Guo, X.M.; Zhao, D.L.; Zhang, L.J.; Wang, H.G.; Kang, S.F.; Lin, L.K. C band transhorizon signal characterisations in evaporation duct propagation environment over Bohai Sea of China. IET Microw. Antennas Propag. 2019, 13, 407–413. [Google Scholar] [CrossRef]
- Ruck, D.W.; Rogers, S.K.; Kabrisky, M.; Oxley, M.E.; Suter, B.W. The multilayer perceptron as an approximation to a Bayes optimal discriminant function. IEEE Trans. Neural Networks 1990, 1, 296–298. [Google Scholar] [CrossRef]
- Isaakidis, S.A.; Dimou, I.N.; Xenos, T.D.; Dris, N.A. An artificial neural network predictor for tropospheric surface duct phenomena. Nonlinear Process. Geophys. 2007, 14, 569–573. [Google Scholar] [CrossRef]
- Sit, H.; Earls, C.J. Characterizing evaporation ducts within the marine atmospheric boundary layer using artificial neural networks. Radio Sci. 2019, 54, 1181–1191. [Google Scholar] [CrossRef]
- Zhou, Z.H. Machine Learning; Tsinghua University Press: Beijing, China, 2016. [Google Scholar]
- Minnis, P.; Mack, S.S.; Chen, Y.; Chang, F.; Yost, C.R. CERES MODIS Cloud Product Retrievals for Edition 4—Part I: Algorithm Changes. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2744–2780. [Google Scholar] [CrossRef]
- Vinod, N.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines Vinod Nair. In Proceedings of the International Conference on Machine Learning Omnipress, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Kingma, P.D.; Jimmy, B. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Molchanov, P.; Tyree, S.; Karras, T.; Aila, T.; Kautz, J. Pruning convolutional neural networks for resource efficient transfer learning. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).