DSANet: A Deep Supervision-Based Simple Attention Network for Efficient Semantic Segmentation in Remote Sensing Imagery
Abstract
1. Introduction
- (1)
- To alleviate the VHR images interpretation mistake in the age of large data, an efficient deep-layer and shallow-channel network with spatial and semantic enhancement losses (DSANet) is developed.
- (2)
- Without inference speed costs, two multiscale feature losses are proposed: improved multiscale spatial detail (MSD) and hierarchical semantic enhancement (HSE). The MSD loss is intended to improve the model’s extraction of underlying spatial information, whilst the HSE loss assists the model in understanding the observed distribution of categories.
- (3)
- The addition of the embedding attention module (EAM) decreases the attention module’s complexity from quadratic (self-attention) to linear with equivalent accuracy, as well as increasing inference speed for large images.
- (4)
- On the ISPRS Potsdam and Vaihingen benchmark data-sets, we attain outstanding results. Using an RTX 3090 GPU, we achieve mean intersection over unions (mIoUs) of 79.19% on the Potsdam test set and 72.26% on the Vaihingen test set, with a speed of 470.07 frames per second (FPS) on 512 × 512 images and 5.46 FPS on 6000 × 6000 images.
2. Related Works
2.1. Efficient Network Designs
2.2. Efficient Semantic Segmentation Methods
2.3. Information Enhancement Modules
2.4. Attention Mechanisms
3. Methodology
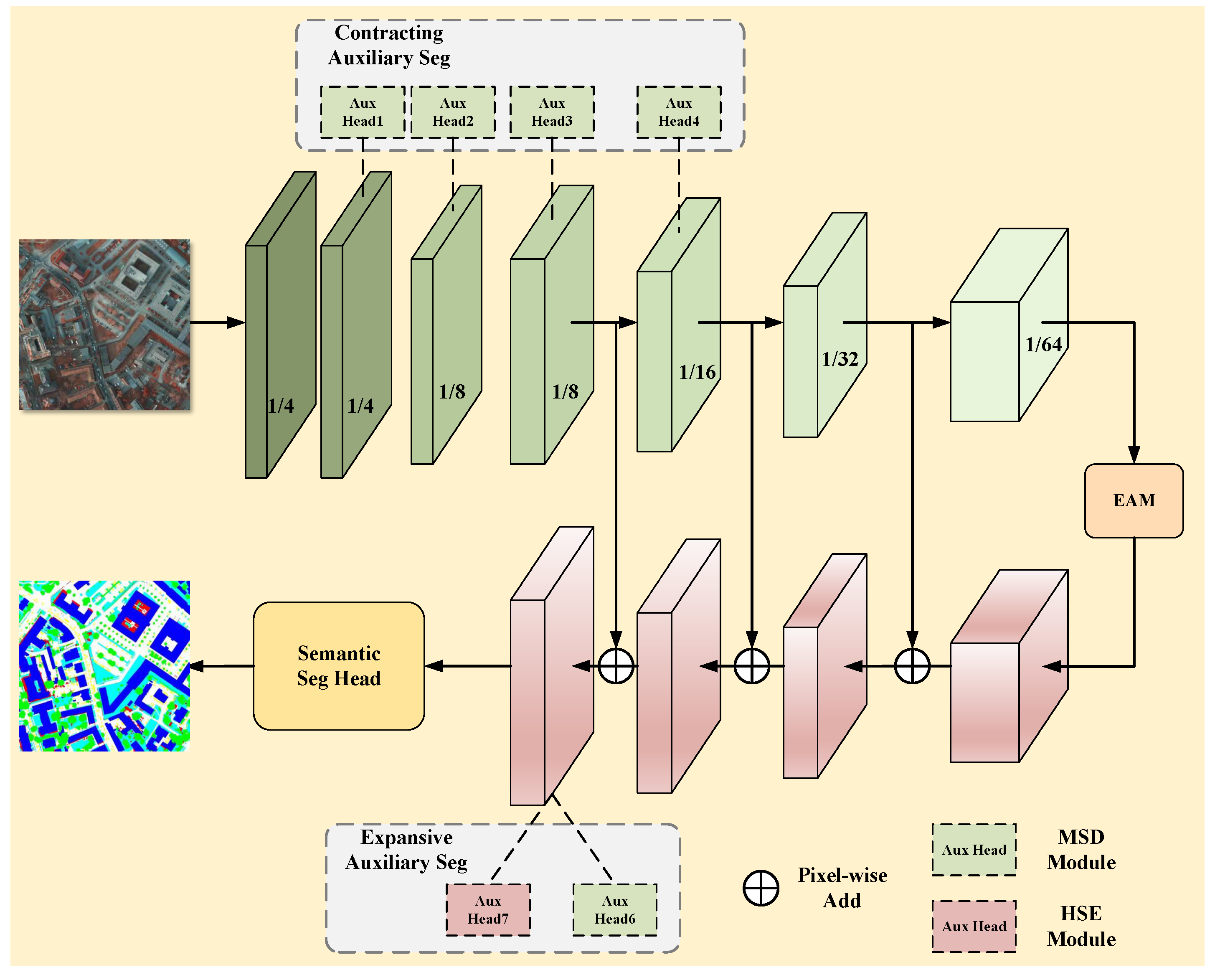
3.1. Network Architecture of the Proposed Method
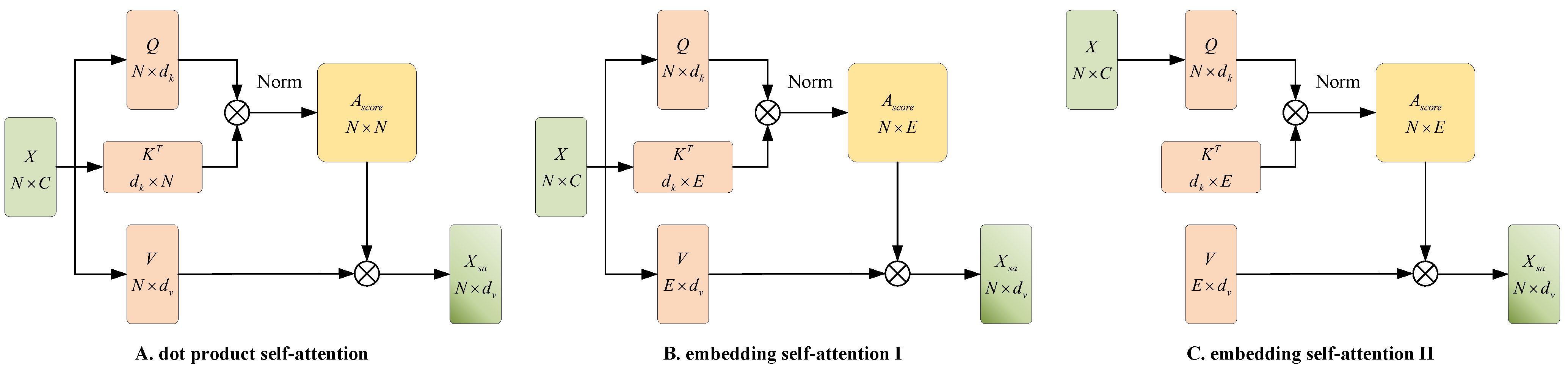
3.2. EAM
- (1)
- In accordance with the fundamental structure of self-attention, the feature vector X is linearly transformed to generate Q, K and V. The difference is that the dimensions of K and V are altered from to , where E is the embedding dimensionality. The first dimension of K and V from N to E simulates the process of selecting the top E most important elements from N. Due to probable image size changes between training and test data, N cannot be predicted in advance for the semantic segmentation task; thus, adaptively pooling the feature vector X in advance is essential to achieve N with fixed dimensions. Theoretically, without considering adaptive pooling, the computational complexity of embedding self-attention I (Figure 3B) is . In the real case, the computational complexity will be better than this value, satisfying a lower linear computational complexity.
- (2)
- Unlike the first two attentional approaches, embedding self-attention II (Figure 2C) generates only Q using the feature vectors X, while the memory K and V are pre-generated random matrices in and optimised during training phase. This strategy may successfully overcome the difficulty associated with the unpredictability of N and reduce calculation time for K and V. Due to the fact that K and V are fully independent of the feature vector X, the interactions between components are weak, making it difficult for EAM II to establish genuine attentional connections. We employ the approach in [65] to normalize the rows and columns of A independently, as it is possible that strengthening the connections between components using a single softmax function, which is often used in self-attention mechanisms, may not yield optimal results. L1 normalization is specifically applied following softmax activation. This method’s computational complexity is also . The following are the precise formulae for the softmax and L1 normalization functions.
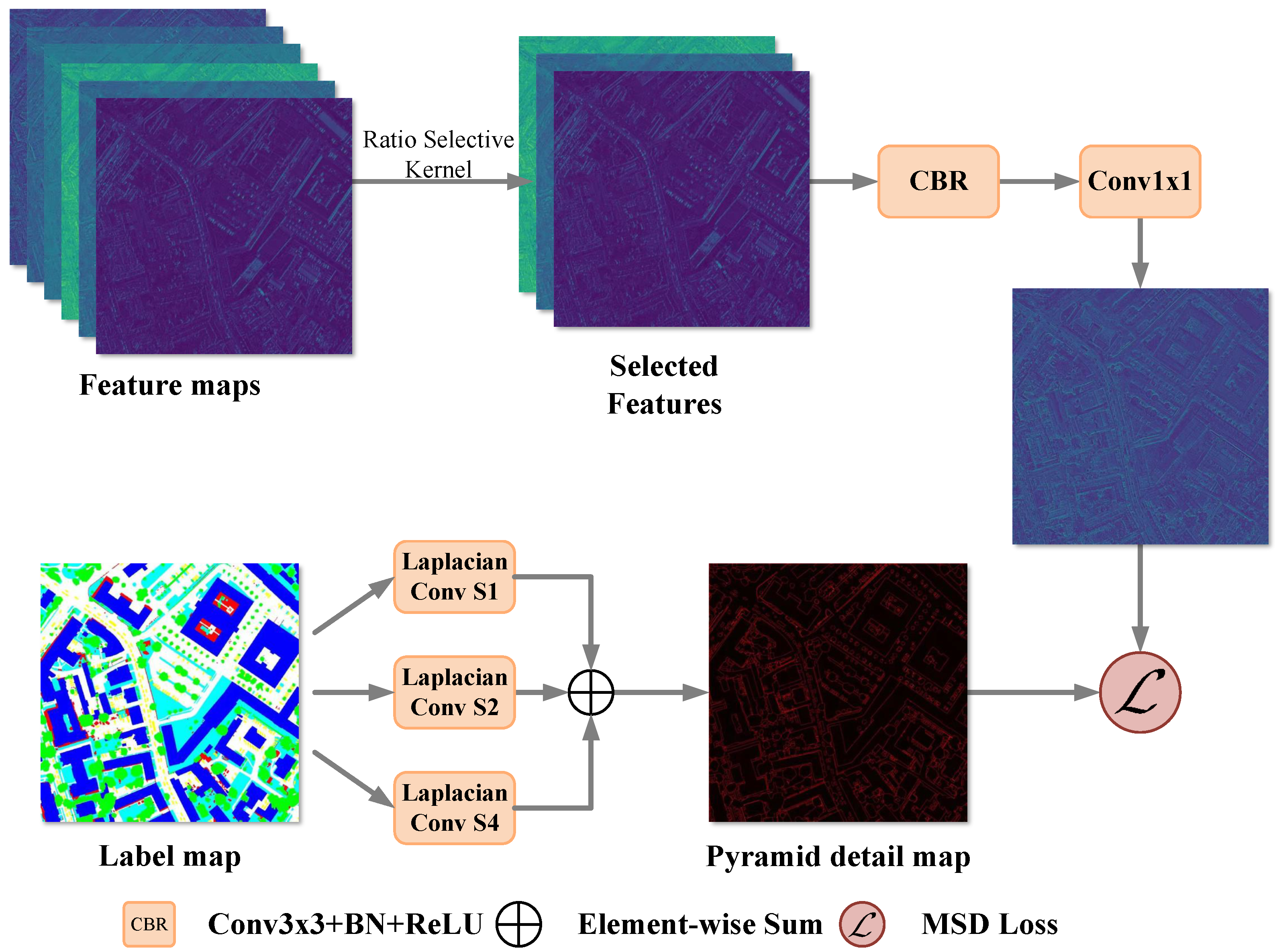
3.3. MSD Loss
3.4. HSE Loss
- (1)
- Set the hierarchical semantic boundary. Semantic boundaries at different locations can capture the distributions of categories in different local regions, and semantic boundaries at different scales can reflect the multiscale characteristics of category distribution features. Assume that boundary levels and the boundary level of n slice the label map in patches along the length and width, respectively. The label patches are set as , where is the set of feature patches in level n and .
- (2)
- Calculate the local frequency distribution. The category distribution is calculated separately for each label patch , where j is the sequence number of the label patch set.
- (3)
- Aggregate the global distribution vector. The label patches at boundary level n are concatenated to generate the global frequency distribution vector . The same processing flow is applied to the prediction map output from network stage in the decoder to obtain the vector . The HSE vector of prediction is , and that of the label map . The HSE loss is obtained by computing the BCE between the HSE vector of the prediction and the HSE vector of the label map .
| Algorithm 1: HSE loss for the deep supervision module. |
 |
4. Data Set and Experimental Details
4.1. Benchmark Description
- (1)
- ISPRS Potsdam Dataset (https://www.isprs.org/education/benchmarks/UrbanSemLab/2d-sem-label-potsdam.aspx (accessed on 2 September 2021).)
- (2)
- ISPRS Vaihingen Dataset (https://www.isprs.org/education/benchmarks/UrbanSemLab/2d-sem-label-vaihingen.aspx (accessed on 2 September 2021).)
4.2. Evaluation Metrics
4.3. Data Preprocessing and Augmentation
4.4. Implementation Details
5. Experimental Results
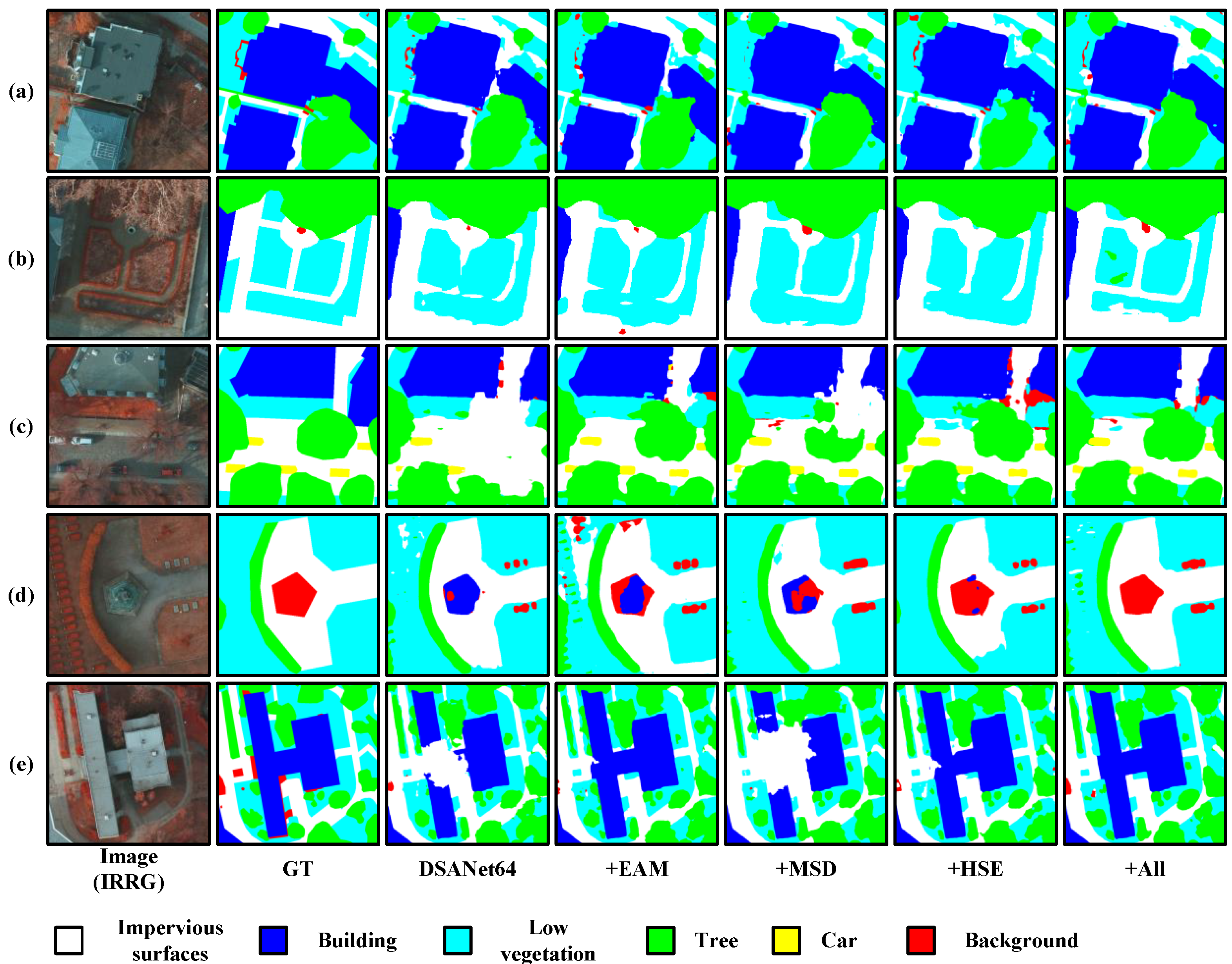
5.1. Ablation Study
5.1.1. Effectiveness of the EAM
5.1.2. Effectiveness of the MSD loss and HSE loss
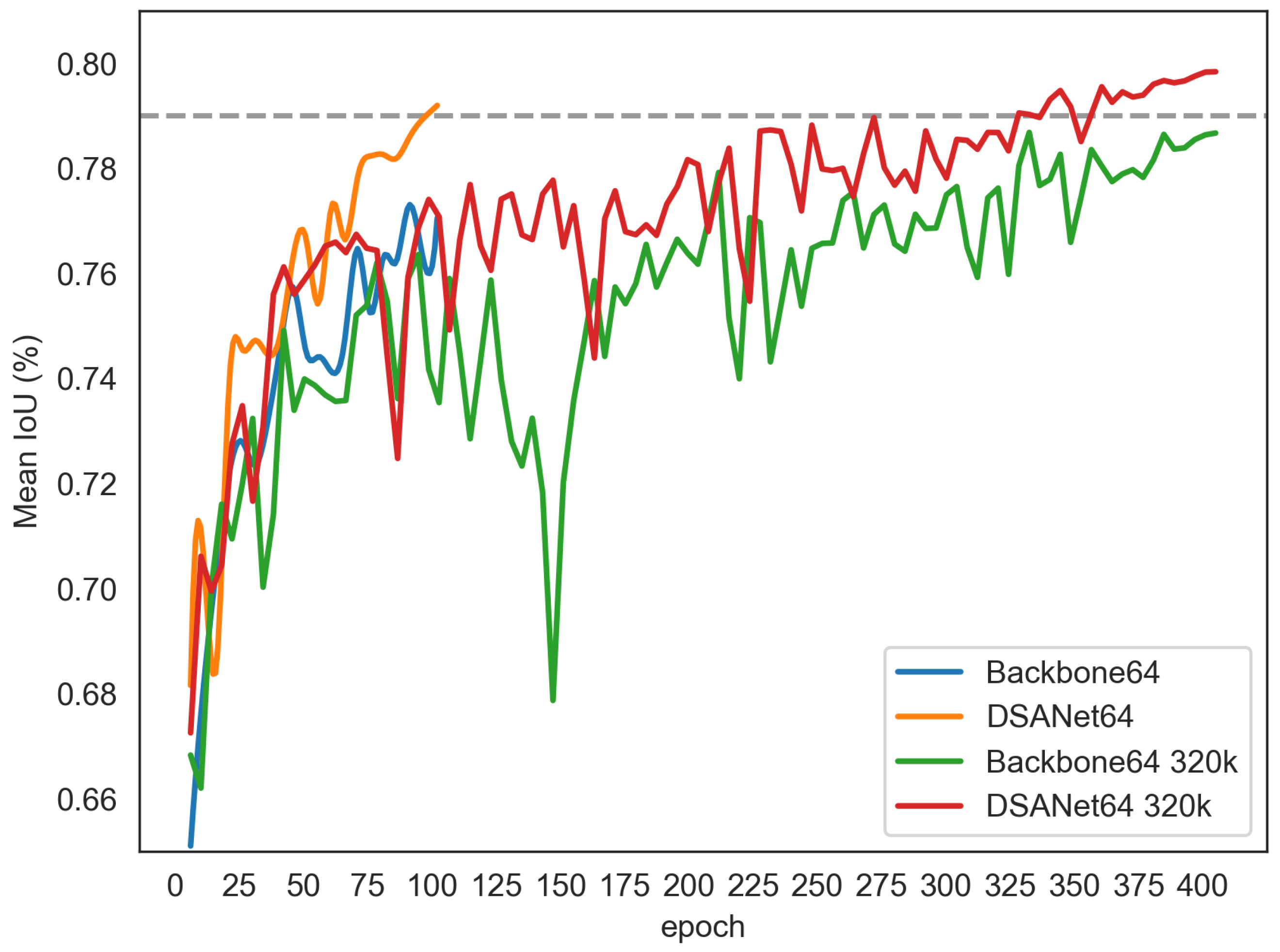
5.1.3. Effectiveness of DSANet
5.2. Qualitative Analysis of Features
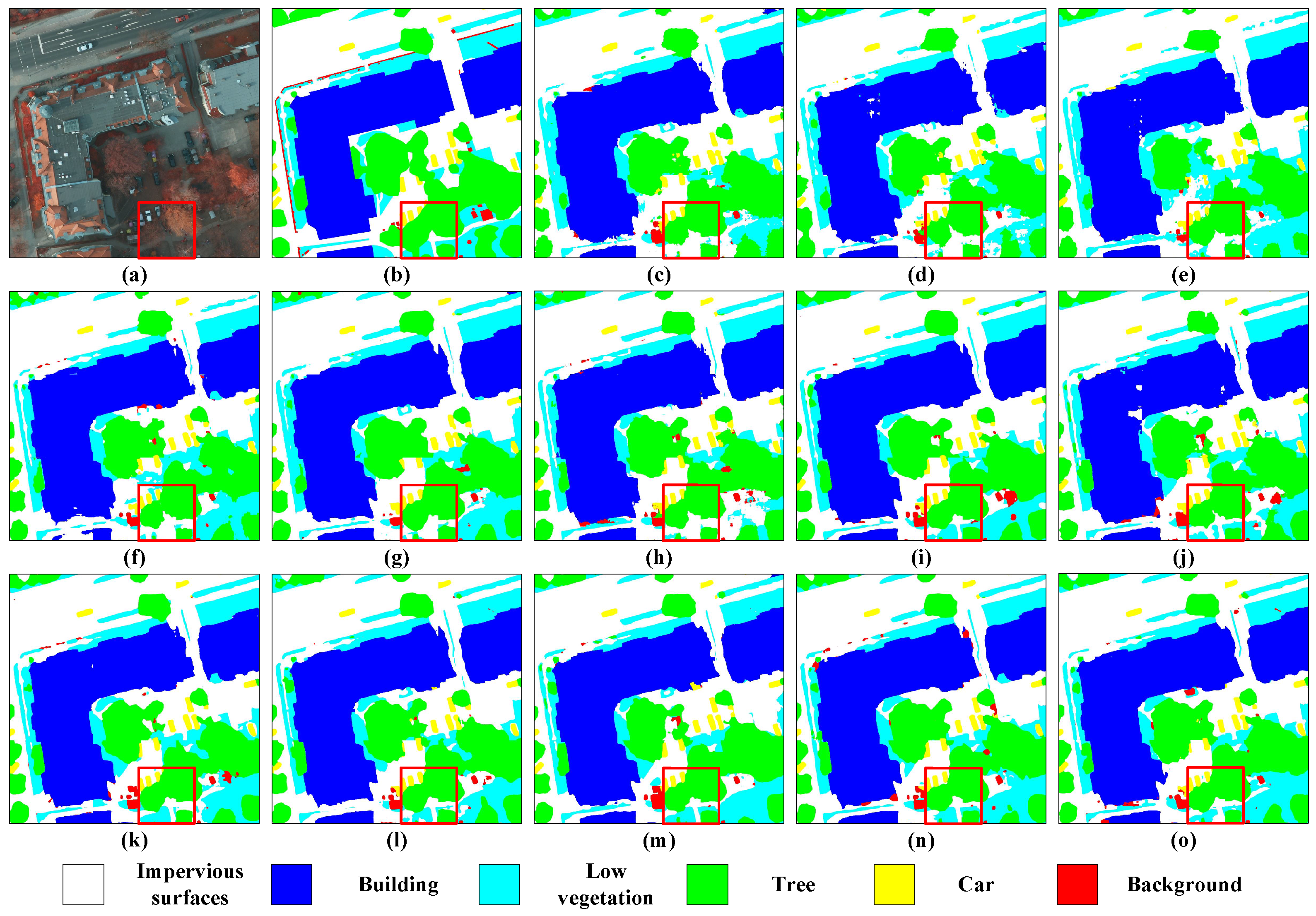
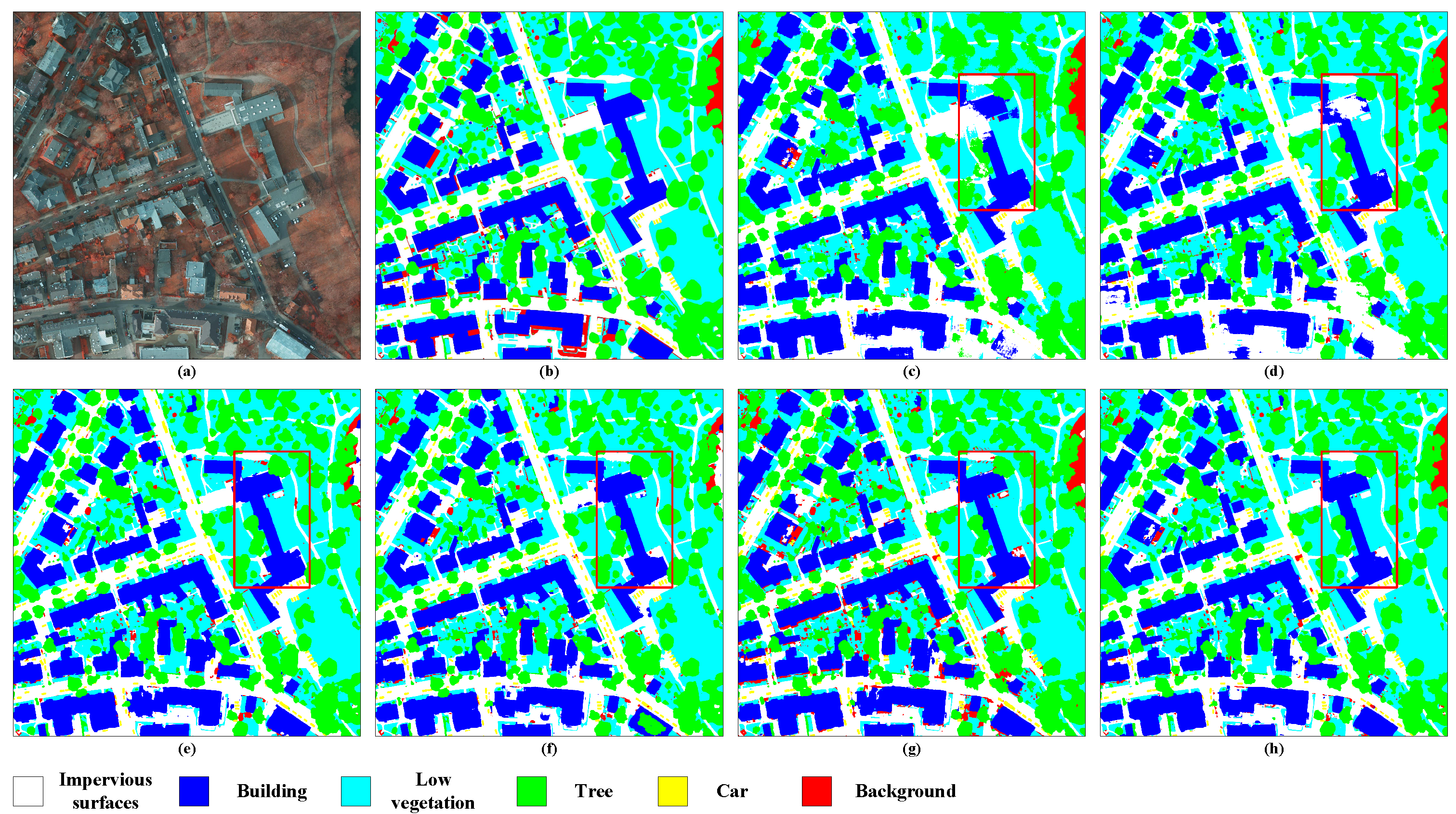
5.3. Quantitative Comparison with State-of-the-Art Methods
5.3.1. Segmentation Performances Achieved on the Potsdam Dataset
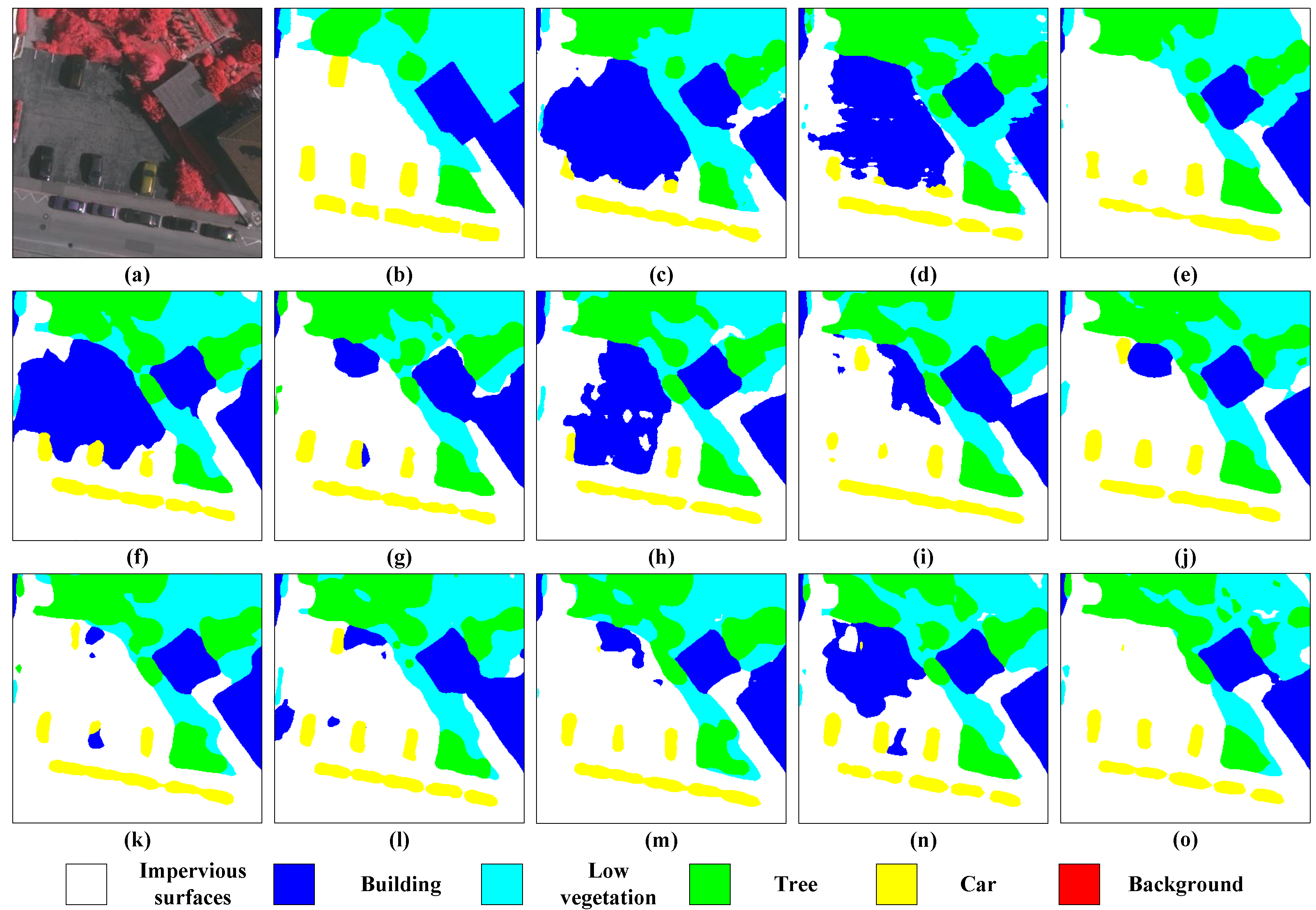
5.3.2. Segmentation Performances Achieved on the Vaihingen Dataset
5.3.3. Inference Speeds
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| RSIs | Remote Sensing Images |
| VHR | Very High-resolution |
| EAM | Embedding Attention Module |
| MSD | Multiscale Spatial Detail |
| HSE | Hierarchical Semantic Enhancement |
| mIoU | Mean Intersection over Union |
| FPS | Frames Per Second |
| FLOPs | Floating Point Operations |
References
- Liu, P. A survey of remote-sensing big data. Front. Environ. Sci. 2015, 3, 5. [Google Scholar] [CrossRef]
- Laney, D. 3D data management: Controlling data volume, velocity and variety. META Group Res. Note 2001, 6, 1. [Google Scholar]
- der Sande, C.V.; Jong, S.D.; Roo, A.D. A segmentation and classification approach of IKONOS-2 imagery for land cover mapping to assist flood risk and flood damage assessment. Int. J. Appl. Earth Obs. Geoinf. 2003, 4, 217–229. [Google Scholar] [CrossRef]
- Costa, H.; Foody, G.M.; Boyd, D.S. Supervised methods of image segmentation accuracy assessment in land cover mapping. Remote Sens. Environ. 2018, 205, 338–351. [Google Scholar] [CrossRef]
- Im, J.; Jensen, J.; Tullis, J. Object-based change detection using correlation image analysis and image segmentation. Int. J. Remote Sens. 2008, 29, 399–423. [Google Scholar] [CrossRef]
- Chen, G.; Hay, G.J.; Carvalho, L.M.; Wulder, M.A. Object-based change detection. Int. J. Remote Sens. 2012, 33, 4434–4457. [Google Scholar] [CrossRef]
- Du, S.; Du, S.; Liu, B.; Zhang, X. Mapping large-scale and fine-grained urban functional zones from VHR images using a multi-scale semantic segmentation network and object based approach. Remote Sens. Environ. 2021, 261, 112480. [Google Scholar] [CrossRef]
- Wang, J.; Hu, X.; Meng, Q.; Zhang, L.; Wang, C.; Liu, X.; Zhao, M. Developing a method to extract building 3d information from GF-7 data. Remote Sens. 2021, 13, 4532. [Google Scholar] [CrossRef]
- Li, P.; Guo, J.; Song, B.; Xiao, X. A multilevel hierarchical image segmentation method for urban impervious surface mapping using very high resolution imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 4, 103–116. [Google Scholar] [CrossRef]
- Miao, Z.; Fu, K.; Sun, H.; Sun, X.; Yan, M. Automatic water-body segmentation from high-resolution satellite images via deep networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 602–606. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Zhang, Z.; Liu, Q.; Wang, Y. Road extraction by deep residual u-net. IEEE Geosci. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef]
- Heidler, K.; Mou, L.; Baumhoer, C.; Dietz, A.; Zhu, X.X. Hed-unet: Combined segmentation and edge detection for monitoring the antarctic coastline. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Yang, J.; Guo, J.; Yue, H.; Liu, Z.; Hu, H.; Li, K. CDnet: CNN-based cloud detection for remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6195–6211. [Google Scholar] [CrossRef]
- Liu, S.; Cheng, J.; Liang, L.; Bai, H.; Dang, W. Light-weight semantic segmentation network for UAV remote sensing images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8287–8296. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Xie, S.; Gallagher, P.; Zhang, Z.; Tu, Z. Deeply-Supervised Nets. In Machine Learning Research, Proceedings of the Eighteenth International Conference on Artificial Intelligence and Statistics; Lebanon, G., Vishwanathan, S.V.N., Eds.; PMLR: San Diego, CA, USA, 2015; Volume 38, pp. 562–570. [Google Scholar]
- Deng, C.; Liang, L.; Su, Y.; He, C.; Cheng, J. Semantic segmentation for high-resolution remote sensing images by light-weight network. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 3456–3459. [Google Scholar]
- Liu, S.; Ding, W.; Liu, C.; Liu, Y.; Wang, Y.; Li, H. ERN: Edge loss reinforced semantic segmentation network for remote sensing images. Remote Sens. 2018, 10, 1339. [Google Scholar] [CrossRef]
- Yuan, W.; Xu, W. Neighborloss: A loss function considering spatial correlation for semantic segmentation of remote sensing image. IEEE Access 2021, 9, 641–675. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Maaten, L.V.D.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.-C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for mobilenetv3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Long Beach, CA, USA, 16–20 June 2019; pp. 1314–1324. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6848–6856. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.-T.; Sun, J. Shufflenet v2: Practical guidelines for efficient CNN architecture design. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 14–18 September 2018; pp. 116–131. [Google Scholar]
- Paszke, A.; Chaurasia, A.; Kim, S.; Culurciello, E. Enet: A deep neural network architecture for real-time semantic segmentation. arXiv 2016, arXiv:1606.02147. [Google Scholar]
- Li, G.; Yun, I.; Kim, J.; Kim, J. Dabnet: Depth-wise asymmetric bottleneck for real-time semantic segmentation. In Proceedings of the British Machine Vision Conference (BMVC), Cardiff, UK, 9–12 September 2019; pp. 186.1–186.12. [Google Scholar]
- Lo, S.-Y.; Hang, H.-M.; Chan, S.-W.; Lin, J.-J. Efficient dense modules of asymmetric convolution for real-time semantic segmentation. In Proceedings of the ACM Multimedia Asia, Nice, France, 21–25 October 2019; pp. 1–6. [Google Scholar]
- Romera, E.; Alvarez, J.M.; Bergasa, L.M.; Arroyo, R. Erfnet: Efficient residual factorized convnet for real-time semantic segmentation. IEEE Trans. Intell. Transp. Syst. 2017, 19, 263–272. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Z.; Wu, Q.J.; Cai, L.; Lu, D.; Li, X. Fast semantic segmentation for scene perception. IEEE Trans. Industr. Inform. 2018, 15, 1183–1192. [Google Scholar] [CrossRef]
- Fan, M.; Lai, S.; Huang, J.; Wei, X.; Chai, Z.; Luo, J.; Wei, X. Rethinking bisenet for real-time semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Montreal, QC, Canada, 11–17 October 2021; pp. 9716–9725. [Google Scholar]
- Chaurasia, A.; Culurciello, E. Linknet: Exploiting encoder representations for efficient semantic segmentation. In Proceedings of the 2017 IEEE Visual Communications and Image Processing (VCIP), Venice, Italy, 22–29 October 2017; pp. 1–4. [Google Scholar]
- Liu, M.; Yin, H. Feature pyramid encoding network for real-time semantic segmentation. arXiv 2019, arXiv:1909.08599. [Google Scholar]
- Wang, Y.; Zhou, Q.; Liu, J.; Xiong, J.; Gao, G.; Wu, X.; Latecki, L.J. Lednet: A lightweight encoder-decoder network for real-time semantic segmentation. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22—25 September 2019; pp. 1860–1864. [Google Scholar]
- Poudel, R.P.; Liwicki, S.; Cipolla, R. Fast-scnn: Fast semantic segmentation network. arXiv 2019, arXiv:1902.04502. [Google Scholar]
- Poudel, R.P.; Bonde, U.; Liwicki, S.; Zach, C. Contextnet: Exploring context and detail for semantic segmentation in real-time. arXiv 2018, arXiv:1805.04554. [Google Scholar]
- Yu, C.; Wang, J.; Peng, C.; Gao, C.; Yu, G.; Sang, N. Bisenet: Bilateral segmentation network for real-time semantic segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 325–341. [Google Scholar]
- Yu, C.; Gao, C.; Wang, J.; Yu, G.; Shen, C.; Sang, N. Bisenet v2: Bilateral network with guided aggregation for real-time semantic segmentation. Int. J. Comput. Vis. 2021, 129, 3051–3068. [Google Scholar] [CrossRef]
- Li, H.; Xiong, P.; Fan, H.; Sun, J. Dfanet: Deep feature aggregation for real-time semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9522–9531. [Google Scholar]
- Li, X.; You, A.; Zhu, Z.; Zhao, H.; Yang, M.; Yang, K.; Tan, S.; Tong, Y. Semantic flow for fast and accurate scene parsing. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 775–793. [Google Scholar]
- Hong, Y.; Pan, H.; Sun, W.; Jia, Y. Deep dual-resolution networks for real-time and accurate semantic segmentation of road scenes. arXiv 2021, arXiv:2101.06085. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Semantic image segmentation with deep convolutional nets and fully connected crfs. arXiv 2014, arXiv:1412.7062. [Google Scholar]
- Chen, L.C.; Papreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Yuan, Y.; Chen, X.; Wang, J. Object-contextual representations for semantic segmentation. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2020; pp. 173–190. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Park, J.; Woo, S.; Lee, J.-Y.; Kweon, I.S. Bam: Bottleneck attention module. arXiv 2018, arXiv:1807.06514. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Meng, Q.; Zhao, M.; Zhang, L.; Shi, W.; Su, C.; Bruzzone, L. Multilayer feature fusion network with spatial attention and gated mechanism for remote sensing scene classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Ambartsoumian, A.; Popowich, F. Self-attention: A better building block for sentiment analysis neural network classifiers. arXiv 2018, arXiv:1812.07860. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Bench, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Wang, W.; Xie, E.; Li, X.; Fan, D.-P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 568–578. [Google Scholar]
- Li, R.; Zheng, S.; Zhang, C.; Duan, C.; Wang, L.; Atkinson, P.M. Abcnet: Attentive bilateral contextual network for efficient semantic segmentation of fine-resolution remotely sensed imagery. ISPRS J. Photogramm. Remote Sens. 2021, 181, 84–98. [Google Scholar] [CrossRef]
- Wang, S.; Li, B.Z.; Khabsa, M.; Fang, H.; Ma, H. Linformer: Self-attention with linear complexity. arXiv 2020, arXiv:2006.04768. [Google Scholar]
- Guo, M.-H.; Liu, Z.-N.; Mu, T.-J.; Hu, S.-M. Beyond self-attention: External attention using two linear layers for visual tasks. arXiv 2021, arXiv:2105.02358. [Google Scholar] [CrossRef]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional Neural Networks for Large-Scale Remote-Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 645–657. [Google Scholar] [CrossRef]
- Wu, T.; Tang, S.; Zhang, R.; Cao, J.; Zhang, Y. Cgnet: A light-weight context guided network for semantic segmentation. IEEE Trans. Image Process. 2020, 30, 1169–1179. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, Q.; Xiong, J.; Wu, X.; Jin, X. Esnet: An efficient symmetric network for real-time semantic segmentation. In Chinese Conference on Pattern Recognition and Computer Vision (PRCV); Springer: Berlin/Heidelberg, Germany, 2019; pp. 41–52. [Google Scholar]



| Module | Params (M) | FLOPs (G) | Inference Time (ms) |
|---|---|---|---|
| SP | 0.685 | 9.586 | 3.84 |
| ARM32 | 4.521 | 1.023 | 0.74 |
| ARM16 | 2.323 | 2.048 | 21.94 |
| FFM | 0.984 | 1.836 | 4.56 |
| All | 8.513 | 14.493 | 31.08 |
| Stages | Output Size | KSize | S | DSANet32 | DSANet64 | ||
|---|---|---|---|---|---|---|---|
| R | C | R | C | ||||
| Image | 512 × 512 | 3 | 3 | ||||
| Stage 0 | 256 × 256 128 × 128 | 3 × 3 | 2 2 | 1 1 | 32 | 1 1 | 64 |
| Stage 1 | 128 × 128 | 3 × 3 | 1, 1 | 2 | 32 | 2 | 64 |
| Stage 2 | 64 × 64 64 × 64 | 3 × 3 | 2, 1 1, 1 | 1 1 | 32 | 1 1 | 64 |
| Stage 3 | 64 × 64 | 3 × 3 | 1, 1 | 2 | 64 | 2 | 128 |
| Stage 4 | 32 ×32 32 × 32 | 3 × 3 | 2, 1 1, 1 | 1 1 | 64 | 1 1 | 128 |
| Stage 5 | 16 × 16 | 3 × 3 | 2 | 1 | 64 | 1 | 128 |
| Stage6 | 8 × 8 | 3 × 3 | 2 | 1 | 128 | 1 | 256 |
| FLOPs | 2.09G | 7.46G | |||||
| Params | 1.14M | 4.58M | |||||
| Method | Norm | E | mF1 (%) | mIoU (%) |
|---|---|---|---|---|
| DSANet64 | - | - | 86.90 | 77.05 |
| +SA | Softmax | - | 87.63 | 78.20 |
| +EAM I | Softmax | 64 | 85.98 | 75.54 |
| +EAM II | Softmax | 64 | 86.61 | 76.60 |
| +EAM II | Softmax+Softmax | 64 | 86.80 | 76.84 |
| +EAM II | Softmax+L1 | 32 | 87.52 | 78.02 |
| +EAM II | Softmax+L1 | 64 | 87.61 | 78.17 |
| Method | Stage | mF1 (%) | mIoU (%) | 512 FPS | 6000 FPS |
|---|---|---|---|---|---|
| DSANet64 | - | 86.90 | 77.05 | 503.77 | 5.83 |
| +SA | 6 | 87.63 | 77.20 | 478.57 | 4.35 |
| +EAM | 6 | 87.61 | 78.17 | 470.07 | 5.46 |
| +EAM | 6/7 | 87.75 | 78.40 | 405.00 | 4.15 |
| +EAM | 6/7/8 | 87.76 | 78.41 | 278.34 | 2.33 |
| Method | MSD Ratio | mF1 (%) | mIoU (%) |
|---|---|---|---|
| DSANet32 | 0 | 86.09 | 75.80 |
| 0.25 | 86.47 | 76.41 | |
| 0.5 | 86.77 | 76.87 | |
| 0.75 | 86.30 | 76.13 | |
| 1.0 | 86.51 | 76.46 | |
| DSANet64 | 0 | 86.89 | 77.05 |
| 0.25 | 87.35 | 77.76 | |
| 0.5 | 87.48 | 77.96 | |
| 0.75 | 87.13 | 77.43 | |
| 1.0 | 86.98 | 77.17 |
| Method | MSD Stage | mF1 (%) | mIoU (%) |
|---|---|---|---|
| DSANet64 | no | 86.89 | 77.05 |
| Stage 1 | 87.04 | 77.28 | |
| Stage 2 | 87.21 | 77.53 | |
| Stage 3 | 87.04 | 77.29 | |
| Stage 4 | 87.31 | 77.70 | |
| Stage 5 | 86.97 | 77.15 | |
| Stage 6 | 87.07 | 77.32 | |
| Stage 7 | 86.81 | 76.92 | |
| Stage 8 | 86.93 | 77.12 | |
| Stage 9 | 87.16 | 77.49 | |
| Stages 1–9 | 87.32 | 77.73 | |
| Stages 1–4 + Stage 9 | 87.48 | 77.96 |
| Method | EAM | MSD | HSE | mIoU (%) | mF1 (%) |
|---|---|---|---|---|---|
| DSANet64 | 77.05 | 86.90 | |||
| ✓ | 78.17 | 87.60 | |||
| ✓ | 77.96 | 87.48 | |||
| ✓ | 77.33 | 87.39 | |||
| ✓ | ✓ | 79.06 | 88.17 | ||
| ✓ | ✓ | ✓ | 79.20 | 88.25 |
| Method | Per-Class mIoU (%) | mIoU (%) | mF1 (%) | Params (M) | ||||
|---|---|---|---|---|---|---|---|---|
| Imperious Surface | Building | Low Vegetation | Tree | Car | ||||
| FPENet [40] | 76.55 | 86.30 | 65.56 | 66.48 | 67.16 | 72.41 | 83.64 | 0.11 |
| FSSNet [37] | 79.90 | 86.83 | 68.69 | 69.40 | 75.20 | 76.00 | 86.20 | 0.17 |
| CGNet [67] | 78.08 | 84.88 | 66.86 | 68.32 | 72.17 | 74.06 | 84.93 | 0.48 |
| EDANet [35] | 79.83 | 87.50 | 69.24 | 70.73 | 72.16 | 75.89 | 86.13 | 0.67 |
| ContextNet [43] | 79.37 | 86.86 | 68.70 | 69.38 | 71.96 | 75.25 | 85.71 | 0.86 |
| LEDNet [41] | 82.45 | 89.12 | 71.17 | 72.51 | 74.28 | 77.91 | 87.42 | 0.89 |
| Fast-SCNN [37] | 78.15 | 83.29 | 68.76 | 69.74 | 70.89 | 74.17 | 85.05 | 1.45 |
| DSANet32 | 82.04 | 88.79 | 70.70 | 72.09 | 75.58 | 77.84 | 87.38 | 1.28 |
| ESNet [68] | 82.31 | 88.16 | 71.94 | 73.37 | 78.09 | 78.77 | 88.00 | 1.66 |
| DABNet [34] | 81.30 | 88.23 | 70.95 | 73.24 | 73.20 | 77.38 | 87.10 | 1.96 |
| ERFNet [36] | 80.38 | 88.18 | 70.81 | 72.30 | 74.89 | 77.31 | 87.06 | 2.08 |
| DDRNet23-slim [48] | 81.27 | 89.09 | 69.91 | 72.37 | 72.99 | 77.13 | 86.91 | 5.81 |
| STDCNet [38] | 82.07 | 89.41 | 71.45 | 73.49 | 76.78 | 78.64 | 87.90 | 8.57 |
| LinkNet [39] | 80.71 | 88.08 | 70.75 | 72.13 | 76.11 | 77.56 | 87.22 | 11.54 |
| BiSeNetV1 [44] | 81.91 | 88.95 | 71.83 | 73.21 | 80.18 | 79.22 | 88.27 | 13.42 |
| BiSeNetV2 [45] | 81.23 | 89.21 | 71.03 | 72.6 | 73.29 | 77.47 | 87.14 | 14.77 |
| SFNet [47] | 80.52 | 84.97 | 71.37 | 72.92 | 79.94 | 77.94 | 87.51 | 13.31 |
| DDRNet23 [48] | 82.58 | 90.07 | 71.56 | 73.55 | 75.44 | 78.64 | 87.89 | 20.59 |
| DSANet64 | 83.02 | 89.50 | 71.86 | 74.26 | 77.34 | 79.20 | 88.25 | 4.65 |
| Method | Per-Class mIoU (%) | mIoU (%) | mF1 (%) | ||||
|---|---|---|---|---|---|---|---|
| Imperious Surface | Building | Low Vegetation | Tree | Car | |||
| FPENet [40] | 78.37 | 84.24 | 63.44 | 73.79 | 44.39 | 68.85 | 80.67 |
| FSSNet [37] | 76.88 | 83.75 | 62.96 | 73.03 | 45.74 | 68.47 | 80.51 |
| CGNet [67] | 77.86 | 84.63 | 64.88 | 74.90 | 47.80 | 70.01 | 81.61 |
| EDANet [35] | 78.76 | 84.56 | 64.51 | 74.32 | 51.65 | 70.76 | 82.36 |
| ContextNet [43] | 77.77 | 83.65 | 61.99 | 73.15 | 50.32 | 69.38 | 81.31 |
| LEDNet [41] | 79.25 | 85.00 | 65.67 | 74.72 | 50.73 | 71.07 | 82.48 |
| Fast-SCNN [37] | 76.21 | 82.08 | 61.06 | 71.47 | 44.45 | 67.05 | 79.48 |
| DSANet32 | 79.17 | 85.30 | 64.30 | 74.05 | 53.74 | 71.31 | 82.74 |
| ESNet [68] | 79.74 | 86.24 | 64.35 | 74.47 | 53.77 | 71.71 | 82.99 |
| DABNet [34] | 78.48 | 84.42 | 63.92 | 73.90 | 54.16 | 70.98 | 82.55 |
| ERFNet [36] | 79.34 | 85.68 | 64.07 | 74.51 | 54.01 | 71.52 | 82.88 |
| DDRNet23-slim [48] | 78.81 | 84.53 | 64.55 | 73.96 | 52.92 | 70.95 | 82.49 |
| STDC1 [38] | 79.03 | 85.76 | 64.27 | 73.69 | 48.71 | 70.29 | 81.84 |
| LinkNet [39] | 79.94 | 85.94 | 64.60 | 74.29 | 54.32 | 71.82 | 83.09 |
| BiSeNetV1 [44] | 78.84 | 85.55 | 64.23 | 74.15 | 50.50 | 70.65 | 82.17 |
| BiSeNetV2 [45] | 79.14 | 84.91 | 64.26 | 74.09 | 55.59 | 71.60 | 83.00 |
| DSANet64 | 79.50 | 85.98 | 63.86 | 73.60 | 58.35 | 72.26 | 83.49 |
| Method | mIoU (%) | FPS | ||
|---|---|---|---|---|
| 512 | 1024 | 6000 | ||
| FPENet [40] | 72.41 | 173.47 | 73.13 | 2.44 |
| FSSNet [37] | 76.00 | 527.26 | 183.30 | 6.27 |
| CGNet [67] | 74.06 | 127.51 | 66.78 | 0.58 |
| EDANet [35] | 75.89 | 390.17 | 135.50 | 4.37 |
| ContextNet [43] | 75.25 | 688.70 | 257.25 | 8.59 |
| LEDNet [41] | 77.91 | 293.48 | 104.92 | 3.74 |
| Fast-SCNN [37] | 74.17 | 670.82 | 261.43 | 8.60 |
| DSANet32 | 77.84 | 648.49 | 245.66 | 8.78 |
| ESNet [68] | 78.77 | 295.33 | 100.27 | 2.77 |
| DABNet [34] | 77.38 | 173.47 | 73.13 | 2.44 |
| ERFNet [36] | 77.31 | 282.66 | 96.00 | 2.65 |
| DDRNet23-slim [48] | 77.13 | 429.09 | 208.38 | 6.98 |
| STDC1 [38] | 78.64 | 437.41 | 147.07 | 5.00 |
| BiSeNetV1 [44] | 79.22 | 351.89 | 128.64 | 3.92 |
| BiSeNetV2 [45] | 77.47 | 242.27 | 114.15 | 3.87 |
| DDRNet23 [48] | 78.64 | 256.65 | 99.58 | 3.46 |
| DSANet64 | 79.20 | 470.07 | 172.16 | 5.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Meng, Q.; Zhang, L.; Zhao, M.; Su, C.; Jancsó, T. DSANet: A Deep Supervision-Based Simple Attention Network for Efficient Semantic Segmentation in Remote Sensing Imagery. Remote Sens. 2022, 14, 5399. https://doi.org/10.3390/rs14215399
Shi W, Meng Q, Zhang L, Zhao M, Su C, Jancsó T. DSANet: A Deep Supervision-Based Simple Attention Network for Efficient Semantic Segmentation in Remote Sensing Imagery. Remote Sensing. 2022; 14(21):5399. https://doi.org/10.3390/rs14215399
Chicago/Turabian StyleShi, Wenxu, Qingyan Meng, Linlin Zhang, Maofan Zhao, Chen Su, and Tamás Jancsó. 2022. "DSANet: A Deep Supervision-Based Simple Attention Network for Efficient Semantic Segmentation in Remote Sensing Imagery" Remote Sensing 14, no. 21: 5399. https://doi.org/10.3390/rs14215399
APA StyleShi, W., Meng, Q., Zhang, L., Zhao, M., Su, C., & Jancsó, T. (2022). DSANet: A Deep Supervision-Based Simple Attention Network for Efficient Semantic Segmentation in Remote Sensing Imagery. Remote Sensing, 14(21), 5399. https://doi.org/10.3390/rs14215399






