Abstract
Remote sensing has been used for decades to produce vector-borne disease risk maps aiming at better targeting control interventions. However, the coarse and climatic-driven nature of these maps largely hampered their use in the fight against malaria in highly heterogeneous African cities. Remote sensing now offers a large panel of data with the potential to greatly improve and refine malaria risk maps at the intra-urban scale. This research aims at testing the ability of different geospatial datasets exclusively derived from satellite sensors to predict malaria risk in two sub-Saharan African cities: Kampala (Uganda) and Dar es Salaam (Tanzania). Using random forest models, we predicted intra-urban malaria risk based on environmental and socioeconomic predictors using climatic, land cover and land use variables among others. The combination of these factors derived from different remote sensors showed the highest predictive power, particularly models including climatic, land cover and land use predictors. However, the predictive power remained quite low, which is suspected to be due to urban malaria complexity and malaria data limitations. While huge improvements have been made over the last decades in terms of remote sensing data acquisition and processing, the quantity and quality of epidemiological data are not yet sufficient to take full advantage of these improvements.
1. Introduction
The Sustainable Development Goals (SDGs) defined malaria incidence reduction as a target (SDG indicator 3.3.3), which comes along with the huge efforts that have been made to control the disease over recent decades [1,2,3]. Better measurements of key malaria indicators through nationally representative household surveys have aided the latter [3]. However, malaria is far from being under control, with causal deaths still estimated at 627,000 in 2020, with almost 95% registered in sub-Saharan Africa (SSA) [3]. Most of these deaths were caused by the parasite Plasmodium falciparum (Pf) transmitted by Anopheles mosquitoes (An. gambiae, An. arabiensis and An. funestus) [4,5]. After a strong and continuous reduction in malaria cases and deaths between 2000 and 2015, progress has slowed or even stagnated between 2015 and 2019, and the year 2020 was marked by a significant increase in malaria cases and deaths, probably partly due to the COVID-19 pandemic that disrupted health services [3]. Remote sensing has long been used in the field of spatial epidemiology to help identify disease hotspots and predict the spatial distribution of infectious diseases [6,7,8]. In particular, risk maps are particularly useful to help in the fight against infectious diseases as they support improved decision-making by enabling better targeting interventions, especially in limited-resource settings [9,10,11]. The spatial distribution of vector-borne diseases such as malaria has been extensively modelled at coarse spatial scales these last two decades mainly because of its clear association with satellite-derived environmental variables [12,13,14], see for example the well-known Malaria Atlas Project [15]. Besides, malaria studies and national control programs have long focused on characterising the vector and pathogen habitat suitability and mapping the spatial limits of stable/unstable transmission mainly based on climatic variables [12].
Nonetheless, the coarse spatial resolution of such large-scale mapping studies, although sufficient for rural environments, prevents the targeting of control interventions in cities. Recent work started to investigate intra-urban variations in malaria prevalence given that malaria hotspots are observed in highly heterogeneous SSA megacities [16,17]. Intra-urban variations in malaria prevalence have been shown to be related to spatially-varying factors such as land cover and land use [9,18], climate [19] or socioeconomic factors [18]. Following [20], malaria risk can be decomposed into two components: the hazard and the vulnerability of the societies to this hazard. Environmental risk factors such as temperature, humidity, vegetation cover, proximity to water bodies, altitude or percentage of built-up areas [9,21,22] are expected to create suitable habitats for the vector and the pathogen and are therefore mainly associated with the hazard. Yet, socioeconomic factors such as housing quality, education [18], human behaviour such as the use of preventive measures [23] and human mobility [24,25] are expected to influence the vulnerability of people to the hazard. Environmental and socioeconomic malaria risk factors are still rarely combined in existing predictive models.
While environmental risk factors are usually and easily derived from remote sensing imagery, socioeconomic factors are traditionally measured via large-scale health surveys as the Demographic and Health Surveys (DHS) and Malaria Indicator Surveys (MIS). However, such survey-based datasets are often expensive and time-consuming to collect and process. Besides, in urban extents, survey geographic coordinates are usually displaced up to 2 km (5 km in rural extents) in a random direction to protect the privacy of the survey participants [26,27,28,29], while it is known that both the environmental and socioeconomic contexts of a city may greatly vary over that range [30]. Several studies showed that this displacement hampers the creation of spatial interpolation surfaces of socioeconomic factors from these survey data, at least in urban settings [26,30]. Instead, remote sensing technologies now allow to automatically (compared to time-consuming surveys) derive alternative socioeconomic variables such as specific land use classes, i.e., industrial areas, commercial areas, informal and planned residential settlements, which, although not directly characterising the human behaviour regarding the use of preventive measures, still allow to describe the urban socioeconomic context [18].
The aim of the present paper is to test the ability of different geospatial datasets exclusively derived from satellite sensors to predict malaria risk in two SSA cities: Kampala (Uganda) and Dar es Salaam (Tanzania). Highly detailed Pf malaria risk models are developed using state-of-the-art remote sensing techniques to include both the most detailed environmental and socioeconomic predictors using climatic, land cover and land use variables among others. More specifically, we aim at (i) comparing the predictive performance of these different geospatial datasets and (ii) evaluating the added-value of combining satellite sensors of varying spatial, temporal and thematic resolutions for mapping vector-borne diseases.
2. Materials and Methods
2.1. Data Preparation and Selection
2.1.1. Malaria Prevalence Data
Malaria prevalence data were extracted from an open online malaria database recording survey data from several sources such as scientific papers, national surveys and health surveys from 1985 to 2016 [31]. The data present as georeferenced points (called data-points). Each point is the centroid of a survey cluster at a specific location where GPS coordinates were registered and malaria prevalence measured. The prevalence is measured as the Pf Parasite Rate standardised over the 2 to 10 age range (PfPR2−10), which corresponds to the proportion of people infected by P. falciparum. PfPR is standardised to the 2 to 10 age range to ensure comparability between surveys sampling different age ranges [32]. In order to use the most spatially-accurate and temporally-consistent data possible, while keeping a sufficient number of observations, we excluded surveys meeting one of these three criteria: (i) surveys conducted outside the 2005–2016 period, assuming there were no important changes in malaria prevalence over that time period, (ii) surveys including adults (i.e., people older than 16 years old) as they are more mobile than children and may hence participate to continuous pathogen re-introductions [24,25], and (iii) non-geolocated surveys or surveys geolocated with a low spatial accuracy (e.g., DHS (https://www.dhsprogram.com/, accessed on 20 October 2022), which are randomly displaced within 2 km buffer zones in urban settings). This resulted in a selection of 39 data-points for Kampala (out of 76) and 90 for Dar es Salaam (out of 241).
2.1.2. Predictor Data
We used three geospatial datasets built from three different mid- and high-resolution satellite data sources to study the intra-urban risk of malaria: (i) a pseudo-climate dataset (CCLM), (ii) Local Climate Zones (LCZ) and (iii) a Land Cover (LC) and Land Use (LU) dataset (Table 1). Each of these datasets was produced in the frame of the REACT (Remote Sensing for Epidemiology in African Cities; https://react.ulb.be/, accessed on 20 October 2022) project with the goal of improving spatial resolution and accuracy to serve for intra-urban epidemiological applications, in comparison to existing products. As an example, the LC and LU covariates in Kampala have a spatial resolution of 0.5 m and 20 m with an overall accuracy of 86% and 81% [33,34]. In comparison, the Land Cover products from the Copernicus Global Land Service (CGLS-LC100) have a spatial resolution of 100 m with 80% accuracy on average [35], which suits better large-scale mapping applications. As the production of each set of predictors was in itself a different topic, we do not describe in details here the methods and techniques employed to derive them. Instead, for more information on how these geospatial datasets were produced, see the corresponding sources in Table 1.
The pseudo-climate dataset consists of 1 km resolution raster grids produced by the Regional Climate Model COSMO-CLM (CCLM), i.e., the climate mode of the atmospheric model used for weather prediction, developed by the German Weather Service [36]. The urban climate model TERRA_URB coupled to the CCLM regional model was activated to represent the urban impact on the local climate and account for the specificities of the urban climates, like the famous Urban Heat Island [37]. The output raster grids represent different climate variables as aggregate values (average, maximum or minimum) for the dry season (June to September 2014) [38]. We also derived a temperature suitability index (TSI) and a temperature suitability index relative humidity (TSI-RH) from CCLM, and hence refer to the term ’pseudo’-climate for this dataset (Table 1). These indexes describe the suitability of a climatic environment for the survival of the mosquito vector in terms of air temperature and relative humidity [37].
The LCZ dataset is a 100 m resolution raster grid that classifies pixels into areas of uniform surface cover and structure with a specific temperature regime [39]. These maps were derived from the Google Earth Engine [40] random forest (RF) classification algorithm applied to Landsat, USGS and Sentinel imagery from 2017 to 2019 [19] (Table 1). The RF classification relies on training areas that were generated during a mapathon organised in November 2019 [19].
The LC and LU dataset consists of LC maps at a resolution of 0.5 m and LU maps at a resolution of 20 m. The LC maps were derived from Pleiades satellite images acquired in 2013 for Kampala and in 2016 and 2018 for Dar es Salaam. These images were processed using Computer Assisted Photo Interpretation, Geographic Object Based Image Analysis (GEOBIA) and machine learning algorithms in order to perform a LC classification [33]. As for the LU maps, they were produced using spatial metrics computed from the LC maps and linear information (parcels and street networks) extracted from OpenStreetMap (OSM) [34]. The output LCZ, LC and LU maps are binary maps showing the presence and absence of one specific type of LCZ, LC or LU class.

Table 1.
Geospatial datasets used as predictors.
Table 1.
Geospatial datasets used as predictors.
| Geospatial Dataset | Variables | Spatial Resolution (m) | Type | Source |
|---|---|---|---|---|
| Pseudo-climate variables (CCLM) | Average specific humidity at two meters—QV2M | 1000 | Direct extraction | CCLM model derived [38] |
| Average relative humidity at two meters—RH2M Average temperature at surface—TS | ||||
| Average temperature at two meters—T2M Minimum precipitation | ||||
| Maximum precipitation | ||||
| Mean precipitation Temperature suitability index—TSI Temperature suitability index relative humidity—TSI-RH | ||||
| Local climate zones (LCZ) | Compact built areas | 100 | Distances & Proportions within 1 km buffer | Derived from Landsat, USGS and Sentinel imagery [19] and available from the LCZ generator [41] |
| Sparsely built areas Open built areas Wetlands Water bodies Lowlands Trees Informal settlements Industrial areas Mineral areas | ||||
| Land cover (LC) | Bare ground Building Low vegetation (humid, riparian, grasses, bushes) Tall vegetation Water | 0.5 | Proportions within 1 km buffer | Derived from Pleiades imagery [33] |
| Land use (LU) | Administrative Commercial Service (ACS) | 20 | Proportions within 1 km buffer | Derived from LC maps and OSM [34] |
| Wetlands, streams, marshes, rivers (mixed class) Planned residential Informal residential |
Along with the three main geospatial datasets, and following [19], we included (i) the Normalized Difference Vegetation Index (NDVI), which ranges between −1 (water bodies) and 1 (dense vegetation) and is extracted from Landsat 5 and 8 over the 2005–2019 period (100 m resolution), (ii) the Normalized Difference Water Index (NDWI) extracted from the same images (100 m resolution), and (iii) the elevation from the Shuttle Radar Topography Mission (SRTM) (30 m resolution).
Covariate pixel values were directly extracted for each malaria prevalence data-point for covariates available at 1 km resolution, i.e., CCLM variables. For finer resolution covariates (LCZ, LC, LU, NDVI, NDWI and elevation), we extracted the average values within 1 km buffers around malaria data-points. To be consistent with [19], we also computed the minimum distance to each LCZ class within 1 km buffers around malaria data-points.
2.2. Random Forest Modelling
We used a random forest (RF) model to assess the relationships between PfPR2−10 and predictor variables, as this machine learning method allows to handle non-linear relationships and already showed interesting results in modelling intra-urban malaria risk [18,19,42]. This method is based on bagging, which overcomes overfitting and decorrelates trees, resulting in more reliable predictions [43]. The RF models were built by spatial cross-validation (ten repetitions of a five-fold division leading to 50 models) with training and test sets representing 80% and 20% of the data respectively, using the ranger [44] and mlr packages [45] in R software [46]. By spatially subdividing the test and training datasets, the spatial cross-validation prevents the model from having biased predictive performance due to spatial autocorrelation [43]. The hyperparameter tuning was performed for each of the five folds by subdividing the training set into two folds to define among 50 random values of hyperparameters, the optimal (i) minimum number of observations per terminal node (nodesize, ranging from one to 10), (ii) number of covariates to be used for splitting at each tree node (mtry, ranging from one to the number of predictors minus one), and (iii) sample fraction (ranging from 0.2 to 0.9), i.e., the fraction of observations to be used in each tree. The number of trees was defined as 500, as an increased number of trees did not lead to an increased performance. The performance of the 50 models built in spatial cross-validation was assessed based on three goodness-of-fit indices (GoF, computed on the test set): (i) the coefficient of determination, R-squared (computed with Equation (1)), (ii) the root mean square error (RMSE), and (iii) the mean absolute error (MAE).
with being the observed values of PfPR2−10, the number of observed values, the value of observation and its predicted value.
Following [47], we used a recursive feature elimination (RFE) procedure to select relevant variables, as our model was likely to contain correlated covariates. In this method, the covariate with the lowest average importance (across the 50 models built by spatial cross-validation) is iteratively removed from the set of predictors until the RF model predictive performance is at the highest [47]. The covariate importance is the increase in mean squared error after permutation divided by the standard deviation of the covariate: the higher the increase, the higher the importance of a covariate [48].
We built different models on both cities to compare the added value of the different geospatial datasets for predicting intra-urban malaria risk:
- ‘Base model’ that only includes NDVI, NDWI and the elevation (Base);
- Model including the variables from the Base model and LCZ variables (Base + LCZ);
- Model corresponding to the second model with the addition of CCLM climate variables (Base + LCZ + CCLM);
- Model corresponding to the second model with the addition of LULC variables (Base + LCZ + LULC);
- Model including all datasets (Base + LCZ + CCLM + LULC).
A RFE was used in each model to select relevant covariates (and hence discard redundant covariates and covariates that are not good predictors of PfPR2−10 [47]), except for the Base model as it contains only three covariates. These five models were then compared based on the three GoF indices. The best model was selected such as to optimise all three GoF indices (R-squared, RMSE and MAE).
We produced predictive maps at 1 km resolution, using the best model selected by our RFE and the predictor data aggregated at 1 km grid resolution.
3. Results
3.1. Comparison of the Geospatial Datasets
Figure 1 and Table 2 present the performance of the five models presented above for the two cities. Model performances (computed on the test sets) are averaged over 50 RF models built in spatial cross-validation and are provided in terms of R-squared, RMSE and MAE. Including LULC and CCLM datasets among the predictors generally provided intra-urban malaria risk models of higher predictive performance in both cities (Figure 1). More specifically, in Dar es Salaam, both models including LULC dataset (Base + LCZ + LULC and Base + LCZ + CCLM + LULC) showed a higher performance according to the three GoF indices, with an average R-squared of 0.32 (±0.03) and 0.33 (±0.03), average RMSE of 6.01 (±0.58) and 6.14 (±0.46) and average MAE of 5.00 (±0.50) and 5.01 (±0.41) (Table 2). In Kampala, the model including all types of variables (Base + LCZ + CCLM + LULC) showed a higher performance than other models, in terms of all three GoF indices, with an average R-squared of 0.21 (±0.05), average RMSE of 6.11 (±0.34) and average MAE of 4.82 (±0.31). The other model including the CCLM variables (Base + LCZ + CCLM) also showed a higher performance than other models, but only in terms of R-squared, with an average R-squared of 0.16 (±0.05) (Figure 1 and Table 2).
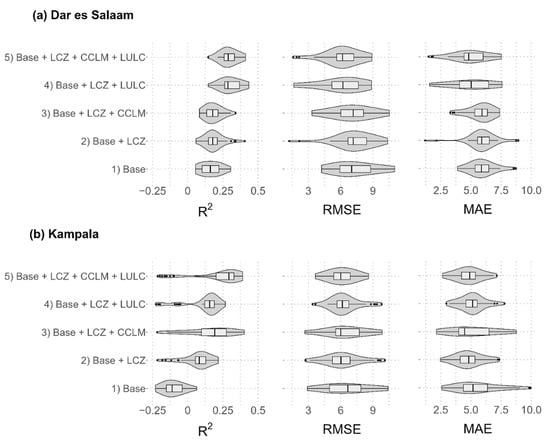
Figure 1.
Comparison of model performances obtained with the five models for (a) Dar es Salaam and (b) Kampala: Base model, Base + LCZ model, Base + LCZ + CCLM model, Base + LCZ + LUCL model, and Base + LCZ + CCLM + LULC model. A recursive feature elimination (RFE) was used, except for the Base model, and this RFE was implemented independently for each model. Model performances are computed on the test sets and provided for the 50 RF models built in spatial cross-validation in terms of R-squared, root mean square error (RMSE) and mean absolute error (MAE).

Table 2.
Model performances (average with 95% confidence intervals and median) in terms of R-squared, RMSE and MAE for the five different models of (a) Dar es Salaam and (b) Kampala. The table also includes the covariates remaining after the RFE variable selection.
Models with only LCZ variables added to the Base model (Base + LCZ) showed low R-squared averages (0.19 (±0.02) for Dar es Salaam and 0.05 (±0.04) for Kampala). Including LCZ variables improved the model performance in Kampala in terms of RMSE and MAE, but it did not considerably improve the model performance in terms of those two GoF indices in Dar es Salaam compared with the Base model.
3.2. Model Performance Assessment and Predictive Maps
The RFE variable selection implemented on all datasets (Base + LCZ + CCLM + LULC) resulted in a best model including 5 covariates in Dar es Salaam and 4 covariates in Kampala, without any common covariate (Figure 2). The best model in Dar es Salaam included the proportion of LC bare ground, water and tall vegetation, the distance to LCZ compact built areas and the proportion of LU ACS. While the pseudo-climate variables were absent from the best model in Dar es Salaam, LC classes reflecting environmental conditions remained important covariates (e.g., LC water and tall vegetation). The best model for Kampala included the LU informal residential, the pseudo-climate temperature suitability index, the relative humidity at two meters, and the distance to LCZ water bodies, translating again the importance of combining both pseudo-climate and LULC datasets to predict malaria risk in Kampala. Partial dependence plots for the covariates included in the best models can be found in Figure S1 for Dar es Salaam and Figure S2 for Kampala.
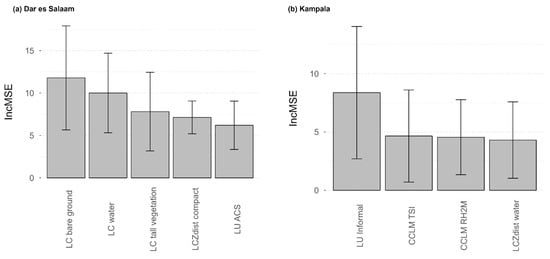
Figure 2.
Covariate importance in the best model (Base + LCZ + CCLM + LULC) for (a) Dar es Salaam and (b) Kampala. The covariate importance is an average increase in mean squared error (Inc MSE) computed across the 50 models built in spatial cross-validation. The error bars represent the standard deviation computed across these 50 models.
Model performances remained quite low (R-squared ≤ 0.33) and results show a high variability in covariate importance, which is not surprising given that we used a spatial cross-validation. Figure 3 shows the predicted PfPR2−10 maps for Dar es Salaam and Kampala at 1 km raster level (Figure 3a,c) and aggregated by administrative unit (Figure 3b,d).
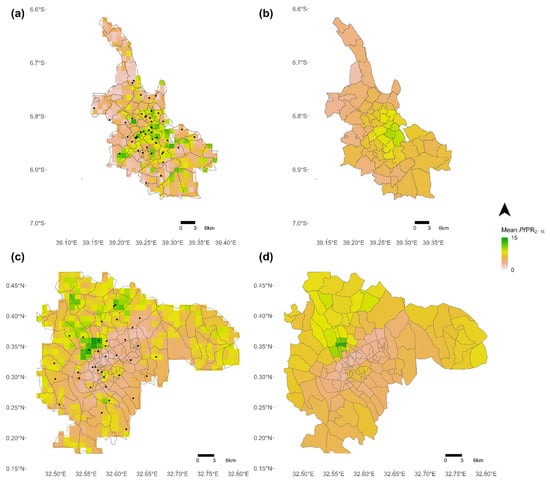
Figure 3.
Predictive maps of the risk of malaria. (a) Predicted PfPR2−10 at 1 km raster level in Dar es Salaam, (b) Average PfPR2−10 aggregated at administrative level (admin 5) in Dar es Salaam, (c) Predicted PfPR2−10 at 1 km raster level in Kampala, and (d) Average PfPR2−10 aggregated at administrative level (admin 5) in Kampala. The black dots represent georeferenced malaria prevalence data-points.
4. Discussion
By combining satellite-derived data from various high and very-high-resolution sensors, this paper aimed at modelling and mapping intra-urban variations in Pf malaria risk in Kampala (Uganda) and Dar es Salaam (Tanzania). With the aim of combining environmental and socioeconomic predictors, we related the hazard and human vulnerability components of malaria risk, as defined by [20]. The results showed that for both cities, a combination of factors derived from different remote sensors provided the best results, and more specifically models including both climatic variables derived from models using remote sensor inputs (CCLM, or LCZ, to a lesser extent) and LULC factors derived from very-high-resolution images.
The main predictors were however different for Kampala versus Dar es Salaam, with differences between models that suggest different malaria driving factors in the two cities. For example, pseudo-climate variables were more important in Kampala, suggesting that the specific climate conditions of the city better explain intra-urban variations. In Dar es Salaam, intra-urban malaria risk was better predicted by LULC variables. The spatial distribution of predicted intra-urban malaria risk also differed between cities. While the predicted PfPR2−10 gradually increases from the city centre to the periphery in Kampala, it is more heterogenous in Dar es Salaam and hotspots are located in the city centre (Figure 3). These results are in line with previous studies showing that malaria risk does not always follow a gradual increasing trend from the city centre to the outskirts given the socioeconomic and environmental contexts of the cities [18,49,50]. Henceforth, these differences between cities, in terms of both predictors and distribution of predicted malaria risk, may result from different socioeconomic and environmental contexts; among others, the two cities are not located in the same malaria endemic zones and Dar es Salaam is a coastal city, which is not the case of Kampala. However, no conclusion can be drawn here given that statistical associations do not imply causality and that the variance explained remained quite low (0.21–0.33). In addition, RF models are arguably less interpretable than other statistical models such as linear regressions. Caution should also be taken regarding the prediction-explanation fallacy, which occurs when explanations are based on prediction-optimised models [51].
The relatively low predictive performance of the models, with R-squared values reaching only 0.33 at best, is suspected to be due to the complexity of urban malaria on the one hand, but also to malaria data limitations. Survey-based malaria data indeed suffer from quantity and quality issues that limit their representativeness and comparability. First, malaria surveys were extracted for the 2005–2016 period and our models therefore assumed a temporal stationarity over that period. The quantity of malaria surveys is too limited to consider any temporal or seasonal variation in malaria risk. Second, an important number of surveys were discarded from the present analysis due to insufficient accuracy in survey geolocation. In particular, DHS data needed to be excluded due to the random displacement of up to 2 km applied to the survey points. In highly heterogeneous African cities, this displacement may completely modify the urban landscape around the data-points and significantly blur statistical associations. Further studies should focus on testing the ability of spatial optimisation methods to overcome the effect of DHS point displacement, such as proposed by [26].
The present study also suffers from some limitations in geospatial datasets used as predictors. As for the malaria data, temporal variations were not captured, as the date of acquisition of satellite images varies from one source to the other and does not necessarily match with the malaria data. For example, pseudo-climate covariates were acquired during the dry season, while other covariates were collected during the wet season or yearly aggregated. Some covariates were aggregated over a longer time period (i.e., 10 years) whenever allowed by the data (e.g., NDVI and NDWI) in order to smooth temporal fluctuations. Finally, we did not include in this study information about human behaviour regarding preventive measures and other socioeconomic factors directly characterising education or household assets, which cannot be retrieved from remote sensing data. We encourage future work to further investigate the combination of remote sensing and surveys such as DHS to create interpolation surfaces of socioeconomic variables.
Mapping intra-urban malaria risk requires high-resolution data both on the disease outcomes (i.e., malaria prevalence) and on the disease determinants (i.e., malaria driving factors). With huge improvements have been made over the last decades in terms of remote-sensing data acquisition and processing, the spatio-temporal heterogeneity of the disease determinants can now be captured to a large extent by remote sensing techniques, as this study has shown. However, the quantity and quality of epidemiological data are not yet sufficient to fully describe the disease outcomes, even for malaria, which is currently the only vector-borne disease for which standardised data are regularly collected. We however expect that epidemiological data will improve in both quality and quantity in the future. At the moment, predictive maps such as the ones created in this study cannot directly be used to target malaria control interventions given their low accuracy, but they could be used in combination with other decision-making tools and with the knowledge of local experts in the field, as they already provide insights into where high-risk areas tend to be located. For better mapping vector-borne diseases, multi-satellite data should become available at finer resolution, cover wider areas (including both rural and urban spaces), and include both environmental and socioeconomic risk factors. Such expected improvements in both epidemiological and remote sensing data call for the integration of intra-urban predictive models into large-scale mapping studies, such as the Malaria Atlas Project, in order to refine large-scale predictive maps of malaria risk within cities.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14215381/s1, Figure S1: Partial dependence plots for the covariates included in the best model (Base + LCZ + CCLM + LULC) for Dar es Salaam. Each thin line is the result of one model among the 50 models built by spatial cross-validation, the plain line is the median line, the dotted lines represent the median added and subtracted by the standard deviation. Figure S2: Partial dependence plots for the covariates included in the best model (Base + LCZ + CCLM + LULC) for Kampala. Each thin line is the result of one model among the 50 models built by spatial cross-validation, the plain line is the median line, the dotted lines represent the median added and subtracted by the standard deviation.
Author Contributions
Conceptualization, C.C., S.D. and C.L.; methodology, C.M., C.C. and S.G.; formal analysis, C.M. and C.C.; investigation, C.M. and C.C.; resources, S.G., O.B. and J.V.d.W.; Software, C.M., C.C., S.G. and O.B.; writing—original draft preparation, C.M. and C.C.; writing—review and editing, C.M., S.G., O.B., J.V.d.W., N.P.M.v.L., E.W., S.D. and C.L.; supervision, S.D. and C.L.; project administration, C.L.; funding acquisition, N.P.M.v.L., E.W. and C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by BELSPO (Belgian Federal Science Policy Office) in the frame of the STEREO III program, as part of the REACT (SR/00/337) and REACTION (SR/13/218) projects. O.B. is funded by the Wellcome HEROIC Project (216035/Z/19/Z).
Data Availability Statement
R scripts and related files needed to run the analyses are available at https://github.com/CamilleMorlighem/REACT2cities (accessed on 20 October 2022). The malaria prevalence data that were used in this study are freely available in the Harvard Dataverse Repository [31]. LC and LU products are publicly accessible from Zenodo repositories [52,53,54]. LCZ maps are downloadable from the LCZ Generator (https://lcz-generator.rub.de/, accessed on 20 October 2022) [41]. CCLM data are also available from the GitHub repository mentioned above. Finally, SRTM and Landsat 5 and 8 images (from which we computed the NDVI and NDWI) can all be extracted from https://www.usgs.gov/ (accessed on 20 October 2022).
Acknowledgments
Authors thank Robert W. Snow (Population Health Unit, KEMRI-Wellcome Trust Research Programme, Nairobi, Kenya and Centre for Tropical Medicine & Global Health, Nuffield Department of Clinical Medicine, University of Oxford, Oxford, UK) for helping in the selection and extraction of malaria prevalence datasets.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Snow, R.W.; Sartorius, B.; Kyalo, D.; Maina, J.; Amratia, P.; Mundia, C.W.; Bejon, P.; Noor, A.M. The prevalence of Plasmodium falciparum in sub-Saharan Africa since 1900. Nature 2017, 550, 515–518. [Google Scholar] [CrossRef] [PubMed]
- Rowe, A.K. Assessing the Health Impact of Malaria Control Interventions in the MDG/Sustainable Development Goal Era: A New Generation of Impact Evaluations. Am. J. Trop. Med. Hyg. 2017, 97, 6–8. [Google Scholar] [CrossRef]
- World Health Organization. World Malaria Report 2021; World Health Organization: Geneva, Switzerland, 2021. [Google Scholar]
- Sinka, M.E.; Bangs, M.J.; Manguin, S.; Coetzee, M.; Mbogo, C.M.; Hemingway, J.; Patil, A.P.; Temperley, W.H.; Gething, P.W.; Kabaria, C.W.; et al. The dominant Anopheles vectors of human malaria in Africa, Europe and the Middle East: Occurrence data, distribution maps and bionomic précis. Parasites Vectors 2010, 3, 117. [Google Scholar] [CrossRef] [PubMed]
- Sinka, M.E.; Bangs, M.J.; Manguin, S.; Rubio-Palis, Y.; Chareonviriyaphap, T.; Coetzee, M.; Mbogo, C.M.; Hemingway, J.; Patil, A.P.; Temperley, W.H.; et al. A global map of dominant malaria vectors. Parasites Vectors 2012, 5, 69. [Google Scholar] [CrossRef] [PubMed]
- Huh, O.K.; Malone, J.B. New tools: Potential medical applications of data from new and old environmental satellites. Acta Trop. 2001, 79, 35–47. [Google Scholar] [CrossRef]
- Hay, S.I.; Tatem, A.J.; Graham, A.J.; Goetz, S.J.; Rogers, D.J. Global environmental data for mapping infectious disease distribution. Adv. Parasitol. 2006, 62, 37–77. [Google Scholar] [PubMed]
- Rogers, D.J.; Randolph, S.E. Studying the global distribution of infectious diseases using GIS and RS. Nat. Rev. Microbiol. 2003, 1, 231–237. [Google Scholar] [CrossRef]
- Kabaria, C.W.; Molteni, F.; Mandike, R.; Chacky, F.; Noor, A.M.; Snow, R.W.; Linard, C. Mapping intra-urban malaria risk using high resolution satellite imagery: A case study of Dar es Salaam. Int. J. Health Geogr. 2016, 15, 26. [Google Scholar] [CrossRef] [PubMed]
- Hay, S.I.; Snow, R.W. The Malaria Atlas Project: Developing Global Maps of Malaria Risk. PLoS Med. 2006, 3, e473. [Google Scholar] [CrossRef] [PubMed]
- Kraemer, M.U.G.; Reiner, R.C.; Brady, O.J.; Messina, J.P.; Gilbert, M.; Pigott, D.M.; Yi, D.; Johnson, K.; Earl, L.; Marczak, L.B.; et al. Past and future spread of the arbovirus vectors Aedes aegypti and Aedes albopictus. Nat. Microbiol. 2019, 4, 854–863. [Google Scholar] [CrossRef] [PubMed]
- Gething, P.W.; Van Boeckel, T.P.; Smith, D.L.; Guerra, C.A.; Patil, A.P.; Snow, R.W.; Hay, S.I. Modelling the global constraints of temperature on transmission of Plasmodium falciparum and P. vivax. Parasites Vectors 2011, 4, 92. [Google Scholar] [CrossRef]
- Hay, S.I.; Guerra, C.A.; Gething, P.W.; Patil, A.P.; Tatem, A.J.; Noor, A.M.; Kabaria, C.W.; Manh, B.H.; Elyazar, I.R.; Brooker, S.; et al. A World Malaria Map: Plasmodium falciparum Endemicity in 2007. PLoS Med. 2009, 6, e1000048. [Google Scholar] [CrossRef]
- Gething, P.W.; Patil, A.P.; Smith, D.L.; Guerra, C.A.; Elyazar, I.R.F.; Johnston, G.L.; Tatem, A.J.; Hay, S.I. A new world malaria map: Plasmodium falciparum endemicity in 2010. Malar. J. 2011, 10, 378. [Google Scholar] [CrossRef] [PubMed]
- Malaria Atlas Project. Welcome to the Malaria Atlas Project—MAP [Interent]. 2022. Available online: https://malariaatlas.org/ (accessed on 15 February 2022).
- Mathanga, D.P.; Tembo, A.K.; Mzilahowa, T.; Bauleni, A.; Mtimaukenena, K.; Taylor, T.E.; Valim, C.; Walker, E.D.; Wilson, M.L. Patterns and determinants of malaria risk in urban and peri-urban areas of Blantyre, Malawi. Malar. J. 2016, 15, 590. [Google Scholar] [CrossRef] [PubMed]
- Brown, B.J.; Manescu, P.; Przybylski, A.A.; Caccioli, F.; Oyinloye, G.; Elmi, M.; Shaw, M.J.; Pawar, V.; Claveau, R.; Shawe-Taylor, J.; et al. Data-driven malaria prevalence prediction in large densely populated urban holoendemic sub-Saharan West Africa. Sci. Rep. 2020, 10, 15918. [Google Scholar] [CrossRef] [PubMed]
- Georganos, S.; Brousse, O.; Dujardin, S.; Linard, C.; Casey, D.; Milliones, M.; Parmentier, B.; van Lipzig, N.P.M.; Demuzere, M.; Grippa, T.; et al. Modelling and mapping the intra-urban spatial distribution of Plasmodium falciparum parasite rate using very-high-resolution satellite derived indicators. Int. J. Health Geogr. 2020, 19, 38. [Google Scholar] [CrossRef] [PubMed]
- Brousse, O.; Georganos, S.; Demuzere, M.; Dujardin, S.; Lennert, M.; Linard, C.; Snow, R.W.; Thiery, W.; van Lipzig, N.P.M. Can we use local climate zones for predicting malaria prevalence across sub-Saharan African cities? Environ. Res. Lett. 2020, 15, 124051. [Google Scholar] [CrossRef] [PubMed]
- Kienberger, S.; Hagenlocher, M. Spatial-explicit modeling of social vulnerability to malaria in East Africa. Int. J. Health Geogr. 2014, 13, 29. [Google Scholar] [CrossRef] [PubMed]
- Boyce, M.R.; Katz, R.; Standley, C.J. Risk Factors for Infectious Diseases in Urban Environments of Sub-Saharan Africa: A Systematic Review and Critical Appraisal of Evidence. Trop. Med. Infect. Dis. 2019, 4, 123. [Google Scholar] [CrossRef] [PubMed]
- McMahon, A.; Mihretie, A.; Ahmed, A.A.; Lake, M.; Awoke, W.; Wimberly, M.C. Remote sensing of environmental risk factors for malaria in different geographic contexts. Int. J. Health Geogr. 2021, 20, 28. [Google Scholar] [CrossRef] [PubMed]
- Noor, A.M.; Mutheu, J.J.; Tatem, A.J.; Hay, S.I.; Snow, R.W. Insecticide-treated net coverage in Africa: Mapping progress in 2000-07. Lancet 2009, 373, 58–67. [Google Scholar] [CrossRef]
- Buckee, C.O.; Wesolowski, A.; Eagle, N.N.; Hansen, E.; Snow, R.W. Mobile phones and malaria: Modeling human and parasite travel. Travel Med. Infect. Dis. 2013, 11, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Wesolowski, A.; Eagle, N.; Tatem, A.J.; Smith, D.L.; Noor, A.M.; Snow, R.W.; Buckee, C.O. Quantifying the Impact of Human Mobility on Malaria. Science 2012, 338, 267–270. [Google Scholar] [CrossRef] [PubMed]
- Georganos, S.; Gadiaga, A.N.; Linard, C.; Grippa, T.; Vanhuysse, S.; Mboga, N.; Wolff, E.; Dujardin, S.; Lennert, M. Modelling the Wealth Index of Demographic and Health Surveys within Cities Using Very High-Resolution Remotely Sensed Information. Remote Sens. 2019, 11, 2543. [Google Scholar] [CrossRef]
- Corsi, D.J.; Neuman, M.; Finlay, J.E.; Subramanian, S. Demographic and health surveys: A profile. Int. J. Epidemiol. 2012, 41, 1602–1613. [Google Scholar] [CrossRef]
- Ozodiegwu, I.D.; Ambrose, M.; Battle, K.E.; Bever, C.; Diallo, O.; Galatas, B.; Runge, M.; Gerardin, J. Beyond national indicators: Adapting the Demographic and Health Surveys’ sampling strategies and questions to better inform subnational malaria intervention policy. Malar. J. 2021, 20, 122. [Google Scholar] [CrossRef]
- Burgert, C.R.; Colston, J.M.; Roy, T.; Zachary, B. (Eds.) Geographic displacement procedure and georeferenced data release policy for the Demographic and Health Surveys. In DHS Spatial Analysis Reports No 7; ICF International: Calverton, MD, USA, 2013. [Google Scholar]
- Gething, P.W.; Tatem, A.J.; Bird, T.J.; Burgert-Brucker, C.R. (Eds.) Creating spatial interpolation surfaces with DHS data. In DHS Spatial Analysis Reports No 11; ICF International: Rockville, MD, USA, 2015. [Google Scholar]
- Snow, R.W. The Prevalence of Plasmodium Falciparum in Sub Saharan Africa Since 1900, V1 ed.; Harvard Dataverse: Cambridge, MA, USA, 2017. [Google Scholar]
- Smith, D.L.; Guerra, C.A.; Snow, R.W.; Hay, S.I. Standardizing estimates of the Plasmodium falciparum parasite rate. Malar. J. 2007, 6, 131. [Google Scholar] [CrossRef]
- Grippa, T.; Lennert, M.; Beaumont, B.; Vanhuysse, S.; Stephenne, N.; Wolff, E. An Open-Source Semi-Automated Processing Chain for Urban Object-Based Classification. Remote Sens. 2017, 9, 358. [Google Scholar] [CrossRef]
- Grippa, T.; Georganos, S.; Zarougui, S.; Bognounou, P.; Diboulo, E.; Forget, Y.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E. Mapping Urban Land Use at Street Block Level Using OpenStreetMap, Remote Sensing Data, and Spatial Metrics. ISPRS Int. J. Geo-Inf. 2018, 7, 246. [Google Scholar] [CrossRef]
- Buchhorn, M.; Smets, B.; Bertels, L.; De Roo, B.; Lesiv, M.; Tsendbazar, N.-E.; Li, L.; Tarko, A. Copernicus Global Land Service: Land Cover 100m: Version 3 Globe 2015-2019: Product User Manual (Dataset v3.0, Doc Issue 3.3); Zenodo: Geneva, Switzerland, 2020. [Google Scholar]
- Rockel, B.; Will, A.; Hense, A. The regional climate model COSMO-CLM (CCLM). Meteorol. Z. 2008, 17, 347–348. [Google Scholar] [CrossRef]
- Brousse, O.; Georganos, S.; Demuzere, M.; Vanhuysse, S.; Wouters, H.; Wolff, E.; Linard, C.; van Lipzig, N.P.M.; Dujardin, S. Using Local Climate Zones in Sub-Saharan Africa to tackle urban health issues. Urban Clim. 2019, 27, 227–242. [Google Scholar] [CrossRef]
- Brousse, O.; Wouters, H.; Demuzere, M.; Thiery, W.; Van de Walle, J.; van Lipzig, N.P.M. The local climate impact of an African city during clear-sky conditions—Implications of the recent urbanization in Kampala (Uganda). Int. J. Climatol. 2020, 40, 4586–4608. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R. Local Climate Zones for Urban Temperature Studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Demuzere, M.; Kittner, J.; Bechtel, B. LCZ Generator: A Web Application to Create Local Climate Zone Maps. Front. Environ. Sci. 2021, 9, 637455. [Google Scholar] [CrossRef]
- Kapwata, T.; Gebreslasie, M.T. Random forest variable selection in spatial malaria transmission modelling in Mpumalanga Province, South Africa. Geospat. Health 2016, 11, 434. [Google Scholar] [CrossRef]
- Lovelace, R.; Nowosad, J.; Muenchow, J. Chapter 14 Ecology in: Geocomputation with R; Chapman and Hall/CRC: New York, NY, USA, 2019. [Google Scholar]
- Wright, M.N.; Ziegler, A. ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. arXiv 2015, arXiv:1508.04409. [Google Scholar] [CrossRef]
- Bischl, B.; Lang, M.; Kotthoff, L.; Schiffner, J.; Richter, J.; Studerus, E.; Casalicchio, G.; Jones, Z.M. mlr: Machine Learning in R. J. Mach. Learn. Res. 2016, 17, 5938–5942. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Gregorutti, B.; Michel, B.; Saint-Pierre, P. Correlation and variable importance in random forests. Stat. Comput. 2017, 27, 659–678. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Mourou, J.-R.; Coffinet, T.; Jarjaval, F.; Cotteaux, C.; Pradines, E.; Godefroy, L.; Kombila, M.; Pagès, F. Malaria transmission in Libreville: Results of a one year survey. Malar. J. 2012, 11, 40. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.J.; Lengeler, C.; Smith, T.A.; Vounatsou, P.; Akogbeto, M.; Tanner, M. Rapid Urban Malaria Appraisal (RUMA) IV: Epidemiology of urban malaria in Cotonou (Benin). Malar. J. 2006, 5, 45. [Google Scholar] [CrossRef] [PubMed]
- Del Giudice, M. The Prediction-Explanation Fallacy: A Pervasive Problem in Scientific Applications of Machine Learning. PsyArXiv 2021. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T. Dar Es Salaam Very-High-Resolution Land Cover Map; Zenodo: Geneva, Switzerland, 2020. [Google Scholar]
- Georganos, S.; Grippa, T. Kampala Very-High-Resolution Land Cover Map; Zenodo: Geneva, Switzerland, 2020. [Google Scholar]
- Georganos, S. Malaria in High-Resolution: Modelling and Mapping Plasmodium falciparum Parasite Rate using Very-High-Resolution Satellite Derived Indicators in Sub-Saharan African Cities; Zenodo: Geneva, Switzerland, 2020. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).