Unsupervised Cluster-Wise Hyperspectral Band Selection for Classification
Abstract
1. Introduction
- The use of a cluster-wise approach to solving the unsupervised band selection problem;
- Once two clusters were formed, the selection of bands was based on the parameters of a hyperplane defined by a single-layer neural network;
- Fine-tuning of the selected bands based on cluster separability in the feature space.
2. Method
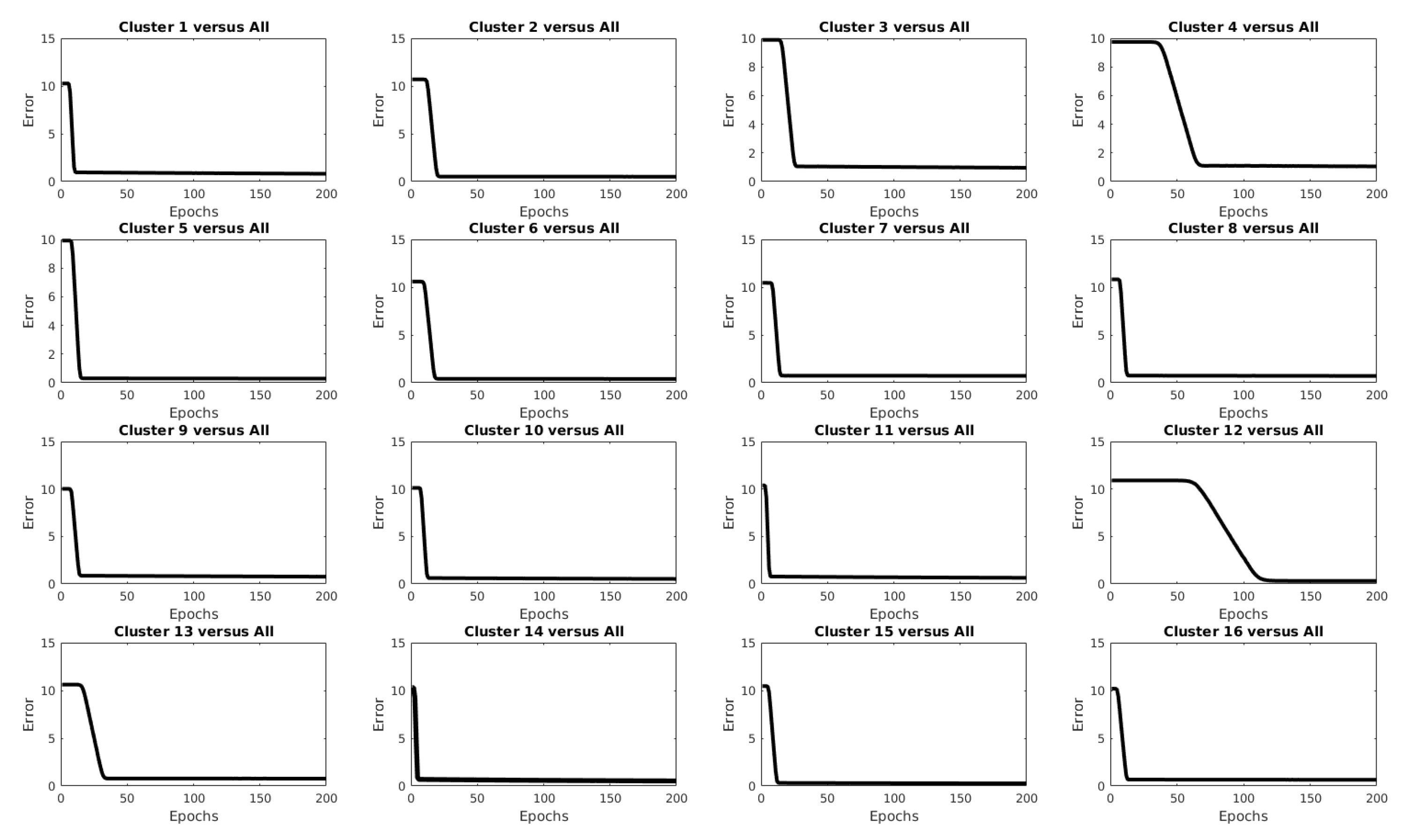
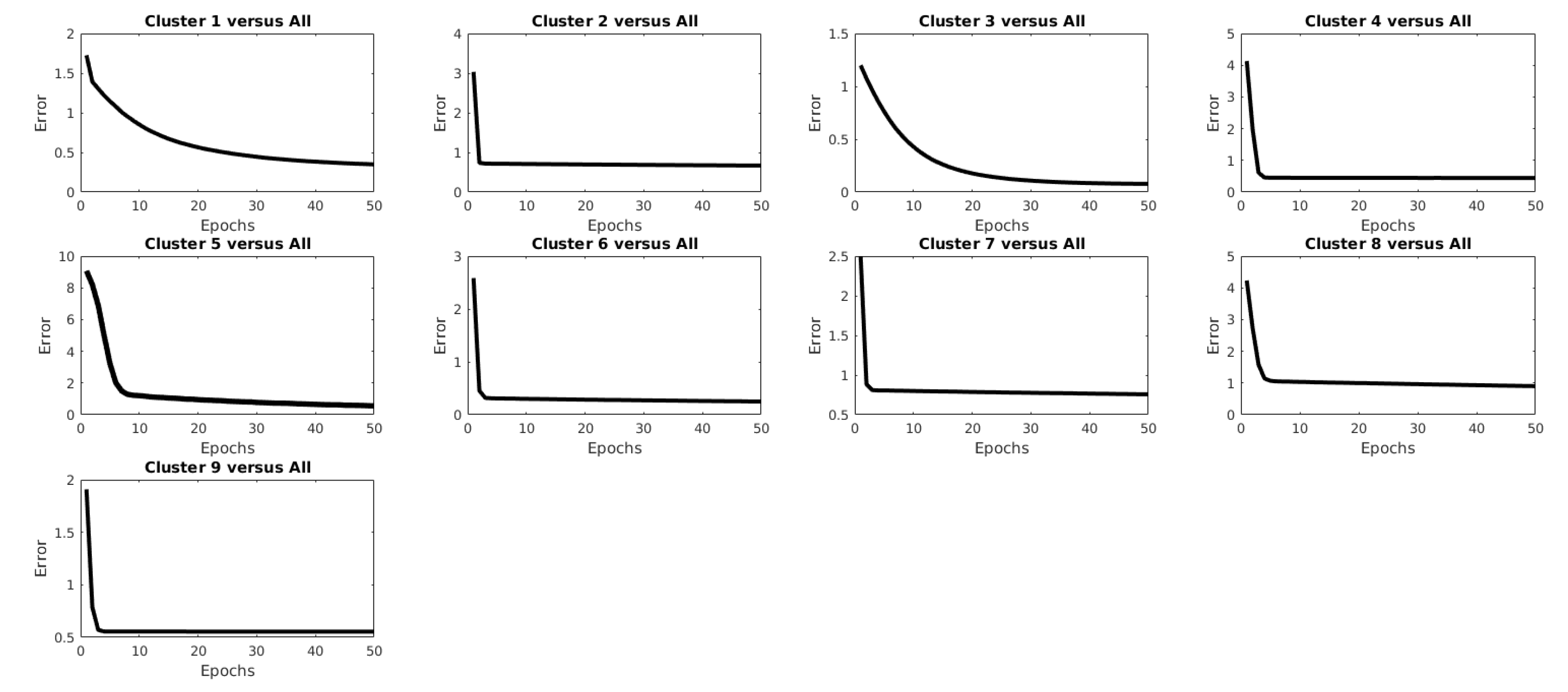
2.1. Data Clustering
Choice of the Clustering Algorithm
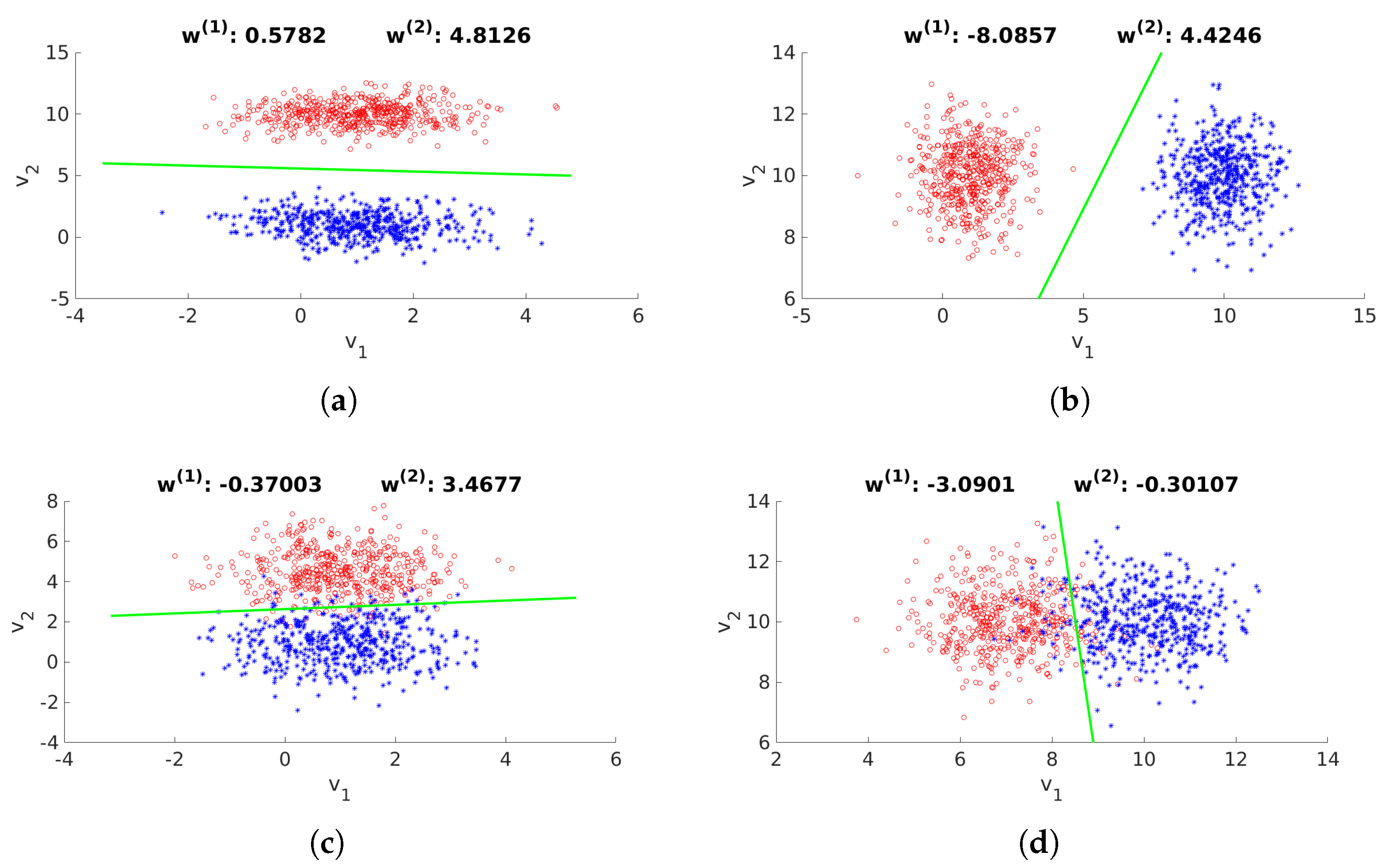
2.2. Selection of Bands of Interest
2.2.1. Selection of Candidate Bands
- , for ;
- ;
- , with and .
- , then ,
- , then ,
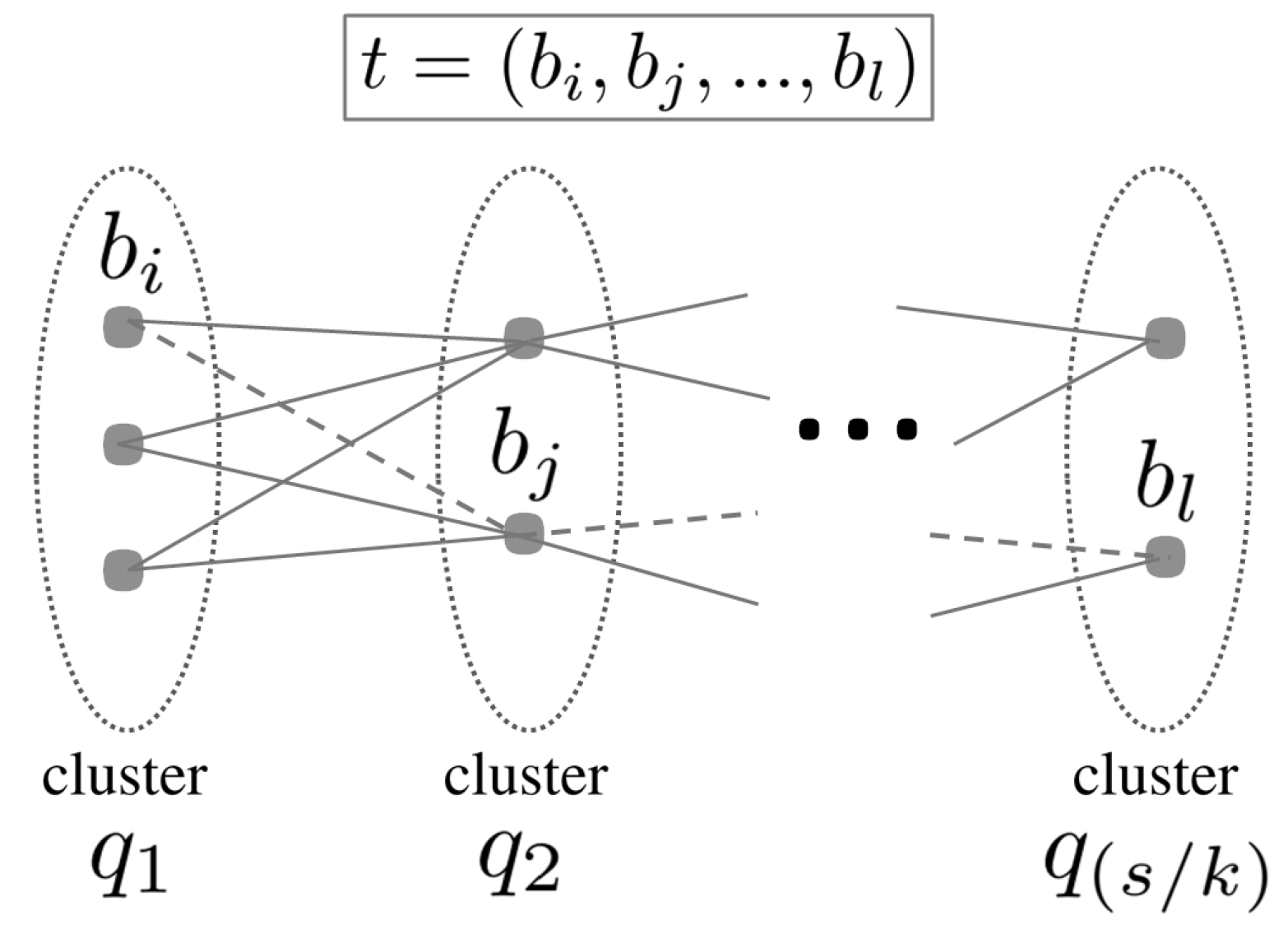
2.2.2. Fine-Tuning
2.3. Redundancy Reduction
| Algorithm 1 Most correlated bands |
| 1: ▷ Pearson’s correlation 2: Initialize matrix 3: 4: for all the columns do 5: ▷ 6: 7: 8: for i = 2 : d do 9: for j = 1 : d do 10: if then 11: 12: Break 13: Return: |
| Algorithm 2 The most correlated bands to a given subset |
| 1: Input: , 2: 3: for j = 1 : do ▷ Vector cardinality 4: for l = 1 : do 5: if then 6: 7: Return: |
2.4. Proposed Method’s Overview
| Algorithm 3 Proposed band selection algorithm |
| 1: Input: Data set , number k of classes 2: ▷ Subset of selected bands 3: ▷ Subset of bands to be discarded 4: Proceed to k-means clustering (cosine distance) of into k clusters 5: for i = 1 : k do 6: Proceed to a binary classification between clusters and (one-versus-all) using a single-layer neural net 7: Select the bands related to the biggest separating hyperplane parameters , according to (4) 8: Proceed to the band selection fine-tuning, according to Section 2.2.2 9: Update subset of selected bands according to (7) 10: Update subset according to (8) 11: Update data set according to (9) 12: Return: S |
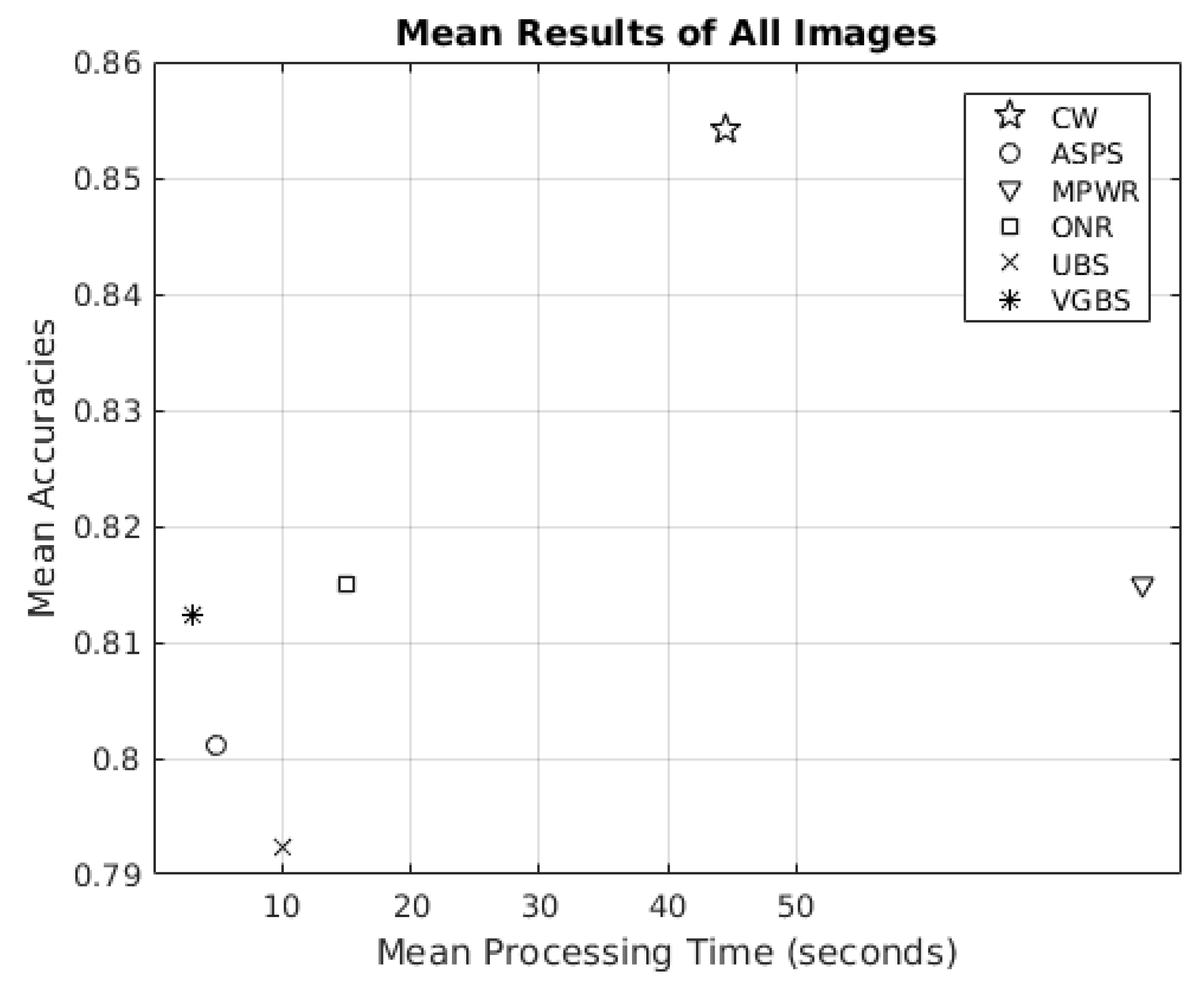
3. Results
3.1. Competitors
3.1.1. ASPS
3.1.2. MPWR
3.1.3. ONR
3.1.4. UBS
3.1.5. VGBS
3.2. Experimental Results
3.2.1. (Case 1) Botswana HSI
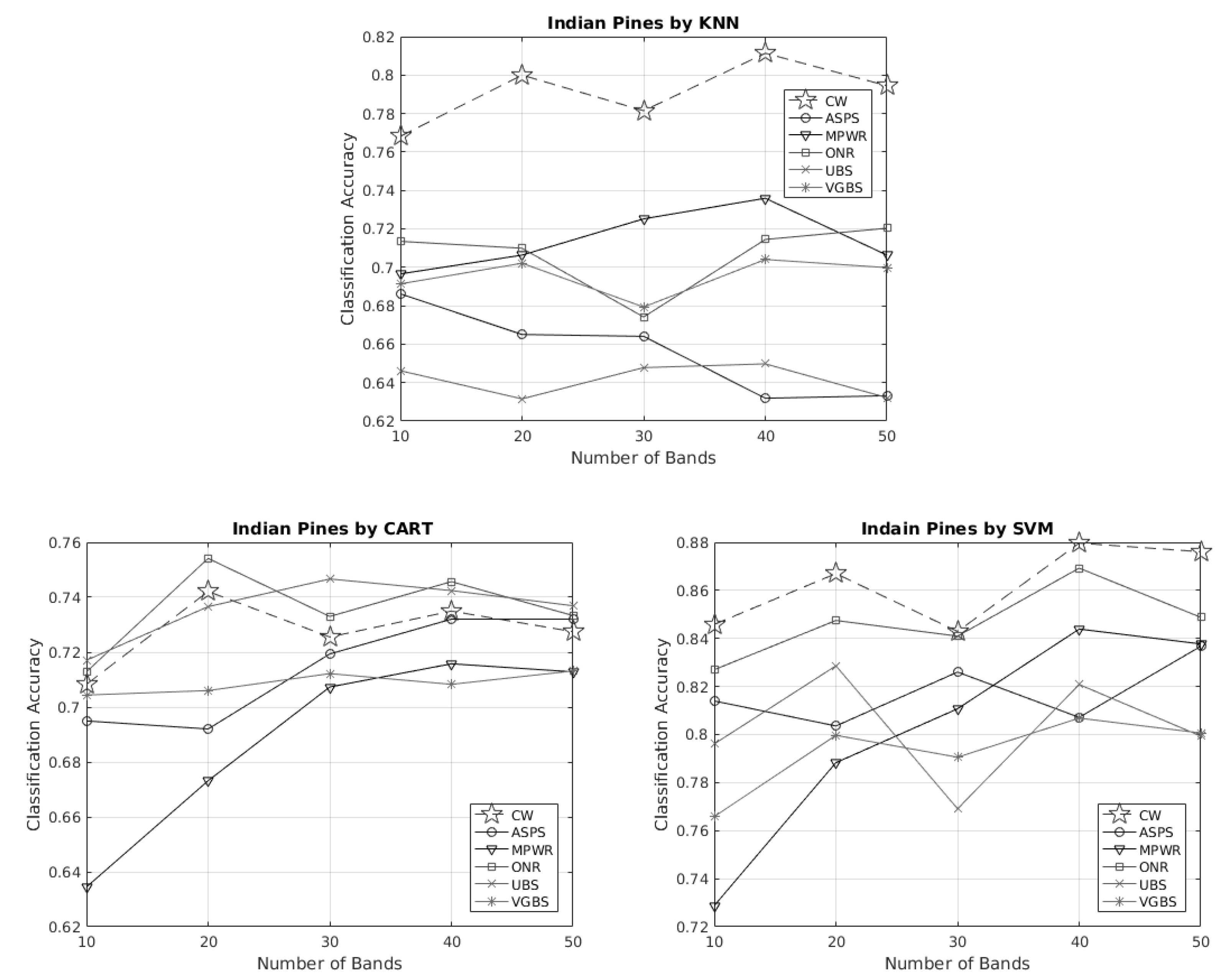
3.2.2. (Case 2) Indian Pines HSI
3.2.3. (Case 3) Pavia University HSI
3.3. Remark
4. Discussion
4.1. Pros
4.2. Cons
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Chen, C.H. Statistical Pattern Recognition, 1st ed.; Spartan Books: Washington, DC, USA, 1973. [Google Scholar]
- Habermann, M.; Frémont, V.; Shiguemori, E.H. Supervised band selection in hyperspectral images using single-layer neural networks. Int. J. Remote Sens. 2019, 40, 3900–3926. [Google Scholar] [CrossRef]
- Houle, M.E.; Kriegel, H.P.; Kröger, P.; Schubert, E.; Zimek, A. Can Shared-Neighbor Distances Defeat the Curse of Dimensionality? In Scientific and Statistical Database Management; Gertz, M., Ludäscher, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 482–500. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Haykin, S.S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Kuncheva, L.I.; Matthews, C.E.; Arnaiz-González, Á.; Rodríguez, J.J. Feature Selection from High-Dimensional Data with Very Low Sample Size: A Cautionary Tale. arXiv 2020, arXiv:abs/2008.12025. [Google Scholar]
- Shang, X.; Song, M.; Wang, Y.; Yu, C.; Yu, H.; Li, F.; Chang, C. Target-Constrained Interference-Minimized Band Selection for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6044–6064. [Google Scholar] [CrossRef]
- Zeng, M.; Cai, Y.; Cai, Z.; Liu, X.; Hu, P.; Ku, J. Unsupervised Hyperspectral Image Band Selection Based on Deep Subspace Clustering. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1889–1893. [Google Scholar] [CrossRef]
- Feng, J.; Chen, J.; Sun, Q.; Shang, R.; Cao, X.; Zhang, X.; Jiao, L. Convolutional Neural Network Based on Bandwise-Independent Convolution and Hard Thresholding for Hyperspectral Band Selection. IEEE Trans. Cybern. 2021, 51, 4414–4428. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Li, H.; Yang, J.; Dale, P.; Chen, X.; Jiang, C.; Zhang, S. An Improved Ant Colony Algorithm for Optimized Band Selection of Hyperspectral Remotely Sensed Imagery. IEEE Access 2020, 8, 25789–25799. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Berthoumieu, Y. Multiple-Feature Kernel-Based Probabilistic Clustering for Unsupervised Band Selection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6675–6689. [Google Scholar] [CrossRef]
- Tang, J.; Alelyani, S.; Liu, H. Feature selection for classification: A review. In Data Classification; CRC Press: Boca Raton, FL, USA, 2014; pp. 37–64. [Google Scholar] [CrossRef]
- Liu, T.; Xiao, J.; Huang, Z.; Kong, E.; Liang, Y. BP Neural Network Feature Selection Based on Group Lasso Regularization. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 2786–2790. [Google Scholar] [CrossRef]
- Cao, X.; Xiong, T.; Jiao, L. Supervised Band Selection Using Local Spatial Information for Hyperspectral Image. IEEE Geosci. Remote Sens. Lett. 2016, 13, 329–333. [Google Scholar] [CrossRef]
- Gao, J.; Du, Q.; Gao, L.; Sun, X.; Wu, Y.; Zhang, B. Ant colony optimization for supervised and unsupervised hyperspectral band selection. In Proceedings of the 2013 5th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Gainesville, FL, USA, 25–28 June 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Habermann, M.; Frémont, V.; Shiguemori, E.H. Problem-based band selection for hyperspectral images. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1800–1803. [Google Scholar] [CrossRef]
- Wei, X.; Cai, L.; Liao, B.; Lu, T. Local-View-Assisted Discriminative Band Selection with Hypergraph Autolearning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2042–2055. [Google Scholar] [CrossRef]
- Feng, J.; Jiao, L.; Liu, F.; Sun, T.; Zhang, X. Mutual-Information-Based Semi-Supervised Hyperspectral Band Selection with High Discrimination, High Information, and Low Redundancy. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2956–2969. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, H.; Bai, X.; Zhang, Z.; Zhou, J. Semi-supervised hyperspectral band selection via sparse linear regression and hypergraph models. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 1474–1477. [Google Scholar] [CrossRef]
- Cao, X.; Wei, C.; Ge, Y.; Feng, J.; Zhao, J.; Jiao, L. Semi-Supervised Hyperspectral Band Selection Based on Dynamic Classifier Selection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1289–1298. [Google Scholar] [CrossRef]
- Bai, J.; Xiang, S.; Shi, L.; Pan, C. Semisupervised Pair-Wise Band Selection for Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2798–2813. [Google Scholar] [CrossRef]
- Karoui, M.S.; Djerriri, K.; Boukerch, I. Unsupervised Hyperspectral Band Selection by Sequentially Clustering A Mahalanobis-Based Dissimilarity of Spectrally Variable Endmembers. In Proceedings of the 2020 Mediterranean and Middle-East Geoscience and Remote Sensing Symposium (M2GARSS), Tunis, Tunisia, 9–11 March 2020; pp. 33–36. [Google Scholar] [CrossRef]
- Sui, C.; Tian, Y.; Xu, Y.; Xie, Y. Unsupervised Band Selection by Integrating the Overall Accuracy and Redundancy. IEEE Geosci. Remote Sens. Lett. 2015, 12, 185–189. [Google Scholar] [CrossRef]
- Yang, C.; Bruzzone, L.; Zhao, H.; Tan, Y.; Guan, R. Superpixel-Based Unsupervised Band Selection for Classification of Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7230–7245. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F.; Li, X. Optimal Clustering Framework for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5910–5922. [Google Scholar] [CrossRef]
- Xu, B.; Li, X.; Hou, W.; Wang, Y.; Wei, Y. A Similarity-Based Ranking Method for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9585–9599. [Google Scholar] [CrossRef]
- Datta, A.; Ghosh, S.; Ghosh, A. Combination of Clustering and Ranking Techniques for Unsupervised Band Selection of Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2814–2823. [Google Scholar] [CrossRef]
- Jia, S.; Tang, G.; Zhu, J.; Li, Q. A Novel Ranking-Based Clustering Approach for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 88–102. [Google Scholar] [CrossRef]
- Xie, W.; Lei, J.; Yang, J.; Li, Y.; Du, Q.; Li, Z. Deep Latent Spectral Representation Learning-Based Hyperspectral Band Selection for Target Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2015–2026. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, Q.; Li, X. Hyperspectral image band selection via global optimal clustering. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Tang, G.; Jia, S.; Li, J. An enhanced density peak-based clustering approach for hyperspectral band selection. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1116–1119. [Google Scholar] [CrossRef]
- Sun, W.; Peng, J.; Yang, G.; Du, Q. Correntropy-Based Sparse Spectral Clustering for Hyperspectral Band Selection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 484–488. [Google Scholar] [CrossRef]
- Kumar, V.; Hahn, J.; Zoubir, A.M. Band selection for hyperspectral images based on self-tuning spectral clustering. In Proceedings of the 21st European Signal Processing Conference (EUSIPCO 2013), Marrakech, Morocco, 9–13 September 2013; pp. 1–5. [Google Scholar]
- Dou, Z.; Gao, K.; Zhang, X.; Wang, H.; Han, L. Band Selection of Hyperspectral Images Using Attention-Based Autoencoders. IEEE Geosci. Remote Sens. Lett. 2021, 18, 147–151. [Google Scholar] [CrossRef]
- Damodaran, B.B.; Courty, N.; Lefèvre, S. Sparse Hilbert Schmidt Independence Criterion and Surrogate-Kernel-Based Feature Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2385–2398. [Google Scholar] [CrossRef]
- Sun, W.; Peng, J.; Yang, G.; Du, Q. Fast and Latent Low-Rank Subspace Clustering for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3906–3915. [Google Scholar] [CrossRef]
- Kohavi, R.; John, G.H. Wrappers for Feature Subset Selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, X.; Cai, Z. BS-Nets: An End-to-End Framework for Band Selection of Hyperspectral Image. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1969–1984. [Google Scholar] [CrossRef]
- Habermann, M.; Frémont, V.; Shiguemori, E.H. Unsupervised Hyperspectral Band Selection Using Clustering and Single-Layer Neural Network. Revue Française de Photogrammétrie et de Télédétection 2018, 217–218, 33–42. [Google Scholar] [CrossRef]
- Graña, M.; Veganzons, M.A.; Ayerdi, B. Hyperspectral Remote Sensing Scenes. Available online: http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes (accessed on 16 August 2022).
- Fu, X.; Shang, X.; Sun, X.; Yu, H.; Song, M.; Chang, C.I. Underwater Hyperspectral Target Detection with Band Selection. Remote Sens. 2020, 12, 1056. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Q.; Li, X. Hyperspectral Band Selection via Adaptive Subspace Partition Strategy. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4940–4950. [Google Scholar] [CrossRef]
- Sui, C.; Li, C.; Feng, J.; Mei, X. Unsupervised Manifold-Preserving and Weakly Redundant Band Selection Method for Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1156–1170. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F.; Li, X. Hyperspectral Band Selection via Optimal Neighborhood Reconstruction. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8465–8476. [Google Scholar] [CrossRef]
- Chang, C.-I.; Du, Q.; Sun, T.-L.; Althouse, M.L.G. A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef]
- Geng, X.; Sun, K.; Ji, L.; Zhao, Y. A Fast Volume-Gradient-Based Band Selection Method for Hyperspectral Image. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7111–7119. [Google Scholar] [CrossRef]




| Clustering Algorithm | r |
|---|---|
| K-means (Euclidean) | 0.6997 |
| K-means (cityblock) | 0.7382 |
| K-means (cosine) | 0.7941 |
| K-means (correlation) | 0.7170 |
| K-medoids (Euclidean) | 0.7062 |
| K-medoids (Mahalanobis) | 0.7685 |
| K-medoids (cityblock) | 0.7402 |
| K-medoids (Minkowski) | 0.7396 |
| K-medoids (Chebychev) | 0.7269 |
| K-medoids (Spearman) | 0.7674 |
| K-medoids (Jaccard) | 0.6146 |
| Method | 10 Bands | 20 Bands | 30 Bands | 40 Bands | 50 Bands |
|---|---|---|---|---|---|
| KNN classifier | |||||
| CW | 90.86 ± 0.69 | 88.81 ± 0.27 | 90.86 ± 0.91 | 91.48 ± 0.97 | 93.22 ± 0.69 |
| ASPS | 85.63 ± 0.75 | 89.73 ± 0.94 | 91.07 ± 0.76 | 89.01 ± 0.63 | 91.58 ± 0.72 |
| MPWR | 81.52 ± 0.99 | 86.45 ± 1.43 | 90.76 ± 0.56 | 90.35 ± 1.05 | 90.25 ± 0.89 |
| ONR | 90.66 ± 0.91 | ± 0.53 | 89.94 ± 0.64 | 91.38 ± 0.89 | 91.99 ± 0.86 |
| UBS | 88.50 ± 1.07 | 89.53 ± 1.05 | 87.99 ± 0.86 | 89.94 ± 0.66 | 90.04 ± 0.96 |
| VGBS | 88.09 ± 0.79 | 90.55 ± 1.00 | 88.50 ± 1.30 | 87.17 ± 1.29 | 88.09 ± 1.10 |
| CART classifier | |||||
| CW | 84.80 ± 1.23 | 86.55 ± 1.27 | 84.91 ± 1.49 | 85.93 ± 1.03 | 86.04 ± 1.13 |
| ASPS | 81.72 ± 1.04 | 85.32 ± 1.27 | 83.78 ± 1.15 | 83.98 ± 1.38 | 84.50 ± 0.96 |
| MPWR | 72.59 ± 1.27 | 81.31 ± 1.13 | 84.29 ± 1.02 | 85.52 ± 1.13 | 85.01 ± 1.47 |
| ONR | 83.37 ± 0.74 | 84.80 ± 1.35 | 84.91 ± 1.06 | 84.60 ± 1.01 | 84.70 ± 1.46 |
| UBS | 80.39 ± 1.14 | 83.26 ± 1.07 | 83.68 ± 1.36 | 85.32 ± 0.84 | 85.01 ± 0.98 |
| VGBS | 83.98 ± 0.81 | 85.22 ± 0.95 | 82.24 ± 1.35 | 83.47 ± 0.65 | 86.24 ± 1.44 |
| SVM classifier | |||||
| CW | 89.73 ± 0.72 | 94.76 ± 0.91 | 94.97 ± 0.69 | 93.94 ± 0.61 | 94.15 ± 0.56 |
| ASPS | 87.78 ± 0.67 | 91.27 ± 0.67 | 93.84 ± 0.66 | 92.09 ± 0.69 | 94.05 ± 0.55 |
| MPWR | 87.06 ± 1.06 | 90.86 ± 0.97 | 93.73 ± 0.67 | 94.76 ± 0.75 | 94.15 ± 0.61 |
| ONR | 92.91 ± 0.36 | 94.25 ± 0.48 | 93.83 ± 0.62 | 94.76 ± 0.46 | 94.14 ± 0.77 |
| UBS | 89.42 ± 0.82 | 92.50 ± 0.98 | 92.71 ± 0.67 | 93.42 ± 0.86 | 92.91 ± 0.89 |
| VGBS | 90.04 ± 0.97 | 92.81 ± 0.58 | 93.63 ± 1.06 | 93.01 ± 0.68 | 93.53 ± 0.65 |
| Method | 10 Bands | 20 Bands | 30 Bands | 40 Bands | 50 Bands |
|---|---|---|---|---|---|
| KNN classifier | |||||
| CW | 76.81 ± 1.13 | 80.00 ± 0.54 | 78.14 ± 0.31 | 81.13 ± 0.59 | 79.45 ± 0.70 |
| ASPS | 68.61 ± 0.68 | 66.50 ± 0.93 | 66.41 ± 0.90 | 63.19 ± 0.33 | 63.32 ± 0.27 |
| MPWR | 69.66 ± 0.89 | 70.63 ± 0.59 | 72.52 ± 0.43 | 73.59 ± 0.49 | 70.63 ± 1.12 |
| ONR | 71.35 ± 0.35 | 70.99 ± 0.61 | 67.41 ± 1.62 | 71.45 ± 0.57 | 72.03 ± 0.96 |
| UBS | 64.62 ± 0.52 | 63.15 ± 0.69 | 64.78 ± 1.09 | 64.98 ± 0.82 | 63.22 ± 0.72 |
| VGBS | 69.14 ± 0.80 | 70.21 ± 0.90 | 67.94 ± 0.74 | 70.41 ± 0.55 | 69.98 ± 0.61 |
| CART classifier | |||||
| CW | 70.82 ± 0.78 | 74.21 ± 0.67 | 72.55 ± 0.86 | 73.50 ± 0.70 | 72.75 ± 0.81 |
| ASPS | 69.49 ± 0.41 | 69.20 ± 0.33 | 71.94 ± 0.46 | 73.20 ± 0.77 | 73.20 ± 0.58 |
| MPWR | 63.45 ± 0.66 | 67.32 ± 0.73 | 70.73 ± 0.70 | 71.58 ± 0.65 | 71.28 ± 0.88 |
| ONR | 71.28 ± 0.99 | 75.41 ± 0.76 | 73.30 ± 1.40 | 74.57 ± 1.22 | 73.33 ± 0.82 |
| UBS | 71.71 ± 0.96 | 73.66 ± 0.78 | 74.67 ± 0.83 | 74.24 ± 1.12 | 73.69 ± 0.86 |
| VGBS | 70.44 ± 0.30 | 70.60 ± 0.57 | 71.22 ± 1.28 | 70.83 ± 0.75 | 71.32 ± 0.78 |
| SVM classifier | |||||
| CW | 84.58 ± 0.80 | 86.70 ± 0.16 | 84.29 ± 5.14 | 87.97 ± 4.48 | 87.61 ± 0.78 |
| ASPS | 81.39 ± 0.58 | 80.36 ± 0.65 | 82.60 ± 0.58 | 80.72 ± 0.52 | 83.68 ± 0.20 |
| MPWR | 72.88 ± 0.95 | 78.82 ± 0.64 | 81.07 ± 0.82 | 84.39 ± 0.50 | 83.77 ± 0.50 |
| ONR | 82.70 ± 0.31 | 84.75 ± 0.70 | 84.10 ± 0.60 | 86.93 ± 0.82 | 84.88 ± 4.00 |
| UBS | 79.61 ± 0.51 | 82.86 ± 0.23 | 76.91 ± 0.61 | 82.08 ± 0.37 | 79.94 ± 3.60 |
| VGBS | 76.59 ± 0.70 | 79.97 ± 0.79 | 79.06 ± 0.52 | 80.68 ± 0.75 | 80.07 ± 1.04 |
| Method | 10 Bands | 20 Bands | 30 Bands | 40 Bands | 50 Bands |
|---|---|---|---|---|---|
| KNN classifier | |||||
| CW | 92.19 ± 0.26 | 92.12 ± 0.48 | 91.73 ± 0.15 | 90.37 ± 0.24 | 90.99 ± 0.15 |
| ASPS | 87.67 ± 0.11 | 90.24 ± 0.39 | 89.90 ± 0.39 | 89.33 ± 0.29 | 90.54 ± 0.40 |
| MPWR | 91.80 ± 0.39 | 90.99 ± 0.14 | 92.37 ± 0.93 | 90.45 ± 0.41 | 91.19 ± 1.19 |
| ONR | 88.89 ± 0.19 | 92.30 ± 0.15 | 91.82 ± 0.29 | 91.02 ± 0.16 | 91.60 ± 0.11 |
| UBS | 86.00 ± 0.42 | 88.15 ± 0.44 | 87.84 ± 0.22 | 88.10 ± 0.22 | 88.17 ± 0.10 |
| VGBS | 84.26 ± 0.39 | 87.77 ± 0.34 | 86.42 ± 0.28 | 87.24 ± 0.39 | 88.30 ± 0.60 |
| CART classifier | |||||
| CW | 89.54 ± 0.12 | 89.18 ± 0.35 | 89.31 ± 0.29 | 89.04 ± 0.39 | 89.04 ± 0.37 |
| ASPS | 83.23 ± 0.35 | 86.69 ± 0.26 | 86.74 ± 0.48 | 87.06 ± 0.37 | 86.47 ± 0.10 |
| MPWR | 89.29 ± 0.67 | 88.82 ± 0.83 | 89.67 ± 0.71 | 89.03 ± 0.95 | 88.81 ± 0.81 |
| ONR | 85.37 ± 0.13 | 89.63 ± 0.23 | 89.03 ± 0.26 | 88.69 ± 0.16 | 89.00 ± 0.25 |
| UBS | 85.02 ± 0.49 | 87.27 ± 0.43 | 86.26 ± 0.31 | 86.50 ± 0.23 | 87.42 ± 0.36 |
| VGBS | 85.79 ± 0.23 | 88.26 ± 0.31 | 88.12 ± 0.32 | 88.49 ± 0.20 | 88.04 ± 0.31 |
| SVM classifier | |||||
| CW | 94.97 ± 2.38 | 90.77 ± 12.59 | 75.56 ± 16.17 | 68.26 ± 16.51 | 67.01 ± 15.36 |
| ASPS | 89.58 ± 9.48 | 88.67 ± 9.41 | 40.19 ± 12.39 | 48.71 ± 15.96 | 40.56 ± 10.81 |
| MPWR | 94.93 ± 3.95 | 91.85 ± 8.64 | 70.66 ± 13.81 | 39.13 ± 17.51 | 54.86 ± 15.50 |
| ONR | 91.31 ± 12.39 | 52.29 ± 24.56 | 46.62 ± 10.86 | 43.36 ± 21.41 | 43.48 ± 12.96 |
| UBS | 89.32 ± 2.49 | 54.75 ± 18.87 | 53.18 ± 13.99 | 38.06 ± 16.05 | 45.21 ± 13.29 |
| VGBS | 91.29 ± 13.59 | 89.74 ± 14.54 | 74.77 ± 17.88 | 50.58 ± 8.86 | 51.20 ± 12.23 |
| Number of Bands | Selected Bands |
|---|---|
| Botswana image | |
| 10 | 4 11 17 21 24 41 69 101 105 120 |
| 20 | 7 10 12 28 32 33 37 39 40 49 55 58 59 65 67 73 75 76 113 124 |
| 30 | 2 4 5 7 21 27 29 30 32 33 34 35 37 43 44 47 54 56 57 58 61 62 71 74 78 80 82 118 120 124 |
| 40 | 2 3 4 5 6 8 13 14 16 27 28 31 32 33 34 35 36 39 41 42 52 54 58 60 63 65 69 70 72 74 78 88 89 92 97 100 101 105 135 142 |
| 50 | 1 2 4 5 6 8 10 16 19 21 22 23 24 25 26 27 30 31 32 33 34 36 41 42 47 57 58 59 66 67 69 72 74 75 77 78 87 89 94 96 98 100 101 102 104 109 110 113 130 144 |
| Indian Pines image | |
| 10 | 16 20 21 33 34 39 92 97 119 128 |
| 20 | 8 10 15 16 17 19 26 27 30 33 36 43 46 47 64 78 97 98 117 133 |
| 30 | 5 6 7 8 9 15 27 30 35 37 39 40 46 56 57 62 63 64 71 73 74 75 76 78 82 92 98 168 173 174 |
| 40 | 4 6 7 9 10 16 17 19 27 30 32 33 34 35 36 40 46 50 52 53 57 63 69 72 74 84 92 93 97 99 100 117 121 122 126 137 139 140 142 199 |
| 50 | 6 9 11 12 15 20 22 23 25 26 29 30 31 32 33 36 41 42 43 44 45 46 49 50 51 55 56 59 65 71 73 74 75 76 77 84 92 95 98 102 114 117 119 121 122 130 138 168 172 199 |
| Pavia University image | |
| 10 | 21 42 55 70 72 73 75 83 85 98 |
| 20 | 15 18 28 46 49 55 56 60 61 63 65 71 83 85 88 89 91 95 99 103 |
| 30 | 10 16 20 22 31 36 38 40 50 54 59 61 62 64 65 67 70 72 74 77 80 83 85 91 92 94 96 98 100 102 |
| 40 | 3 10 11 14 16 17 18 20 23 27 38 39 44 46 51 56 58 59 61 62 63 65 67 69 71 72 74 75 76 78 80 83 84 85 91 94 96 98 100 103 |
| 50 | 9 10 11 13 15 17 18 20 23 25 26 28 29 31 33 35 37 40 41 44 56 57 59 61 62 63 65 66 67 69 71 72 73 75 77 79 81 83 84 85 88 90 92 94 95 96 98 100 102 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habermann, M.; Shiguemori, E.H.; Frémont, V. Unsupervised Cluster-Wise Hyperspectral Band Selection for Classification. Remote Sens. 2022, 14, 5374. https://doi.org/10.3390/rs14215374
Habermann M, Shiguemori EH, Frémont V. Unsupervised Cluster-Wise Hyperspectral Band Selection for Classification. Remote Sensing. 2022; 14(21):5374. https://doi.org/10.3390/rs14215374
Chicago/Turabian StyleHabermann, Mateus, Elcio Hideiti Shiguemori, and Vincent Frémont. 2022. "Unsupervised Cluster-Wise Hyperspectral Band Selection for Classification" Remote Sensing 14, no. 21: 5374. https://doi.org/10.3390/rs14215374
APA StyleHabermann, M., Shiguemori, E. H., & Frémont, V. (2022). Unsupervised Cluster-Wise Hyperspectral Band Selection for Classification. Remote Sensing, 14(21), 5374. https://doi.org/10.3390/rs14215374