Haiti Earthquake (Mw 7.2): Magnetospheric–Ionospheric–Lithospheric Coupling during and after the Main Shock on 14 August 2021
Abstract
1. Introduction
2. Data and Methods
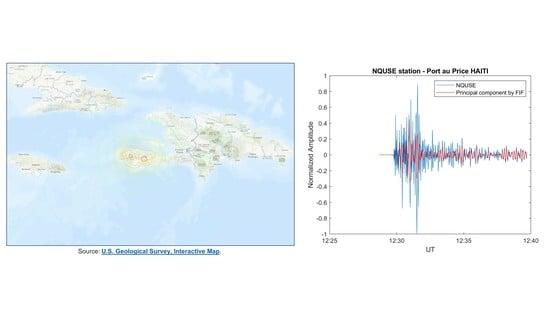
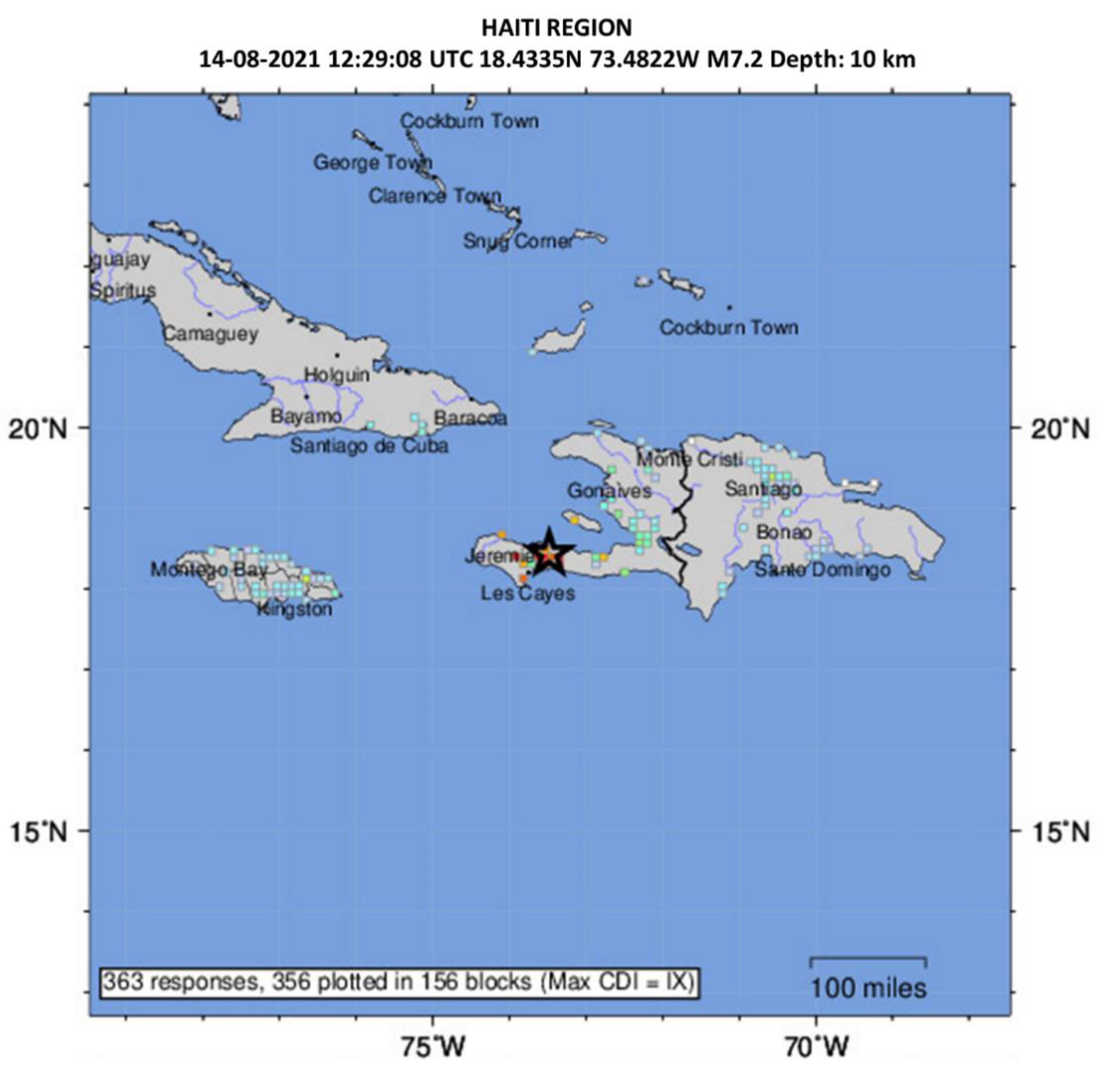
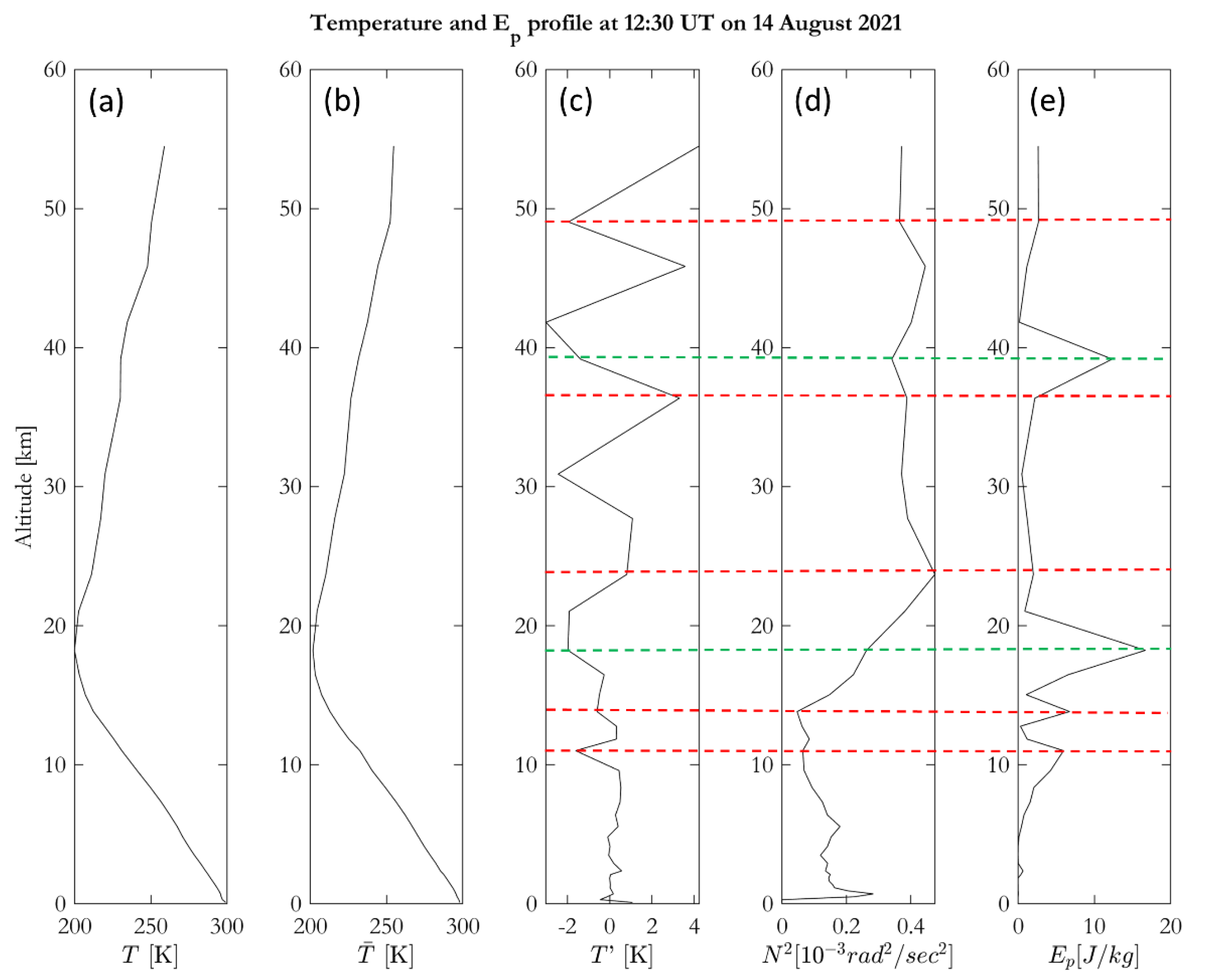
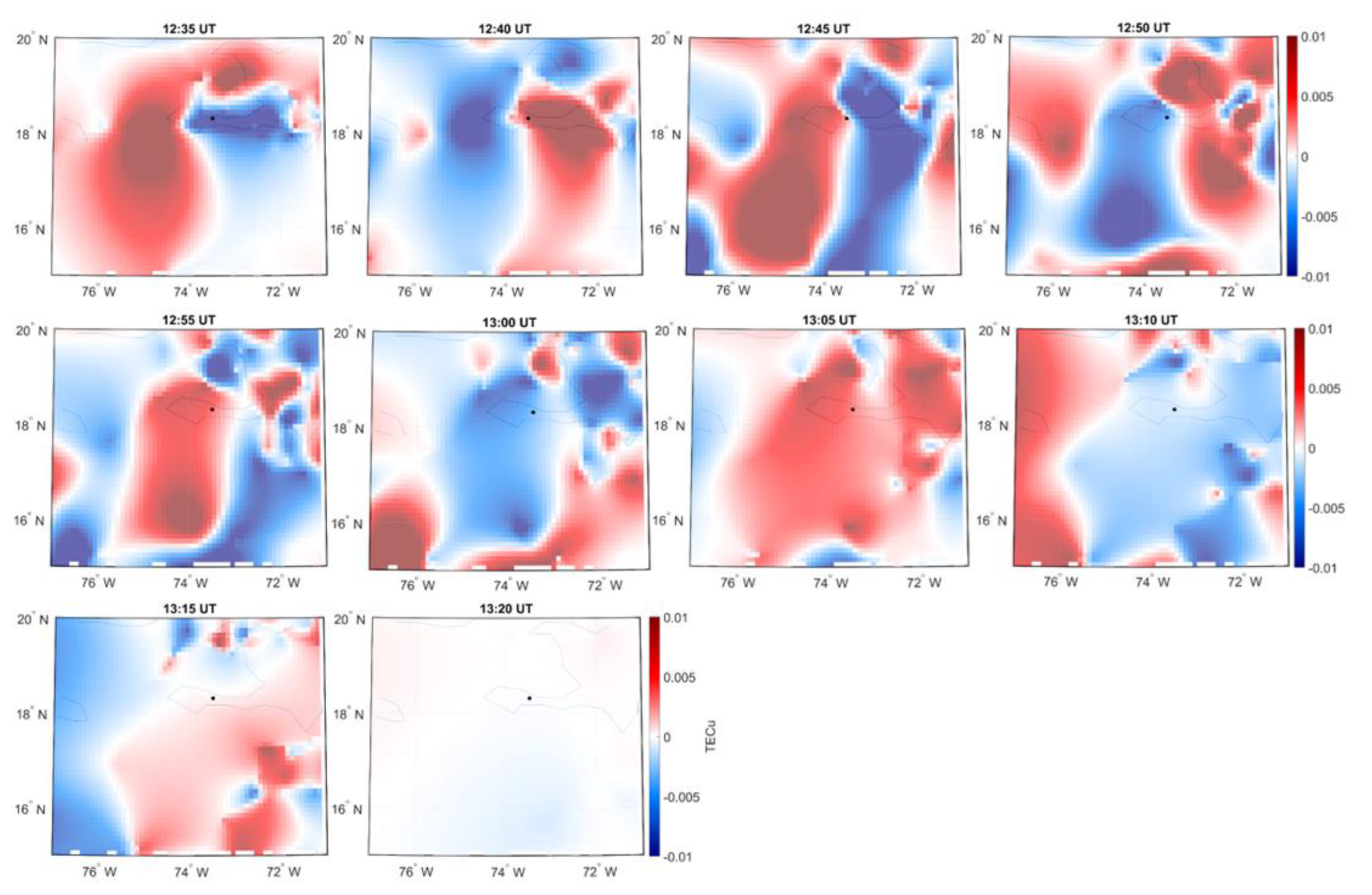
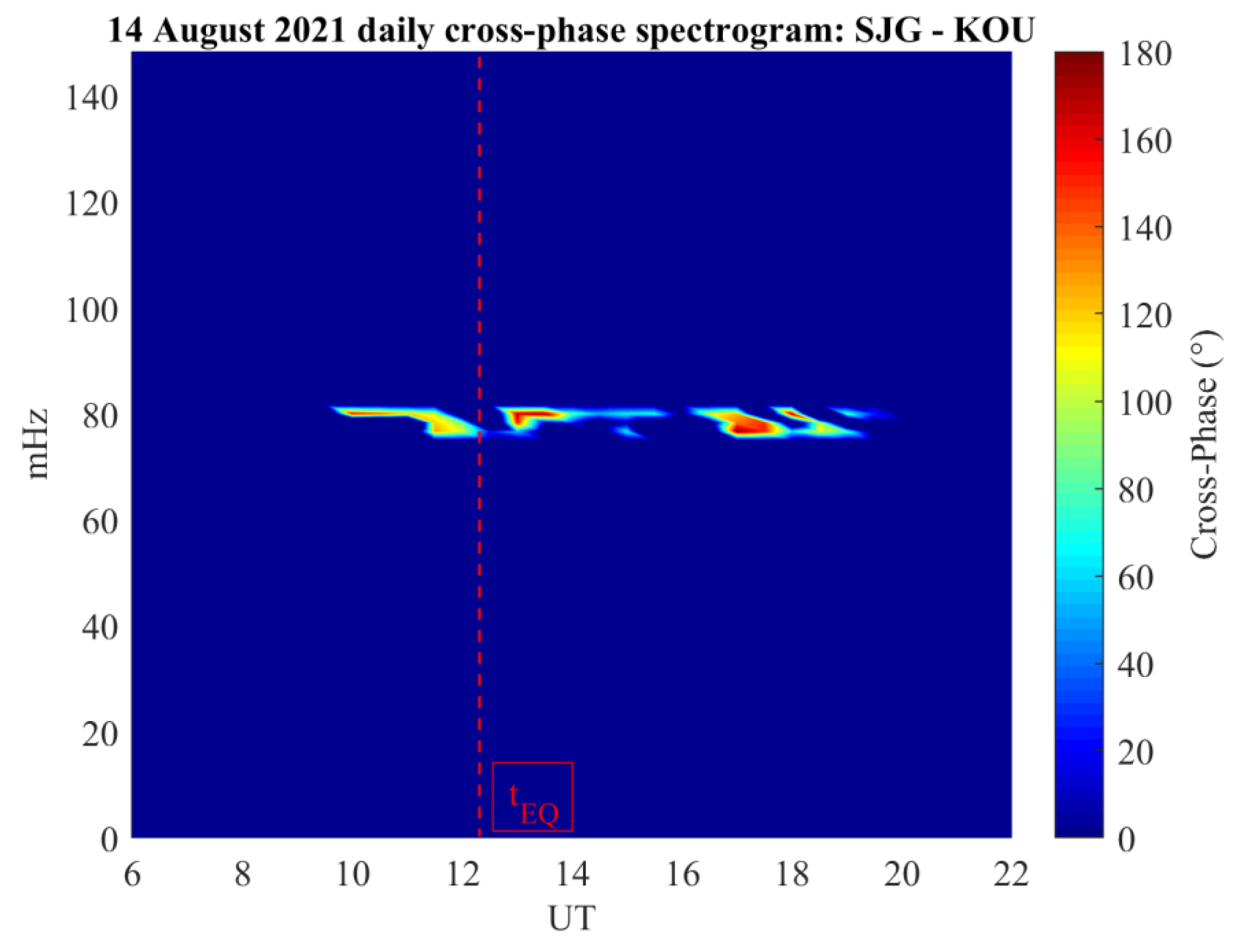
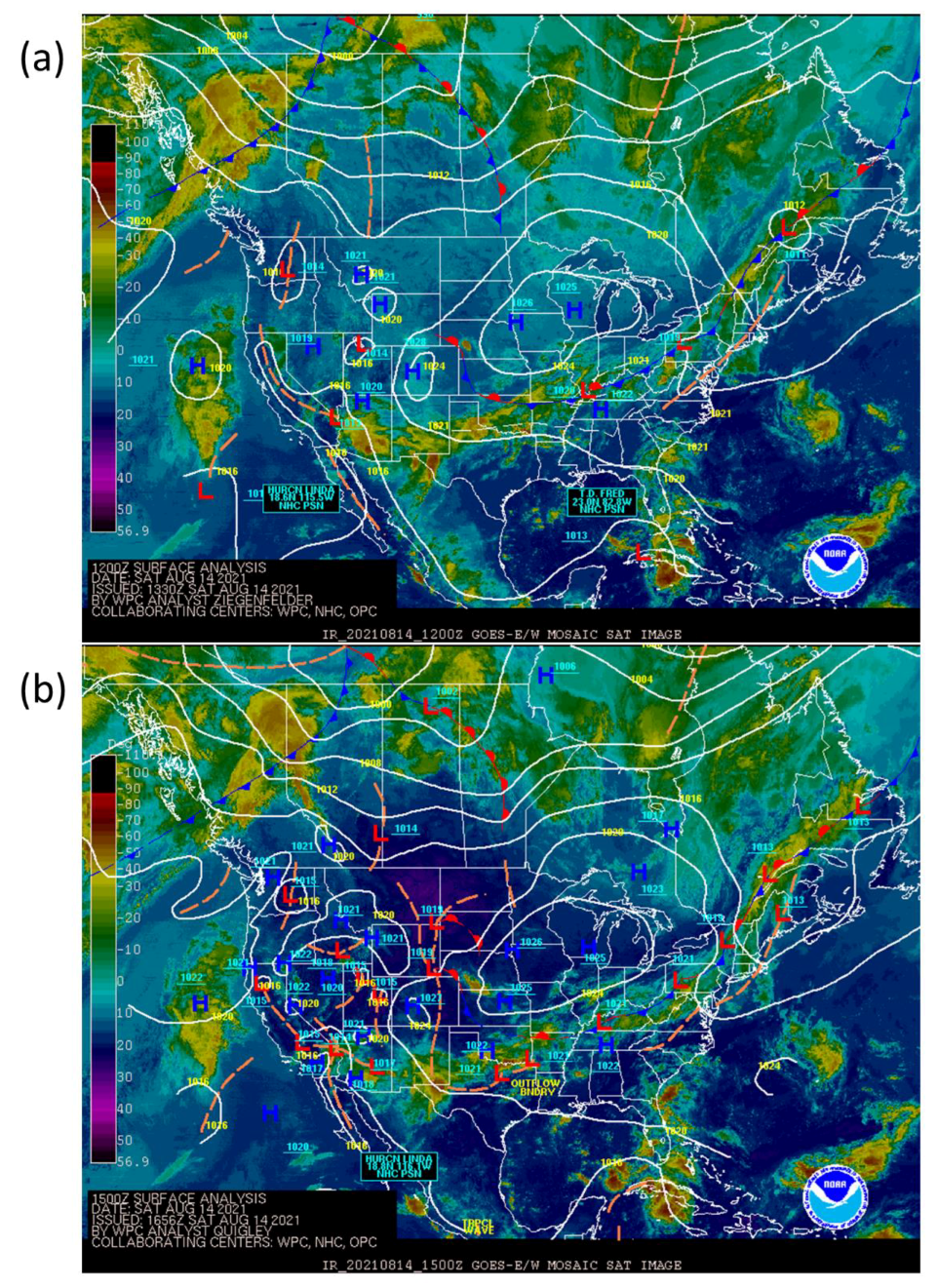
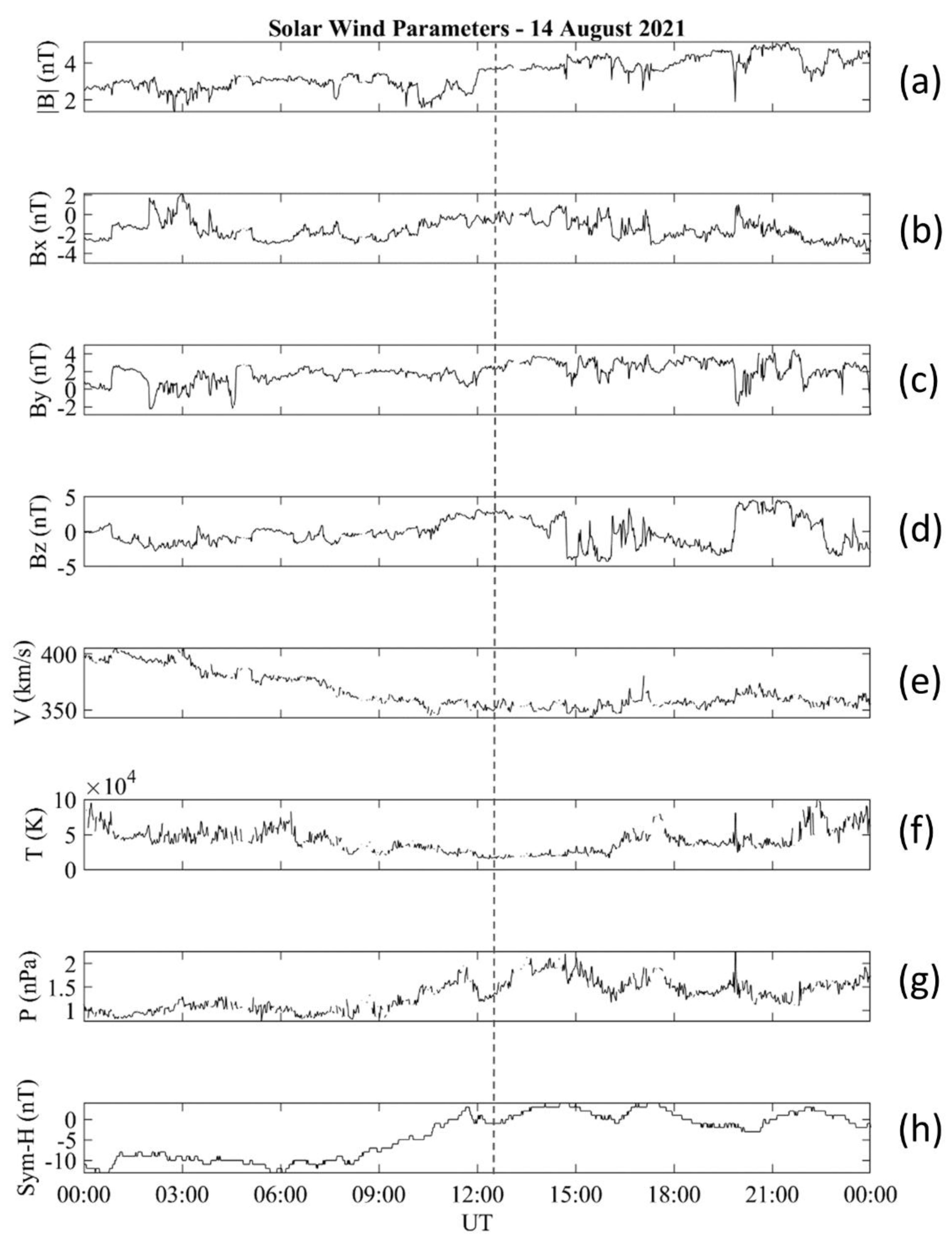
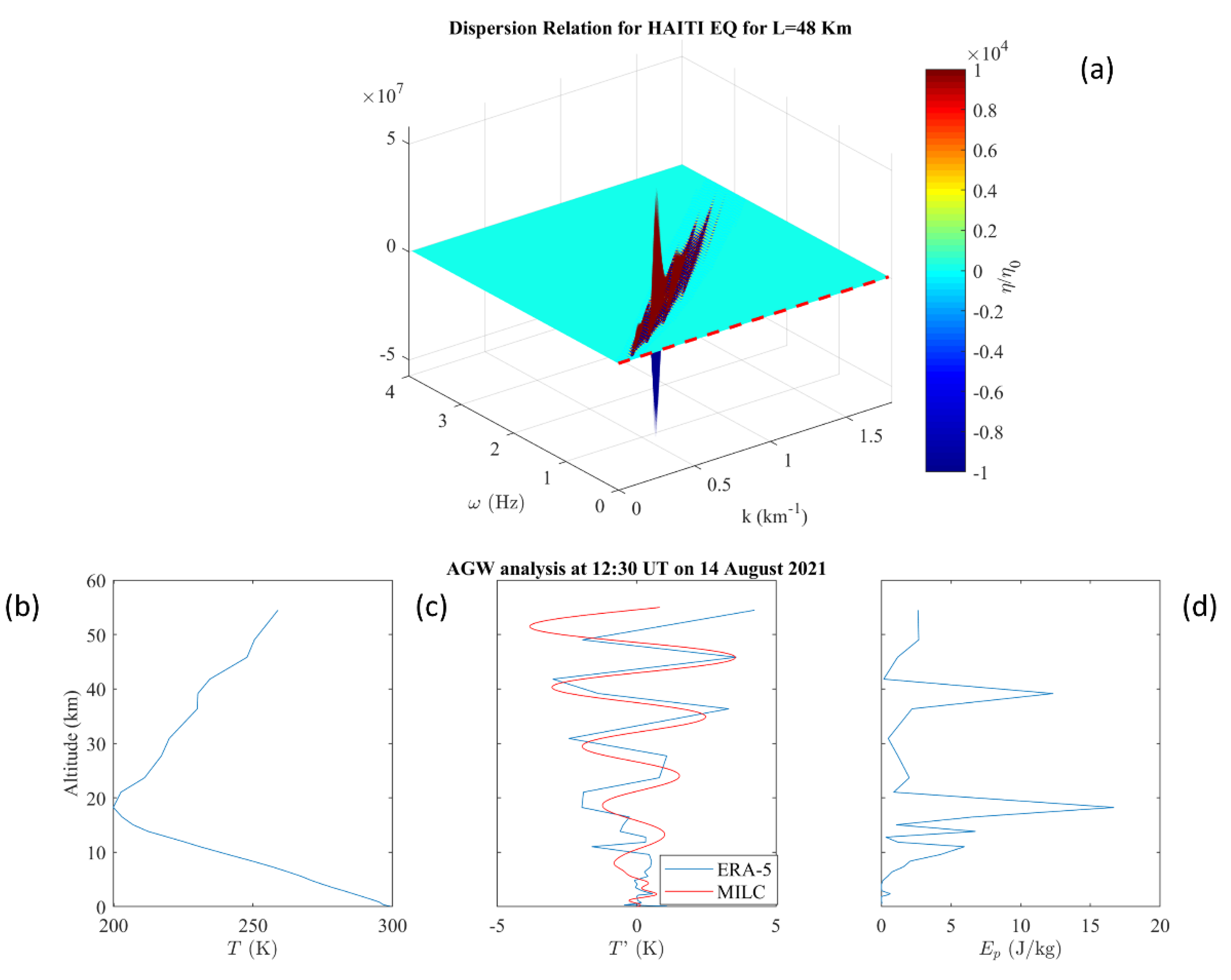
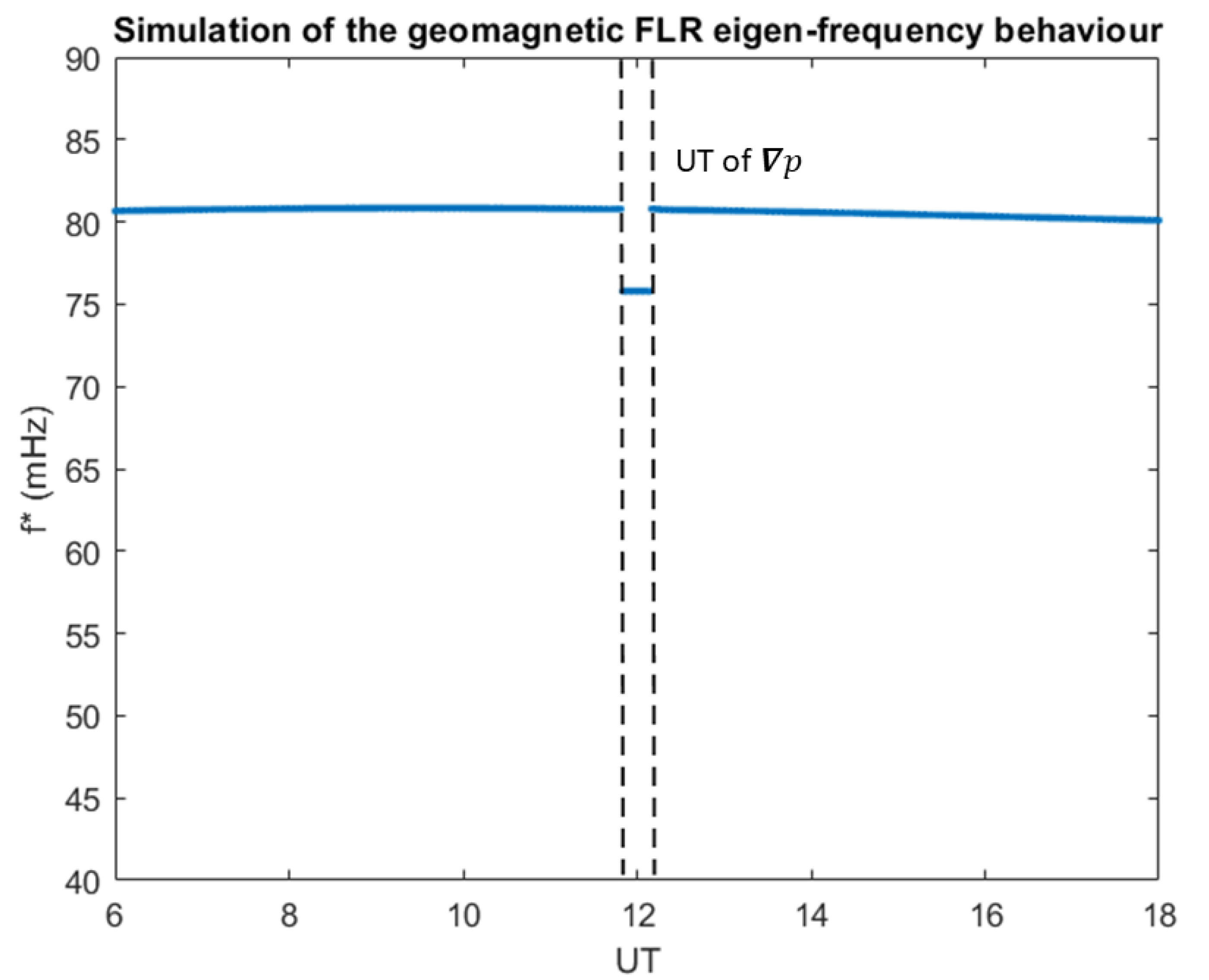
3. Results
4. Discussion
5. Conclusions
- An AGW in the atmosphere;
- A TID in the ionosphere;
- A change in the magnetospheric FLR eigenfrequency.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiong, H. Recent advances in the research on seismo-electromagnetic emissions. Acta Seismol. Sin. 1992, 5, 407–412. [Google Scholar] [CrossRef]
- Pulinets, S.; Boyarchuk, K. Ionospheric Precursors of Earthquakes; Springer Science & Business Media: Berlin, Germany, 2004. [Google Scholar]
- Battiston, R.; Vitale, V. First evidence for correlations between electron fluxes measured by NOAA-POES satellites and large seismic events. Nucl. Phys. B-Proc. Suppl. 2013, 243, 249–257. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sasmal, S.; Basak, T.; Chakrabarti, S.K. Comparative study of charged particle precipitation from Van Allen radiation belts as observed by NOAA satellites during a land earthquake and an ocean earthquake. Adv. Space Res. 2019, 64, 719–732. [Google Scholar] [CrossRef]
- Sgrigna, V.; Carota, L.; Conti, L.; Corsi, M.; Galper, A.; Koldashov, S.; Murashov, A.; Picozza, P.; Scrimaglio, R.; Stagni, L. Correlations between earthquakes and anomalous particle bursts from SAMPEX/PET satellite observations. J. Atmos. Sol.-Terr. Phys. 2005, 67, 1448–1462. [Google Scholar] [CrossRef]
- Astafyeva, E.I.; Afraimovich, E.L. Long-distance traveling ionospheric disturbances caused by the great Sumatra-Andaman earthquake on 26 December. Earth Planets Space 2006, 58, 1025–1031. [Google Scholar] [CrossRef]
- Calais, E.; Minster, J.B. GPS detection of ionospheric perturbations following the January 17, 1994, Northridge earthquake. Geophys. Res. Lett. 1995, 22, 1045–1048. [Google Scholar] [CrossRef]
- Heki, K.; Otsuka, Y.; Choosakul, N.; Hemmakorn, N.; Komolmis, T.; Maruyama, T. Detection of ruptures of Andaman fault segments in the 2004 great Sumatra earthquake with coseismic ionospheric disturbances. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Liu, J.; Tsai, H.; Lin, C.; Kamogawa, M.; Chen, Y.; Lin, C.; Huang, B.; Yu, S.; Yeh, Y. Coseismic ionospheric disturbances triggered by the Chi-Chi earthquake. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Bonan, G.B. Land-atmosphere interactions for climate system models: Coupling biophysical, biogeochemical, and ecosystem dynamical processes. Remote Sens. Environ. 1995, 51, 57–73. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Perevalova, N.P.; Plotnikov, A.; Uralov, A. The shock-acoustic waves generated by earthquakes. Ann. Geophys. 2001, 19, 395–409. [Google Scholar] [CrossRef]
- Meng, X.; Vergados, P.; Komjathy, A.; Verkhoglyadova, O. Upper atmospheric responses to surface disturbances: An observational perspective. Radio Sci. 2019, 54, 1076–1098. [Google Scholar] [CrossRef]
- Pokhotelov, O.; Parrot, M.; Fedorov, E.; Pilipenko, V.; Surkov, V.; Gladychev, V. Response of the ionosphere to natural and man-made acoustic sources. Ann. Geophys. 1995, 13, 1197–1210. [Google Scholar] [CrossRef]
- Piersanti, M.; Materassi, M.; Battiston, R.; Carbone, V.; Cicone, A.; D’Angelo, G.; Diego, P.; Ubertini, P. Magnetospheric–ionospheric–lithospheric coupling model. 1: Observations during the 5 August 2018 Bayan Earthquake. Remote Sens. 2020, 12, 3299. [Google Scholar] [CrossRef]
- Carbone, V.; Piersanti, M.; Materassi, M.; Battiston, R.; Lepreti, F.; Ubertini, P. A mathematical model of lithosphere–atmosphere coupling for seismic events. Sci. Rep. 2021, 11, 8682. [Google Scholar] [CrossRef] [PubMed]
- Piersanti, M.; Burger, W.J.; Carbone, V.; Battiston, R.; Iuppa, R.; Ubertini, P. On the Geomagnetic Field Line Resonance Eigenfrequency Variations during Seismic Event. Remote Sens. 2021, 13, 2839. [Google Scholar] [CrossRef]
- Yang, S.S.; Pan, C.-J.; Das, U. Investigating the Spatio-Temporal Distribution of Gravity Wave Potential Energy over the Equatorial Region Using the ERA5 Reanalysis Data. Atmosphere 2021, 12, 311. [Google Scholar] [CrossRef]
- De la Torre, A.; Alexander, P.; Giraldez, A. The kinetic to potential energy ratio and spectral separability from high-resolution balloon soundings near the Andes Mountains. Geophys. Res. Lett. 1999, 26, 1413–1416. [Google Scholar] [CrossRef]
- VanZandt, T. A model for gravity wave spectra observed by Doppler sounding systems. Radio Sci. 1985, 20, 1323–1330. [Google Scholar] [CrossRef]
- Cai, X.; Yuan, T.; Liu, H.-L. Large-scale gravity wave perturbations in the mesopause region above Northern Hemisphere midlatitudes during autumnal equinox: A joint study by the USU Na lidar and Whole Atmosphere Community Climate Model. Ann. Geophys. 2017, 35, 181–188. [Google Scholar] [CrossRef]
- Lu, X.; Chu, X.; Fong, W.; Chen, C.; Yu, Z.; Roberts, B.R.; McDonald, A.J. Vertical evolution of potential energy density and vertical wave number spectrum of Antarctic gravity waves from 35 to 105 km at McMurdo (77.8 S, 166.7 E). J. Geophys. Res. Atmos. 2015, 120, 2719–2737. [Google Scholar] [CrossRef]
- Tsuda, T.; Nishida, M.; Rocken, C.; Ware, R.H. A global morphology of gravity wave activity in the stratosphere revealed by the GPS occultation data (GPS/MET). J. Geophys. Res. Atmos. 2000, 105, 7257–7273. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Hennermann, K.; Berrisford, P. ERA5 Data Documentation; Copernicus Knowledge Base. 2017. Available online: https://confluence.ecmwf.int/display/CKB/ERA5%3A+data+documentation (accessed on 20 October 2022).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis, QJ Roy. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Ciraolo, L.; Azpilicueta, F.; Brunini, C.; Meza, A.; Radicella, S.M. Calibration errors on experimental slant total electron content (TEC) determined with GPS. J. Geod. 2007, 81, 111–120. [Google Scholar] [CrossRef]
- Cesaroni, C.; Spogli, L.; Alfonsi, L.; De Franceschi, G.; Ciraolo, L.; Monico, J.F.G.; Scotto, C.; Romano, V.; Aquino, M.; Bougard, B. L-band scintillations and calibrated total electron content gradients over Brazil during the last solar maximum. J. Space Weather. Space Clim. 2015, 5, A36. [Google Scholar] [CrossRef]
- Cicone, A.; Zhou, H. Numerical analysis for iterative filtering with new efficient implementations based on FFT. Numer. Math. 2021, 147, 1–28. [Google Scholar] [CrossRef]
- Lin, L.; Wang, Y.; Zhou, H. Iterative filtering as an alternative algorithm for empirical mode decomposition. Adv. Adapt. Data Anal. 2009, 1, 543–560. [Google Scholar] [CrossRef]
- Piersanti, M.; Alberti, T.; Bemporad, A.; Berrilli, F.; Bruno, R.; Capparelli, V.; Carbone, V.; Cesaroni, C.; Consolini, G.; Cristaldi, A. Comprehensive analysis of the geoeffective solar event of 21 June 2015: Effects on the magnetosphere, plasmasphere, and ionosphere systems. Sol. Phys. 2017, 292, 169. [Google Scholar] [CrossRef]
- Cicone, A.; Pellegrino, E. Multivariate fast iterative filtering for the decomposition of nonstationary signals. IEEE Trans. Signal Process. 2022, 70, 1521–1531. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Cicone, A. Iterative filtering as a direct method for the decomposition of nonstationary signals. Numer. Algorithms 2020, 85, 811–827. [Google Scholar] [CrossRef]
- Flandrin, P. Time-Frequency/Time-Scale Analysis; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Crowley, G.; Rodrigues, F. Characteristics of traveling ionospheric disturbances observed by the TIDDBIT sounder. Radio Sci. 2012, 47, 1–12. [Google Scholar] [CrossRef]
- Menk, F.W.; Waters, C.L. Magnetoseismology: Ground-Based remote Sensing of Earth’s Magnetosphere; VCH: Weinheim, Germany, 2013; p. 251. ISBN 978-3-527-41027-9. [Google Scholar]
- Okuwaki, R.; Fan, W. Oblique Convergence Causes Both Thrust and Strike-Slip Ruptures During the 2021 M 7.2 Haiti Earthquake. Geophys. Res. Lett. 2022, 49, e2021GL096373. [Google Scholar] [CrossRef]
- Tsuda, T.; Murayama, Y.; Nakamura, T.; Vincent, R.; Manson, A.; Meek, C.; Wilson, R. Variations of the gravity wave characteristics with height, season and latitude revealed by comparative observations. J. Atmos. Terr. Phys. 1994, 56, 555–568. [Google Scholar] [CrossRef]
- Waters, C.; Samson, J.; Donovan, E. Variation of plasmatrough density derived from magnetospheric field line resonances. J. Geophys. Res. Space Phys. 1996, 101, 24737–24745. [Google Scholar] [CrossRef]
- Vellante, M.; Piersanti, M.; Pietropaolo, E. Comparison of equatorial plasma mass densities deduced from field line resonances observed at ground for dipole and IGRF models. J. Geophys. Res. Space Phys. 2014, 119, 2623–2633. [Google Scholar] [CrossRef]
- Šindelářová, T.; Burešová, D.; Chum, J. Observations of acoustic-gravity waves in the ionosphere generated by severe tropospheric weather. Stud. Geophys. Et Geod. 2009, 53, 403–418. [Google Scholar] [CrossRef]
- King, J.; Papitashvili, N. Solar wind spatial scales in and comparisons of hourly Wind and ACE plasma and magnetic field data. J. Geophys. Res. Space Phys. 2005, 110. [Google Scholar] [CrossRef]


| IAGA Code | Name | Country | Latitude | Longitude | Magnetic Latitude | Magnetic LONGITUDE |
|---|---|---|---|---|---|---|
| KOU | Kourou | French Guiana | 5.21° | 307.27° | 10.89° | 235.91° |
| SJG | San Juan | USA | 18.11° | 293.85° | 25.08° | 224.44° |
| Date | L (km) | ωs | PGA (g) | α (s) | vs | ks 10−5 | ωs | |
|---|---|---|---|---|---|---|---|---|
| Haiti | 14 August 2021 | 48 | 0.041 | 0.6 | 48.5 | 2.2 | 1.8 | 0.058 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Angelo, G.; Piersanti, M.; Battiston, R.; Bertello, I.; Carbone, V.; Cicone, A.; Diego, P.; Papini, E.; Parmentier, A.; Picozza, P.; et al. Haiti Earthquake (Mw 7.2): Magnetospheric–Ionospheric–Lithospheric Coupling during and after the Main Shock on 14 August 2021. Remote Sens. 2022, 14, 5340. https://doi.org/10.3390/rs14215340
D’Angelo G, Piersanti M, Battiston R, Bertello I, Carbone V, Cicone A, Diego P, Papini E, Parmentier A, Picozza P, et al. Haiti Earthquake (Mw 7.2): Magnetospheric–Ionospheric–Lithospheric Coupling during and after the Main Shock on 14 August 2021. Remote Sensing. 2022; 14(21):5340. https://doi.org/10.3390/rs14215340
Chicago/Turabian StyleD’Angelo, Giulia, Mirko Piersanti, Roberto Battiston, Igor Bertello, Vincenzo Carbone, Antonio Cicone, Piero Diego, Emanuele Papini, Alexandra Parmentier, Piergiorgio Picozza, and et al. 2022. "Haiti Earthquake (Mw 7.2): Magnetospheric–Ionospheric–Lithospheric Coupling during and after the Main Shock on 14 August 2021" Remote Sensing 14, no. 21: 5340. https://doi.org/10.3390/rs14215340
APA StyleD’Angelo, G., Piersanti, M., Battiston, R., Bertello, I., Carbone, V., Cicone, A., Diego, P., Papini, E., Parmentier, A., Picozza, P., Plainaki, C., Recchiuti, D., Sparvoli, R., & Ubertini, P. (2022). Haiti Earthquake (Mw 7.2): Magnetospheric–Ionospheric–Lithospheric Coupling during and after the Main Shock on 14 August 2021. Remote Sensing, 14(21), 5340. https://doi.org/10.3390/rs14215340