Feasibility Analysis of GPS L2C Signals for SSV Receivers on SBAS GEO Satellites
Abstract
1. Introduction
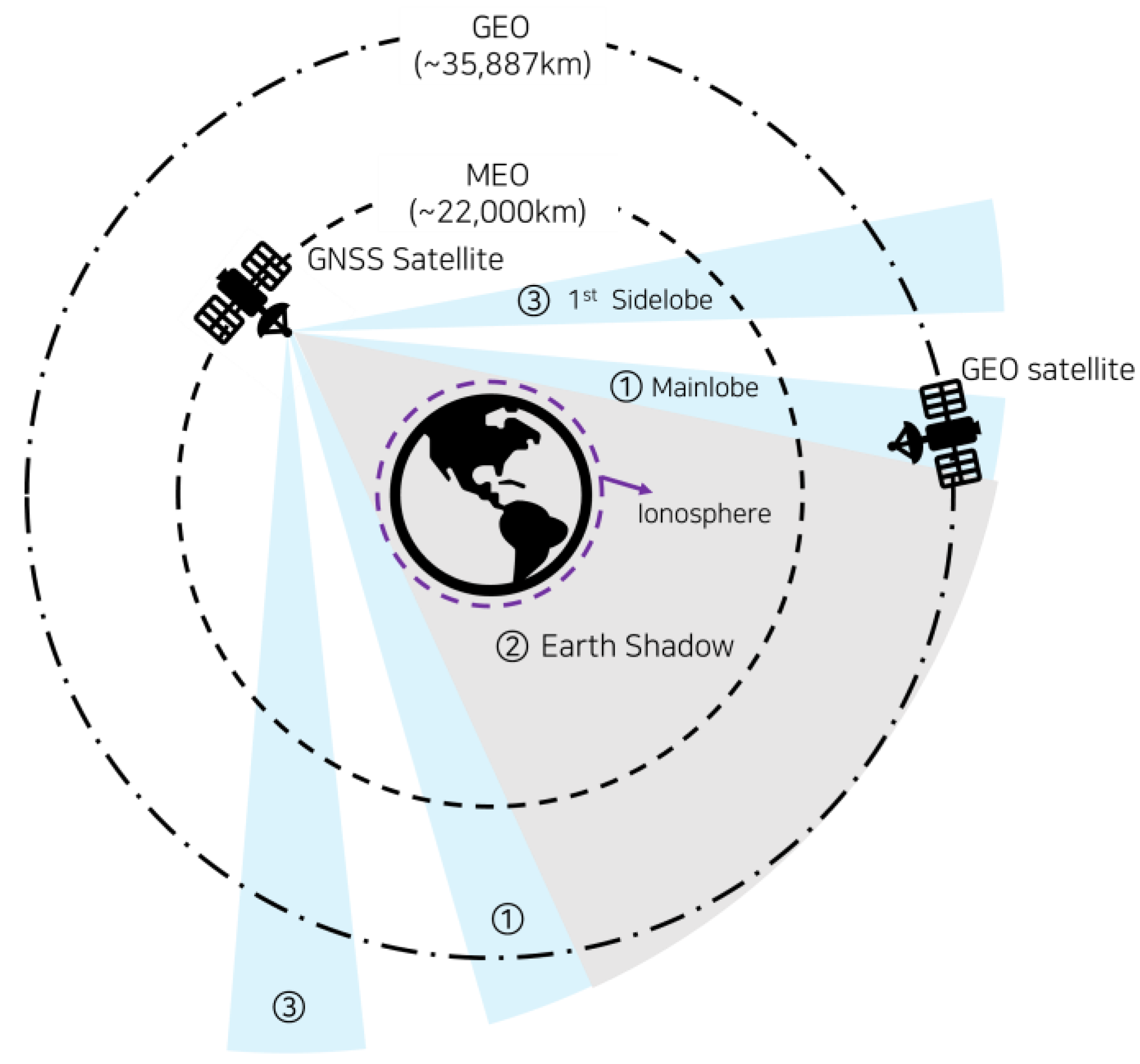
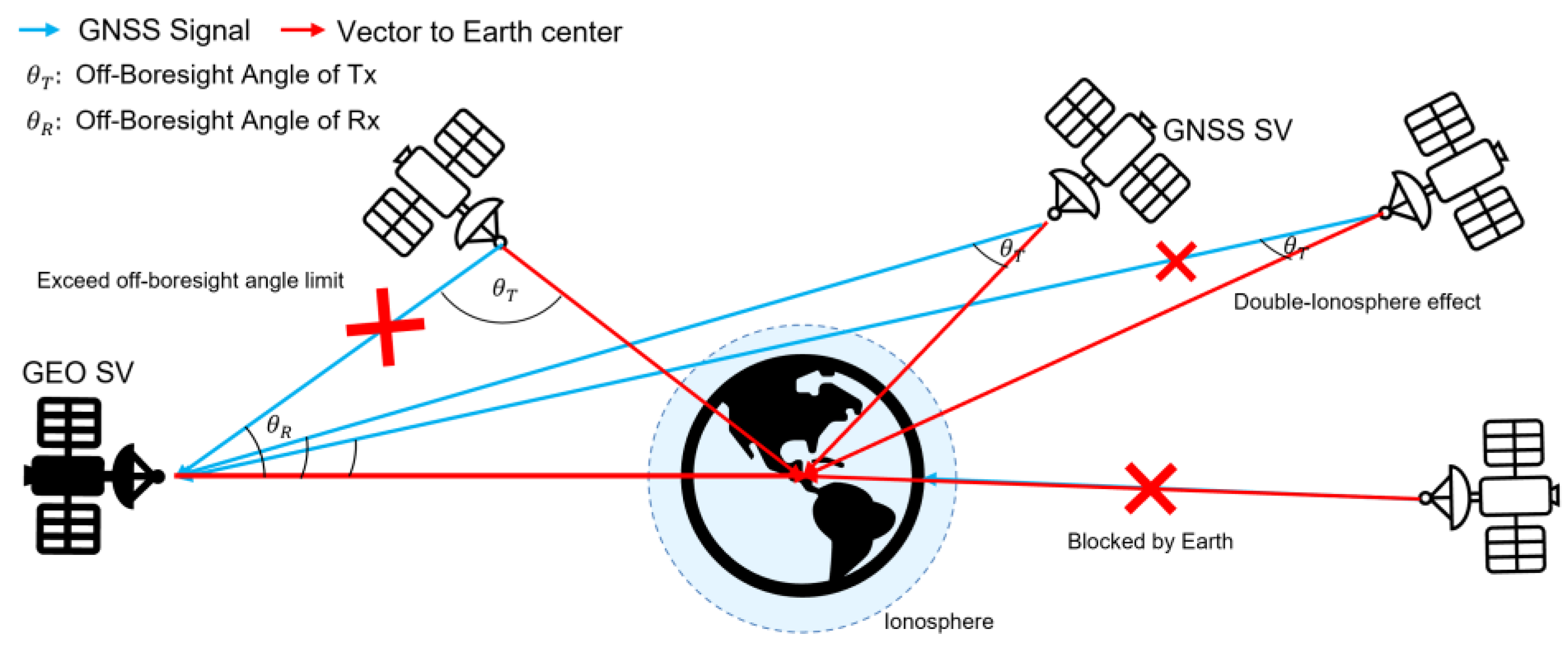
2. Assumption of Isolation between GNSS and SBAS signals
3. Feasibility Analysis
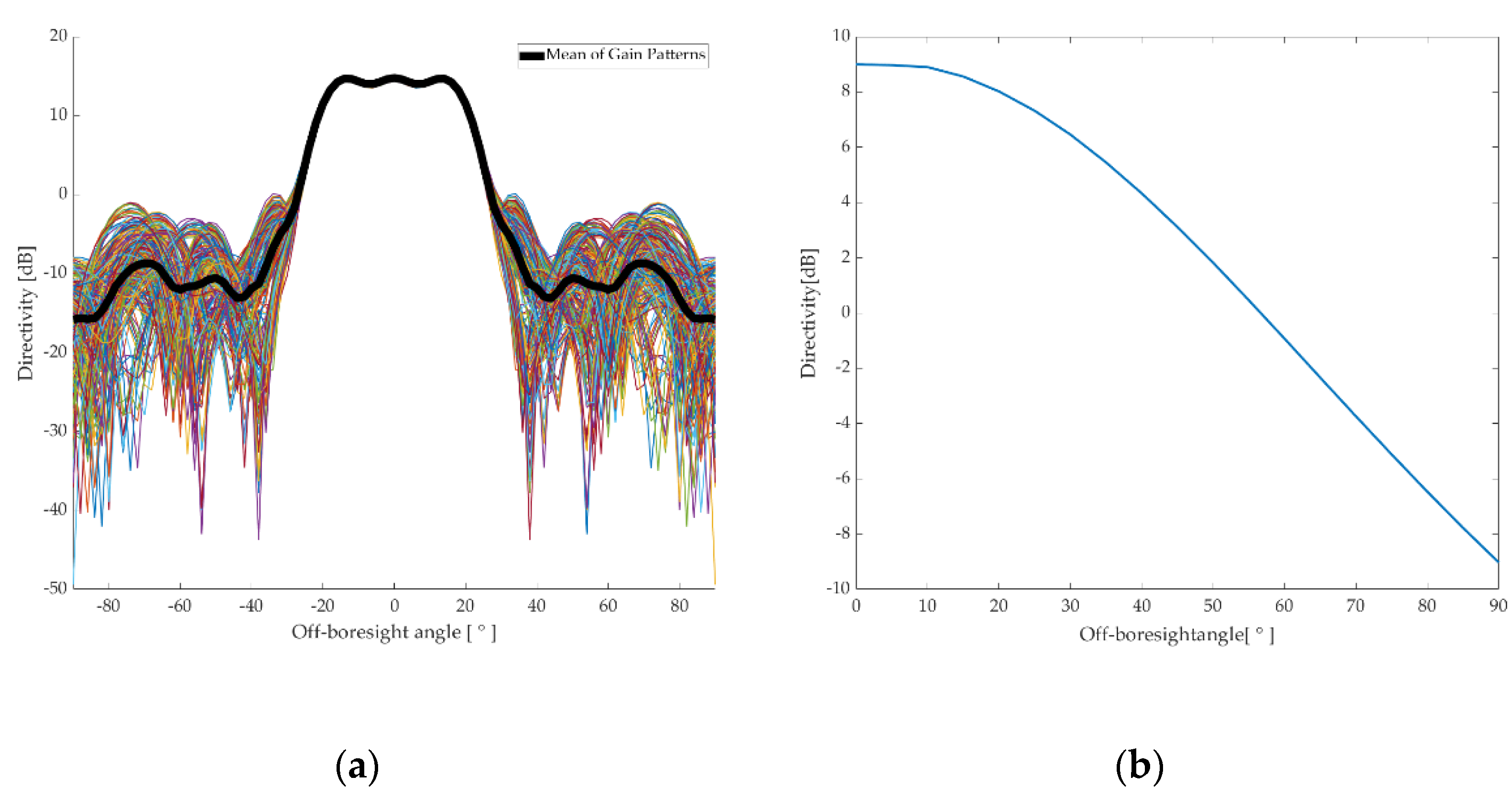
3.1. Satellite Visibility Analysis
3.2. GDOP and Navigation Error
4. Results
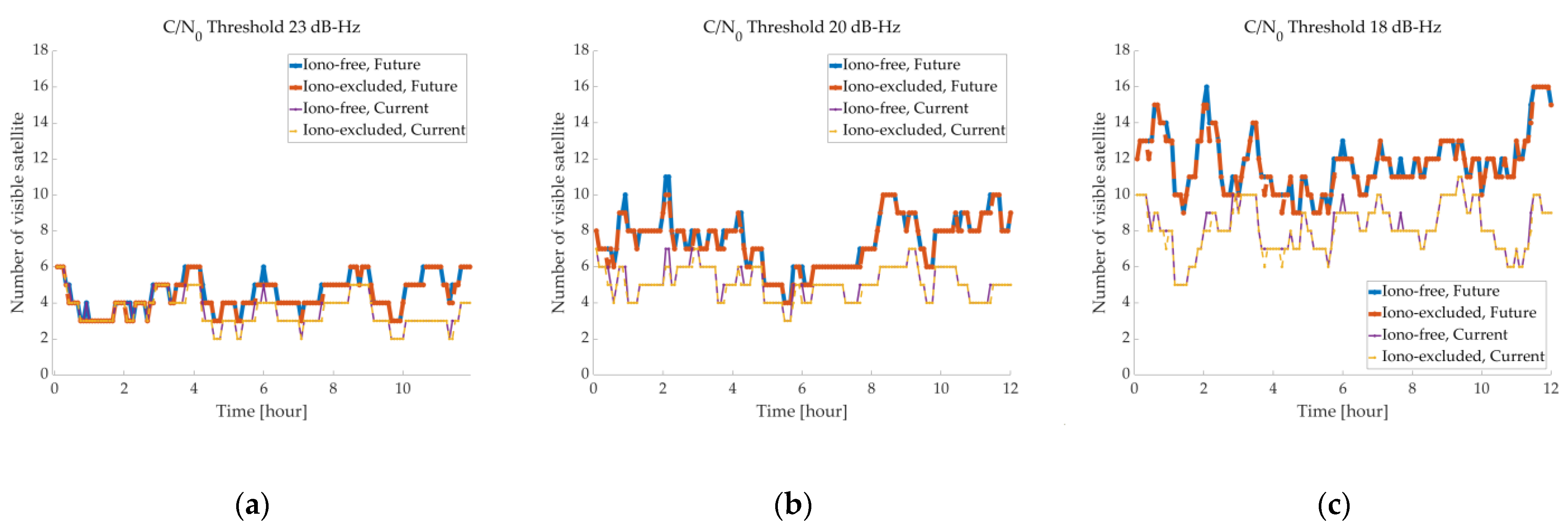
4.1. Satellite Visibility
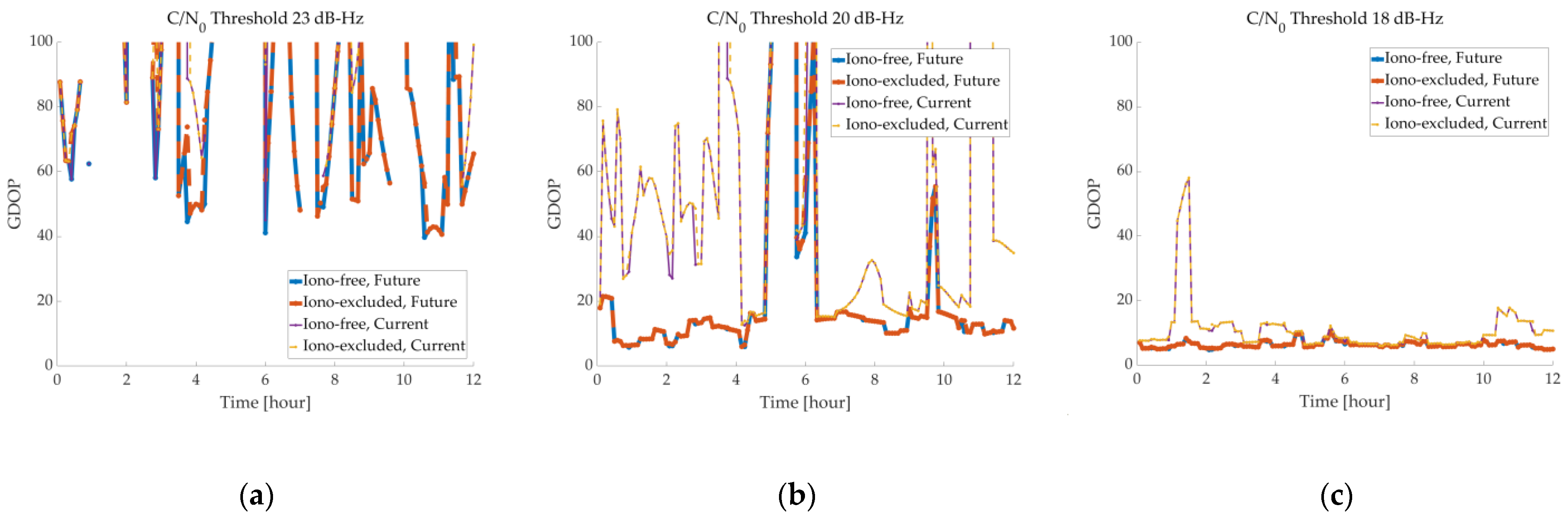
4.2. GDOP
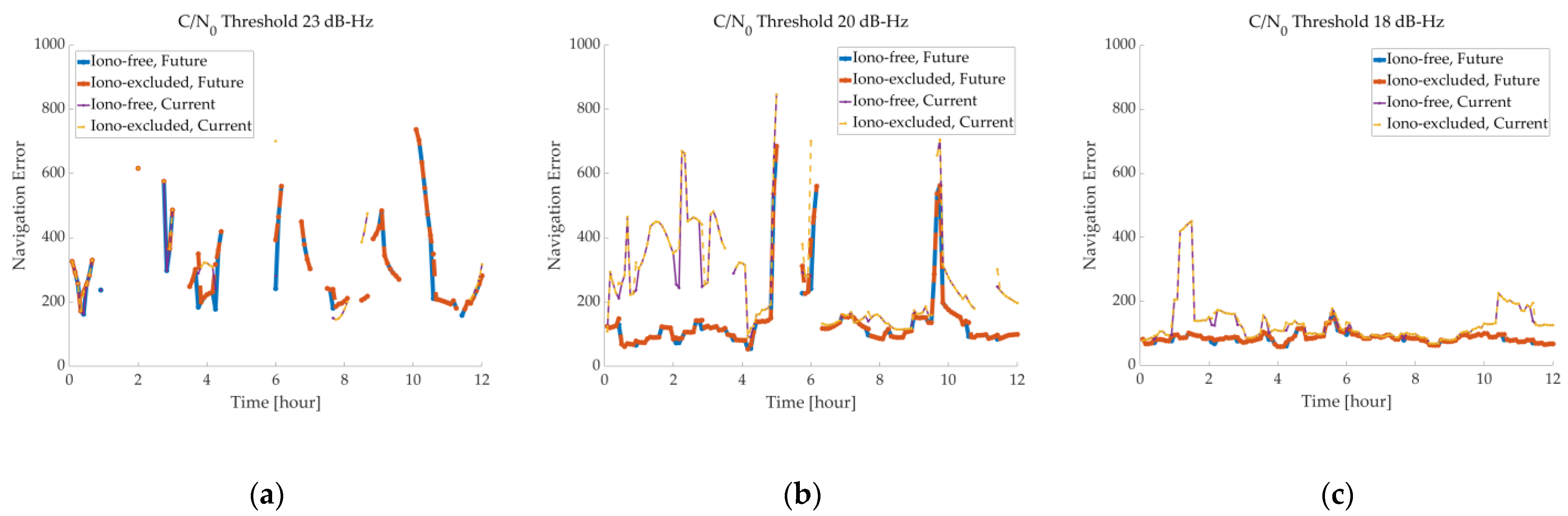
4.3. Navigation Error
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bauer, F.H.; Moreau, M.C.; Dahle-Melsaether, M.E.; Petrofski, W.P.; Stanton, B.J.; Thomason, S.; Harris, G.A.; Sena, R.P.; Parker, T., III. The GPS space service volume. In Proceedings of the 19th International Technical meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2006), Fort Worth, TX, USA, 26–29 September 2006. [Google Scholar]
- Park, Y.; Kwon, K.-H.; Won, J.-H. Performance analysis of multi-constellation and multi-frequency GNSS receivers in deep space. In Proceedings of the 30th International Technical meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 1127–1132. [Google Scholar]
- Enderle, W.; Gini, F.; Boomkamp, H.; Parker, J.J.; Ashman, B.W.; Welch, B.W.; Koch, M.; Sands, O.S. Space user visibility benefits of the multi-GNSS Space Service Volume: An internationally-coordinated, global and mission-specific analysis. In Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 1191–1207. [Google Scholar]
- United Nations. The Interoperable Global Navigation Satellite Systems Space Service Volume; United Nations Office for Outer Space Affairs: Vienna, Austria, 2018. [Google Scholar]
- Moreau, M.C.; Davis, E.P.; Carpenter, J.; Russell, K.; David, D.; George, W.; Axelrad, P. Results from the GPS Flight Experiment on the High Earth Orbit AMSAT OSCAR-40 Spacecraft. In Proceedings of the 15th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2002), Portland, OR, USA, 24–27 September 2002. [Google Scholar]
- Su, X.; Geng, T.; Li, W.; Zhao, Q.; Xie, X. Chang’E-5T orbit determination using onboard GPS observations. Sensors 2017, 17, 1260. [Google Scholar] [CrossRef] [PubMed]
- Winkler, S.; Ramsey, G.; Frey, C.; Chapel, J.; Chu, D.; Freesland, D.; Krimchansky, A.; Concha, M. GPS receiver on-orbit performance for the GOES-R spacecraft. In Proceedings of the 10th International ESA Conference on Guidance, Navigation & Control Systems, Salzburg, Austria, 29 May–2 June 2017. [Google Scholar]
- Ji, G.-H.; Kwon, K.-H.; Won, J.-H. GNSS signal availability analysis in SSV for geostationary satellites utilizing multi-GNSS with first side lobe signal over the Korean Region. Remote Sens. 2021, 13, 3852. [Google Scholar] [CrossRef]
- Ji, G.-H.; Shin, H.; Won, J.-H. Analysis of multi-constellation GNSS receiver performance utilizing 1-st side-lobe signal on the use of SSV for KPS satellites. IET Radar Sonar Navig. 2021, 15, 485–499. [Google Scholar] [CrossRef]
- Lin, K.; Zhan, X.; Yang, R.; Shao, F.; Huang, J. BDS Space Service Volume characterizations considering side-lobe signals and 3D antenna pattern. Aerosp. Sci. Technol. 2020, 106, 106071. [Google Scholar] [CrossRef]
- Bunce, D. Wide area augmentation system (WAAS) status and history. In Proceedings of the 27th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2014), Tampa, FL, USA, 8–12 September 2014. [Google Scholar]
- European Union Agency for the Space Programme. Available online: https://www.euspa.europa.eu/european-space/egnos/egnos-system (accessed on 4 May 2022).
- GAGAN Redefining Navigation. Available online: https://gagan.aai.aero/gagan/content/gagan-working (accessed on 4 May 2022).
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS/GNSS Principles and Applications, 3rd ed.; Artech House: Norwood, MA, USA, 2017; pp. 662–668. [Google Scholar]
- CelesTrak, GPS Yuma Almanacs. Available online: https://celestrak.com/GPS/almanac/Yuma/ (accessed on 4 May 2022).
- GPS.gov. Available online: https://www.gps.gov/systems/gps/space/ (accessed on 4 May 2022).
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2006; ISBN 9780970954411. [Google Scholar]
- Marquis, W.A.; Reigh, D.L. The GPS Block IIR and IIR-M Broadcast L-band Antenna Panel: Its Pattern and Performance. Navig. J. Inst. Navig. 2015, 62, 329–347. [Google Scholar] [CrossRef]
- Dunn, M.J. NAVSTAR GPS Space Segment/Navigation User Interfaces, IS-GPS-200M; U.S. Space Force: Washington, DC, USA, 2021; pp. 15–17. [Google Scholar]
- Betz, J.W.; Kolodziejski, K.R. Generalized theory of GPS code tracking accuracy with an Early-Late discriminator. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1538–1564. [Google Scholar] [CrossRef]
- Betz, J.W.; Kolodziejski, K.R. Extended theory of Early-Late code tracking for a bandlimited GPS receiver. J. Inst. Navig. 2000, 47, 211–226. [Google Scholar] [CrossRef]
- Jiang, K.; Li, M.; Wang, M.; Zhao, Q.; Li, W. TJS-2 geostationary satellite orbit determination using onboard GPS measurements. GPS Solut. 2018, 22, 87. [Google Scholar] [CrossRef]
| Required Isolation Performance (dB) | |||||||
|---|---|---|---|---|---|---|---|
| EIRP | Receiving Signal Power Compensation | Margin | Total | ||||
| 62 | 130 | 10 | 202 | ||||
| Theoretical Maximum Isolation Performance (dB) | |||||||
| Antenna Isolation | Antenna Directivity Isolation | Antenna Polarization | Physical Shielding | Total | |||
| 42.4 | 60 | 20 | 30 | 152.4 | |||
| Block Type | PRN |
|---|---|
| IIR | 2, 13, 16, 19, 20, 21, 22, 28 |
| IIR-M | 5, 7, 12, 15, 17, 29, 31 |
| IIF | 1, 3, 6, 8, 9, 10, 24, 25, 26, 27, 30, 32 |
| III | 4, 14, 18, 23 |
| Block Type | Minimum Received Power |
|---|---|
| IIR-M/IIF | −160.0 dB·W |
| III | −158.5 dB·W |
| Parameter | Configuration | |
|---|---|---|
| Simulation time | 12 h, time epoch: 300 s (5 min) | |
| GPS constellation | Current/future | |
| User position | GEO (over the Korean peninsula, 128 °E, 36,000 km) | |
| Rx antenna | High-gain antenna (up to 9 dBi) | |
| Ionosphere height | 400 km (iono-excluded)/0 km (iono-free) | |
| Receiver parameters | C/N0 threshold | 18/20/23 dB·Hz |
| DLL noise bandwidth () | 1 Hz | |
| Frond-end bandwidth () | 4 MHz | |
| Early–late correlator spacing (D) | 0.1 chips | |
| Coherent integration time (T) | 20 ms | |
| Code chip width () | 1/0.5115 µs | |
| C/N0 Threshold (dB·Hz) | Current | Future | |||
|---|---|---|---|---|---|
| Iono-Free | Iono-Excluded | Iono-Free | Iono-Excluded | ||
| Average number of visible SV | 23 | 3.59 | 3.51 | 4.52 | 4.44 |
| 20 | 5.16 | 5.08 | 7.47 | 7.39 | |
| 18 | 8.22 | 8.15 | 11.83 | 11.75 | |
| Visible SV > 4 (%) | 23 | 47.92 | 43.75 | 84.03 | 81.94 |
| 20 | 97.92 | 97.92 | 100 | 100 | |
| 18 | 100 | 100 | 100 | 100 | |
| C/N0 Threshold (dB·Hz) | Current | Future | |||
|---|---|---|---|---|---|
| Iono-Free | Iono-Excluded | Iono-Free | Iono-Excluded | ||
| Average GDOP | 23 | 75.88 | 79.18 | 64.59 | 65.85 |
| 20 | 36.19 | 36.52 | 16.03 | 16.25 | |
| 18 | 10.94 | 11.01 | 6.34 | 6.37 | |
| Time ratio of GDOP < 100 (%) | 23 | 25.00 | 21.53 | 53.47 | 51.39 |
| 20 | 85.42 | 84.72 | 93.75 | 93.75 | |
| 18 | 100 | 100 | 100 | 100 | |
| C/N0 Threshold (dB·Hz) | Current | Future | |||
|---|---|---|---|---|---|
| Iono-Free | Iono-Excluded | Iono-Free | Iono-Excluded | ||
| Mean range error | 23 | 4.59 | 4.66 | 4.47 | 4.81 |
| 20 | 7.70 | 7.79 | 8.82 | 8.90 | |
| 18 | 12.65 | 12.76 | 13.51 | 13.60 | |
| Mean navigation error (m) | 23 | 293.89 | 317.86 | 302.79 | 315.47 |
| 20 | 263.97 | 273.39 | 136.33 | 139.44 | |
| 18 | 130.21 | 132.16 | 85.35 | 86.35 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.-B.; Kwon, K.-H.; Won, J.-H. Feasibility Analysis of GPS L2C Signals for SSV Receivers on SBAS GEO Satellites. Remote Sens. 2022, 14, 5329. https://doi.org/10.3390/rs14215329
Lee H-B, Kwon K-H, Won J-H. Feasibility Analysis of GPS L2C Signals for SSV Receivers on SBAS GEO Satellites. Remote Sensing. 2022; 14(21):5329. https://doi.org/10.3390/rs14215329
Chicago/Turabian StyleLee, Hak-Beom, Ki-Ho Kwon, and Jong-Hoon Won. 2022. "Feasibility Analysis of GPS L2C Signals for SSV Receivers on SBAS GEO Satellites" Remote Sensing 14, no. 21: 5329. https://doi.org/10.3390/rs14215329
APA StyleLee, H.-B., Kwon, K.-H., & Won, J.-H. (2022). Feasibility Analysis of GPS L2C Signals for SSV Receivers on SBAS GEO Satellites. Remote Sensing, 14(21), 5329. https://doi.org/10.3390/rs14215329





