1. Introduction
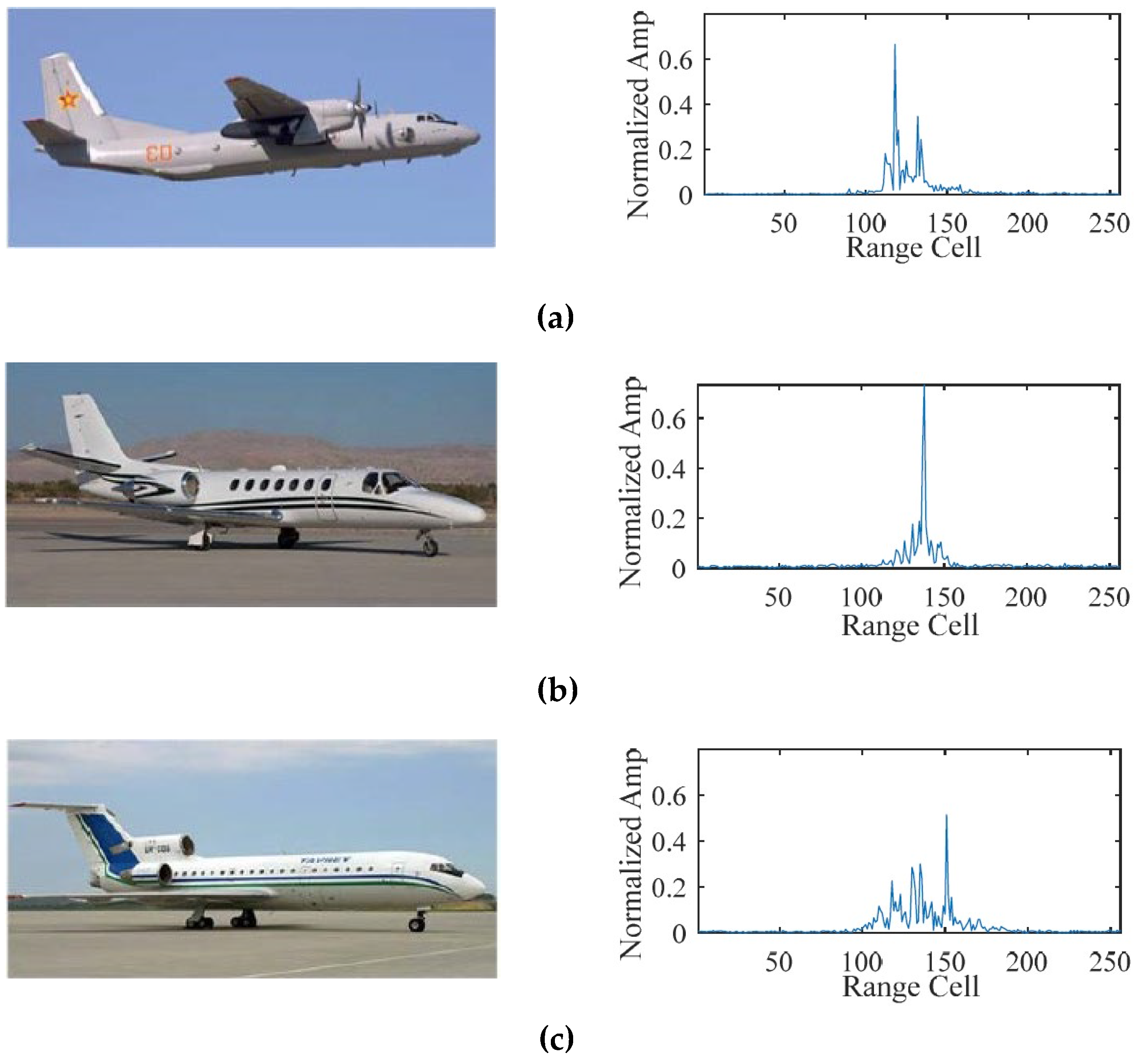
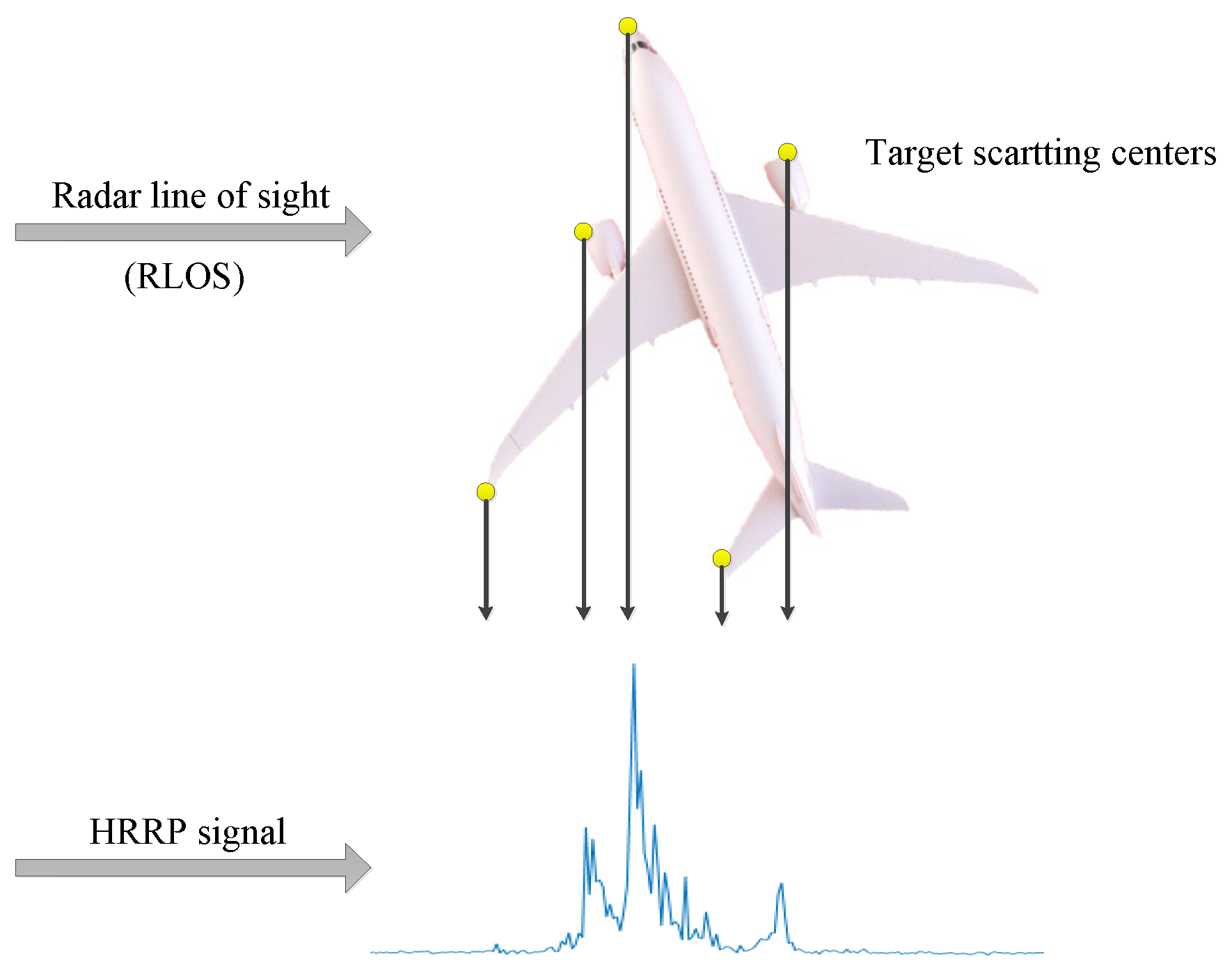
The high-resolution range profile (HRRP) of a target represents the 1D projection of its scattering centers along the radar line of sight (LOS), as shown in
Figure 1. Compared with the 2D inverse synthetic aperture radar (ISAR) image, the HRRP is easier to acquire, store, and process. Moreover, it contains abundant structural signatures of the target such as the shape, size, and location of the main parts. Currently, automatic radar target recognition based on HRRP has received increasing attention in the radar automatic target recognition (RATR) community [
1,
2,
3,
4,
5].
HRRP recognition can be achieved by traditional methods and deep learning. Traditional HRRP recognition methods [
6,
7,
8,
9,
10,
11,
12] mainly depend on manually designed features and classifiers, which require extensive domain knowledge. Additionally, their heavy computational burden and poor generalization performance hinder practical application. Recently, HRRP recognition based on deep learning has avoided the tedious process of feature design and selection, and achieved much better performance than traditional approaches [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22].
In real-world situations, however, the existence of strong noise will lead to a low signal-to-noise ratio (SNR) and hinder effective feature extraction. To deal with this issue, the available methods implement denoising firstly and then carry out feature extraction and recognition [
19]. In terms of deep neural networks, however, such two-stage processing prohibits end-to-end training, resulting in complicated processing as well as long operational time. Furthermore, decoupling denoising from recognition ignores the potential requirements for noise suppression and signal extraction when fulfilling effective recognition. Therefore, it is natural to study the network structure integrating denoising and recognition to boost the performance and efficiency.
Traditional HRRP recognition methods are mainly divided into three categories: (1) feature domain transformation [
6,
7,
8]; (2) statistical modeling [
3,
4,
5,
9,
10]; and (3) kernel methods [
11,
12]. The first category obtains features in the transformation domain, e.g., the bispectra domain [
6], by data projection, and then designs proper classifiers for HRRP recognition. The over-dependency on the prior knowledge, however, induces degraded performance and robustness in complex scenarios where priors are improper or unavailable. The second category establishes statistical models by imposing specific distributions, e.g., Gaussian [
5], on the HRRP, which may result in limited data description capability, optimization space, and generalization performance. The third category projects the HRRP to higher feature space through kernels. In order to obtain satisfying recognition and generalization performance, however, the kernels should be carefully designed, such as kernel optimization based on the localized kernel fisher criterion [
12].
In recent years, deep learning [
14] has received intensive attention in HRRP recognition. Unlike traditional methods that rely heavily on hand-designed features, methods based on deep learning are data-driven, i.e., they could extract features of the HRRP automatically, through typical structures such as the autoencoder (AE) [
15,
16], the convolutional neural network (CNN) [
17,
18,
19,
20], and the recurrent neural network (RNN) [
21,
22], etc. The proposed method belongs to deep learning. Constituted by the encoder and the decoder, the AE attempts to output a copy of the input data by reconstructing it in an unsupervised fashion. In particular, the encoded, i.e., compressed data in the middle, serves as the recognition feature, which is then fed into the classifier for recognition [
15,
16]. The traditional CNN [
17] extracts hierarchical spatial features from the input by cascaded convolutional and pooling layers, whereas it fails to capture the temporal information [
18,
19,
20]. In view of this, RNN [
21] has sequential architecture to process the current input and historical information simultaneously, so that to capture the temporal information of the target. However, it assumes that both the target and noise regions contribute equally to HRRP recognition, which may result in limited performance [
22].
Mimicking the human vision, the attention mechanism [
23,
24,
25,
26] captures long-term information and dependencies between input sequence elements by measuring the importance of the input to the output. Traditional attention models designed for HRRP recognition [
27,
28,
29,
30,
31], such as the target-attentional convolutional neural network (TACNN) [
28], the target-aware recurrent attentional network (TARAN) [
29], and the stacked CNN–Bi-RNN (CNN–Bi-RNN) [
30]. TACNN, which is based on CNN, fails to make full use of the temporal correlation of HRRP, whereas TARAN, which is based on RNN and its variants, has difficulties in network training, parallelization, and long-term memory representation. Furthermore, CNN–Bi-RNN fuses the advantages of CNN and RNN and uses an attention mechanism to adjust the importance of features. In recent years, self-attention [
32], which relates different positions of a single sequence to compute a global representation, has achieved efficient and parallel sequence modeling and feature extraction. Specifically, it acquires the attention score by calculating the correlation between the query vector and the key vector, and then weights it to the value vector as the output. Since the self-attention mechanism explicitly models the interactions between all elements in the sequence, it is a feature extractor of global information with long-term memory. Moreover, the global random access of the self-attention mechanism facilitates the fast and parallel modeling of long sequences. For HRRP recognition, the self-attention is added before the convolutional long short-term memory (ConvLSTM) [
33] in order to focus on more significant range cells. Because the main recognition structure, i.e., the LSTM, is still a variant of RNN, it fails to directly use the different importance between features for recognition. In addition, although the networks proposed by the existing methods have certain noise robustness, they fail to achieve better recognition results under the condition of low SNR.
Traditionally, HRRP denoising is implemented prior to feature extraction, and typical denoising methods include least mean square (LMS) [
34,
35], recursive least square (RLS) [
36], and eigen subspace techniques [
37], etc. Such techniques, however, rely heavily on domain expertise and fail to estimate the model-order (i.e., the number of signal components) accurately with low SNR. Recently, the generative adversarial network (
GAN) has been introduced as a novel way to train a generative model, which could learn the complex distributions through the adversarial training between the generator and the discriminator [
38]. Currently,
GAN has been successfully applied to data generation [
39,
40], image conversion and classification [
41,
42], speech enhancement [
43] and so on, which provides an effective way to blind HRRP denoising.
In a nutshell, the separated HRRP denoising and recognition processes, the inability to distinguish the contribution of the target regions and noisy regions during the feature extraction process, the incompetence in long-term/global dependency acquisition hinder effective recognition of the noisy HRRP. Specifically, the output of the classifier cannot be fed back to the denoising process, thus significant signal components may be suppressed during denoising. Meanwhile, the different intensity information of each component of the HRRP cannot be effectively utilized in the identification process. Therefore, it is natural to integrate the tasks of denoising and recognition through elaborately deigned deep architectures, under the guidance of proper loss.
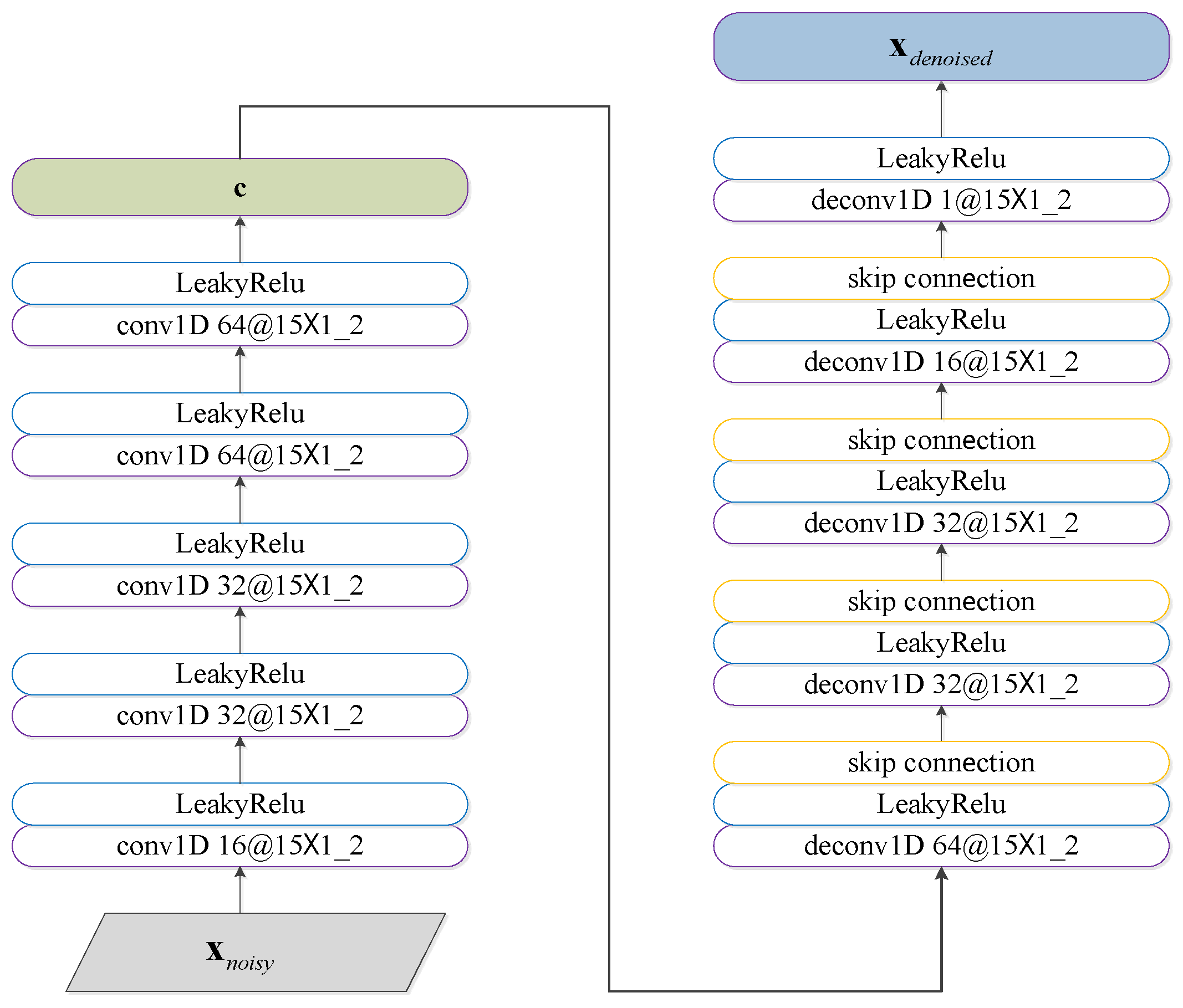
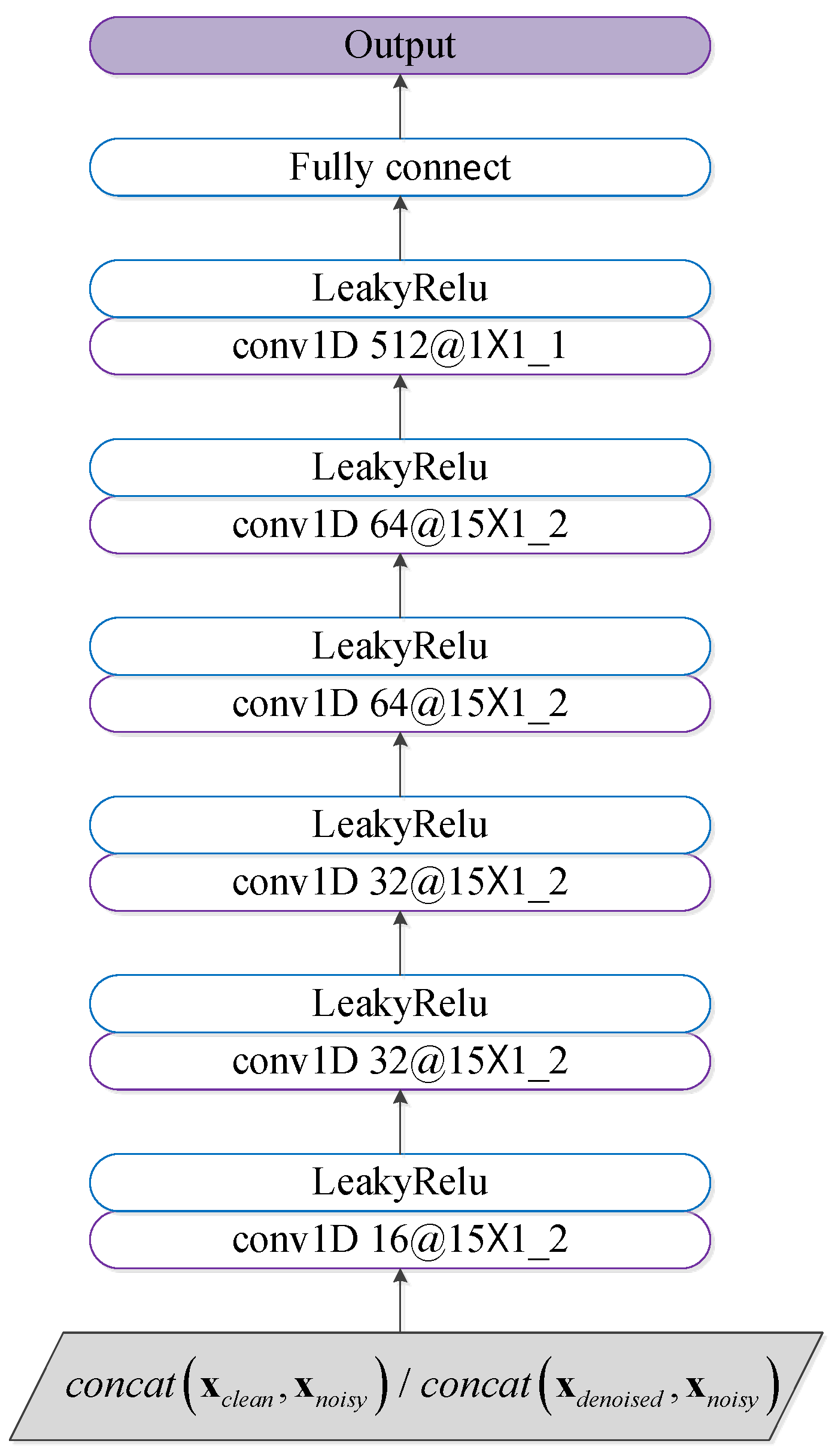
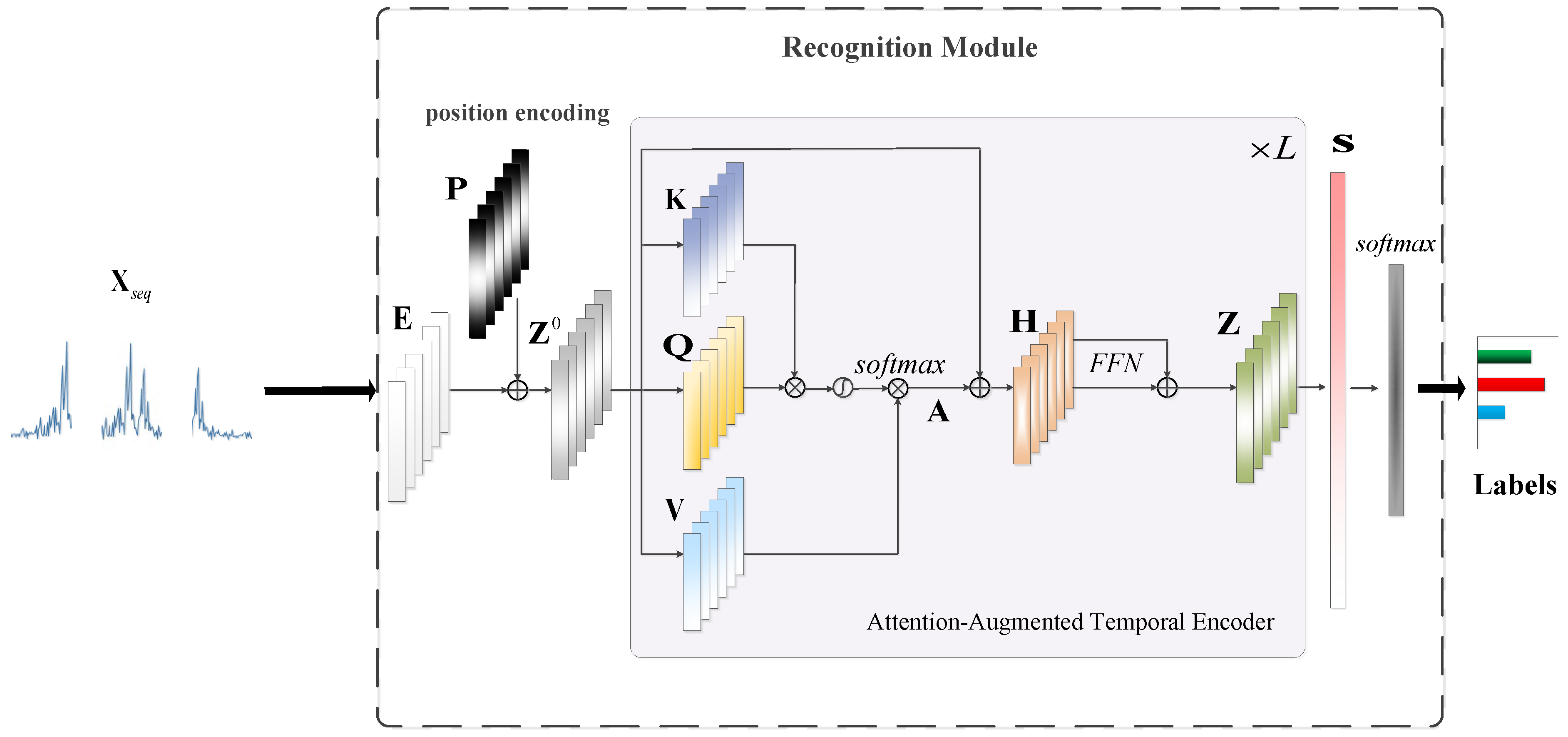
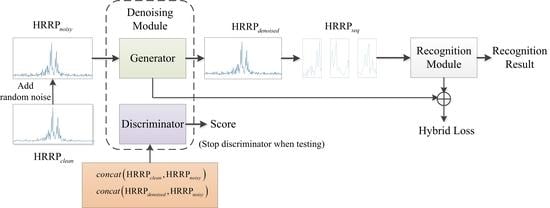
Aiming at the above issues, this paper proposes the integrated denoising and recognition network, namely, IDR-Net, to achieve effective HRRP denoising and recognition. The network consists of two modules, i.e., the denoising module and the recognition module. Specifically, the generator in the denoising module maps the noisy HRRP to the denoised one after adversarial training, which is then fed into the attention-augmented recognition module to output the target label. In particular, a new hybrid loss function is used to guide the denoising of HRRP. The main contributions of this paper include the following: (a) To tackle the issue that separated HRRP denoising and recognition hinder end-to-end training and may suppress signal components that are significant for recognition, an integrated denoising and recognition model, i.e., the IDR-Net is designed, denoising the low SNR HRRP through the denoising module and outputs the category label through the recognition module. To the best of our knowledge, our method integrates denoising and recognition for the first time, realizing end-to-end training, and achieving better recognition performance. (b) To tackle the issue of long-term and global dependency acquisition of HRRP, the recognition module adopts the attention-augmented temporal encoder with parallelized and global sequential feature extraction. In particular, the attention score is generated with emphasis on the important input data to weight the feature vector and facilitate recognition. (c) Propose a new hybrid loss, and for the first time in the recognition of HRRP using such a combination of denoising loss and classification loss as loss function. By these means, the recognition module is integrated with the generator, thereby reducing the information loss during denoising, and enhancing the inter-class dissimilarity.
The remainder of this paper is organized as follows:
Section 2 discusses the related work, including the modelling of HRRP and the basic principles of
GAN.
Section 3 provides the detailed structure of the proposed IDR-Net.
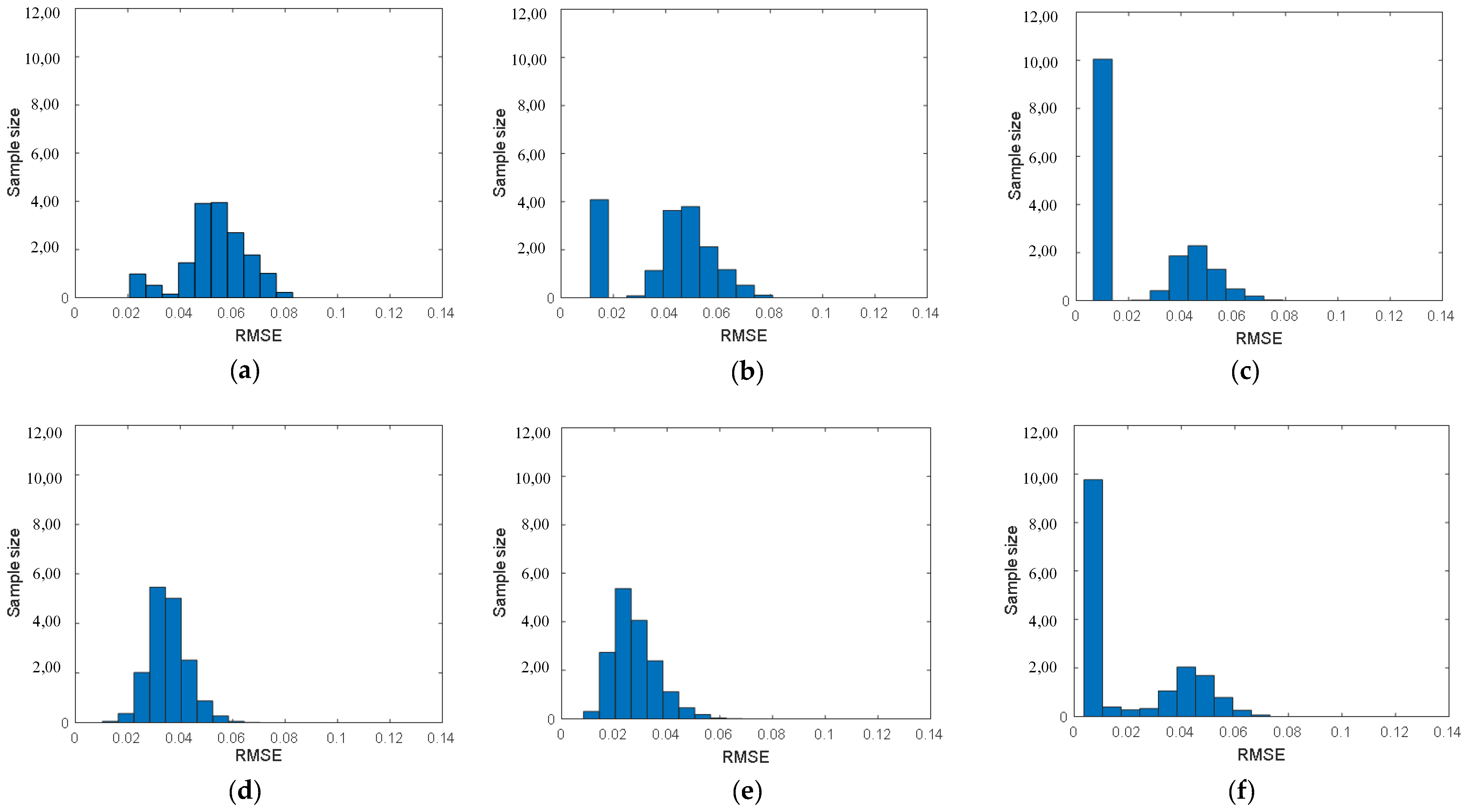
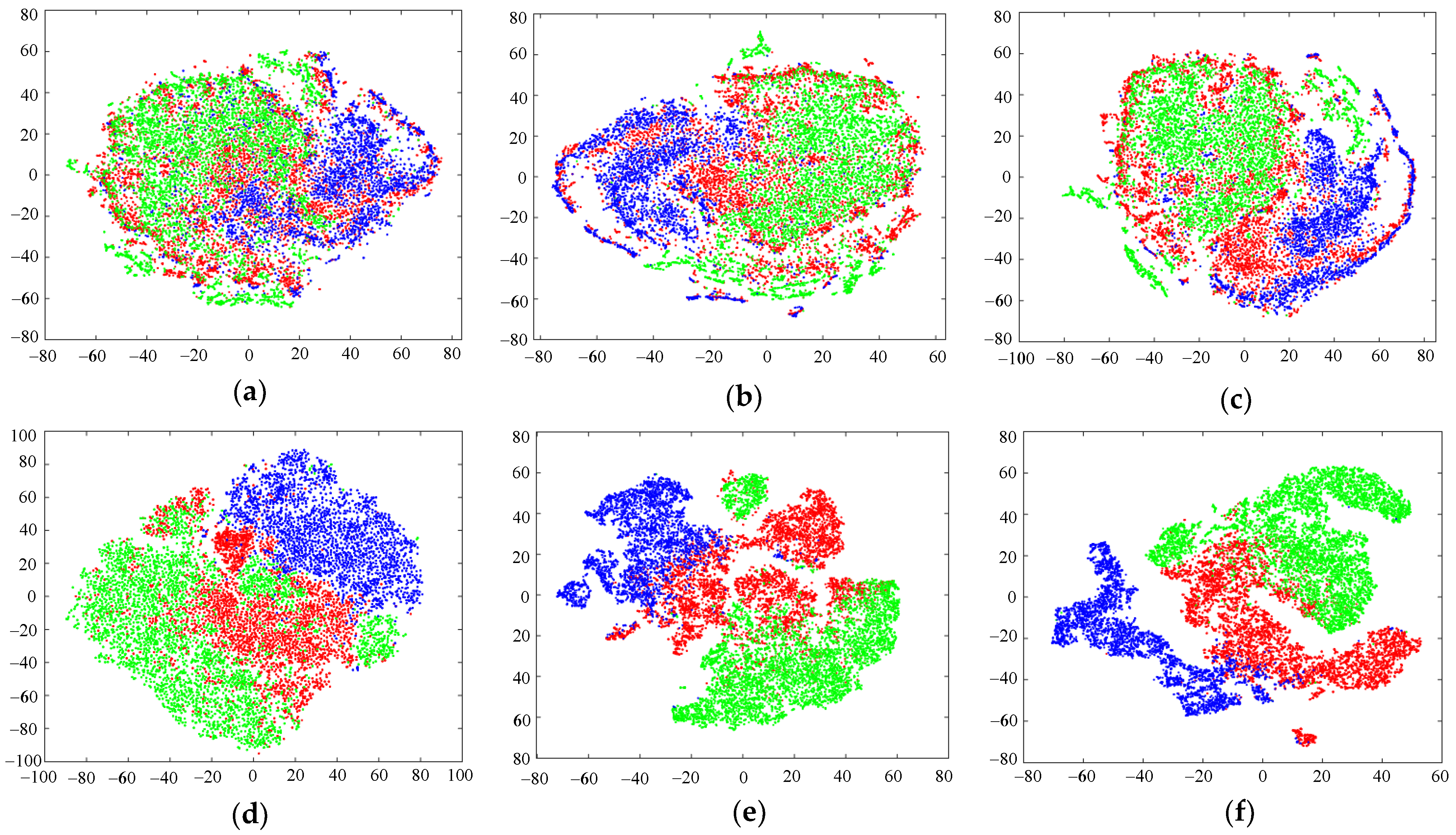
Section 4 presents the data set and experimental results with detailed analysis. Finally,
Section 5 concludes this paper and discusses the future work.