Abstract
Remote sensing data comprise a valuable information source for many ecological landscape studies that may be under-utilized because of an overwhelming amount of processing methods and derived variables. These complexities, combined with a scarcity of quality control studies, make the selection of appropriate remote sensed variables challenging. Quality control studies are necessary to evaluate the predictive power of remote sensing data and also to develop parsimonious models underpinned by functional variables, i.e., cause rather than solely correlation. Cause-based models yield superior model transferability across different landscapes and ecological settings. We propose two basic guidelines for conducting such quality control studies that increase transferability and predictive power. The first is to favor predictors that are causally related to the response. The second is to include additional variables controlling variation in the property of interest and testing for optimum processing method and/or scale. Here, we evaluated these principles in predicting ground vegetation cover, soil moisture and pH under challenging conditions with forest canopies hindering direct remote sensing of the ground. Our model using lidar data combined with natural resource maps explained most of the observed variation in soil pH and moisture, and somewhat less variation of ground vegetation cover. Soil pH was best predicted by topographic position, sediment type and site index (R2 = 0.90). Soil moisture was best predicted by topographic position, radiation load, sediment type and site index (R2 = 0.83). The best model for predicting ground vegetation cover was a combination of lidar-based estimates for light availability below canopy and forest type, including an interaction between these two variables (R2 = 0.65).
1. Introduction
The use of remote sensing (RS) technologies has been a breakthrough for ecology, which has long struggled with the field-based means for mapping spatial properties. Since the first aerial photographs were taken in the mid-1800s, the range of remote sensing technology has evolved greatly [1]. From multispectral satellite images to aerial laser data, remote sensing is now utilized in a range of ecological contexts, such as for monitoring biodiversity [2], assessing ecosystem services [3] and mapping terrestrial and aquatic habitats [4,5]. With such methods, it should be possible to characterize large areas with respect to environmental demands of vulnerable and threatened species in a more efficient way.
When using RS data, a demanding step is the choice of processing method to obtain derived variables. These processed RS variables should predict the property of interest as accurately as possible. Without the resources needed to perform a pilot study, the best alternative is to utilize previous studies testing alternative RS indices’ predictive power for the variables of interest, preferably in a similar landscape context. Hence, generating many such studies in a variety of contexts is important, given that the results are transferable to other study areas.
To increase transferability, models should not merely be built on predictive power, but favor processed RS variables representing a causal, functional relationship between predictor and response. This would make it more likely that the predictions will hold across landscapes, under a range of conditions [6]. Sometimes, such causal data may be scarce or lacking, which may favor including predictors with purely correlative relationships to the response to increase predictive power. This type of predictor should be restricted to those where the correlational relationship is well understood. However, too often, model emphasis seems to be on maximizing predictive power, with the inclusion of predictors with more vague relationships to the response (e.g., the use of “altitude” as a predictor for soil pH [7] and soil moisture [8]). This may compromise transferability to other landscape and ecological settings.
An additional way of maximizing the predictive power of RS-based models, which still may be more in line with maintaining transferability, is to include more causal factors determining the variation in the focal property, and testing for the optimal processing method and/or spatial scale. When testing the predictive power of RS variables, focus has often been on meticulously testing variations of RS-based variables representing the same functional factor. For example, when predicting soil moisture from RS data, Oltean et al. [9] focused on the topographical control of water drainage, testing a single RS processing method and its predictive power across various spatial scales. Similarly, Aagren et al. [8] compared two processing methods for estimating topographically controlled water drainage, and also across varying spatial scales. Although both studies included one variable representing the effect of sunlight on evaporation (aspect), this was not evaluated in the same meticulous way. There are several processing methods for estimating solar radiation load [10,11], and aspect may not be the optimum representative for this factor with respect to predictive power. We suggest including several RS indices representing important factors causally related to the predictors and testing them with a similar level of meticulousness. Following this guideline, one may increase predictive power without turning to variables with a vague predictor–response relationship.
Working with RS data in forested areas is particularly challenging because forest canopies obscure the ground, making direct sensing of the soil or below-canopy vegetation more difficult [12]. Under such conditions, we may be unable to map the property of interest directly (through direct remote sensing), and therefore resort to indirect prediction via variables representing the mechanisms that control its distribution and/or variation.
Soil pH, soil moisture and ground vegetation cover all have high ecological predictive relevance in terrestrial habitat studies [13,14], in biodiversity assessments [15,16] and when addressing ecosystem services [17,18,19]. Therefore, we evaluated the potential for building RS-based predictive models for these ecologically relevant spatial properties, adhering to the guidelines suggested above.
For soil pH, parent material (bedrock and/or sediment type) can be important, due to variations in calcium content and release rate of basic cations, and differences in dominant particle size which affects the leaching rate [20]. Topography may also affect soil pH, due to its control over water drainage patterns [21]. In addition, coniferous forests are often associated with lower soil pH than deciduous forests [22], due to differences in litter acidity, litter decomposition, nutrient uptake and leaching rate [20,23]. Moreover, site index, i.e., forest productivity estimated from tree height at a certain age [24], is closely related to soil nutrient and moisture conditions [25]. Soil pH is closely related to nutrient availability and recycling [26], and thus is likely strongly correlated with site index. For soil moisture, topography is an important factor because it affects the pattern and rate of water drainage and accumulation [27]. Soil properties, such as particle size and soil depth, may affect soil moisture via differences in the water holding capacity and drainage rate [20]. In addition, solar radiation load may affect soil moisture through its effect on evapotranspiration [28]. Furthermore, forest type may show correlation to soil moisture due to differences in the tree species requirements with respect to soil moisture conditions, i.e., Pinus sylvestris being more drought tolerant than Picea Abies [29]. For ground vegetation cover, an important controlling factor is light availability, presumably modulated by forest type [30]. Unfavorable growing conditions due to poor nutrient or moisture conditions, or unstable masses on steep slopes, may also affect ground cover due to lower plant establishment and growth [31,32,33]. In addition, ground vegetation cover may correlate with soil depth, because areas with thin soils are more likely to have patches of bare rock.
Therefore, in this study we address the question: Can we build RS-based models with high predictive power, using mainly variables that have a causal relationship to the three ecological properties of soil pH, soil moisture and ground vegetation cover?
2. Materials and Methods
2.1. Study Area
We collected vegetation data from two areas in southeastern Norway, including a range in topographical relief, dominating vegetation and sediment types. The two areas are approximately 50 km apart and span from the boreonemoral to the middle boreal vegetation zone. The first area (59°38′02.6″N, 9°18′07.8″E; Figure 1) is a hilly area 250–560 m.a.s.l. covered by coniferous forest (Pinus sylvestris (74%), Picea Abies (21%)) with patches of mixed forest (5%, covered by Betula pubescens, Populus tremula). The second area (59°50′27.5″N, 10°13′47.5″E; Figure 1), 40–410 m.a.s.l., includes a broad valley with agricultural land and patches of forest, and east-facing hills. The main sediment type is marine clay, and here, forest patches are dominated by temperate deciduous tree species (86%, Ulmus glabra, Fraxinus excelsior, Acer platanoides), with smaller areas dominated by spruce (9%) and pine (5%). At higher elevations (>200 m.a.s.l), the marine clay layer is replaced by glacial tills dominated by coniferous forest (spruce (64%), pine (24%)), with patches of deciduous forest (12%).
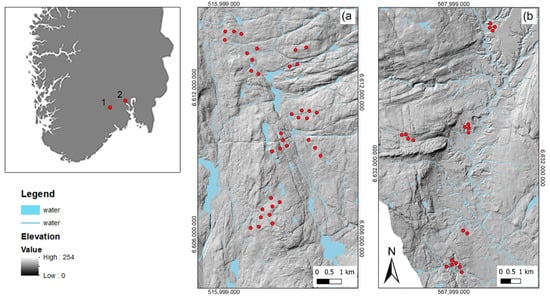
Figure 1.
Map showing the location of study area 1 and 2 in southeastern Norway. The distribution of sample plots is shown relative to topography and surface water in (a) study area 1 (n = 36) and (b) study area 2 (n = 20). Coordinate system: ETRS89: UTM 32 N.
2.2. Field Data Collection and Processing
Forest-covered areas inside the two study areas were delimited using ArcMap v10.7.1 (excluding clear-cuts and young forests). Random sampling points were generated in QGIS v3.16.3, with a minimum distance of 200 m between points to tentatively reduce the likelihood of spatial autocorrelation. This was also achieved in area 2, where small patches of forest within the agricultural area led to sample plots becoming very clustered. During the field survey, conducted in June 2021, a high-precision GPS (Topcon HiPer SR) was used to mark the exact coordinates at the center of each plot. Around each sampling point, a 10 × 10 m sampling square was marked, 56 squares in total (area 1: n = 36, area 2: n = 20). Within each square, data on ground vegetation cover (%), vascular plant species, dominating tree species, soil depth (cm) and vegetation type were recorded. Vegetation type was determined following the Norwegian system “Nature in Norway” (NIN) [34,35]. From the collected data, the mean Ellenberg indicator value for soil pH was calculated [36]. The NIN vegetation types were used to quantify soil moisture, as they are ordered on an ordinal scale after vegetation drought tolerance (4 levels). In addition, we included an additional level for vegetation affected by ground water, increasing the number of levels to 5. Using vegetational bioindicators to represent soil pH and soil moisture has some advantages and disadvantages. On the positive side, vegetation patterns are a more stable expression of the abiotic conditions that often fluctuate with time [37]. On the negative side, using vegetation as a bioindicator depends on how well one can identify a representative number of the species present. This can be difficult when vegetation cover is suppressed, such as under low light conditions.
The ground vegetation was initially defined as all vascular plants lower than 50 cm, and percent cover was estimated visually. Lichen cover was later included in the definition of ground vegetation cover to reduce model complexity and because the light lichen cover can easily be delimited later using satellite images. Lastly, soil depth was measured using a thin metal rod (max. 30 cm) to approximate the depth of the soil available for the ground vegetation [38]. Soil depth was measured in the center of the 10 × 10 m plot, and in each 5 × 5 m square created when dividing the plot into four equal pieces. The average was then taken for each plot.
2.3. Generating Predictor Variables from Remote Sensing Data
Recent lidar (light detection and ranging) data were acquired from the national map service [39,40,41]. The data have a medium to high point density (2–5 per m2).
Five remote sensing indices representing topographically controlled water drainage was included: Saga Wetness Index (SWI), depth-to-water table (DTW), topographic position (TPI), deviation from elevation (DEV) and slope (SLOP) (Table 1). To represent variation in spatial scale, SWI was generated from terrain models with different resolutions (1, 5, 10 and 30 m) using the Saga plugin in QGIS [42]. DTW was generated with a range in drainage area sizes (1, 2, 4, 6, 8 and 10 ha) using ArcMap v10.7.1 and the D8 flow algorithm [43]. TPI was estimated by subtracting the elevation at each cell from the mean elevation of the surrounding neighborhood. DEV was calculated the same way, but in addition normalized by the standard deviation to account for local surface roughness [44]. The effect of the neighborhood size was assessed using a radius of 10, 30 and 100 m. Slope was estimated from a 1 m resolution terrain model. Representing light conditions or radiation load, four different remote sensing indices were included: canopy cover (CC), heat load index (HLI), Subcanopy Solar Radiation model (SSR) and a modified version of SSR accounting for forest gaps (GAP) (Table 1). A canopy height model at 1 m resolution was used to calculate canopy cover (%, canopies were defined as vegetation > 2 m height). A 2 m resolution DEM was used to calculate HLI at each study site, using the “area solar radiation tool” in ArcGIS v10.7.1. To model sub-canopy solar radiation, the heat load index was multiplied with a light penetration index (LPI) [10]. LPI is the proportion of laser beams reaching the forest floor when accounting for the filtering effect of the canopy. LPI was corrected for solar angle using a moving kernel that “smooths” the canopy at a certain angle dictated by the sun angle. Furthermore, gaps and edges in the canopy were accounted for in the GAP model [10]. Spatial scale was assessed only for canopy cover. Here, the mean was taken for the 10 × 10 m plot, but also for an area of 20 × 20 m and 30 × 30 m around the plot center. The remaining light indices were assessed with respect to radiation properties: diffuse, direct and a combination of direct and diffuse radiation proportionate to conditions in southeastern Norway (52% diffuse, 48% direct) during the growing season.

Table 1.
Predictors used to model soil pH, soil moisture and ground vegetation cover.
2.4. Additional Information Included
Decent maps based on broad-scale field surveys are available for some spatial properties with high utility for many purposes. We included existing maps for quaternary sediments, calcium content in bedrock and site index (Table 1). A disadvantage of predicting soil pH based on bedrock calcium content is that the thick layer of marine clay likely decouples the topsoil from the bedrock. Thus, we created a map using the calcium content map as the base and exchanging the calcium content value for all areas covered by clay to the second-highest level for calcium content (level 4). These maps had a considerably lower resolution compared to the remote sensing data, with sediments and bedrock in 1:50,000–1:250,000 scale and site index 1:5000. The low-resolution data can be a problem when used for predictions together with high-resolution lidar data, as they likely will lead to some inaccuracies when making predictions on a finer scale. On the other hand, including them may increase the model’s explanatory power and may thus give better predictions than when not included.
In addition, we included forest type based on field observations (Table 1). However, this variable can also be generated using remote sensing data [52]. Finally, soil depth from field measures was included in the analysis, although it could been approximated using remotely sensed data [53].
2.5. Statistical Analysis
A generalized least-squares linear model with Gaussian distribution was used for the analysis of soil pH, using the nlme R package [54]. Soil moisture was analyzed using proportional odds ordinal regression with a logit link via R packages rms [55] and MASS [56]. Here, the proportional odds assumption was checked for all predictor variables using the brant R package [57]. For the analysis of ground vegetation cover, we used beta regression with a logit link via the betareg R package [58]. All statistical analyses were performed in R v4.0.4 [59].
First, simple predictor–response regressions were used to identify the “best” alternative predictor variable representing topographic wetness (SWI, DTW), topographic position (TPI, DEV), solar radiation load (CC, SSR, GAP, HLI) and soil properties (sediment type, bedrock calcium content) for each response, with some exceptions. For soil moisture, we chose sediment type to be the most relevant based on existing knowledge [20]. When analyzing soil pH, solar radiation load was not deemed relevant. AICc was used for model selection using the MuMIn R package [60]. In case the predictor had a nonlinear relationship to the response, we included polynomial terms. The variables representing light availability/radiation load were centered because of large values, and topographic position variables were centered for easier interpretation [47]. Residuals were checked for spatial autocorrelation using Moran’s I index from the ape R package [61]. If found to be an issue, the model selection procedure was performed including either location or a spatial correlation term in all models compared.
After finding the best alternative variable for topographic wetness (SWI, DTW), topographic position (TPI, DEV), solar radiation (CC, SSR, GAP, HLI) and soil properties (SED, CA.sed, CA.bed) (Table 1), these predictors were included in a second model selection procedure to find the best combination of variables, using multiple regressions and AICc score to rank models. Location was included as a fixed effect, and whereas slope, soil depth, site index and forest type were included in all the multiple regression analyses, soil depth was excluded in the soil pH model. In the analysis of ground vegetation cover, an interaction between light and forest type was included as part of the multiple regression model selection. Model diagnostics on top-ranked models were performed using R packages Dharma [62] and Sure [63], and prediction plots were generated using sjPlot [64].
3. Results
3.1. Soil pH
For soil pH, the best variable representing soil properties was sediment type (AICc weight = 0.99), which was clearly better than the second-best variable bedrock calcium content + clay (AICc weight = 0.01) (Table S1). Topographic wetness was best represented by SWI at 1 m resolution (AICc weight = 0.51), followed by DTW with a flow initiation threshold of 8 ha (AICc weight = 0.13). DEV30m was the best variable representing topographic position (AICc weight = 0.86), followed by TPI30m (AICc weight = 0.14) (Table S1).
The multiple regression model comparison ranked these models as the top three:
- Soil pH = a + b1(SED) + b2(LOC) + b3(BON) + b4(DEV30M)2 + e
- Soil pH = a + b1(SED) + b2(LOC) + b3(BON) + b4(DEV30M)2 + b5(SWI1m) +e
- Soil pH = a + b1(SED) + b2(LOC) + b3(BON) + b4(DEV30M)2 + b5(SLOP) + e
The best model carried 45% of the cumulative model weight and explained a high amount of the observed variation (adj. R2 = 0.91, or 0.90 if the location was excluded). Including SWI1m or slope did not improve model fit (Table 2).

Table 2.
The top three highest-ranked multiple regression models explaining variation in soil pH, soil moisture and ground vegetation cover. Included is the adjusted R2 for the top-ranked soil pH model, and pseudo-R2 for the top-ranked models for soil moisture and ground vegetation cover.
The top-ranked model predicted soil pH to be highest in area 2, but the confidence intervals were overlapping with area 1 (Figure 2). Topographic position predicted higher soil pH in terrain depressions and foot slopes and decreasing soil pH when moving upslope, with the lowest soil pH predicted at terrain ridges. For sediment type, soil pH was highest for clay sediments. The effect of the other sediment types could not be clearly distinguished from each other, though sites with thin layers of glacial tills and bare rock tended to predict somewhat higher soil pH than thicker layers of glacial tills. For peat sediments, we only had two observations, which makes the predictions less reliable. Soil pH was predicted to be lower on sites with low site index compared to medium. High site index predicted medium soil pH, but confidence intervals were overlapping with both low and medium site index (Figure 2).
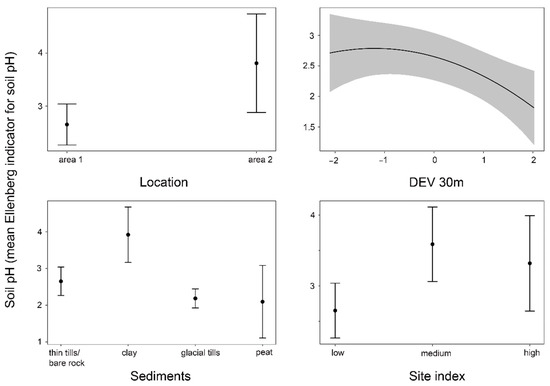
Figure 2.
Predictive plots for each variable included in the top-ranked model explaining soil pH (mean Ellenberg indicator value for soil pH).
3.2. Soil Moisture
For soil moisture, the best topographical wetness variable was SWI1m (AICc weight = 0.31), but DTW with a flow initiation threshold of 1 and 2 ha were both clustered within ΔAICc less than 1, indicating similar support as for the top-ranked model (Table S2). Topographic position was best represented by DEV30M (AICc weight = 0.71), followed by TPI30m (AICc weight = 0.29). The best variable representing light availability was the SSR global model (AICc weight = 0.28); however, the SSR diffuse light model, HLI diffuse light model and SSR direct light model all had ΔAICc less than 1, indicating that they had similar support as the top-ranked model (Table S2).
The three top-ranked models were:
- Soil moist. = a + b1(BON) + b2(SED) + b3(SSRglob) + b4(DEV30M) + e
- Soil moist. = a + b1(BON) + b2(LOC) + b3(SSRglob) + b4(DEV30M) + e
- Soil moist. = a + b1(BON) + b2(SED) + b3(SSRglob) + b4(DEV30M) + b5(DEP)+ e
The top model carried 20% of the cumulative weight and explained 83% of the observed variation (Table 2). In the second-best model, sediment type was replaced by location. Including soil depth did not improve model fit (third-ranked model, Table 2).
Medium site index predicted a higher probability for high soil moisture (level 0) compared to low and high site index (Figure 3), the latter predicting a higher probability for somewhat moist areas (level 1). Site index did not separate between semi-dry and dry areas (levels 2 and 3). The moistest sites were somewhat more probable in areas with low radiation load, although the effect was uncertain. The semi-most sites were most probable in areas with medium radiation load, but the confidence intervals were wide at both high and low amounts of radiation, suggesting that the effect was uncertain (Figure 3). Semi-dry or dry areas did not seem to be predicted by solar radiation, though confidence intervals did suggest that areas with high solar radiation load may predict semi-dry areas. High soil moisture sites were not clearly predicted by any sediment type. Semi-moist areas were most probable on clay. Thin glacial tills and bare rock areas did also seem to predict semi-moist areas, but here, confidence intervals were wider, indicating predictions with low precision. Semi-dry areas were most probable in areas with thicker glacial tills, but with high uncertainty. The driest areas did not seem to be predicted by any sediment type. For topographic position, terrain depressions predicted the wettest areas, and semi-moist areas were predicted by all other topographic positions, except terrain depression. However, the wide confidence intervals suggested that the effect may be uncertain (Figure 3). In general, the model did not perform well at predicting the driest soil moisture class (level 3). This was most likely due to the low sample size, i.e., four observations.
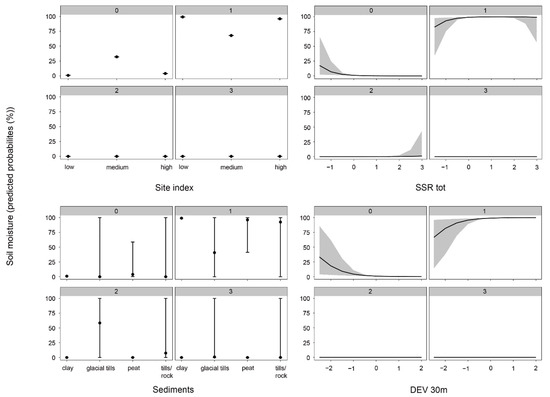
Figure 3.
Predictive plots for each variable included in the top-ranked model explaining soil moisture (predicted probabilities (%)).
3.3. Ground Vegetation Cover
For ground vegetation cover, the best variable representing light availability was the SSR model with diffuse light (AICc weights = 0.43), followed by canopy cover with a 30 m resolution (AICc weight = 0.13) (Table S3). Topographical wetness was best represented by DTW with a flow initiation threshold of 10 ha (AICc weight = 0.15), but the alternative variables were all within ΔAICc less than 2, implying that they had similar support. DEV30M was the best variable representing topographical position (AICc weight = 0.28), but not clearly better than the other variables that were all clustered within ΔAICc less than 1. CA.sed was the best variable for soil properties (AICc weight = 0.65), followed by CA.bed (AICc weight = 0.32) (Table S3).
For the multiple regression model selection, these models were ranked as the top three:
- G. veg. cov. = a + b1(FOR) + b2(SSRdif) + b3(FOR) × (SSRdif) + e
- G. veg. cov. = a + b1(FOR) + b2(SSRdif) + b3(FOR) × (SSRdif) + b4(DEV30M) + e
- G. veg. cov. = a + b1(FOR) + b2(SSRdif) + b3(FOR) × (SSRdif) + b4(SLOP) + e
The top-ranked model carried a rather low amount of the cumulative weight (18%) but explained a fair amount of the observed variation (pseudo-R2 = 0.65). Including topographical position or slope did not improve model fit (Table 2).
Ground vegetation cover was predicted to be higher in pine and deciduous forest compared to spruce forests (Figure 4). Pine and deciduous forest were more similar, with overlapping confidence intervals. Vegetation cover was predicted to increase almost linearly to an increasing amount of diffuse light. The uncertainty was highest under low light conditions. The effect of light availability on ground vegetation cover varied with forest type. In spruce forest, vegetation cover increased rapidly with an increasing amount of light but leveled off when the light levels reached around two-thirds of the maximum level. The predictions in the deciduous forest were similar, but here, the ground vegetation cover was predicted to be somewhat higher than in the spruce forest, under the same light conditions (Figure 4). When light levels reached around two-thirds of the maximum level, the predicted ground vegetation cover in the deciduous forest started to converge with that in the spruce forest. In the pine forest, the predicted ground vegetation cover was higher than in the other forest types under low light conditions. Under high light availability, ground vegetation cover was lower in pine forest compared to the other forest types (Figure 4).
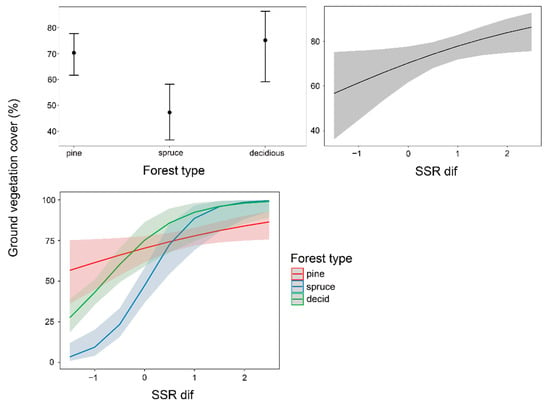
Figure 4.
Predictive plots for each variable included in the top-ranked model explaining ground vegetation cover (%).
4. Discussion
By combining RS data and natural resource information, we were able to build models explaining moderate to high amounts of the observed variation in soil pH, soil moisture and ground vegetation cover.
Sediment type was an important variable for predicting both soil pH and soil moisture. For soil pH, the effect of sediment type was due to the difference between clay and glacial tills. Similarly, Lamarche et al. [65] found that forest soils had higher pH when originating from clay compared to glacial tills. The effect may partly be caused by differences in soil texture, with clay having finer and easier weatherable particles, releasing basic cations at a higher rate compared to coarser particles. In addition, finer particles bind cations better, dampening the leaching rate [20]. However, both clay and glacial tills may vary in mineral content [66,67], which may lead to differing effects on soil pH (e.g., Gruba and Socha [68] found that clay content was positively correlated with total acidity). Calibrating the model with soil samples may be sensible when using it in areas with differing sediment conditions. This will still be less resource-demanding than creating field-based maps of soil pH where sediment type varies less than soil pH. For soil moisture, the effect of sediment type was also due to the difference between clay and glacial tills, clay being related to higher soil moisture than tills. This was expected since clay has a higher water holding capacity than glacial tills [20]. In a similar study, sediment type was found to be an important variable in predicting soil moisture [69]. Here, glacial tills were also the driest sediment type (clay was not included). In contrast, a similar study found that sediment type, including clay and glacial tills, was not important for predicting soil moisture [8]. This study included plots from a large geographical area, meaning that large-scale processes likely were more important in this study compared to ours. In addition, contrary to our study, they included elevation in the analysis. We omitted this variable due to its correlation with sediment type, and since sediment type has a more direct relationship to soil moisture. Including variables that possibly correlate with several factors affecting the response variable may bring about results where variables that have indirect and vague relationships to the response outperform variables that are more directly related to it. This can give the impression that the indirect variable is important when predicting soil moisture in general, but this may not be the case when moving outside the study area.
We expected that bedrock calcium content would be an important predictor of soil pH, as it has been in other similar studies [70,71]. This was not the case in our study, even when we accounted for the decoupling effect of the thick layers of marine clay in study area 2. One explanation may be the glacial movement and transportation of material, which leads to the calcium content of the sediments likely better representing upstream bedrock type. The coarse scale of the bedrock map may also have played a part, as it does not capture all small-scale variations.
Topography is important when explaining soil pH and soil moisture, as indicated by DEV30M being represented in the top-ranked models for both properties. This is most likely due to its control over water drainage and accumulation, including transportation of material and basic cations [21]. Similar studies have found that topography is related to soil pH and moisture, but it is not clear which topographic variable best represents this mechanism. Li et al. [7] found that slope and cross-slope curvature explained soil pH better than topographic wetness (topographic position was not included) in a broad-leaved forest in China. Contrarily, Baltensweiler et al. [72] found that terrain wetness explained more of the variation in soil pH than cross-slope curvature in a mountain forest in the Swiss Alps. Similarly, Aagren et al. [73] found that depth-to-water table was a better predictor of soil moisture compared to topographic position in a boreal forest in Sweden. In Finland, Kemppinen [70] had more success predicting soil moisture using the Saga Wetness Index (SWI) than a Topographical Position Index (TPI). This contrasts with our study, as we found that topographic position was a better variable than both DTW and SWI. It is not clear why the best variable varies between studies, but it has been suggested that soil transmissivity, variation in topography and local climate may affect the performance of topographic indices and what represents the optimum scale [73].
Site index was included in the top-ranked model for both soil moisture and soil pH. Since most plots with high site index were located on clay sediments, the effect was confounded, and high site index was most likely caused by the clay sediment. Medium and low site index differentiated between higher and lower soil pH and moisture for the plots located on glacial tills. Site index represents forest productivity, which is caused by the combined effect of soil moisture, soil pH and climatic conditions. Thus, it can be used as an indicator for these three factors, as shown in our analysis. We did not use a remote sensing-based version of the index, but it can be estimated with relatively high accuracy using bitemporal lidar data [74].
Light availability or radiation load was included in the top-ranked model for both soil moisture and ground vegetation cover. For soil moisture, the association was most likely due to the effect of radiation load on evapotranspiration [28,75]. Here, the best variable was one of the most comprehensive variables, including the effect of solar angle, topography, canopy and both direct and diffuse radiation. This suggests that higher precision can be achieved when using more complex estimations of solar radiation load, in comparison to using more simple methods, such as topographic aspect.
As expected, ground vegetation cover increased with higher light availability. Although light is known to be an important limiting factor for plant establishment and growth [30], this does not always translate into a detectable association between light availability and vegetation cover. For example, Tinya et al. [76] did not find a correlation between the herbaceous cover and the amount of measured diffuse light inside a mixed temperate forest in Hungary. This was assumed to be due to poor establishment of herbaceous species in nutrient-poor soils. This suggests that how one defines the ground vegetation cover is important. We included species that can tolerate both nutrient-poor soils (dwarf shrubs) and dry soils (lichen); thus, we did not experience the same lack of correlation. Our top-ranked model did, however, have other issues. Of the three ecological properties included in our analysis, we had the least success explaining ground vegetation cover, possibly because we did not account for dead trunks and snags in our model, which led to lower estimated vegetation cover. In addition, estimating vegetation cover visually is not a precise form of measurement. Measurement errors are unavoidable and create noise in the data.
Forest type was included in the top-ranked model for ground vegetation cover, both as an additive factor and in interaction with light availability. The amount of light reaching the forest floor depends on the amount of absorption, reflection and transmittance of the light as it travels through the canopy [77]. Tree species may modulate these three factors through differences in leaf angle, canopy structure and density [28]. These differences are probably not fully accounted for by the lidar-based variables, so including tree species or forest types gives better predictions. In our study, deciduous forests had higher estimated light availability than spruce forests. Unlike us, Renaud et al. [78] found that deciduous forests had lower levels of available light below the canopy compared to spruce forests. In their study, the deciduous forests consisted mostly of beech (Fagus sylvatica), which are generally much darker than the deciduous forests in our study area. This means that dominating tree species may be a better predictor than forest type.
5. Conclusions
In this study, we found that soil pH, soil moisture and ground vegetation cover may be modeled using a combination of remotely sensed data and natural resource maps. By choosing variables based on causal or well-known correlational relationships to the response, we were able to build more easily interpretable models that explained medium to high amounts of the observed variation. We found that topographically controlled water drainage patterns, which may affect both soil moisture and pH, are one of the more challenging variables to select in advance because the optimum method and/or scale seem to vary between study areas. However, it may be possible to select the best variable based on existing knowledge of a selected study area (e.g., sediment types, local climate) and some measures of topographic variation estimated from digital elevation models. Future studies should focus on testing the relationship between these factors and the optimum topographical wetness variable for a better understanding of why and when the optimum processing method and spatial scale vary, and how to select the optimum variable without performing a pre-study field survey. If this can be sorted out, it would be helpful for future ecological studies and other types of studies, as well for management projects, where remote sensing data can be of great use.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14205207/s1, Table S1: Ranking of single regression models for soil pH using AICc scores.; Table S2: Ranking of single regression models for soil moisture using AICc scores.; Table S3: Ranking of single regression models for ground vegetation cover using AICc scores.; Table S4: Model summary of the highest ranked multiple regression models for soil pH, soil moisture and ground vegetation cover.
Author Contributions
Conceptualization, H.H.; methodology, O.D. and H.H.; formal analysis, H.H. and O.D.; investigation, H.H.; resources, J.H.; writing—original draft preparation, H.H.; writing—review and editing, K.Ø., A.L., J.H. and O.D.; visualization, H.H.; supervision, A.L., J.H., K.Ø. and O.D.; project administration, A.L. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
Data will be shared upon reasonable request to the corresponding author.
Acknowledgments
The authors would like to thank Børre Dervo and Antonio Bjørn Stefano Poleo for their advice regarding this project and their comments on the manuscript. We would also like to thank the University of South-Eastern Norway for the lending of high-precision GPS used during the field survey.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Chuvieco, E. Fundamentals of Satellite Remote Sensing: An Environmental Approach, 3rd ed.; CRC Press: New York, NY, USA, 2020. [Google Scholar]
- Randin, C.F.; Ashcroft, M.B.; Bolliger, J.; Cavender-Bares, J.; Coops, N.C.; Dullinger, S.; Dirnböck, T.; Eckert, S.; Ellis, E.; Fernández, N.; et al. Monitoring biodiversity in the Anthropocene using remote sensing in species distribution models. Remote Sens. Environ. 2020, 239, 111626. [Google Scholar] [CrossRef]
- de Araujo Barbosa, C.C.; Atkinson, P.M.; Dearing, J.A. Remote sensing of ecosystem services: A systematic review. Ecol. Indic. 2015, 52, 430–443. [Google Scholar] [CrossRef]
- Poursanidis, D.; Traganos, D.; Reinartz, P.; Chrysoulakis, N. On the use of Sentinel-2 for coastal habitat mapping and satellite-derived bathymetry estimation using downscaled coastal aerosol band. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 58–70. [Google Scholar] [CrossRef]
- Ackers, S.H.; Davis, R.J.; Olsen, K.A.; Dugger, K.M. The evolution of mapping habitat for northern spotted owls (Strix occidentalis caurina): A comparison of photo-interpreted, Landsat-based, and lidar-based habitat maps. Remote Sens. Environ. 2015, 156, 361–373. [Google Scholar] [CrossRef]
- Wenger, S.J.; Olden, J.D. Assessing transferability of ecological models: An underappreciated aspect of statistical validation. Methods Ecol. Evol. 2012, 3, 260–267. [Google Scholar] [CrossRef]
- Li, X.; Chang, S.X.; Liu, J.; Zheng, Z.; Wang, X. Topography-soil relationships in a hilly evergreen broadleaf forest in subtropical China. J. Soils Sediments 2016, 17, 1101–1115. [Google Scholar] [CrossRef]
- Aagren, A.M.; Larson, J.; Paul, S.S.; Laudon, H.; Lidberg, W. Use of multiple LIDAR-derived digital terrain indices and machine learning for high-resolution national-scale soil moisture mapping of the Swedish forest landscape. Geoderma 2021, 404, 115280. [Google Scholar] [CrossRef]
- Oltean, G.S.; Comeau, P.G.; White, B. Linking the depth-to-water topographic index to soil moisture on boreal forest sites in Alberta. For. Sci. 2016, 62, 154–165. [Google Scholar] [CrossRef]
- Bode, C.A.; Limm, M.P.; Power, M.E.; Finlay, J.C. Subcanopy Solar Radiation model: Predicting solar radiation across a heavily vegetated landscape using LiDAR and GIS solar radiation models. Remote Sens. Environ. 2014, 154, 387–397. [Google Scholar] [CrossRef]
- Zellweger, F.; Baltensweiler, A.; Schleppi, P.; Huber, M.; Küchler, M.; Ginzler, C.; Jonas, T. Estimating below-canopy light regimes using airborne laser scanning: An application to plant community analysis. Ecol. Evol. 2019, 9, 9149–9159. [Google Scholar] [CrossRef]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating soil moisture remote sensing with observations from the UK TechDemoSat-1 satellite mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef]
- Baines, D.; Moss, R.; Dugan, D. Capercaillie breeding success in relation to forest habitat and predator abundance. J. Appl. Ecol. 2004, 41, 59–71. [Google Scholar] [CrossRef]
- Telagathoti, A.; Probst, M.; Peintner, U. Habitat, Snow-Cover and Soil pH, Affect the Distribution and Diversity of Mortierellaceae Species and Their Associations to Bacteria. Front. Microbiol. 2021, 12, 669784. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.-T.; Zheng, Y.-M.; Hu, H.-W.; Zhang, L.-M.; Li, J.; He, J.-Z. Soil pH determines the alpha diversity but not beta diversity of soil fungal community along altitude in a typical Tibetan forest ecosystem. J. Soils Sediments 2015, 15, 1224–1232. [Google Scholar] [CrossRef]
- Erlandson, S.; Savage, J.; Cavender-Bares, J.; Peay, K. Soil moisture and chemistry influence diversity of ectomycorrhizal fungal communities associating with willow along an hydrologic gradient. FEMS Microbiol. Ecol. 2016, 92, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, M.-C.; Wardle, D.A. Understory Vegetation as a Forest Ecosystem Driver: Evidence from the Northern Swedish Boreal Forest. Front. Ecol. Environ. 2005, 3, 421–428. [Google Scholar] [CrossRef]
- Liu, L.; Gudmundsson, L.; Hauser, M.; Qin, D.; Li, S.; Seneviratne, S.I. Soil moisture dominates dryness stress on ecosystem production globally. Nat. Commun. 2020, 11, 4892. [Google Scholar] [CrossRef]
- Emmett, B.A.; Cooper, D.; Smart, S.; Jackson, B.; Thomas, A.; Cosby, B.; Evans, C.; Glanville, H.; McDonald, J.E.; Malham, S.K.; et al. Spatial patterns and environmental constraints on ecosystem services at a catchment scale. Sci. Total Environ. 2016, 572, 1586–1600. [Google Scholar] [CrossRef]
- Weil, R.R.; Brady, N.C.; Weil, R.R. The Nature and Properties of Soils, 5th ed.; Pearson: Harlow, UK, 2017. [Google Scholar]
- Seibert, J.; Stendahl, J.; Sørensen, R. Topographical influences on soil properties in boreal forests. Geoderma 2007, 141, 139–148. [Google Scholar] [CrossRef]
- Barbier, S.; Gosselin, F.; Balandier, P. Influence of tree species on understory vegetation diversity and mechanisms involved—A critical review for temperate and boreal forests. For. Ecol. Manag. 2008, 254, 1–15. [Google Scholar] [CrossRef]
- Augusto, L.; De Schrijver, A.; Vesterdal, L.; Smolander, A.; Prescott, C.; Ranger, J. Influences of evergreen gymnosperm and deciduous angiosperm tree species on the functioning of temperate and boreal forests: Spermatophytes and forest functioning. Biol. Rev. Camb. Philos. Soc. 2015, 90, 444–466. [Google Scholar] [CrossRef] [PubMed]
- Amaro, A.; Reed, D.; Soares, P. Modelling Forest Systems; CABI: Yuen Long, Hong Kong, 2003. [Google Scholar]
- Farrelly, N.; Ní Dhubháin, Á.; Nieuwenhuis, M. Site index of Sitka spruce (Picea sitchensis) in relation to different measures of site quality in Ireland. Rev. Can. De Rech. For. 2011, 41, 265–278. [Google Scholar] [CrossRef]
- Neina, D. The Role of Soil pH in Plant Nutrition and Soil Remediation. Appl. Environ. Soil Sci. 2019, 2019, 5794869. [Google Scholar] [CrossRef]
- Western, A.W.; Grayson, R.B.; Blöschl, G. SCALING OF SOIL MOISTURE: A Hydrologic Perspective. Annu. Rev. Earth Planet. Sci. 2002, 30, 149–180. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Routledge: London, UK, 1987; p. 464. [Google Scholar]
- Lid, J.; Lid, D.T.; Elven, R.; Alm, T. Norsk Flora, 7th ed.; Samlaget: Oslo, Norway, 2005. [Google Scholar]
- Hart, S.A.; Chen, H.Y.H. Understory Vegetation Dynamics of North American Boreal Forests. Crit. Rev. Plant Sci. 2006, 25, 381–397. [Google Scholar] [CrossRef]
- Asbjornsen, H.; Goldsmith, G.R.; Alvarado-Barrientos, M.S.; Rebel, K.T.; Osch, F.v.; Rietkerk, M.G.; Chen, J.; Gotsch, S.; Tobon, C.; Geissert, D.R.; et al. Ecohydrological advances and applications in plant-water relations research: A review. Plant Ecol. 2011, 4, 3. [Google Scholar] [CrossRef]
- Burke, I.C.; Lauenroth, W.K.; Vinton, M.A.; Hook, P.B.; Kelly, R.H.; Epstein, H.E.; Aguiar, M.R.; Robles, M.D.; Aguilera, M.O.; Murphy, K.L.; et al. Plant-soil interactions in temperate grasslands. Biogeochemistry 1998, 42, 121–143. [Google Scholar] [CrossRef]
- Bochet, E.; García-Fayos, P. Factors Controlling Vegetation Establishment and Water Erosion on Motorway Slopes in Valencia, Spain. Restor. Ecol. 2004, 12, 166–174. [Google Scholar] [CrossRef]
- Natur i Norge. Available online: https://artsdatabanken.no/NiN (accessed on 14 January 2022).
- Halvorsen, R.; Skarpaas, O.; Bryn, A.; Bratli, H.; Erikstad, L.; Simensen, T.; Lieungh, E.; Zarnetske, P. Towards a systematics of ecodiversity: The EcoSyst framework. Glob. Ecol. Biogeogr. 2020, 29, 1887–1906. [Google Scholar] [CrossRef]
- Ellenberg, H.; Leuschner, C. Vegetation Mitteleuropas mit den Alpen; Ulmer Verlag: Stuttgart, Germany, 2010; Volume 6. [Google Scholar]
- Zonneveld, I.S. Principles of Bio-Indication. In Ecological Indicators for the Assessment of the Quality of Air, Water, Soil, and Ecosystems; Best, E.P.H., Haeck, J., Eds.; Springer: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Rose, J.P.; Malanson, G.P. Microtopographic heterogeneity constrains alpine plant diversity, Glacier National Park, MT. Plant Ecol. 2012, 213, 955–965. [Google Scholar] [CrossRef]
- Kartverket. NDH Lifjell-MælefjellSauherad-Notodden 2 pkt 2017; Kartverket: Hønefoss, Norway, 2017. [Google Scholar]
- Kartverket. NDH Notodden-SauheradHjartdal 5pkt 2017. 2017. Available online: https://hoydedata.no/LaserInnsyn2/ (accessed on 3 June 2022).
- Kartverket. NDH Lier-Røyken-HurumSvelvik 5 pkt 2017. 2017. Available online: https://hoydedata.no/LaserInnsyn2/ (accessed on 3 June 2022).
- Boehner, J.; Conrad, O. SAGA-GIS Module Library Documentation (v2.2.2). Available online: https://saga-gis.sourceforge.io/saga_tool_doc/2.2.2/ta_hydrology_15.html (accessed on 5 May 2022).
- O’Callaghan, J.F.; Mark, D.M. The extraction of drainage networks from digital elevation data. Comput. Vis. Graph. Image Processing 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Gallant, J.C.; Wilson, J.P. Terrain Analysis: Principles and Applications; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Boehner, J.; Selige, T. Spatial prediction of soil attributes using terrain analysis and climate regionalisation. Goettinger Geogr. Abh. 2006, 115, 13–28. [Google Scholar]
- Murphy, P.N.C.; Ogilvie, J.; Connor, K.; Arp, P.A. Mapping Wetlands: A Comparison of Two Different Approaches for New Brunswick, Canada. Wetl. (Wilmington N.C.) 2007, 27, 846–854. [Google Scholar] [CrossRef]
- Weiss, A.D. Topographic Position and Landforms Analysis; The Nature Conservancy: Arlington County, VA, USA, 2001. [Google Scholar]
- ESRI. Area Solar Radiation (Spatial Analyst). Available online: https://desktop.arcgis.com/en/arcmap/latest/tools/spatial-analyst-toolbox/area-solar-radiation.htm (accessed on 1 June 2022).
- NGU. Produktark: Løsmasser N50/N250; NGU: Tigerville, SC, USA, 2016. [Google Scholar]
- Heldal, T.; Torgersen, E. Miljøvariabel Kalkinnhold i Berggrunn: Metode for å Etablere Nasjonale Dataset; Norges Geologiske Undersøkelser (NGU): Trondheim, Norway, 2020. [Google Scholar]
- NIBIO. AR5 Klassifikasjonssystem: Klassifisering av Arealressurser; NIBIO: Aas, Norway, 2019; Volume 5. [Google Scholar]
- Dalponte, M.; Ørka, H.O.; Ene, L.T.; Gobakken, T.; Næsset, E. Tree crown delineation and tree species classification in boreal forests using hyperspectral and ALS data. Remote Sens. Environ. 2014, 140, 306–317. [Google Scholar] [CrossRef]
- Taylor, J.A.; Jacob, F.; Galleguillos, M.; Prévot, L.; Guix, N.; Lagacherie, P. The utility of remotely-sensed vegetative and terrain covariates at different spatial resolutions in modelling soil and watertable depth (for digital soil mapping). Geoderma 2013, 193–194, 83–93. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D. R_Core_Team. nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 2022, 3, 1–89. [Google Scholar]
- Harrell, F.E. Package ‘Rms’; Vanderbilt University: Nashville, TN, USA, 2022. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S; Springer Science & Business Media: Berlin, Germany, 2002. [Google Scholar]
- Brant, R. Assessing proportionality in the proportional odds model for ordinal logistic regression. Biometrics 1990, 46, 1171–1178. [Google Scholar] [CrossRef]
- Francisco, C.-N.; Achim, Z. Beta Regression in R. J. Stat. Softw. 2010, 34, 1–24. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Barton, K. Mu-MIn: Multi-model inference. 2009. Available online: https://www.scirp.org/(S(i43dyn45teexjx455qlt3d2q))/reference/ReferencesPapers.aspx?ReferenceID=753578 (accessed on 14 January 2022).
- Paradis, E.; Schliep, K. ape 5.0: An environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics 2019, 35, 526–528. [Google Scholar]
- Hartig, F.; Lohse, L. DHARMa: Residual Diagnostics for Hierarchical (Multi-Level/Mixed) Regression Models. 2022. [Google Scholar]
- Greenwell, B.; McCarthy, A.; Boehmke, B.; Liu, D. sure: Surrogate Residuals for Ordinal and General Regression Models. 2017. Available online: https://cran.r-project.org/web/packages/DHARMa/vignettes/DHARMa.html (accessed on 14 January 2022).
- Lüdecke, D. sjPlot: Data Visualization for Statistics in Social Science. R Package 2021, 1308357. [Google Scholar]
- Lamarche, J.; Bradley, R.L.; Paré, D.; Légaré, S.; Bergeron, Y. Soil parent material may control forest floor properties more than stand type or stand age in mixedwood boreal forests. Écoscience (St. -Foy) 2004, 11, 228–237. [Google Scholar] [CrossRef]
- Keller, W.D.; Matlack, K. The pH of clay suspensions in the field and laboratory, and methods of measurement of their pH. Appl. Clay Sci. 1990, 5, 123–133. [Google Scholar] [CrossRef]
- Jørgensen, P.; Sørensen, R.; Haldorsen, S. Kvartærgeologi, 2nd ed.; Landbruksforl.: Oslo, Norway, 1997. [Google Scholar]
- Gruba, P.; Socha, J. Effect of parent material on soil acidity and carbon content in soils under silver fir (Abies alba Mill.) stands in Poland. Catena (Giess.) 2016, 140, 90–95. [Google Scholar] [CrossRef]
- Kemppinen, J.; Niittynen, P.; Riihimäki, H.; Luoto, M. Modelling soil moisture in a high-latitude landscape using LiDAR and soil data. Earth Surf. Processes Landf. 2018, 43, 1019–1031. [Google Scholar] [CrossRef]
- Zhang, Y.-Y.; Wu, W.; Liu, H. Factors affecting variations of soil pH in different horizons in hilly regions. PLoS ONE 2019, 14, e0218563. [Google Scholar] [CrossRef]
- Reuter, H.I.; Lado, L.R.; Hengl, T.; Montanarella, L. Continental-Scale Digital Soil Mapping Using European Soil Profile Data: Soil PH.; University of Hamburg: Hamburg, Germany, 2008; pp. 91–102. [Google Scholar]
- Baltensweiler, A.; Heuvelink, G.B.M.; Hanewinkel, M.; Walthert, L. Microtopography shapes soil pH in flysch regions across Switzerland. Geoderma 2020, 380, 114663. [Google Scholar] [CrossRef]
- Aagren, A.M.; Lidberg, W.; Strömgren, M.; Ogilvie, J.; Arp, P.A. Evaluating digital terrain indices for soil wetness mapping—A Swedish case study. Hydrol. Earth Syst. Sci. 2014, 18, 3623–3634. [Google Scholar] [CrossRef]
- Bollandsås; Ørka; Dalponte; Gobakken; Næsset. Modelling Site Index in Forest Stands Using Airborne Hyperspectral Imagery and Bi-Temporal Laser Scanner Data. Remote Sens. (Basel Switz.) 2019, 11, 1020. [CrossRef]
- Western, A.W.; Grayson, R.B.; Blöschl, G.; Willgoose, G.R.; McMahon, T.A. Observed spatial organization of soil moisture and its relation to terrain indices. Water Resour. Res. 1999, 35, 797–810. [Google Scholar] [CrossRef]
- Tinya, F.; Márialigeti, S.; Király, I.; Németh, B.; Ódor, P. The Effect of Light Conditions on Herbs, Bryophytes and Seedlings of Temperate Mixed Forests in Őrség, Western Hungary. Plant Ecol. 2009, 204, 69–81. [Google Scholar] [CrossRef]
- Hagemeier, M.; Leuschner, C. Leaf and Crown Optical Properties of Five Early-, Mid- and Late-Successional Temperate Tree Species and Their Relation to Sapling Light Demand. Forests 2019, 10, 925. [Google Scholar] [CrossRef]
- Renaud, V.; Innes, J.L.; Dobbertin, M.; Rebetez, M. Comparison between open-site and below-canopy climatic conditions in Switzerland for different types of forests over 10 years (1998–2007). Theor. Appl. Climatol. 2010, 105, 119–127. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).