The Influence of Image Degradation on Hyperspectral Image Classification
Abstract
1. Introduction
- Five common degradations in HSIs are outlined and modeled by reliable mathematical or physical knowledge. These well-established or refined degradation models can be used to generate simulated hyperspectral images with different types and degrees of degradation, which can be utilized as supplementary data for evaluating the robustness of classification methods or developing new classification methods.
- A huge volume of HSI data containing single-type and mixed-type degradations are produced and presented. The degraded HSI data with five individual degradation types are constructed from four HSI data in different scenes, while the degraded data with mixed-type degradation are real data which show the situation in a real imaging scene.
- Comparative experimental results of typical HSI classification methods on the degraded HSI data are given. The effects of five image degradation on HSI classification are analyzed separately. Supplementary experiments on real degraded HSI with mixed-type degradation are also conducted and analyzed. In addition, according to the analysis and discussion, suggestions are provided for both selections of proper images and methods in complex classification applications.
2. Related Work
2.1. HSI Classification
2.2. HSI Degradation
3. Proposed Analysis Framework
3.1. Data Preparation
- Pavia University: It was captured by the reflective optics system imaging spectrometer (ROSIS-3) during a flight over the city of Pavia, northern Italy, in 2003. The image consists of 115 spectral bands within the wavelength range of 0.43–0.86 m. Among them, 12 bands were discarded due to noise, and the remaining 103 spectral bands were used in this study. Pavia University contains 610 × 340 pixels with a geometric resolution of 1.3 m. The image is divided into 9 classes in the urban scene, including trees, asphalt roads, bricks, meadows, etc., where 42,776 pixels are labeled;
- Salinas: This scene was gathered by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) sensor over the Salinas Valley in California, USA. Its spatial resolution reaches 3.7 m with 224 spectral bands ranging from 370 nm to 2480 nm. After removing the channels with poor imaging quality (1–2 and 221–224) or related to water absorption (104–113 and 148–167), there remained 188 channels for experiments. The image comprises 512 × 217 pixels, of which 56,975 are background pixels and 54,129 are labeled for classification. Salinas’s ground truth contains 16 categories, including fallow, celery, etc.;
- Cuprite: Cuprite was also acquired by the AVIRIS sensor, covering cuprite mining areas in Las Vegas, NV, USA. Similar to the Salinas data, there also remained 188 bands after preprocessing. A subimage of 479 × 507 pixels that corresponds to the mineral mapping areas of copper mining reported by the spectral Laboratory of the United States Geological Survey (USGS) [81] was selected for later tests. The ground truth was drawn manually according to the released map (download link: http://speclab.cr.usgs.gov/PAPERS/tetracorder/ (accessed on 1 September 2022)), and was labeled with eight classes, including Alunite, Kaolinite, Calcite, Muscovite, etc. Consistent with the released map, there also exist categories containing two or three kinds of mixed minerals in the manually interpreted ground truth. The total number of labeled pixels is 33,302.
- Yellow River Estuary coastal wetland (YRE coastal wetland): This data, obtained by the Gaofen-5 satellite, covers the Yellow River Estuary coastal wetland between Bohai Bay and Laizhou Bay, which is the most important representative of the coastal wetland ecosystem in China [82]. The YRE coastal wetland image contains 740 × 761 pixels with 296 spectral bands. The ground sample distance (GSD) of the image is 30 m. According to the records of field observation, the image contains 8 kinds of ground objects, including water, reed, Tamarix, Spartina, etc. There are 415,101 labeled pixels.
3.1.1. Hyperspectral Data with Single-Type Degradation
- Low spatial resolution: To better study the impact of low spatial resolution on image classification, we constructed a series of degraded data with low spatial resolution. The source images were downsampled according to the resolution reduction ratio () and then upsampled to the same size as the original images for display. The whole process can be described as:where g denotes the interpolation kernel, stands for the sampling function and its two parameters are used to control the sampling process. Given the resolution reduction ratio , represents the downsampling process, which transforms the image from to . Conversely, describes the upsampling process, which transforms the image from to since . In the subsequent simulation, the bicubic kernel [83] was chosen and the resolution reduction ratio was selected as 81%, 64%, 49%, 36%, 25%, and 16%. Clearly, the spatial resolution decreases as decreases, and the image becomes more and more blurred in the visual display.
- Gaussian noise: Gaussian noise is the most common kind of noise, which is caused by random interference in the process of image capture, transmission, or processing. Since Gaussian noise can be regarded as additive noise, we simulated Gaussian noise degraded data series as:where represents the additive Gaussian noise, whose probability density function at each pixel in each band obeys the distribution as the name implies:where , are the expectation and variance of the Gaussian distribution, respectively. To simulate different noise levels, the mean value was fixed as 0, and the variance of Gaussian noise was adjusted to 0.001, 0.005, 0.01, 0.02, 0.03, and 0.04.
- Stripe noise: Stripe noise is a kind of directional noise, with pixel values brighter or darker than their adjacent normal image rows/columns, which is usually caused by inconsistent responses of imaging detectors due to unevenness, dark current influence, and environmental interference. For different imaging systems, stripe noise can be randomly distributed or periodically distributed in the image. Considering that the push-broom imaging system is used in hyperspectral imaging, only the randomly distributed stripe noise was simulated in HSIs. The stripe degradation process can be written as:When constructing stripe data, three variables are involved. They are the amplitude of the stripe , the density of the stripe , and the number of affected bands in hyperspectral images. The calculation of , , are separately given as follows:where stands for the ratio of the specific variable and the function refers to the three-dimensional mean calculation on the whole hyperspectral data. In the simulation process, the amplitude of the added stripe was a random number obeying the normal distribution with the mean value as . The degree of density referred to the number of striped columns in one band, and the locations of stripes were distributed randomly. The number of the affected bands of stripe noise was determined by . In addition, we added positive stripes to the random half of the striping locations and negative stripes to the other half to simulate the light and dark distribution of stripe noise. The ratio of the three variables was tested at 6 levels: 10%, 20%, 40%, 50%, 60%, and 80%. It should be noted that in the process of stripe simulation, when one variable was considered for adjustment, the ratio of the other two variables was fixed at 30%.
- Fog: In foggy weather, hyperspectral imaging records the reflected energy of fog and ground objects at the same time, that is, there is a deviation in the spectral information of ground objects. Then, whether the foggy image affects the hyperspectral classification and to what degree has become a problem worthy of study.In order to reasonably add fog to a clean hyperspectral image and make it closer to a real situation, we used the model proposed in [4] for fog simulation, in which the foggy hyperspectral image was modeled as the superposition of the clean image and fog image. Specifically, the authors in [4] first calculated a foggy density map by comparing the average values from visible and infrared bands, since the fog had an obvious effect on the visible bands and almost no effect on the infrared bands. Then, based on the foggy density map and reflectance differences between pixels, fog abundances in different spectral bands were estimated. Finally, by solving the fog model, the fog in the degraded image was removed. Contrary to the fog removal process, we added fog to clean hyperspectral images according to the formulation given in (6). The foggy density map and fog abundance were both extracted from real foggy datasets.where represents the vector at the ith pixel in the simulated image . represents the vector at the ith pixel in the original clean image . stands for the fog abundance estimated from the real foggy HSI. denotes the fog intensity map, and represents its ith pixel. In order to evaluate the effects of different fog degradation levels, we simulated the data as follows:where stands for the fog degradation levels and ⊗ represents the Kronecker product. To be specific, we adjusted the value of to 0.6, 0.8, 1.0, 1.2, 1.4, and 1.6.
- Shadow: Shadows in the image represent a significant brightness loss of the ground surface radiation recorded by imagers. Here, we only discuss a shadow caused by inadequate lighting when the sun is blocked, regardless of the shadow caused by tall buildings when the angle of sunlight changes considering that the spatial resolution of hyperspectral images is usually not high enough to generate a large area of building shadows. Since there are few physical models of shadow in hyperspectral images in the current literature, we extended the shadow model of natural images given in [72] to realize a hyperspectral shadow simulation.The model proposed in [72] is based on the image formation equation that an observed image is the pixelwise product of the reflectance and illumination [84]. By denoting and as vectors of the illumination and reflectance at the ith pixel, the value of then satisfies the following formula: , where ∘ represents the elementwise product. At the same time, the illumination can be described as the sum of direct illumination (illumination generated by the main light source) and ambient illumination (illumination generated by the surrounding environment), i.e., . Therefore, for each pixel in the shadow area, its ambient illumination intensity can be regarded as unchanged, but the direct illumination intensity reduces significantly. To effectively separate shadows from shadow-affected areas, the corresponding relationship between shadow pixels and intact pixels is established based on texture similarity. The whole model is shown as:where denotes an optimized illumination restoration operator, and represents its ith pixel. represents the vector at the ith pixel in the simulated image . is vectorized and describes the degree to which shadows reduce illumination. can be computed by minimizing the energy equation in the closed-form matting method [85], and represents the ith pixel in . In the energy equation, is the Laplacian matrix, is a diagonal matrix whose diagonal elements are 1 for constrained pixels and 0 for other pixels, and is a vector which records the specified values for constrained pixels and 0 for other pixels.When extending the model (8) to hyperspectral images, we firstly used a real shadow hyperspectral image caused by a single light source occlusion to extract the optimized illumination restoration operator and then estimated by following [85]. The calculation of is given in (9). Finally, we added the shadow to the clean image according to the operation displayed as:where represents the shadow degradation levels, which were set as 0.1, 0.2, 0.4, 0.5, 0.6, and 0.8.
3.1.2. Hyperspectral Data with Mixed-Type Degradation
3.2. Training and Testing Methods
- Support vector machines (SVMs) [7]: As a spectral-based classification method, the support vector machine (SVM) is one of the most classical and widely used methods whose basic model is the linear classifier with the largest interval defined in the feature space. An SVM was initially designed as a binary linear classification method. However, when the kernel technique is adopted, an SVM can also be used for nonlinear classification in hyperspectral multiclass problems.
- Extended morphological profiles (EMP) [20]: The extended morphological profiles (EMP) method is a spectral–spatial classification method based on mathematical morphology. The EMP method constructs extended morphological profiles according to the principal components of the hyperspectral data. It mainly considers the spatial information of HSIs and is a preprocessing method, thus generally used together with feature extraction techniques.
- Edge-preserving filtering (EPF) [29]: Edge-preserving filtering (EPF) is a spectral–spatial classification method based on postprocessing. In this method, the hyperspectral image is first classified by a pixel classifier to obtain a probability map. Then, the probability map is postprocessed by edge-preserving filtering, where the category of each pixel is determined according to the principle of maximum probability. Due to the high computational efficiency, EPF can get considerable classification results at a smaller time cost.
- Markov random field (MRF) [86]: A Markov random field (MRF) is also a postprocessing spectral–spatial method. Different from EPF, its probability map is optimized through the model of a Markov random field. Specifically, the class of a pixel is determined jointly by the output of the pixelwise classifier, the spatial correlation of adjacent pixels, and the solution of a MRF related minimization problem.
- Multiscale total variation (MSTV) [87]: Multiscale total variation (MSTV) consists of two steps. The first step is a multiscale structure feature construction where the relative total variation is applied to the dimension-reduced hyperspectral images. Then, multiple principal components are fused by a kernel principal component analysis (KPCA). MSTV can be regarded as a hybrid method since spatial and spectral information is well coupled throughout the classification process.
- Convolutional neural networks (CNN) [41]: As a data-driven technique, deep learning has been proven to be an effective image classification method due to its accurate semantic interpretation. There are many existing deep learning architectures for remote sensing hyperspectral image classification. Among them, the 3D convolutional neural network can establish a deep comprehension of input images and enables the joint processing of spectral and spatial information for classification. The 3DCNN method was implemented through the source code released in [88].
- Robust self-ensembling network (RSEN) [89]: The robust self-ensembling network (RSEN) is a recent work that first introduces self-ensembling learning into hyperspectral image classification. An RSEN implements a base network and an ensemble network learning from each other to assist the spectral–spatial network training. A novel consistency filtering strategy was also proposed to enhance the robustness of self-ensembling learning. It is claimed that RSEN can achieve a high accuracy with a small amount of labeled data.
3.3. Evaluation
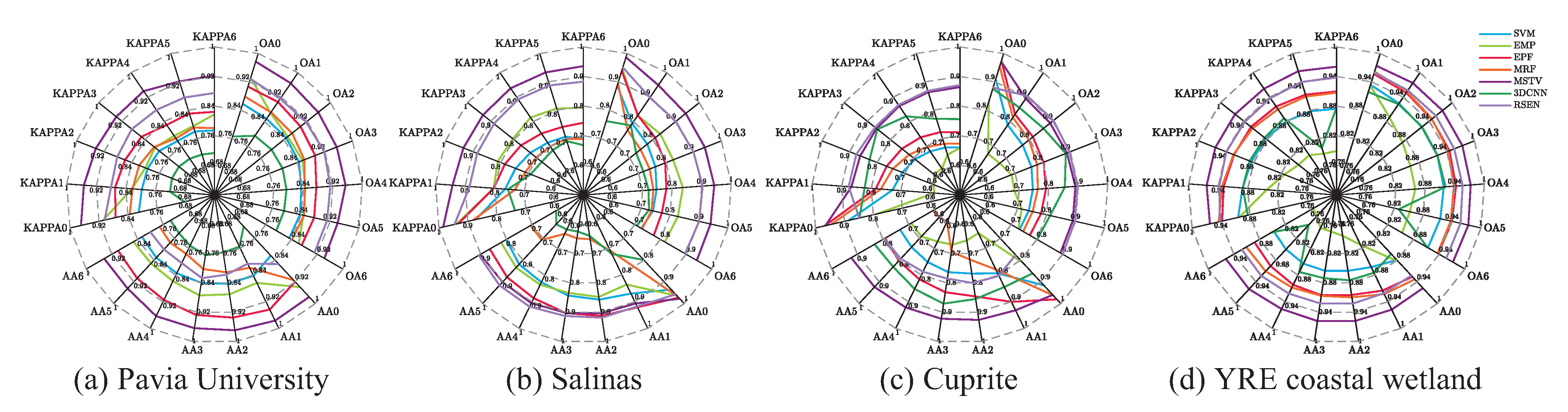
4. Effects of Degraded Images on Hyperspectral Image Classification
4.1. Effect Analysis of Single-Type Image Degradation
4.1.1. Effects of Low Spatial Resolution on Hyperspectral Image Classification
4.1.2. Effects of Gaussian Noise on Hyperspectral Image Classification
4.1.3. Effects of Stripe Noise on Hyperspectral Image Classification
4.1.4. Effects of Fog on Hyperspectral Image Classification
4.1.5. Effects of Shadow on Hyperspectral Image Classification
4.2. Effect Analysis of Mixed-Type Image Degradation
5. Discussion
5.1. Method Selection to Handle Degraded HSIs in Classification
5.2. Data Preparation to Handle Degraded HSI in Classification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Shaw, G.; Manolakis, D. Signal processing for hyperspectral image exploitation. IEEE Signal Process. Mag. 2002, 19, 12–16. [Google Scholar] [CrossRef]
- Zare, A.; Ho, K. Endmember Variability in Hyperspectral Analysis: Addressing Spectral Variability During Spectral Unmixing. IEEE Signal Process. Mag. 2014, 31, 95–104. [Google Scholar] [CrossRef]
- Kang, X.; Fei, Z.; Duan, P.; Li, S. Fog Model-Based Hyperspectral Image Defogging. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5512512. [Google Scholar] [CrossRef]
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in Hyperspectral Image and Signal Processing: A Comprehensive Overview of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef]
- Li, C.; Liu, X.; Kang, X.; Li, S. A Comparative Study of Noise Sensitivity on Different Hyperspectral Classification Methods. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 3689–3692. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, L. An Adaptive Artificial Immune Network for Supervised Classification of Multi-/Hyperspectral Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 894–909. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Fisher, R.A. The Use of Multiple Measurements in Taxonomic Problems. Ann. Hum. Genet. 2012, 7, 179–188. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of Hyperspectral Images with Regularized Linear Discriminant Analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Plaza, A.; Bioucas-Dias, J.M. A Subspace-Based Multinomial Logistic Regression for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2105–2109. [Google Scholar] [CrossRef]
- Liew, S.C.; Chang, C.W.; Lim, K.H. Hyperspectral land cover classification of EO-1 Hyperion data by principal component analysis and pixel unmixing. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 6, pp. 3111–3113. [Google Scholar] [CrossRef]
- Villa, A.; Benediktsson, J.A.; Chanussot, J.; Jutten, C. Hyperspectral Image Classification With Independent Component Discriminant Analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4865–4876. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral–Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Jia, X.; Kuo, B.C.; Crawford, M.M. Feature Mining for Hyperspectral Image Classification. Proc. IEEE 2013, 101, 676–697. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral Image Classification Using Dictionary-Based Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Kang, X.; Benediktsson, J.A. Spectral–Spatial Hyperspectral Image Classification via Multiscale Adaptive Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7738–7749. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Marpu, P.R.; Pedergnana, M.; Dalla Mura, M.; Benediktsson, J.A.; Bruzzone, L. Automatic Generation of Standard Deviation Attribute Profiles for Spectral–Spatial Classification of Remote Sensing Data. IEEE Geosci. Remote Sens. Lett. 2013, 10, 293–297. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Gomez-Chova, L.; Munoz-Mari, J.; Vila-Frances, J.; Calpe-Maravilla, J. Composite kernels for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2006, 3, 93–97. [Google Scholar] [CrossRef]
- Li, J.; Marpu, P.R.; Plaza, A.; Bioucas-Dias, J.M.; Benediktsson, J.A. Generalized Composite Kernel Framework for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4816–4829. [Google Scholar] [CrossRef]
- Lu, T.; Li, S.; Fang, L.; Jia, X.; Benediktsson, J.A. From Subpixel to Superpixel: A Novel Fusion Framework for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4398–4411. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Duan, W.; Ren, J.; Benediktsson, J.A. Classification of Hyperspectral Images by Exploiting Spectral–Spatial Information of Superpixel via Multiple Kernels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6663–6674. [Google Scholar] [CrossRef]
- Ghamisi, P.; Maggiori, E.; Li, S.; Souza, R.; Tarablaka, Y.; Moser, G.; De Giorgi, A.; Fang, L.; Chen, Y.; Chi, M.; et al. New Frontiers in Spectral-Spatial Hyperspectral Image Classification: The Latest Advances Based on Mathematical Morphology, Markov Random Fields, Segmentation, Sparse Representation, and Deep Learning. IEEE Geosci. Remote Sens. Mag. 2018, 6, 10–43. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–Spatial Hyperspectral Image Segmentation Using Subspace Multinomial Logistic Regression and Markov Random Fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–823. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Ghamisi, P.; Contreras, C.; Gloaguen, R. Subspace Multinomial Logistic Regression Ensemble for Classification of Hyperspectral Images. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 5740–5743. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Spectral–Spatial Hyperspectral Image Classification with Edge-Preserving Filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2666–2677. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–Spatial Classification of Hyperspectral Data Using Loopy Belief Propagation and Active Learning. IEEE Trans. Geosci. Remote Sens. 2013, 51, 844–856. [Google Scholar] [CrossRef]
- Ghamisi, P.; Plaza, J.; Chen, Y.; Li, J.; Plaza, A.J. Advanced Spectral Classifiers for Hyperspectral Images: A review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–32. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Bordes, A.; Glorot, X.; Weston, J. Joint Learning of Words and Meaning Representations for Open-Text Semantic Parsing. In Proceedings of the Artificial intelligence and statistics, La Palma, Spain, 21–23 April 2012. [Google Scholar]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Wei, H.; Yangyu, H.; Li, W.; Fan, Z.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 258619. [Google Scholar]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar] [CrossRef]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised Deep Feature Extraction for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1349–1362. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral–Spatial Feature Extraction for Hyperspectral Image Classification: A Dimension Reduction and Deep Learning Approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Ben Hamida, A.; Benoit, A.; Lambert, P.; Ben Amar, C. 3-D Deep Learning Approach for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled Nonnegative Matrix Factorization Unmixing for Hyperspectral and Multispectral Data Fusion. IEEE Trans. Geosci. Remote Sens. 2012, 50, 528–537. [Google Scholar] [CrossRef]
- Li, S.; Dian, R.; Fang, L.; Bioucas-Dias, J.M. Fusing Hyperspectral and Multispectral Images via Coupled Sparse Tensor Factorization. IEEE Trans. Image Process. 2018, 27, 4118–4130. [Google Scholar] [CrossRef]
- Dian, R.; Li, S. Hyperspectral Image Super-Resolution via Subspace-Based Low Tensor Multi-Rank Regularization. IEEE Trans. Image Process. 2019, 28, 5135–5146. [Google Scholar] [CrossRef]
- Lin, C.H.; Ma, F.; Chi, C.Y.; Hsieh, C.H. A Convex Optimization-Based Coupled Nonnegative Matrix Factorization Algorithm for Hyperspectral and Multispectral Data Fusion. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1652–1667. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution Via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image Super-Resolution Using Dense Skip Connections. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4809–4817. [Google Scholar] [CrossRef]
- Mei, S.; Jiang, R.; Li, X.; Du, Q. Spatial and Spectral Joint Super-Resolution Using Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4590–4603. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Z.; Wen, B.; Yang, J.; Han, W.; Huang, T.S. Robust Single Image Super-Resolution via Deep Networks With Sparse Prior. IEEE Trans. Image Process. 2016, 25, 3194–3207. [Google Scholar] [CrossRef]
- Liu, X.; Shen, H.; Yuan, Q.; Lu, X.; Zhou, C. A Universal Destriping Framework Combining 1-D and 2-D Variational Optimization Methods. IEEE Trans. Geosci. Remote Sens. 2018, 56, 808–822. [Google Scholar] [CrossRef]
- Fischer, A.D.; Thomas, T.J.; Leathers, R.A.; Downes, T.V. Stable Scene-based Non-uniformity Correction Coefficients for Hyperspectral SWIR Sensors. In Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007; pp. 1–14. [Google Scholar] [CrossRef]
- Corsini, G.; Diani, M.; Walzel, T. Striping removal in MOS-B data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1439–1446. [Google Scholar] [CrossRef]
- Chen, J.; Shao, Y.; Guo, H.; Wang, W.; Zhu, B. Destriping CMODIS data by power filtering. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2119–2124. [Google Scholar] [CrossRef]
- Tsai, F.; Chen, W.W. Striping Noise Detection and Correction of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4122–4131. [Google Scholar] [CrossRef]
- Asner, G.; Heidebrecht, K. Imaging spectroscopy for desertification studies: Comparing AVIRIS and EO-1 Hyperion in Argentina drylands. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1283–1296. [Google Scholar] [CrossRef]
- Rakwatin, P.; Takeuchi, W.; Yasuoka, Y. Stripe Noise Reduction in MODIS Data by Combining Histogram Matching with Facet Filter. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1844–1856. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L. A MAP-Based Algorithm for Destriping and Inpainting of Remotely Sensed Images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1492–1502. [Google Scholar] [CrossRef]
- Bouali, M.; Ladjal, S. Toward Optimal Destriping of MODIS Data Using a Unidirectional Variational Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2924–2935. [Google Scholar] [CrossRef]
- Liu, X.; Lu, X.; Shen, H.; Yuan, Q.; Jiao, Y.; Zhang, L. Stripe Noise Separation and Removal in Remote Sensing Images by Consideration of the Global Sparsity and Local Variational Properties. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3049–3060. [Google Scholar] [CrossRef]
- Jia, J.; Zheng, X.; Guo, S.; Wang, Y.; Chen, J. Removing Stripe Noise Based on Improved Statistics for Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2020, 19, 5501405. [Google Scholar] [CrossRef]
- Yang, D.; Yang, L.; Zhou, D. Stripe removal method for remote sensing images based on multi-scale variation model. In Proceedings of the 2019 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Dalian, China, 20–23 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Behnood, R.; Paul, S.; Pedram, G.; Giorgio, L.; Jocelyn, C. Noise Reduction in Hyperspectral Imagery: Overview and Application. Remote Sens. 2018, 10, 482. [Google Scholar]
- Rasti, B.; Ulfarsson, M.O.; Ghamisi, P. Automatic Hyperspectral Image Restoration Using Sparse and Low-Rank Modeling. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2335–2339. [Google Scholar] [CrossRef]
- Jiang, T.X.; Zhuang, L.; Huang, T.Z.; Bioucas-Dias, J.M. Adaptive Hyperspectral Mixed Noise Removal. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 4035–4038. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Single Image Haze Removal Using Dark Channel Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2341–2353. [Google Scholar] [CrossRef] [PubMed]
- Cai, B.; Xu, X.; Jia, K.; Qing, C.; Tao, D. DehazeNet: An End-to-End System for Single Image Haze Removal. IEEE Trans. Image Process. 2016, 25, 5187–5198. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Su, Y.; Li, Q.; Li, J. Single fog image restoration via multi-scale image fusion. In Proceedings of the 2017 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; pp. 1873–1878. [Google Scholar] [CrossRef]
- Makarau, A.; Richter, R.; Müller, R.; Reinartz, P. Haze Detection and Removal in Remotely Sensed Multispectral Imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5895–5905. [Google Scholar] [CrossRef]
- Guo, Q.; Hu, H.M.; Li, B. Haze and Thin Cloud Removal Using Elliptical Boundary Prior for Remote Sensing Image. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9124–9137. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Xiao, C. Shadow Remover: Image Shadow Removal Based on Illumination Recovering Optimization. IEEE Trans. Image Process. 2015, 24, 4623–4636. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.H.; Bennamoun, M.; Sohel, F.; Togneri, R. Automatic Shadow Detection and Removal from a Single Image. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 431–446. [Google Scholar] [CrossRef]
- Liu, Y.; Bioucas-Dias, J.; Li, J.; Plaza, A. Hyperspectral cloud shadow removal based on linear unmixing. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1000–1003. [Google Scholar] [CrossRef]
- Zhang, G.; Cerra, D.; Muller, R. Towards the Spectral Restoration of Shadowed Areas in Hyperspectral Images Based on Nonlinear Unmixing. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Windrim, L.; Ramakrishnan, R.; Melkumyan, A.; Murphy, R.J. A Physics-Based Deep Learning Approach to Shadow Invariant Representations of Hyperspectral Images. IEEE Trans. Image Process. 2018, 27, 665–677. [Google Scholar] [CrossRef]
- Liu, D.; Cheng, B.; Wang, Z.; Zhang, H.; Huang, T.S. Enhance Visual Recognition Under Adverse Conditions via Deep Networks. IEEE Trans. Image Process. 2019, 28, 4401–4412. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, H.; Meng, Y.; Fu, M. Classification of Hyperspectral Image by CNN Based on Shadow Area Enhancement Through Dynamic Stochastic Resonance. IEEE Access 2019, 7, 134862–134870. [Google Scholar] [CrossRef]
- Luo, R.; Liao, W.; Zhang, H.; Zhang, L.; Scheunders, P.; Pi, Y.; Philips, W. Fusion of Hyperspectral and LiDAR Data for Classification of Cloud-Shadow Mixed Remote Sensed Scene. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3768–3781. [Google Scholar] [CrossRef]
- Fu, P.; Sun, Q.; Ji, Z.; Geng, L. A Superpixel-Based Framework for Noisy Hyperspectral Image Classification. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September– 2 October 2020; pp. 834–837. [Google Scholar] [CrossRef]
- Duarte-Carvajalino, J.M.; Castillo, P.E.; Velez-Reyes, M. Comparative Study of Semi-Implicit Schemes for Nonlinear Diffusion in Hyperspectral Imagery. IEEE Trans. Image Process. 2007, 16, 1303–1314. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Zhang, J.; Ma, Y.; An, J.; Ren, G.; Li, X. Hyperspectral Coastal Wetland Classification Based on a Multiobject Convolutional Neural Network Model and Decision Fusion. IEEE Geosci. Remote. Sens. Lett. 2019, 16, 1110–1114. [Google Scholar] [CrossRef]
- Keys, R. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Barrow, H.; Tenenbaum, J. Recovering Intrinsic Scene Characteristics From Images. Comput. Vis. Syst. 1978, 2, 3–26. [Google Scholar]
- Levin, A.; Lischinski, D.; Weiss, Y. A Closed-Form Solution to Natural Image Matting. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 228–242. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Fauvel, M.; Chanussot, J.; Benediktsson, J.A. SVM- and MRF-Based Method for Accurate Classification of Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 736–740. [Google Scholar] [CrossRef]
- Duan, P.; Kang, X.; Li, S.; Ghamisi, P. Noise-Robust Hyperspectral Image Classification via Multi-Scale Total Variation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1948–1962. [Google Scholar] [CrossRef]
- Audebert, N.; Le Saux, B.; Lefevre, S. Deep Learning for Classification of Hyperspectral Data: A Comparative Review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 159–173. [Google Scholar] [CrossRef]
- Xu, Y.; Du, B.; Zhang, L. Robust Self-Ensembling Network for Hyperspectral Image Classification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–14. [Google Scholar] [CrossRef] [PubMed]














Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Li, Z.; Liu, X.; Li, S. The Influence of Image Degradation on Hyperspectral Image Classification. Remote Sens. 2022, 14, 5199. https://doi.org/10.3390/rs14205199
Li C, Li Z, Liu X, Li S. The Influence of Image Degradation on Hyperspectral Image Classification. Remote Sensing. 2022; 14(20):5199. https://doi.org/10.3390/rs14205199
Chicago/Turabian StyleLi, Congyu, Zhen Li, Xinxin Liu, and Shutao Li. 2022. "The Influence of Image Degradation on Hyperspectral Image Classification" Remote Sensing 14, no. 20: 5199. https://doi.org/10.3390/rs14205199
APA StyleLi, C., Li, Z., Liu, X., & Li, S. (2022). The Influence of Image Degradation on Hyperspectral Image Classification. Remote Sensing, 14(20), 5199. https://doi.org/10.3390/rs14205199






