Estimation of Aboveground Biomass of Potatoes Based on Characteristic Variables Extracted from UAV Hyperspectral Imagery
Abstract
1. Introduction
2. Materials and Methods
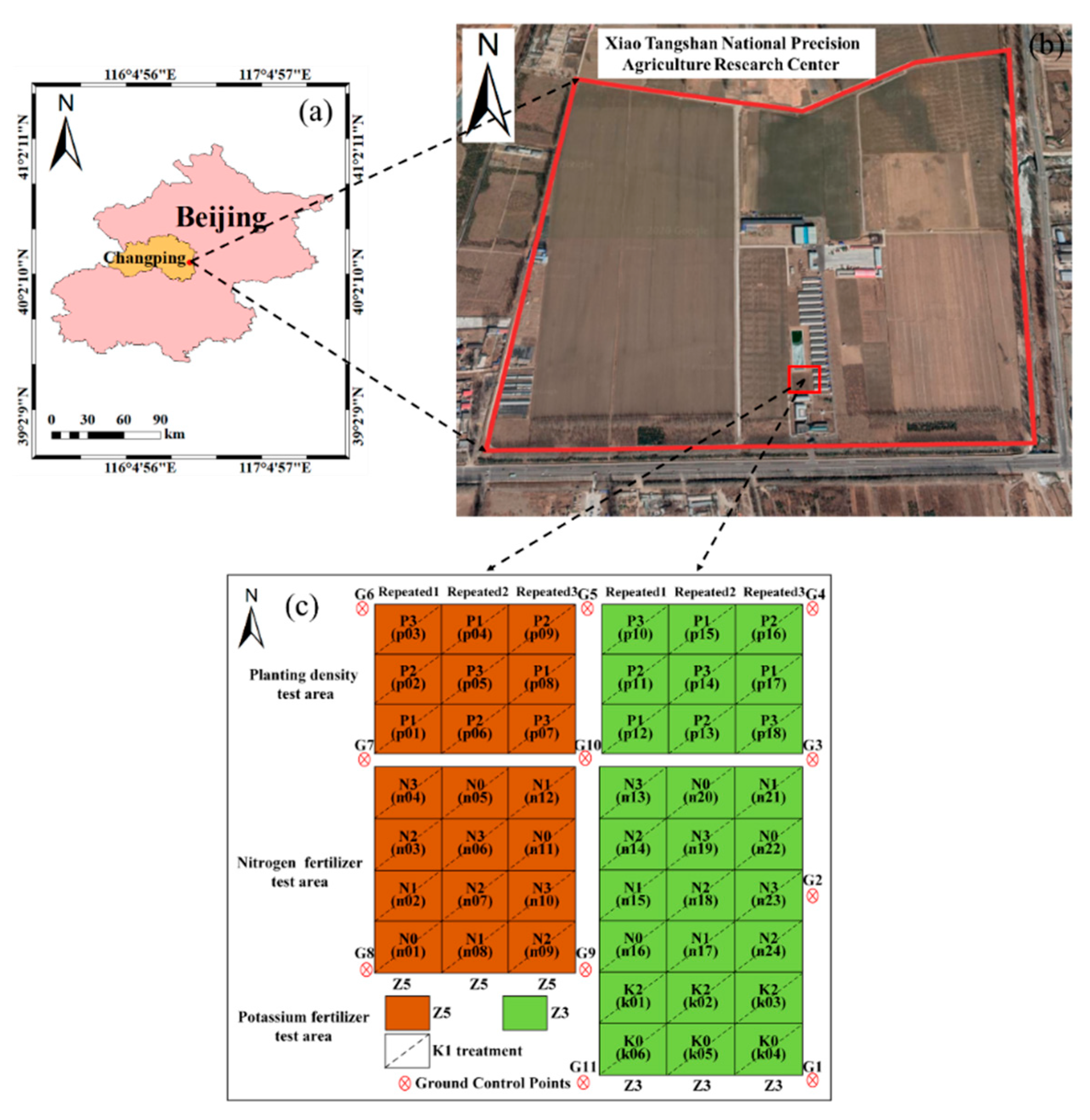
2.1. Experimental Design
2.2. Ground-Data Collection and Processing
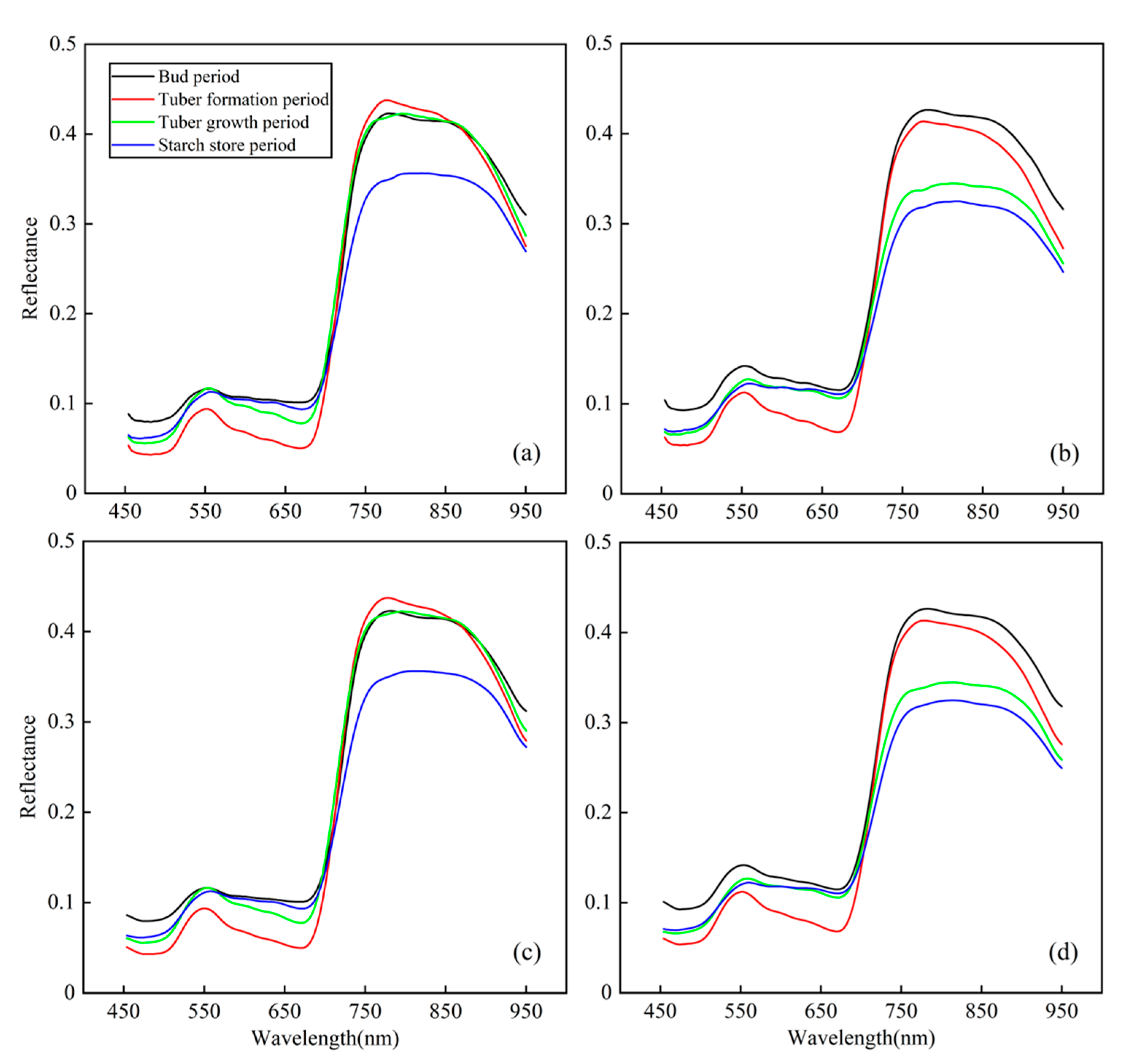
2.3. UAV Hyperspectral Data Acquisition and Processing
- (i)
- Image mosaic and terrain correction. First, with the help of the Agisoft Photoscan software, which is based on a motion structure algorithm, image mosaic and terrain correction were carried out in combination with the position of ground control points (the correction error of each growth period is less than 2 cm). Second, hyperspectral and grayscale images were fused by using the Cubert Cube-Pilot software to form new hyperspectral digital orthophotos [40].
- (ii)
- Extraction of canopy spectral reflectance. According to the ratio method, the digital number value of the hyperspectral image is converted into the surface reflectance based on the black and white panel data collected on the ground. To eliminate the boundary effect, ArcGIS 10.2 software was used to draw the maximum region of interest (a total of 48 plots) for each plot. Based on ENVI 5.3 software, the average spectral reflectance of all pixels in each region of interest was calculated, and the average spectrum obtained served as the spectral reflectance of the potato canopy for each experimental plot [41].
2.4. Selection of Model Parameters
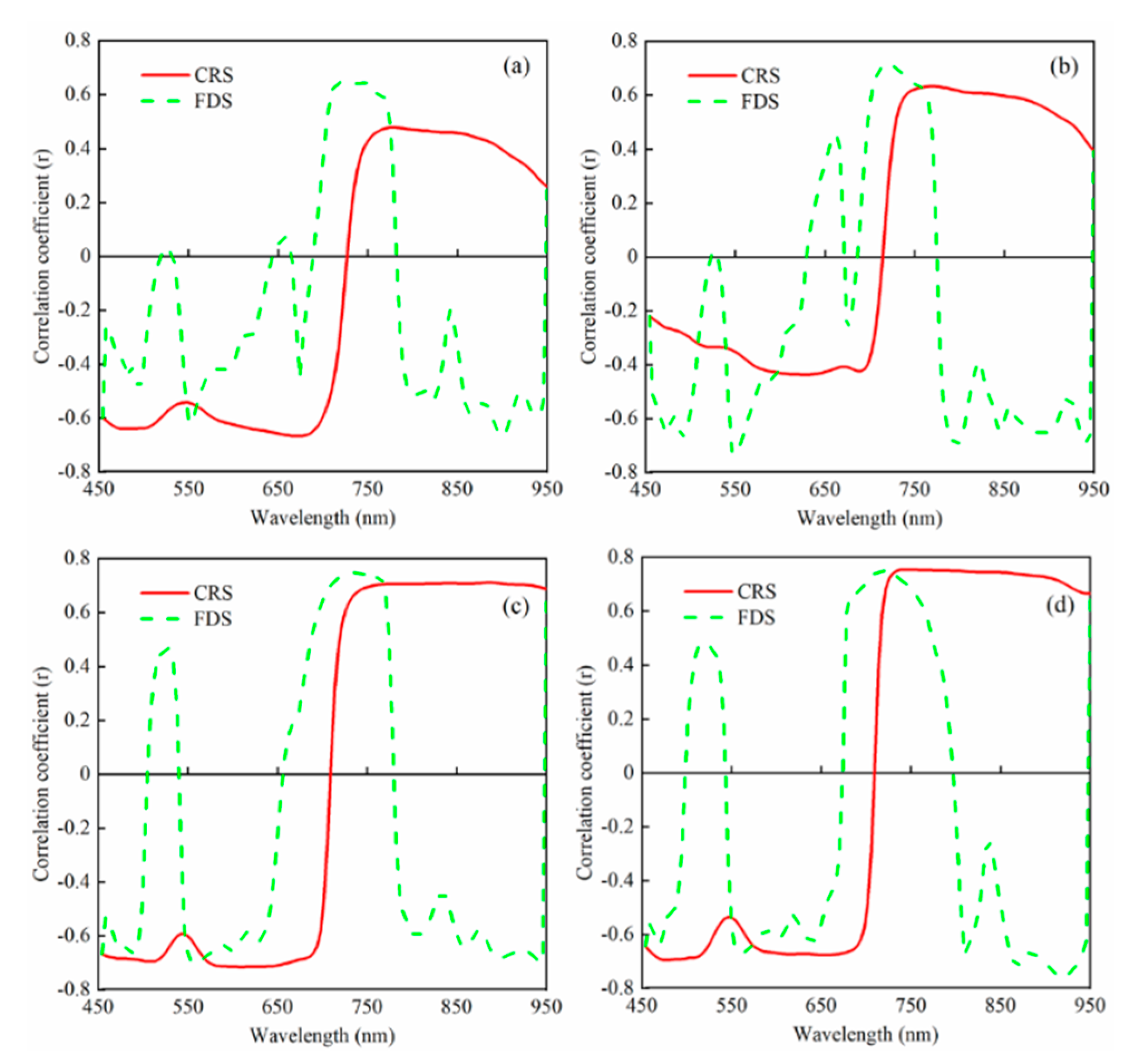
2.4.1. Extraction of Spectral-Reflection Features
2.4.2. Extraction of Spectral-Position Features
2.4.3. Selection of Vegetation Indexes
2.5. Analysis Method
2.6. Accuracy Evaluation
3. Results and Analysis
3.1. Estimation of AGB Using Spectral-Reflectance Features
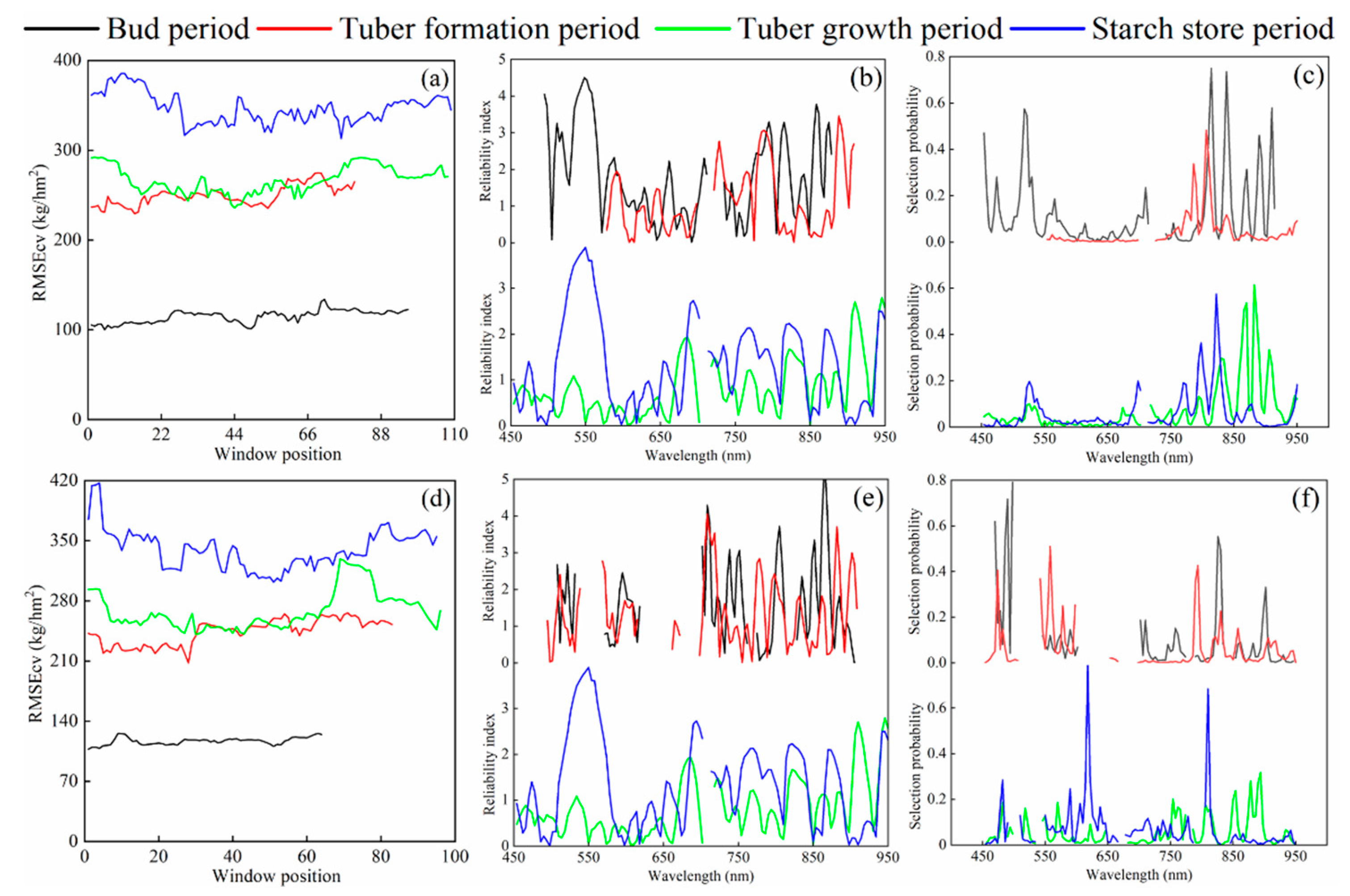
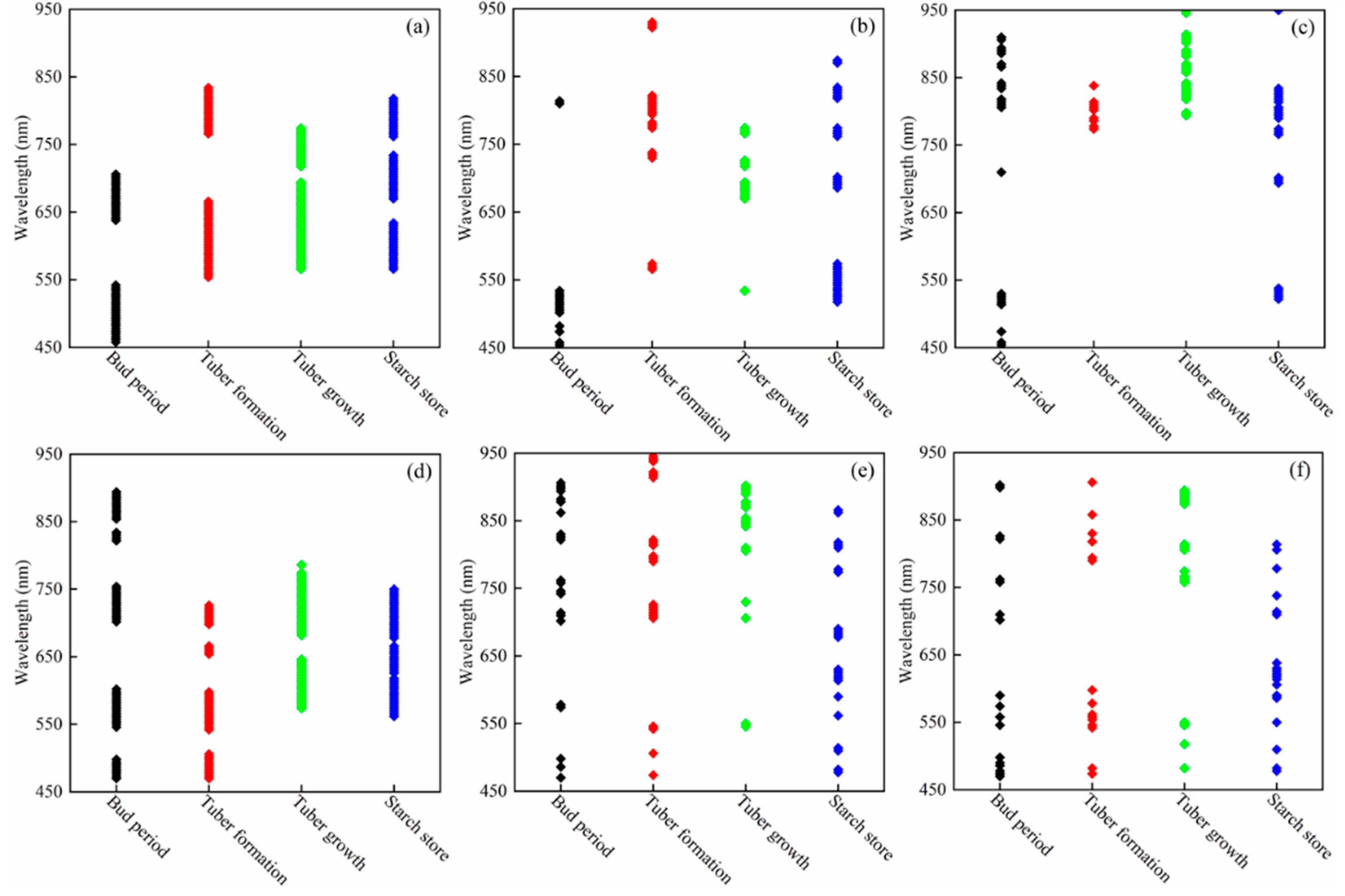
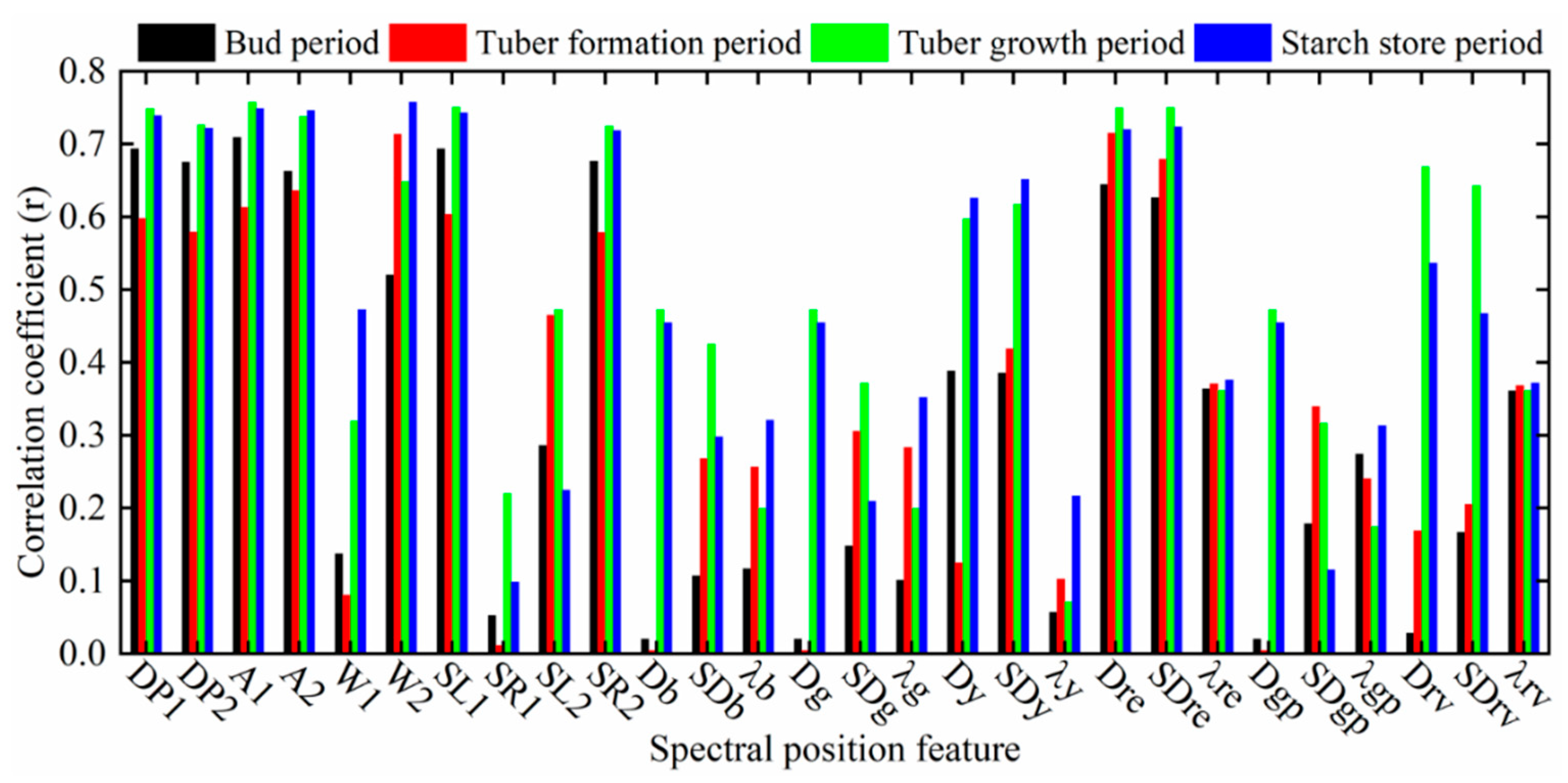
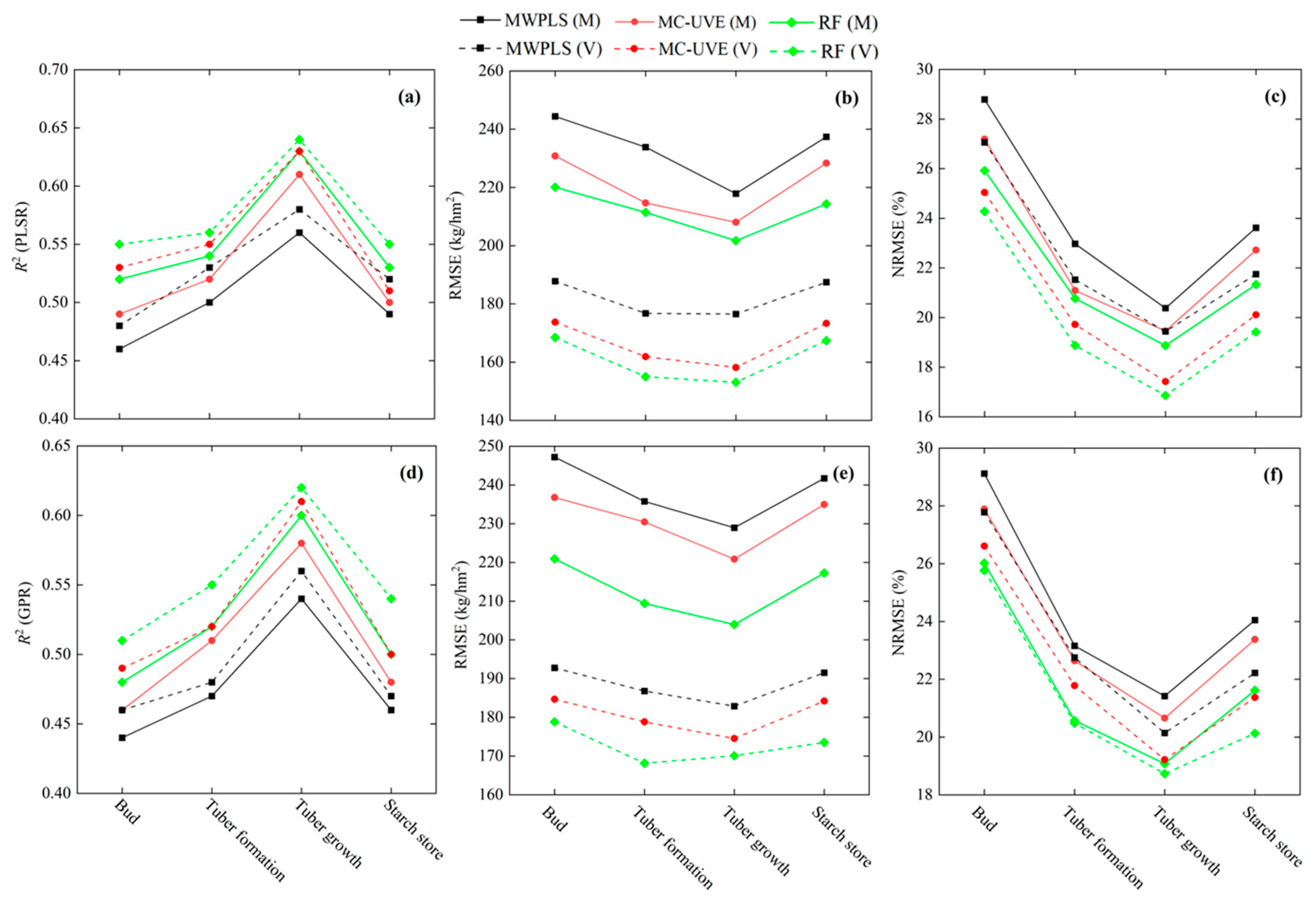
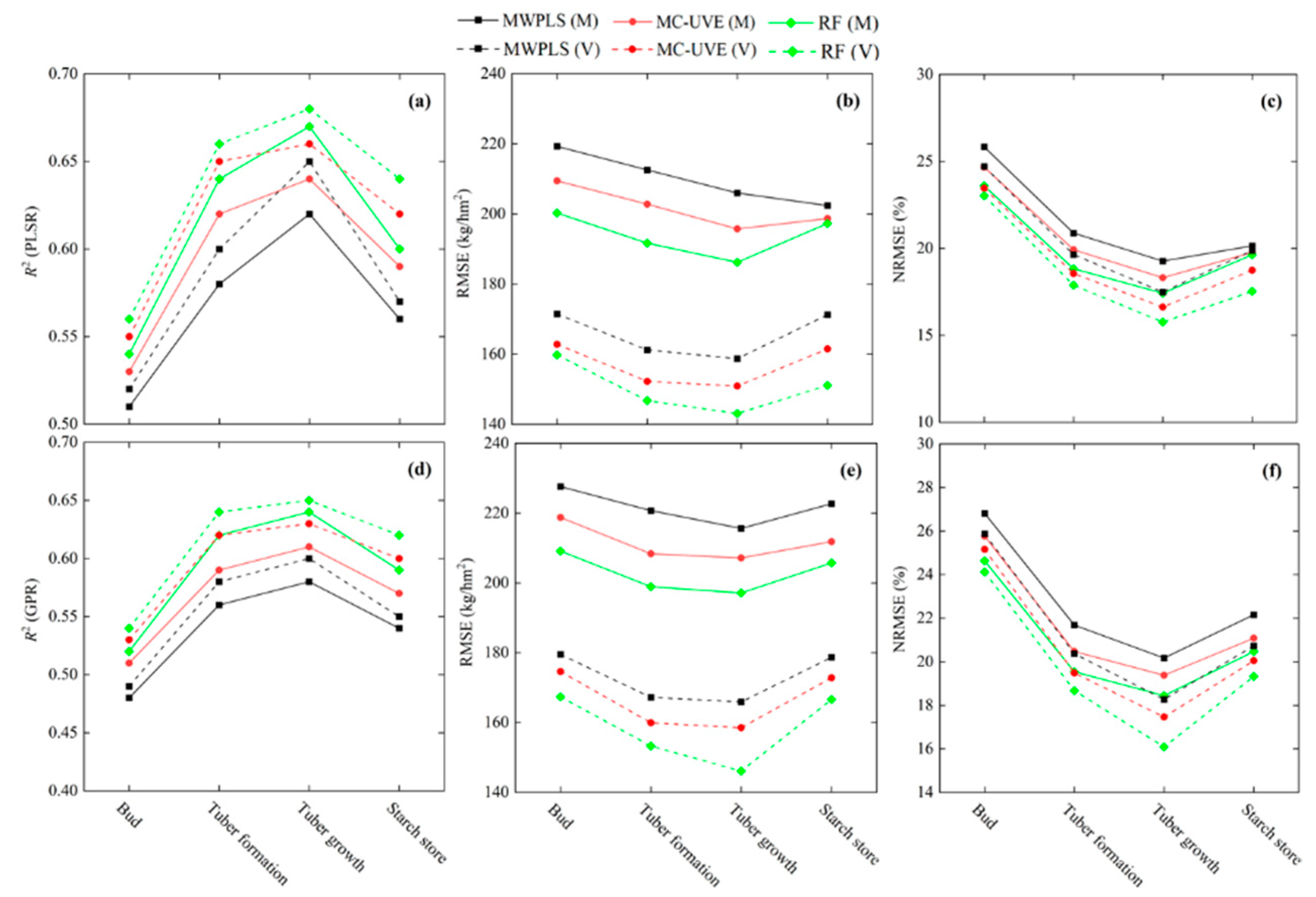
3.2. Estimation of AGB Using Spectral-Position Features
3.3. Estimation of AGB Using Vegetation Indexes
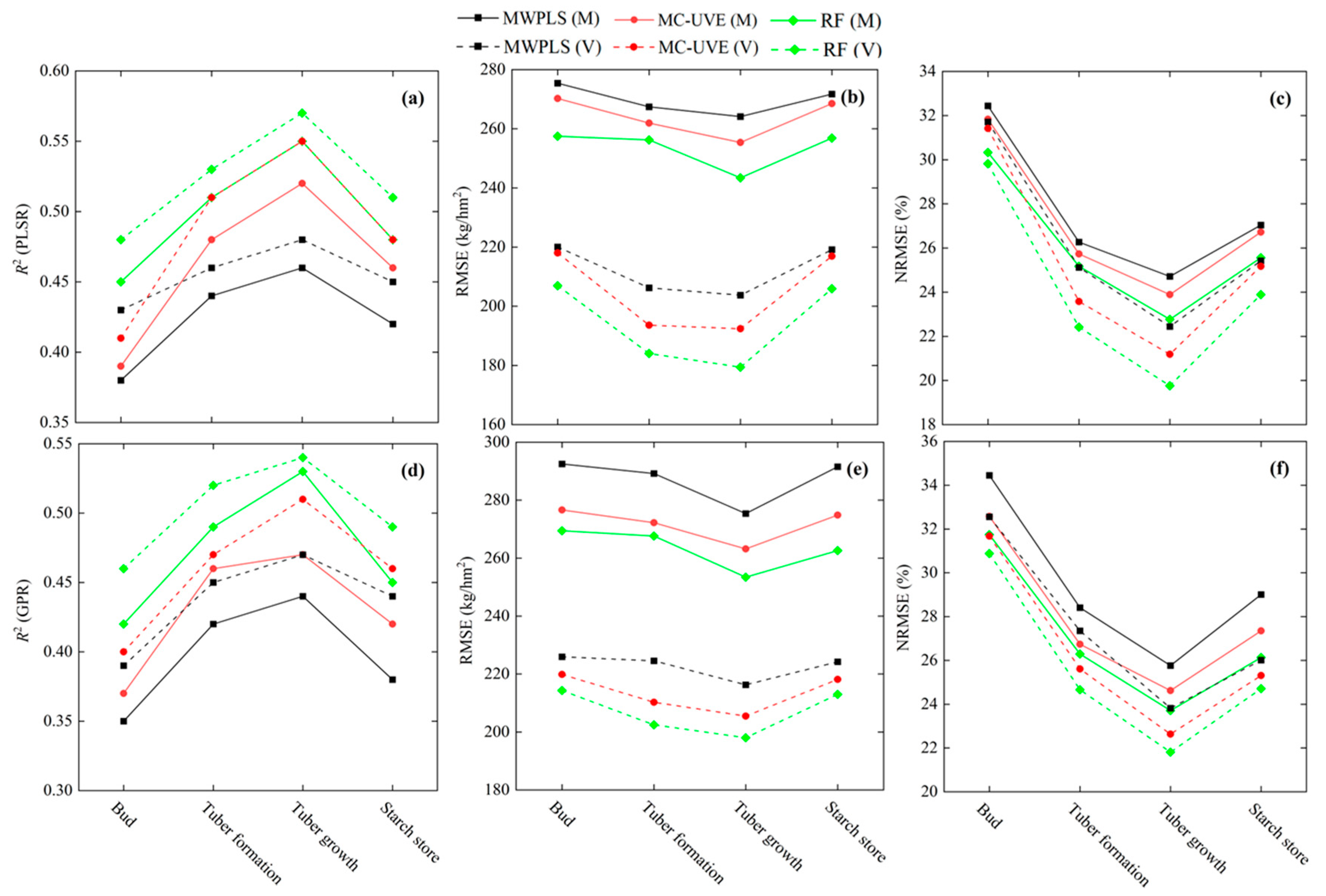
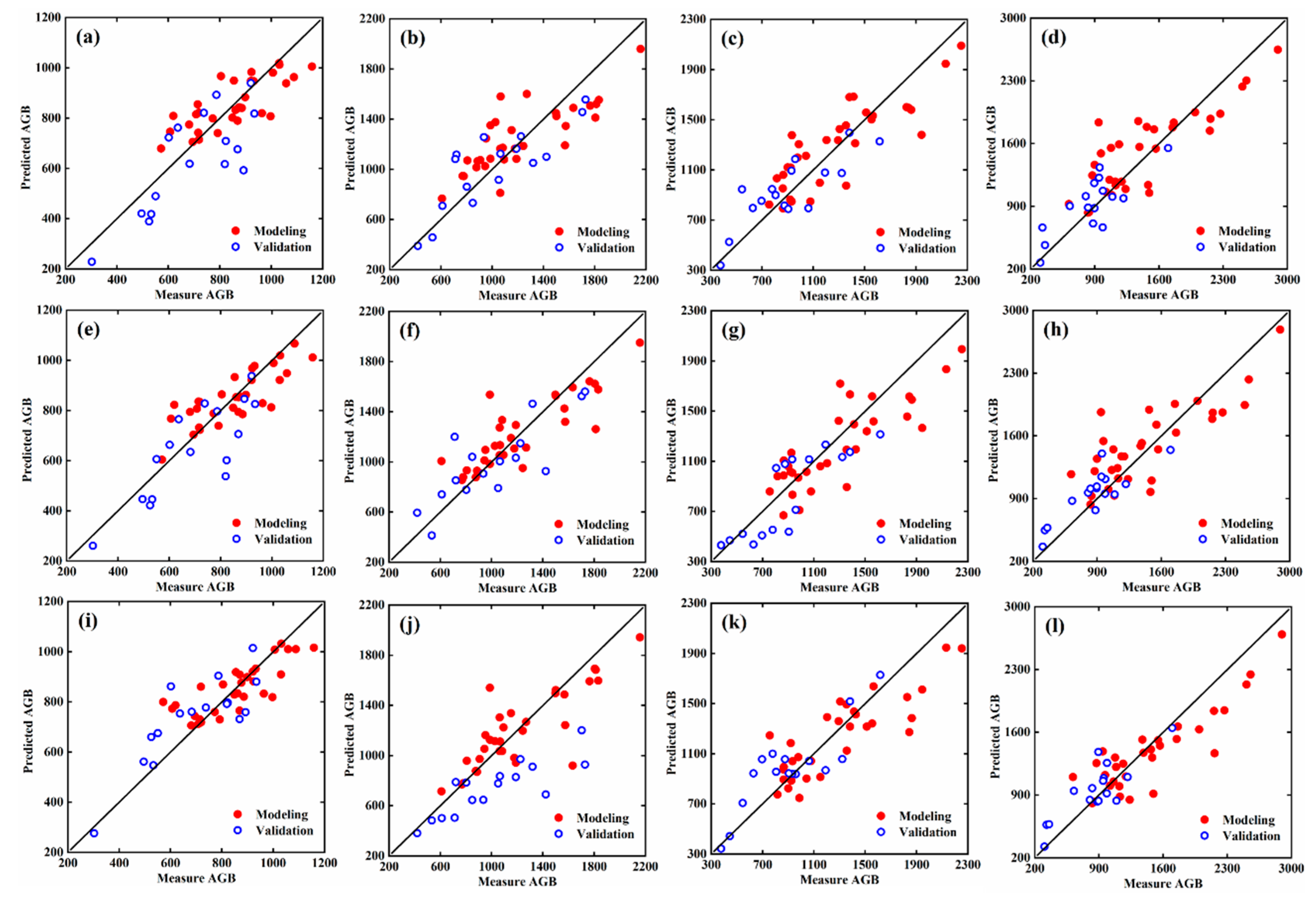
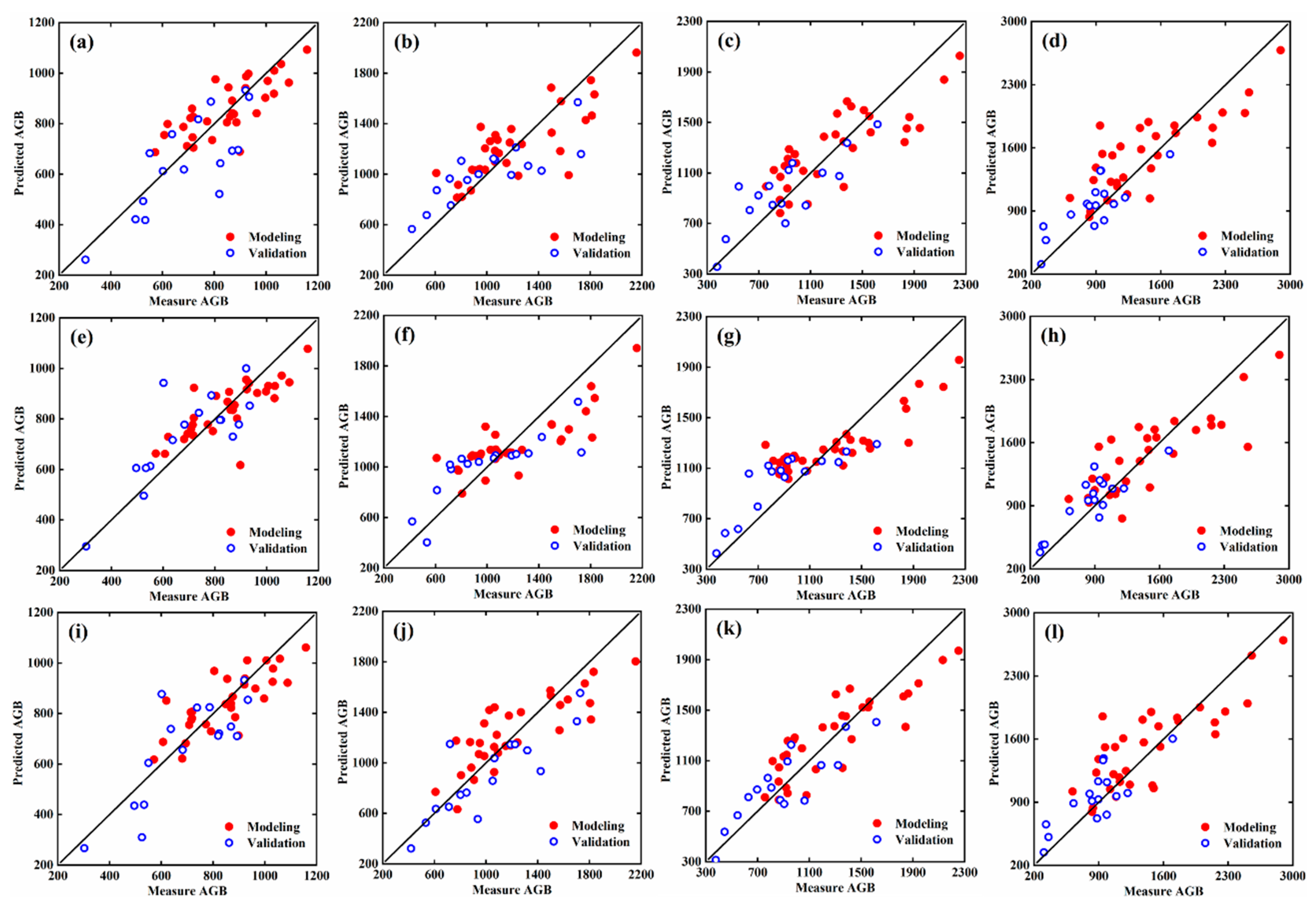
3.4. Estimation of AGB Using Composite Variables
4. Discussion
4.1. Correlation between Three Types of Spectral Features and AGB
4.2. Estimation of AGB Effect Based on Three Spectral Features
4.3. Estimation of AGB Based on Different Variable-Screening Methods
4.4. Estimation of AGB Based on Different Modeling Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Banerjee, B.P.; Spangenberg, G.; Kant, S. Fusion of spectral and structural information from aerial images for improved biomass estimation. Remote Sens. 2020, 12, 3164. [Google Scholar] [CrossRef]
- Banerjee, B.P.; Raval, S.; Cullen, P.J. UAV-hyperspectral imaging of spectrally complex environments. Int. J. Remote Sens. 2020, 41, 4136–4159. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, B.M.; Ni, X.Y.; Tao, L.Z.; Yu, L.X.; Yang, Y.; Feng, M.X.; Zhong, W.J.; Wu, Y.J. Rice productivity and profitability with slow-release urea containing organic-inorganic matrix materials. Pedosphere 2021, 31, 511–520. [Google Scholar] [CrossRef]
- Morier, T.; Cambouris, A.N.; Chokmani, K. In-season nitrogen status assessment and yield estimation using hyperspectral vegetation indices in a potato crop. Agron. J. 2015, 107, 1295–1309. [Google Scholar] [CrossRef]
- Mahlein, A.K.; Rumpf, T.; Welke, P.; Dehne, H.W.; Plumer, L.; Steiner, U.; Oerke, E.C. Development of spectral indices for detecting and identifying plant diseases. Remote Sens. Environ. 2013, 128, 21–30. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Smith, R.B.; Pauw, E.D. Hyperspectral vegetation indices and their relationships with agricultural crop characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Kumar, A.; Tewari, S.; Sing, H.; Kumar, P.; Kumar, N.; Bisht, S.; Devi, S. Biomass accumulation and carbon stock in different agroforestry systems prevalent in the Himalayan foothills, India. Curr. Sci. 2021, 120, 1083–1088. [Google Scholar] [CrossRef]
- Virlet, N.; Sabermanesh, K.; Sadeghi, P.; Hawkesford, M.J. Field Scanalyzer: An automated robotic field phenotyping platform for detailed crop monitoring. Funct. Plant Biol. 2016, 44, 143–153. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Du, H.Y.; Zhang, C.K.; Zhang, L.P. An automated early-season method to map winter wheat using time-series Sentinel-2 data: A case study of Shandong, China. Comput. Electron. Agric. 2021, 182, 105962–105977. [Google Scholar] [CrossRef]
- Huang, J.X.; Sedano, F.; Huang, Y.B.; Ma, H.Y.; Li, X.L.; Liang, S.L.; Tian, L.Y. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation. Agric. For. Meteorol. 2016, 216, 188–202. [Google Scholar] [CrossRef]
- Tao, H.L.; Feng, H.K.; Xu, L.J.; Miao, M.K.; Yang, G.J.; Yang, X.D. Estimation of the yield and plant height of winter wheat using UAV-based hyperspectral images. Sensors 2020, 20, 1231. [Google Scholar] [CrossRef] [PubMed]
- Yue, J.B.; Feng, H.K.; Yang, G.J.; Li, Z.H. A comparison of regression techniques for estimation of above-ground winter wheat biomass using near-surface spectroscopy. Remote Sens. 2018, 10, 66. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Yu, N.; Li, L.; Schmitz, N.; Tian, L.F.; Greenberg, J.A.; Diers, B.W. Development of methods to improve soybean yield estimation and predict plant maturity with an unmanned aerial vehicle based platform. Remote Sens. Environ. 2016, 187, 91–101. [Google Scholar] [CrossRef]
- Lydia, S.; Iolanda, F.; Josep, P. Remote sensing of biomass and yield of winter wheat under different nitrogen supplies. Crop Sci. 2000, 40, 723–731. [Google Scholar] [CrossRef]
- David, A.J.; Hernan, D.B.; Jocelyn, C. Graph-based data fusion applied to: Change detection and biomass estimation in rice crops. Remote Sens. 2020, 12, 2683. [Google Scholar] [CrossRef]
- Kanemasu, E.T. Seasonal canopy reflectance patterns of wheat, sorghum, and soybean. Remote Sens. Environ. 1974, 3, 43–47. [Google Scholar] [CrossRef]
- Kooistra, L.; Clevers, J.W. Estimating potato leaf chlorophyll content using ratio vegetation indices. Remote Sens. Lett. 2016, 7, 611–620. [Google Scholar] [CrossRef]
- Daughtry, C.T.; Walthall, C.L.; Kim, M.S.; Colstoun, E.B.; Mcmurtrey, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Poley, L.G.; McDermid, G.J. A systematic review of the factors influencing the estimation of vegetation aboveground biomass using unmanned aerial systems. Remote Sens. 2020, 12, 1052. [Google Scholar] [CrossRef]
- Behmann, J.; Mahlein, A.K.; Rumpf, T.; Romer, C.; Plumer, L. A review of advanced machine learning methods for the detection of biotic stress in precision crop protection. Precis. Agric. 2015, 16, 239–260. [Google Scholar] [CrossRef]
- Andres, V.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Melian, J.M.; Jimenez, A.; Diaz, M.; Morales, A.; Horstrand, P.; Guerra, R.; Lopez, S. Real-time hyperspectral data transmission for UAV-based acquisition platform. Remote Sens. 2021, 13, 850. [Google Scholar] [CrossRef]
- Guerra, R.; Lopez, S.; Sarmiento, R. A computationally efficient algorithm for fusing multispectral and hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5712–5728. [Google Scholar] [CrossRef]
- Guo, A.T.; Huang, W.J.; Dong, Y.Y.; Ye, H.C.; Ma, H.Q.; Liu, B. Wheat yellow rust detection using UAV-based hyperspectral technology. Remote Sens. 2021, 13, 123. [Google Scholar] [CrossRef]
- Li, C.C.; Ma, C.Y.; Cui, Y.Q.; Lu, G.Z. UAV hyperspectral remote sensing estimation of soybean yield based on physiological and ecological parameter and meteorological factor in China. J. Indian Soc. Remote Sens. 2021, 49, 873–886. [Google Scholar] [CrossRef]
- Liu, T.; Shi, T.Z.; Zhang, H.; Wu, C. Detection of rise damage by leaf folder (Cnaphalocrocis medinalis) using unmanned aerial vehicle based hyperspectral data. Sustainability 2020, 12, 9343. [Google Scholar] [CrossRef]
- Pugh, N.A.; Horne, D.W.; Murray, S.C.; Carvalho, G.; Malambo, L.; Jung, J.H. A Temporal estimates of crop growth in sorghum and maize breeding enabled by unmanned aerial systems. Plant Phenome J. 2017, 28, 170006–170016. [Google Scholar] [CrossRef]
- Astor, T.; Dayananda, S.; Nautiyal, S. Vegetable crop biomass estimation using hyperspectral and RGB 3D UAV data. Agronomy 2020, 10, 1600. [Google Scholar] [CrossRef]
- Wang, Y.; Li, F.L.; Wang, W.D.; Chen, X.K.; Chang, Q.R. Hyperspectral remote sensing of shoot biomass of winter wheat based on SPA and transformation spectra. J. Triticeae Crops 2020, 40, 1389–1398. [Google Scholar] [CrossRef]
- Jia, M.; Li, W.; Wang, K.; Zhou, C.; Cheng, T.; Tian, Y.; Zhu, Y.; Cao, W. A newly developed method to extract the optimal hyperspectral feature for monitoring leaf biomass in wheat. Comput. Electron. Agric. 2019, 165, 104942. [Google Scholar] [CrossRef]
- Kong, Q.M.; Su, Z.B.; Shen, W.Z.; Zhang, B.F.; Wang, J.B.; Ji, N. Research of straw biomass based on NIR by wavelength selection of IPLS-SPA. Spectrosc. Spectr. Anal. 2015, 35, 1233–1238. [Google Scholar] [CrossRef]
- Tao, H.L.; Feng, H.K.; Xu, X.J.; Miao, M.K.; Long, H.L.; Yue, J.B.; Li, Z.H. Estimation of crop growth parameters using UAV-based hyperspectral remote sensing data. Sensors 2020, 20, 1296. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.Y.; Wang, J.H.; Yang, G.J.; Song, X.Y.; Xu, X.G.; Feng, H.K. Band depth analysis and partial least square regression based winter wheat biomass estimation using hyperspectral measurements. Spectrosc. Spectr. Anal. 2013, 33, 1315–1319. [Google Scholar] [CrossRef]
- Gnyp, M.L.; Bareth, G.; Li, F.; Lenz-Wiedemann, V.S.; Koppe, W.G.; Miao, Y.X.; Hennig, S.D. Development and implementation of a multiscale biomass model using hyperspectral vegetation indices for winter wheat in the North China Plain. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 232–242. [Google Scholar] [CrossRef]
- Jin, X.L.; Li, Z.H.; Feng, H.K.; Ren, Z.B.; Li, S.K. Estimation of maize yield by assimilating biomass and canopy cover derived from hyperspectral data into the Aqua Crop model. Agric. Water Manag. 2019, 227, 105846–105856. [Google Scholar] [CrossRef]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Y.; Lu, Y.H.; Liao, Y.L.; Nie, J.; Yuan, X.L. Use of a leaf chlorophyll content index to improve the prediction of above-ground biomass and productivity. PeerJ 2019, 6, 6240–6255. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, H.K.; Yue, J.B.; Li, Z.H.; Yang, G.J. Remote-sensing estimation of potato above-ground biomass based on spectral and spatial features extracted from high-definition digital camera images. Comput. Electron. Agric. 2022, 198, 107089–107099. [Google Scholar] [CrossRef]
- Li, T.S.; Zhu, Z.; Cui, J.; Chen, J.H.; Shi, X.Y.; Zhao, X. Monitoring of leaf nitrogen content of winter wheat using multi-angle hyperspectral data. Int. J. Remote Sens. 2021, 42, 4676–4696. [Google Scholar] [CrossRef]
- Arroyo-Mora, J.P.; Kalacska, M.; Loke, T.; Schlapfer, D.; Coops, N.C.; Lucanus, O. Assessing the impact of illumination on UAV pushbroom hyperspectral imagery collected under various cloud cover conditions. Remote Sens. Environ. 2021, 258, 112396–112410. [Google Scholar] [CrossRef]
- Fan, L.L.; Zhao, J.L.; Xu, X.G.; Liang, D.; Yang, G.J.; Feng, H.K.; Yang, H. Hyperspectral-based estimation of leaf nitrogen content in corn using optimal selection of multiple spectral variables. Sensors 2019, 19, 2898. [Google Scholar] [CrossRef] [PubMed]
- Marabel, M.; Alvarez-Taboada, F. Spectroscopic determination of aboveground biomass in grasslands using spectral transformations, support vector machine and partial least squares regression. Sensors 2014, 13, 10027. [Google Scholar] [CrossRef] [PubMed]
- Kokaly, R.F.; Clark, R.N. Spectroscopic determination of leaf biochemistry using band-depth analysis of absorption features and stepwise multiple linear regression. Remote Sens. Environ. 1999, 67, 267–287. [Google Scholar] [CrossRef]
- Han, X.; Wong, Y.S.; Song, M.H.; Tam, N.Y. Feasibility of using microalgal biomass cultured in domestic wastewater for the removal of chromium pollutants. Water Environ. Res. 2008, 80, 647–653. [Google Scholar] [CrossRef]
- Yang, H.B.; Li, F.; Wang, W.; Yu, K. Estimating above-ground biomass of potato using random forest and optimized hyperspectral indices. Remote Sens. 2021, 13, 2339. [Google Scholar] [CrossRef]
- Zhe, L.; Lee, Y.S.; Chen, J.H.; Qian, Y.W. Developing variable moving window PLS models: Using case of NOx emission prediction of coal-fired power plants. Fuel 2021, 296, 120441–120457. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, X.Y.; Cai, W.S.; Shao, X.G. A variable importance criterion for variable selection in near-infrared spectral analysis. Sci. China Chem. 2019, 62, 271–279. [Google Scholar] [CrossRef]
- Fan, N.Y.; Liu, G.S.; Zhang, J.J.; Zhang, C.; Yuan, R.R.; Ban, J.J. Hyperspectral model optimization for protein of tan mutton based on Box-Behnken. Spectrosc. Spectr. Anal. 2021, 41, 918–923. [Google Scholar] [CrossRef]
- Kang, X.Y.; Zhang, A.W.; Pang, H.Y. Estimation of grassland above ground biomass from UAV-mounted hyperspectral image by optimized spectral reconstruction. Spectrosc. Spectr. Anal. 2021, 41, 250–256. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Gitelson, A.; Delegido, J.; Moreno, J.; Camps-Valls, G. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar] [CrossRef]
- Chen, J.; Gu, S.; Shen, M.G.; Tang, Y.H.; Matsushita, B. Estimating above ground biomass of grassland having a high canopy cover: An exploratory analysis of in situ hyperspectral data. Int. J. Remote Sens. 2009, 30, 6497–6517. [Google Scholar] [CrossRef]
- Gong, Z.; Kawamura, K.; Ishikawa, N.; Inaba, M.; Alateng, D. Estimation of herbage biomass and nutritive status using band depth features with partial least squares regression in Inner Mongolia grassland, China. Grassl. Sci. 2016, 62, 45–54. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.; Corsi, F.; Sobhan, I. Estimation of green grass/herb biomass from airborne hyperspectral imagery using spectral indices and partial least squares regression. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 414–424. [Google Scholar] [CrossRef]
- Fu, Y.Y.; Yang, G.J.; Wang, J.; Feng, H.K.; Xu, B. Winter wheat biomass estimation based on spectral indices, band depth analysis and partial least squares regression using hyperspectral measurements. Comput. Electron. Agric. 2014, 100, 51–59. [Google Scholar] [CrossRef]
- Niu, Y.X.; Zhang, L.Y.; Zhang, H.H.; Han, W.T.; Peng, X.S. Estimating above-ground biomass of maize using features derived from UAV-based RGB imagery. Remote Sens. 2019, 11, 1261. [Google Scholar] [CrossRef]
- Acquach, G.E.; Via, B.K.; Fasina, O.; Eckhardt, L.G. Non-destructive prediction of the properties of forest biomass for chemical and bioenergy applications using near infrared spectroscopy. J. Near Infrared Spectrosc. 2015, 23, 93–102. [Google Scholar] [CrossRef]
- Sun, L.; Chen, X.; Wu, J.J.; Feng, X.W.; Bao, A.M.; Ma, Y.Q. Study on the biomass change derived from the hyperspectral data of cotton leaves in canopy under moisture stress. Chin. Sci. Bull. 2006, 51, 173–178. [Google Scholar] [CrossRef]
- Li, C.C.; Cui, Y.Q.; Ma, C.Y.; Niu, Q.L.; Li, J.B. Hyperspectral inversion of maize biomass coupled with plant height data. Crop Sci. 2021, 61, 2067–2079. [Google Scholar] [CrossRef]
- Kanke, Y.; Tubana, B.; Dalen, M.; Harrell, D. Evaluation of red and red-edge reflectance-based vegetation indices for rice biomass and grain yield prediction models in paddy fields. Precis. Agric. 2016, 17, 507–530. [Google Scholar] [CrossRef]
- Akhtar, K.; Wang, W.Y.; Khan, A.; Ren, G.X.; Afridi, M.Z.; Feng, Y.Z. Wheat straw mulching offset soil moisture deficient for improving physiological and growth performance of summer sown soybean. Agric. Water Manag. 2019, 211, 16–25. [Google Scholar] [CrossRef]
- Yang, B.H.; Chen, J.L.; Chen, L.H.; Cao, W.X.; Yao, X.; Zhu, Y. Estimation model of wheat canopy nitrogen content based on sensitive bands. Trans. Chin. Soc. Agric. Eng. 2015, 31, 176–182. [Google Scholar] [CrossRef]
- Liu, Y.; Feng, H.K.; Huang, J.; Yang, F.Q.; Wu, Z.C.; Sun, Q.; Yang, G.J. Estimation of potato above-ground biomass based on hyperspectral characteristic parameters of UAV and plant height. Spectrosc. Spectr. Anal. 2021, 41, 903–911. [Google Scholar] [CrossRef]
- Fu, Y.Y.; Yang, G.J.; Li, Z.H.; Song, X.Y.; Li, Z.H.; Xu, X.G.; Wang, P.; Zhao, C.J. Winter wheat nitrogen status estimation using UAV-based RGB imagery and Gaussian processes regression. Remote Sens. 2020, 12, 3778. [Google Scholar] [CrossRef]
- Sun, H.; Zheng, T.; Liu, N.; Li, M.Z.; Zhang, Q. Vertical distribution of chlorophyll in potato plants based on hyperspectral imaging. Trans. Chin. Soc. Agric. Eng. 2018, 34, 149–156. [Google Scholar] [CrossRef]



| Parameter Names | Variables | Definition and Description |
|---|---|---|
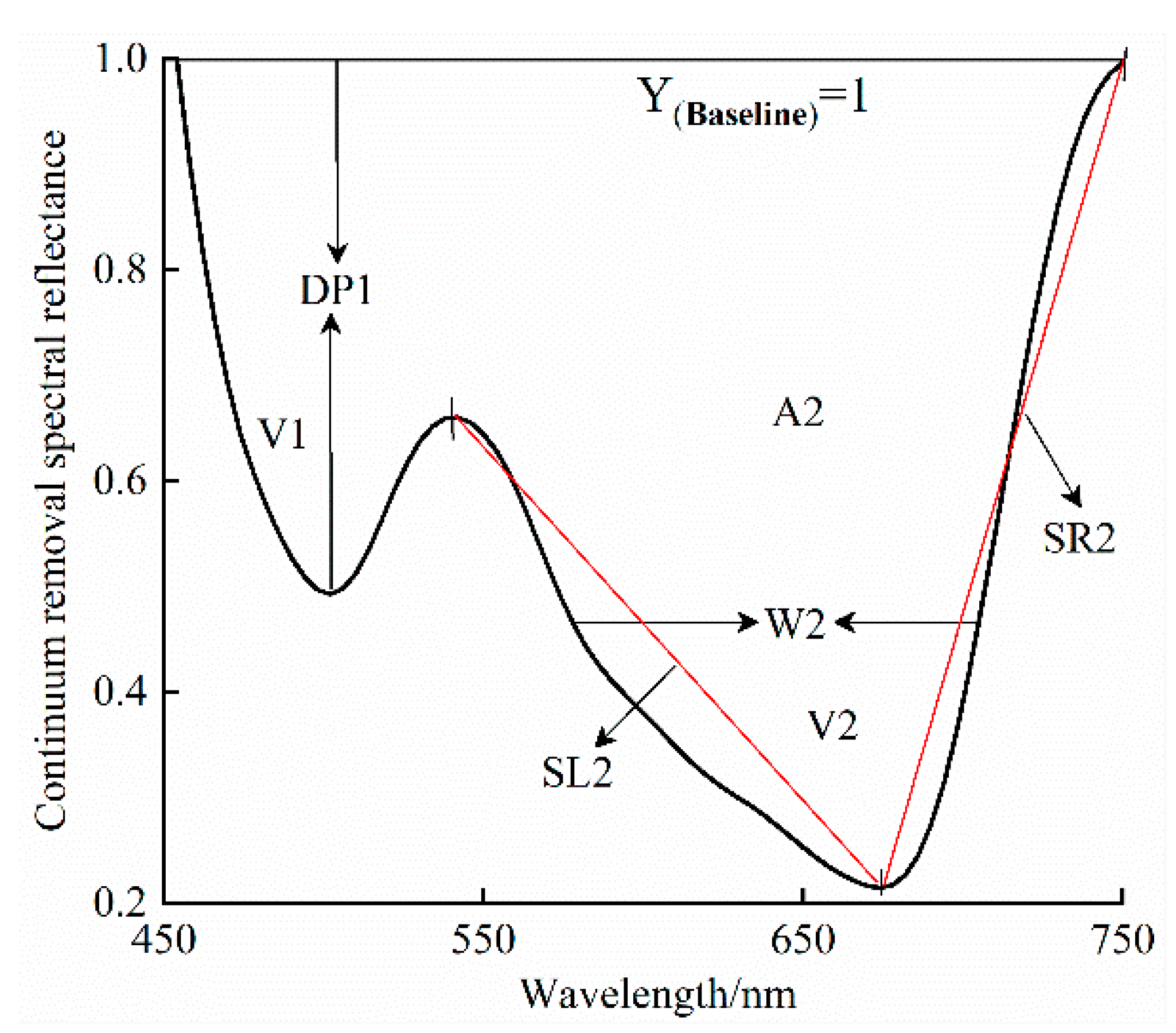
| Absorption valley depth | DP | The distance from the lowest point of the absorption valley to the baseline |
| Absorption valley area | A | Absorption valley integration of continuous removal spectra |
| Absorption valley width | W | Distance on either side of the absorption valley at half the depth |
| Slope of the left side of the absorption valley | SL | Slope of the line connecting the starting point on the left side of the absorption valley with the bottom point of the absorption valley |
| Slope of the right side of the absorption valley | SR | The slope of the line connecting the starting point on the right side of the absorption valley with the bottom point of the absorption valley |
| Green edge amplitude | Dg | Maximum value of the 1st derivative with a green edge (502–554 nm) |
| Green edge position | λg | Wavelength at Dg |
| Green edge area | SDg | Sum of the 1st derivative values within the green edge |
| Blue edge amplitude | Db | Maximum value of the 1st derivative with a blue edge (490–530 nm) |
| Blue edge position | λb | Wavelength at Db |
| Blue edge area | SDb | Sum of the 1st derivative values within the blue edge |
| Yellow edge amplitude | Dy | Maximum value of the 1st derivative with a yellow edge (562–638 nm) |
| Yellow edge position | λy | Wavelength at Dy |
| Yellow edge area | SDy | Sum of the 1st derivative values within the yellow edge |
| Red edge amplitude | Dre | Maximum value of the 1st derivative with a red edge (682–758 nm) |
| Red edge position | λre | Wavelength at Dre |
| Red edge area | SDre | Sum of the 1st derivative values within the red edge |
| Red valley amplitude | Drv | Maximum value of the 1st derivative with a red valley (650–690 nm) |
| Red valley position | λrv | Wavelength at Drv |
| Red valley area | SDrv | Sum of the 1st derivative values within the red valley |
| Green peak amplitude | Dgp | Maximum value of the 1st derivative with a green peak (510–558 nm) |
| Green peak position | λgp | Wavelength at Dgp |
| Green peak area | SDgp | Sum of the 1st derivative values within the green peak |
| Vegetation Indices | Equation | Reference |
|---|---|---|
| MCARI (modified chlorophyll absorption ratio index) | [(R700 − R670) − 0.2 × (R700R550)](R700/R670) | [33] |
| TCARI (transformed chlorophyll absorption reflectance index) | 3 × [(R700 − R670) − 0.2(R700 − R550)(R700/R670)] | [33] |
| TVI (triangular vegetation index) | 0.5 × [120(R750 − R550) − 200 × (R670 − R550)] | [24] |
| NDVI (normalized difference index) | (R800 − R680)/(R800 + R680) | [35] |
| SIPI (structure-insensitive pigment index) | (R800 − R445)/(R800 + R680) | [11] |
| GNDVI (green normalized difference vegetation index) | (R800 − R570)/(R800 + R570) | [12] |
| RDVI (re-normalized difference vegetation index) | (R800 − R670)/(R800 + R670)1/2 | [12] |
| OSAVI (optimized soil adjusted vegetation index) | 1.16 × (R800 − R670)/(R800 + R670 + 0.16) | [33] |
| MSR (modified simple ratio index) | (R800/R670 − 1)/(R800/R670 + 1)1/2 | [33] |
| NDRE (normalized difference red edge) | (R790 − R720)/(R790 + R720) | [11] |
| EVI (enhanced vegetation index) | 2.5 × (R800 − R670)/(1 + R800 + 6 × R670 − 7.5 × R500) | [12] |
| PSND (pigment specific normalized difference) | (R800 − R470)/(R800 + R470) | [33] |
| SPVI (spectral polygon vegetation index) | 0.4 × [3.7(R800 − R670) − 1.2 × |R530 − R670|] | [33] |
| PSRI (plant senescence reflectance index) | (R680 − R500)/R750 | [11] |
| SAVI (soil adjusted vegetation index) | 1.5 × (R800 − R670)/(R800 + R670 + 0.5) | [12] |
| NRI (nitrogen reflectance index) | (R570 − R670)/(R570 + R670) | [12] |
| CRI (carotenoid reflectance index) | 1/R570 + 1/R800 | [12] |
| NDI (normalized difference index) | (R850 − R710)/(R850 + R680) | [12] |
| WDRVI (modified wide dynamic range vegetation index) | (0.1 × R800 − R670)/(0.1 × R800 + R670) | [12] |
| LCI (linear combination index) | (R850 − R710)/(R850 + R670)1/2 | [33] |
| Growth Stage | Variable Selection Method | ||
|---|---|---|---|
| MWPLS | MC-UVE | RF | |
| Bud period | DP2, A1, A2, W2, SL1 | A1, SR2, Dre, SDre, λrv | DP1, SR2, SDy, Dre, SDre |
| Tuber formation period | W2, SL1, SL2, SR2, SDy, Dre, SDre, λre | DP2, A2, W2, SL2, SR2, SDy, Dre, SDre | W1, DP2, SL1, SR2, SDy, Dre, SDre |
| Tuber growth period | DP2, A1, A2, SL1, SR2, Db | W1, W2, λre, λrv | DP1, DP2, A1, W1, W2, SL1, SR2, SDy |
| Starch store period | SR2, Db, Dg | DP2, A1, A2, SDg Drv, SDrv | SL1, SL2, SR2, SDy, Drv, SDrv |
| Growth Stage | Variable Selection Method | ||
|---|---|---|---|
| MWPLS | MC-UVE | RF | |
| Bud period | NDVI, SIPI, GNDVI, NDRE, EVI, PSND | SIPI, PSND, NDI, WDRVI, LCI | SIPI, RDVI, NDRE, EVI, SAVI, NDI |
| Tuber formation period | NDVI, SIPI, GNDVI, RDVI, OSAVI, MSR, NDRE, EVI, PSND, SPVI | TVI, SIPI, EVI, SPVI, PSRI, NRI, CRI, WDRVI | NDVI, SIPI, MSR, PSRI |
| Tuber growth period | TVI, NDVI, SIPI, GNDVI, RDVI, OSAVI | MCARI, TCARI, NDVI, NDRE, PSRI | MCARI, NDVI, SIPI, GNDVI, NDRE, PSRI |
| Starch store period | TVI, NDVI, SIPI, SAVI, NRI, NDI | NDVI, SIPI, SPVI, NRI, NDI, WDRVI | TCARI, EVI, SPVI, NDI, WDRVI, LCI |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Feng, H.; Yue, J.; Li, Z.; Jin, X.; Fan, Y.; Feng, Z.; Yang, G. Estimation of Aboveground Biomass of Potatoes Based on Characteristic Variables Extracted from UAV Hyperspectral Imagery. Remote Sens. 2022, 14, 5121. https://doi.org/10.3390/rs14205121
Liu Y, Feng H, Yue J, Li Z, Jin X, Fan Y, Feng Z, Yang G. Estimation of Aboveground Biomass of Potatoes Based on Characteristic Variables Extracted from UAV Hyperspectral Imagery. Remote Sensing. 2022; 14(20):5121. https://doi.org/10.3390/rs14205121
Chicago/Turabian StyleLiu, Yang, Haikuan Feng, Jibo Yue, Zhenhai Li, Xiuliang Jin, Yiguang Fan, Zhihang Feng, and Guijun Yang. 2022. "Estimation of Aboveground Biomass of Potatoes Based on Characteristic Variables Extracted from UAV Hyperspectral Imagery" Remote Sensing 14, no. 20: 5121. https://doi.org/10.3390/rs14205121
APA StyleLiu, Y., Feng, H., Yue, J., Li, Z., Jin, X., Fan, Y., Feng, Z., & Yang, G. (2022). Estimation of Aboveground Biomass of Potatoes Based on Characteristic Variables Extracted from UAV Hyperspectral Imagery. Remote Sensing, 14(20), 5121. https://doi.org/10.3390/rs14205121










