Abstract
Deep learning is a popular topic in machine learning and artificial intelligence research and has achieved remarkable results in various fields. In geological remote sensing, mineral mapping is an appealing application of hyperspectral remote sensing for geological surveyors. Whether deep learning can improve the mineral identification ability in hyperspectral remote sensing images, especially for the discrimination of spectrally similar and intimately mixed minerals, needs to be evaluated. In this study, shortwave airborne spectrographic imager (SASI) hyperspectral images of the Baiyanghe uranium deposit in Northwestern Xinjiang, China, were used as experimental data. Three deep neural network (DNN) models were designed: a fully connected neural network (FCNN), a one-dimensional convolutional neural network (1D CNN), and a one-dimensional and two-dimensional convolutional neural network (1D and 2D CNN). A sample dataset containing five minerals was constructed for model training and validation, which was divided into training, validation and test sets at a ratio of 6:2:2. The final test accuracies of the FCNN, 1D CNN, and 1D and 2D CNN were 91.24%, 93.67% and 94.77%, respectively. The three DNNs were used for mineral identification and mapping of SASI hyperspectral images of the Baiyanghe uranium mining area. The mapping results were compared with the mapping results of the support vector machine (SVM) and the mixture-tuned matched filtering (MTMF) method. Combined with the ground spectral data obtained by the spectrometer, spectral verification and interpretation were carried out on sections that the two kinds of methods identified differently. The verification results show that the mapping results of the 1D and 2D CNN were more accurate than those of the other methods. More importantly, for minerals with similar spectral characteristics, such as short-wavelength white mica and medium-wavelength white mica, the 1D and 2D CNN model had a more accurate discrimination effect than the other DNN models, indicating that the introduction of spatial information can improve the mineral identification ability in hyperspectral remote sensing images. In general, CNNs have good application prospects in geological mapping of hyperspectral remote sensing images and are worthy of further development in future work.
1. Introduction
Hyperspectral remote sensing is a technology for continuous remote sensing imaging of ground objects with narrow and continuous spectral channels, which essentially changes the traditional remote sensing monitoring targets and enables the direct detection of undetectable substances in wide-band remote sensing. Mineral mapping is a key application direction in hyperspectral remote sensing in geological and mineral exploration, especially for hydrothermal alteration minerals that indicate prospecting, such as white mica group minerals (which have different aluminum contents), chlorite group minerals (which have different aluminum, magnesium and iron contents), and carbonate minerals [1,2,3,4]. The identification of altered minerals is critical in regional mineral surveys.
In essence, each pixel spectrum in a hyperspectral remote sensing image is a mixed spectrum, and a set of mineral abundance maps is the final product of the hyperspectral remote sensing processing chain. However, many geological surveyors do not understand the abundance map, and they believe that a distribution map of minerals (especially altered minerals) makes them more convenient to use in the field. Technically, remote sensing mineral mapping is to identify the dominant minerals in each pixel of the image and display their spatial distribution, which belongs to the category of object detection.
In geological remote sensing, there are two broad categories of analytical techniques that are used widely for mineral mapping of hyperspectral remote sensing images: spectrum matching techniques and subpixel methods [5]. The spectrum matching techniques strive to find a measure of mathematical or physical similarity between a known reference spectrum and an unknown test (target) spectrum. Representative methods include spectral angle mapper (SAM), cross-correlogram spectral matching (CCSM), spectral information divergence (SID), etc. [6]. However, the major problem associated with similarity measures is their inability to deal with mixed spectra as well as subjective thresholding [7]. Subpixel methods comprise techniques to unmix hyperspectral images with the aim of quantifying the relative abundance of various materials within a pixel. The mixture-tuned matched filtering (MTMF) is a typical subpixel method that is often used to generate mineral abundance maps [8]. Their output is a single score or percent per pixel, which bear some resemblance to similarity measures, leading to the threshold problem that still exists for mineral mapping using the subpixel method.
In real geological environments, there is a complex mixture of minerals with similar spectra. In such cases, distinctive absorption features happen very close to or overlap with each other and relevant spectra are highly correlated. This correlation hinders any attempts to identify or discriminate the minerals in routine ways. The discrimination of spectrally similar and intimately mixed minerals and prediction of their abundances in the mixture are long-standing issues in mineral mapping. The polynomial fitting method can effectively track the changes in wavelength positions related to component changes, such as Al-OH and Mg-OH [9,10]. However, this method is mainly applied to composition mapping of specific mineral types. It is obviously more appealing to map various types of minerals simultaneously, including mineral subtypes with similar spectra and different components, in a single remote sensing image.
In recent years, machine learning methods, as a subdomain of artificial intelligence, have been increasingly introduced into remote sensing geology or mineral exploration, including support vector machine (SVM), random forest (RF), and artificial neural network (ANN) [11,12,13,14]. Machine learning methods are data-driven and can automatically learn the relationship between spectral data and desired features. Moreover, these methods are robust in processing spectral data against noise and uncertainties, and can reliably analyze and efficiently classify hyperspectral remote sensing image data [15,16].
In the field of machine learning, deep learning is currently the most focused technology due to its achievements in speech recognition, visual object recognition, object detection and various other domains [17,18,19]. Deep learning is a method of feature learning through deep neural networks (DNNs). Some scholars have introduced deep learning into hyperspectral image classification, achieving high classification accuracies of more than 90% or even 95% [20,21,22,23,24,25,26]. Although the above studies have demonstrated that deep learning can improve the classification accuracy of ground objects in hyperspectral images, most of the studied objects were stable and uniform artificial ground objects in farmland, woodland or water, which are considerably different from minerals in geological environments.
To date, there are a few studies concerned with the application of deep learning in processing remote sensing data for mineral exploration [16]. In the past two years, some scholars have used deep learning technology to identify minerals from hyperspectral images or spectral data of rock samples obtained under laboratory conditions. For example, Okada et al. proposed an automatic mineral identification system based on a deep learning method, and established a convolutional neural network (CNN) model for deep learning of 400–1000 nm hyperspectral data obtained by a Specim hyperspectral camera, which greatly improved the classification accuracy of five types of minerals: galena, chalcopyrite, hematite with large particles, hematite with small particles, and hematite with very small particles [27]. Jahoda et al. used machine learning methods including CNNs, to evaluate the mineral classification accuracy of different spectral data measured in the laboratory (Raman spectra, visible-near infrared spectra and laser spectra), and the results demonstrated that machine learning techniques can successfully combine the spectra of two analytical instruments to improve mineral classification accuracy [28]. Zeng et al. designed a spatial-spectral residual CNN that can successfully detect minerals from hyperspectral images. Unfortunately, the accuracy assessments of specific minerals are not shown [29]. In summary, for mineral mapping of hyperspectral remote sensing images, the application of deep learning has not yet been fully explored, and this research aims to contribute to its advancement in geological remote sensing. Whether deep learning methods can improve hyperspectral image mineral identification, especially for the discrimination of spectrally similar and intimately mixed minerals, requires further evaluation.
The Baiyanghe uranium deposit is a typical hydrothermal uranium deposit in Northwestern Xinjiang, China, which is comprised of a rich variety of altered minerals with little vegetation cover, thus providing a suitable target for hyperspectral remote sensing mineral mapping. In this research, the Baiyanghe uranium deposit is also a suitable test area for evaluating hyperspectral remote sensing mineral mapping based on DNN methods. The reasons are as follows: First, this area is rich in white mica group minerals. The spectral characteristics of its subtypes are very similar and often mixed with each other, which allows us to test the ability of deep learning methods to distinguish these mineral subtypes. Second, we carried out airborne hyperspectral remote sensing measurements in this area, and obtained mineral mapping results based on the MTMF method, which can be used to compare the new results [30]. Most importantly, we conducted extensive field investigations and spectral measurements in this area, and the ground spectra collected can be used to validate airborne hyperspectral identification results [2,31].
In addition to the deep learning method, we also use some other methods in the field of machine learning for comparison in the experiment, such as the SVM method in supervised classification, which has achieved good results in remote sensing lithology classification [32,33]. In the design of the DNN model, we also use more than one model structure to test, evaluate, and compare their accuracy and mapping effect, providing a reference for the future application of deep learning technology in hyperspectral remote sensing mineral mapping.
2. Test Area and Data Source
2.1. Geological Setting of the Test Area
The Baiyanghe uranium deposit (46°33′–46°35′N; 84°49′–84°58′E) is located in the northwest of Xinjiang Province, China, and the western part of the Xuemisitan volcanic belt in Western Junggar. It is tectonically located in the late Paleozoic mature island arc in the Paleozoic continental margin active belt of the northwestern margin of the Kazakhstan-Junggar plate [34].
The Baiyanghe deposit is a uranium-beryllium symbiotic deposit in the western Xuemisitan area that has industrial significance and considerable exploration prospects. This area has a complex geological structure, with an extremely developed fault structure and multiple periods of tectonic and magmatic activity [35]. The outcropping deposit strata include Devonian continental volcaniclastic rocks, Carboniferous marine sedimentary detrital rocks with andesitic porphyrite, basic volcanic rocks, intermediate-acid volcanic rocks, and volcaniclastic rocks characterized as marine facies and marine-continental interactive facies. Additionally, the region includes Permian granite porphyry and tuffaceous sandstone [35]. A series of granite porphyry intrusions are distributed in the mining area, including the Yangzhuang rock body, Asuda rock body, and small Baiyanghe rock body. Uranium mineralization was discovered located near the northern rim contact zone of the eastern section of the Yangzhuang rock body (Figure 1).
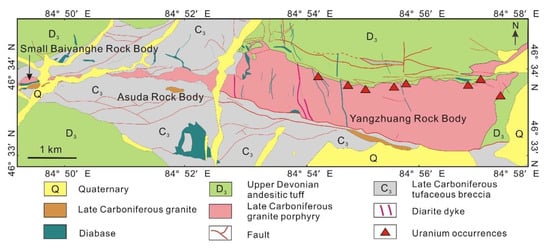
Figure 1.
Geological map of the Baiyanghe uranium deposit (modified from [2,35]).
The Baiyanghe uranium deposit is a typical hydrothermal uranium deposit in Northwestern Xinjiang, China, that includes rich altered minerals. According to previous studies, the wall rocks in the Baiyanghe uranium deposit feature various alterations, including sericitization, illitization, carbonatization, fluoritization, hematitization, silicification, and chloritization [36]. A fade zone was formed by hydrothermal alterations near the ore body, and the zone was light green to white in color. Previous studies have shown significant spatial correlations between uranium mineralization and hematitization, sericitization or illite alterations [37].
2.2. Hyperspectral Remote Sensing Data Source
Airborne hyperspectral remote sensing data were obtained using the Shortwave Airborne Spectrographic Imager (SASI), a hyperspectral shortwave infrared imager manufactured by ITRES Research Limited, Canada. This instrument is a pushbroom hyperspectral sensor that operates in the shortwave infrared (SWIR) spectral region. The SASI acquires 100 spectral bands with continuous spectral coverage in the wavelength range of 950–2450 nanometers (nm) for each of its 600 across-track imaging pixels. The spectral range covers the absorption spectra of many hydrothermal alteration minerals, including silicate minerals, sulphate, and carbonate. The technical specifications of the SASI sensor are given in Table 1.

Table 1.
Technical specifications of the acquired airborne hyperspectral data.
The airborne hyperspectral data of the Baiyanghe mining area were collected in September 2011, and the flight time was at approximately noon. At the same time, a FieldSpec ASD spectrometer was used to conduct ground quasi-synchronized spectral measurements on standard calibrated light and dark materials, which were used for subsequent atmospheric corrections and reflectance spectrum reconstruction. The ground calibration site is laid on a flat ground in the northeast of the Baiyanghe deposit, which consists of black, white and gray materials, as shown in Figure 2.
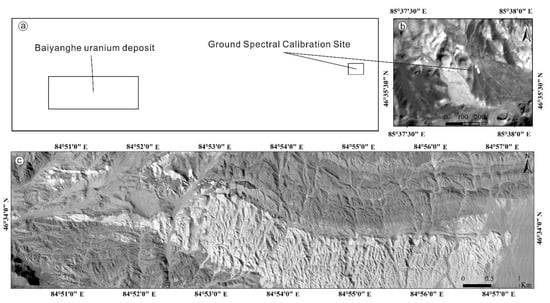
Figure 2.
(a) Diagram of the test area and ground spectral calibration site, (b) SASI image (band 5) of the ground spectral calibration site, and (c) SASI image (band 5) of the test area, consisting of two adjacent airborne images.
3. Methodology
3.1. Working Method
The working process of this research includes airborne hyperspectral data processing, sample dataset construction, deep learning and its applications, as shown in Figure 3. Airborne hyperspectral data processing includes a series of preprocessing processes, where radiometric calibration and ortho-corrections are performed by ITRES software, and atmospheric corrections and elimination of bad bands are performed by ENVI software (version 5.3) developed by Exelis Visual Information Solutions (EVIS), Boulder, CO, USA.
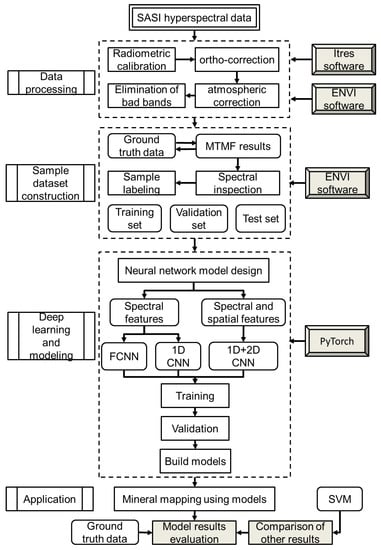
Figure 3.
Workflow of the experimental process in this paper.
Considering the different scales of ground data and airborne hyperspectral data, we use airborne scale data as samples. The sample dataset is constructed based on MTMF mapping results validated with ground truth data from previous studies, and each type of mineral was examined by spectral inspection to ensure its reliability. When all the samples were labeled, the sample dataset was divided into training, validation and test sets at a ratio of 6:2:2. Sixty percent of the samples were used to train the DNN model. Twenty percent of the samples were used as the validation set for feedback of the output result of training. Twenty percent of the samples were used as the test set and did not participate in training; these samples were applied to evaluate the generalization capability of the DNN model.
Then, three DNNs were designed according to the characteristics of the airborne hyperspectral data in the PyTorch deep learning framework. In this study, the fully connected neural network (FCNN) and CNN were used as the basic architecture. FCNNs and CNNs are the two most widely used network structures in deep learning. In general, CNNs are more suitable for processing images than FCNNs [23,38]. However, hyperspectral images are considerably different from general RGB images, as hyperspectral images combine images with spectra. Since the spectral resolution of hyperspectral images is very high, these images can be used not only to identify ground objects with large spectral features in a group of ground objects, but also to theoretically distinguish ground objects with slight spectral differences in groups of ground objects through feature mining. Therefore, an FCNN was still considered in our experiments, and the results were compared with those of a CNN. Because airborne hyperspectral data have both high spectral resolution and high spatial resolution, two structures of CNNs were designed for this study. One is the 1D CNN based on the spectral information, and the other is the 1D and 2D CNN considering the spectral and spatial information.
The model was trained on the training set and validated on the test set of the sample dataset, and then the model was established according to the accuracy results. Finally, the model was applied to identify minerals in airborne hyperspectral images of the test area, and the mapping results were verified and evaluated based on the ground truth data. In addition, to increase the contrast, SVM as a competitor, using the same training set for supervised learning, was applied to the airborne hyperspectral mineral mapping in the test area.
The DNN models applied in this study are based on the Python language and PyTorch deep learning framework. The program design, code writing, debugging and running processes were carried out in the PyCharm integrated development environment.
3.2. Hyperspectral Remote Sensing Data Preprocessing
The radiometric and geometric corrections of the SASI data were performed using preprocessing software provided by ITRES. Because the Baiyanghe mining area has certain topographic fluctuations, the SASI data were orthorectified in combination with digital elevation model data. The empirical line method was used for atmospheric corrections, and a regression equation was established based on the synchronous hyperspectral data of standard calibrated light and dark materials. After radiometric and atmospheric corrections, the DN values of the SASI hyperspectral images were converted to reflectance values. Finally, the abnormal values affected by water vapor absorption near 1400 nm and 1900 nm and beyond 2420 nm were removed. The removed bands included 9 bands at 1340–1460 nm, 12 bands at 1790–1970 nm and 3 bands beyond 2420 nm, yielding a total of 76 bands.
3.3. Construction of the Mineral Sample Dataset
The deep learning task requires a suitable sample dataset to mine feature information in the data and abstract advanced information to map to the output. When DNNs are applied to identify minerals in airborne hyperspectral images, sample datasets of various minerals for feature mining must be established. Deep learning technology operates as a black box that provides stable processing through a large number of inputs and given results. Therefore, the greater the number of training samples, the more stable and better the working performance of the black box [39]. In addition to a large number of samples, deep learning methods need to ensure the reliability of the samples.
In theory, ground truth data are the most reliable. However, deep learning has a great demand for the number of samples, and there is a direct scale difference between ground data and airborne hyperspectral data. Therefore, we use the image spectrum to construct a sample dataset. In previous studies, SASI hyperspectral mineral mapping in the Baiyanghe mining area was completed by using the MTMF method, and the mapping results were verified in a certain amount in the field [30,31]. To improve the efficiency of sample selection various mineral samples were selected based on the MTMF mapping results (Figure 4a,c). All selected samples are from one of two images in the test area, as shown in Figure 4b,d. In the process, the locations of ground truth data obtained by the FieldSpec4 ASD spectrometer were used to guide sample selection, and errors were eliminated pixel by pixel through visual spectral inspection according to the spectral curve shape and wavelength of the absorption peak. A total of 13,186 pixel samples were inspected, of which 11,074 pixels were accurately identified by the MTMF method; therefore, the mineral mapping accuracy of this method was estimated to be 84%.
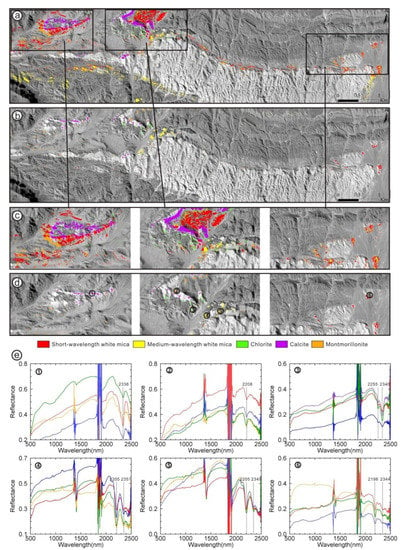
Figure 4.
Sample distribution map of the test area. (a) MTMF mapping results of SASI images in the test area, (b) The distribution of samples in the image, (c) The MTMF mapping results in three sample selection areas, (d) Distribution of samples in three corresponding areas and location of ground truth data points numbered ①–⑥, and (e) Spectral measurement results for corresponding ground points, where the spectral curves of different colors represent the measurement results of different outcrops at the point, obtained by the FieldSpec4 ASD spectrometer.
Five types of altered minerals were sampled in the Baiyanghe area, Figure 4e shows the spectral curves of minerals measured by an ASD spectrometer. The spectra at point 1 were interpreted as calcite in carbonate minerals, which exhibits one absorption feature near 2338 nm. The spectra at point 2 were interpreted as montmorillonite, which exhibits one absorption feature near 2208 nm. The spectra at point 3 were interpreted as chlorite and epidote, which are often mixed with each other. Chlorite and epidote exhibit two absorption features near 2255 nm and 2340 nm. Through visual spectral inspection, we found that the corresponding pixel spectrum is closer to the spectrum of chlorite (possibly mixed with a small amount of epidote), so the sample is named chlorite. The spectra at points 4 and 5 were interpreted as medium-wavelength white mica, which exhibits two absorption features near 2205 nm and 2350 nm. The spectra at point 6 were interpreted as short-wavelength white mica, which exhibits two absorption features near 2198 nm and 2344 nm. The feature difference between the two types of white mica is mainly reflected in the different wavelength positions of Al-OH near 2200 nm. Each class of minerals in the sample dataset was assigned a code or label that was expressed in the numbers 1–5.
The sample dataset also includes the image backgrounds in addition to the five types of mineral samples. Obviously, the number of background pixels substantially exceeds the sum of the five kinds of mineral pixels. If all nonmineral pixels are input into the DNN model as background samples, due to the large gap between the number of mineral samples and the number of background samples, it may lead to difficulties in training the neural network or poor effects while testing the model. According to the number of pixels of the five types of mineral samples and the total number of pixels, the background spectrum was sampled by extracting the pixel spectra from the image at certain intervals to construct a preliminary background spectrum library. Then, the position of the preliminarily collected background samples was inspected in the image, the background samples that overlapped with the mineral samples were eliminated, and the remaining samples were taken as the final background samples.
The number of samples selected for this experiment is shown in Table 2. The average spectral curves of six kinds of objects in the sample dataset were calculated. As shown in Figure 5, the main characteristic absorption peaks of the average spectral curves of various minerals after 2000 nm are roughly consistent with the ground truth spectra, indicating that the selected samples are representative and reliable. Because the spectral resolution of SASI airborne hyperspectral data is 15 nm, the absorption peak wavelength position of some minerals deviates from that of the ground truth spectrum; however, the deviation range is within 5 nm. In addition, the average background spectra are considerably different from the spectra of all minerals.

Table 2.
Sample dataset of the test area.
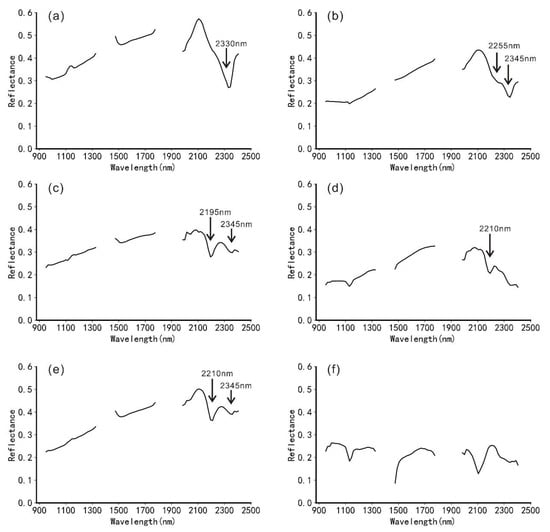
Figure 5.
Sample mean spectrum. (a) Spectral curve of calcite. (b) Spectral curve of chlorite. (c) Spectral curve of short-wavelength white mica. (d) Spectral curve of montmorillonite. (e) Spectral curve of medium-wavelength white mica. (f) Spectral curve of the background.
3.4. Deep Neural Network Model Design
3.4.1. FCNN
A DNN is a generalized concept that includes FCNNs, CNNs, and recurrent neural networks (RNNs). A narrow DNN has a fully connected neuron structure; that is, a narrow DNN is an FCNN. An FCNN is a simplified abstraction of the human brain structure and operation mechanism. Each node in an FCNN has an operational relationship with all nodes in the next layer. An FCNN includes a multilayer perceptron that identifies the most reasonable and robust hyperplane between classes [40]. FCNNs include an input layer, hidden layer and output layer, and the hidden layer can contain multiple layers.
As an important deep learning algorithm, the FCNN was used as one of the basic structures for mineral identification in airborne hyperspectral data in this study. The structure of the FCNN is shown in Figure 6. By considering factors such as the number of samples, the model complexity, the calculation time and ensuring that the parameters were not overfit, the hidden layer included four layers, and the number of neurons in each layer was set to 128, 256, 256 and 64. The number of neurons in the input layer was set to the number of bands of the spectral data, and the number of neurons in the output layer was set to the number of categories in the sample dataset. The softmax function was used in the last layer of the entire network. The ReLU function was used as the activation function for the hidden layers.
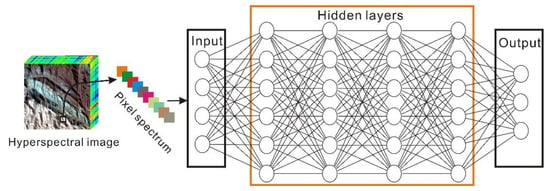
Figure 6.
The FCNN structure for hyperspectral remote sensing data classification.
The activation function is an important tool for realizing nonlinear neural networks. In the absence of an activation function, the input to each layer of nodes is a linear combination of the outputs of the previous layer, which is similar to the most primitive perceptron, severely limiting the approximation and fitting abilities of the network. Thus, nonlinear functions were introduced as activation functions to ensure that neural networks can approximate almost any function and can better address nonlinear problems. Typical activation functions include the sigmoid, tanh, and ReLU activation functions. Sigmoid and tanh are saturated activation functions that often lead to the vanishing gradient problem, making it difficult to train neural network models [41]. To solve this problem, Krizhevsky et al. proposed ReLU, a nonsaturated activation function, and achieved excellent results in the ImageNet ILSVRC competition [42]. Compared with the sigmoid and tanh functions, the ReLU function has good sparsity and small amount of calculation. It not only avoids gradient disappearance, but also speeds up network training [43,44]. Therefore, the ReLU function quickly becomes the mainstream activation function commonly used in deep learning.
3.4.2. CNN
A CNN is a traditional model and representative algorithm in the field of deep learning that is mainly used in image pattern recognition tasks. At present, CNNs play a critical role in the field of computer vision [45]. A CNN is a kind of feedforward neural network that includes convolution calculations and a deep structure. A CNN consists of a stack of alternating convolution layers and pooling layers. At the end of the network, several fully connected layers are usually used as classifiers. In the convolutional layers, image patches with spatial context information are convoluted with a set of kernels. Then, the pooling layers reduce the size of the feature maps generated by the convolutional layers to obtain more general and abstract features. Finally, the feature maps are transformed into feature vectors by several fully connected layers [23,46].
Two CNN structures were designed: the 1D CNN based on the spectral information and the 1D and 2D CNN considering the spectral and spatial information. The structure of the 1D CNN is shown in Figure 7. The spectral features are extracted through several alternating 1D convolutional layers and pooling layers, and a fully connected layer is used for classification. The structure of the 1D and 2D CNN is shown in Figure 8. The spatial features are extracted by adding a series of alternating 2D convolution layers and pooling layers and fused with the spectral features extracted by the 1D convolution layers. Finally, a fully connected layer is used for classification.
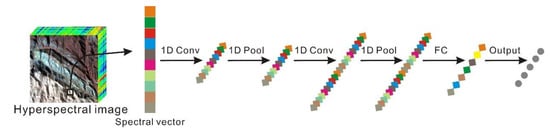
Figure 7.
The 1D CNN structure for hyperspectral remote sensing data classification.
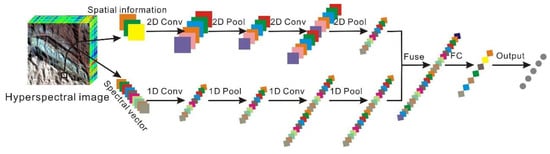
Figure 8.
The 1D and 2D CNN structure for hyperspectral remote sensing data classification.
The CNN model also uses ReLU as its activation function. The convolution kernel sizes of the convolution layers are set to 3 × 3 and 2 × 2 in turn. The pooling layer uses the commonly used maximum pooling method. The concat method in PyTorch is used to fuse the spatial and spectral features in the neural network with 1D and 2D convolutions. The softmax function is used in the last layer of the entire network.
Due to the high spatial resolution of airborne hyperspectral images, they contain rich spatial texture information. However, the data correlations between adjacent hyperspectral bands are high. Thus, in the convolution operation, if all pixels in the hyperspectral band data are taken as inputs to the model, the calculation costs are considerable. Therefore, before spatial information is extracted from the hyperspectral images, the dimensionality of the original hyperspectral images must be reduced. Principal component analysis (PCA) is used to reduce the dimensions of the SASI images. This method uses the variance as an information measure to extract features from the original data [47]. Principal component analyses and eigenvalue calculations were performed on the preprocessed SASI images. The results show that the first principal component contained 98% of the information in the whole image, the second principal component contained 1% of the information, and the third principal component contained only a few thousandths of the information in the image. Figure 9 shows the first twenty principal component images after principal component analysis of the SASI image. From these images, the texture of the first principal component image is the most complex and rich; by the 13th principal component image, it is difficult to see the original spatial contour information; by the 17th principal component image, the spatial information is almost blurred. Therefore, to retain as much spatial information as possible, the first sixteen principal components after PCA of the SASI image were input into the 2D CNN for spatial feature extraction. The input principal components contain 99.99% of the information.

Figure 9.
The first 20 principal component images after PCA of the SASI image, the total information content contained in the corresponding principal component and all upper principal components, and the horizontal and vertical axes of the image represent the number of image pixels.
3.5. Model Training and Validation
Every machine learning algorithm has an objective function, and the solution process of the algorithm involves optimizing this objective function. In classification or regression problems, the loss function is usually used as the objective function of the model. The loss function evaluates the difference between the predicted and true values of the model. Different deep learning tasks use various objective functions. For example, in regression tasks, the mean squared error loss function is commonly used, while classification tasks typically apply the cross-entropy loss function. At present, the cross-entropy loss function is the most commonly used classification loss function in convolutional neural networks [48]. Therefore, in this study, the cross-entropy loss function was applied in the neural network models.
The neural network model continuously optimized its parameters through training. The network parameters usually refer to the connection weights between neurons. Deep neural networks gradually adjust the connection weights of each neuron by repeatedly training the known information in the input sample dataset to “learn” the relationship between the input and output data. During the training process, the neural network measures the distance between the output and the expected value through the loss function after initializing the output and uses this distance value as a feedback signal to adjust the weight value and reduce the loss value of the current example. The training process implements the backpropagation algorithm. The algorithm for updating parameters is usually called an optimizer, and the most commonly used optimizer is the gradient descent algorithm. Thus, the neural network was trained by combining the backpropagation algorithm and the gradient descent method.
Before model training, the sample dataset was divided into a training set, a validation set and a test set at a ratio of 6:2:2. Considering that the activation function used in DNN models is ReLU, Kaiming initialization was used to initialize the parameters of the DNNs [49]. In terms of the parameter settings of the model training process, the batch size was set to 64, the learning rate was set to 0.001, the number of training epochs was set to 2000, and the optimizer was Adam, which adaptively adjusts the learning rate and has high computational efficiency [50]. After each training epoch, the model performance was evaluated by using the validation set.
Considering the differences in the experimental results of the three DNN models in the Baiyanghe uranium mining area, to evaluate the performance of these models, several evaluation indices were used to assess the accuracy of the models. The indices used in this paper include the overall accuracy, producer’s accuracy, average accuracy and Kappa coefficient, which are important evaluation indices for remote sensing classification models [51,52].
The overall accuracy is defined as the ratio of the number of correctly classified samples to the total number of samples. The producer’s accuracy is defined as the probability that the true reference data of each category are correctly classified, which can be calculated as the number of correctly classified samples divided by the total number of samples in each category. The average accuracy is defined as the average of the producer’s accuracies of all categories, which reduces accuracy deviations caused by unbalanced numbers of samples. The Kappa coefficient is a statistics indicator that measures the consistency between two variables. When the two variables are replaced by the classification results and true values, the Kappa coefficient can be used to evaluate model accuracy. In general, the Kappa coefficient varies between 0 and 1, and the larger the Kappa value is, the higher the classification accuracy. In the training process, with the increase in training epochs, the accuracies of the models on the training set and the validation set were observed to judge whether the model was overfitting. According to the accuracies of the models on the validation set, the hyperparameters can be adjusted to obtain better model performance. In this study, we only adjusted the learning rates of the three DNN models, respectively, and obtained good model performance. As shown in Figure 10, the training and validation accuracies of the three models were all more than 90%. Each network model converged, and the final training and validation accuracies are shown in Table 3. Among the three models, the 1D and 2D CNN had the highest training accuracy and validation accuracy of 97.039% and 93.003%, respectively.
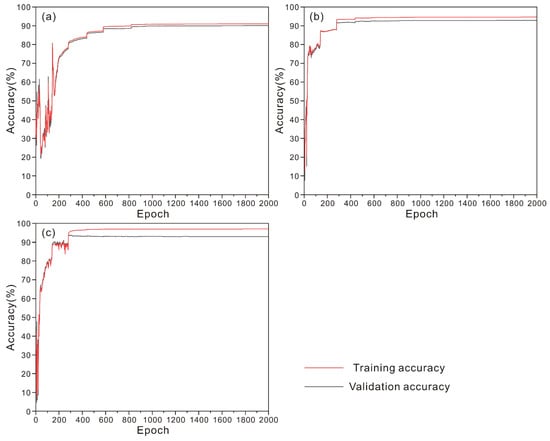
Figure 10.
Training and validation accuracies of DNN models. (a) Training and validation accuracies of the FCNN as the number of epochs increases. (b) Curves of the training and validation accuracies of the 1D CNN as the number of epochs increases. (c) Curves of the training and validation accuracies of the 1D and 2D CNN as the number of epochs increases.

Table 3.
Training accuracy and validation accuracy of the DNN models.
After the model training was completed, the test set was used to evaluate the final performance of the models. For a more comprehensive evaluation, confusion matrix was used to standardize the classification results and calculate the accuracy index. Each column in the confusion matrix represents a prediction category, and the sum of each column represents the total number of data points predicted for that category. Each row represents the true data category, and the sum of each row represents the number of data instances in that category. Based on the confusion matrix, the correct and incorrect classification ratios of each category can be calculated.
As the final purpose of the application of the DNN model, to better verify its practical effect in hyperspectral remote sensing mineral mapping, the trained DNN models were used to perform mineral identification in the SASI airborne hyperspectral images of the Baiyanghe uranium mining area, and the mineral identification results were output by the models. The results were visualized through the ArcGIS software platform to realize mineral mapping.
4. Results
4.1. Model Evaluation
Table 4 and Table 5 show various evaluation indices for the three DNN models on the test dataset and show the corresponding indices of the SVM on the test dataset after supervised learning on the training set. The overall accuracy of the three DNN models was more than 90% and is consistent with their accuracy ranking on the training set and the validation set, showing the good stability and generalization capability of these models. In terms of the various indices, the 1D and 2D CNN has the best performance. The overall accuracy of this model is 94.77%, the average accuracy is 94.23%, and the Kappa coefficient is 0.9477, which is higher than the values of the other models. In contrast, the overall accuracy, average accuracy and Kappa coefficient of the SVM are lower than those of the three DNN models, indicating that the deep learning method has better overall performance in this experiment.

Table 4.
Test accuracy of the DNN models and SVM.

Table 5.
Producer’s accuracy of the DNN models and SVM.
For specific categories, the producer’s accuracies of calcite and background in the four methods are high, all greater than 95%, so the errors mainly come from the other four categories. For each method tested, the producer’s accuracy of short-wavelength white mica is the lowest among all categories, indicating that it is the main source of error for each method. The producer’s accuracies of chlorite and short-wavelength white mica of SVM are lower than 70%, which affects its overall accuracy. The case of the FCNN model is similar to that of the SVM. With the exception of short-wavelength white mica, the producer’s accuracies of the other categories of the 1D and 2D CNN model are more than 90%, and the producer’s accuracy of short-wavelength white mica is close to 90%, indicating that the model has a relatively balanced identification ability in this region. The 1D CNN model is somewhat partial. Although the producer’s accuracies of other categories of the model are more than 90% or close to 90%, the producer’s accuracy of short-wavelength white mica is only 80%.
The confusion matrices of the three DNN models and SVM on the test dataset are shown in Figure 11. The confusion matrices of the models on the test dataset show that the model errors are mainly due to the misclassification of certain categories. The errors in the FCNN model are due to the misclassification of chlorite as the background, the mutual misclassification of short-wavelength white mica and medium-wavelength white mica, and the misclassification of short-wavelength white mica as montmorillonite. The main misclassification errors in the 1D CNN model are due to the misclassification of chlorite as the background and mutual misclassification between short-wavelength white mica and medium-wavelength white mica. The main misclassification errors in the 1D and 2D CNN model are due to the mutual misclassification between short-wavelength white mica and medium-wavelength white mica. The main misclassification errors in the SVM method are due to the misclassification of chlorite as the background and mutual misclassification between short-wavelength white mica and medium-wavelength white mica.
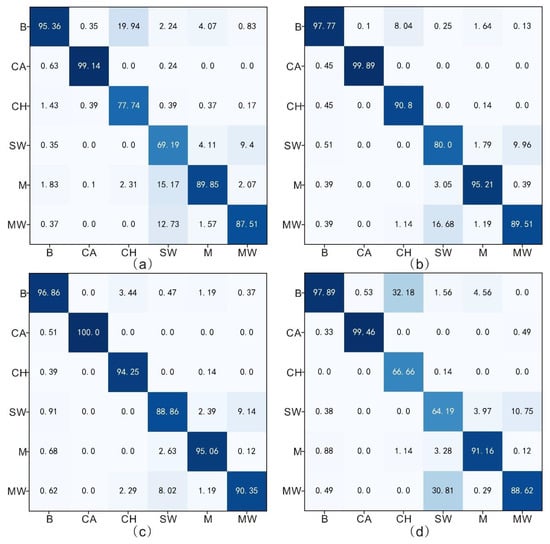
Figure 11.
(a) The confusion matrix of the FCNN model for the test set. (b) The confusion matrix of the 1D CNN model for the test set. (c) The confusion matrix of the 1D and 2D CNN model for the test set. (d) The confusion matrix of the SVM method for the test set. CA represents calcite, CH represents chlorite, SW represents short-wavelength white mica, MW represents medium-wavelength white mica, M represents montmorillonite and B represents the background.
Among the misclassifications identified in the above confusion matrix analysis, a large proportion of the misclassification errors is the mutual misclassification between short-wavelength white mica and medium-wavelength white mica. The main reason for this result is that the two minerals have high spectral similarity, and the only difference between the two is the wavelength position of the absorption peak at 2200 nm. Actually, in the geologic environment, the variation from short-wavelength white mica to medium-wavelength white mica commonly continues, which causes them to mix with each other on SASI images with a spectral resolution of 15 nm, making it difficult to distinguish them. The mutual misclassification rates of the FCNN model and 1D CNN model between short-wavelength white mica and medium-wavelength white mica are both more than 20%, and the misclassification rate of the SVM method is even higher than 40%. In contrast, the mutual misclassification rate of the 1D and 2D CNN model is within 20%, demonstrating that the model can relatively better distinguish white mica subgroups with similar spectral characteristics. In addition, it can be seen from the confusion matrix of each model that the mutual misclassification between montmorillonite and the two types of white mica also accounts for a certain proportion. This is because montmorillonite resembles white mica when only the 2200 nm feature and their spectra have a certain similarity.
4.2. Mineral Mapping
The established DNN models and preprocessed SASI airborne hyperspectral images of the Baiyanghe mining area were input into Python. After running the program, the identification results of each mineral were obtained, and the results were output as vector files. The mineral identification files of the three models were imported into the ArcGIS software platform. The vector coding of each type of mineral was consistent with the classification coding of each mineral in the sample dataset. Different colors were used for various vector codes and superimposed on the airborne hyperspectral base map to complete the mineral mapping process.
Figure 12 shows the SASI airborne hyperspectral mineral mapping results of the three DNN models, the mapping results of the SVM method, the mapping results of the MTMF method in previous studies, and the sample distribution map in the Baiyanghe uranium mining area. Initially, the distribution trends of the various minerals in the mapping results of the SVM and DNN models are generally consistent; however, the results significantly differ from the previous MTMF mapping results in some sections.
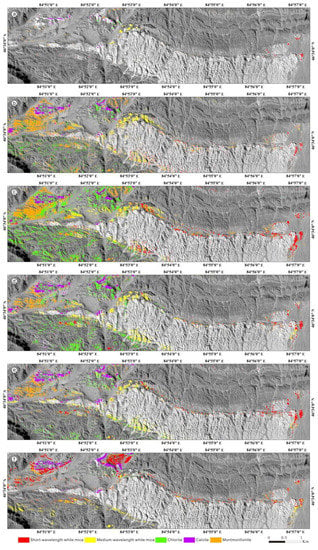
Figure 12.
(a) Sample distribution map of the test area. (b) Mineral mapping results of the SASI hyperspectral data based on the SVM method. (c) Mineral mapping results of the SASI hyperspectral data based on the FCNN model. (d) Mineral mapping results of the SASI hyperspectral data based on the 1D CNN model. (e) Mineral mapping results of the SASI hyperspectral data based on the 1D and 2D CNN model. (f) Mineral mapping results of the SASI hyperspectral data based on the MTMF method.
The differences in the mapping results are mainly concentrated in the northwestern Baiyanghe mining area and part of the northern margin of the Yangzhuang rock body. Specifically, in the fold area of the northwestern Baiyanghe mining area, a large number of montmorillonites are identified by the DNN models, while these sections are identified as short-wavelength white mica by the MTMF method. Near the northwest margin of the Yangzhuang rock body, a large amount of short-wavelength white mica is identified by the MTMF method, but not by the three DNN models and SVM. Instead, a small amount of montmorillonite is identified. Moreover, in some sections in the northern margin of the Yangzhuang rock body and the southwestern margin of the Yangzhuang rock body, the differences in the mapping results are mainly in the distributions of short-wavelength and medium-wavelength white mica.
For DNN models and SVM, the differences between the mapping results are mainly reflected in the distribution ranges of some minerals, especially chlorite and montmorillonite. In comparison, the ranges of chlorite and montmorillonite extracted by the FCNN model are the widest, followed by the 1D CNN model and the SVM method, while the ranges extracted by the 1D and 2D CNN model are smaller. The distribution ranges of calcite and white mica extracted by the above four methods are essentially consistent.
5. Discussion
According to Figure 12, the three DNN models and the SVM method display good consistency between the spatial positions and distribution of the minerals; however, there is a large gap in the number of mineral pixels. In practical work, especially for field geological prospecting, it is sometimes more meaningful to find small-scale alteration outcrops. For a more detailed comparison of the mapping results of different methods, two areas were selected in the test area, and the model accuracy was evaluated through visual interpretation of the pixel spectrum combined with ground truth spectral verification.
The first area was located in the northwest region of the test area and contained abundant mineral information, and the identification results of the DNN models and the SVM were significantly different from the previous identification results of the MTMF method, as shown in Figure 13.
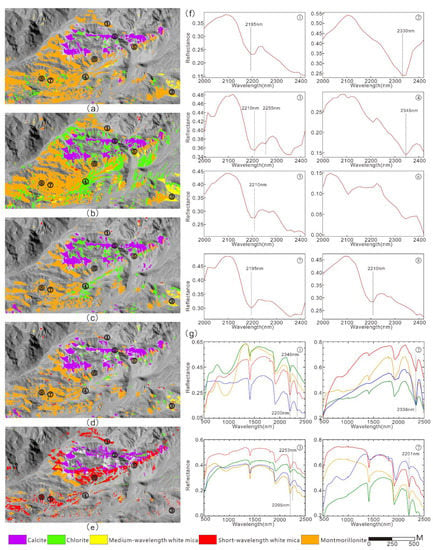
Figure 13.
(a–e) show the mapping results of the SVM, FCNN, 1D CNN, 1D + 2D CNN models and MTMF in the northwest region of the test area, respectively. (f) shows the pixel spectral curves of 8 points numbered ①–⑧ in the SASI images. (g) shows the spectral curves of rock samples collected at the corresponding points measured by ASD spectrometer in the laboratory, and curves with different colors represent the measurement results of different rock samples.
At the point 1 position, the mapping results of the MTMF and 1D and 2D CNN model identified short-wavelength white mica, while the mapping results of the SVM, FCNN and 1D CNN models identified montmorillonite. The spectral curve of the pixel at the point 1 position was verified, and the curve shape was closer to that of montmorillonite. According to the spectral curves of rock samples collected at this point measured by ASD spectrometer in the laboratory, both short-wavelength white mica and montmorillonite are present at this site (Figure 13g). At the point 2 position, the mapping results of the MTMF method identified chlorite, while the mapping results of the three DNN models and the SVM identified calcite. The spectral curve of the pixel at this point was verified, and the spectral curve was closer to that of calcite, which was confirmed by the rock sample spectra at this point (Figure 13g). At the point 3 position, MTMF did not identify any mineral, SVM identified montmorillonite, and three DNN models identified medium-wavelength white mica. The pixel spectral curve was mainly characterized by medium-wavelength white mica, but there was a weak absorption at 2255 nm, indicating the possible mixing of white mica and chlorite. According to the rock sample spectra at this point, although some spectra showed weak absorption near 2253 nm, medium-wavelength white mica was the dominant mineral from the whole spectral morphology (Figure 13g). At the point 4 position, the MTMF and the 1D and 2D CNN model identified nothing, while the SVM, FCNN, and 1D CNN models identified chlorite; however, the pixel spectral curve was interpreted as nonstandard calcite. At the point 5 position, the MTMF identified short-wavelength white mica, while the other methods all identified montmorillonite. The pixel spectrum was closer to that of montmorillonite. At the point 6 position, the mapping results of the MTMF method identified short-wavelength white mica, the mapping results of the SVM and FCNN model identified montmorillonite, and the mapping results of the two CNN models identified the background. The spectral curve of the pixel at this point was the background curve. At the point 7 and 8 positions, the mapping results of the MTMF method identified short-wavelength white mica, while the mapping results of the other methods identified montmorillonite. The pixel spectral curve at point 7 was interpreted as short-wavelength white mica, while the pixel spectral curve at point 8 was interpreted as montmorillonite. The spectral curves of rock samples rock samples collected at point 7 show the coexistence of montmorillonite and white mica (Figure 13f). According to the analysis of the above verification points, as shown in Table 6, the mapping results of the CNN models, especially the 1D and 2D convolutions, are more accurate than the results of the other models.

Table 6.
A comparison table of the verification point results shown in Figure 13.
White mica is one of the important altered minerals in the Baiyanghe uranium deposit and has a high correlation with the uranium mineralization discovered in the mining area. Thus, the distinction of various white mica types is of great significance to the study of uranium mineralization alteration [2,30]. The spectral features of short-wavelength white mica and medium-wavelength white mica are similar, and these two minerals also have similar spectral features to montmorillonite. Thus, their mapping accuracies have certain reference significance for model evaluation. To better verify the distinction between the two types of white mica, a section with rich white mica development in the northeastern margin of the Yangzhuang rock body was selected for spectral verification analysis, as shown in Figure 14.
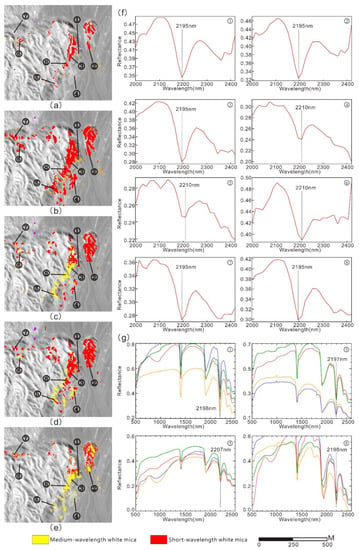
Figure 14.
(a–e) show the mapping results of the SVM, FCNN, 1D CNN, 1D + 2D CNN models and MTMF in the northeast margin of the Yangzhuang rock body, respectively. (f) shows the pixel spectral curves of 8 points numbered ①–⑧ in the SASI images. (g) shows the spectral curves of rock samples collected at the corresponding points measured by an ASD spectrometer in the laboratory, and curves with different colors represent the measurement results of different rock samples.
At points 1, 2, 3, 7 and 8, the MTMF method identifies medium-wavelength white mica, while the pixel spectral interpretation of these points identifies short-wavelength white mica, of which three points were confirmed by the spectral curves of rock samples collected at this point measured by an ASD spectrometer in the laboratory (Figure 14f). Among these five points, the SVM method and the 1D CNN model identify three points accurately, the FCNN model identifies four points accurately, and the 1D and 2D CNN model identifies all points accurately. At the point 6 position, the MTMF identifies nothing, and the pixel spectral curve resembles medium-wavelength white mica. The two CNN models identify this mineral accurately, while the SVM and the FCNN both identify it as short-wavelength white mica. At points 4 and 5, the mapping results of the MTMF method identify medium-wavelength white mica, and only the mapping results of the 1D and 2D CNN model identify medium-wavelength white mica. Based on pixel spectral analyses of these two points, the Al-OH wavelength of white mica is between short-wavelength and medium-wavelength and is closer to the wavelength of medium-wavelength white mica, which may lead to certain deviations in the DNN models. This deviation may also be affected by sample noise. To ensure that the number of deep learning samples has a certain scale, some sample noise is inevitably introduced when delineating the samples. Nevertheless, in general, as shown in Table 7, the identification effect of the CNN models for the two types of white mica is better than that of the MTMF method, the SVM method and the FCNN model, especially the 1D and 2D CNN model. According to the spectral interpretation of white mica and its surrounding pixels, the 1D and 2D CNN distinguish the boundary between short-wavelength white mica and medium-wavelength white mica more accurately than the other models.

Table 7.
A comparison table of the verification point results shown in Figure 14.
A visual interpretation of the pixel spectrum also shows that deep learning can improve the mineral mapping of the traditional MTMF method in the Baiyanghe uranium deposit. SVM is also a good machine learning algorithm, but it lost the competition with the DNN model, which is consistent with the above model accuracy evaluation results. In general, the accuracy and identification effects of the 1D and 2D CNN are better than those of the other models, especially for distinguishing minerals with similar spectra. For this reason, the deep learning method is appealing in geology remote sensing, as many methods currently have difficulty solving this problem. Moreover, the DNN structure used in this study is not complicated but only for basic evaluation. In view of the current development speed of deep learning technology, there is much room for improvement and imagination in model structure optimization in the future.
6. Conclusions
In this paper, to investigate the practical effects of deep learning methods on airborne hyperspectral remote sensing mineral mapping, three DNN structures were designed based on the mainstream deep learning framework. Experiments were carried out in the Baiyanghe uranium deposit in Northwestern Xinjiang, China, which includes a considerable amount of altered minerals, and the results were compared with the hyperspectral remote sensing mineral mapping results of the MTMF and SVM methods. The following conclusions were reached.
(1) The feasibility and effectiveness of deep learning methods for airborne hyperspectral mineral mapping were verified. Compared with the traditional MTMF method, the DNN model improves the mineral identification accuracy. In general, the 1D and 2D CNN model has better identification effects than the other methods, which provides a reference for deep learning applications in hyperspectral remote sensing mineral mapping in future works.
(2) A CNN that combines 1D spectral features with 2D spatial features outperforms the other two DNN models in terms of the identification effect of short-wavelength and medium-wavelength white micas, which indicates that the introduction of spatial information improves the ability of CNNs to distinguish minerals with similar spectral features in airborne hyperspectral remote sensing images. Feature selection is one of the difficulties in hyperspectral remote sensing image object detection. There is no special comparative study on feature selection in this study. Therefore, the performance of the model still has room for further improvement, which is the focus of follow-up work.
In general, CNN is more suitable for image recognition than FCNN. The combination of spatial-spectral information improves the feature expression ability of hyperspectral images, which may accelerate the development of remote sensing geological mapping. In theory, a CNN model that introduces spatial information may be more effective for lithological mapping. For geological prospecting, it is often more critical to distinguish specific altered minerals in different lithologies. Therefore, it is a good idea to develop an integrated lithological and mineral mapping method in the future.
Future work will also include constructing a hyperspectral remote sensing sample library that includes more rock minerals, trying more complex DNN model structures such as 3D CNN, and performing more experimental applications and evaluations.
Author Contributions
C.Z. wrote this paper and performed the hyperspectral data processing and model design. M.Y. wrote the program of deep neural network. F.Y. provided the key suggestions. Q.X. performed the field work. X.L. and Q.G. performed sample inspection. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the Nuclear Power Development Project of China (Study on uranium exploration technology based on airborne hyperspectral remote sensing and gamma spectrometry, No. [2021] 88) and the National Pre-Research Project of China (No. 32101070101).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kruse, F.A. Integrated visible and near-infrared, shortwave infrared, and longwave infrared full range hyperspectral data analysis for geologic mapping. J. Appl. Remote Sens. 2015, 9, 096005. [Google Scholar] [CrossRef]
- Xu, Q.J.; Ye, F.W.; Liu, S.F.; Zhang, Z.X.; Zhang, C. Hyperspectral Alteration Information from Drill Cores and Deep Uranium Exploration in the Baiyanghe Uranium Deposit in the Xuemisitan Area, Xinjiang, China. Remote Sens. 2017, 9, 451. [Google Scholar] [CrossRef]
- Duke, E.F.; Lewis, R.S. Near infrared spectra of white mica in the Belt Supergroup and implications for metamorphism. Am. Mineral. 2010, 95, 908–920. [Google Scholar] [CrossRef]
- Cardoso-Fernandes, J.; Silva, J.; Perrotta, M.M.; Lima, A.; Teodoro, A.C.; Ribeiro, M.A.; Dias, F.; Barrès, O.; Cauzid, J.; Roda-Robles, E. Interpretation of the Reflectance Spectra of Lithium (Li) Minerals and Pegmatites: A Case Study for Mineralogical and Lithological Identification in the Fregeneda-Almendra Area. Remote Sens. 2021, 13, 3688. [Google Scholar] [CrossRef]
- van der Meer, F.D.; van der Werff, H.M.A.; van Ruitenbeek, F.J.A.; Hecker, C.A.; Bakker, W.H.; Noomen, M.F.; van der Meijde, M.; Carranza, E.J.M.; Smeth, J.B.D.; Woldai, T. Multi- and hyperspectral geologic remote sensing: A review. Int. J. Appl. Earth Observ. Geoinf. 2012, 14, 112–128. [Google Scholar] [CrossRef]
- van der Meer, F. The effectiveness of spectral similarity measures for theanalysis of hyperspectral imagery. Int. J. Appl. Earth Observ. Geoinf. 2006, 8, 3–17. [Google Scholar] [CrossRef]
- Asadzadeh, S.; Filho, C.R.D.S. A review on spectral processing methods for geological remote sensing. Int. J. Appl. Earth Observ. Geoinf. 2016, 47, 69–90. [Google Scholar] [CrossRef]
- Boardman, J.W.; Kruse, F.A. Analysis of imaging spectrometer data using N-dimensional geometry and a mixture-tuned matched filtering approach. Geosci. Remote Sens. IEEE Trans. 2011, 49, 4138–4152. [Google Scholar] [CrossRef]
- van der Meer, F. Analysis of spectral absorption features in hyperspectral imagery. Int. J. Appl. Earth Observ. Geoinf. 2004, 5, 55–68. [Google Scholar] [CrossRef]
- Cudahy, T.; Jones, M.; Thomas, M.; Laukamp, C.; Caccetta, M.; Hewson, R.; Rodger, A.; Verrall, M. Next Generation Mineral Mapping: Queensland Airborne HyMap and Satellite ASTER Surveys 2006–2008. In CSIRO Exploration & Mining Report; P2007/364; CSIRO: Canberra, Australia, 2008. [Google Scholar]
- Kuhn, S.; Cracknell, M.J.; Reading, A.M. Lithologic mapping using random forests applied to geophysical and remote-sensing data: A demonstration study from the Eastern Goldfields of Australia. Geophysics 2018, 83, 183–193. [Google Scholar] [CrossRef]
- Bachri, I.; Hakdaoui, M.; Raji, M.; Teodoro, A.C.; Benbouziane, A. Machine learning algorithms for automatic lithological mapping using remote sensing data: A case study from Souk Arbaa Sahel, Sidi Ifni Inlier, Western Anti-Atlas, Morocco. ISPRS Int. J. Geo-Inf. 2019, 8, 248. [Google Scholar] [CrossRef]
- Chung, B.; Yu, J.; Wang, L.; Kim, N.H.; Lee, B.H.; Koh, S.; Lee, S. Detection of magnesite and associated gangue minerals using hyperspectral remote sensing—A laboratory approach. Remote Sens. 2020, 12, 1325. [Google Scholar] [CrossRef]
- Lobo, A.; Garcia, E.; Barroso, G.; Martí, D.; Fernandez-Turiel, J.L.; Ibáñez-Insa, J. Machine Learning for Mineral Identification and Ore Estimation from Hyperspectral Imagery in Tin-Tungsten Deposits: Simulation under Indoor Conditions. Remote Sens. 2021, 13, 3258. [Google Scholar] [CrossRef]
- Gewali, U.B.; Monteiro, S.T.; Saber, E. Machine learning based hyperspectral image analysis: A survey. arXiv 2018, arXiv:1802.08701. [Google Scholar]
- Shirmard, H.; Farahbakhsh, E.; Müller, R.D.; Chandra, R. A review of machine learning in processing remote sensing data for mineral exploration. Remote Sens. Environ. 2022, 268, 112750. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, F.; Hinton, G.E. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Szegedy, C.; Liu, W.; Jia, Y.Q.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Liang, H.M.; Li, Q. Hyperspectral Imagery Classification Using Sparse Representations of Convolutional Neural Network Features. Remote Sens. 2016, 8, 9. [Google Scholar] [CrossRef]
- Zhao, W.Z.; Du, S.H. Spectral-Spatial Feature Extraction for Hyperspectral Image Classification: A Dimension Reduction and Deep Learning Approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.Y.; Wei, L.; Zhang, F.; Li, H.C. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Chen, Y.S.; Jiang, H.L.; Li, C.Y.; Jia, X.P.; Pedram, G. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Lee, H.; Heesung, K. Going deeper with contextual CNN for hyperspectral image classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, H.K.; Shen, Q. Spectral-Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Wu, H.; Saurabh, P. Convolutional Recurrent Neural Networks for Hyperspectral Data Classification. Remote Sens. 2017, 9, 298. [Google Scholar] [CrossRef]
- Okada, N.; Maekawa, Y.; Owada, N.; Haga, K.; Kawamura, Y. Automated Identification of Mineral Types and Grain Size Using Hyperspectral Imaging and Deep Learning for Mineral Processing. Minerals 2020, 10, 809. [Google Scholar] [CrossRef]
- Jahoda, P.; Drozdovskiy, I.; Payler, S.J.; Turchi, L.; Bessone, L.; Sauro, F. Machine learning for recognizing minerals from multispectral data. Analyst 2021, 146, 184–195. [Google Scholar] [CrossRef]
- Zeng, H.; Han, X.Q.; Liu, Q.J. Mineral Detection from Hyperspectral Images Using a Spatial-Spectral Residual Convolution Neural Network. J. Phys. Conf. Ser. 2021, 1894, 012104. [Google Scholar] [CrossRef]
- Zhang, C.; Ye, F.W.; Xu, Q.J.; Liu, H.C.; Meng, S. Mineral mapping and analysis of alteration characteristics using airborne hyperspectral remote sensing data in the Baiyanghe uranium and beryllium ore district, Xinjiang. Remote Sens. Land Res. 2017, 29, 160–166. (In Chinese) [Google Scholar]
- Xu, Q.J.; Liu, S.F.; Ye, F.W.; Zhang, Z.X.; Zhang, C. Application of CASI/SASI and fieldspec4 hyperspectral data in exploration of the Baiyanghe uranium deposit, Hebukesaier, Xinjiang, NW China. Int. J. Remote Sens. 2018, 39, 453–469. [Google Scholar] [CrossRef]
- Yu, L.; Porwal, A.; Holden, E.J.; Dentith, M.C. Towards automatic lithological classification from remote sensing data using support vector machines. Comput. Geosci. 2012, 45, 229–239. [Google Scholar] [CrossRef]
- Othman, A.; Gloaguen, R. Improving lithological mapping by SVM classification of spectral and morphological features: The discovery of a new chromite body in the Mawat ophiolite complex (Kurdistan, NE Iraq). Remote Sens. 2014, 6, 6867–6896. [Google Scholar] [CrossRef]
- Dong, L.H.; Feng, J.; Liu, D.Q.; Tang, Y.L.; Qu, X.; Wang, K.Z.; Yang, Z.F. Research for classification of metallogenic unit of Xinjiang. Xinjiang Geol. 2010, 28, 1–15. (In Chinese) [Google Scholar]
- Wang, M.; Li, X.F.; Wang, G.; Li, Y.L.; Shi, Z.L.; Lu, K.G. Geological characteristics of Baiyanghe beryllium-uranium deposits in Xuemisitan volcanic belt. Xinjiang Miner. Explor. 2012, 3, 34–40. (In Chinese) [Google Scholar]
- Xiu, X.Q.; Fan, H.H.; Ma, H.F.; Yi, L.S. The wall rock alteration and its geochemical characteristics of Baiyanghe uranium and beryllium deposit, Xinjiang. Uranium Geol. 2011, 27, 215–220. (In Chinese) [Google Scholar]
- Lu, K.G.; Wang, G.R.; Yin, S.; Li, X.L. Discussion on the interpretation of volcanic texture from ETM+ map and uranium mineralization. Prog. Rep. China Nucl. Sci. Technol. 2009, 1, 382–395. (In Chinese) [Google Scholar]
- Wan, Y.L.; Zhong, X.W.; Liu, H.; Qian, Y.R. Survey of Application of Convolutional Neural Network in Classification of Hyperspectral Images. Comput. Eng. Appl. 2021, 57, 1–10. (In Chinese) [Google Scholar]
- Sun, C.; Shrivastava, A.; Singh, S.; Gupta, A. Revisiting Unreasonable Effectiveness of Data in Deep Learning Era. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 843–852. [Google Scholar] [CrossRef]
- Lei, X.; Fan, Y.K.; Li, K.C.; Castiglione, A.; Hu, Q. High-precision linearized interpretation for fully connected neural network. Appl. Soft Comput. 2021, 109, 107572. [Google Scholar] [CrossRef]
- Lau, M.M.; Lim, K.H. Review of adaptive activation function in deep neural network. In Proceedings of the IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES), Sarawak, Malaysia, 3–6 December 2018. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Li, Y.Z.; Yuan, Y. Convergence Analysis of Two-layer Neural Networks with ReLU Activation. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 597–607. [Google Scholar]
- Mazumdar, A.; Rawat, A.S. Learning and Recovery in the ReLU Model. In Proceedings of the 57th Allerton Conference, Monticello, IL, USA, 24–27 September 2019; pp. 108–115. [Google Scholar]
- Li, S.T.; Song, W.W.; Fang, L.Y.; Chen, Y.S.; Pedram, G.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. Remote IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Zhou, F.Y.; Jin, L.P.; Dong, J. Review of convolutional neural network. Chin. J. Comput. 2017, 40, 1229–1251. (In Chinese) [Google Scholar]
- Datta, A.; Ghosh, S.; Ghosh, A. PCA, Kernel PCA and Dimensionality Reduction in Hyperspectral Images. In Advances in Principal Component Analysis; Springer: Singapore, 2018; pp. 19–46. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Wang, X.; Zhang, M.C.; Zhu, J.L.; Zheng, R.J.; Wu, Q.T. MPCE: A Maximum Probability based Cross Entropy Loss Function for Neural Network Classification. IEEE Access 2019, 7, 146331–146341. [Google Scholar] [CrossRef]
- He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Liu, C.; Frazier, P.; Kumar, L. Comparative assessment of the measures of thematic classification accuracy. Remote Sens. Environ. 2007, 107, 606–616. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).