Comparison of the Novel Probabilistic Self-Optimizing Vectorized Earth Observation Retrieval Classifier with Common Machine Learning Algorithms
Abstract
:1. Introduction
2. The Challenges of Image Classification
2.1. Training Sample Selection
- The reference dataset should be large enough to populate the feature space with information sufficient to correctly infer labels for new test cases that have not appeared in the training dataset. This implies that the new samples should be very similar to the ones used for classifier training. Such a situation occurs only rarely for simple classification tasks based on a few features. The multi-temporal and multi-spectral remote sensing imagery composed of heterogeneous pixels with mixed classes requires an enormous training dataset to represent all of the potential relationships between the features. The training datasets are usually affected by sampling issues related to an uneven distribution of in situ observations due to limited accessibility (e.g., remote areas, swamps, high mountains), temporal and spatial constraints while collocating different data sources and the subjective selection of training polygons. Consequently, a training dataset may be sparse and under-represented. Therefore, a robust image classifier should be able to generalize available a priori information to unseen cases without overfitting the training dataset. The overfitting implies that a classifier matches the training dataset too well (including noisy cases instead of only the “true” signal). On the contrary, underfitting implies that a classifier performs poorly on the training data, presumably due to crude assumptions or incorrectly selected hyper-parameters or classification features.
- The training dataset should feature low spatial and temporal autocorrelation in order to maximize information within the feature space and to objectively assess the quality of the generated classification. If pixels are highly correlated, then their spectral signatures are mostly redundant. Consequently, a classifier has little information to learn from and to generalize to new test cases. Such a situation often occurs in the case of visual image interpretation, where an operator marks a few large polygons covering the same class. Even though a large number of pixels are selected, very limited spectral information is actually used to train a classifier. Moreover, if a subset of those pixels is used for the evaluation of classification quality, then the derived statistics are inflated and unreliable. Thus, as suggested by [36], the most robust solution to this problem is a random selection of pixels forming training and validation datasets. Furthermore, it is advantageous to temporarily decouple both datasets so that the training dataset is acquired at a different time (e.g., a different year) than the validation dataset.
- The reference dataset should reflect the same proportion of classes as the one occurring in the classified image. This is especially important for Bayesian classifiers, which rely on the a priori probability of class occurrence [37]. Similar conclusions were reported by [36] in the case of decision tree algorithms.
- The reference data should be of high quality, with as few mislabeled pixels as possible. This obvious statement is difficult to implement in reality, where the reference data may originate from: (1) other classification products featuring their own uncertainty; (2) in situ observations altered by instrumental malfunction or typographical errors; (3) crowdsourcing data featuring many subjective observations; and (4) poorly delineated training polygons. Furthermore, in the case of low-resolution imagery covering a heterogeneous landscape, pixels are usually composed of mixed classes, which ultimately have to be classified into a single class. Alternatively, some sub-pixel classification techniques [38,39,40] can be applied to infer the fractional proportion of classes within such pixels. Nevertheless, from the perspective of an image classifier, the mislabeled pixels introduce noise, which has to be dissected from the true spectral signature associated with a certain class. A limited number of studies have elaborated on the sensitivity of the image classifiers to mislabeled input data. In [34], it is found that the random forest algorithm is less sensitive to class mislabeling than support vector machines (SVMs) thanks to the bootstrap and random split operations incorporated into the random forest method. The robust multi-class AdaBoost (Rob_MulAda) classifier [41] was proposed to overcome the class overfitting problem of the standard AdaBoost algorithm, where there are mislabeled noisy training datasets. In [42], the Naive Bayes classifier was found to be less sensitive to class mislabeling as compared to the decision tree classifier [43], IBk instance-based learner [44] and the Sequential Minimal Optimization (SMO) support vector machine classifier [45]. Recently, in [46], a novel CMR-NLD method has been proposed to filter out the mislabeled samples by the thresholding of a covariance matrix calculated between sample dimensions. Ultimately, it has to be emphasized that a reliable training dataset is a prerequisite for the high accuracy of supervised image classification. Thus, it is advisable to perform data screening prior to classification instead of relying on a classifier to cope with noise in the input data.
2.2. Feature Selection
2.3. Imbalanced Distribution of Classes
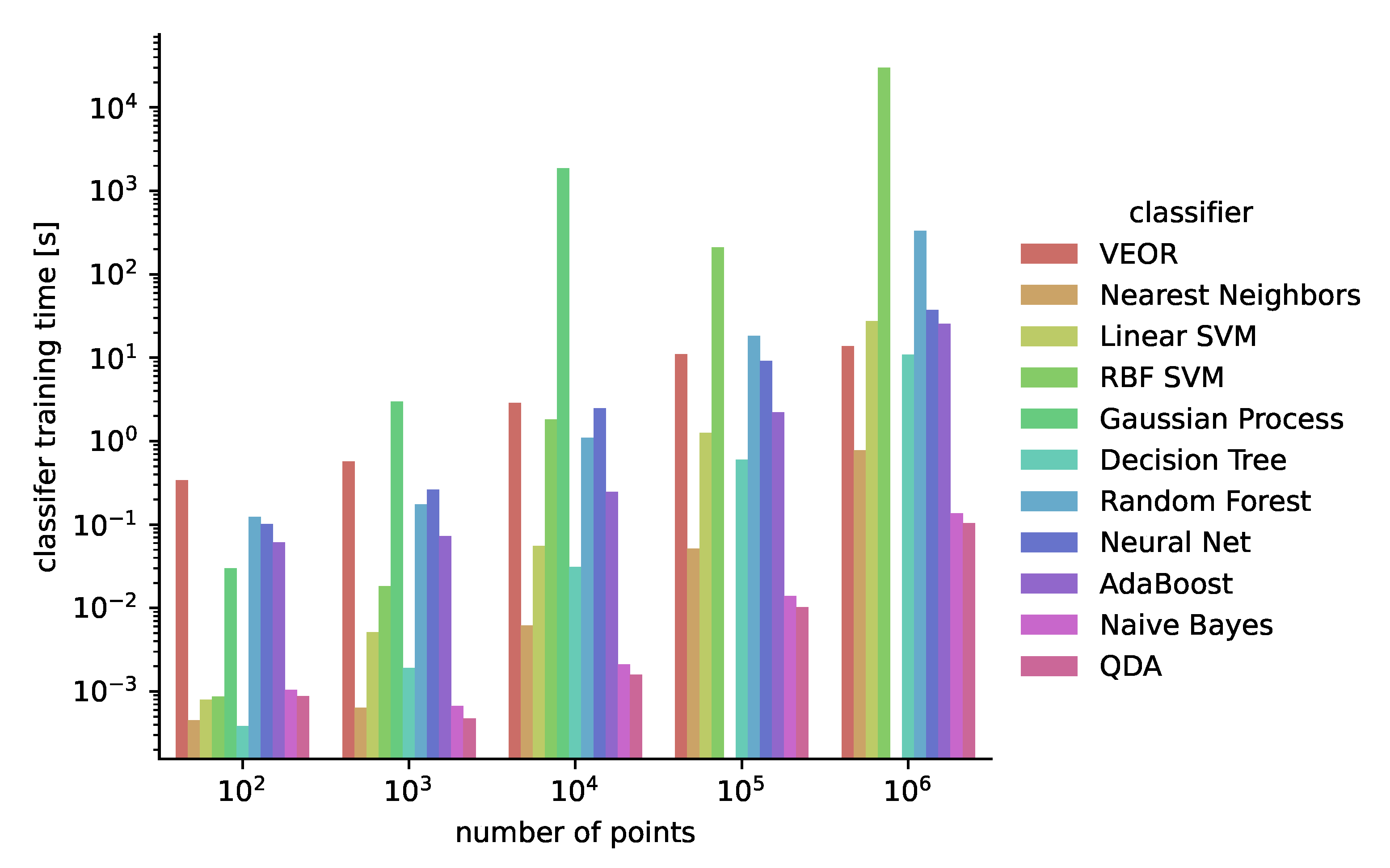
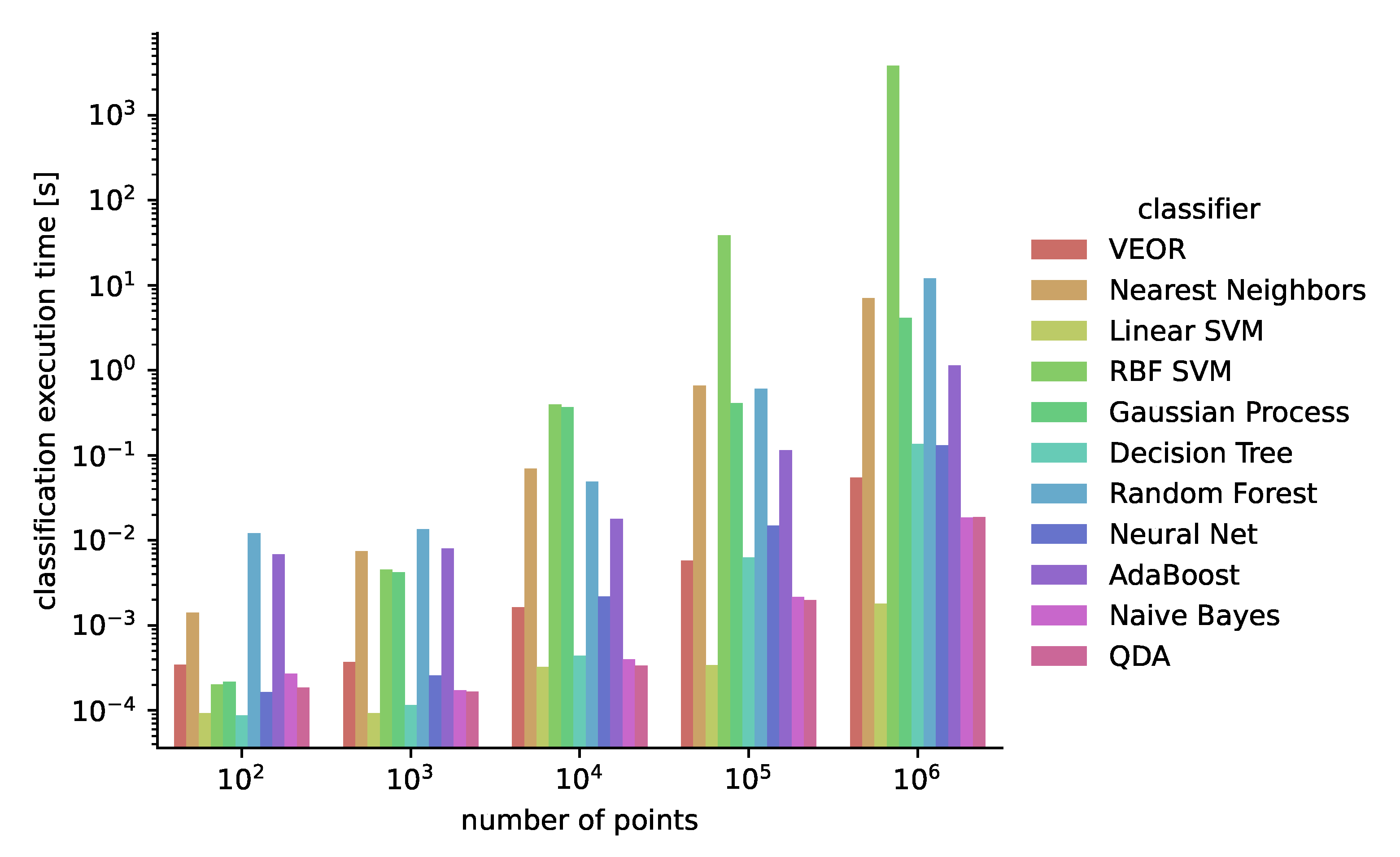
2.4. Classifier Numerical Performance
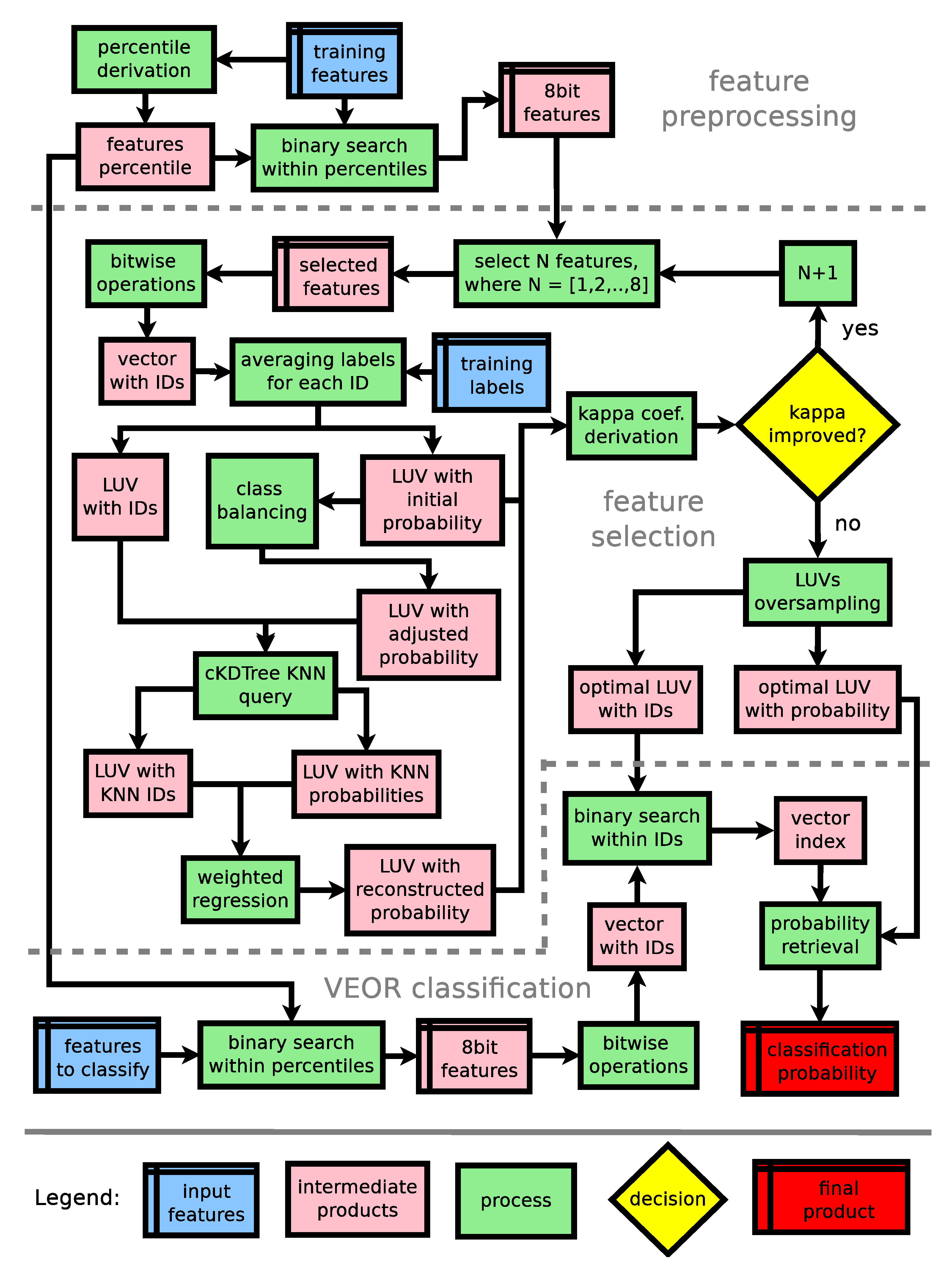
3. The Vectorized Earth Observation Retrieval Classifier
3.1. Derivation of Look-Up Vectors (LUV)
- —classification probability within cell x;
- N—number of samples within cell x;
- —binary label of a sample within cell x.
3.2. Feature Selection
- —reconstructed probability value for cell x;
- K—number of nearest neighbouring cells in the vicinity of cell x;
- —Euclidean distance between cell k and cell x expressed as a percentile number;
- —number of samples within cell k;
- —binary label of a sample within cell k.
3.3. Inclusion of Discrete Features
3.4. Classification of New Data
4. Description of Selected Classifiers Implemented in the Python Scikit-Learn Library
4.1. Nearest Neighbor Classifier
4.2. Decision Tree (DT) Classifier
4.3. Random Forest (RF) Classifier
4.4. AdaBoost Classifier
4.5. Support Vector Machine (SVM) Classifier
4.6. Artificial Neural Network (ANN) Classifier
4.7. Gaussian Process (GP) Classifier
4.8. Naive Bayes Classifier
4.9. Quadratic Discriminant Analysis (QDA) Classifier
5. Experimental Design
5.1. Generation of Synthetic Datasets
- easy—perfectly balanced with 10% noise;
- moderate—40%/60% class imbalance with 20% noise;
- difficult—30%/70% class imbalance with 30% noise.
- linear dataset—adapted from the “classifier comparison” script with a linear boundary between groups;
- moons dataset—adapted from the routine “make_moons” from the “sklearn.datasets” module with a non-linear boundary between groups;
- circles dataset—adapted from the routine “make_circles” from the “sklearn.datasets” module with one group forming a ring surrounding another.
5.2. Real Case Datasets
5.3. Optimization of Classifiers: Forward Feature Selection and Hyper-Parameter Tuning
5.4. Evaluation of Classifiers
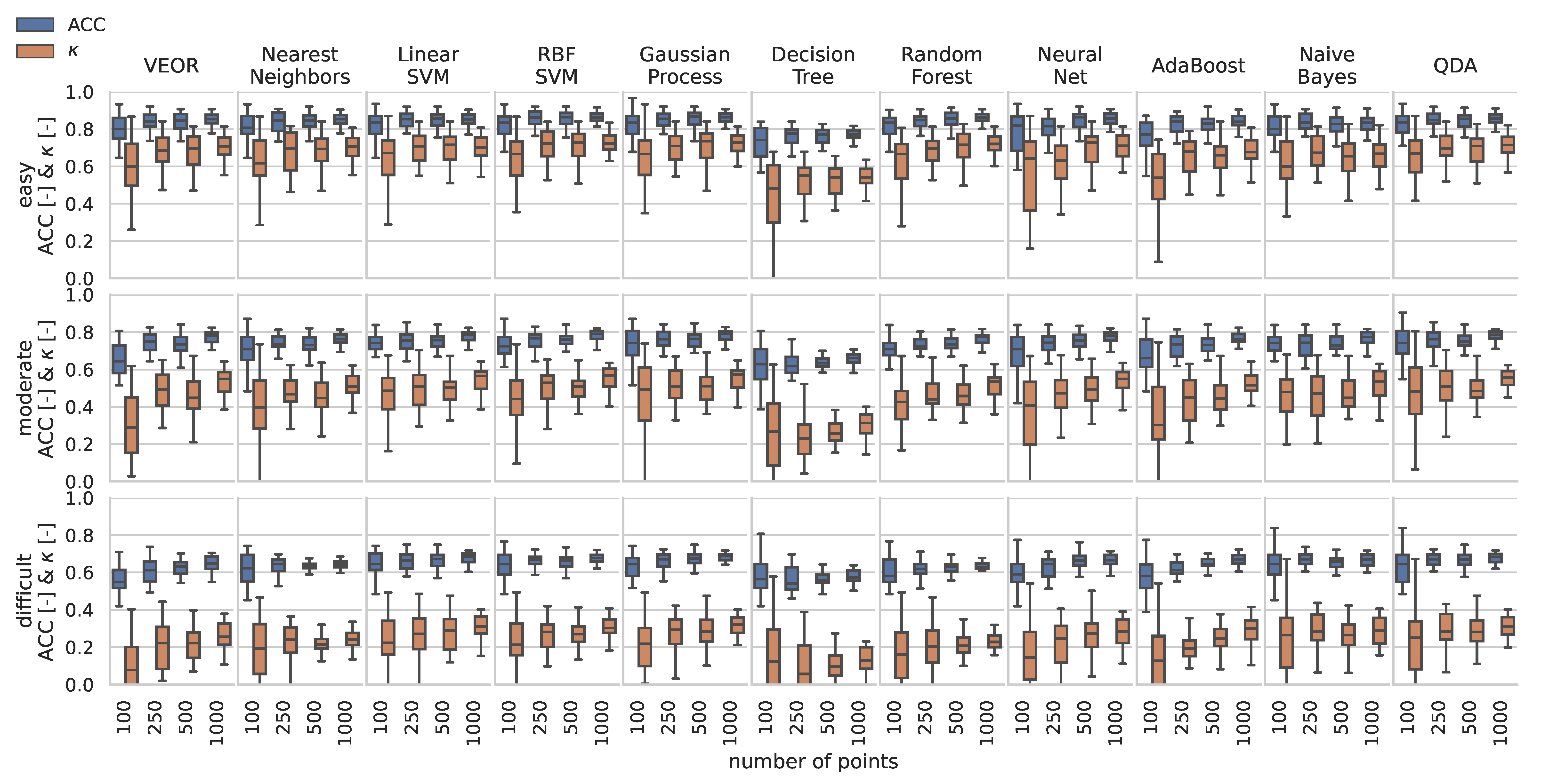
6. Results
6.1. Classification of Synthetic 2D Datasets
6.2. Classification of Synthetic 7D Datasets
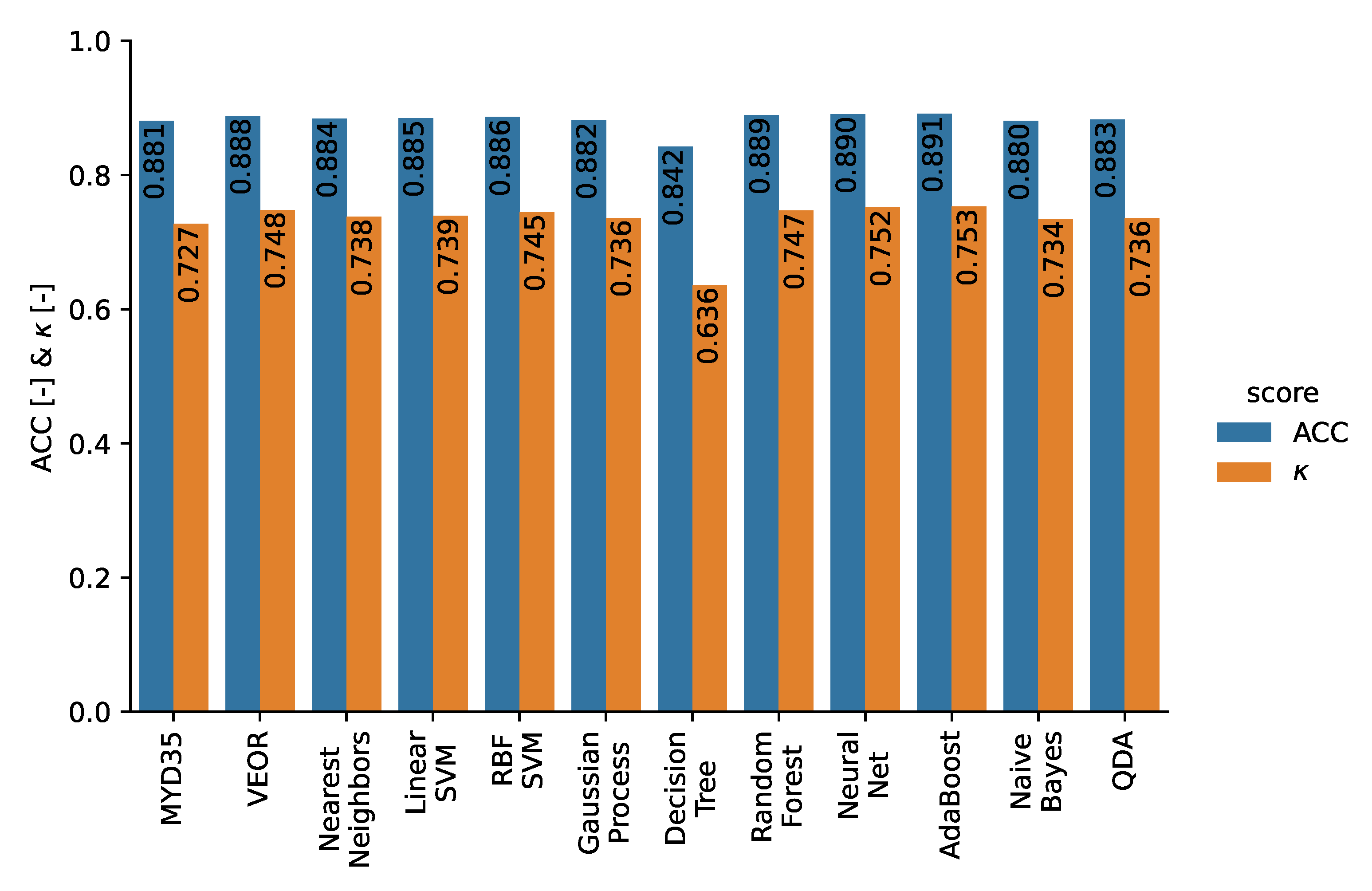
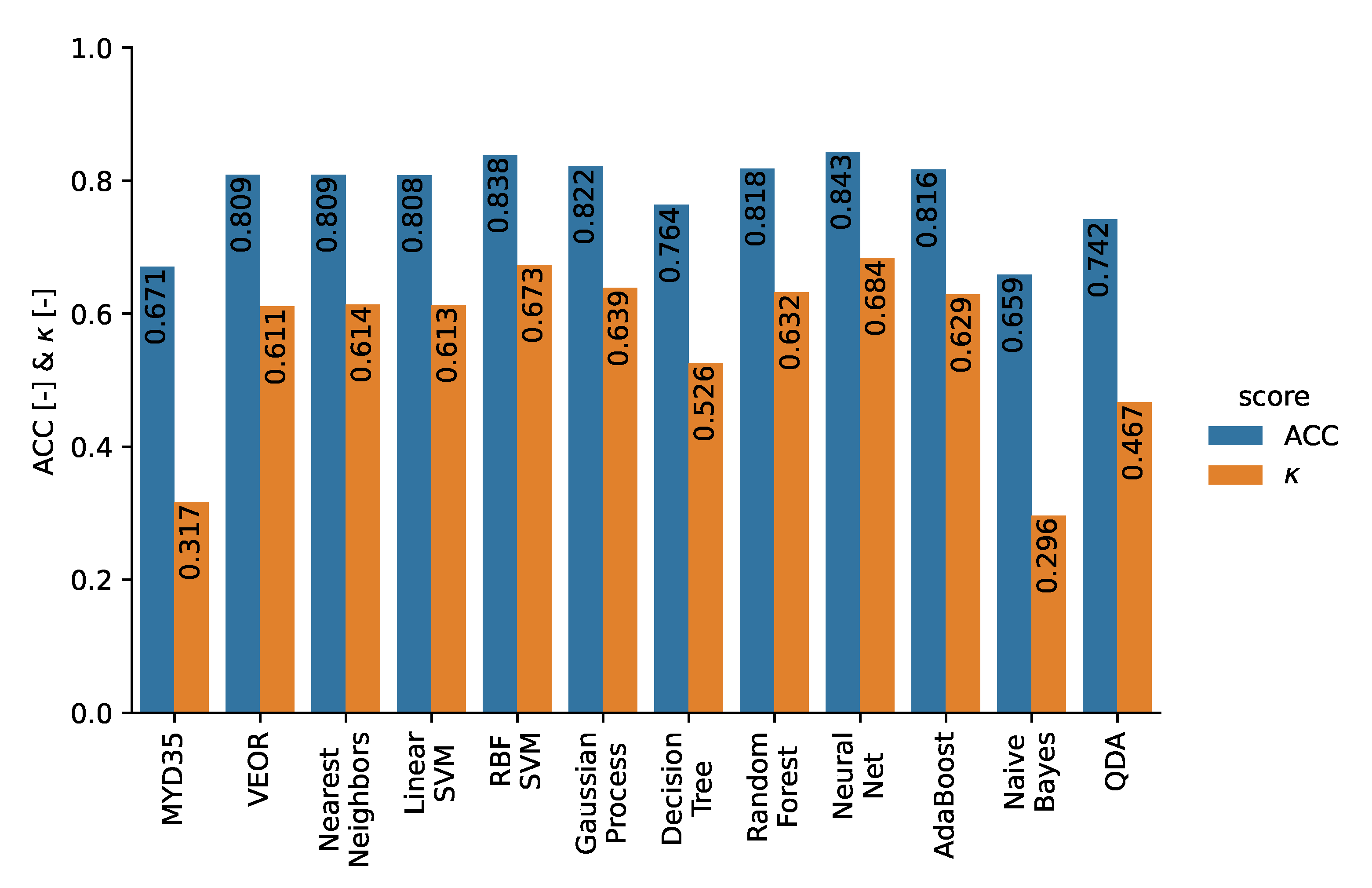
6.3. Cloud Detection Using Daytime MODIS Spectral Measurements and a Reference Cloud Mask Derived from Combined CALIOP and CPR Data
6.3.1. Cloud Detection over Water Surfaces
6.3.2. Cloud Detection over Ice/Snow Surfaces
6.4. Numerical Performance Evaluation
7. Discussion
8. Conclusions
- numerically efficient probabilistic classification of large, multidimensional datasets;
- an internal feature selection method that allows the minimal feature subset required for optimal classification results to be identified;
- the ranking of classification skills for analyzed feature combinations according to Cohen’s kappa coefficient;
- intuitive interpretation of derived optimal algorithm settings (including selected features);
- easily expandable LUV whenever new data have to be added to a training dataset.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Classifier | MODIS Water | MODIS Snow |
|---|---|---|
| VEOR | B18_936nm, B32_12020nm, sunz, B30_9730nm | B7_2130nm, B18_936nm, B26_1375nm, B3_469nm |
| Multi-layer perceptron | scat, B18_936nm, B32_12020nm, B29_8550nm_B31_11030nm_diff | B7_2130nm, B18_936nm, B27_6715nm, B32_12020nm |
| K-nearest neighbor classifier | suna, B18_936nm, B26_1375nm, B32_12020nm | B7_2130nm, B18_936nm, B28_7325nm, B29_8550nm_B28_7325nm_diff |
| Support vector classification with a linear kernel | B7_2130nm, B33_13335nm, NDVI, B29_8550nm_B31_11030nm_diff | sunz, B7_2130nm, B29_8550nm_B31_11030nm_diff, B29_8550nm_B28_7325nm_diff |
| Support vector classification with a Radial Basis Function (RBF) kernel | razi, B18_936nm, B31_11030nm_B20_3750nm_diff, B29_8550nm_B31_11030nm_diff | B7_2130nm, B18_936nm, B27_6715nm, B33_13335nm |
| Gaussian process classification | razi, B18_936nm, B29_8550nm_B31_11030nm_diff, B29_8550nm_B28_7325nm_diff | B3_469nm, B7_2130nm, B19_940nm, B27_6715nm |
| Decision tree classifier | suna, B18_936nm, B32_12020nm, B31_11030nm_B20_3750nm_diff | B7_2130nm, B19_940nm, B31_11030nm, B29_8550nm_B28_7325nm_diff |
| Random forest classifier | scat, B18_936nm, B26_1375nm, B32_12020nm_B20_3750nm_diff | B7_2130nm, B18_936nm, B20_3750nm, B28_7325nm |
| AdaBoost-SAMME classifier | scat, B18_936nm, B26_1375nm, B31_11030nm_B20_3750nm_diff | B7_2130nm, B18_936nm, B27_6715nm, B28_7325nm_B31_11030nm_diff |
| Gaussian Naive Bayes classifier | suna, scat, NDVI, B29_8550nm_B31_11030nm_diff | B5_1240nm, B28_7325nm, B32_12020nm_B20_3750nm_diff, B29_8550nm_B28_7325nm_diff |
| Quadratic Discriminant Analysis | scat, B27_6715nm, NDVI, B29_8550nm_B31_11030nm_diff | B7_2130nm, B32_12020nm_B20_3750nm_diff, B28_7325nm_B31_11030nm_diff, B29_8550nm_B28_7325nm_diff |
Appendix B
| Algorithm A1: Pseudocode for the VEOR classification |
 |
| Algorithm A2: Pseudocode for the VEOR classifier training |
 |
References
- Anderson, J.R. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; US Government Printing Office: Washington, DC, USA, 1976; Volume 964. [Google Scholar]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Inglada, J.; Vincent, A.; Arias, M.; Tardy, B.; Morin, D.; Rodes, I. Operational high resolution land cover map production at the country scale using satellite image time series. Remote Sens. 2017, 9, 95. [Google Scholar] [CrossRef] [Green Version]
- Talukdar, S.; Singha, P.; Mahato, S.; Pal, S.; Liou, Y.A.; Rahman, A. Land-use land-cover classification by machine learning classifiers for satellite observations—A review. Remote Sens. 2020, 12, 1135. [Google Scholar] [CrossRef] [Green Version]
- Defourny, P.; Bontemps, S.; Bellemans, N.; Cara, C.; Dedieu, G.; Guzzonato, E.; Hagolle, O.; Inglada, J.; Nicola, L.; Rabaute, T.; et al. Near real-time agriculture monitoring at national scale at parcel resolution: Performance assessment of the Sen2-Agri automated system in various cropping systems around the world. Remote Sens. Environ. 2019, 221, 551–568. [Google Scholar] [CrossRef]
- Kussul, N.; Lavreniuk, M.; Skakun, S.; Shelestov, A. Deep learning classification of land cover and crop types using remote sensing data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 778–782. [Google Scholar] [CrossRef]
- Li, R.; Xu, M.; Chen, Z.; Gao, B.; Cai, J.; Shen, F.; He, X.; Zhuang, Y.; Chen, D. Phenology-based classification of crop species and rotation types using fused MODIS and Landsat data: The comparison of a random-forest-based model and a decision-rule-based model. Soil Tillage Res. 2021, 206, 104838. [Google Scholar] [CrossRef]
- Sonobe, R.; Tani, H.; Wang, X.; Kobayashi, N.; Shimamura, H. Random forest classification of crop type using multi-temporal TerraSAR-X dual-polarimetric data. Remote Sens. Lett. 2014, 5, 157–164. [Google Scholar] [CrossRef] [Green Version]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: A review. Wetl. Ecol. Manag. 2010, 18, 281–296. [Google Scholar] [CrossRef]
- Bourgeau-Chavez, L.; Kasischke, E.; Brunzell, S.; Mudd, J.; Smith, K.; Frick, A. Analysis of space-borne SAR data for wetland mapping in Virginia riparian ecosystems. Int. J. Remote Sens. 2001, 22, 3665–3687. [Google Scholar] [CrossRef]
- DeLancey, E.R.; Simms, J.F.; Mahdianpari, M.; Brisco, B.; Mahoney, C.; Kariyeva, J. Comparing deep learning and shallow learning for large-scale wetland classification in Alberta, Canada. Remote Sens. 2020, 12, 2. [Google Scholar] [CrossRef] [Green Version]
- McCarthy, M.J.; Radabaugh, K.R.; Moyer, R.P.; Muller-Karger, F.E. Enabling efficient, large-scale high-spatial resolution wetland mapping using satellites. Remote Sens. Environ. 2018, 208, 189–201. [Google Scholar] [CrossRef]
- Carroll, M.L.; Townshend, J.R.; DiMiceli, C.M.; Noojipady, P.; Sohlberg, R.A. A new global raster water mask at 250 m resolution. Int. J. Digit. Earth 2009, 2, 291–308. [Google Scholar] [CrossRef]
- Donchyts, G.; Baart, F.; Winsemius, H.; Gorelick, N.; Kwadijk, J.; Van De Giesen, N. Earth’s surface water change over the past 30 years. Nat. Clim. Chang. 2016, 6, 810–813. [Google Scholar] [CrossRef]
- Feng, M.; Sexton, J.O.; Channan, S.; Townshend, J.R. A global, high-resolution (30-m) inland water body dataset for 2000: First results of a topographic–spectral classification algorithm. Int. J. Digit. Earth 2016, 9, 113–133. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Wu, M.; Wei, X.; Song, H. Water identification from high-resolution remote sensing images based on multidimensional densely connected convolutional neural networks. Remote Sens. 2020, 12, 795. [Google Scholar] [CrossRef] [Green Version]
- Martin, M.; Newman, S.; Aber, J.; Congalton, R. Determining forest species composition using high spectral resolution remote sensing data. Remote Sens. Environ. 1998, 65, 249–254. [Google Scholar] [CrossRef]
- Hościło, A.; Lewandowska, A. Mapping forest type and tree species on a regional scale using multi-temporal Sentinel-2 data. Remote Sens. 2019, 11, 929. [Google Scholar] [CrossRef] [Green Version]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support vector machine vs. random forest for remote sensing image classification: A meta-analysis and systematic review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- Tang, L.; Shao, G. Drone remote sensing for forestry research and practices. J. For. Res. 2015, 26, 791–797. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. MODIS snow and sea ice products. In Earth Science Satellite Remote Sensing; Springer: Berlin/Heidelberg, Germany, 2006; pp. 154–181. [Google Scholar]
- Cannistra, A.F.; Shean, D.E.; Cristea, N.C. High-resolution CubeSat imagery and machine learning for detailed snow-covered area. Remote Sens. Environ. 2021, 258, 112399. [Google Scholar] [CrossRef]
- Schneider, A.; Friedl, M.A.; Potere, D. A new map of global urban extent from MODIS satellite data. Environ. Res. Lett. 2009, 4, 044003. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Li, C.; Ying, Q.; Cheng, X.; Wang, X.; Li, X.; Hu, L.; Liang, L.; Yu, L.; Huang, H.; et al. China’s urban expansion from 1990 to 2010 determined with satellite remote sensing. Chin. Sci. Bull. 2012, 57, 2802–2812. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Qin, K.; Bi, Q.; Cui, W.; Li, G. Landscape Patterns and Building Functions for Urban Land-Use Classification from Remote Sensing Images at the Block Level: A Case Study of Wuchang District, Wuhan, China. Remote Sens. 2020, 12, 1831. [Google Scholar] [CrossRef]
- Heidinger, A.K.; Evan, A.T.; Foster, M.J.; Walther, A. A naive Bayesian cloud-detection scheme derived from CALIPSO and applied within PATMOS-x. J. Appl. Meteorol. Climatol. 2012, 51, 1129–1144. [Google Scholar] [CrossRef]
- Karlsson, K.G.; Johansson, E.; Devasthale, A. Advancing the uncertainty characterisation of cloud masking in passive satellite imagery: Probabilistic formulations for NOAA AVHRR data. Remote Sens. Environ. 2015, 158, 126–139. [Google Scholar] [CrossRef] [Green Version]
- Marchant, B.; Platnick, S.; Meyer, K.; Arnold, G.T.; Riedi, J. MODIS Collection 6 shortwave-derived cloud phase classification algorithm and comparisons with CALIOP. Atmos. Meas. Tech. 2016, 9, 1587–1599. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Håkansson, N.; Adok, C.; Thoss, A.; Scheirer, R.; Hörnquist, S. Neural network cloud top pressure and height for MODIS. Atmos. Meas. Tech. 2018, 11, 3177–3196. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Platnick, S.; Meyer, K.; Zhang, Z.; Zhou, Y. A machine-learning-based cloud detection and thermodynamic-phase classification algorithm using passive spectral observations. Atmos. Meas. Tech. 2020, 13, 2257–2277. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Mantero, P.; Moser, G.; Serpico, S.B. Partially supervised classification of remote sensing images through SVM-based probability density estimation. IEEE Trans. Geosci. Remote Sens. 2005, 43, 559–570. [Google Scholar] [CrossRef]
- Pelletier, C.; Valero, S.; Inglada, J.; Champion, N.; Marais Sicre, C.; Dedieu, G. Effect of training class label noise on classification performances for land cover mapping with satellite image time series. Remote Sens. 2017, 9, 173. [Google Scholar] [CrossRef] [Green Version]
- Musial, J.P.; Verstraete, M.M.; Gobron, N. Comparing the effectiveness of recent algorithms to fill and smooth incomplete and noisy time series. Atmos. Chem. Phys. 2011, 11, 7905–7923. [Google Scholar] [CrossRef] [Green Version]
- Millard, K.; Richardson, M. On the importance of training data sample selection in random forest image classification: A case study in peatland ecosystem mapping. Remote Sens. 2015, 7, 8489–8515. [Google Scholar] [CrossRef] [Green Version]
- Langley, P.; Sage, S. Induction of selective Bayesian classifiers. In Uncertainty Proceedings 1994; Elsevier: Amsterdam, The Netherlands, 1994; pp. 399–406. [Google Scholar]
- Foody, G.M. The continuum of classification fuzziness in thematic mapping. Photogramm. Eng. Remote Sens. 1999, 65, 443–452. [Google Scholar]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Li, Y.; Lu, T.; Li, S. Subpixel-pixel-superpixel-based multiview active learning for hyperspectral images classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4976–4988. [Google Scholar] [CrossRef]
- Sun, B.; Chen, S.; Wang, J.; Chen, H. A robust multi-class AdaBoost algorithm for mislabeled noisy data. Knowl.-Based Syst. 2016, 102, 87–102. [Google Scholar] [CrossRef]
- Nettleton, D.F.; Orriols-Puig, A.; Fornells, A. A study of the effect of different types of noise on the precision of supervised learning techniques. Artif. Intell. Rev. 2010, 33, 275–306. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: London, UK, 2017. [Google Scholar]
- Aha, D.W.; Kibler, D.; Albert, M.K. Instance-based learning algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef] [Green Version]
- Platt, J. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines; Technical Report; Microsoft: Redmond, WA, USA, 1997. [Google Scholar]
- Tu, B.; Kuang, W.; He, W.; Zhang, G.; Peng, Y. Robust Learning of Mislabeled Training Samples for Remote Sensing Image Scene Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5623–5639. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Cai, J.; Luo, J.; Wang, S.; Yang, S. Feature selection in machine learning: A new perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
- Amaldi, E.; Kann, V. On the approximability of minimizing nonzero variables or unsatisfied relations in linear systems. Theor. Comput. Sci. 1998, 209, 237–260. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Denker, J.; Solla, S. Optimal brain damage. Adv. Neural Inf. Process. Syst. 1989, 2, 598–605. [Google Scholar]
- Uddin, M.P.; Mamun, M.A.; Hossain, M.A. PCA-based feature reduction for hyperspectral remote sensing image classification. IETE Tech. Rev. 2021, 38, 377–396. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef] [Green Version]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef] [Green Version]
- Krishnaiah, P.R.; Kanal, L.N. Classification Pattern Recognition and Reduction of Dimensionality; Elsevier: Amsterdam, The Netherlands, 1982; Volume 2. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Hanssen, A.; Kuipers, W. On the Relationship between the Frequency of Rain and Various Meteorological Parameters (with Reference to the Problem of Objective Forecasting); Koninklijk Nederlands Meteorologisch Instituut: De Bilt, The Netherlands, 1965.
- Van Rijsbergen, C.J. A theoretical basis for the use of co-occurrence data in information retrieval. J. Doc. 1977, 33, 106–119. [Google Scholar] [CrossRef]
- Kubat, M.; Holte, R.C.; Matwin, S. Machine learning for the detection of oil spills in satellite radar images. Mach. Learn. 1998, 30, 195–215. [Google Scholar] [CrossRef] [Green Version]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Finn, J.T. Use of the average mutual information index in evaluating classification error and consistency. Int. J. Geogr. Inf. Sci. 1993, 7, 349–366. [Google Scholar] [CrossRef]
- López, V.; Fernández, A.; Moreno-Torres, J.G.; Herrera, F. Analysis of preprocessing vs. cost-sensitive learning for imbalanced classification. Open problems on intrinsic data characteristics. Expert Syst. Appl. 2012, 39, 6585–6608. [Google Scholar] [CrossRef]
- Thabtah, F.; Hammoud, S.; Kamalov, F.; Gonsalves, A. Data imbalance in classification: Experimental evaluation. Inf. Sci. 2020, 513, 429–441. [Google Scholar] [CrossRef]
- Quinlan, J.R. Improved estimates for the accuracy of small disjuncts. Mach. Learn. 1991, 6, 93–98. [Google Scholar] [CrossRef] [Green Version]
- Zadrozny, B.; Elkan, C. Learning and making decisions when costs and probabilities are both unknown. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001; pp. 204–213. [Google Scholar]
- Wu, G.; Chang, E.Y. Class-boundary alignment for imbalanced dataset learning. In Proceedings of the ICML 2003 Workshop on Learning from Imbalanced Data Sets II, Washington, DC, USA, 21 August 2003; pp. 49–56. [Google Scholar]
- Carvajal, K.; Chacón, M.; Mery, D.; Acuna, G. Neural network method for failure detection with skewed class distribution. Insight-Non Test. Cond. Monit. 2004, 46, 399–402. [Google Scholar] [CrossRef] [Green Version]
- Bermejo, P.; Gámez, J.A.; Puerta, J.M. Improving the performance of Naive Bayes multinomial in e-mail foldering by introducing distribution-based balance of datasets. Expert Syst. Appl. 2011, 38, 2072–2080. [Google Scholar] [CrossRef]
- Musial, J.P.; Hüsler, F.; Sütterlin, M.; Neuhaus, C.; Wunderle, S. Probabilistic approach to cloud and snow detection on Advanced Very High Resolution Radiometer (AVHRR) imagery. Atmos. Meas. Tech. 2014, 7, 799–822. [Google Scholar] [CrossRef] [Green Version]
- Musial, J.P.; Hüsler, F.; Sütterlin, M.; Neuhaus, C.; Wunderle, S. Daytime low stratiform cloud detection on AVHRR imagery. Remote Sens. 2014, 6, 5124–5150. [Google Scholar] [CrossRef] [Green Version]
- Musiał, J.P.; Bojanowski, J.S. AVHRR LAC satellite cloud climatology over Central Europe derived by the Vectorized Earth Observation Retrieval (VEOR) method and PyLAC software. Geoinf. Issues 2017, 9, 39–51. [Google Scholar]
- Musial, J. CM SAF Visiting Scientist Activity CM_VS18_01 Report: Assessing the VEOR Technique for Bayesian Cloud Detection for the Generation of CM SAF Cloud Climate Data Records; Technical Report; The Satellite Application Facility on Climate Monitoring: Darmstadt, Germany, 2018. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming; Pearson Education: London, UK, 1997; Volume 3. [Google Scholar]
- Maneewongvatana, S.; Mount, D.M. It’s okay to be skinny, if your friends are fat. In Proceedings of the Center for Geometric Computing 4th Annual Workshop on Computational Geometry, San Francisco, CA, USA, 28–30 May 1999; Volume 2, pp. 1–8. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef] [Green Version]
- Goldberger, J.; Hinton, G.E.; Roweis, S.T.; Salakhutdinov, R.R. Neighbourhood components analysis. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; pp. 513–520. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Bernardo, J.; Berger, J.; Dawid, A.; Smith, A. Regression and classification using Gaussian process priors. Bayesian Stat. 1998, 6, 475. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Rosset, S.; Zhu, J.; Zou, H. Multi-class adaboost. Stat. Its Interface 2009, 2, 349–360. [Google Scholar] [CrossRef] [Green Version]
- Chan, T.F.; Golub, G.H.; LeVeque, R.J. Updating formulae and a pairwise algorithm for computing sample variances. In COMPSTAT 1982 5th Symposium Held at Toulouse 1982; Springer: Berlin/Heidelberg, Germany, 1982; pp. 30–41. [Google Scholar]
- Tharwat, A. Linear vs. quadratic discriminant analysis classifier: A tutorial. Int. J. Appl. Pattern Recognit. 2016, 3, 145–180. [Google Scholar] [CrossRef]
- Pal, M.; Mather, P.M. An assessment of the effectiveness of decision tree methods for land cover classification. Remote Sens. Environ. 2003, 86, 554–565. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Zhang, H. The optimality of naive Bayes. AA 2004, 1, 3. [Google Scholar]
- Guyon, I. Design of experiments of the NIPS 2003 variable selection benchmark. In Proceedings of the NIPS 2003 Workshop on Feature Extraction and Feature Selection, Whistler, BC, Canada, 11–13 December 2003; Volume 253. [Google Scholar]
- Mace, G.G.; Zhang, Q. The CloudSat radar-lidar geometrical profile product (RL-GeoProf): Updates, improvements, and selected results. J. Geophys. Res. Atmos. 2014, 119, 9441–9462. [Google Scholar] [CrossRef]
- Partain, P. CloudSat MODIS-AUX Auxiliary Data Process Description and Interface Control Document; Cooperative Institute for Research in the Atmosphere, Colorado State University: Fort Collins, CO, USA, 2007; p. 23. [Google Scholar]
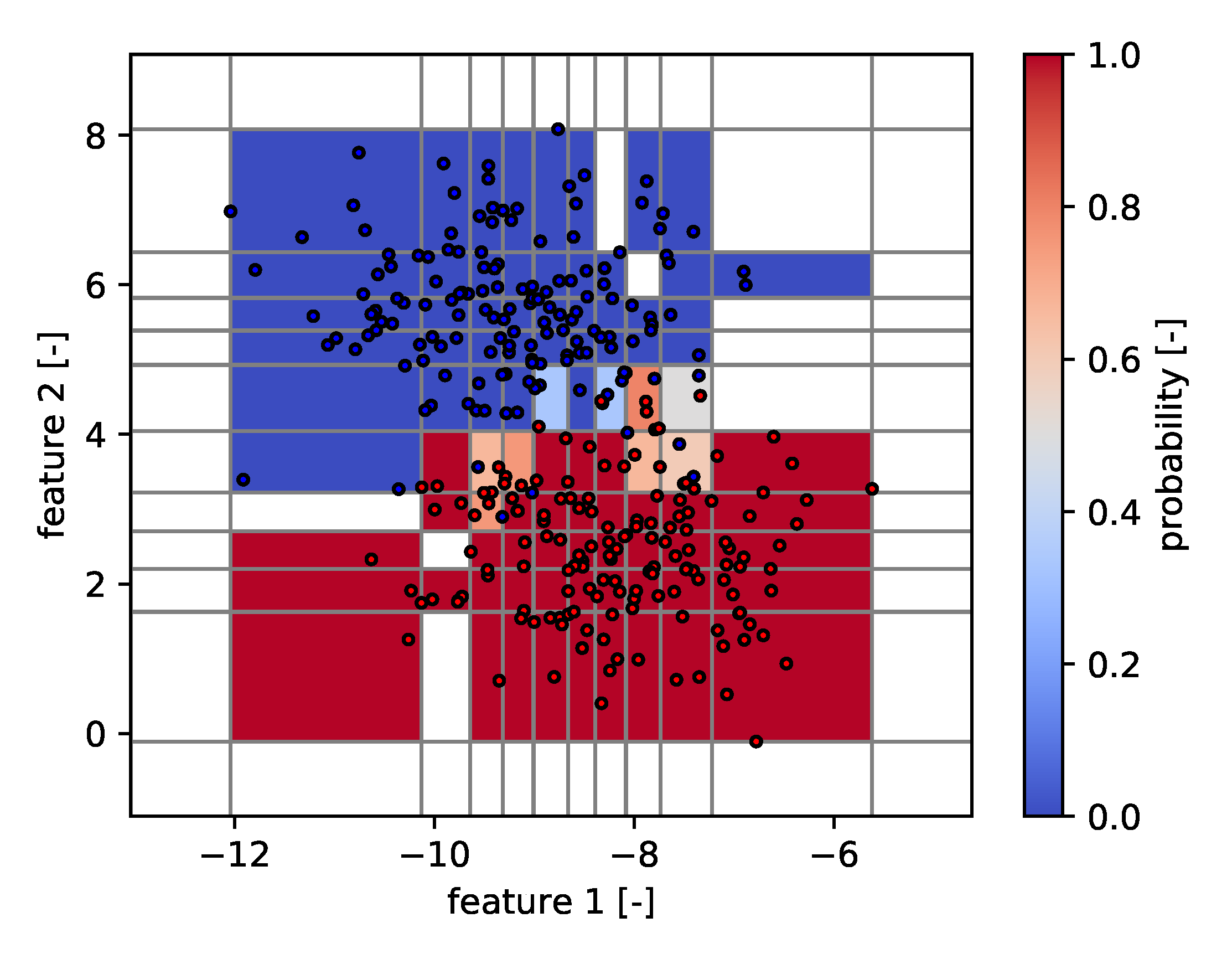
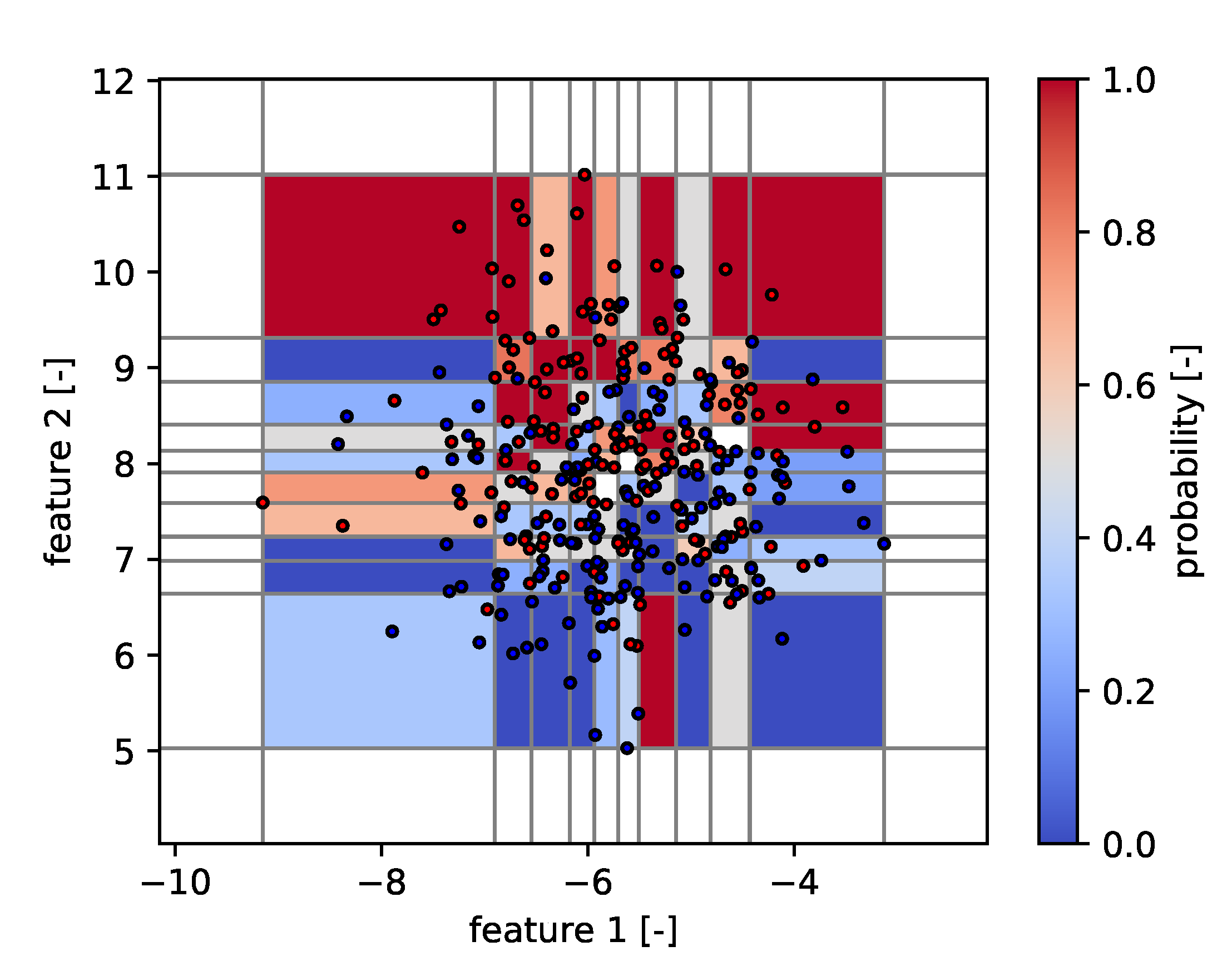


| Algorithm | Module/Routine |
|---|---|
| Multi-layer perceptron classifier that optimizes the log-loss function using the limited memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) gradient descent algorithm [76,77] | sklearn.neural_network/MLPClassifier |
| K-nearest neighbor classifier [78] | sklearn.neighbors/KneighborsClassifier |
| Support vector classification with a linear kernel [79] | sklearn.svm/LinearSVC |
| Support vector classification with a Radial Basis Function (RBF) kernel [79] | sklearn.svm/SVC |
| Gaussian process classification (GPC) based on the Laplace approximation [80] | sklearn.gaussian_process/ GaussianProcessClassifier |
| Decision tree classifier [43] | sklearn.tree/DecisionTreeClassifier |
| Random forest classifier [81] | sklearn.ensemble/RandomForestClassifier |
| AdaBoost-SAMME classifier [82,83] | sklearn.ensemble/AdaBoostClassifier |
| Gaussian Naive Bayes classifier [84] | sklearn.naive_bayes/GaussianNB |
| Quadratic Discriminant Analysis [85] | sklearn.discriminant_analysis/ QuadraticDiscriminantAnalysis |
| number of features | 2, 7 |
| number of samples | 100, 250, 500, 1000 |
| fraction of mislabeled samples (in %) | 10, 20, 30 |
| class imbalance (in %) | 30/70, 40/60, 50/50 |
| Abbreviation | Full Name |
|---|---|
| B1_645nm | Band 1 reflectance at 645 nm |
| B2_858nm | Band 2 reflectance at 858 nm |
| B3_469nm | Band 3 reflectance at 469 nm |
| B4_555nm | Band 4 reflectance at 555 nm |
| B5_1240nm | Band 5 reflectance at 1.240 m |
| B7_2130nm | Band 7 reflectance at 2.130 m |
| B17_905nm | Band 17 reflectance at 905 nm |
| B18_936nm | Band 18 reflectance at 936 nm |
| B19_940nm | Band 19 reflectance at 940 nm |
| B26_1375nm | Band 26 reflectance at 1.375 m |
| B20_3750nm | Band 20 brightness temperature at 3.750 m |
| B27_6715nm | Band 27 brightness temperature at 6.715 m |
| B28_7325nm | Band 28 brightness temperature at 7.325 m |
| B29_8550nm | Band 29 brightness temperature at 8.550 m |
| B30_9730nm | Band 30 brightness temperature at 9.730 m |
| B31_11030nm | Band 31 brightness temperature at 11.030 m |
| B32_12020nm | Band 32 brightness temperature at 12.020 m |
| B33_13335nm | Band 33 brightness temperature at 13.335 m |
| B34_13635nm | Band 34 brightness temperature at 13.635 m |
| B35_13935nm | Band 35 brightness temperature at 13.935 m |
| B36_14235nm | Band 36 brightness temperature at 14.235 m |
| B1_645nm_B2_858nm_ratio | Reflectance ratio between Bands 1 and 2 |
| B31_11030nm_B20_3750nm_diff | Brightness temperature difference between Bands 31 and 20 |
| B32_12020nm_B20_3750nm_diff | Brightness temperature difference between Bands 32 and 20 |
| B31_11030nm_B32_12020nm_diff | Brightness temperature difference between Bands 31 and 32 |
| B28_7325nm_B31_11030nm_diff | Brightness temperature difference between Bands 28 and 31 |
| B29_8550nm_B31_11030nm_diff | Brightness temperature difference between Bands 29 and 31 |
| B29_8550nm_B28_7325nm_diff | Brightness temperature difference between Bands 29 and 28 |
| sunz | Sun zenith angle |
| satz | Satellite zenith angle |
| suna | Sun azimuth angle |
| sata | Satellite azimuth angle |
| razi | Relative azimuth angle |
| scat | Scattering angle |
| NDVI | Normalized Difference Vegetation Index |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Musial, J.P.; Bojanowski, J.S. Comparison of the Novel Probabilistic Self-Optimizing Vectorized Earth Observation Retrieval Classifier with Common Machine Learning Algorithms. Remote Sens. 2022, 14, 378. https://doi.org/10.3390/rs14020378
Musial JP, Bojanowski JS. Comparison of the Novel Probabilistic Self-Optimizing Vectorized Earth Observation Retrieval Classifier with Common Machine Learning Algorithms. Remote Sensing. 2022; 14(2):378. https://doi.org/10.3390/rs14020378
Chicago/Turabian StyleMusial, Jan Pawel, and Jedrzej Stanislaw Bojanowski. 2022. "Comparison of the Novel Probabilistic Self-Optimizing Vectorized Earth Observation Retrieval Classifier with Common Machine Learning Algorithms" Remote Sensing 14, no. 2: 378. https://doi.org/10.3390/rs14020378
APA StyleMusial, J. P., & Bojanowski, J. S. (2022). Comparison of the Novel Probabilistic Self-Optimizing Vectorized Earth Observation Retrieval Classifier with Common Machine Learning Algorithms. Remote Sensing, 14(2), 378. https://doi.org/10.3390/rs14020378






