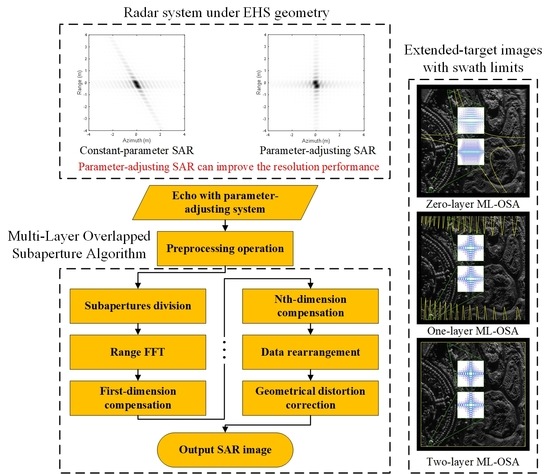
Multi-Layer Overlapped Subaperture Algorithm for Extremely-High-Squint High-Resolution Wide-Swath SAR Imaging with Continuously Time-Varying Radar Parameters
Abstract
:1. Introduction
- A more accurate signal model with time-varying parameters is employed. Comparing to the existing ones, the new signal model includes the complete expansion of two-dimensional Taylor series and hence is able to describe the residual PWA phase errors with a much improved accuracy.
- A more precise phase error compensation method is proposed via multi-level coarse-to-fine focusing. Coarsely focused images are used as references for compensator generation to remove spatially variant PWA phase errors. The new processing describes the coarse image distortion caused by the linear components of the PWA phase error with a much improved accuracy and hence contributes to much less residual phase error.
- The accuracy of the proposed ML-OSA is analytically presented in the form of swath limit in a certain resolution level. The algorithm accuracy analysis is more accurate than the existing ones by considering the effects of both the precision of signal model and multi-level phase compensation.
2. Overview of Parameter-Adjusting SAR
2.1. Geometry and Signal Model
2.2. Limit of Constant-Parameter SAR with EHS Geometry
2.3. Parameter-Adjusting SAR
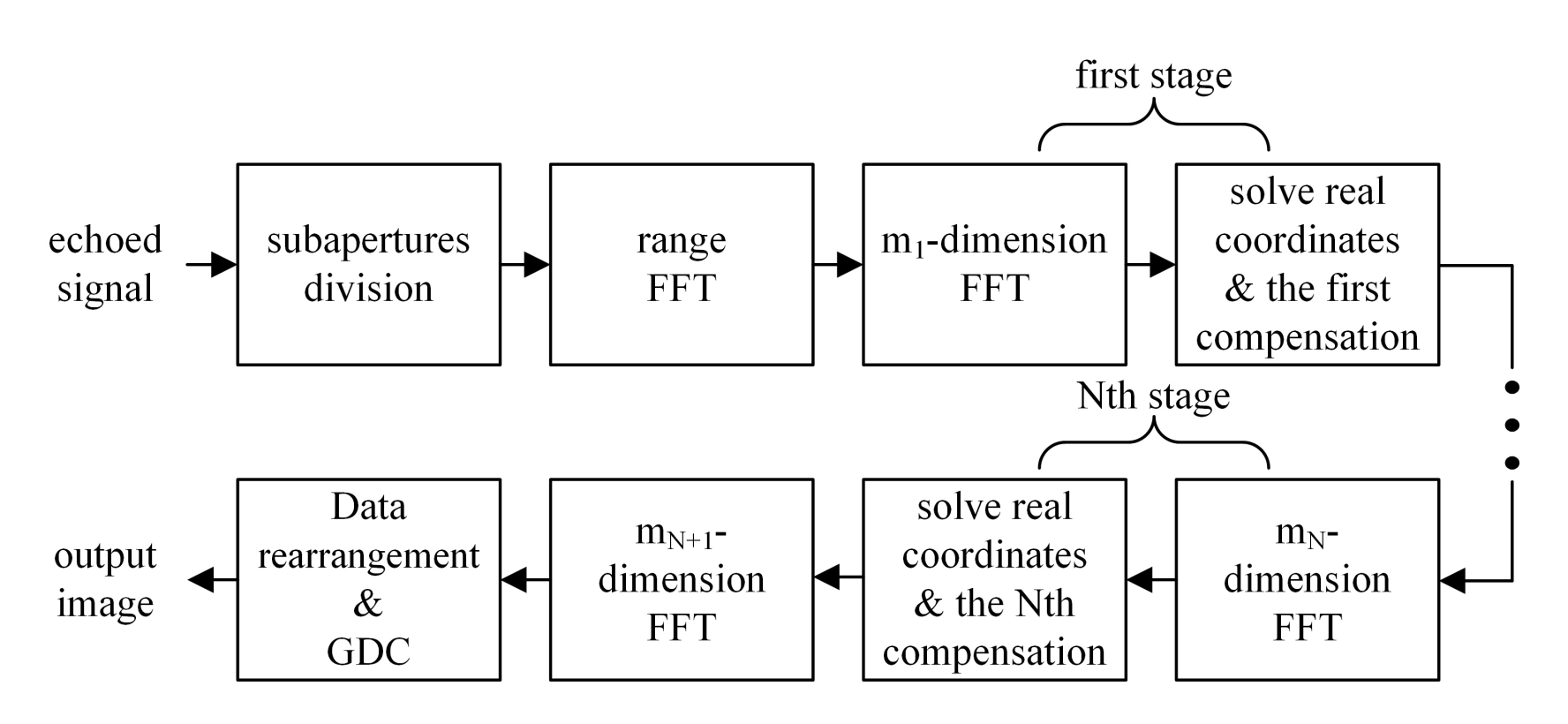
3. Multi-Layer Overlapped Subaperture Algorithm
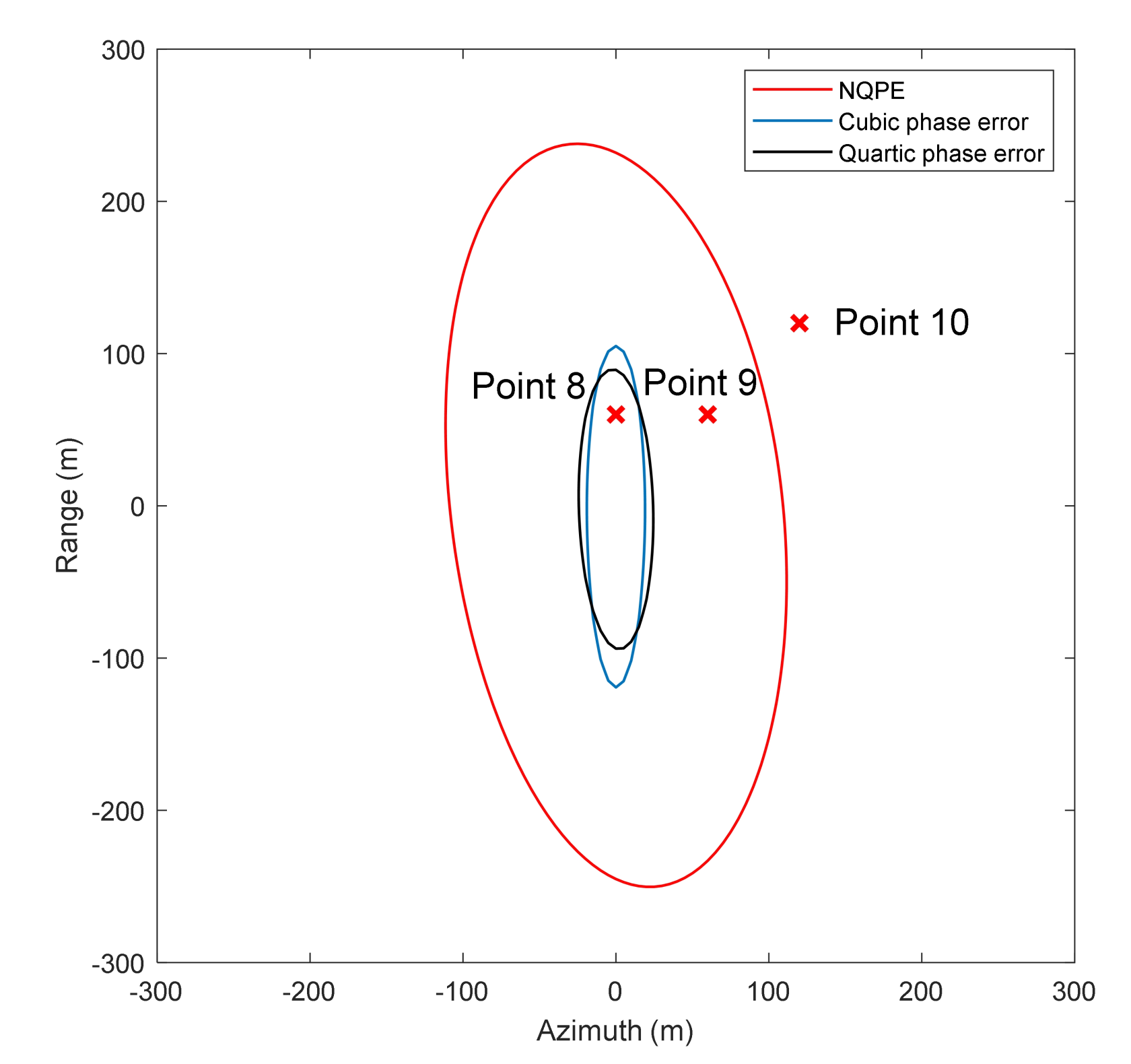
3.1. Analysis of the PWA Phase Error
3.2. Derivation of the ML-OSA
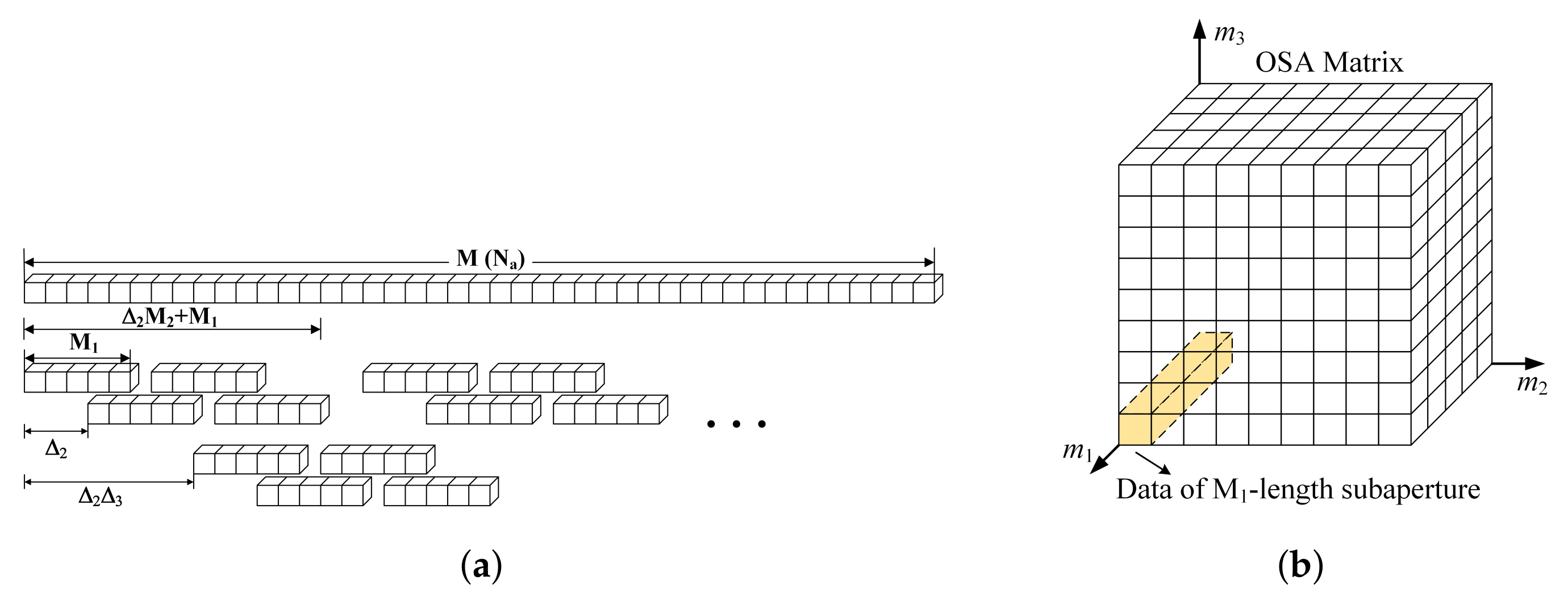
3.2.1. Azimuth Subaperture Division and Range Compression
3.2.2. 1st to the Nth-Dimensional Azimuth Processing
3.2.3. (N+1)th-Dimensional Azimuth Processing
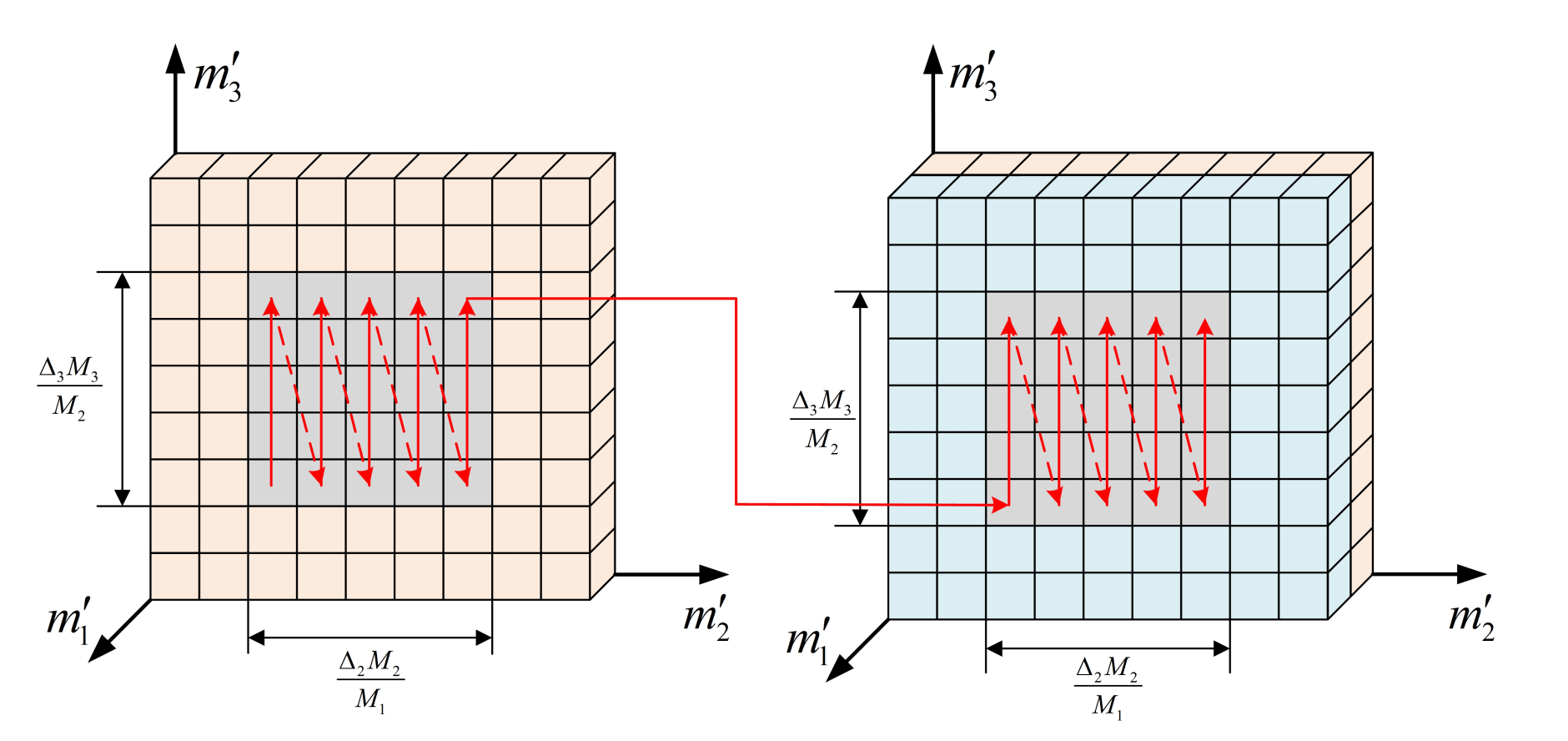
3.2.4. Data Stitching and Geometrical Distortion Correction
3.2.5. Computation Load Analysis
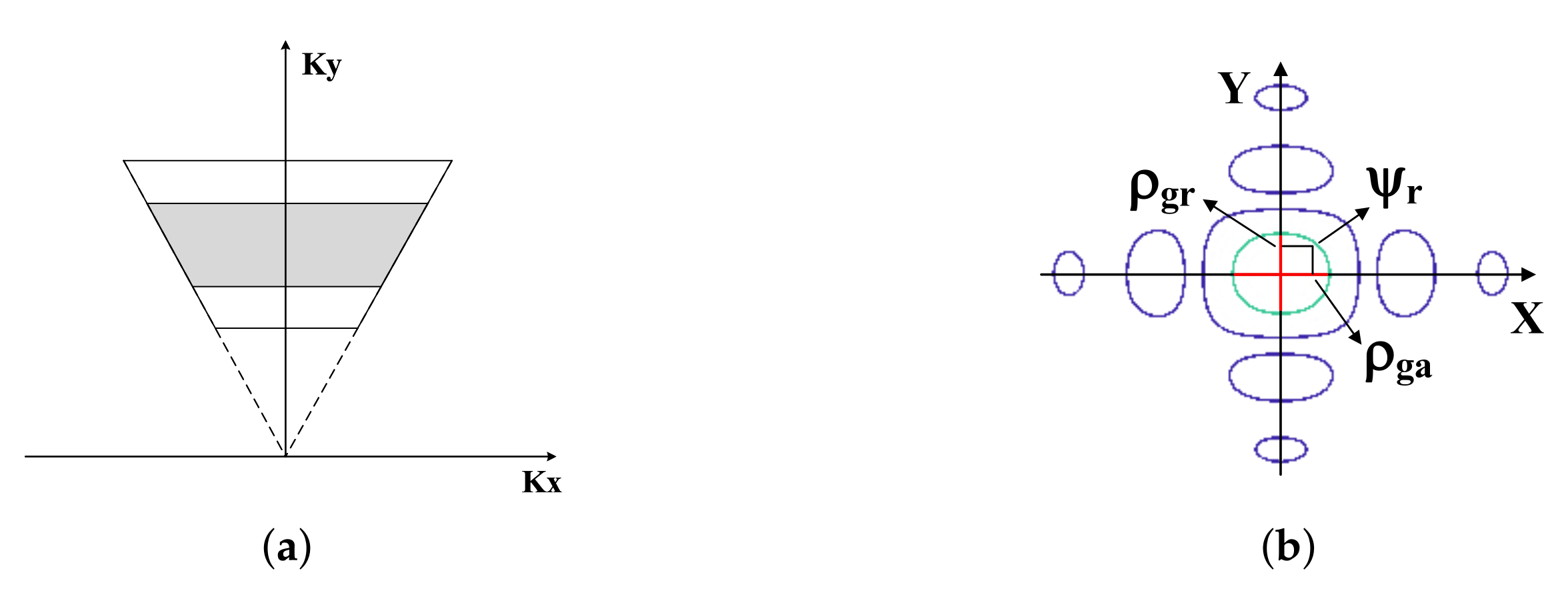
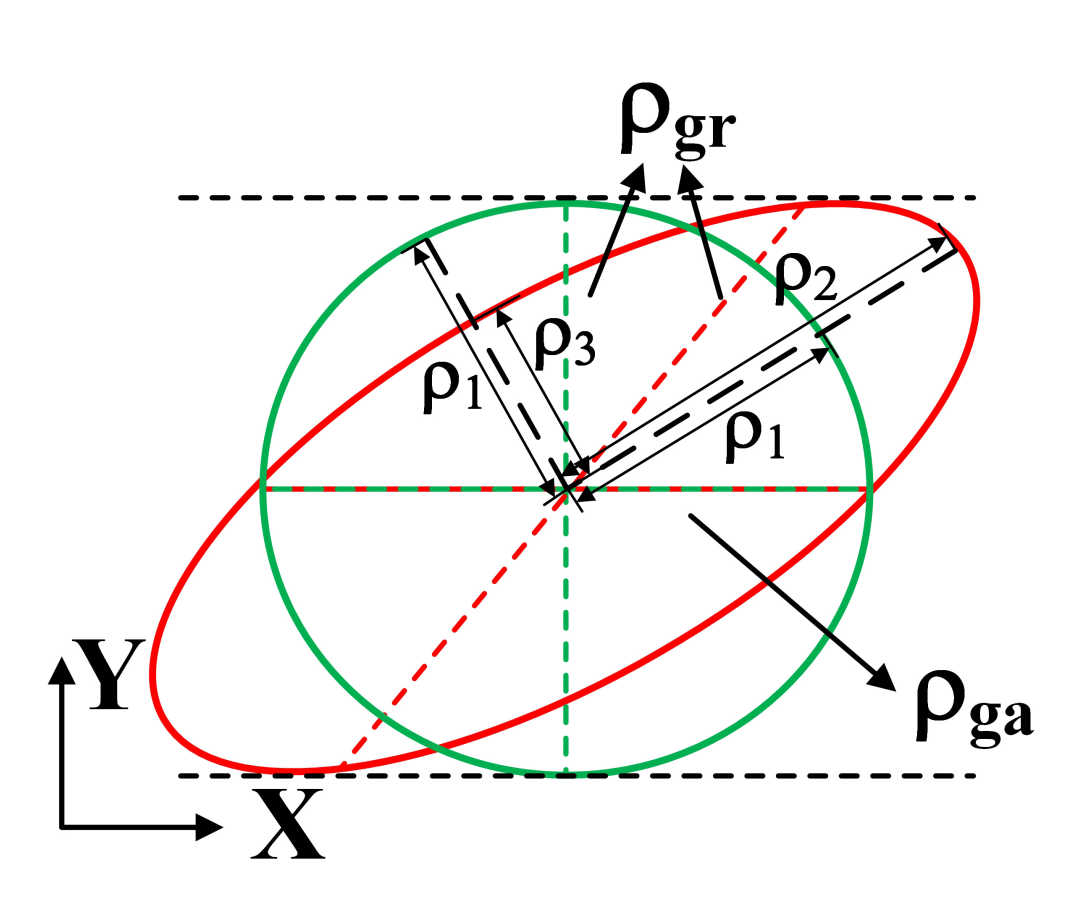
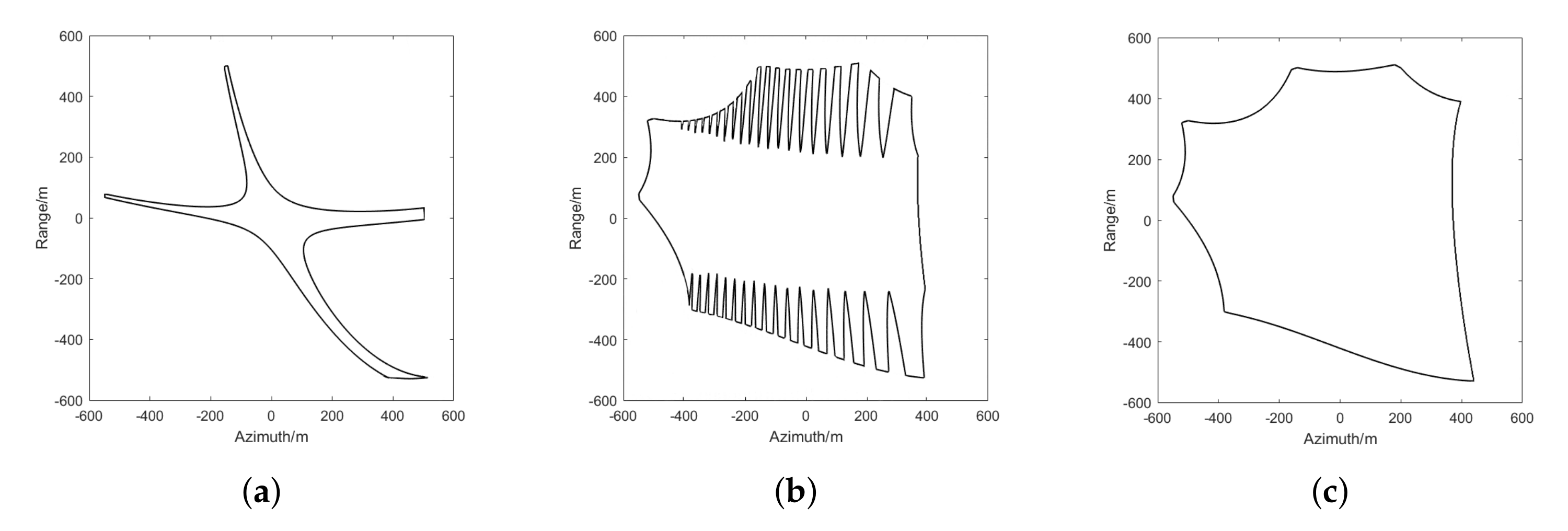
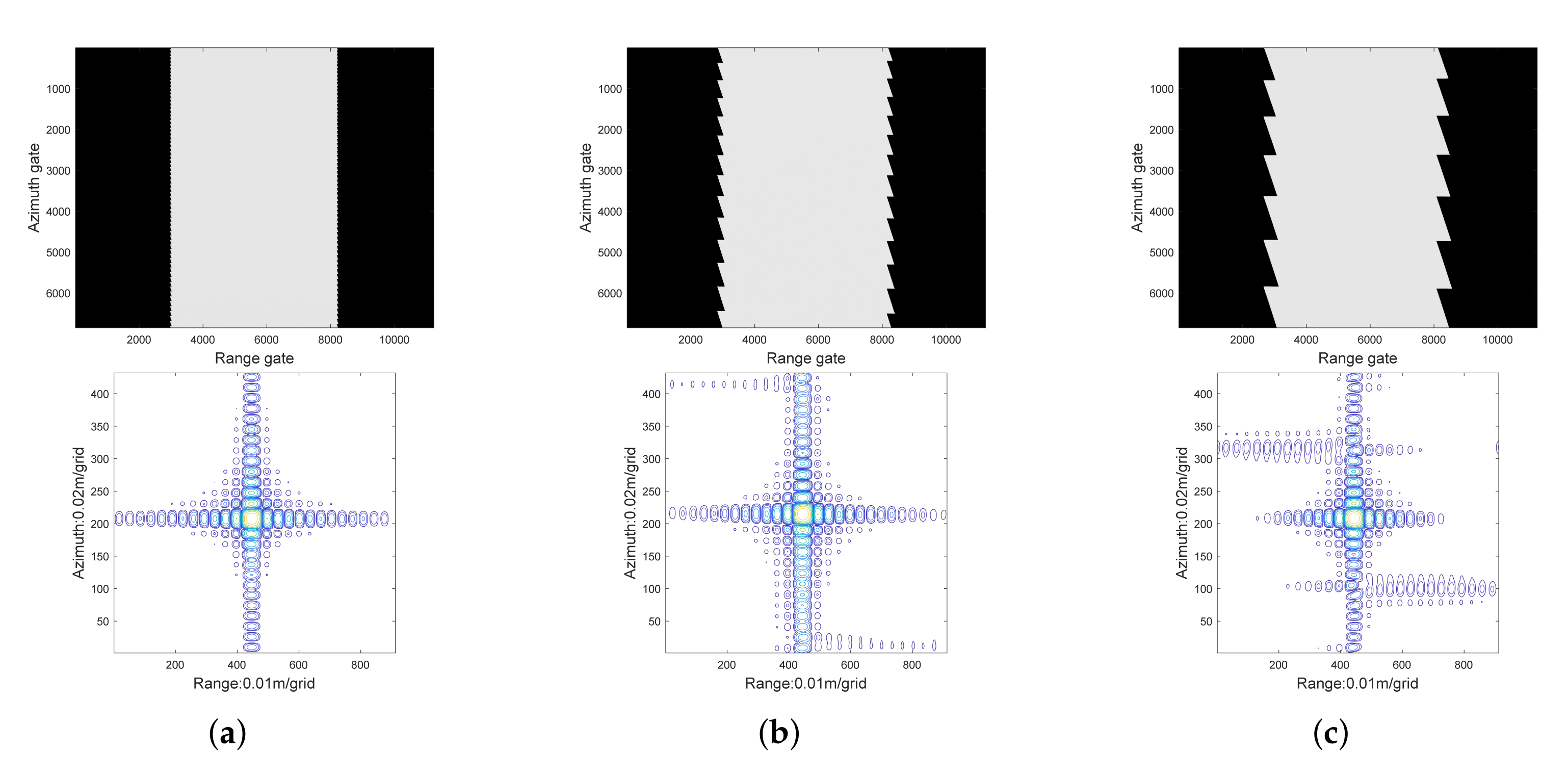
4. Swath Limit Analysis
4.1. Signal Model Accuracy
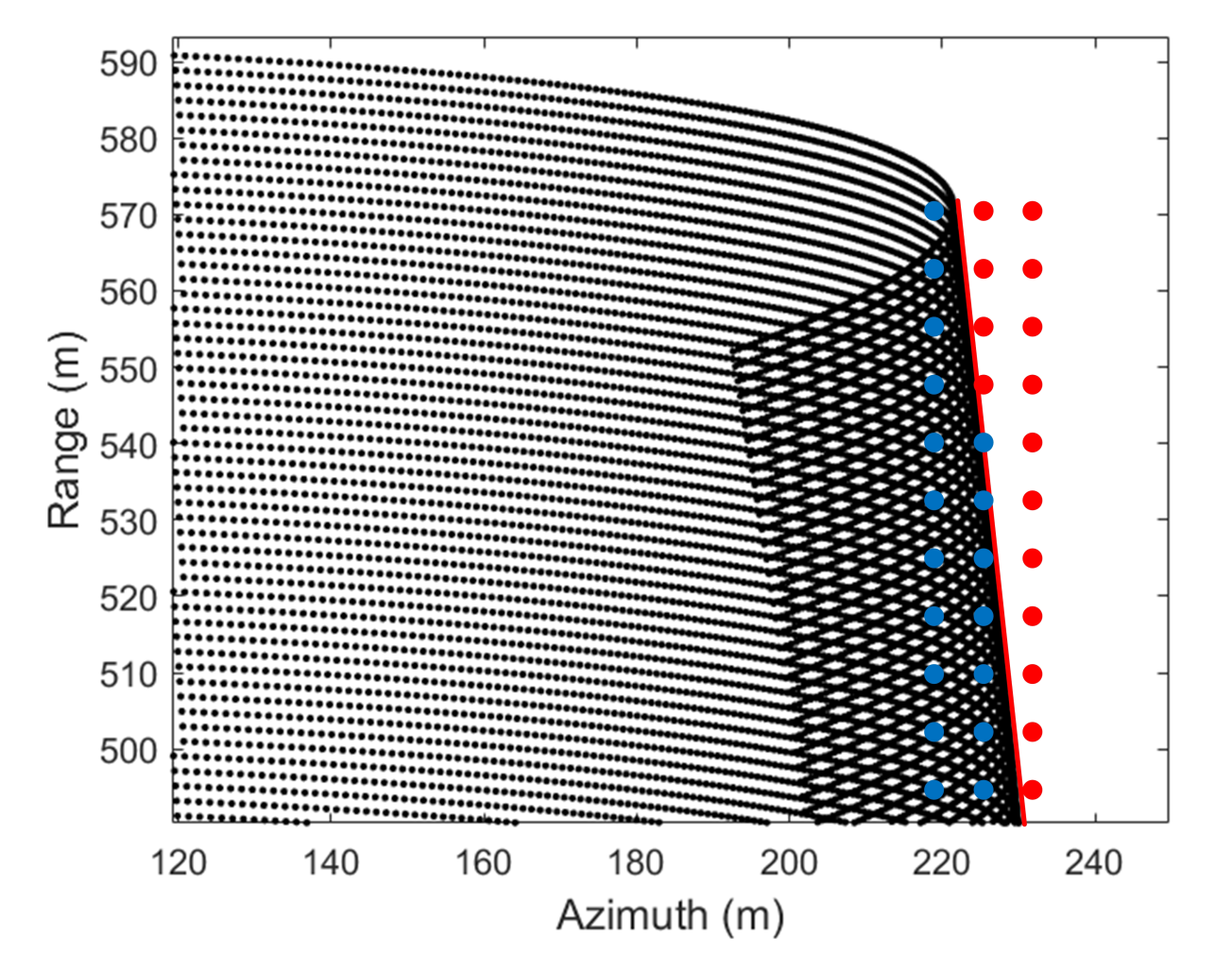
4.2. Folding Phenomenon in Subaperture Compensation Generation
4.3. Residual Phase Error of the ML-OSA
5. Discussion
5.1. Measurable Motion Error
5.2. Unmeasurable Motion Error
5.3. Segment-by-Segment Parameter Adjustment
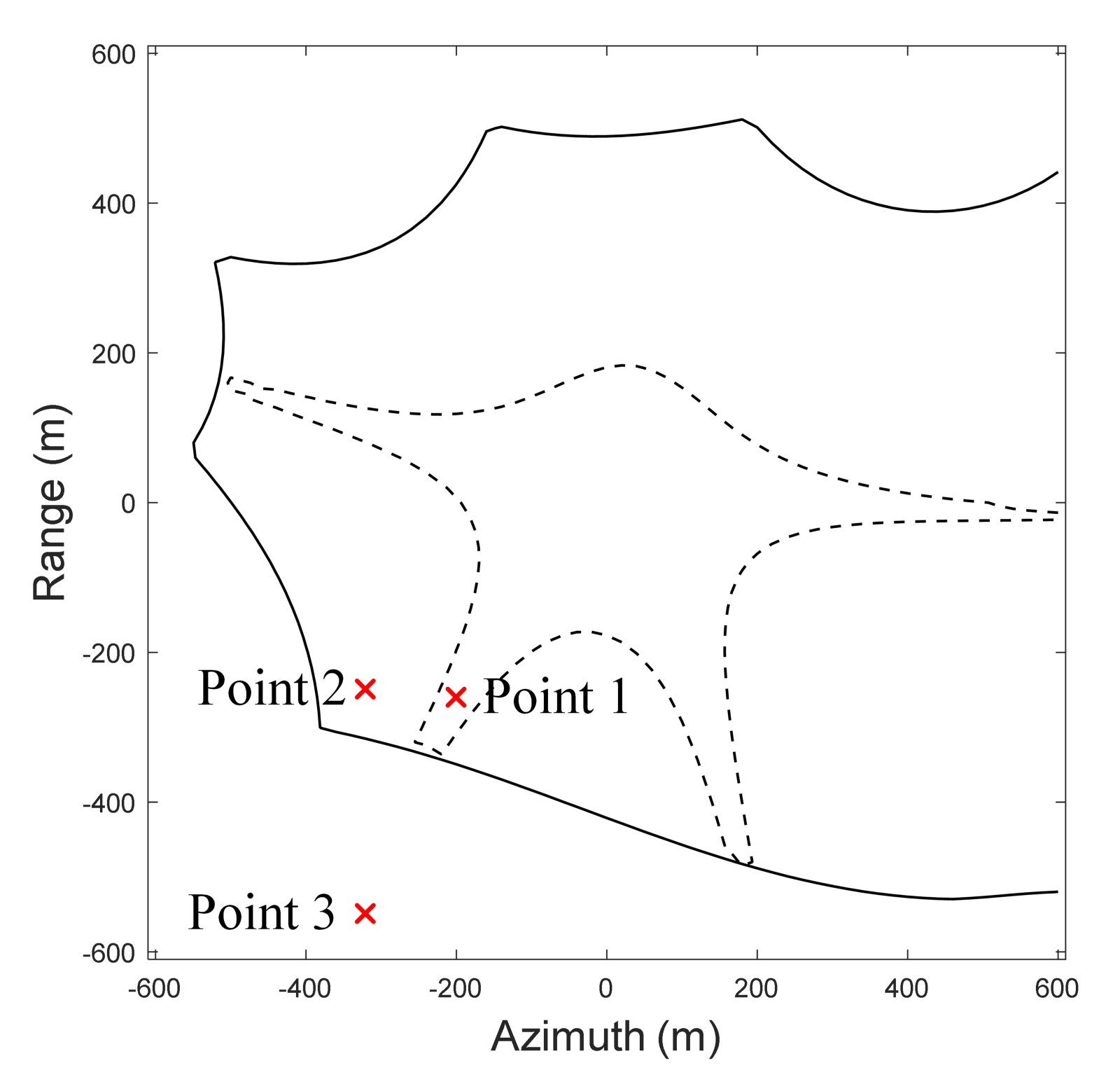
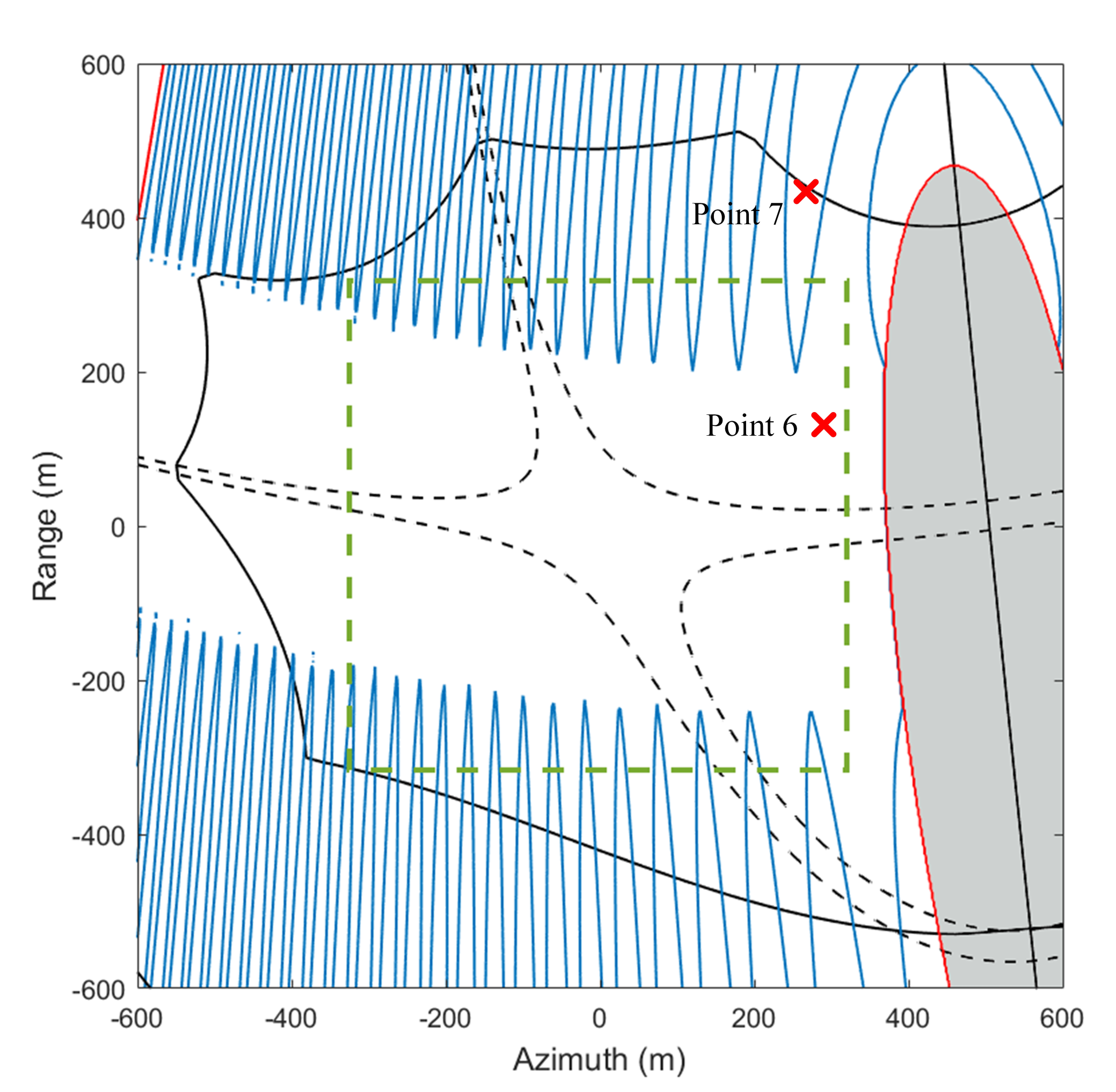
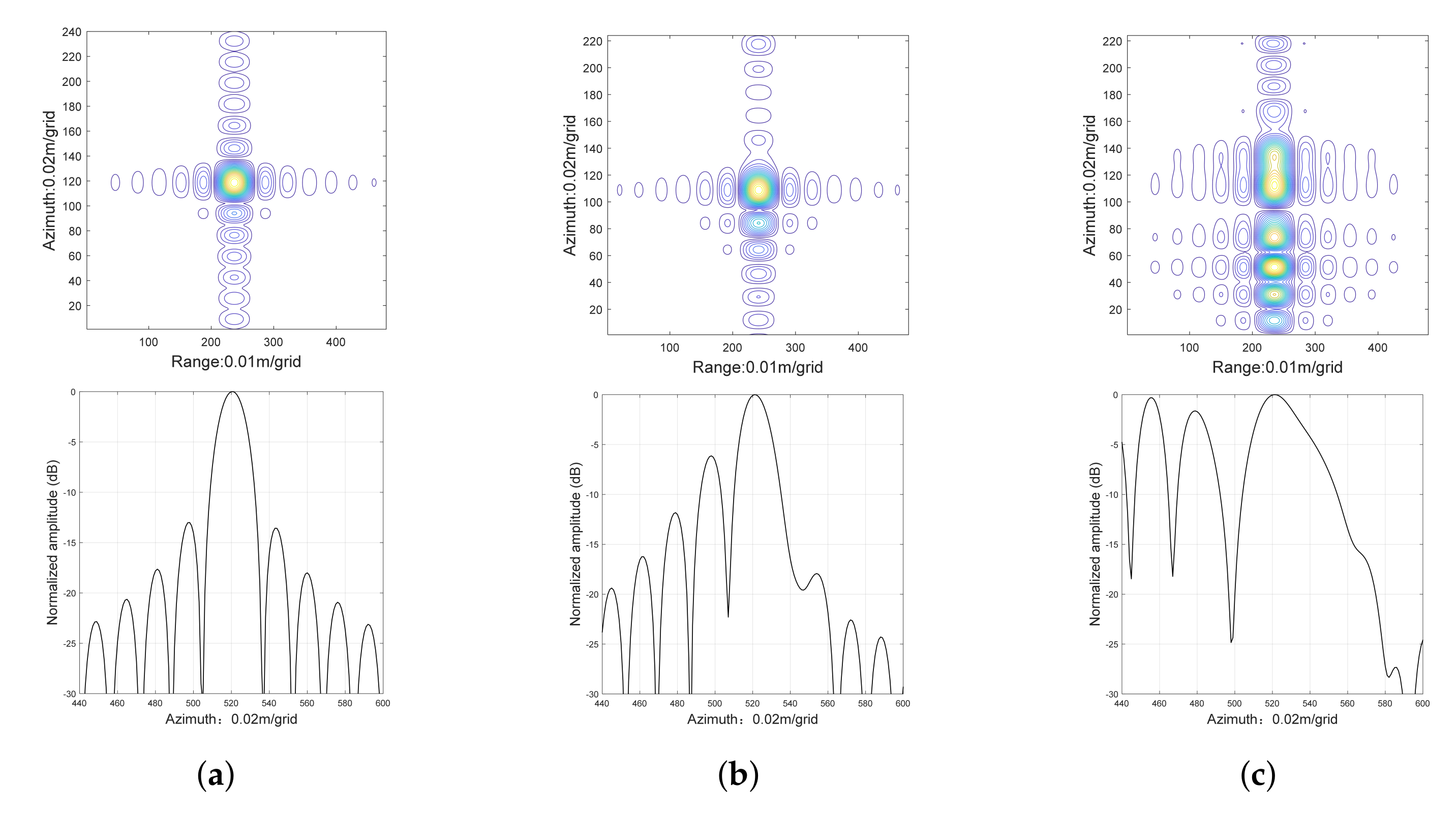
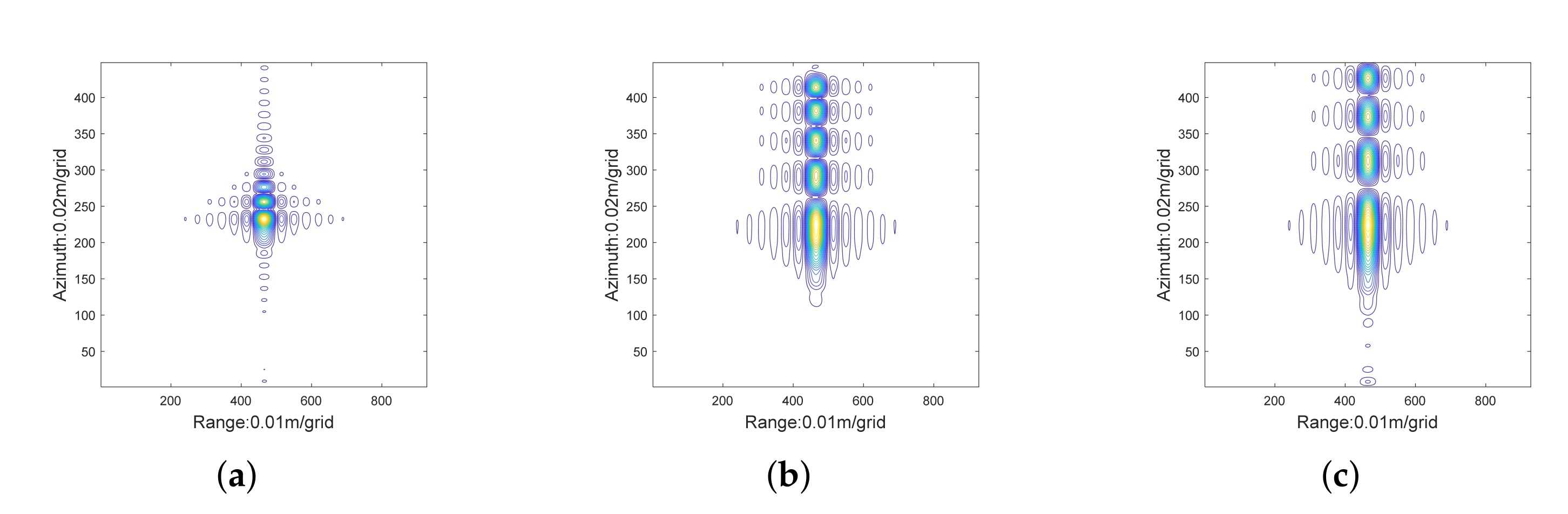
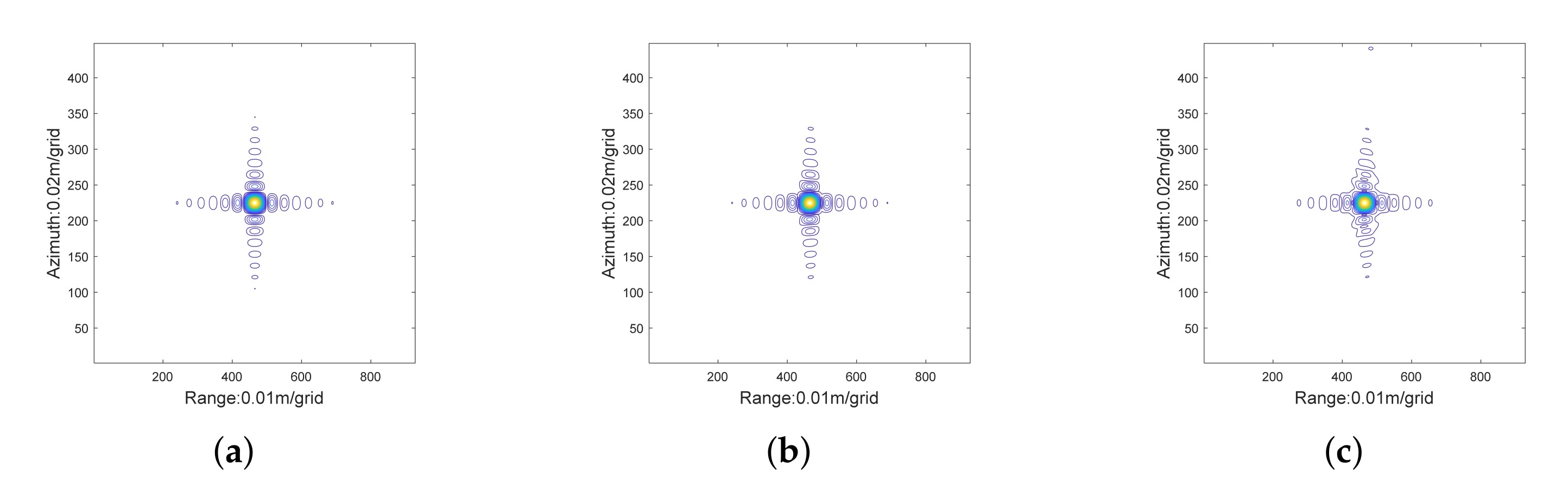
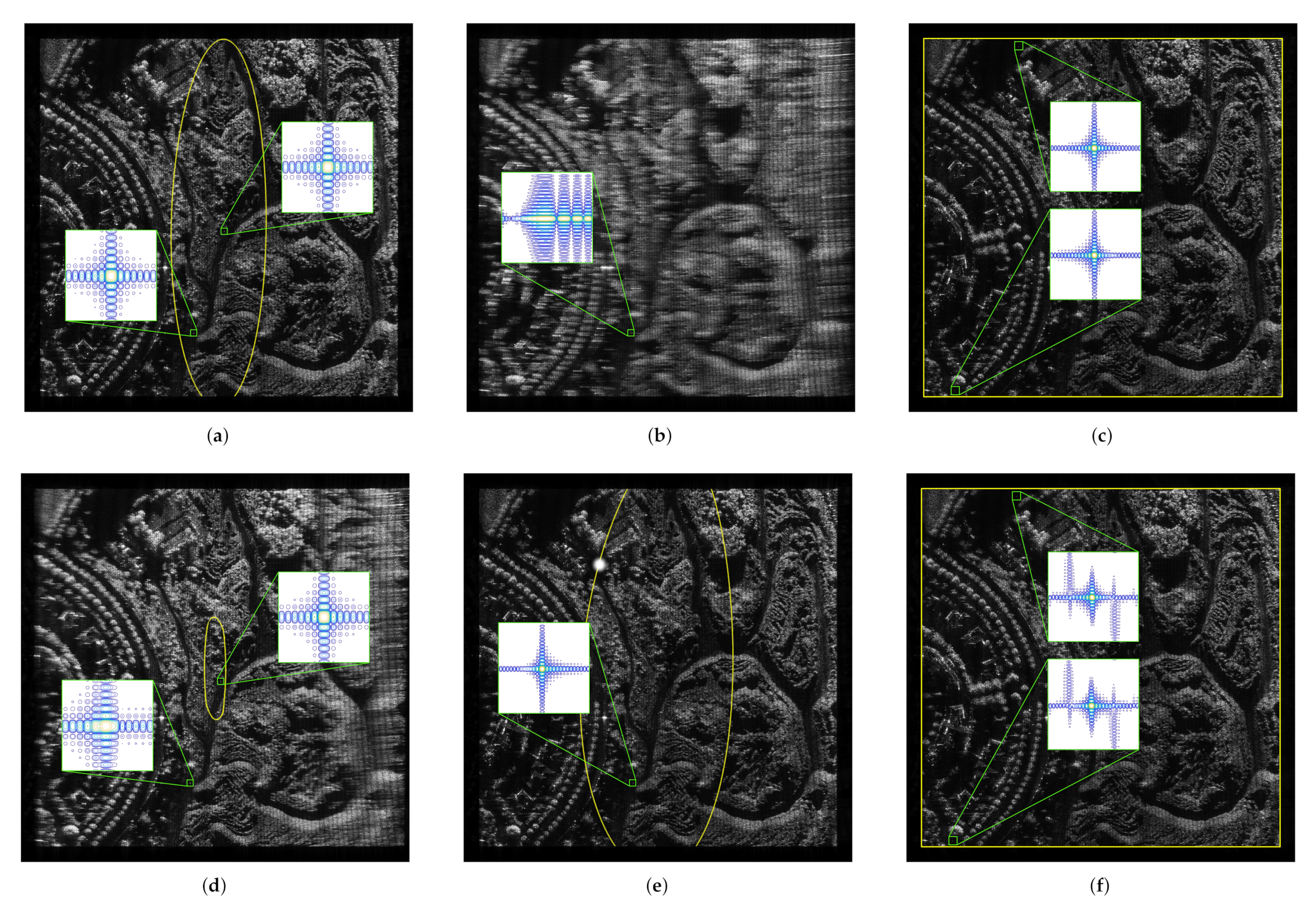
6. Extended-Target Simulations
6.1. Ideal Case
6.2. Non-Ideal Case
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Wavenumber Spectrum Distortion Caused by EHS Geometry
Appendix B. PWA Phase Error with Continuously Time-Varying Parameters
Appendix C. Coordinate Mapping between Distorted Target Coordinates and Real Coordinates
References
- Carrara, W.G.; Goodman, R.S.; Majewski, R.M. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms; Artech House: Boston, MA, USA, 1995. [Google Scholar]
- Lin, Y.; Hong, W.; Li, Y.; Tan, W.; Yu, L.; Hou, L.; Wang, J.; Liu, Y.; Wang, W. Study on fine feature description of multi-aspect SAR observations. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5682–5685. [Google Scholar]
- Chen, S.; Yuan, Y.; Zhang, S.; Zhao, H.; Chen, Y. A New Imaging Algorithm for Forward-Looking Missile-Borne Bistatic SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1543–1552. [Google Scholar] [CrossRef]
- Zeng, T.; Li, Y.; Ding, Z.; Long, T.; Yao, D.; Sun, Y. Subaperture Approach Based on Azimuth-Dependent Range Cell Migration Correction and Azimuth Focusing Parameter Equalization for Maneuvering High-Squint-Mode SAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6718–6734. [Google Scholar] [CrossRef]
- Zhou, Z.; Ding, Z.; Zhang, T.; Wang, Y. High-Squint SAR Imaging for Noncooperative Moving Ship Target Based on High Velocity Motion Platform. In Proceedings of the 2018 China International SAR Symposium (CISS), Shanghai, China, 10–12 October 2018; pp. 1–5. [Google Scholar]
- Xu, X.; Su, F.; Gao, J.; Jin, X. High-Squint SAR Imaging of Maritime Ship Targets. IEEE Trans. Geosci. Remote Sens. 2020, 60, 1–16. [Google Scholar] [CrossRef]
- Davidson, G.; Cumming, I. Signal properties of spaceborne squint-mode SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 611–617. [Google Scholar] [CrossRef] [Green Version]
- Beard, G.S. Performance Factors for Airborne Short-Dwell Squinted Radar Sensors. Ph.D. Thesis, UCL (University College London), London, UK, 2011. [Google Scholar]
- Zhang, Q.; Yin, W.; Ding, Z.; Zeng, T.; Long, T. An Optimal Resolution Steering Method for Geosynchronous Orbit SAR. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1732–1736. [Google Scholar] [CrossRef]
- Ding, Z.; Yin, W.; Zeng, T.; Long, T. Radar Parameter Design for Geosynchronous SAR in Squint Mode and Elliptical Orbit. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2720–2732. [Google Scholar] [CrossRef]
- Zeng, T.; Cherniakov, M.; Long, T. Generalized approach to resolution analysis in BSAR. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 461–474. [Google Scholar] [CrossRef]
- Xiong, T.; Xing, M.; Xia, X.G.; Bao, Z. New applications of omega-K algorithm for SAR data processing using effective wavelength at high squint. IEEE Trans. Geosci. Remote Sens. 2012, 51, 3156–3169. [Google Scholar] [CrossRef]
- Moreira, A.; Huang, Y. Airborne SAR processing of highly squinted data using a chirp scaling approach with integrated motion compensation. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1029–1040. [Google Scholar] [CrossRef]
- Davidson, G.; Cumming, I.; Ito, M. An approach for improved processing in squint mode SAR. In Proceedings of the IGARSS ’93—IEEE International Geoscience and Remote Sensing Symposium, Tokyo, Japan, 18–21 August 1993; pp. 1173–1175. [Google Scholar]
- Wang, Y.; Li, J.; Chen, J.; Xu, H.; Sun, B. A Parameter-Adjusting Polar Format Algorithm for Extremely High Squint SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2014, 52, 640–650. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Li, J. Theoretical Application of Overlapped Subaperture Algorithm for Quasi-Forward-Looking Parameter-Adjusting Spotlight SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 144–148. [Google Scholar] [CrossRef]
- Min, R.; Wang, Y.; Ding, Z.; Li, L. Spatial Resolution Improvement via Radar Parameter Adjustment for Extremely-High-Squint Spotlight SAR. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2963–2966. [Google Scholar]
- Li, Y.; Liang, D. A refined range doppler algorithm for airborne squinted SAR imaging under maneuvers. In Proceedings of the 2007 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 5–9 November 2007; pp. 389–392. [Google Scholar]
- Wang, W.; Wu, W.; Su, W.; Zhan, R.; Zhang, J. High squint mode SAR imaging using modified RD algorithm. In Proceedings of the IEEE China Summit and International Conference on Signal and Information Processing, Beijing, China, 6–10 July 2013; pp. 589–592. [Google Scholar]
- Fan, W.; Zhang, M.; Li, J.; Wei, P. Modified Range-Doppler Algorithm for High Squint SAR Echo Processing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 422–426. [Google Scholar] [CrossRef]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR processing using chirp scaling. IEEE Trans. Geosci. Remote Sens. 1994, 32, 786–799. [Google Scholar] [CrossRef]
- Davidson, G.; Cumming, I.G.; Ito, M. A chirp scaling approach for processing squint mode SAR data. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 121–133. [Google Scholar] [CrossRef]
- Mittermayer, J.; Moreira, A. Spotlight SAR processing using the extended chirp scaling algorithm. In Proceedings of the 1997 IEEE International Geoscience and Remote Sensing Symposium, IGARSS’97, Singapore, 3–8 August 1997; pp. 2021–2023. [Google Scholar]
- An, D.; Huang, X.; Jin, T.; Zhou, Z. Extended nonlinear chirp scaling algorithm for high-resolution highly squint SAR data focusing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3595–3609. [Google Scholar] [CrossRef]
- Li, Z.; Xing, M.; Liang, Y.; Gao, Y.; Chen, J.; Huai, Y.; Zeng, L.; Sun, G.C.; Bao, Z. A Frequency-Domain Imaging Algorithm for Highly Squinted SAR Mounted on Maneuvering Platforms With Nonlinear Trajectory. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4023–4038. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Xu, F.; Yang, J. A New Nonlinear Chirp Scaling Algorithm for High-Squint High-Resolution SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2225–2229. [Google Scholar] [CrossRef]
- Zhong, H.; Zhang, Y.; Chang, Y.; Liu, E.; Tang, X.; Zhang, J. Focus High-Resolution Highly Squint SAR Data Using Azimuth-Variant Residual RCMC and Extended Nonlinear Chirp Scaling Based on a New Circle Model. IEEE Geosci. Remote Sens. Lett. 2018, 15, 547–551. [Google Scholar] [CrossRef]
- Li, Z.; Liang, Y.; Xing, M.; Huai, Y.; Zeng, L.; Bao, Z. Focusing of Highly Squinted SAR Data With Frequency Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2016, 13, 23–27. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, J.; Li, Z.; Huang, Y.; Yang, J. Highly Squint SAR Data Focusing Based on Keystone Transform and Azimuth Extended Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2015, 12, 145–149. [Google Scholar]
- Berens, P. Extended range migration algorithm for squinted spotlight SAR. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; pp. 4053–4055. [Google Scholar]
- Wang, G.; Zhang, L.; Hu, Q. A novel range cell migration correction algorithm for highly squinted SAR imaging. In Proceedings of the 2016 CIE International Conference on Radar, Guangzhou, China, 10–13 October 2016; pp. 1–4. [Google Scholar]
- Li, Z.; Liang, Y.; Xing, M.; Huai, Y.; Gao, Y.; Zeng, L.; Bao, Z. An Improved Range Model and Omega-K-Based Imaging Algorithm for High-Squint SAR With Curved Trajectory and Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2016, 13, 656–660. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Zhao, Y. An Omega-K Algorithm for Highly Squinted Missile-Borne SAR With Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1569–1573. [Google Scholar] [CrossRef]
- Jakowatz, C.V.J.; Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Thompson, P.A. Spotlight-Mode Synthetic Aperture Radar: A signal Processing Approach; Springer: Berlin, Germany, 1996; pp. 330–332. [Google Scholar]
- Scherreik, M.D.; Gorham, L.A.; Rigling, B.D. New Phase Error Corrections for PFA with Squinted SAR. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2637–2641. [Google Scholar] [CrossRef]
- Gorham, L.A.; Rigling, B.D. Scene size limits for polar format algorithm. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 73–84. [Google Scholar] [CrossRef]
- Doerry, A.W. Wavefront Curvature Limitations and Compensation to Polar Format Processing for Synthetic Aperture Radar Images; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 2006. [Google Scholar]
- Li, P.; Mao, X.; Ding, L. Wavefront curvature correction for missile borne spotlight SAR polar format image. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–4. [Google Scholar]
- Mao, X.; Zhu, D.; Zhu, Z. Polar format algorithm wavefront curvature compensation under arbitrary radar flight path. IEEE Geosci. Remote Sens. Lett. 2011, 9, 526–530. [Google Scholar] [CrossRef]
- Doerry, A. Synthetic Aperture Radar Processing with Tiered Subapertures; NASA STI/Recon Technical Report N; U.S. Department of Energy Office of Scientific and Technical Information: Washington, DC, USA, 1994; pp. 111–170. [Google Scholar]
- Tang, Y.; Zhang, B.; Xing, M.; Bao, Z.; Guo, L. Azimuth Overlapped Subaperture Algorithm in Frequency Domain for Highly Squinted Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2013, 10, 692–696. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Xing, M.; Yu, H.; Liang, B.; Peng, J.; Sun, G. Motion Compensation/Autofocus in Airborne Synthetic Aperture Radar: A Review. IEEE Geosci. Remote Sens. Mag. 2021, 1, 2–23. [Google Scholar] [CrossRef]
- Wahl, D.; Eichel, P.; Ghiglia, D.; Jakowatz, C. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef] [Green Version]
- Ran, L.; Liu, Z.; Zhang, L.; Li, T.; Xie, R. An Autofocus Algorithm for Estimating Residual Trajectory Deviations in Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3408–3425. [Google Scholar] [CrossRef]


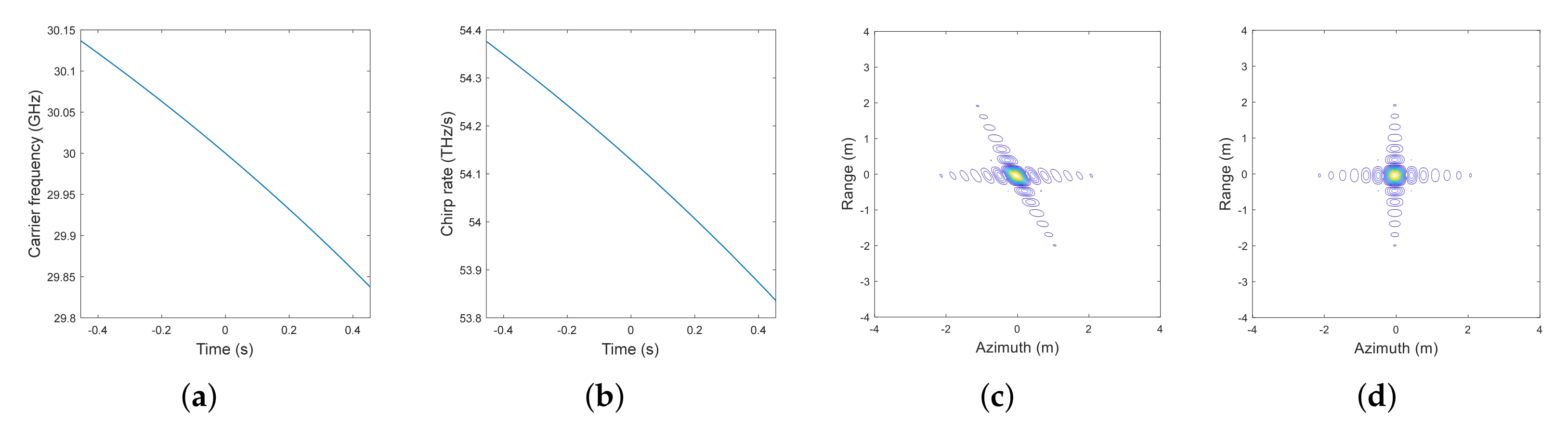
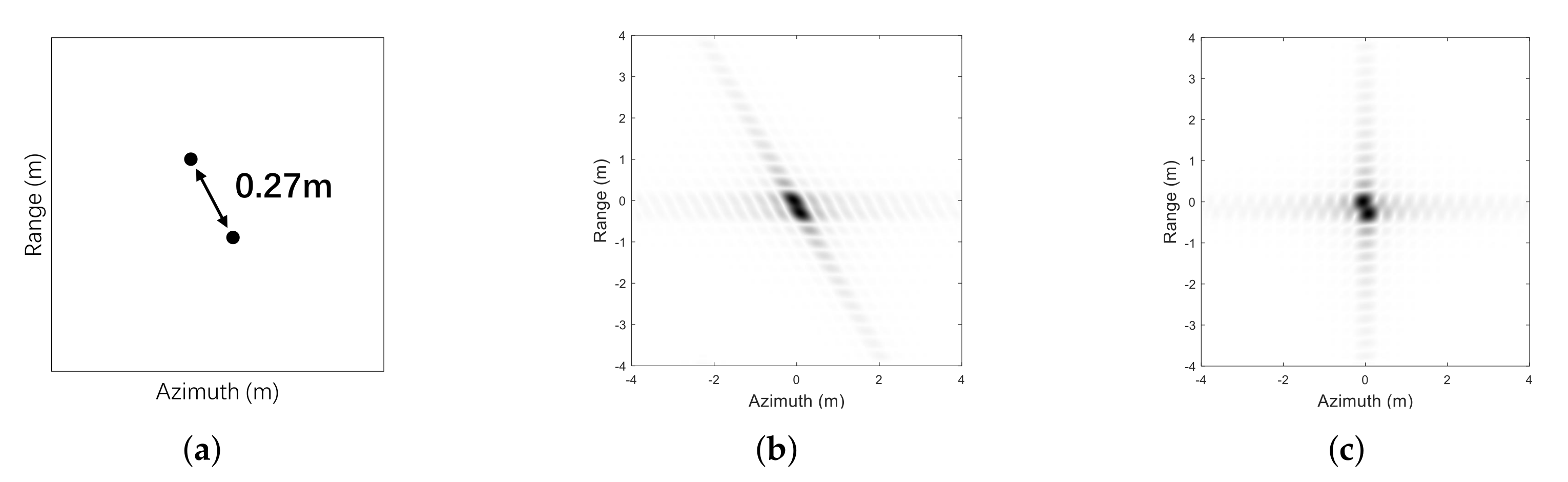





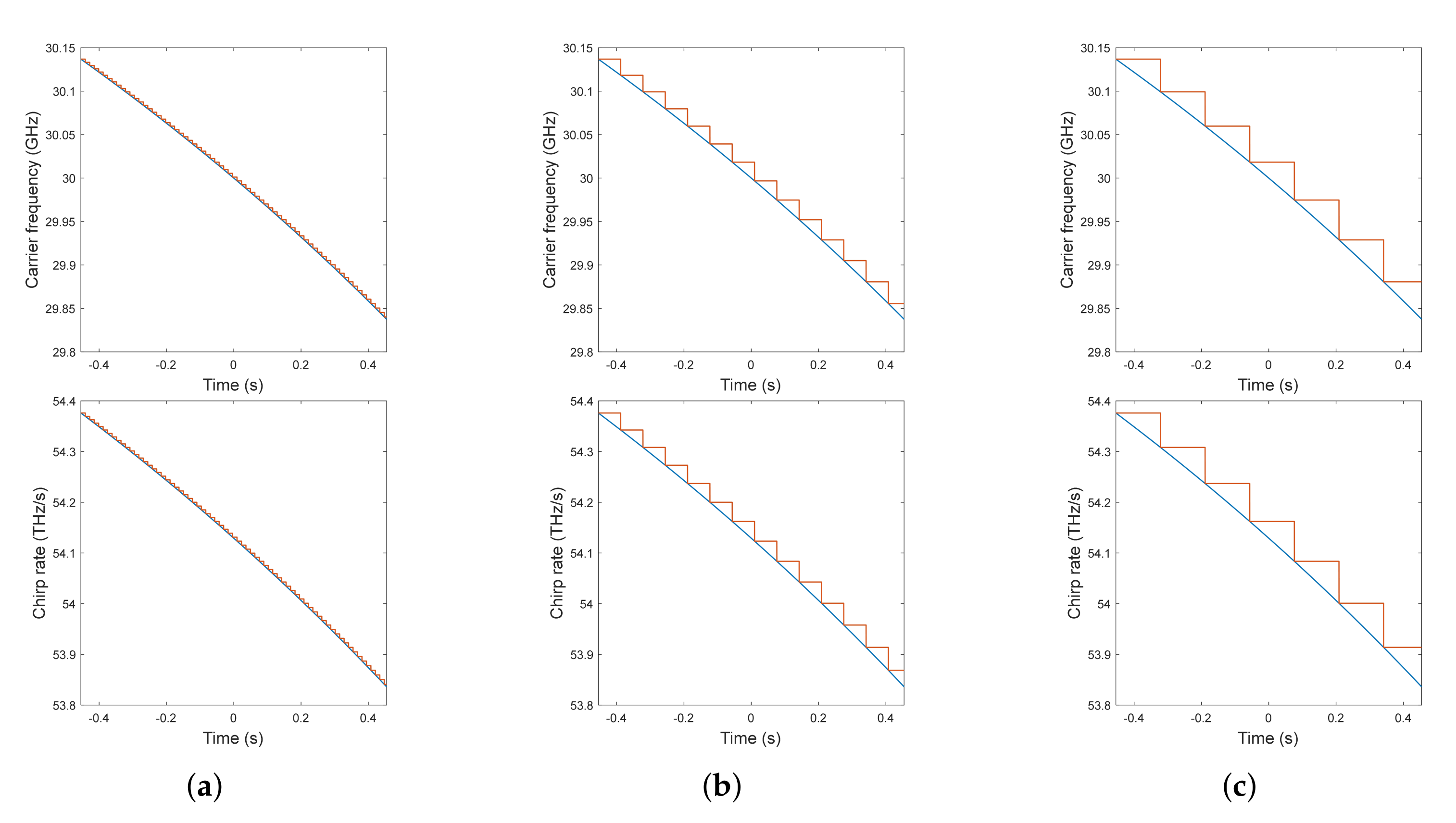


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Carrier frequency | 30.11∼29.83 GHz | Bandwidth | 540 MHz |
| Pulse width | 10 s | Chirp rate | 54.23∼53.74 THz/s |
| Sensor velocity | 1000 m/s | Sensor acceleration | 100 m/s |
| Pulse repeat frequency | 7540 Hz | Central altitude | 2 km |
| Central slant range | 5.2 km | Central incidence angle | 67.3 |
| Dive angle | 30 | Squint angle | 80.9 |
| Resolution | 0.3 m × 0.3 m | Scene size | 1200 m × 1200 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Min, R.; Ding, Z.; Zeng, T.; Li, L. Multi-Layer Overlapped Subaperture Algorithm for Extremely-High-Squint High-Resolution Wide-Swath SAR Imaging with Continuously Time-Varying Radar Parameters. Remote Sens. 2022, 14, 365. https://doi.org/10.3390/rs14020365
Wang Y, Min R, Ding Z, Zeng T, Li L. Multi-Layer Overlapped Subaperture Algorithm for Extremely-High-Squint High-Resolution Wide-Swath SAR Imaging with Continuously Time-Varying Radar Parameters. Remote Sensing. 2022; 14(2):365. https://doi.org/10.3390/rs14020365
Chicago/Turabian StyleWang, Yan, Rui Min, Zegang Ding, Tao Zeng, and Linghao Li. 2022. "Multi-Layer Overlapped Subaperture Algorithm for Extremely-High-Squint High-Resolution Wide-Swath SAR Imaging with Continuously Time-Varying Radar Parameters" Remote Sensing 14, no. 2: 365. https://doi.org/10.3390/rs14020365
APA StyleWang, Y., Min, R., Ding, Z., Zeng, T., & Li, L. (2022). Multi-Layer Overlapped Subaperture Algorithm for Extremely-High-Squint High-Resolution Wide-Swath SAR Imaging with Continuously Time-Varying Radar Parameters. Remote Sensing, 14(2), 365. https://doi.org/10.3390/rs14020365