Forest Canopy Height Mapping by Synergizing ICESat-2, Sentinel-1, Sentinel-2 and Topographic Information Based on Machine Learning Methods
Abstract
:1. Introduction
- Evaluate the accuracy for height metric (RH95) provided by ATL08 product by comparing with the height metrics derived from ALS data, and determine the best spatial resolution for these two kinds of height metrics in study area;
- Establish canopy height estimation models for different forest types using multi-source remote sensing data based on machine learning algorithms (RF and GBDT) at the spatial resolution determined in Step (1). Evaluate the accuracy of the estimation models and compare the accuracy of established model for different forest types;
- Obtain forest canopy height map for study area based on the estimation models for different forest types established in Step (2), and conduct accuracy assessment for the forest canopy height map by comparing with existing forest canopy height map;
- Obtain optimal variables for different forest types based on machine learning algorithms. Compare the optimal variables corresponding to different forest types and analyze the importance of variables for different forest types.
2. Materials and Methods
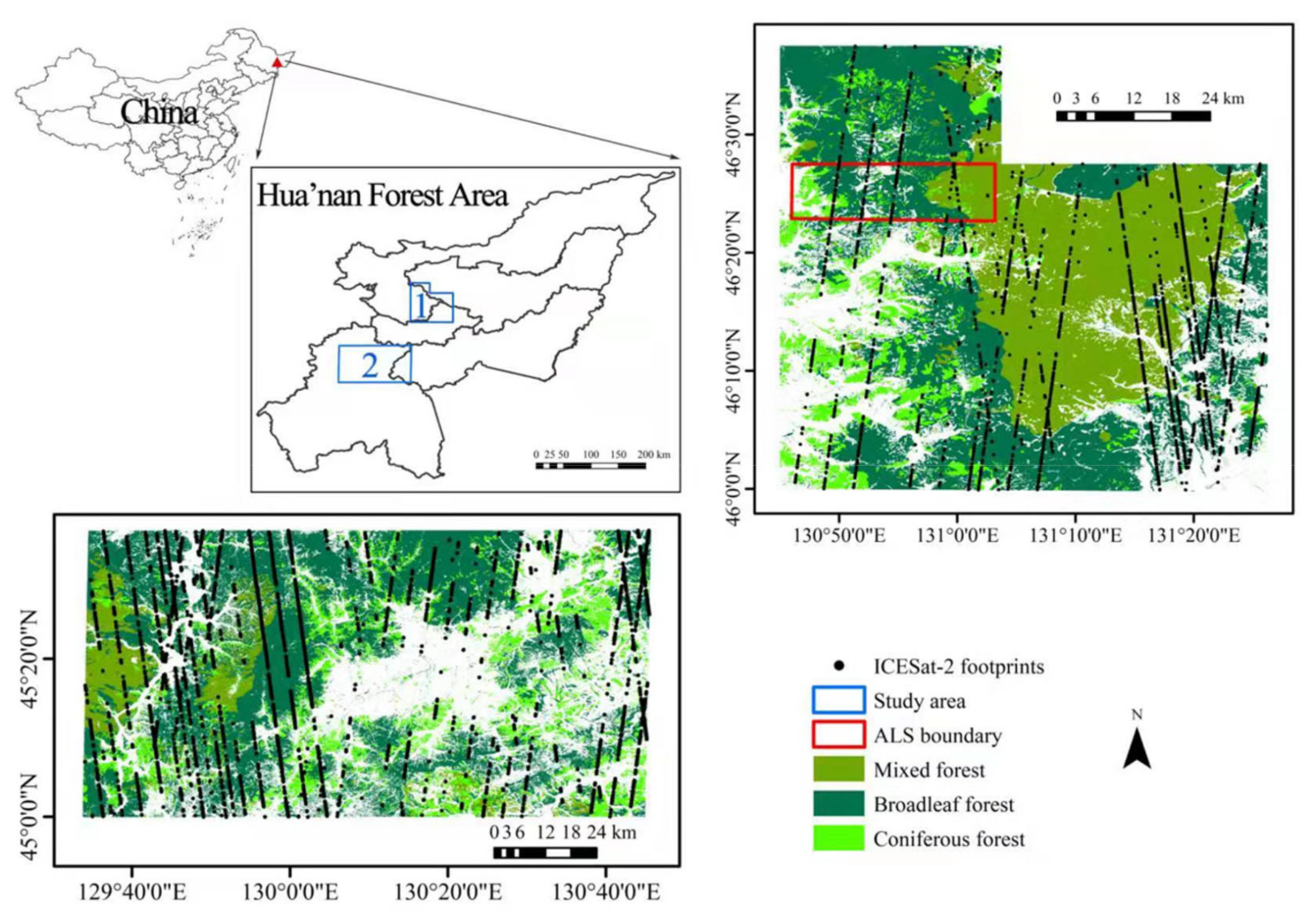
2.1. Study Area
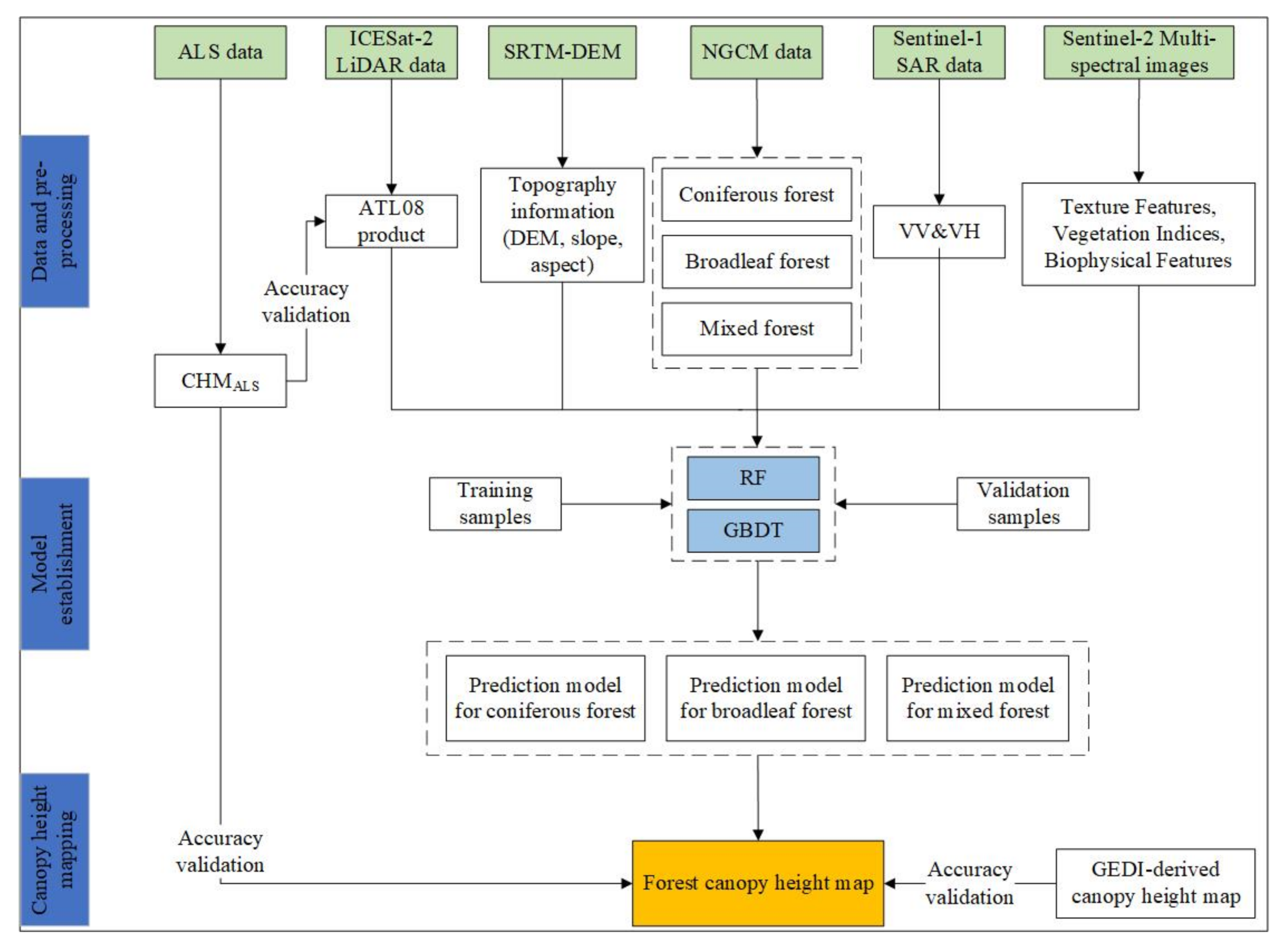
2.2. Data Collection and Preprocessing
2.2.1. ICESat-2 Data
2.2.2. Sentinel-1 SAR Data
2.2.3. Sentinel-2 Multi-Spectral Images
2.2.4. Topographic Information
2.2.5. NGCM Data
2.2.6. ALS Data
2.3. Forest Canopy Height Prediction
2.3.1. Random Forest
2.3.2. Gradient Boosting Decision Tree
3. Results
3.1. Accuracy of ATL08 Product and Sample Selection
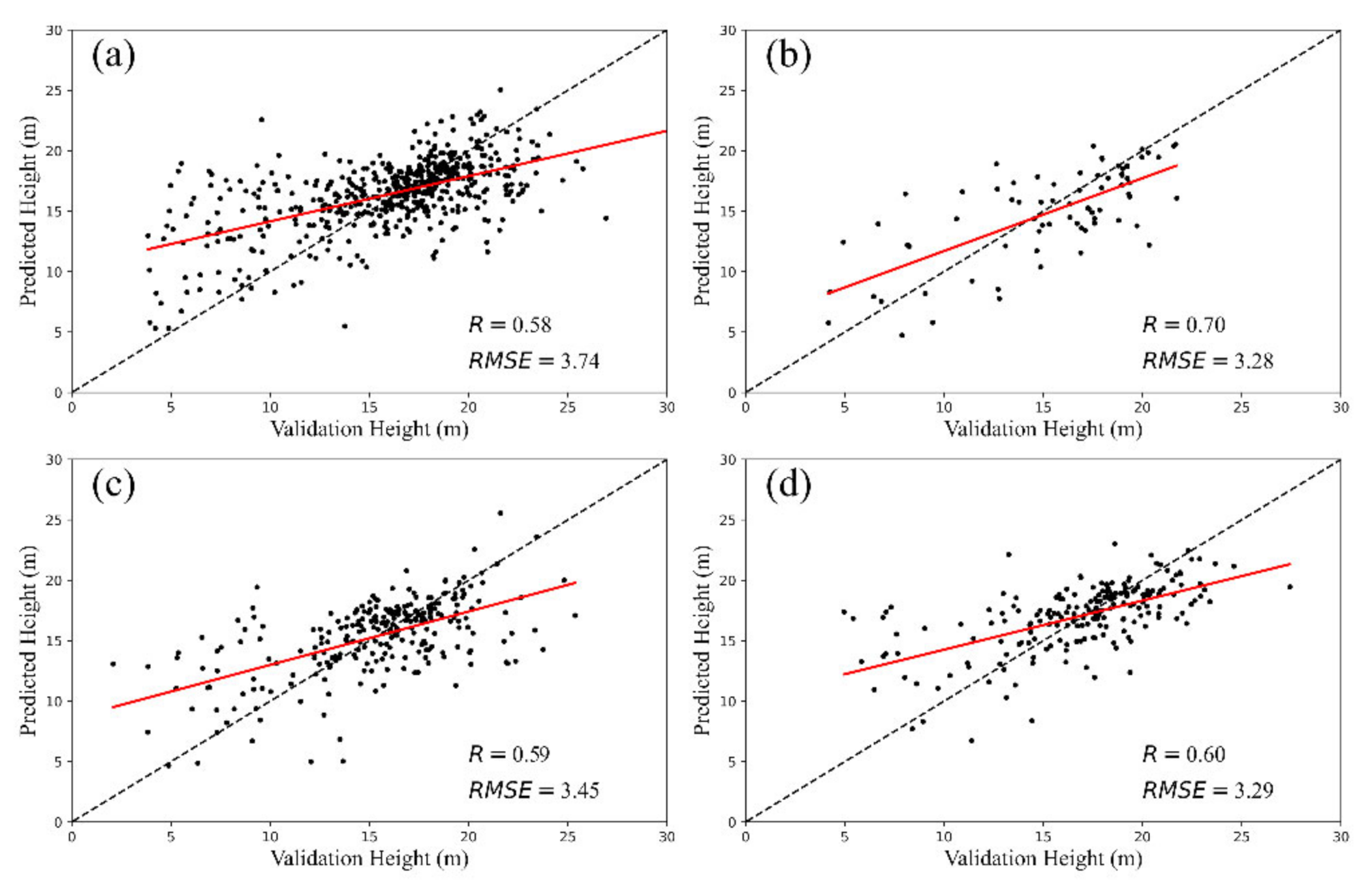
3.2. Forest Canopy Heights Prediction by RF and GBDT
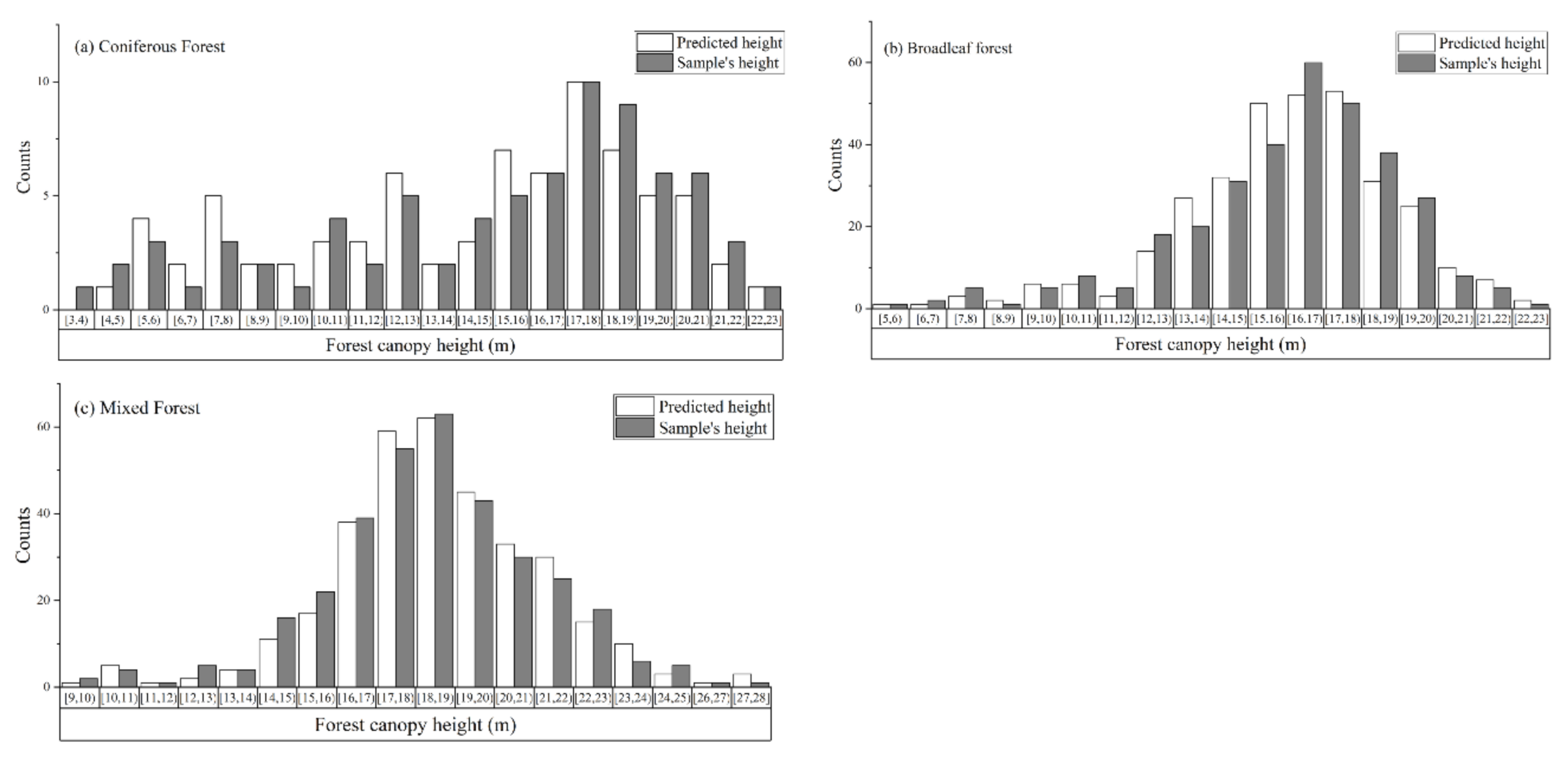
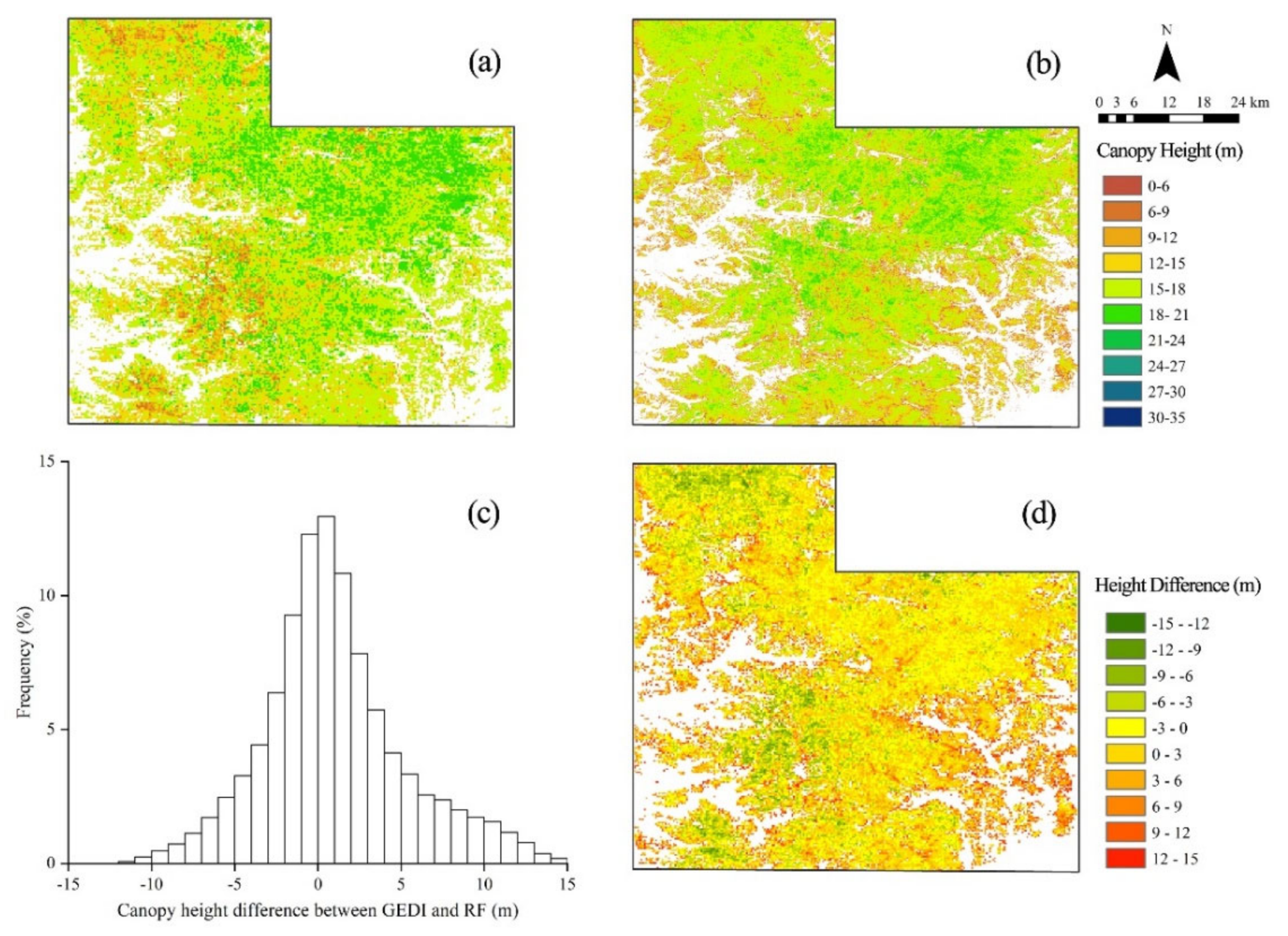
3.3. Forest Canopy Height Mapping
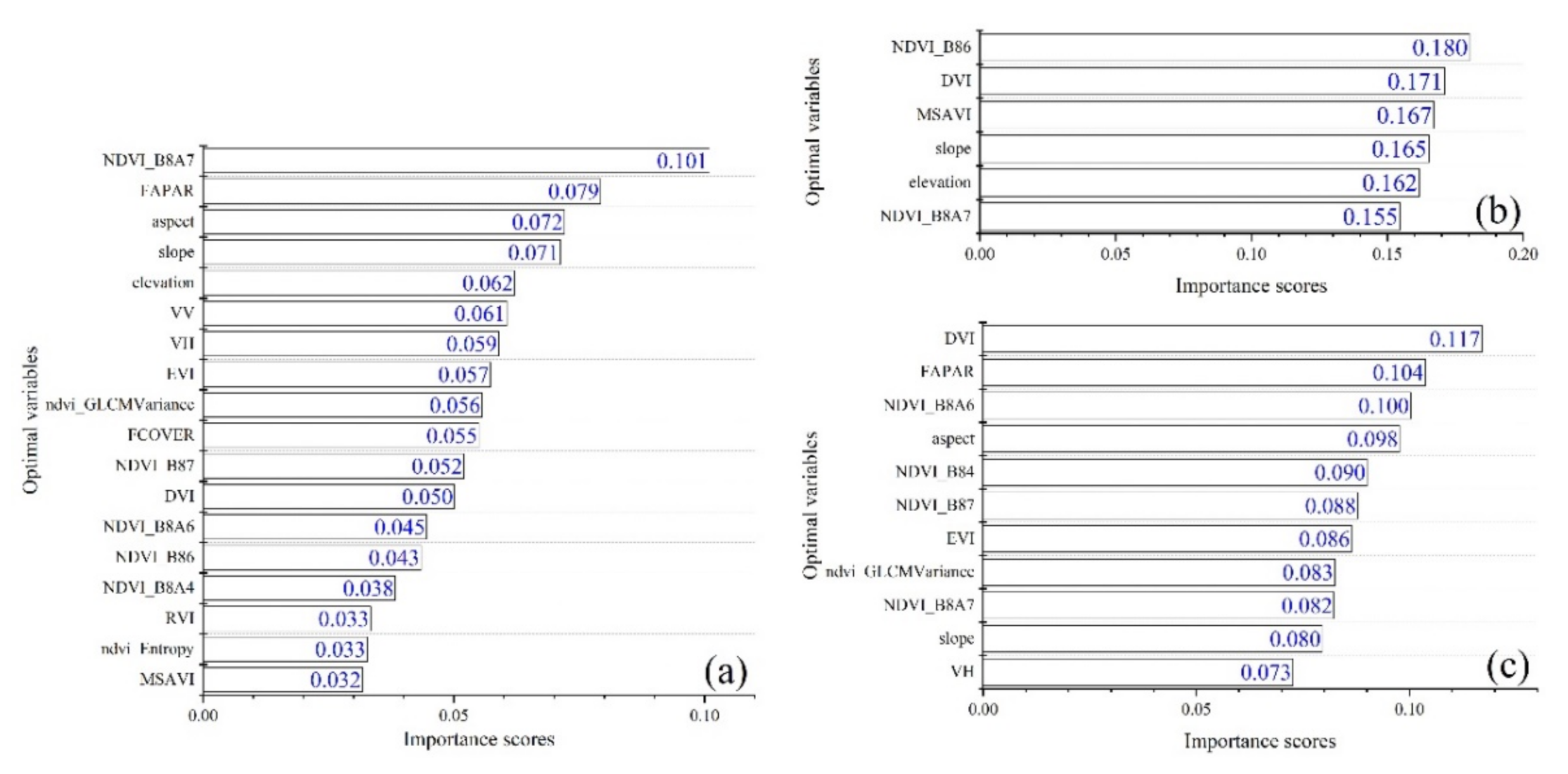
3.4. Optimal Variables and Importance Scores
4. Discussion
4.1. Comparison of RF and GBDT for Forest Canopy Height Modelling
4.2. Comparison of Estimation Models for Different Forest Types
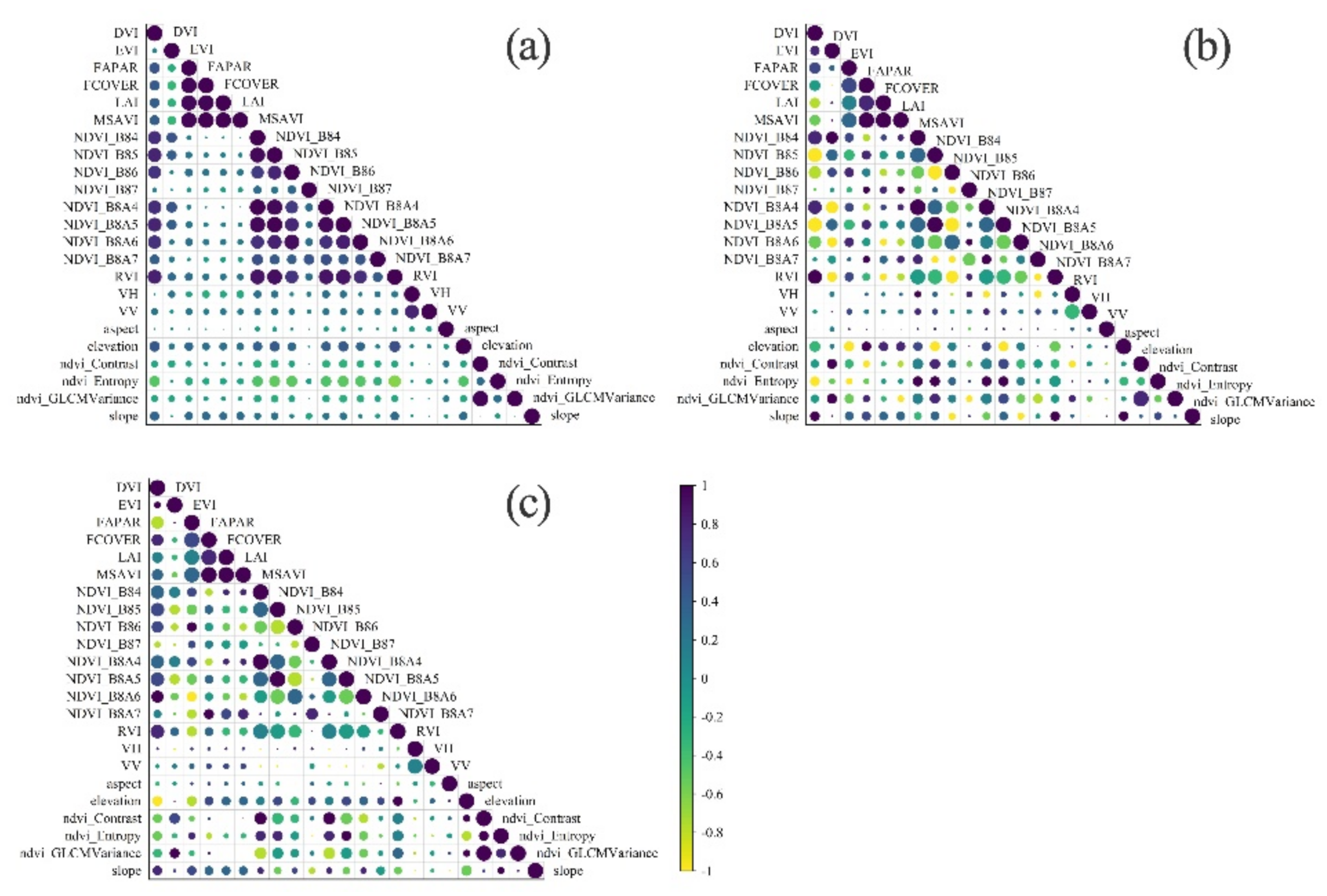
4.3. Comparison of Optimal Variables for Different Forest Types
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, J.; Kaufmann, R.K.; Myneni, R.B.; Tucker, C.J.; Kauppi, P.E.; Liski, J.; Buermann, W.; Alexeyev, V.; Hughes, M.K. Remote sensing estimates of boreal and temperate forest woody biomass: Carbon pools, sources, and sinks. Remote Sens. Environ. 2003, 84, 393–410. [Google Scholar] [CrossRef] [Green Version]
- Lefsky, M.A.; Cohen, W.B.; Harding, D.J.; Parker, G.G.; Acker, S.A.; Gower, S.T. Lidar remote sensing of above-ground biomass in three biomes. Glob. Ecol. Biogeogr. 2002, 11, 393–399. [Google Scholar] [CrossRef] [Green Version]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Rosenqvist, A.; Milne, A.; Lucas, R.; Imhoff, M.; Dobson, C. A review of remote sensing technology in support of the Kyoto protocol. Environ. Sci. Policy 2003, 6, 441–455. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef] [Green Version]
- Alexander, C.; Korstjens, A.H.; Hill, R.A. Influence of micro-topographic and crown characteristics on tree height estimations in tropical forests based on LiDAR canopy height models. Int. J. Appl. Earth Obs. Geoinf. 2018, 65, 105–113. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D. The ice, cloud, and land elevation satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Magruder, L.A.; Brunt, K.M. Performance analysis of airborne photon- counting lidar data in preparation for the ICESat-2 mission. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2911–2918. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. Canopy and Terrain Height Retrievals with ICESat-2: A First Look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef] [Green Version]
- Xing, Y.; Huang, J.; Gruen, A.; Qin, L. Assessing the Performance of ICESat-2/ATLAS Multi-Channel Photon Data for Estimating Ground Topographic in Forested Terrain. Remote Sens. 2020, 12, 2084. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Lin, X.; Xu, M.; Cao, C.; Dang, Y.; Bashir, B.; Xie, B.; Huang, Z. Estimates of Forest height Using a Combination of ICESat-2/ATLAS Data and Stereo-Photogrammetry. Remote Sens. 2020, 12, 3649. [Google Scholar] [CrossRef]
- Lang, N.; Schindler, K.; Wegner, J.D. Country-wide high-resolution vegetation height mapping with Sentinel-2. Remote Sens. Environ. 2019, 233, 111347. [Google Scholar] [CrossRef] [Green Version]
- Jiang, F.; Zhao, F.; Ma, K.; Li, D.; Sun, H. Mapping the Forest height in Northern China by Synergizing ICESat-2 with Sentinel-2 Using a Stacking Algorithm. Remote Sens. 2021, 13, 1535. [Google Scholar] [CrossRef]
- Nandy, S.; Srinet, R.; Padalia, H. Mapping Forest Height and Aboveground Biomass by Integrating ICESat-2, Sentinel-1 and Sentinel-2 Data Using Random Forest Algorithm in Northwest Himalayan Foothills of India. Geophys. Res. Lett. 2021, 14, e2021GL093799. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, W.; Xing, Y.; Hu, X.; Gong, J. Estimation of the forest stand mean height and aboveground biomass in Northeast China using SAR Sentinel-1B, multispectral Sentinel-2A, and DEM imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 277–289. [Google Scholar] [CrossRef]
- Liu, T.; Abd-Elrahman, A.; Morton, J.; Wilhelm, V.L. Comparing fully convolutional networks, random forest, support vector machine, and patch-based deep convolutional neural networks for object-based wetland mapping using images from small unmanned aircraft system. GISci. Remote Sens. 2018, 55, 243–264. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Belgiu, M.; Drăgut, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; White, J.C. Characterizing stand-level forest canopy cover and height using Landsat time series, samples of airborne LiDAR, and the Random Forest algorithm. ISPRS J. Photogramm. Remote Sens. 2015, 101, 89–101. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Tian, X.; Li, Z.; Su, Z.; Chen, E.; van der Tol, C.; Li, X.; Guo, Y.; Li, L.; Ling, F. Estimating montane forest above-ground biomass in the upper reaches of the Heihe River Basin using Landsat-TM data. Int. J. Remote Sens. 2014, 35, 7339–7362. [Google Scholar] [CrossRef] [Green Version]
- Liang, Z.; Wang, C.; Khan, K.U.J. Application and Comparison of Different Ensemble Learning Machines Combining with a Novel Sampling Strategy for Shallow Landslide Susceptibility Mapping. Stoch. Environ. Res. Risk Assess 2021, 35, 1243–1256. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, L.; Li, S.; Ren, F.; Du, Q. A Hybrid Model Considering Spatial Heterogeneity for Landslide Susceptibility Mapping in Zhejiang Province, China. CATENA 2020, 188, 104425. [Google Scholar] [CrossRef]
- He, Q.; Jiang, Z.; Wang, M.; Liu, K. Landslide and Wildfire Susceptibility Assessment in Southeast Asia Using Ensemble Machine Learning Methods. Remote Sens. 2021, 13, 1572. [Google Scholar] [CrossRef]
- Liu, L.; Ji, M.; Buchroithner, M. Combining Partial Least Squares and the Gradient-Boosting Method for Soil Property Retrieval Using Visible Near-Infrared Shortwave Infrared Spectra. Remote Sens. 2017, 9, 1299. [Google Scholar] [CrossRef] [Green Version]
- Heilongjiang Meteorological Bureau. Available online: http://http://hl.cma.gov.cn/ (accessed on 10 March 2021).
- Neumann, T.; Martino, A.; Markus, T.; Bae, S.; Bock, M.; Brenner, A.; Brunt, K.; Cavanaugh, J.; Fernandes, S.; Hancock, D.; et al. The Ice, Cloud, and Land Elevation Satellite-2 Mission: A global geolocated photon product derived from the Advanced Topographic Laser Al-timeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef] [PubMed]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Neuenschwander, A.L. Ice, Cloud, and Land Elevation Satellite-2 Algorithm Theoretical Basis Document for Land—Vegetation Along-Track Products. Available online: https://icesat-2.gsfc.nasa.gov/sites/default/files/files/ATL08_15June2018.pdf (accessed on 20 May 2021).
- Day, F.P.; Monk, C.D. Vegetation patterns on a southern Appalachian watershed. Ecology 1974, 55, 1064–1074. [Google Scholar] [CrossRef] [Green Version]
- Ying, W.; Wanxing, Z.; Liqiong, Z.; Jing, W. Analysis of correlation between terrain and forest spatial distribution based on DEM. J. Northeast For. Univ. 2012, 11, 96–98. [Google Scholar]
- Zhang, J.; Liu, J.; Zhai, L.; Hou, W. Implementation of Geographical Conditions Monitoring in Beijing-Tianjin-Hebei, China. ISPRS Int. J. Geo-Inf. 2016, 5, 89. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Cai, Y. The application of the national geographic census results in quality inspection of basic surveying and mapping. Geomat. Spat. Inform. Technol. 2016, 39, 139–145. [Google Scholar]
- Yang, R.; Dong, C.; Zhang, Y. Method of population spatialization under the support of geographic national conditions data. Sci. Surv. Mapp. 2017, 42, 76–81. [Google Scholar]
- Fu, R.; Fan, Z.J. Analysis on the Error of the Data Processing and Quality Control in First Survey of National Geographical Conditions. Geomat. Spat. Inform. Technol. 2015, 38, 118–122. [Google Scholar]
- Li, H.; Song, S.; Wang, G.; Gu, J. Comprehensive statistical analysis study based on national geographic condition survey data: The case of Bei’an agricultural farmland as the pilot area. Geomat. Spat. Inform. Technol. 2014, 37, 137–139. [Google Scholar]
- Wu, C.; Venevsky, S.; Sitch, S.; Yang, Y.; Wang, M.; Wang, L.; Gao, Y. Present-day and future contribution of climate and fires to vegetation composition in the boreal forest of China. Ecosphere 2017, 8, e01917. [Google Scholar] [CrossRef] [Green Version]
- Mandianpari, M.; Salehi, B.; Mohammadimanesh, F.; Motagh, M. Random forest wetland classification using ALOS-2 L-band, RADARSAT-2 C-band, and TerraSAR-X imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 13–31. [Google Scholar] [CrossRef]
- Tian, S.; Zhang, X.; Tian, J.; Sun, Q. Random Forest Classification of Wetland Landcovers from Multi-Sensor Data in the Arid Region of Xinjiang, China. Remote Sens. 2016, 8, 954. [Google Scholar] [CrossRef] [Green Version]
- Dong, J.W.; Xiao, X.M.; Sheldon, S.; Biradar, C.; Duong, N.D.; Hazarika, M. A comparison of forest cover maps in Mainland Southeast Asia from multiple sources: PALSAR, MERIS, MODIS and FRA. Remote Sens. Environ. 2012, 127, 60–73. [Google Scholar] [CrossRef]
- Shao, Z.; Yang, K.; Zhou, W. Performance Evaluation of Single-Label and Multi-Label Remote Sensing Image Retrieval Using a Dense Labeling Dataset. Remote Sens. 2018, 10, 964. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Niu, Z.; Liang, X.; Li, Z.; Huang, N.; Gao, S.; Wang, C.; Muhammad, S. Geostatistical modeling using LiDAR-derived prior knowledge with SPOT-6 data to estimate temperate forest canopy cover and above-ground biomass via stratified random sampling. Int. J. Appl. Earth Obs. Geoinf. 2015, 41, 88–98. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D.; Paramanik, S. Canopy Height Estimation Using Sentinel Series Images through Machine Learning Models in a Mangrove Forest. Remote Sens. 2020, 12, 1519. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sens. Environ. 2020, 112165. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Xue, W.; Shahabi, H.; Li, S.; Hong, H.; Wang, X.; Bian, H.; Zhang, S.; Pradhan, B.; et al. Modeling Flood Sus-ceptibility Using Data-Driven Approaches of Naïve Bayes Tree, Alternating Decision Tree, and Random Forest Methods. Sci. Total Environ. 2020, 701, 134979. [Google Scholar] [CrossRef] [PubMed]
- Staben, G.; Lucieer, A.; Scarth, P. Modelling LiDAR derived tree canopy height from Landsat TM, ETM+ and OLI satellite im-agery-a machine learning approach. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 666–681. [Google Scholar] [CrossRef]
- Mielcarek, M.; Stereńczak, K.; Khosravipour, A. Testing and evaluating different LiDAR-derived canopy height model gen-eration methods for tree height estimation. Int. J. Appl. Earth Obs. Geoinf. 2018, 71, 132–143. [Google Scholar] [CrossRef]
- Pascual, C.; Cohen, W.; Garcíaabril, A.; Arroyo, L.A.; Valbuena, R.; Martífernández, S.; Manzanera, J.A.; Hill, R.; Rosette, J.; Suárez, J. Mean height and variability of height derived from lidar data and Landsat images relationship. In Proceedings of the International Conference Silvilaser, Edinburgh, UK, 17–19 September 2008. [Google Scholar]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S.J. Large-area mapping of Cana-dian boreal forest cover, height, biomass and other structural attributes using Landsat composites and lidar plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]




| Canopy Height Metrics | Description |
|---|---|
| h_max_canopy | Relative maximum of individual canopy heights. |
| h_mean_canopy | Relative mean of individual canopy heights. |
| h_min_canopy | Relative minimum of individual canopy heights. |
| RH90/RH95/RH98 | Height metrics calculated at 90/95/98 percentiles. |
| Types | Features | Description | Reference |
|---|---|---|---|
| Biophysical Features | LAI | Leaf area index, reflecting the density, structure, and growth of vegetation. | [17] |
| FAPAR | Fraction of absorbed photosynthetically active radiation, representing growth state of vegetation. | [17] | |
| FCOVER | Fraction of vegetation cover, quantifying the spatial extent of vegetation. | [17] | |
| Vegetation Indices | RVI | NIR/R, distinguishing vegetation/non vegetation areas. | [16] |
| EVI | 2.5 × ((NIR-R)/(NIR + 6 × R − 7.5 × B + 1)), analyzing the changes of vegetation, especially describing the differences of vegetation in a specific climate zone. | [16] | |
| DVI | NIR-R, reflecting change of vegetation coverage. | [16] | |
| MSAVI | (2 × NIR + 1 − sqrt((2 × NIR + 1)2 − 8 × (NIR − R)))/2 | [16] | |
| NDVI_B84 | (NIR − R)/(NIR + R) | [17] | |
| NDVI_B85 | (NIR − RE1)/(NIR + RE) | [17] | |
| NDVI_B86 | (NIR − RE2)/(NIR + RE2) | [17] | |
| NDVI_B87 | (NIR − RE3)/(NIR + RE3) | [17] | |
| NDVI_B8A4 | (NIR2 − R)/(NIR2 + R) | [17] | |
| NDVI_B8A5 | (NIR2 − RE1)/(NIR2 + RE) | [17] | |
| NDVI_B8A6 | (NIR2 − RE2)/(NIR2 + RE2) | [17] | |
| NDVI_B8A7 | (NIR2 − RE3)/(NIR2 + RE3) | [17] | |
| Texture Features | ndvi_Contrast | Contrast provided by Grey Level Co-occurrence Matrix, making use of spatial information inherent in images for image classification. | [12] |
| ndvi_Entropy | Entropy provided by Grey Level Co-occurrence Matrix, making use of spatial information inherent in images for image classification. | [12] | |
| ndvi_GLCM Variance | GLCM Variance provided by Grey Level Co-occurrence Matrix, making use of spatial information inherent in images for image classification. | [12] | |
| / | VV | Backscatter value extracted from VV-polarization image, penetrating forest, and interacting with branches. | [12] |
| VH | Backscatter value extracted from VH-polarization image, penetrating forest, and interacting with branches. | [17] | |
| Topographic Information | elevation | Elevation extracted from DEM, closely relating to the distribution and growth of vegetation. | [17] |
| aspect | Aspect extracted from DEM, closely relating to the distribution and growth of vegetation. | [17] | |
| slope | Slope extracted from DEM, closely relating to the distribution and growth of vegetation. | [17] |
| Resolution | 10 m | 30 m | 250 m | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ALS Metric | |||||||||||||||
| R | 0.56 | 0.23 | 0.68 | 0.69 | 0.71 | 0.59 | 0.54 | 0.73 | 0.70 | 0.68 | 0.72 | 0.68 | 0.80 | 0.76 | 0.75 |
| RMSE/m | 3.08 | 3.29 | 2.75 | 2.71 | 2.69 | 2.90 | 2.98 | 2.59 | 2.64 | 2.87 | 2.21 | 2.45 | 1.98 | 2.10 | 2.18 |
| Types | Training Samples | Validation Samples | Total |
|---|---|---|---|
| Whole forest | 2117 | 530 | 2647 |
| Coniferous forest | 292 | 74 | 366 |
| Broadleaf forest | 1028 | 258 | 1286 |
| Mixed forest | 796 | 199 | 995 |
| Types | Number of Samples | R | RMSE (m) |
|---|---|---|---|
| CF | 1121 | 0.67 | 3.16 |
| BF | 2980 | 0.50 | 3.34 |
| MF | 323 | 0.61 | 3.31 |
| CF | BF | MF | |
|---|---|---|---|
| Vegetation Indices | 0.45 | 0.67 | 0.57 |
| Topographic Information | 0.21 | 0.33 | 0.18 |
| Biophysical Variables | 0.13 | 0 | 0.10 |
| Texture Features | 0.09 | 0 | 0.08 |
| VV&VH | 0.12 | 0 | 0.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, Z.; Xu, H.; Xing, Y.; Gong, W.; Chen, G.; Yang, S. Forest Canopy Height Mapping by Synergizing ICESat-2, Sentinel-1, Sentinel-2 and Topographic Information Based on Machine Learning Methods. Remote Sens. 2022, 14, 364. https://doi.org/10.3390/rs14020364
Xi Z, Xu H, Xing Y, Gong W, Chen G, Yang S. Forest Canopy Height Mapping by Synergizing ICESat-2, Sentinel-1, Sentinel-2 and Topographic Information Based on Machine Learning Methods. Remote Sensing. 2022; 14(2):364. https://doi.org/10.3390/rs14020364
Chicago/Turabian StyleXi, Zhilong, Huadong Xu, Yanqiu Xing, Weishu Gong, Guizhen Chen, and Shuhang Yang. 2022. "Forest Canopy Height Mapping by Synergizing ICESat-2, Sentinel-1, Sentinel-2 and Topographic Information Based on Machine Learning Methods" Remote Sensing 14, no. 2: 364. https://doi.org/10.3390/rs14020364
APA StyleXi, Z., Xu, H., Xing, Y., Gong, W., Chen, G., & Yang, S. (2022). Forest Canopy Height Mapping by Synergizing ICESat-2, Sentinel-1, Sentinel-2 and Topographic Information Based on Machine Learning Methods. Remote Sensing, 14(2), 364. https://doi.org/10.3390/rs14020364









