On the Sensitivity of a Ground-Based Tropospheric Lidar to Aitken Mode Particles in the Upper Troposphere
Abstract
1. Introduction
2. Materials and Methods
2.1. Lidar LFA IF-USP
2.2. Lidar Signal Simulation
2.3. Detection Algorithm
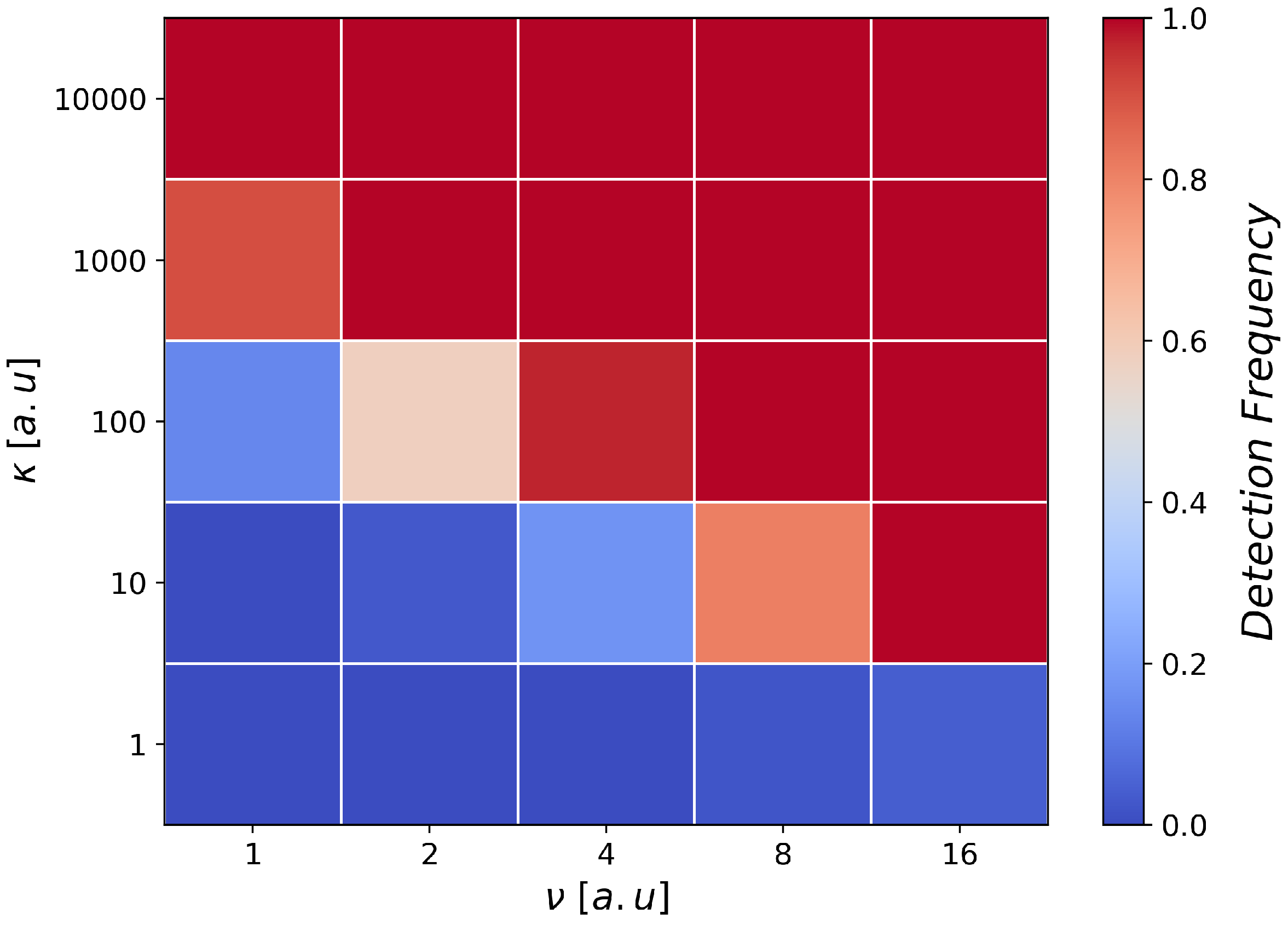
2.4. Sensitivity Experiments
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liou, K.N. Influence of Cirrus Clouds on Weather and Climate Processes: A Global Perspective. Mon. Weather Rev. 1986, 114, 1167–1199. [Google Scholar] [CrossRef]
- Betts, A.K.; Köhler, M.; Zhang, Y. Comparison of river basin hydrometeorology in ERA-Interim and ERA-40 reanalyses with observations. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Collow, A.B.M.; Miller, M.A. The Seasonal Cycle of the Radiation Budget and Cloud Radiative Effect in the Amazon Rain Forest of Brazil. J. Clim. 2016, 29, 7703–7722. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
- Zemp, D.C.; Schleussner, C.F.; Barbosa, H.M.J.; Van der Ent, R.J.; Donges, J.F.; Heinke, J.; Sampaio, G.; Rammig, A. On the importance of cascading moisture recycling in South America. Atmos. Chem. Phys. Discuss. 2014, 14, 17479–17526. [Google Scholar] [CrossRef]
- Marengo, J. On the hydrological cycle of the Amazon Basin: A historical review and current state-of-the-art. Rev. Bras. Meteorol. 2006, 21, 1–19. [Google Scholar]
- Arraut, J.M.; Nobre, C.; Barbosa, H.M.J.; Obregon, G.; Marengo, J. Aerial Rivers and Lakes: Looking at Large-Scale Moisture Transport and Its Relation to Amazonia and to Subtropical Rainfall in South America. J. Clim. 2012, 25, 543–556. [Google Scholar] [CrossRef]
- Davidson, E.A.; de Araújo, A.C.; Artaxo, P.; Balch, J.K.; Brown, I.F.; Bustamante, M.M.C.; Coe, M.T.; DeFries, R.S.; Keller, M.; Longo, M.; et al. The Amazon basin in transition. Nature 2012, 481, 321–328. [Google Scholar] [CrossRef]
- Fu, R.; Yin, L.; Li, W.; Arias, P.A.; Dickinson, R.E.; Huang, L.; Chakraborty, S.; Fernandes, K.; Liebmann, B.; Fisher, R.; et al. Increased dry-season length over southern Amazonia in recent decades and its implication for future climate projection. Proc. Natl. Acad. Sci. USA 2013, 110, 18110–18115. [Google Scholar] [CrossRef]
- Artaxo, P.; Rizzo, L.V.; Brito, J.F.; Barbosa, H.M.J.; Arana, A.; Sena, E.T.; Cirino, G.G.; Bastos, W.; Martin, S.T.; Andreae, M.O.; et al. Atmospheric aerosols in Amazonia and land use change: From natural biogenic to biomass burning conditions. Faraday Discuss. 2013, 165, 203. [Google Scholar] [CrossRef]
- Baars, H.; Ansmann, A.; Althausen, D.; Engelmann, R.; Heese, B.; Müller, D.; Artaxo, P.; Paixao, M.; Pauliquevis, T.; Souza, R. Aerosol profiling with lidar in the Amazon Basin during the wet and dry season. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Videla, F.C.; Barnaba, F.; Angelini, F.; Cremades, P.; Gobbi, G.P. The relative role of Amazonian and non-Amazonian fires in building up the aerosol optical depth in South America: A five year study (2005–2009). Atmos. Res. 2013, 122, 298–309. [Google Scholar] [CrossRef]
- Gatti, L.V.; Basso, L.S.; Miller, J.B.; Gloor, M.; Gatti Domingues, L.; Cassol, H.L.; Tejada, G.; Aragão, L.E.; Nobre, C.; Peters, W.; et al. Amazonia as a carbon source linked to deforestation and climate change. Nature 2021, 595, 388–393. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Vásquez, M.; Arias, P.A.; Martínez, J.A.; Espinoza, J.C. Effects of Amazon basin deforestation on regional atmospheric circulation and water vapor transport towards tropical South America. Clim. Dyn. 2020, 54, 4169–4189. [Google Scholar] [CrossRef]
- Agudelo, J.; Arias, P.A.; Vieira, S.C.; Martínez, J.A. Influence of longer dry seasons in the Southern Amazon on patterns of water vapor transport over northern South America and the Caribbean. Clim. Dyn. 2019, 52, 2647–2665. [Google Scholar] [CrossRef]
- Zemp, D.C.; Schleussner, C.F.; Barbosa, H.M.J.; Rammig, A. Deforestation effects on Amazon forest resilience. Geophys. Res. Lett. 2017, 44, 6182–6190. [Google Scholar] [CrossRef]
- Nobre, C.A.; Sellers, P.J.; Shukla, J. Amazonian Deforestation and Regional Climate Change. J. Clim. 1991, 4, 957–988. [Google Scholar] [CrossRef]
- Laurance, W.F. Gaia’s Lungs: Are rainforests inhaling Earth’s excess carbon dioxide? Nat. Hist. 1999, 108, 96. [Google Scholar]
- Correia, A.; Sena, E.; Dias, M.; Koren, I. Preconditioning, aerosols, and radiation control the temperature of glaciation in Amazonian clouds. Commun. Earth Environ. 2021, 2, 168. [Google Scholar] [CrossRef]
- Gunthe, S.S.; King, S.M.; Rose, D.; Chen, Q.; Roldin, P.; Farmer, D.K.; Jimenez, J.L.; Artaxo, P.; Andreae, M.O.; Martin, S.T.; et al. Cloud condensation nuclei in pristine tropical rainforest air of Amazonia: Size-resolved measurements and modeling of atmospheric aerosol composition and CCN activity. Atmos. Chem. Phys. 2009, 9, 7551–7575. [Google Scholar] [CrossRef]
- Franco, M.A.; Ditas, F.; Kremper, L.A.; Machado, L.A.T.; Andreae, M.O.; Araújo, A.; Barbosa, H.M.J.; de Brito, J.F.; Carbone, S.; Holanda, B.A.; et al. Occurrence and growth of sub-50 nm aerosol particles in the Amazonian boundary layer. Atmos. Chem. Phys. 2022, 22, 3469–3492. [Google Scholar] [CrossRef]
- Andreae, M.O. The Aerosol Nucleation Puzzle. Science 2013, 339, 911–912. [Google Scholar] [CrossRef] [PubMed]
- Varanda Rizzo, L.; Roldin, P.; Brito, J.; Backman, J.; Swietlicki, E.; Krejci, R.; Tunved, P.; Petäjä, T.; Kulmala, M.; Artaxo, P. Multi-year statistical and modeling analysis of submicrometer aerosol number size distributions at a rain forest site in Amazonia. Atmos. Chem. Phys. 2018, 18, 10255–10274. [Google Scholar] [CrossRef]
- Wimmer, D.; Buenrostro Mazon, S.; Manninen, H.E.; Kangasluoma, J.; Franchin, A.; Nieminen, T.; Backman, J.; Wang, J.; Kuang, C.; Krejci, R.; et al. Ground-based observation of clusters and nucleation-mode particles in the Amazon. Atmos. Chem. Phys. 2018, 18, 13245–13264. [Google Scholar] [CrossRef]
- Andreae, M.O.; Afchine, A.; Albrecht, R.; Holanda, B.A.; Artaxo, P.; Barbosa, H.M.J.; Borrmann, S.; Cecchini, M.A.; Costa, A.; Dollner, M.; et al. Aerosol characteristics and particle production in the upper troposphere over the Amazon Basin. Atmos. Chem. Phys. 2018, 18, 921–961. [Google Scholar] [CrossRef]
- Wang, J.; Krejci, R.; Giangrande, S.; Kuang, C.; Barbosa, H.M.J.; Brito, J.; Carbone, S.; Chi, X.; Comstock, J.; Ditas, F.; et al. Amazon boundary layer aerosol concentration sustained by vertical transport during rainfall. Nature 2016, 539, 416–419. [Google Scholar] [CrossRef]
- Kupc, A.; Williamson, C.J.; Hodshire, A.L.; Kazil, J.; Ray, E.; Bui, T.P.; Dollner, M.; Froyd, K.D.; McKain, K.; Rollins, A.; et al. The potential role of organics in new particle formation and initial growth in the remote tropical upper troposphere. Atmos. Chem. Phys. 2020, 20, 15037–15060. [Google Scholar] [CrossRef]
- Martin, S.T.; Artaxo, P.; Machado, L.A.T.; Manzi, A.O.; Souza, R.A.F.; Schumacher, C.; Wang, J.; Andreae, M.O.; Barbosa, H.M.J.; Fan, J.; et al. Introduction: Observations and Modeling of the Green Ocean Amazon (GoAmazon2014/5). Atmos. Chem. Phys. 2016, 16, 4785–4797. [Google Scholar] [CrossRef]
- Wendisch, M.; Pöschl, U.; Andreae, M.O.; Machado, L.A.T.; Albrecht, R.; Schlager, H.; Rosenfeld, D.; Martin, S.T.; Abdelmonem, A.; Afchine, A.; et al. ACRIDICON–CHUVA Campaign: Studying Tropical Deep Convective Clouds and Precipitation over Amazonia Using the New German Research Aircraft HALO. Bull. Am. Meteorol. Soc. 2016, 97, 1885–1908. [Google Scholar] [CrossRef]
- Baars, H.; Ansmann, A.; Althausen, D.; Engelmann, R.; Artaxo, P.; Pauliquevis, T.; Souza, R. Further evidence for significant smoke transport from Africa to Amazonia. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Kulmala, M.; Asmi, A.; Lappalainen, H.K.; Baltensperger, U.; Brenguier, J.L.; Facchini, M.C.; Hansson, H.C.; Hov, Ø.; O’Dowd, C.D.; Pöschl, U.; et al. General overview: European Integrated project on Aerosol Cloud Climate and Air Quality interactions (EUCAARI); integrating aerosol research from nano to global scales. Atmos. Chem. Phys. 2011, 11, 13061–13143. [Google Scholar] [CrossRef]
- Martin, S.T.; Andreae, M.O.; Althausen, D.; Artaxo, P.; Baars, H.; Borrmann, S.; Chen, Q.; Farmer, D.K.; Guenther, A.; Gunthe, S.S.; et al. An overview of the Amazonian Aerosol Characterization Experiment 2008 (AMAZE-08). Atmos. Chem. Phys. 2010, 10, 11415–11438. [Google Scholar] [CrossRef]
- Marenco, F.; Johnson, B.; Langridge, J.M.; Mulcahy, J.; Benedetti, A.; Remy, S.; Jones, L.; Szpek, K.; Haywood, J.; Longo, K.; et al. On the vertical distribution of smoke in the Amazonian atmosphere during the dry season. Atmos. Chem. Phys. 2016, 16, 2155–2174. [Google Scholar] [CrossRef]
- Barbosa, H.M.J.; Barja, B.; Pauliquevis, T.; Gouveia, D.A.; Artaxo, P.; Cirino, G.G.; Santos, R.M.N.; Oliveira, A.B. A permanent Raman lidar station in the Amazon: Description, characterization, and first results. Atmos. Meas. Tech. 2014, 7, 1745–1762. [Google Scholar] [CrossRef]
- Holben, B.; Eck, T.; Slutsker, I.; Tanré, D.; Buis, J.; Setzer, A.; Vermote, E.; Reagan, J.; Kaufman, Y.; Nakajima, T.; et al. AERONET—A Federated Instrument Network and Data Archive for Aerosol Characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Licel. Licel PM-HV Photomultiplier Module R9880U—Manual; Licel GmbH: Berlin, Germany, 2022; Available online: https://licel.com/manuals/pmtmanual.pdf (accessed on 28 July 2022).
- Whiteman, D.N. Examination of the traditional Raman lidar technique. I. Evaluating the temperature-dependent lidar equations. Appl. Opt. 2003, 42, 2571–2592. [Google Scholar] [CrossRef]
- Bucholtz, A. Rayleigh-scattering calculations for the terrestrial atmosphere. Appl. Opt. 1995, 34, 2765–2773. [Google Scholar] [CrossRef]
- Bodhaine, B.A.; Wood, N.B.; Dutton, E.G.; Slusser, J. On Rayleigh Optical Depth Calculations. J. Atmos. Ocean. Technol. 1999, 16, 1854–1861. [Google Scholar] [CrossRef]
- Anderson, G.; Clough, S.; Kneizys, F.; Chetwynd, J.; Shettle, E. AFGL Atmospheric Constituent Profiles (0.120 km); Tech. Report AFGL-TR-0208, Environmental Research Papers, No. 954; Air Force Geophysics Laboratory, Hanscom AFB: Bedford, MA, USA, 1986; Available online: https://apps.dtic.mil/sti/pdfs/ADA175173.pdf (accessed on 28 July 2022).
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations—description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Smirnov, A.; Sinyuk, A.; Schafer, J.; Giles, D.; Dubovik, O. Aeronet’s Version 2.0 quality assurance criteria. In Proceedings of the SPIE Asia-Pacific Remote Sensing, Goa, India, 13–17 November 2006; Volume 6408, pp. 134–147. [Google Scholar] [CrossRef]
- Klett, J.D. Lidar inversion with variable backscatter/extinction ratios. Appl. Opt. 1985, 24, 1638–1643. [Google Scholar] [CrossRef]
- Fernald, F.G. Analysis of atmospheric lidar observations: Some comments. Appl. Opt. 1984, 23, 652–653. [Google Scholar] [CrossRef] [PubMed]
- Gouveia, D.A.; Barja, B.; Barbosa, H.M.J.; Seifert, P.; Baars, H.; Pauliquevis, T.; Artaxo, P. Optical and geometrical properties of cirrus clouds in Amazonia derived from 1 year of ground-based lidar measurements. Atmos. Chem. Phys. 2017, 17, 3619–3636. [Google Scholar] [CrossRef]
- Rocadenbosch, F.; Frasier, S.; Kumar, D.; Lange Vega, D.; Gregorio, E.; Sicard, M. Backscatter Error Bounds for the Elastic Lidar Two-Component Inversion Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4791–4803. [Google Scholar] [CrossRef]
- Whiteman, D.N.; Demoz, B.; Rush, K.; Schwemmer, G.; Gentry, B.; Girolamo, P.D.; Comer, J.; Veselovskii, I.; Evans, K.; Melfi, S.H.; et al. Raman Lidar Measurements during the International H2O Project. Part I: Instrumentation and Analysis Techniques. J. Atmos. Ocean. Technol. 2006, 23, 157–169. [Google Scholar] [CrossRef]
- Torres, O.; Jethva, H.; Bhartia, P.K. Retrieval of Aerosol Optical Depth above Clouds from OMI Observations: Sensitivity Analysis and Case Studies. J. Atmos. Sci. 2012, 69, 1037–1053. [Google Scholar] [CrossRef]
- Thorsen, T.J.; Ferrare, R.A.; Hostetler, C.A.; Vaughan, M.A.; Fu, Q. The impact of lidar detection sensitivity on assessing aerosol direct radiative effects. Geophys. Res. Lett. 2017, 44, 9059–9067. [Google Scholar] [CrossRef]
- Winker, D.M.; Vaughan, M.A.; Omar, A.; Hu, Y.; Powell, K.A.; Liu, Z.; Hunt, W.H.; Young, S.A. Overview of the CALIPSO Mission and CALIOP Data Processing Algorithms. J. Atmos. Ocean. Technol. 2009, 26, 2310–2323. [Google Scholar] [CrossRef]
- Winker, D.M.; Pelon, J.; Coakley, J.A.; Ackerman, S.A.; Charlson, R.J.; Colarco, P.R.; Flamant, P.; Fu, Q.; Hoff, R.M.; Kittaka, C.; et al. The CALIPSO Mission: A Global 3D View of Aerosols and Clouds. Bull. Am. Meteorol. Soc. 2010, 91, 1211–1230. [Google Scholar] [CrossRef]
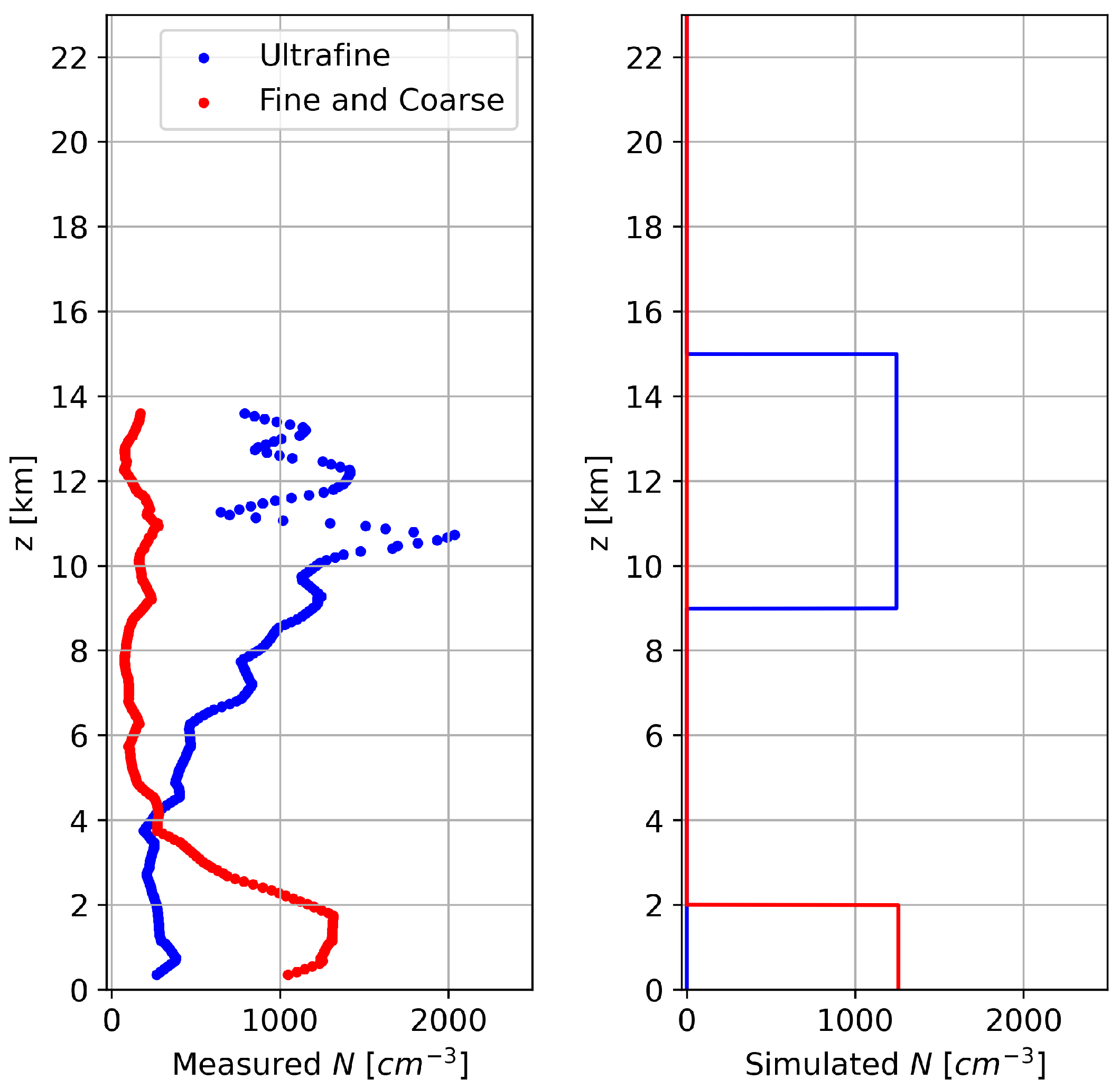
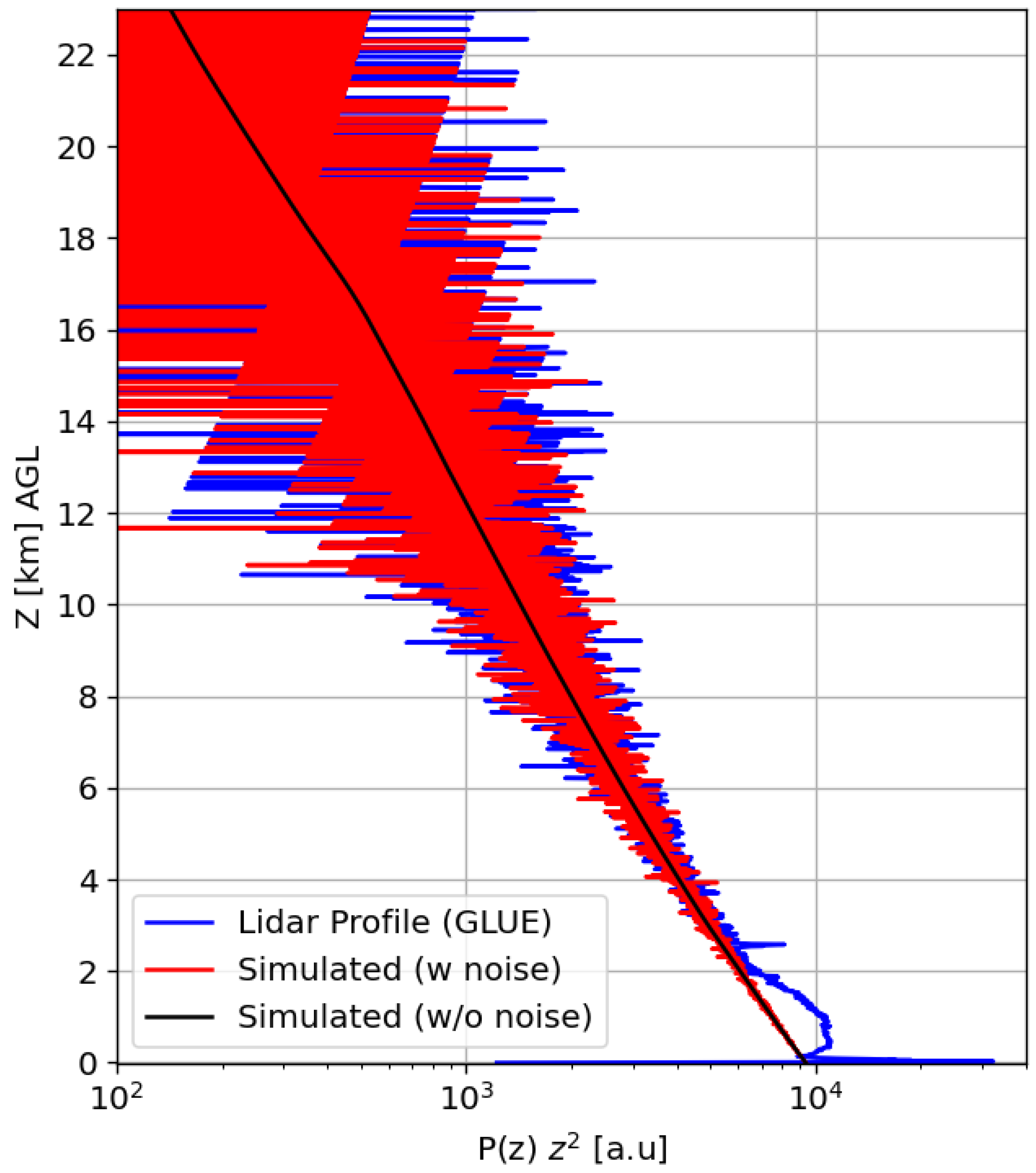
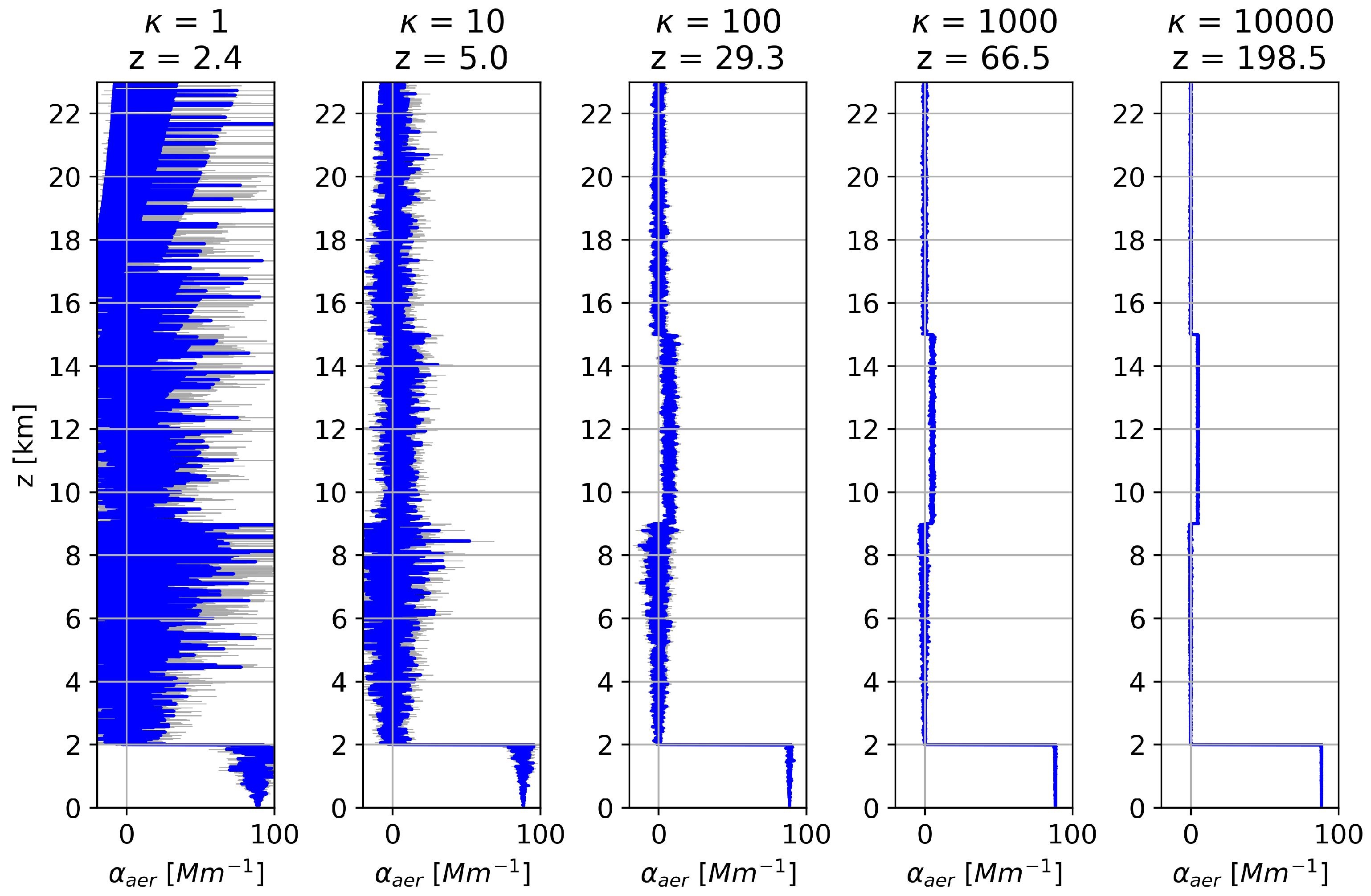
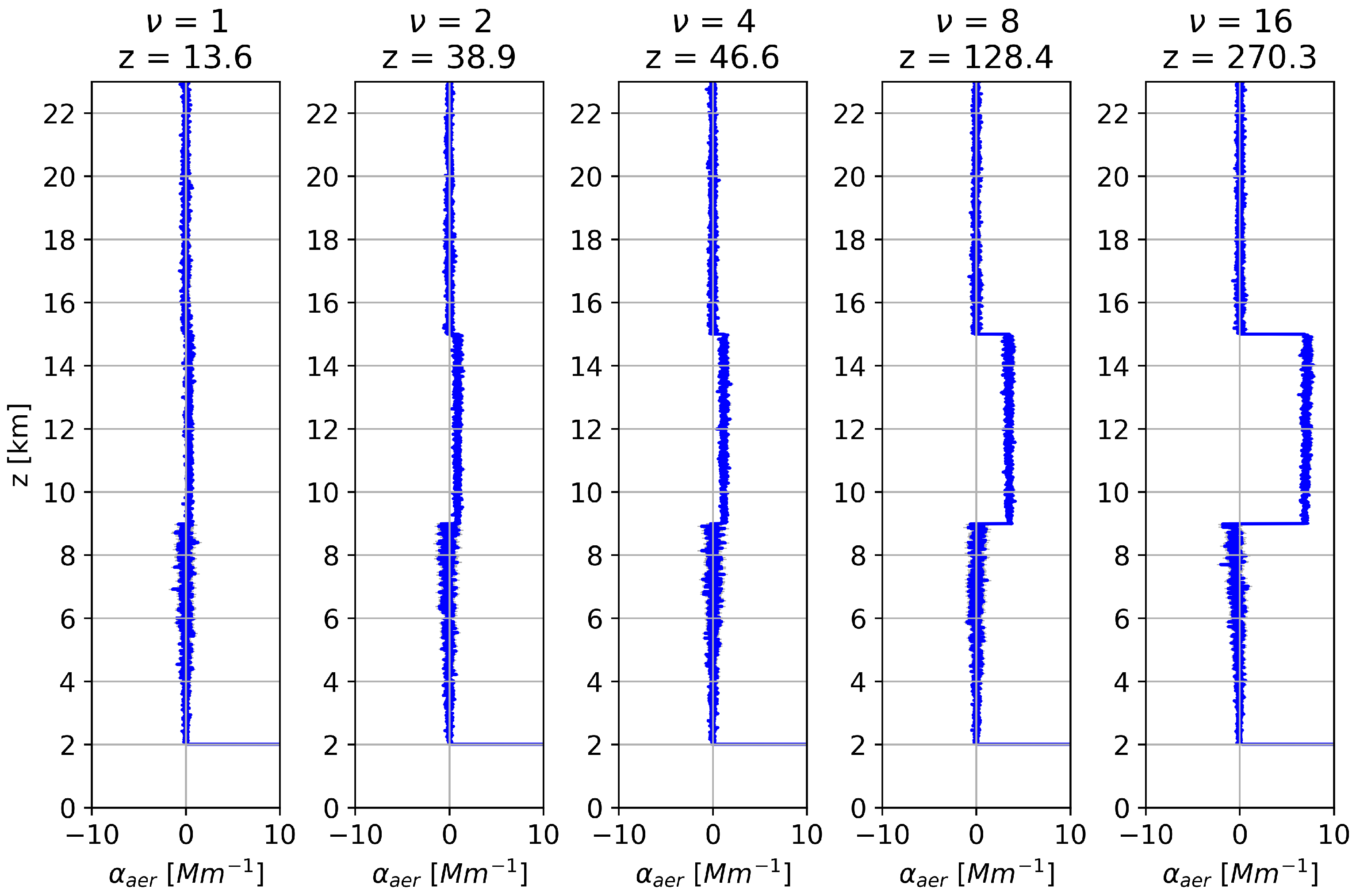


| Parameters | Upper Troposphere | Planetary Boundary Layer |
|---|---|---|
| R (nm) | 23 | 85 and 236 |
| 1.6 | 1.5 and 2.4 | |
| ℜ (440 nm) | [1.40 to 1.56] | 1.46 |
| ℑ (440 nm) | [0.00052 to 0.00944] | 0.0021 |
| L (sr) | [20.2 to 23.5] | 60.3 |
| Layer Top (km) | 15 | 2 |
| Layer Base (km) | 9 | 0 |
| Number Conc. (cm) | N | N and 4.9 |
| Mass Conc. (g m) | 0.25 | 11.2 and 16.0 |
| Extinction (Mm) | 0.37 | 88.4 |
| AOD | 0.0022 | 0.18 |
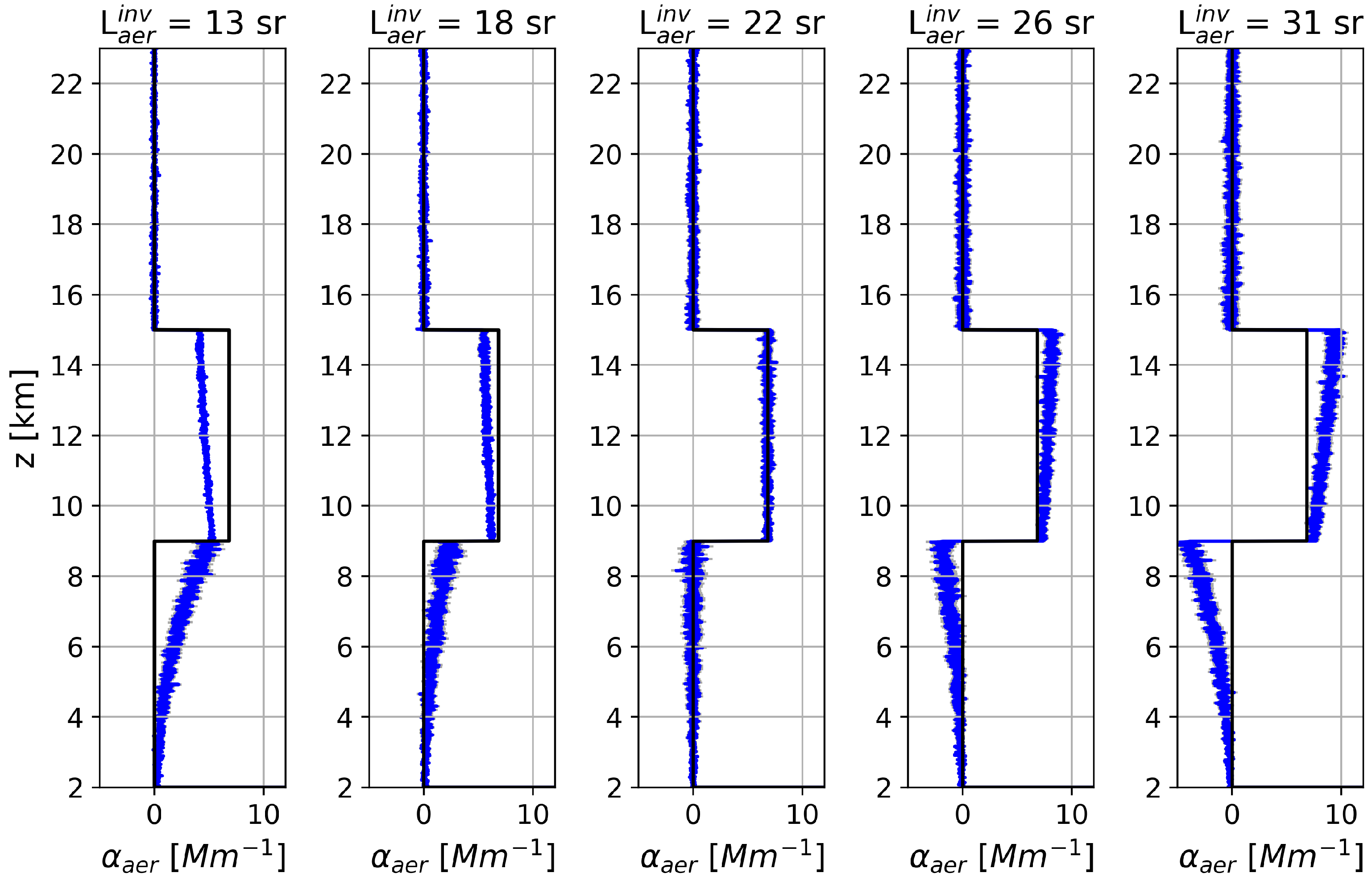
| L (sr) | 13 | 18 | 22 | 26 | 31 |
|---|---|---|---|---|---|
| AOD | 0.02791 | 0.03495 | 0.04105 | 0.04629 | 0.05112 |
| 0.00008 | 0.00010 | 0.00011 | 0.00013 | 0.00014 | |
| z-score | 346 | 351 | 361 | 365 | 368 |
| Bias AOD (%) | 0 | 13 | 25 | ||
| Bias (%) | 0 | 14 | 23 | ||
| Bias z-score (%) | 0 | 1.1 | 1.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, M.T.; Guerrero-Rascado, J.L.; Correia, A.L.; Gouveia, D.A.; Barbosa, H.M.J. On the Sensitivity of a Ground-Based Tropospheric Lidar to Aitken Mode Particles in the Upper Troposphere. Remote Sens. 2022, 14, 4913. https://doi.org/10.3390/rs14194913
Silva MT, Guerrero-Rascado JL, Correia AL, Gouveia DA, Barbosa HMJ. On the Sensitivity of a Ground-Based Tropospheric Lidar to Aitken Mode Particles in the Upper Troposphere. Remote Sensing. 2022; 14(19):4913. https://doi.org/10.3390/rs14194913
Chicago/Turabian StyleSilva, Matheus T., Juan Luis Guerrero-Rascado, Alexandre L. Correia, Diego A. Gouveia, and Henrique M. J. Barbosa. 2022. "On the Sensitivity of a Ground-Based Tropospheric Lidar to Aitken Mode Particles in the Upper Troposphere" Remote Sensing 14, no. 19: 4913. https://doi.org/10.3390/rs14194913
APA StyleSilva, M. T., Guerrero-Rascado, J. L., Correia, A. L., Gouveia, D. A., & Barbosa, H. M. J. (2022). On the Sensitivity of a Ground-Based Tropospheric Lidar to Aitken Mode Particles in the Upper Troposphere. Remote Sensing, 14(19), 4913. https://doi.org/10.3390/rs14194913







