Abstract
The stability and accuracy of the on-orbit radiometric calibration of hyperspectral sensors are prerequisites for the quantitative application of satellite hyperspectral data. The Zhuhai-1 micro-nano satellite constellation is composed of eight hyperspectral satellite missions. The Orbita Hyperspectral Sensor (OHS) on board each satellite has a gradient filter spectroscopic design. When observing the Earth, eight integration stages can be set for each band according to different lighting conditions. Due to high manufacturing costs, OHSs are not equipped with on-board calibration devices. Therefore, it is very difficult to accurately calibrate OHSs for all of the integration stages. On the other hand, it is extremely important to ensure radiometric consistency between different OHSs within the Zhuhai-1 micro-nano satellite constellation. To carry out the rapid radiometric calibration of the Zhuhai-1 constellation, an on-orbit radiometric calibration model considering all of the integration stages related to hyperspectral sensors was built based on the BOA reflectance and atmosphere parameters published by the Committee on Earth Observation Satellites (CEOS) radiometric calibration network (RadCalNet). The RadCalNet product was used to derive the TOA radiance base in the Second Simulation of the Satellite Signal in the Solar Spectrum (6S) radiative transfer (RT) model. In this paper, we analyzed the radiometric stability of the same sensor and the consistency of different calibration results regarding four RadCalNet sites, and the on-orbit radiometric performance evaluation of OHSs was also carried out. The data retrieved from OHSs regarding hyperspectral surface reflectance were preliminarily validated using site-synchronous surface reflectance measurements.
1. Introduction
In recent years, with the gradual implementation of China’s commercial space policy, several Chinese commercial remote sensing satellites have been launched by commercial companies. The Zhuhai-1 constellation from Orbita, Zhuhai, China is composed of 12 satellite missions, including eight hyperspectral satellites. The first four satellites were launched on 26 April 2018, and the remaining four satellites were launched on 19 September 2019. The Orbita Hyperspectral Sensor (OHS) on board each micro-nano satellite has similar electro-optics, with three complementary metal oxide semiconductor (CMOS) detectors designed with eight integration stages. To maintain reduced costs, none of the satellites are equipped with on-board calibrators (OBCs). Therefore, the combination of multiple CMOS detectors and multiple integration level settings makes the on-orbit radiometric calibration of the Zhuhai-1 micro-nano hyperspectral satellite constellation extremely complex and difficult. The sensor parameters are shown in Table 1.

Table 1.
Sensor parameters of OHS.
Zhuhai-1 constellation calibration and validation (Cal&Val) tasks are used to calibrate all of the CMOS detectors for all of the integration stages. In addition, it is essential to ensure that data from different OHSs in the whole Zhuhai-1 constellation are of high quality and consistency. Vicarious calibration [1] (VC) based on site campaigns is one of the current state-of-the-art radiometric calibration methods used for optical satellite sensors. Several calibration sites (e.g., Dunhuang, Baotou) are located in China and have been regularly used for the radiometric calibration of Chinese satellites. However, site campaigns are so expensive and labor-intensive that the frequent VC of all of the Zhuhai-1 OHSs is an impossible task. The radiometric calibration of similar satellite constellations, such as the SkySat constellation from Planet, is conducted using the Libya site without field measurements [2]. The bottom of atmosphere (BOA) data used to simulate TOA values are generated from Sentinel-2 BOA reflectance time series.
Cross-calibration [3] is another important and widely used method that can be used for the radiometric calibration of most optical sensors. Usually, simultaneous or near-simultaneous observations from different satellite sensors are used to derive the calibration coefficients through band-by-band comparisons. As site measurement is not required, it can be used at high frequencies and is associated with low costs. For example, the Dove constellation is calibrated using cross-calibration with RapidEye, and it is validated using cross-calibration with Landsat8 and Sentinel, with lunar, and with RadCalNet site measurements. The choice of high-precision reference sensors is critical for cross-calibration [4]. Regarding hyperspectral sensors on board the Zhuhai-1 constellation, it is very difficult to match suitable reference bands for all of the calibrated bands.
The radiometric calibration network [5,6] (RadCalNet) was initiated by the Working Group on Calibration and Validation (WGCV) of the Committee on Earth Observation Satellites (CEOS) in 2014. Moreover, the ground observation data of RadCalNet have been shown to be accurate and effective [7,8], and the data can be widely used in the radiometric calibration of satellite sensors such as visible light and near-infrared sensors [9,10,11]. The aim of RadCalNet is to provide a time-continuous, SI-traceable top-of-atmosphere (TOA) reflectance product to satellite operators, at a 10 nm spectral sampling interval, in the spectral range of 380 nm to 2500 nm. Currently, there are five sites involved in RadCalNet, which are located in the United States, France, Namibia, and China. Each site is equipped with automated ground instruments that are used to measure surface and atmospheric parameters for the simulation of TOA reflectance. The uncertainty associated with RadCalNet BOA reflectance, TOA reflectance, and atmosphere parameters is presented in the RadCalNet product. This allows users to understand the error and uncertainty related to RadCalNet-based calibration results. At present, the RadCalNet product, which includes BOA reflectance, TOA reflectance, and atmosphere parameters, has been widely used in the on-orbit radiometric calibration and validation of many optical satellite sensors, such as Landsat-8/OLI [12], Sentinel-2A/2B/MSI [13,14,15], SV-1/MUX [16], ZY-3/MUX [17], etc. As they benefit from time continuity and multi-site collaboration, the RadCalNet product is suitable for use in the on-orbit radiometric calibration of a constellation of identical sensors such as the Zhuhai-1 satellite constellation. The standardization, traceability and high frequency of the RadCalNet product mean it is useful in ensuring radiometric consistency between different satellite measurements.
With the aim of calibrating the Zhuhai-1 satellite constellation with multi-hyperspectral sensors and multi-integration stages, an on-orbit radiometric calibration model considering all of the integration stages of hyperspectral sensors was proposed based on the RadCalNet product (i.e., BOA reflectance and atmosphere parameters) from four sites. In this paper, we analyzed the consistency of the calibration results from different RadCalNet sites, and then, we also conducted the on-orbit radiometric stability evaluation of OHSs. To further validate the reliability of the calibration results, we compared the retrieved hyperspectral reflectance from OHSs with site surface reflectance measurements.
2. Materials and Methods
2.1. Satellite Constellation and RadCalNet Sites
2.1.1. The Zhuhai-1 Constellation and Hyperspectral Sensors
To maintain lower costs, Zhuhai-1 micro-nano satellite hyperspectral sensors have a gradient filter spectroscopic design. Compared to a traditional narrow-band filter, a linear gradient filter has a nearly continuous spectral channel; therefore, a higher spectral resolution can be obtained by using a linear gradient filter to split light. In this study, the camera was composed of three CMOS sensors. Figure 1 shows the splicing method used with this hyperspectral camera. The number of pixels in the sensor was 5056 × 2968, and the pixel size was 4.25 µm. The light in the wavelength range of 400 nm–1000 nm was equally divided into 32 spectral bands (see the spectral response function (SRF) of OHS-F CMOS2 in Figure 2). The specific row position of each spectral band on the sensor was determined using the width of the slit (i.e., area of interest, AOI), and each spectral band used up to eight rows of pixels for eight-level integral imaging. Therefore, we defined eight integration stages of a band as 1 to 8, which were used to adapt to different irradiation stages during imaging. According to changes in the Sun’s altitude angle, four groups of common integration stage configurations were set for the satellite on-orbit operation to achieve optimal imaging under the conditions of different solar incident angles. The integration stage settings in a single CMOS were basically the same, but they were different between different satellites or CMOSs. The spectral assignment of sensor pixel rows is shown in Figure 3. When the hyperspectral camera on board Zhuhai-1 micro-nano satellites observed the Earth in orbit, 32 bands of the sensor along the flight direction of the satellite were sequentially imaged, as shown in Figure 3. The integrated imaging principle of each band of the sensor is shown in Figure 4.
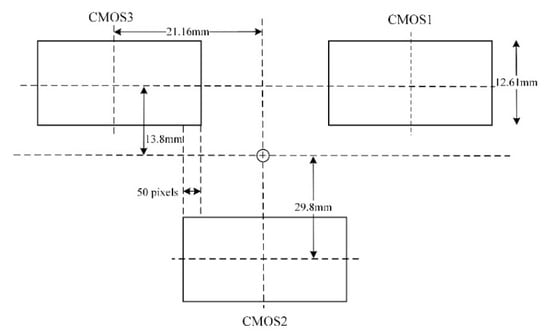
Figure 1.
Focal plane arrangement for the hyperspectral camera. The width of each CMOS image is 50 km, and the inter slice overlap is 50 pixels.
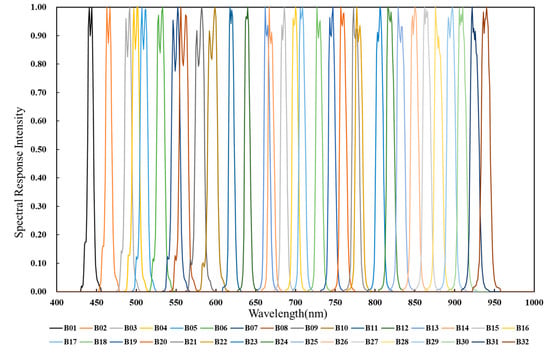
Figure 2.
The spectral response function of OHS-F COMS2 sensor.
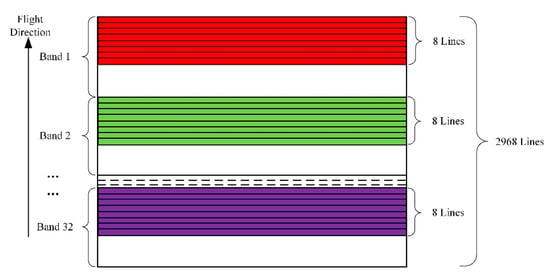
Figure 3.
Sensor spectrum distribution.
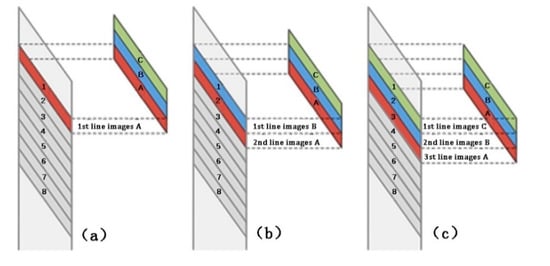
Figure 4.
Integral imaging principle. (a) is the first line of the sensor in a certain spectral band to image object A; (b) is with the movement of the satellite, the first line is to image object B, and the second line is to image object A; (c) is the image of object A with the movement of the satellite. For the movement of the satellite, the first line images object C, the second line images object B, and the third line images object A, and so on, to achieve eight integral images of the same scene in each line.
As is shown in Figure 3, the light wave ranging from 400 nm to 1000 nm was divided into 32 spectral segments on average, and each spectral band accounted for approximately 92 lines on the sensor. Due to low resolution and low signal-to-noise ratio, only eight lines of pixels were used for eight-level integration imaging in each spectral band.
2.1.2. RadCalNet Sites
In this study, we used four RadCalNet sites (i.e., Baotou, Gobabeb, La Crau, and Railroad Valley) [10]. The calibration product (i.e., BOA reflectance and atmosphere parameters) published by RadCalNet was downloaded and processed from December 2019 to December 2021. Detailed information regarding the four RadCalNet sites is shown in Table 2, and the selected regions of interest (ROIs) in the calibration sites are shown in the yellow boxes in Figure 5.

Table 2.
Calibration site information.

Figure 5.
Four RadCalNet sites and corresponding regions of interest.
Figure 6 shows the BOA reflectance provided by RadCalNet (located on website: https://www.radcalnet.org/#!, accessed on 12 July 2022), which was used in this study to simulate the TOA radiance and the atmosphere parameters shown in Table 3. As shown in Figure 6, the BOA reflectance in RVUS is very high: it is higher than 0.4 at 700 nm. The LCFR site has the lowest surface reflectance, and the reflectance of the other two fields (i.e., BTCN and GBNA) falls between these values. In terms of the atmospheric parameters, the threshold of AOD was set to 0.2, which means that the corresponding date of AOD below this threshold value was used in the following calibration procedure.
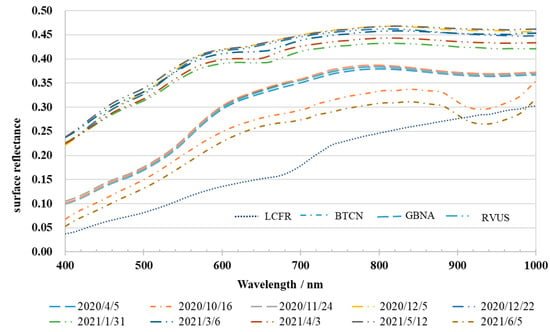
Figure 6.
The BOA reflectance provided by RadCalNet used to calibrate OHS-F CMOS2.

Table 3.
The atmosphere parameters when the satellites pass over the RadCalNet sites.
2.2. Methods
2.2.1. The Proposed Calibration Method for OHS
In the laboratory tests of the OHS before launch, an integrating sphere system was used to evaluate the relationship between the measured counts of the OHS and the integration stages. The sphere’s spectral radiance was varied to test the sensor at different radiance levels. The test results are shown in Figure 7a, which shows that the DN value increased linearly with the increase in the integration stage. We also calculated the ratio of measured counts at integration stages 2–8 to that at integration stage 1, which is shown in Figure 7b. The ratios were approximately constant when the radiance level of the integrating sphere changed. Therefore, assuming the relationship between the measured counts of the OHS and the integral stages was linear, we established the radiometric calibration equation considering different integration stages.
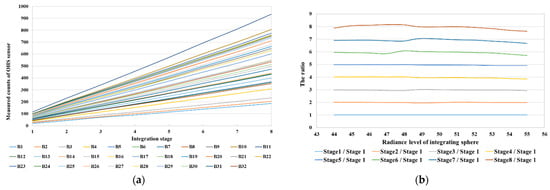
Figure 7.
Laboratory test results regarding the relationship between the measured counts of OHS and integration stages. (a) The change in the measured counts of OHS when the integration stage varied; (b) the ratio between the measured counts at different integration stages (B3).
Regarding OHSs with multiple integral stages, based on the traditional radiometric calibration equation, as shown in Equation (1), a new comprehensive gain is defined as Equation (2). For a specific band of an OHS, assuming is fixed:
where is the physical gain, is the DN value, is the offset in calibration equation, is the integral stage, and is the apparent radiance.
Combining Equations (1) and (2), the radiometric calibration equation for an OHS considering different integral stages is obtained, as shown in Equation (3).
According to the calibration equation shown above, using OHS images with different integration stages and the corresponding ground measurement data provided by RadCalNet, the comprehensive gain of different bands can be solved using the least squares method.
Figure 8 shows the procedures in the calibration method proposed for use with OHSs. As shown in the figure above, the main steps of the proposed calibration method are as follows:
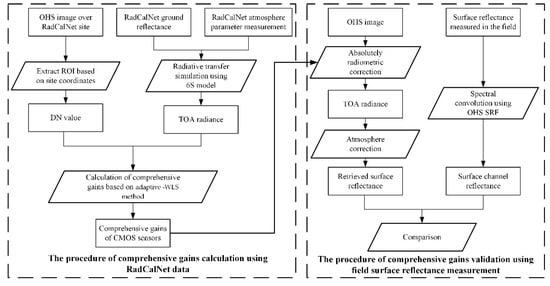
Figure 8.
Flow chart of the proposed calibration method.
- The regions of interest (ROIs) are extracted from OHS images over RadCalNet sites, and the surface reflectance and atmosphere parameters, such as AOD, WCV, and ozone content, are also extracted from the RadCalNet product.
- Then, the Second Simulation of the Satellite Signal in the Solar Spectrum (6S) radiative transfer (RT) model [18] is used to simulate the TOA radiance, which will be used with the DN value to calculate the comprehensive gains.
- An adaptive weighted least squares method is used to solve the comprehensive gains, and then, they will be evaluated. The absolute radiometric correction is carried out using the fitting comprehensive gains to obtain the TOA radiance.
- The atmosphere correction is then conducted to obtain the retrieved surface reflectance, which is compared to the ground measured reflectance. The closer they are, the more accurate the comprehensive gains are.
2.2.2. RadCalNet Data Process
Based on the automatic ground measurement data of four calibration sites provided by RadCalNet, the 6S atmospheric radiative transfer model was used to calculate the at-sensor TOA radiance. The BOA reflectance and atmosphere parameters (i.e., aerosol optical depth, water vapor content, and ozone content) were extracted from the RadCalNet output file based on the satellite overpass time. The RadCalNet ground measurement data, observation geometry parameters, and sensor spectral response function were input into the 6S model to simulate the quantities in the atmospheric radiative transfer equation, which is simplified as the following Equation (4):
where is the upward scattering reflectance generated by the atmosphere, is the surface reflectance, are the solar zenith angle, sensor zenith angle, solar azimuth angle, and sensor azimuth angle, respectively, is the total absorption transmittance of the atmosphere taken into account in both incident and observation directions, is the scattering transmittance in the observation direction, is the scattering transmittance in the incident direction of the solar, and is the hemispherical reflectance of the atmosphere.
Then, the at-sensor radiance (i.e., TOA radiance) is calculated according to the following Equation (5):
where is the correction factor for the distance between the Sun and the Earth, is the TOA reflectance, and is the solar irradiance.
2.2.3. Comprehensive Gain Calculation
Using satellite data with different integration stages acquired on different dates and the corresponding RadCalNet ground measurement data, several groups of , , could be obtained and then used to solve the comprehensive gain by using the adaptive weighted least squares (WLS) method. The cost function is shown as Equation (6):
where is the given weight factor of the k-th sample, N is the number of samples, and is the fitting mean square error, which reflects the fitting effect of the calibration model on the observed values. The smaller the value, the better the fitting effect.
2.2.4. Evaluation Method of Calibration Results
First, we calculated the comprehensive gain corresponding to a certain integration stage individually, assuming the offset in Equation (2) was zero. The standard deviation (SD) of the differences between the comprehensive gains on different dates and the corresponding mean value was calculated, and then, the relative bias (RB) was computed by using the SD divided by the mean comprehensive gain. The RB value was used as the characterization of the stability of calibration results at different sites and different integration stages in the same year. The formulas of SD and RB are shown in the following Equations (7) and (8), respectively:
where j = (1, 2, …, N) represents the index of the calibration results at different sites and different integration stages, represents the j-th comprehensive gain obtained by the j-th calibration, and represents the mean value of multiple comprehensive gains.
The fitting comprehensive gain for a given year was solved through Equation (6) using satellite data and RadCalNet data at different sites and different integration stages. Assuming the comprehensive gain was applicable to all of the integration stages of the CMOS sensor, in this paper, we evaluated the accuracy of the fitting comprehensive gain. The fitting comprehensive gain was applied to the satellite data to obtain the satellite radiance, and the corresponding simulated radiance was calculated using the RadCalNet data. In this paper, we used the average relative difference %RE and root mean square error %RMSE, which are shown in Equations (9) and (10), respectively.
where is the simulated radiance calculated using the RadCalNet data, is the satellite radiance calculated using the fitted comprehensive gain, represents the number of samples, represents different dates, and represents different bands.
In addition, the measured surface reflectance in the field was used to evaluate the fitted comprehensive gains. The radiometric calibration of the satellite image was carried out first, and the atmospheric correction on the radiance image using the 6S radiative transfer model was then carried out to obtain the surface reflectance image. Finally, the reflectance retrieved from the satellite image was compared with ground measured surface reflectance.
3. Results
3.1. Stability Analysis of Multi-Temporal Calibration Results
According to the processing steps described in the previous section, the comprehensive gains of three CMOS sensors on board the OHS-F satellite were calculated. The SD and RB were also calculated using the comprehensive gains of different CMOS sensors on different dates. The stability of the calibration results of each CMOS sensor was analyzed based on these calculation results.
3.1.1. OHS-F CMOS1 Calibration Results and Analysis
Figure 9 shows the comprehensive gains of the CMOS1 sensor in 2020 and 2021. In 2020, the comprehensive gains at the wavelength range of 550 nm to 880 nm had high consistency, and the maximum RB was about 5%. For the bands outside the wavelength range, the RB of different comprehensive gains was more than 10%, especially for the band with the central wavelength of 896 nm. The comprehensive gains for these bands on 22 May, 3 June, and 26 June 2020 were quite different from those for the other two dates, indicating that the radiometric performance stability of these bands was low. In 2021, the consistency between the comprehensive gains at different dates was significantly better than that in 2020, and only the bands with central wavelength greater than 896 nm had relatively low stability. This shows that the radiometric performance of the CMOS1 sensor tended to be more stable in 2021.
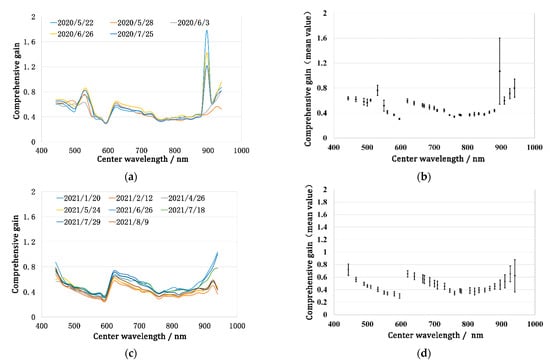
Figure 9.
Calibration results of OHS-F CMOS1. (a) Description of comprehensive gains in 2020; (b) description of averaged value and SD of comprehensive gains in 2020; (c) description of comprehensive gains in 2021; (d) description of averaged value and SD of comprehensive gains in 2021.
3.1.2. OHS-F CMOS2 Calibration Results and Analysis
Figure 10 shows the comprehensive gains of the CMOS2 sensor in 2020 and 2021. In 2020, the consistency between the comprehensive gains on different dates was not very high. The RB of the comprehensive gains for the bands at the wavelength range of 550 nm to 880 nm was basically approximately 15%, while it was up to more than 25% for the bands with central wavelengths outside this wavelength range, indicating that the radiometric stability of the CMOS2 sensor in each band in 2020 was not very good on the whole. In 2021, the consistency between the comprehensive gains on different dates was significantly better than that in 2020. Except for the four bands of 441 nm, 910 nm, 926 nm, and 940 nm, the RB of the comprehensive gains of other bands on different dates was less than 10%, indicating that the radiometric performance of the CMOS2 sensor in 2021 was very stable.
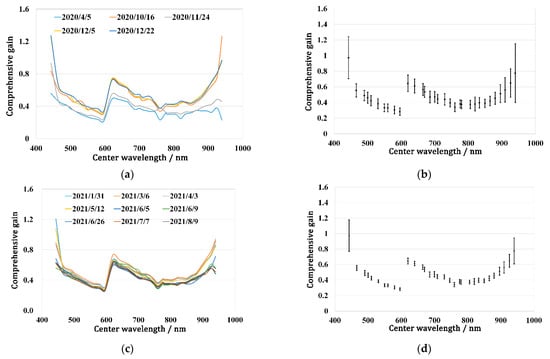
Figure 10.
Calibration results for OHS-F CMOS2. (a) Description of comprehensive gains in 2020; (b) description of averaged value and SD of comprehensive gains in 2020; (c) description of comprehensive gains in 2021; (d) description of averaged value and SD of comprehensive gains in 2021.
3.1.3. OHS-F CMOS3 Calibration Results and Analysis
Figure 11 shows the comprehensive gains of the CMOS3 sensor in 2020 and 2021. In 2020, the RB of the comprehensive gains of the CMOS3 sensor at the wavelength range of 550 nm to 880 nm was basically approximately 10%, while the RB of the comprehensive gains for the bands with central wavelengths outside this wavelength range was higher, with the maximum value exceeding 20%. In 2021, except for the bands of 441 nm, 910 nm, 926 nm, and 940 nm, the RB of the comprehensive gains of the other bands on different dates was about 6%, indicating that the radiometric performance stability of the CMOS3 sensor in 2021 was significantly better than that in 2020.
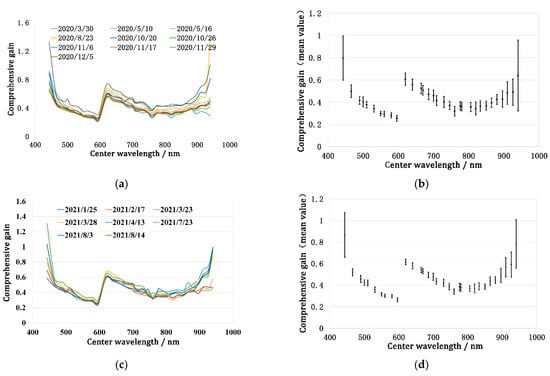
Figure 11.
Calibration results for OHS-F CMOS3. (a) Description of comprehensive gains in 2020; (b) description of averaged value and SD of comprehensive gains in 2020; (c) description of comprehensive gains in 2021; (d) description of averaged value and SD of comprehensive gains in 2021.
It is noted that the radiometric stability of three CMOS sensors on-board the OHS-F satellite in 2020 was lower than that in 2021, which was mainly caused by the great change in radiometric stability in the early stage of the satellite launch. At the same time, the above analysis results also show that the comprehensive gains calculated in different calibration sites and different integral stages had high consistency. Therefore, the use of satellite data in different sites and different integration stages is expected to obtain high-frequency and stable radiometric calibration results, which can more effectively describe the changes in the radiometric performance of satellite sensors and enable the high-frequency calibration of micro-nano satellite constellations.
3.2. Comprehensive Gain Calculation Results
In Section 3.1, the comprehensive gains of different COMS sensors on board the OHS-F satellite calculated using the ground measurement data from different RadCalNet sites were shown, and the consistency of the calibration results and the stability of the sensors’ radiometric performance was analyzed. In this section, the calibration data from different sites on different dates were used to fit the comprehensive gains of three CMOS sensors on board the OHS-F satellite in 2020 and 2021. Taking some bands of CMOS2 as an example, the results are shown in the figure below.
As shown in Figure 12, the adaptive weighted least squares method can be used to eliminate the influence of discrete observation points. Compared to direct linear fitting and simple least squares fitting, the fitting error was the smallest using the adaptive weighted least squares method.
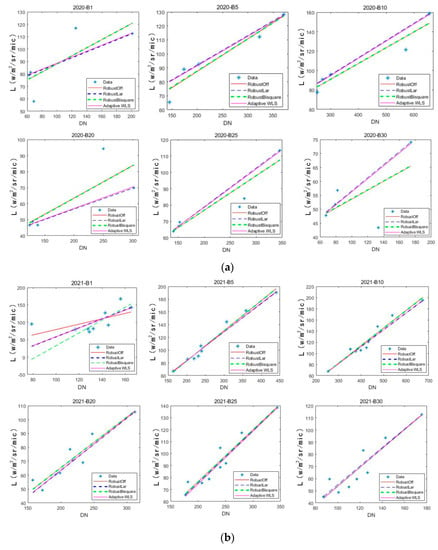
Figure 12.
The radiance and DN value used to fit comprehensive gains for CMOS2. (a) description of 2020; (b) description of 2021.
Figure 13 shows the comprehensive gain fitting results and fitting errors of the CMOS1 sensor on board the OHS-F satellite in 2020 and 2021. It is noted that the overall trend of comprehensive gain in 2020 and 2021 at the wavelength range of 500 nm to 880 nm was very similar, and the gain value was also relatively close. In terms of fitting error, the %RE and %RMSE of these bands were basically within 10%.
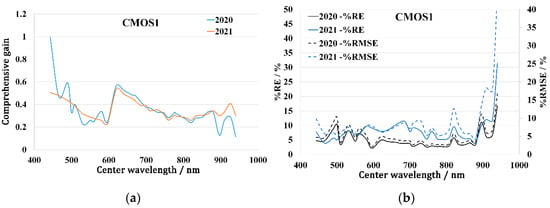
Figure 13.
Comprehensive gain fitting results and fitting errors of OHS-F CMOS1. (a) Description of comprehensive gain fitting results; (b) description of comprehensive gain fitting error.
Figure 14 shows the fitting results and fitting errors of the comprehensive gain of the CMOS2 sensor. The fitting comprehensive gains in 2020 and 2021 were quite different, which was mainly due to the poor radiometric stability of the CMOS2 sensor in 2020 and the large change in the early stage of the launch. In terms of the fitting error, the fitting error of the bands at 443 nm, 760 nm, and 820 nm, and the bands with a central wavelength greater than 910 nm was large, which was basically consistent with the bands with poor stability in the previous analysis.
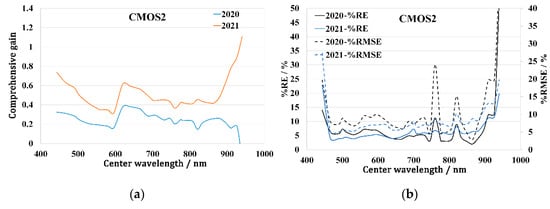
Figure 14.
Comprehensive gain fitting results and fitting errors for OHS-F CMOS2. (a) Description of comprehensive gain fitting results; (b) description of comprehensive gain fitting error.
Figure 15 shows the fitting results and fitting errors of the comprehensive gain of the CMOS3 sensor. The fitting comprehensive gains in 2020 and 2021 basically followed the same trend with the wavelength, and the comprehensive gain of most of the bands was also close in value. In terms of the fitting error, like the CMOS2 sensor, fitting errors greater than 10% were concentrated in the bands of 443 nm, 760 nm, and 820 nm, and in bands with central wavelengths greater than 910 nm.
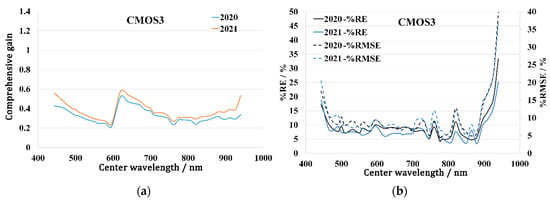
Figure 15.
Comprehensive gain fitting results and fitting errors for OHS-F CMOS3. (a) Description of comprehensive gain fitting results; (b) description of comprehensive gain fitting error.
In summary, the comprehensive gain in 2020 and 2021 based on the least squares fitting was basically the same. The bands with large fitting errors were mainly concentrated in the gas absorption band (such as the bands with central wavelengths near 760 nm) and the bands with low signal-to-noise ratios (such as 443 nm and the bands with central wavelengths greater than 910 nm).
3.3. Validation Using the Ground Measured Reflectance
Based on the above mentioned experimental results, using the 2021 comprehensive gains as the calibration coefficient of the satellite sensor, the satellite data were processed with absolute radiometric correction and atmospheric correction. Then, the satellite reflectance data corresponding to the ground sample points (GSPs) were obtained and compared with the measured surface reflectance of the GSPs. The measured reflectance and retrieved reflectance for each GSP are shown in Figure 16. The solid line represents the measured surface reflectance, and the dotted line indicates the surface reflectance retrieved by satellite data.
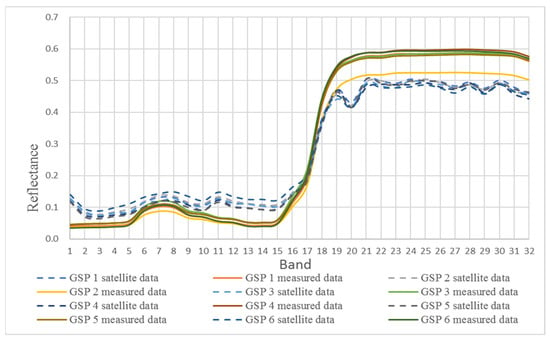
Figure 16.
The satellite reflectance retrieved from OHS-F CMOS2 image and corresponding ground synchronous surface reflectance.
It is noted that the surface reflectance retrieved from satellite data was visually consistent with the measured ground reflectance of cotton and was basically consistent with the measured reflectance curve of cotton with the wavelength. However, the reflectance of the first 16 bands was slightly higher than that measured. In contrast, the latter 16 bands were the opposite. The main reason for this may be an error in the input atmospheric parameters used in the 6S atmospheric correction or a spatial matching error in measurement samples, etc.
4. Discussion
The radiometric calibration results for OHSs on board the Zhuhai-1 micro-nano satellite constellation presented here show that the proposed method can be efficiently used for the fast and low-cost on-orbit radiometric calibration of similar satellite constellations containing a large number of micro-nano satellites. The comprehensive gain defined in this work can effectively establish the relationship between the integration stages and the physical gains. Taking the OHS-F sensor on board the Zhuhai-1 satellite constellation as an example, the calibration of three CMOS sensors under all of the integration stages was conducted based on RadCalNet multi-site automatic continuous monitoring data. The calibration results between different sites and different integration stages were consistent, and the comprehensive gain could also effectively characterize the radiometric response of the sensors. Taking the OHS-F sensor on board the Zhuhai-1 satellite constellation as an example, the calibration of three CMOS sensors under all of the integration stages was conducted based on the RadCalNet multi-site automatic continuous monitoring data. For three CMOS sensors on board the OHS-F satellite, the spectral channels at the wavelength range of 550 nm to 880 nm were relatively stable. For other bands, the stability was relatively poor, mainly because the noise effect on these bands was obvious. Therefore, this also shows that it is necessary to carry out high-frequency radiometric calibration for these bands. In addition, the radiometric calibration results for the three CMOS sensors on board the OHS-F satellite in 2020 and 2021 were consistent, and the radiometric stability in 2021 was higher.
The fitted comprehensive gains of three CMOS sensors applicable to all of the integration stages have been proven to have good accuracy. Except for individual atmospheric absorption bands and low signal-to-noise ratio bands, the fitting error was basically within 10%. Compared to the ground measured reflectance of corn, the retrieved surface reflectance from OHS images was shown to be quite accurate and reliable. The absolute radiometric correction of OHS data was based on the fitted comprehensive gains, which further proved that the fitted comprehensive gains were reliable. In addition to using vegetation reflectance in validation, using other targets such as sandy targets can better validate the accuracy and reliability of the comprehensive gains. Unfortunately, we have not obtained the synchronous reflectance data for these targets, and we will continue to carry out validation work in the future.
5. Conclusions
In this paper, the radiometric calibration of the OHS-F satellite covering all CMOSs and integration stages was carried out using RadCalNet ground-measured reflectance and atmosphere parameters. With the aim of completing the on-orbit radiometric calibration of all sensors on board a satellite constellation at different integration stages with low cost and high efficiency, a normalized radiometric calibration model was proposed and evaluated. The consistency of the calibration results for different RadCalNet sites and different integration stages was also analyzed. The radiometric response performance and change was also evaluated based on the calibration results. The main conclusions of this paper are as follows:
- (1)
- The calibration model developed in this paper is suitable for use with hyperspectral sensors designed with gradient filters, which will be very helpful to the calibration of low-cost commercial micro-nano satellite constellations such as the “Zhuhai-1” satellite constellation.
- (2)
- The comprehensive gains in 2020 and 2021 calculated by using the calibration data for four sites of RadCalNet displayed good consistency, which shows the rationality of the comprehensive gain defined in this paper. Except for a few bands, the relative error of the calibration results in a single observation period was less than 10%.
- (3)
- The consistency of the calibration results for satellite sensors in 2021 was significantly higher than that in 2020, mainly due to the poor radiometric stability of satellite sensors in the early stage of the launch.
- (4)
- The overall trend in the comprehensive gain in 2020 and 2021 fitted by the least squares method was similar, which can reflect the change in the sensors’ radiation performance over time. Except for the individual gas absorption bands and low signal-to-noise ratio bands, the fitting error was below 10% during the calculation of the comprehensive gains.
- (5)
- The radiometric calibration results were applied to obtain the satellite reflectance data. Compared to the reflectance spectrum of cotton measured on the ground, the trend in the surface reflectance curve retrieved by the OHS-F satellite CMOS2 sensor was consistent.
Author Contributions
Conceptualization, J.Y., L.Z. and Z.Y.; methodology, Q.Z. and Y.Z.; software, Q.Z.; validation, J.W., W.L. and Q.Z.; formal analysis, X.J.; investigation, Z.Y. and L.Z.; resources, J.Z.; data curation, Q.Z.; writing—original draft preparation, Q.Z.; writing—review and editing, Y.Z. and J.W.; visualization, W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the 2019 Zhuhai Introduction of Innovation and Entrepreneurship Team (ZH0405-1900-01PWC), the Key project of Aerospace Information Research Institute, Chinese Academy of Sciences (ID. E0Z206010F), the Youth Innovation Promotion Association, Chinese Academy of Sciences (ID. 2022128), Zhuhai Social Development Field in Science and Technology Plan Project (2220004000003) and the Dragon 5 ESA-MOST Cooperation (ID. 59166).
Data Availability Statement
Original data download path: https://www.radcalnet.org/#!/; The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
The authors would like to thank Hongyin Xiang for excellent technical support.
Conflicts of Interest
We declare that we have no financial and personal relationships with other people or organizations that could inappropriately influence our work, and there is no professional or other personal interest of any nature or kind regarding any product, service, and/or company that could be construed as influencing the position presented in, or the review of, the manuscript.
References
- Wei, W. Research on Long Time Series Calibration Method of Satellite Remote Sensor Based on Global Calibration Site Network; University of Science and Technology of China: Hefei, China, 2017. [Google Scholar]
- Saunier, S.; Karakas, G.; Yalcin, I.; Done, F.; Mannan, R.; Albinet, C.; Goryl, P.; Kocaman, S. SkySat Data Quality Assessment within the EDAP Framework. Remote Sens. 2022, 14, 1646. [Google Scholar] [CrossRef]
- Xingfa, G. Principles and Methods of Radiometric Calibration of Aerospace Optical Remote Sensors; Science Press: Beijing, China, 2013. [Google Scholar]
- Wilson, N.; Greenberg, J.; Jumpasut, A.; Collison, A. In-Orbit Radiometric Calibration of the Planet Dove Constellation. 2017. Available online: https://digitalcommons.usu.edu/calcon/CALCON2017/All2017Content/23/ (accessed on 20 October 2017).
- Czapla-Myers, J.; Thome, K.; Wenny, B.; Anderson, N. Railroad Valley Radiometric Calibration Test Site (RadCaTS) as Part of a Global Radiometric Calibration Network (RadCalNet). In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020. [Google Scholar]
- Scanlon, T.; Greenwell, C.; Czapla-Myers, J.; Anderson, N.; Goodman, T.; Thome, K.; Wolliams, E.; Porrovecchio, G.; Linduška, P.; Šmíd, M.; et al. Ground comparisons at RadCalNet sites to determine the equivalence of sites within the network. In Proceedings of the SPIE Remote Sensing, Warsaw, Poland, 29 September 2017; Volume 10423, pp. 255–267. [Google Scholar]
- Jing, X.; Leigh, L.; Teixeira Pinto, C.; Helder, D. Evaluation of RadCalNet Output Data Using Landsat 7, Landsat 8, Sentinel 2A, and Sentinel 2B Sensors. Remote Sens. 2019, 11, 541. [Google Scholar] [CrossRef]
- Ma, L.; Zhao, Y.; Woolliams, E.R.; Dai, C.; Wang, N.; Liu, Y.; Li, L.; Wang, X.; Gao, C.; Li, C.; et al. Uncertainty analysis for RadCalNet instrumented test sites using the Baotou sites BTCN and BSCN as examples. Remote Sens. 2020, 12, 1696. [Google Scholar] [CrossRef]
- Shrestha, M.; Helder, D.; Christopherson, J. DLR Earth Sensing Imaging Spectrometer (DESIS) Level 1 Product Evaluation Using RadCalNet Measurements. Remote Sens. 2021, 13, 2420. [Google Scholar] [CrossRef]
- Bouvet, M.; Thome, K.; Berthelot, B.; Bialek, A.; Czapla-Myers, J.; Fox, N.P.; Goryl, P.; Henry, P.; Ma, L.; Marcq, S.; et al. RadCalNet: A radiometric calibration network for Earth observing imagers operating in the visible to shortwave infrared spectral range. Remote Sens. 2019, 11, 2401. [Google Scholar] [CrossRef]
- Wenny, B.N.; Thome, K.; Czapla-Myers, J. Evaluation of vicarious calibration for airborne sensors using RadCalNet. J. Appl. Remote Sens. 2021, 15, 034501. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, L.; Li, C.; Gao, C.; Wang, N.; Tang, L. Radiometric cross-calibration of Landsat-8/OLI and GF-1/PMS sensors using an instrumented sand site. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3822–3829. [Google Scholar] [CrossRef]
- Alhammoud, B.; Jackson, J.; Clerc, S.; Arias, M.; Bouzinac, C.; Gascon, F.; Cadau, E.G.; Iannone, R.Q.; Boccia, V. Sentinel-2 Level-1 Radiometry Assessment Using Vicarious Methods From DIMITRI Toolbox and Site Measurements From RadCalNet Database. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3470–3479. [Google Scholar] [CrossRef]
- Marcq, S.; Meygret, A.; Bouvet, M.; Fox, N.; Greenwell, C.; Scott, B.; Berthelot, B.; Besson, B.; Guilleminot, N.; Damiri, B. New Radcalnet Site at Gobabeb, Namibia: Installation of the Instrumentation and First Satellite Calibration Results. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Gao, C.; Liu, Y.; Wu, Z.; Ma, L.; Qiu, S.; Li, C.; Zhao, Y.; Han, Q.; Zhao, E.; Qian, Y.; et al. An Approach for Evaluating Multisite Radiometry Calibration of Sentinel-2B/MSI Using RadCalNet Sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8473–8483. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, L.; Li, W.; He, H.; Long, X.; Wang, N.; Liu, Z.; Qian, Y.; Qiu, S.; Liu, Y.; et al. Vicarious Radiometric Calibration of Superview-1 Sensor Using RadCalNet TOA Reflectance Product. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 8130–8133. [Google Scholar]
- Li, W.; Ma, L.; Zhao, Y.; Liu, Y.; Wang, N.; Qian, Y.; Li, K.; Li, C.; Tang, L. Temporal Vicarious Radiometric Calibration of ZY-3 Mux Sensor Using Automatic Ground Measurement of Baotou Sandy Site in China. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 7767–7770. [Google Scholar]
- Vermote, E.F.; Tanré, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).