Next Article in Journal
Determining Ionospheric Drift and Anisotropy of Irregularities from LOFAR Core Measurements: Testing Hypotheses behind Estimation
Next Article in Special Issue
Coastal Waveform Retracking for HY-2B Altimeter Data by Determining the Effective Trailing Edge and the Low Noise Leading Edge
Previous Article in Journal
Responses of Satellite Chlorophyll-a to the Extreme Sea Surface Temperatures over the Arabian and Omani Gulf
Previous Article in Special Issue
Performance of HaiYang-2 Altimetric Data in Marine Gravity Research and a New Global Marine Gravity Model NSOAS22
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 18
10.3390/rs14184654
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluation and Calibration of Remotely Sensed High Winds from the HY-2B/C/D Scatterometer in Tropical Cyclones

by
Xiaohui Li
1,
Jingsong Yang
1,2,*,
Jiuke Wang
3 and
Guoqi Han
4
1
State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, Ministry of Natural Resources, Hangzhou 310012, China
2
Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), Zhuhai 519082, China
3
National Marine Environmental Forecasting Center, Beijing 100081, China
4
Fisheries and Oceans Canada, Institute of Ocean Sciences, Sidney, BC V8L 4B2, Canada
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(18), 4654; https://doi.org/10.3390/rs14184654
Submission received: 12 July 2022 / Revised: 17 August 2022 / Accepted: 9 September 2022 / Published: 17 September 2022
(This article belongs to the Special Issue HY-2 Satellite Microwave Remote Sensing of Ocean for 10 Years: Applications and Advances)
Browse Figures
Review Reports Versions Notes

Abstract

:
Haiyang-2 scatterometers (HY-2A/B/C/D) have limitations in high wind speed retrieval due to the complexity of the remote sensing mechanism and the influence of rainfall on the radar cross section under the conditions of tropical cyclones. In this study, we focus on the evaluation of Chinese scatterometer operational wind products from HY-2B/C/D over the period from July 2019 to December 2021. HY-2B/C/D scatterometer wind products are collocated with SMAP (Soil Moisture Active Passive) L-band radiometer remotely sensed measurements. The results show that the underestimation of high wind speed occurs in the HY-2B/C/D wind speed products. The machine learning algorithms are explored to improve this underestimation issue, including the back propagation neural network (BP-NN), K-nearest neighbor (KNN), support vector machine (SVM), decision tree (DT), random forest (RF), and Bayesian ridge (BR) regression algorithms. Comparisons show that the BP-NN algorithm shows the best performance with a small RMSE (root-mean-square error) of 3.40 m/s, and high correlation coefficient of 0.88, demonstrating an improvement of 20.4% in RMSE (root-mean-square error) compared with the HY-2B/C/D wind speed products. In addition, the revised high winds are in good agreement with the ground truth measurements from the SFMR (Stepped Frequency Microwave Radiometer), which are useful for tropical cyclone disaster prevention and mitigation and are of vital importance in the numerical simulation of storm surges.

Graphical Abstract

1. Introduction

Tropical cyclones are fast rotating storms that originate from the tropical ocean, drawing energy from it in order to develop. Even in their formative stage of development, tropical cyclones are one of the greatest threats to life and property, including different disasters that may individually cause significant impacts, such as wind storms, floods, storm surges, tornadoes, and lightning. The superposition of these disasters will greatly increase the possibility of the loss of life and property. Every year, in the late summer months (July to September in the northern hemisphere and January to March in the southern hemisphere), the nearshore areas hit by cyclones are as far as the coast of China, the Gulf coast of North America, northwest Australia, eastern India, and Bangladesh.
Spaceborne microwave scatterometers are one of the instruments that provide all-weather, all-time capabilities for the field of global ocean wind [1,2]. The HY-2A (Haiyang-2A; “Haiyang” means ocean in Chinese) satellite is China’s first marine dynamic environment monitoring satellite, which is loaded with a microwave scatterometer (as shown in Table 1), scanning microwave radiometer, calibration microwave radiometer, radar altimeter, etc. [3,4,5,6]. The main task of the Haiyang-2 satellite series (namely HY-2A, HY-2B, HY-2C and HY-2D) is to monitor and investigate global marine dynamic phenomena and processes, including important sea-state parameters such as sea surface wind, sea surface height, significant wave height, marine gravity, ocean circulation, and sea surface temperature [7]. This satellite is an important means of monitoring for marine disaster prevention and mitigation [8,9,10,11,12]. Compared with traditional wind measurement methods such as buoys, ships, and aircraft, scatterometers can provide continuous and wide-range datasets [13,14]. These datasets are an important part of the basis for marine disaster prevention and mitigation and are of vital importance in numerical weather prediction (NWP) systems [2,15,16], which has been proven by the long-term application of the remotely sensed winds observed from the HY-2 satellite series [8].
HY-2 can measure more than 90% of the global sea surface per day with an accuracy of 2 m/s or 10% in wind speed and 20 ∘ in wind direction [3,17,18]. The premise of HY-2 scatterometer data application is data evaluation. For example, Xing et al. [18] used buoy, ERA-Interim, and ASCAT data to evaluate HY-2A scatterometer wind vectors for the period 2012–2014, demonstrating the effectiveness of HY-2 data. In addition, previous studies also confirmed that HY-2A meets the operational accuracy requirement (<2 m/s) at medium and low wind speeds (2–24 m/s) [14,19,20,21,22]. The wind speed inversion of the HY-2B/C/D scatterometers also benefits from the achievements of HY-2A. The accuracy of sea surface winds observed by the HY-2B scatterometer was investigated in [23,24,25]. These studies show that the wind speed of HY-2B is in good agreement with the measured data. The effectiveness of HY-2C was also verified in [26], with a wind speed standard deviation of 1.03 m/s and a direction root-mean-square error (RMSE) of 15.9°. Compared to NWP models, the wind speed deviation of the HY-2B/C/D series of scatterometers has similar characteristics in the wind speed range of 4 to 20 m/s [27].
On the whole, the HY-2 microwave scatterometer satellite series in operation can provide accurate sea surface wind field data for medium and low wind speeds (<20 m/s) in rainless areas. However, the sea surface wind field data provided by the HY-2 microwave scatterometer satellite series are not accurate under the conditions of tropical cyclones and heavy rainfall. One reason is the poor quality of the observables from the microwave scatterometer in rainy conditions [28]. Another is that the geophysical model function (GMF) still struggles to effectively retrieve high wind speed in terms of intense air sea interaction under the conditions of tropical cyclones [29].
To date, much work has been done to study the high wind speed retrieval of scatterometers. Many high wind speed algorithms (the forward models and GMFs) for microwave scatterometers and radiometers were established with the goal of retrieving extreme winds under the conditions of tropical cyclones [2,30]. In addition to the traditional inversion algorithm, machine learning has also been applied in the field of high wind speed inversion, with rapid development, especially with regard to the artificial neural network (ANN) algorithm. Cornford et al. [31] proposed a novel scatterometer forward model based on ANN, which has good inversion accuracy in the range of high wind speeds. In addition, the Ku-band has obvious attenuation under rainfall conditions, which directly affects the accuracy of high wind speeds. Stiles and Dunbar [32] successfully applied ANN to improve the performance of the extreme winds retrieved by a scatterometer in the presence of precipitation. For the scatterometer onboard the HY-2 satellite, Chen et al. [33] used the ANN algorithm to retrieve medium and high wind speeds. It was shown that the retrieved wind field can meet the accuracy requirements of the HY-2 microwave scatterometer [33]. The performance of the neural network model depends on the completeness of the training set. However, the data measured during tropical cyclones are not sufficient to support ANN model training and verification [30]. Considering that tropical cyclones have a great impact on the economy and safety of coastal areas, it is necessary to carry out the verification and calibration of the satellite remote sensing of high wind speeds based on limited in situ datasets.
In this paper, we investigate the HY-2 microwave scatterometer as a remote sensing technique for monitoring extreme winds globally during the period 2019–2021. The performance of the Chinese HY-2B/C/D series scatterometer wind product in tropical cyclones is evaluated and analyzed with respect to the remotely sensed measurements of the SMAP (Soil Moisture Active Passive) L-band radiometer. Then, we explore machine learning methods to improve the extreme wind measurements retrieved by HY-2B/C/D series scatterometers. Finally, the stability of machine learning models is verified by the measured data from the SFMR (Stepped Frequency Microwave Radiometer). A description of the datasets for the HY-2B/C/D scatterometers and SMAP radiometer is provided in Section 2. The methodology of the machine learning algorithms is described in Section 3. The comparisons and main results are presented in Section 4. Section 5 provides the discussion and conclusion.

2. Datasets

2.1. HY-2 Series Scatterometer Data of High Wind Speed Vectors

In this study, the Level 2B near-real-time (NRT) wind vectors retrieved by maximum likelihood estimation method are used to evaluate the quality of the HY-2B/C/D operational wind products under the condition of tropical cyclones. These data, with a spatial resolution of 25 × 25 km, are obtained from the National Satellite Ocean Application Service (NSOAS) and are distributed in a daily orbit file. It should be pointed out that the actual spatial resolution (half power footprint diameter) of the HY-2 series scatterometer is 25 × 35 km. In order to ensure data quality, land and sea ice data are eliminated according to the flag.
Since the launch time of the HY-2 satellite series has a sequence as shown in Table 1, the starting times are different, and the end time is 31 December 2021, for HY-2B/C/D, as shown in Table 2. Two pencil beam antennas aboard the HY-2 satellite series can observe 1350 km by horizontal polarization (HH) at the 41 ∘ incident angle and 1700 km by vertical polarization (VV) at the 48 ∘ incident angle, and can cover the global sea surface twice per day. A wide swath is suitable for observing tropical structure globally.

2.2. SMAP Radiometer Data in Tropical Cyclones

It is well known that the passive radiometer (L-band, 1.4 GHz) is significantly less affected by precipitation than the Ku-band of the scatterometer [34,35], which provides a new approach and capability for sea surface remote sensing in tropical cyclones, and complements existing ocean satellites [36,37].
The SMAP L-band wind speed product is obtained from Remote Sensing Systems (https://data.remss.com/smap/wind/, accessed on 1 June 2022). High wind speeds retrieved by satellites in storms are challenging and usually require dedicated GMFs. To help solve this problem, several new algorithms developed by Remote Sensing Systems are used to retrieve reliable high wind speed measurements under the conditions of tropical cyclones and heavy rainfall [38,39,40]. The performance of SMAP under tropical cyclone conditions is evaluated with respect to the Weather Research and Forecasting for Hurricanes (HWRF) model, which models winds with a standard deviation below 4 m/s and strong winds in the range of 10–60 m/s [41]. This approach is suitable for evaluating the Chinese HY-2B/C/D series scatterometer wind products in tropical cyclones.

2.3. High Wind Speed Measurements from SFMR

Due to extreme weather, it is extremely difficult to obtain wind speed during tropical cyclones, resulting in a scarcity of measured data. The National Oceanic and Atmospheric Administration (NOAA)/Hurricane Research Division’s SFMR has made great contributions to monitoring tropical cyclone wind speed by airborne remote sensing instruments for estimating the ocean surface brightness temperature at six frequencies between 4.6 and 7.2 GHz [42,43,44]. With the continuous optimization of the inversion model, the accuracy of its high wind speed measurement is also gradually improving, within ∼3.9 m/s in terms of RMSE [45]. In this paper, the independent SFMR high wind speed measurements are used as the true value to verify the performance and generalization ability of the machine learning models.

3. Methods

3.1. ANN

The back propagation neural network (BP-NN) is a concept proposed by Rumelhart and McClelland in 1986 [46]. It is a multilayer feedforward neural network trained according to the error back propagation algorithm, which is one of the most widely used neural network models [47]. Under the learning of external input samples, the neural network continuously changes the connection weight of the network to make the output of the network close to the expected output. Because of its strong learning ability in regression, the BP-NN algorithm has also been widely used in satellite remote sensing wind speed inversion [25,31,48,49,50]. In this paper, the BP-NN algorithm is applied to revise the high wind speed of HY-2 relative to the SMAP L-band radiometer wind product in tropical cyclones.

3.2. SVM

As one of the kernel learning methods, the support vector machine (SVM) is a kind of generalized linear classifier that classifies data in a supervised learning way [51]. The SVM belongs to the supervised learning methods, which can be used not only for classification, but also for regression. There are many parameters in the regression model of SVM, and the key parameters are the kernel parameter and penalty C parameter. The SVM can effectively solve the classification and regression problems of high-dimensional features, and it has also been well applied in wind speed inversion [52]. Sreelakshmi and Ramakanthkumar [53] pointed out that the SVM has good accuracy in wind speed prediction compared with BP-NN. However, when the training sample size is too large, it leads to the excessive computation of kernel function mapping.

3.3. KNN

The K-nearest neighbor (KNN) algorithm is used to calculate the distance between the predicted points and all points, and to sort the distance. Among the first K points, the distance between two points is found, and it is determined which point is the closest [54]. For KNN, two key parameters are “n_ neighbors” and “Weights” [55]. “n_ neighbors” represents the number of nearest neighbors to be used in the learning process, that is, the k value; “Weights” is the weight function used in the prediction. One option for “Weights” is that all points in each neighborhood are weighted equally; another is weighted by the inverse of their distance, such as the Euclidean distance, Manhattan distance, and Minkowski distance [56].

3.4. Decision Tree and Random Forest

Decision tree (DT) was proposed by Hunt [57] in the early 1960s, being a conditional probability distribution defined in feature space and class space to find the purest division method [58]. The composition of decision tree has four elements: (1) decision nodes; (2) scheme branch; (3) status node; and (4) probability branch. Compared with black box classification models such as neural networks, decision trees can be logically well explained [59].
The random forest (RF) algorithm was developed by L. Breiman in 2001 [60]. As we all know, DT is usually trained by recursively splitting data, but it is easy to overfit. To avoid this problem, RF runs by constructing multiple decision trees simultaneously; then, the prediction is obtained from each sample, and the best solution is finally selected by voting [61]. Compared to ANNs and SVMs, it is more efficient and robust against overfitting and outliers in order to improve the performance, especially when the dataset is large [62,63]. It is suitable for demonstrating the nonlinear effects of variables, and can learn the complex interactions between variables [60,64]. The potential of RF in satellite remote sensing data classification has also been verified [64,65,66].

3.5. Bayesian Ridge Regression

Bayesian ridge regression is mainly proposed because it is difficult to determine the complexity of the model in the maximum likelihood estimation. The penalty parameter (C) added to ridge regression actually solves this problem [67]. On the Bayesian regression, the distribution of parameter ω obeys the Gaussian sphere distribution. The priori parameters α and λ generally follow the γ distribution, which has a conjugate prior relationship with Gaussian distribution, and the accuracy is used to find the maximum a posteriori estimate [68,69,70].

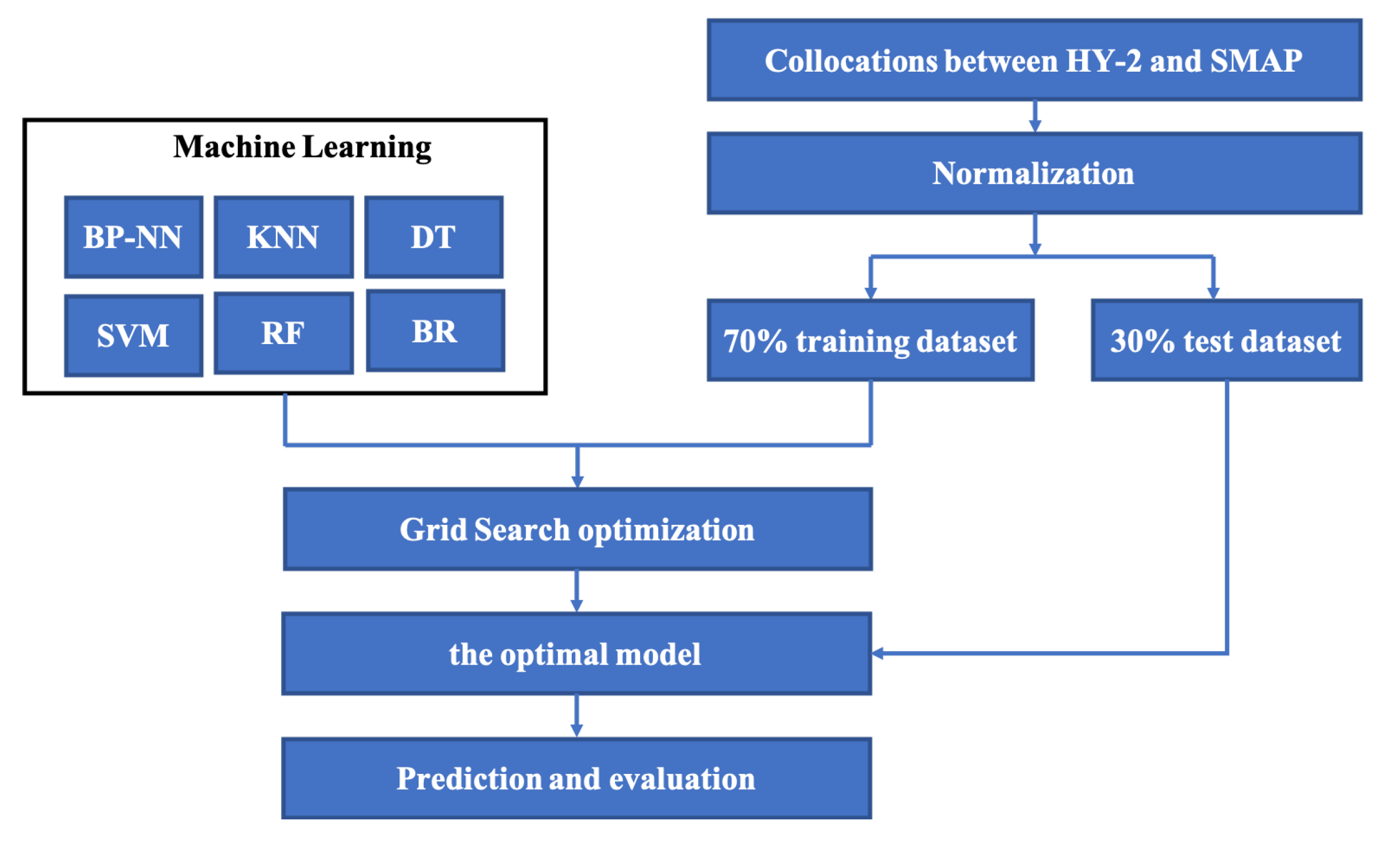
3.6. Method of Machine Learning

In this paper, six machine learning methods are used to optimize the high wind speed accuracy of HY-2, as shown in Figure 1. The data pair of HY-2 and SMAP requires some necessary operations before being input to the machine learning model. First, normalization is a commonly used method in machine learning, which can accelerate the speed of gradient descent to find the optimal solution. In gradient-based algorithms, such as the neural network or SVM, normalization can potentially improve the accuracy. In distance models, such as KNN and K-means clustering, normalization can help improve the accuracy of the model and avoid the impact of a feature with a large value range on distance calculation. DT and its integral algorithm do not need normalization, because this kind of algorithm can handle any data well. Before training, the normalization of the matchups is processed into 0-1 dimensionless data. Then, the dataset is randomly divided into a 70% training set and 30% test set based on the Python sklearn module. These two datasets are used for model training and model accuracy testing, respectively.
In addition, model optimization is one of the most difficult challenges in the implementation of machine learning algorithms [71]. The parameters that need to be manually selected are called hyper-parameters; for example, the number of hidden layers and nodes in each layer in the artificial neural network model, and the number of decision trees in the random forest. The improper selection of hyper-parameters will lead to the problem of underfitting or overfitting. Grid Search and Cross Validation (hereafter GridsearchCV) optimization can be said to be the most basic hyper-parametric optimization method. Using this technique, we only need to build an independent model for all possible hyper-parameters, evaluate the performance of each model, and select the model and hyper-parameter that produce the best results. In this paper, the GridsearchCV optimization is implemented based on the Python sklearn module, in order to find the optimal model parameters in the present models. When the data are limited, the training model can easily cause overfitting; GridsearchCV is mainly used to avoid this problem. In this paper, the 5-fold cross-validation method is used [72].

4. Results

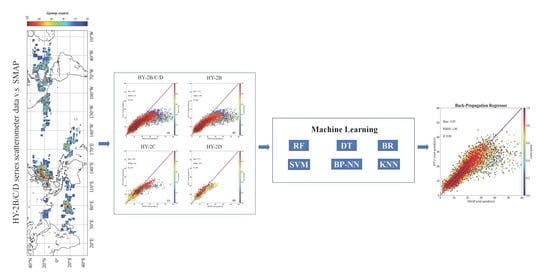
4.1. Collocations of HY-2B/C/D and SMAP

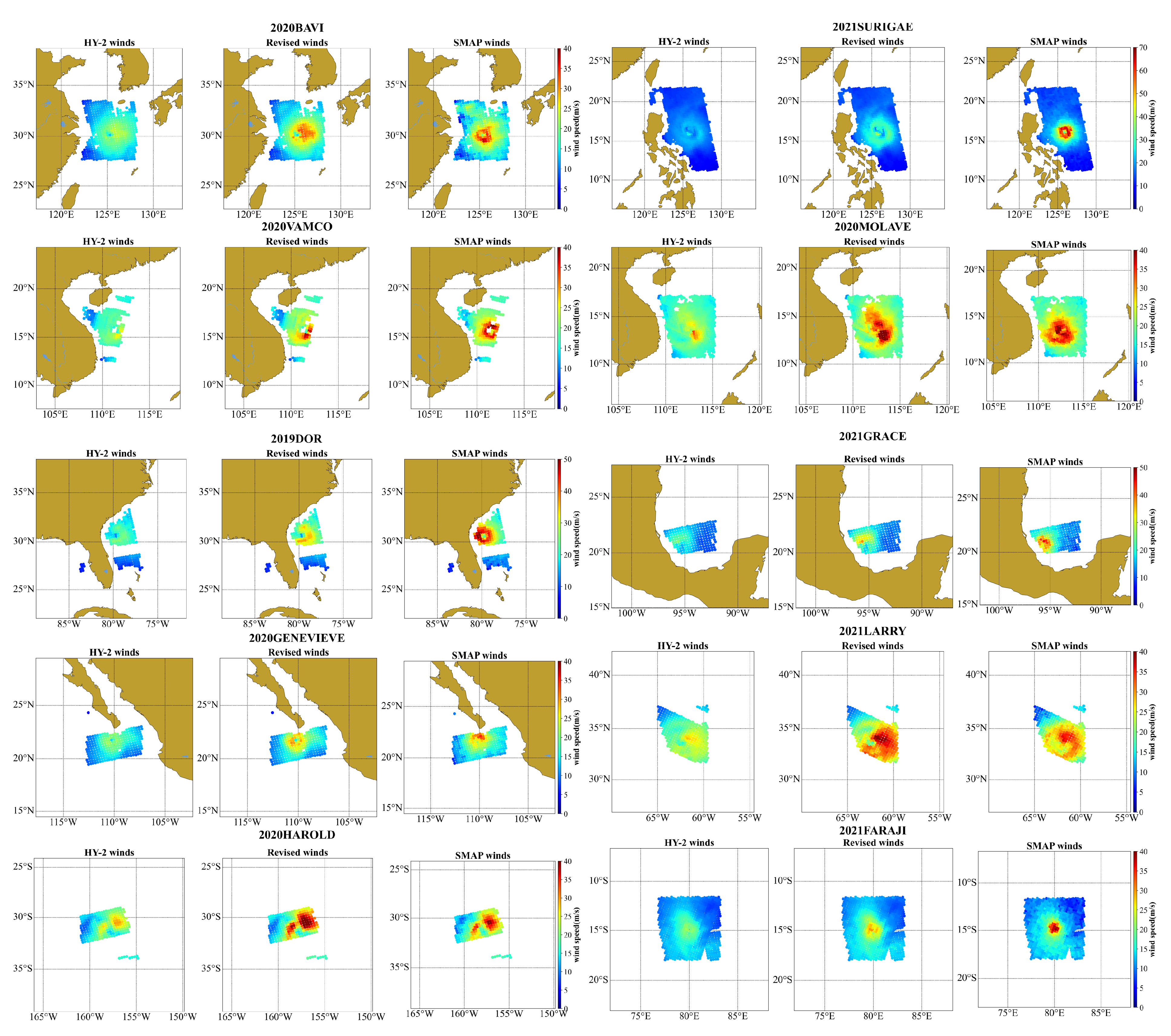
4.1.1. Geographical Distribution

In this paper, the HY-2B/C/D series scatterometer data of high wind speed vectors are compared and evaluated by SMAP measurements within tropical cyclones during 2019–2021. The list of tropical cyclones captured by SMAP is sorted by year and provided by Remote Sensing Systems. Then, according to the center and radius of maximum wind (RMW) of each tropical cyclone, SMAP radiometer and HY-2 scatterometer winds are selected within four times the RMW and with a time difference of no more than 1 h. The storm tracking data are provided by the Joint Typhoon Warning Center (JTWC, https://www.usno.navy.mil/JTWC/, accessed on 1 January 2022) in this study. Since the sea surface state of tropical cyclones varies with the spatial distribution, it is necessary to ensure that the location of the HY-2B/C/D series scatterometer wind speed measurements are as close as possible to SMAP. In this study, collocations from SMAP are collocated by less than 12.5 km.
Figure 2 shows the density map of the distribution of all data pairs after collocation, which suggests that most of the captured tropical cyclone data from both HY-2 and SMAP are distributed in the Northwest Pacific in the northern hemisphere. This is consistent with the high frequency of tropical cyclone occurrence in the Northwest Pacific. In addition, most of the matchups are distributed in the Western Pacific Ocean and Eastern Pacific Ocean (along the coast of America). In the southern hemisphere, it is noted that no tropical cyclone has been observed in South America. In addition, there are some tropical cyclones captured by both HY-2 and SMAP in the open sea in the southern Indian Ocean. From Figure 2a,b, it can be seen that the number of matchups has a similar distribution, and compared to Figure 2c,d, this means that HY-2B captured the main tropical cyclones, and HY-2C/D accounted for a small part.

4.1.2. Tropical Cyclones Jointly Captured by HY-2 and SMAP

In order to count the number of typhoons jointly captured by the two satellites, the ability of SMAP to capture typhoons in 2019–2021 is introduced first. According to the location of tropical cyclones at each time, the global ocean is first divided into the southern hemisphere and the northern hemisphere, and then the northern hemisphere is further divided into the Atlantic Ocean, the Eastern Pacific Ocean, the Central Pacific Ocean, the Western Pacific Ocean, the Northern Indian Ocean, and the southern hemisphere ocean, respectively. However, the tropical cyclone of hurricane Ema in 2019 was captured by SMAP. Therefore, the assessment of HY-2 in this study does not include the Central Pacific Ocean.
Table 3 gives the statistics of tropical cyclones captured by SMAP during the period 2019–2021. There are 41, 45, 29, 11, and 64 tropical cyclones observed by SMAP in the Atlantic Ocean, Western Pacific Ocean, Eastern Pacific Ocean, Indian Ocean, and southern hemisphere, respectively. During these three years, SMAP observed the most tropical cyclones during 2020, and among the six basins, the southern hemisphere contained the largest number of observed tropical cyclones. As shown in Table 3, the number of captured storms is the smallest in the Northern Indian Ocean, which is consistent with the low frequency of occurrence in this area.
After the HY-2 scatterometer data are matched with SMAP, the number of tropical cyclones observed by the two satellites at the same time is also counted, as shown in Table 3. The local times of the ascending/descending node of the HY-2 satellite and SMAP are the same, as shown in Table 1, providing a good opportunity to match the data for instrument inter-calibrations. Since HY-2B (3 July 2019–31 December 2021 for evaluation) was launched the earliest, it has also captured the most tropical cyclones (Figure 2a and Table 3) relative to HY-2C (25 September 2020–31 December 2021 for evaluation) and HY-2D (24 June 2021–31 December 2021 for evaluation), which is consistent with Figure 2b–d.

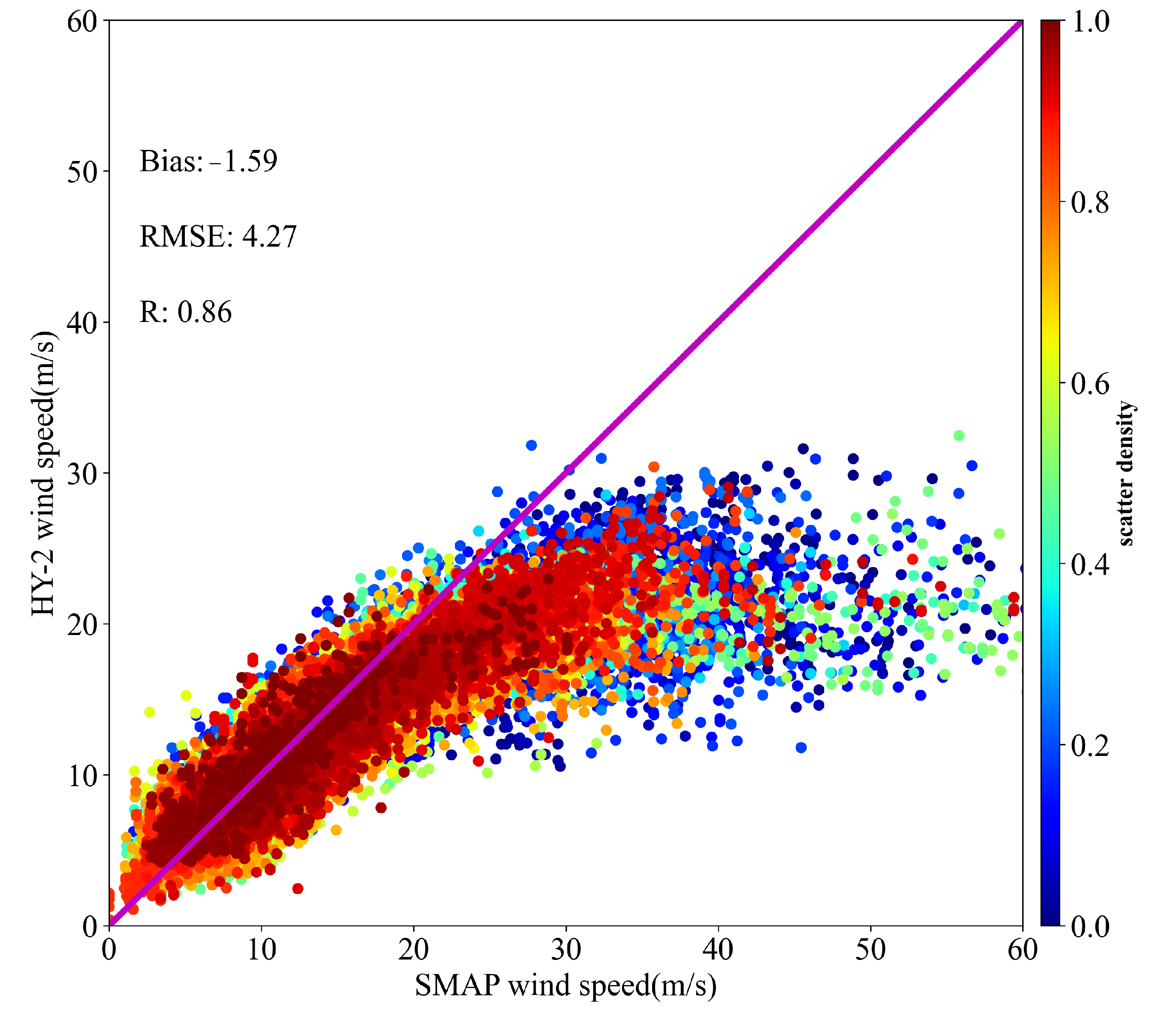
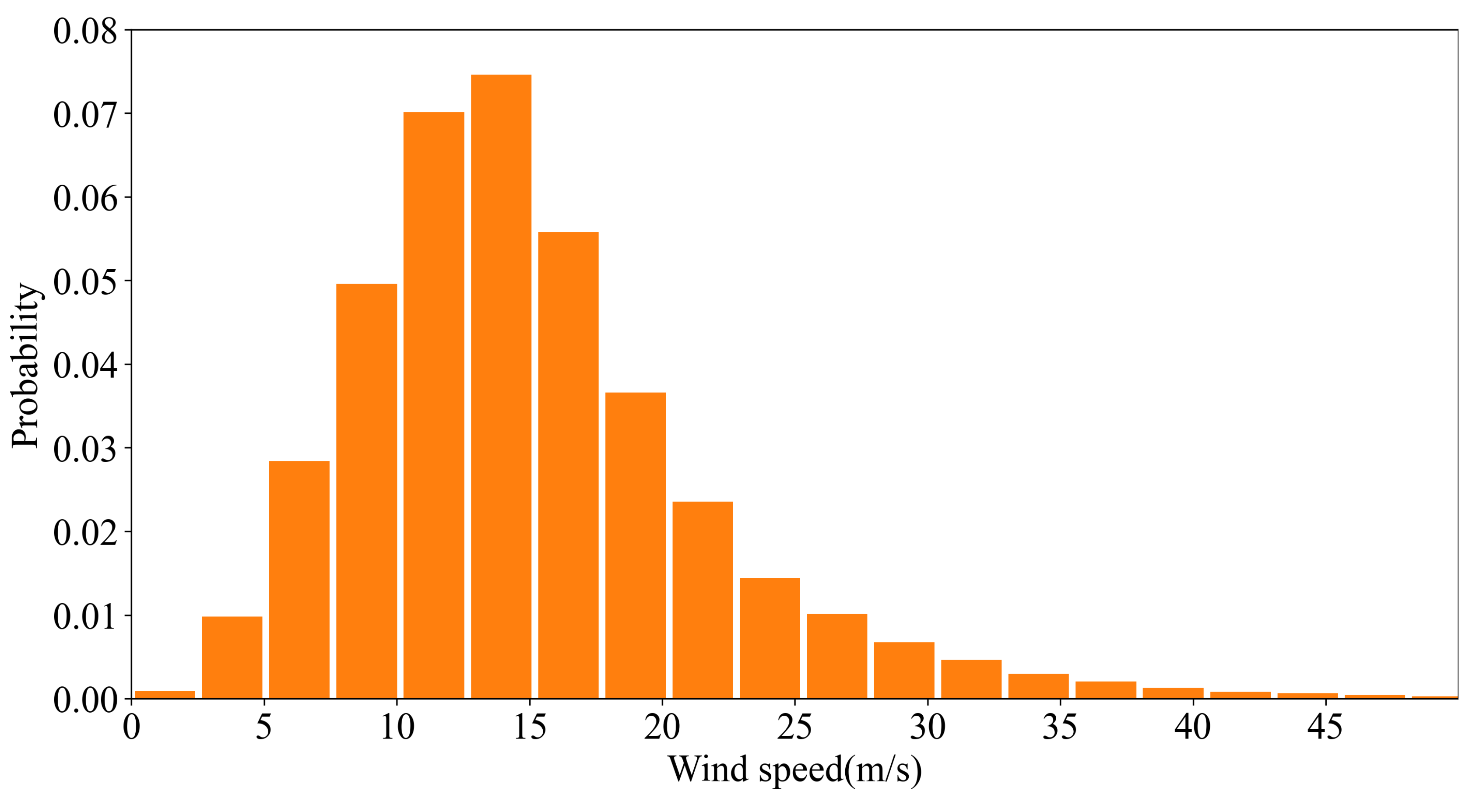
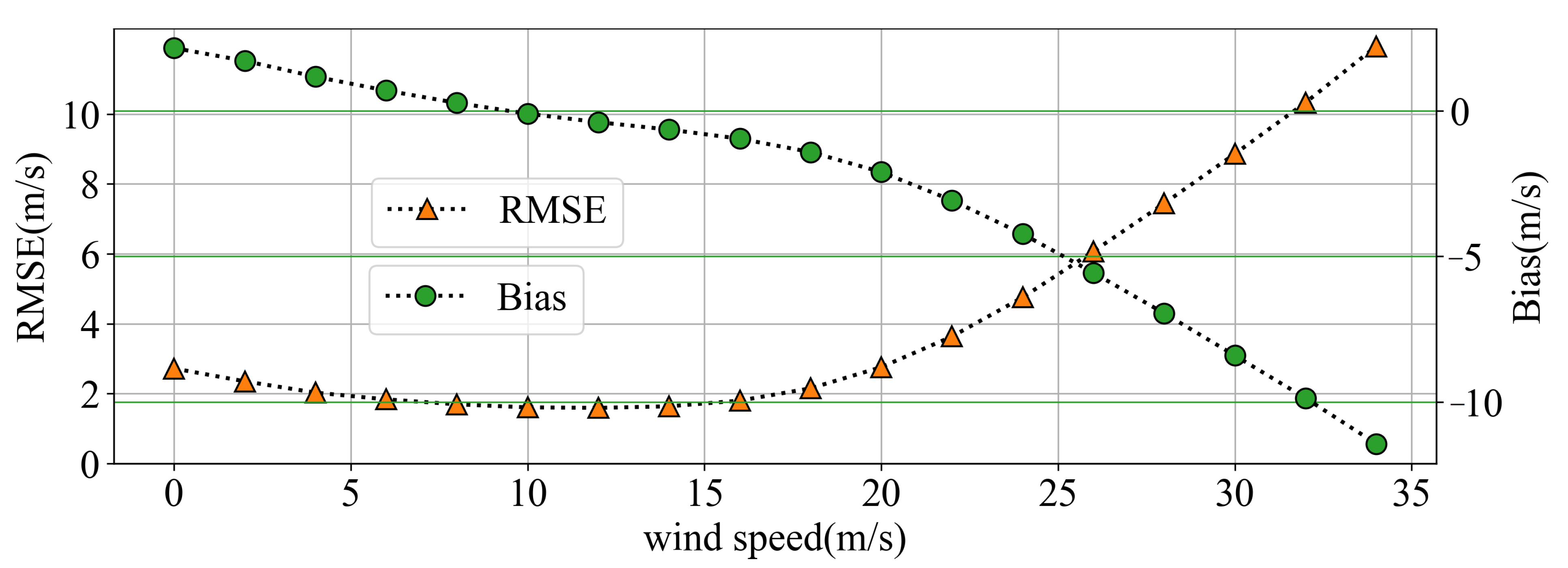
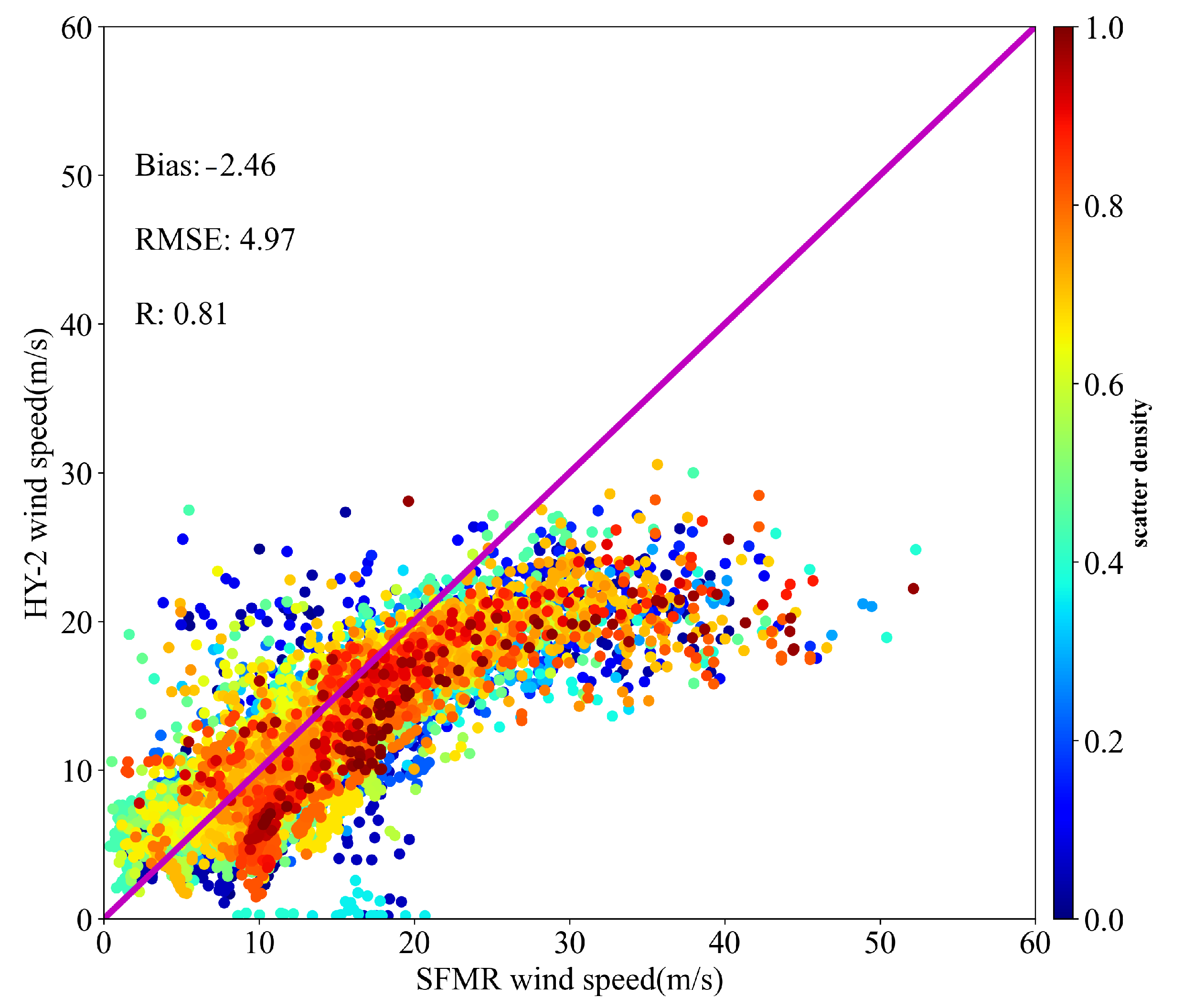
4.2. Statistical Analysis of HY-2 Scatterometer and SMAP Radiometer

To evaluate the performance of HY-2 scatterometer wind retrieval, we collocated these data with SMAP high wind speeds. Figure 3 presents the scatterplot of wind speeds from HY-2B/C/D scatterometers and the SMAP radiometer under tropical cyclone conditions, with summaries of the statistical metrics, including bias (HY-2–SMAP), RMSE, and correlation coefficient (R). However, the wind range of HY-2C/D is less than 30 m/s, and the number of matchups between HY-2 and SMAP is small, which makes it impossible to evaluate the accuracy of its high wind speed. In addition to the HY-2B data volume being enough to evaluate the accuracy of wind speed in tropical cyclones, the other two require more data for support. Therefore, the overall performance is implemented and analyzed by HY-2B/C/D winds. First, HY-2B/C/D slightly underestimate the wind speed with a negative bias of –1.59 m/s in tropical cyclones. A high correlation coefficient of 0.86 implies that the two datasets have good correlation when the wind speeds are below 20 m/s. However, it can be seen from the scatter density diagram that this underestimation is particularly obvious when the wind speeds exceed 20 m/s. The RMSE of the wind speed is 4.27 m/s, demonstrating the accuracy of HY-2 scatterometer wind retrieval.
According to the wind speed of SMAP, the wind speed distribution of HY-2 is statistically analyzed within the range of 0–50 m/s. Considering the amount of data in each wind speed interval, RMSE and bias are counted every 2 m/s at 0–35 m/s to facilitate understanding of the accuracy of HY-2 in each wind speed interval. Figure 4 presents the 2D histogram of the wind speed from the HY-2B/C/D scatterometer, which demonstrates that most of the data are distributed in the range 5–20 m/s. It can be seen from Figure 5 that the RMSEs of the HY-2B/C/D wind speeds are less than 2 m/s in the moderate wind speed range (5–18 m/s), and the biases are generally negligibly small, showing that HY-2 wind speeds are consistent with those measured by SMAP. The HY-2 wind speeds lie within the range 0–2 m/s, and the RMSE also exceeds 2 m/s, as shown in Figure 5. The main reason is that the scatterometer uses the backscattering signal; when the sea surface is too calm (winds < 2 m/s), similar to specular scattering, the backscattering signal is weak and cannot be accurately measured. As can be seen from Figure 5, the deviation (HY-2–SMAP) decreases from 0 to –12 m/s with the increase in wind speed, and RMSE also increases from 2 to 12 m/s. Particularly when the wind speed exceeds 25 m/s, HY-2 fails to accurately retrieve the high wind speed relative to SMAP. Therefore, it is necessary to revise the high wind speed products from HY-2B/C/D according to the relationship between the two, so as to provide a reliable high wind speed estimate for tropical cyclone monitoring.

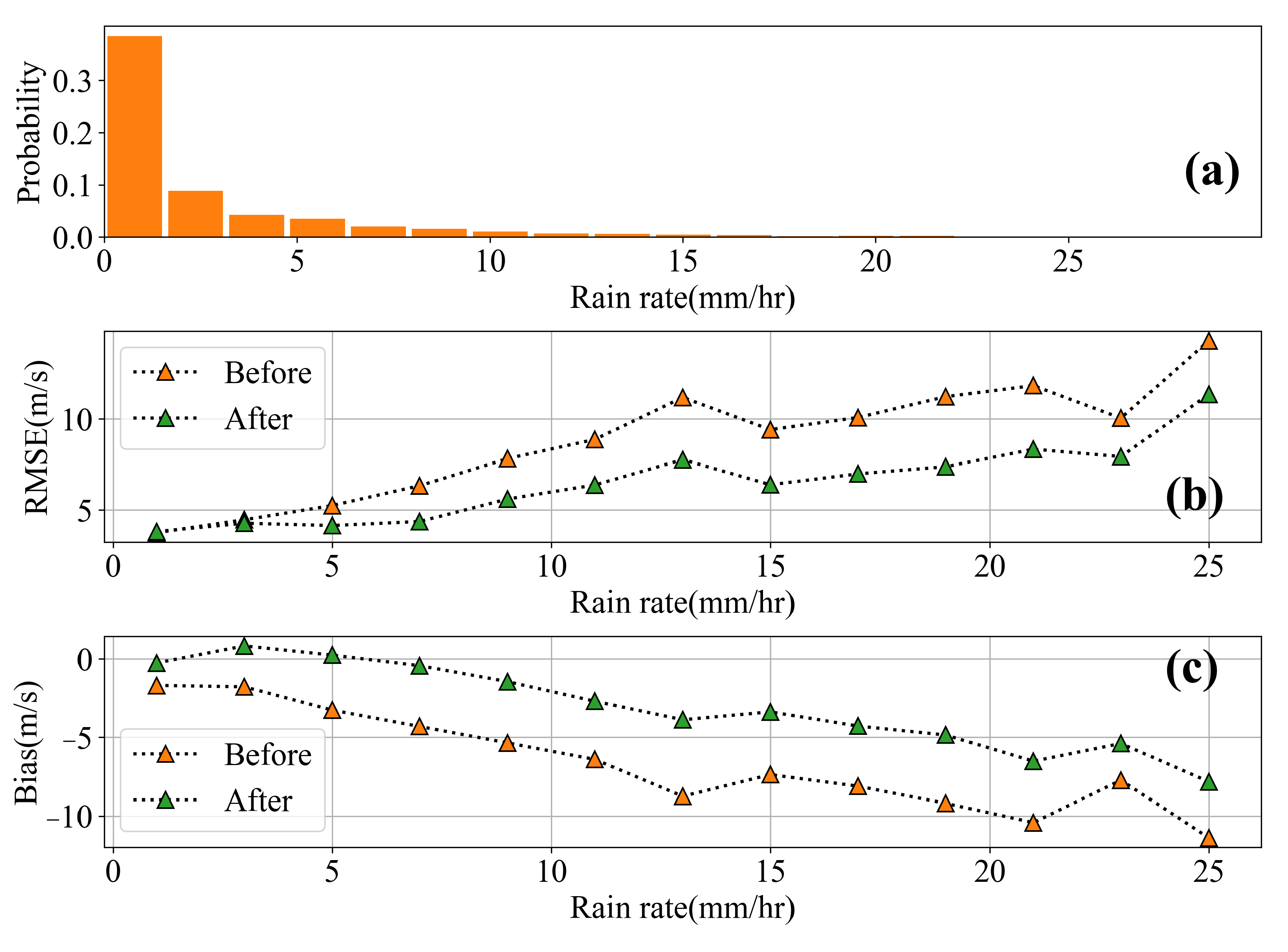
4.3. A Revised Algorithm Based on Machine Learning

From the correlation coefficient between HY-2B/C/D and SMAP wind speed, it can be seen that they have a good correlation, as shown in Figure 3, which also provides the possibility to optimize HY-2 wind speed products for tropical cyclones. It can be seen from Figure 3 that HY-2B/C/D and SMAP wind speed have a nonlinear relationship, and machine learning has an advantage in solving nonlinear problems. In this paper, six machine learning algorithms are used to optimize the wind speed of HY-2B/C/D, including the BP-NN, KNN, DT, SVM, RF, and BR algorithms.

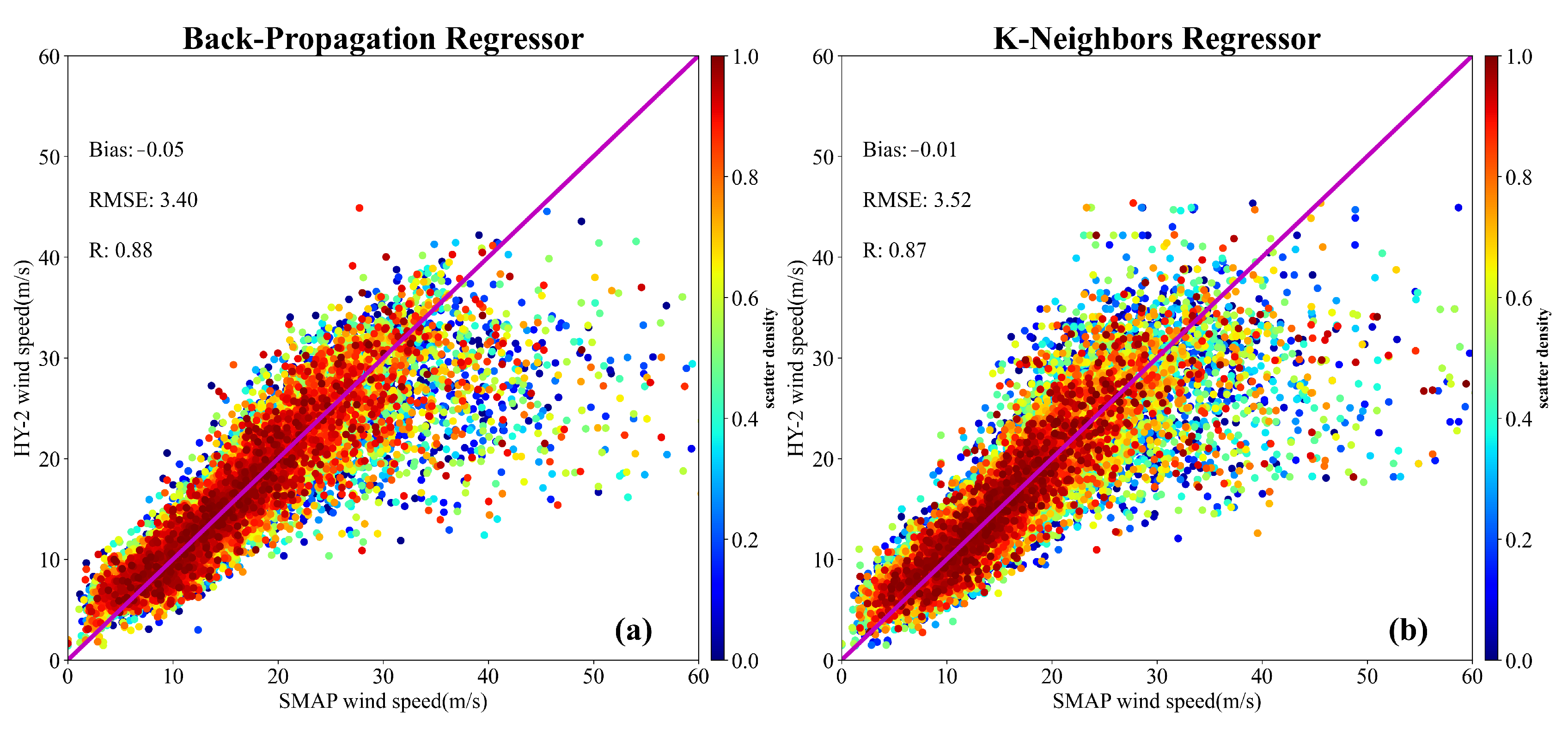
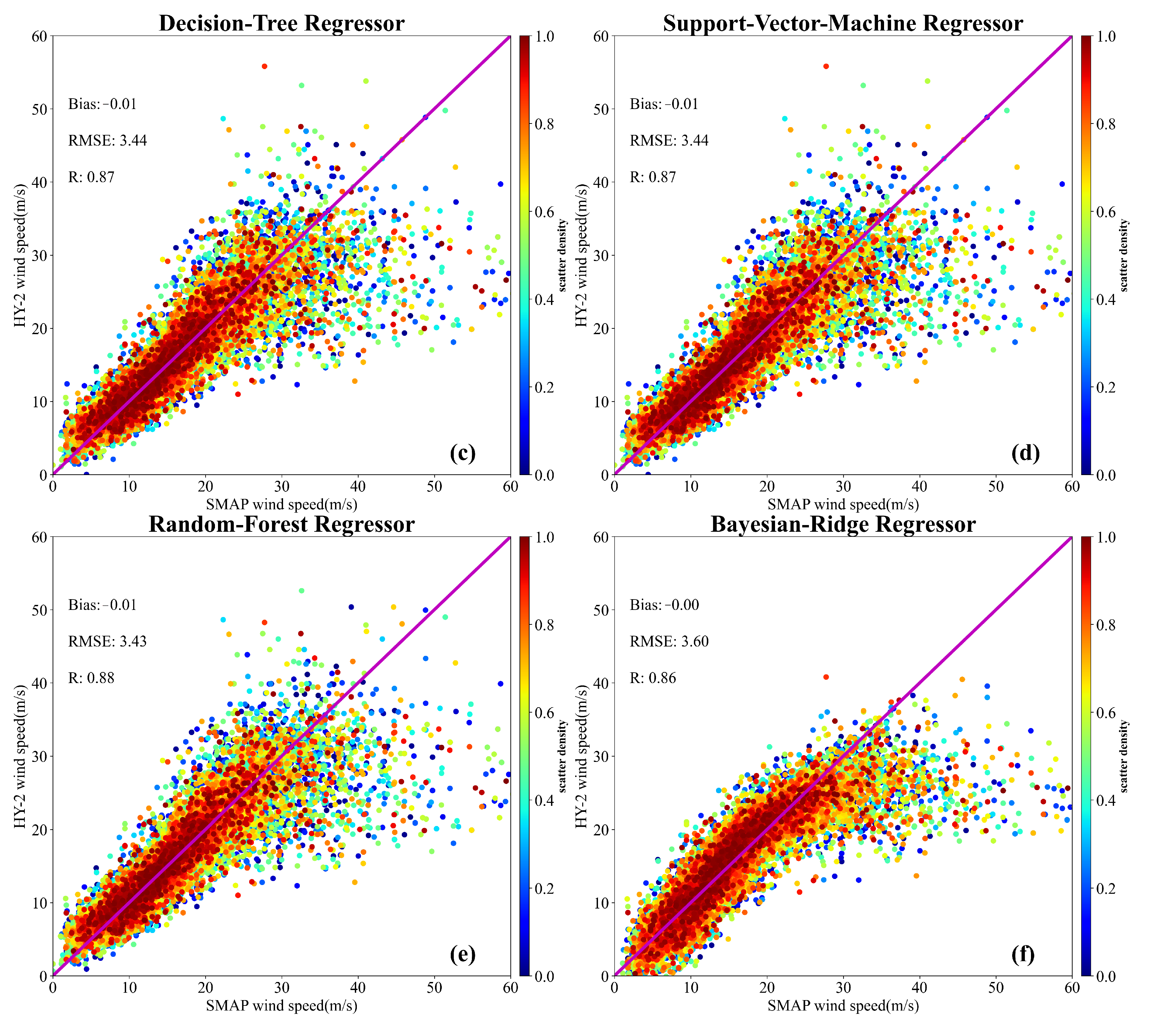
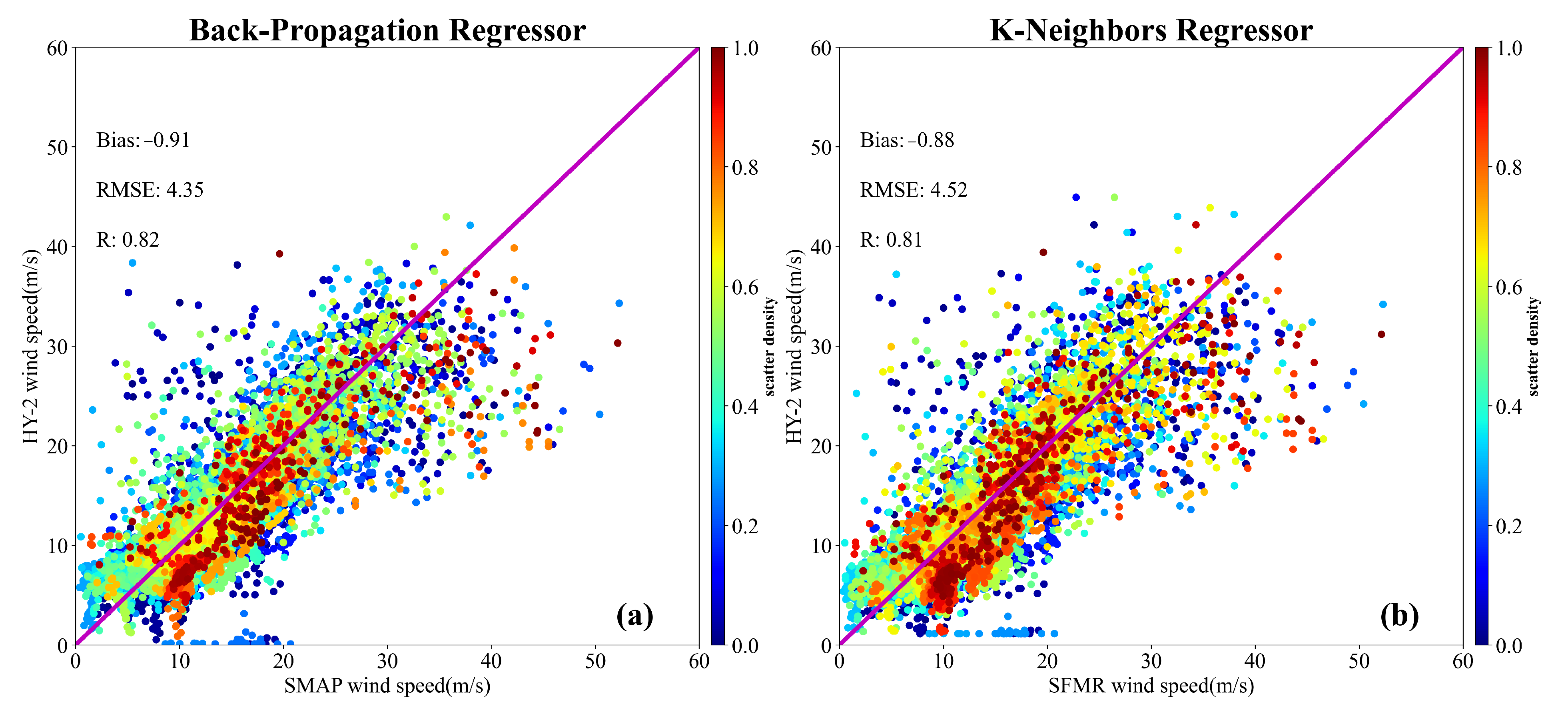
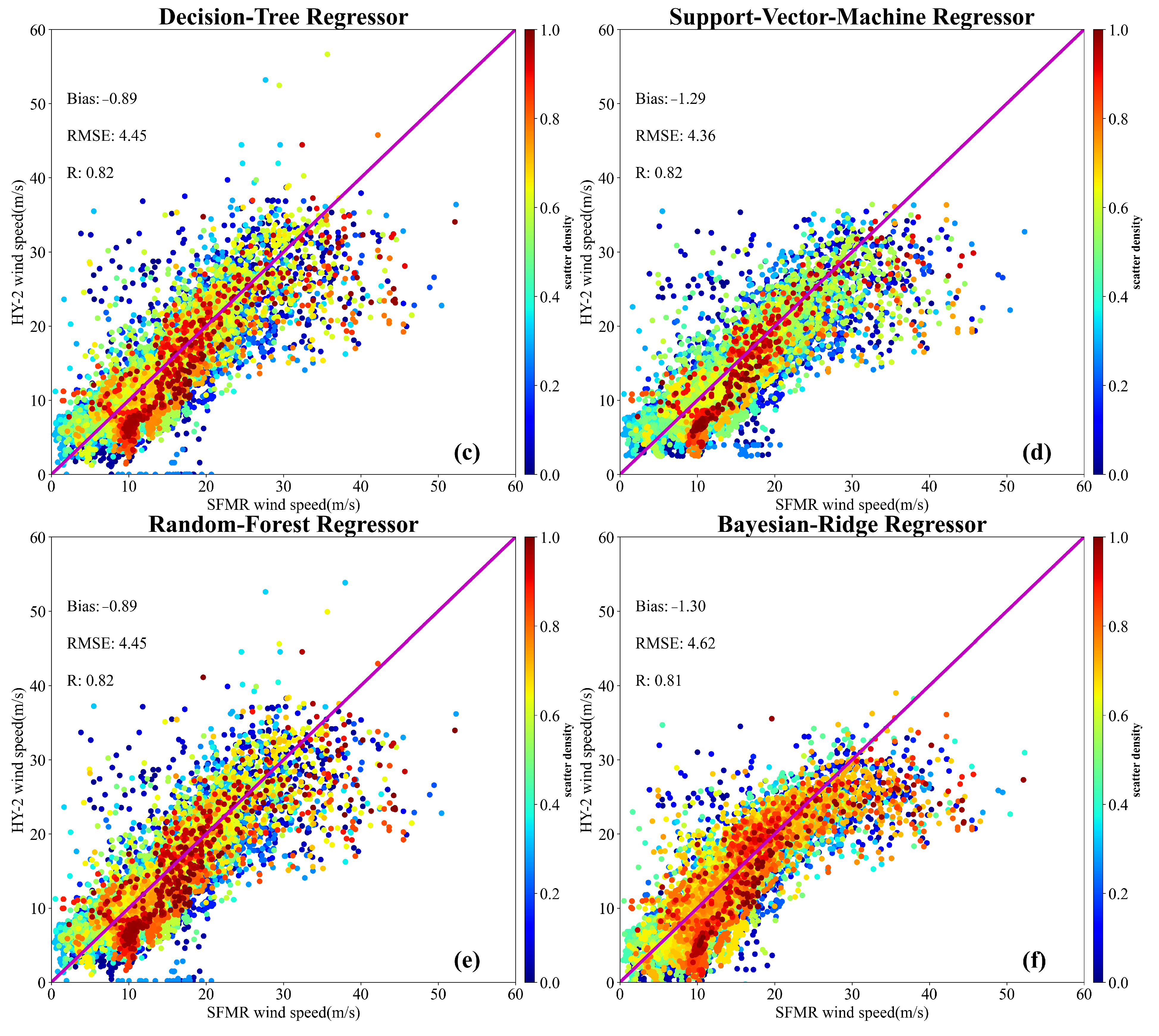
4.3.1. Implementation of Machine Learning Algorithms

Firstly, BP-NN is implemented based on the Python keras module. To prevent overfitting, the model is set to three layers: input layer, hidden layer, and output layer. The number of neurons is 128, 64, and 1, respectively. The activation function of the input layer and the hidden layer is “relu”, and the optimizer is “Adam”. Secondly, from the model trained 10–100 times, the GridsearchCV optimization is used to find the optimal model. In addition, the structure of the BP-NN model, the selection of the optimizer, and the activation function can be further optimized. Here, we only optimized the training times, although other parameters can also be optimized using GridsearchCV optimization.
The KNN, DT, SVM, RF, and BR algorithms are also implemented based on the Python sklearn module. The parameters of KNN include the weights of “uniform” and “distance”, and the number of neighbors ranges from 1 to 10. The GridsearchCV optimization is used to find the optimal KNN model. To facilitate the comparison of these methods, the DT, SVM, RF, and BR algorithms all maintain the default parameters in the sklearn module and seek the optimal parameter settings by GridsearchCV optimization.

4.3.2. Evaluation of Machine Learning Algorithms

Figure 6 presents the comparisons of the revised winds by the six machine learning algorithms and SMAP. From the distribution of the scatter diagram, as shown in Figure 6f, the performance of the BR algorithm in retrieving wind speed is the worst, with a large RMSE of 3.60 m/s and a low correlation coefficient of 0.86. These six machine learning algorithms all exhibit the phenomenon of the scattered points not being concentrated in the high wind speed range. From the perspective of bias, the wind speed retrieved by the six machine learning algorithms is a slight underestimate. In terms of statistical metrics, the BP-NN algorithm achieves the best inversion accuracy with a small RMSE of 3.40 m/s, and high correlation coefficient of 0.88. Compared with the RMSE (4.27 m/s) of the original HY-2B/C/D product with respect to SMAP, the BP-NN algorithm leads to an overall improvement of 20.4%.
Figure 7a shows the histogram of wind speed ranging from 1 to 35 m/s, which demonstrates that most data are distributed in the range 10–20 m/s. Figure 7b,c illustrates the average RMSE and bias for wind speed, ranging from 1 to 35 m/s in 1 m/s intervals of SMAP wind speed. It can be seen from Figure 7b that the RMSEs of the 5–25 m/s wind speed are almost the same before and after revision, and the RMSEs of the revised winds obtained by the BP-NN algorithm are smaller than those of the HY-2B/C/D original winds. This phenomenon also occurs in the evaluation of bias in wind speed before and after revision by the BP-NN algorithm compared to SMAP (Figure 7c). Overall, our proposed method can effectively improve the accuracy of high wind speed measurement.
Through the above statistical analysis, we can confirm the effectiveness of our proposed method based on the BP-NN algorithm. In order to ensure the authenticity of the revised winds, we compared the spatial structure of tropical cyclones with SMAP. A variety of swirling patterns found in the tropical cyclone eye are presented in Figure 8, including Bavi, Vamco, and Molave in 2020, and Urigae in 2021 over the Western North Pacific; Dor in 2019, Genevieve in 2020, and Grace and Larry in 2021 over the Atlantic Ocean and Eastern Pacific Ocean; and Harold in 2020 and Faraji in 2021 over the southern hemisphere ocean. From the spatial distribution of tropical cyclones, the high wind speed of the HY-2 scatterometer is lower than that of the SMAP radiometer, especially during Dor in 2019 (up to 50 m/s) and Urigae in 2021 (up to 70 m/s). After calibration using the BP-NN algorithm, the revised wind speed is in good agreement with SMAP, including wind speed and spatial distribution.

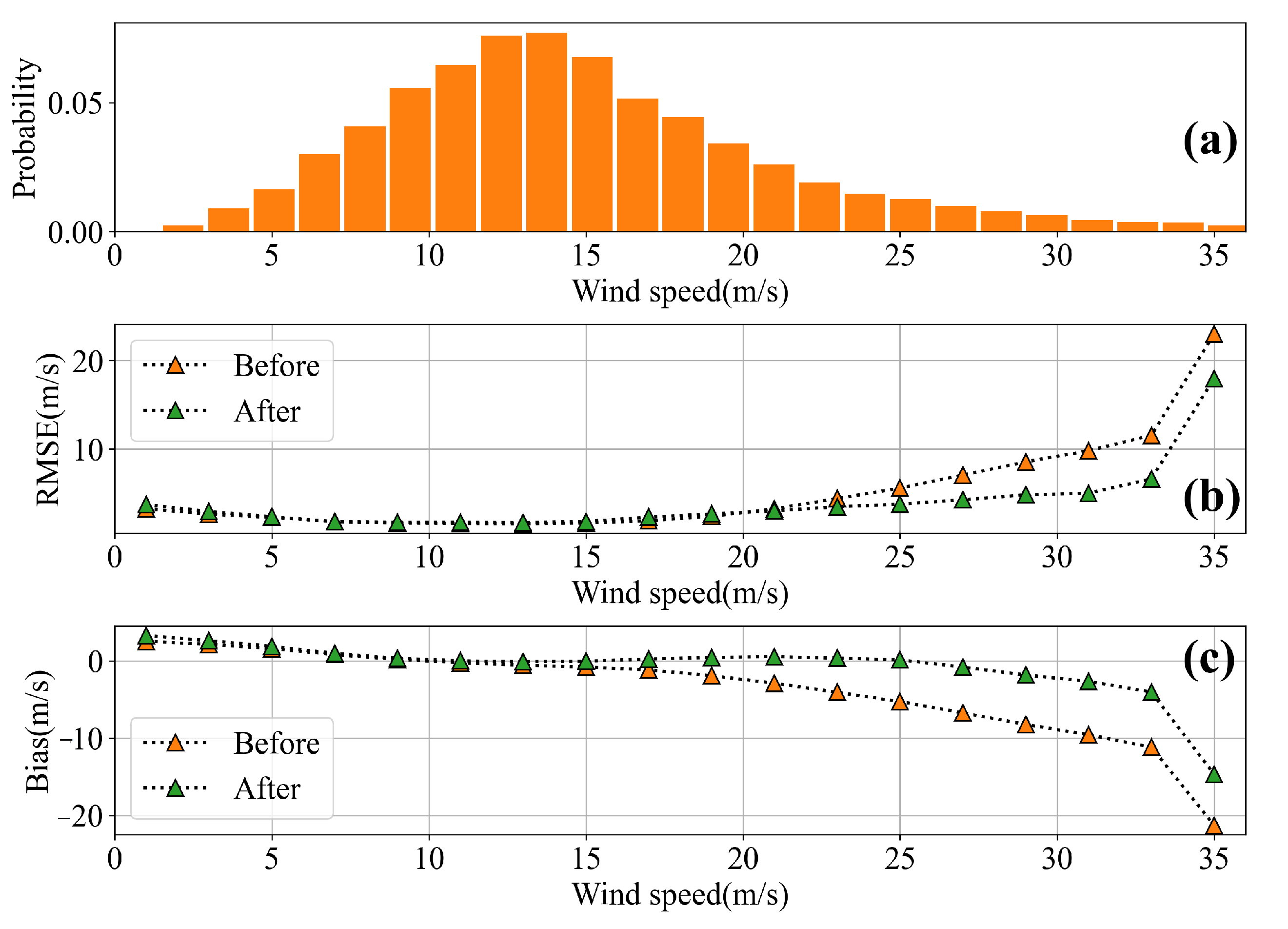
4.4. Comparisons of Revised Winds and SFMR Winds

According to the space–time window, the data of HY-2B/C/D winds from July 2019 to December 2021 are matched with SFMR measurements within the time window of ±30 min. Then, the spatial average of SFMR measurements within 25 km is selected as the reference for comparison. There are 38 tropical cyclones jointly captured by HY-2B/C/D and SFMR during the period 2019–2021, and 12,287 data pairs are used to evaluate the performance of the machine learning models. Figure 9 shows the comparisons of high wind speed between HY-2B/C/D and SFMR from July 2019 to December 2021. The performance of HY-2B/C/D high winds can be obtained with a bias of –2.46 m/s, an RMSE of 4.97 m/s, and an R of 0.81. From the distribution of scattered points in Figure 9, HY-2 also underestimates the wind speed (>20 m/s) relative to SFMR wind speed, which is the same as the result of SMAP comparison. The wind speed of SFMR is up to 50 m/s, while the wind speed of HY-2 is limited to within 30 m/s. In practical application, this underestimation of wind speed is fatal, making it necessary to correct it.
After collocating, the matchups of HY-2B/C/D and SFMR are input to these six machine learning models. Figure 10 demonstrates the performance and generalization ability of the machine learning models, including the (a) BP-NN, (b) KNN, (c) DT, (d) SVM, (e) RF and (f) BR algorithms. First, the BR algorithm shows a performance with a large RMSE of 4.62 m/s and a low correlation coefficient of 0.81, similar to the results of the 30% test dataset verification. From the distribution of scattered points in Figure 10f, it can be seen that the retrieved high wind speed is obviously underestimated. Second, the other five machine learning algorithms show relatively stable inversion performance and generalization ability with respect to those from the SFMR measurements. In particular, BP-NN also gives an optimal accuracy of 4.35 m/s in terms of RMSE, and the accuracy of HY-2B/C/D can be improved by 12.5%. The bias can be decreased from −2.46 m/s to −0.91 m/s and the correlation coefficient can also be improved slightly.
Heavy rainfall is often accompanied by tropical cyclones, which is likely one of the major drivers of algorithm performance [73,74]. The rain rate data are collocated from SFMR by the same procedure of wind collocation. As shown in Figure 11, it is found that the RMSE can be decreased from 5.03 m/s to 4.38 m/s, the bias can be decreased from −2.42 m/s to −0.24 m/s, and the correlation coefficient can also be improved slightly under rainy conditions. The comparison shows that the BP-NN method can also give stable wind speed accuracy under such conditions.
Figure 12a illustrates the histogram distribution of rain rate from 1 to 30 mm/h. Since the HY-2 scatterometer data are all subject to quality control, the rainfall rate of the data matched with the SFMR data is around 1 mm/h; however, the amount of strong rainfall data is not sufficient. From Figure 12b,c, it can be seen that the performance of the revised winds is better than that of the HY-2 scatterometer wind speed measurements, which shows the effectiveness of our model.

5. Conclusions

This work focuses on the evaluation and calibration of remotely sensed winds from the HY-2B/C/D scatterometers in tropical cyclones over the period from July 2019 to December 2021. SMAP high wind speeds are used as a stable reference to investigate the performance of the HY-2B/C/D scatterometers. After matching, it is found that HY-2 has a good ability to capture tropical cyclones globally due to its wide swath of 1700 km. However, comparisons demonstrate that high wind speeds are obviously underestimated by HY-2B/C/D scatterometers. In order to overcome the deficiency of HY-2B/C/D measurements, six machine learning algorithms are used to calibrate the high wind speeds of HY-2B/C/D, including the BP-NN, KNN, DT, SVM, RF, and BR algorithms. Through the verification of the 30% test dataset, it can be seen that the BP-NN algorithm achieves the best inversion accuracy, with a small RMSE of 3.40 m/s, and a high correlation coefficient of 0.88. In addition, the spatial distribution of the revised wind speed is in good agreement with that of SMAP, which will be of benefit for tropical cyclone monitoring by HY-2B/C/D scatterometer satellites. Finally, the performance of the six machine learning algorithms is verified by SFMR data, demonstrating that BP-NN also achieves the best inversion accuracy and that the performance can be improved by 12.5%. We also compared the wind speed accuracy under different rain rates and found that the BP-NN model can also provide stable wind speed accuracy under rainy conditions.
By using the relationship between HY-2B/C/D wind speed measurements and SMAP measurements, the performance of HY-2B/C/D in high wind speeds has been improved significantly based on machine learning algorithms. However, the parameters of each machine learning algorithm can be further optimized by GridsearchCV technology. The revised high wind speed of HY-2B/C/D scatterometers using machine learning algorithms shows good agreement with SMAP and SFMR up to 60 m/s, which is expected to play an important role in tropical cyclone intensity estimation, structure identification, model validation, and the numerical simulation of storm surges.

Author Contributions

Conceptualization, X.L, J.Y. and G.H.; methodology, X.L. and J.W.; software, validation, and formal analysis, X.L.; writing—original draft preparation, X.L. and J.W.; writing—review and editing, J.W., J.Y. and G.H. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Scientific Research Fund of the Second Institute of Oceanography, MNR, grant no. JB2205, and was supported by the Innovation Group Project of Southern Marine Science and Engineering Guangdong Laboratory(Zhuhai) (no. 311021004).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Katsaros, K. Microwave Remote Sensing of Tropical Cyclones from Space. J. Oceanogr. 2002, 58, 137–151. [Google Scholar] [CrossRef]
  2. Xu, X.; Dong, X.; Zhu, D.; Lang, S. High Winds From Combined Active and Passive Measurements of HY-2A Satellite. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 4339–4348. [Google Scholar] [CrossRef]
  3. Lin, M.; Zou, J.; Xie, X.; Zhang, Y. HY-2A Microwave Scatterometer Wind Retrieval Algorithm. Eng. Sci. 2013, 68, 68–74. [Google Scholar]
  4. Lin, M.; Jiang, X. HY-2 Ocean Dynamic Environment Mission and Payloads. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 5167–5170. [Google Scholar] [CrossRef]
  5. Lin, M.; Zhang, Y.; Yuan, X. The Development Course and Trend of Ocean Remote Sensing Satellite. Acta Oceanol. Sin. 2015, 37, 1–10. [Google Scholar] [CrossRef]
  6. Yun, T.; Dong, X. Study of Image Reconstruction Techniques for Spaceborne Scatterometer. Remote Sens. Technol. Appl. 2015, 30, 495–503. [Google Scholar] [CrossRef]
  7. Li, Y.; Min, J.; Rui, Y.; Chen, W. System Design of Microwave Radiometer of HY-2A satellite. Eng. Sci. 2013, 15, 39–43. [Google Scholar] [CrossRef]
  8. Dong, X.; Lang, S.; Wang, T.; Liu, H. Accuracy and Resolution Analysis of the Pencil Beam Radar Scatterometer Onboard China’s HY-2 Satellite. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; p. 44674470. [Google Scholar] [CrossRef]
  9. Jiang, X.; Wang, X. The Technology of Precise Orbit Determination for HY-2A Satellite. Eng. Sci. 2013, 15, 19–24. [Google Scholar]
  10. Xu, X.; Xu, K.; Wang, Z.; Liu, H.; Wang, L. Compensating the PTR and LPF Features of the HY-2A Satellite Altimeter Utilizing Look-Up Tables. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 149–159. [Google Scholar] [CrossRef]
  11. Zhang, Y.; Lin, M.; Song, Q. Evaluation of Geolocation Errors of the Chinese HY-2A Satellite Microwave Scatterometer. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6124–6133. [Google Scholar] [CrossRef]
  12. Zhang, L.; Yu, H.; Wang, Z.; Yin, X.; Yang, L.; Du, H.; Li, B.; Wang, Y.; Zhou, W. Evaluation of the Initial Sea Surface Temperature From the HY-2B Scanning Microwave Radiometer. IEEE Geosci. Remote Sens. Lett. 2020, 18, 137–141. [Google Scholar] [CrossRef]
  13. Martin, S. An Introduction to Ocean Remote Sensing: Passive Microwave Observations of the Atmosphere and Ocean Surface; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
  14. Zhao, K.; Zhao, C.; Chen, G. Evaluation of Chinese Scatterometer Ocean Surface Wind Data: Preliminary Analysis. Earth Space Sci. 2021, 8, e2020EA001482. [Google Scholar] [CrossRef]
  15. Stoffelen, A. Scatterometry. Ph.D. Thesis, University of Utrecht, Utrecht, The Netherlands, 1998. [Google Scholar]
  16. Meissner, T.; Smith, D.; Wentz, F. A 10 year intercomparison between collocated Special Sensor Microwave Imager oceanic surface wind speed retrievals and global analyses. J. Geophys. Res. Oceans 2001, 106, 11731–11742. [Google Scholar] [CrossRef]
  17. Wang, X.; Liu, L.; Shi, H.; Dong, X.; Zhu, D. In-orbit Calibration and Performance Evaluation of HY-2 Scatterometer. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 4614–4616. [Google Scholar] [CrossRef]
  18. Xing, J.; Shi, J.; Lei, Y.; Huang, X.Y.; Liu, Z. Evaluation of HY-2A Scatterometer Wind Vectors Using Data from Buoys, ERA-Interim and ASCAT during 2012–2014. Remote Sens. 2016, 8, 390. [Google Scholar] [CrossRef]
  19. Wang, H.; Zhu, J.; Lin, M.; Huang, X.; Zhao, Y.; Chen, C.; Zhang, Y.; Peng, H. First Six Months Quality Assessment of HY-2A SCAT Wind Products Using in Situ Measurements. Acta Oceanol. Sin. 2013, 32, 27–33. [Google Scholar] [CrossRef]
  20. Yang, X.; Liu, G.; Li, Z.; Yu, Y. Preliminary Validation of Ocean Surface Vector Winds Estimated from China’s HY-2A Scatterometer. Int. J. Remote Sens. 2014, 35, 4532–4543. [Google Scholar] [CrossRef]
  21. Lin, M.; Ye, X.; Yuan, X. The First Quantitative Joint Observation of Typhoon by Chinese GF-3 SAR and HY-2A Microwave Scatterometer. Acta Oceanol. Sin. 2017, 36, 1–3. [Google Scholar] [CrossRef]
  22. Zheng, M.; Li, X.M.; Sha, J. Comparison of Sea Surface Wind Field Measured by HY-2A Scatterometer and WindSat in Global Oceans. Acta Oceanol. Sin. 2019, 37, 9. [Google Scholar] [CrossRef]
  23. Wang, Z.; Stoffelen, A.; Zou, J.; Lin, W.; Verhoef, A.; Zhang, Y.; He, Y.; Lin, M. Validation of New Sea Surface Wind Products From Scatterometers Onboard the HY-2B and MetOp-C Satellites. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4387–4394. [Google Scholar] [CrossRef]
  24. Wang, J.; Aouf, L.; Jia, Y.; Zhang, Y. Validation and Calibration of Significant Wave Height and Wind Speed Retrievals from HY2B Altimeter Based on Deep Learning. Remote Sens. 2020, 12, 2858. [Google Scholar] [CrossRef]
  25. Shi, X.; Duan, B.; Ren, K. A More Accurate Field-to-Field Method towards the Wind Retrieval of HY-2B Scatterometer. Remote Sens. 2021, 13, 2419. [Google Scholar] [CrossRef]
  26. Wang, Z.; Zou, J. Scatterometer Sea Surface Wind Product Validation for HY-2C. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 6156–6164. [Google Scholar] [CrossRef]
  27. Wang, Z.; Zou, J.; Zhang, Y.; Stoffelen, A.; Lin, W.; He, Y.; Feng, Q.; Zhang, Y.; Mu, B.; Lin, M. Intercalibration of Backscatter Measurements among Ku-Band Scatterometers Onboard the Chinese HY-2 Satellite Constellation. Remote Sens. 2021, 13, 4783. [Google Scholar] [CrossRef]
  28. Quilfen, Y.; Prigent, C.; Chapron, B.; Mouche, A.; Houti, N. The Potential of QuikSCAT and WindSat Observations for the Estimation of Sea Surface Wind Vector under Severe Weather Conditions. J. Geophys. Res. Oceans. 2007, 112, C09023. [Google Scholar] [CrossRef]
  29. Weissman, D.; Stiles, B.; Hristova-Veleva, S.; Long, D.; Smith, D.; Hilburn, K.; Jones, W. Challenges to Satellite Sensors of Ocean Winds: Addressing Precipitation Effects. J. Atmos. Ocean. Technol. 2012, 29, 356–374. [Google Scholar] [CrossRef]
  30. Chang, P.; Jelenak, Z.; Said, F.; Sienkiewicz, J. High Wind Observations within Extratropical Cyclones as Observed by Different Microwave Radiometers and Scatterometers. In Proceedings of the JPGU-AGU Joint Meeting 2017, Chiba, Japan, 20–24 May 2017. [Google Scholar]
  31. Cornford, D.; Nabney, I.; Ramage, G. Improved Neural Network Scatterometer Forward Models. J. Geophys. Res. 2001, 106, 22331–22338. [Google Scholar] [CrossRef]
  32. Stiles, B.; Dunbar, R. A Neural Network Technique for Improving the Accuracy of Scatterometer Winds in Rainy Conditions. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3114–3122. [Google Scholar] [CrossRef]
  33. Chen, K.; Dong, X.; Xingou, X.; Lang, S. The Study on Oceanic Vector Wind Field Retrieve Technique based on Neural Networks of Microwave Scatterometer. Remote Sens. Technol. Appl. 2017, 32, 8. [Google Scholar] [CrossRef]
  34. Mouche, A.; Chapron, B.; Zhang, B.; Husson, R. Combined Co- and Cross-Polarized SAR Measurements Under Extreme Wind Conditions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6746–6755. [Google Scholar] [CrossRef]
  35. Zabolotskikh, E.; Mitnik, L.; Chapron, B. New Approach for Severe Marine Weather Study Using Satellite Passive Microwave Sensing. Geophys. Res. Lett. 2013, 40, 3347–3350. [Google Scholar] [CrossRef] [Green Version]
  36. Reul, N.; Tenerelli, J.; Chapron, B.; Vandemark, D.; Quilfen, Y.; Kerr, Y. SMOS Satellite L-band Radiometer: A New Capability for Oceansurface Remote Sensing in Hurricanes. J. Geophys. Res. Oceans 2012, 117, 1–24. [Google Scholar] [CrossRef]
  37. Yueh, S.; Fore, A.; Tang, W.; Hayashi, A.; Stiles, B.; Reul, N.; Weng, Y.; Zhang, F. SMAP L-Band Passive Microwave Observations of Ocean Surface Wind During Severe Storms. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7339–7350. [Google Scholar] [CrossRef]
  38. Meissner, T.; Ricciardulli, L.; Wentz, F. Capability of the SMAP Mission to Measure Ocean Surface Winds in Storms. Bull. Am. Meteorol. Soc. 2017, 98, 1660–1677. [Google Scholar] [CrossRef]
  39. Meissner, T.; Ricciardulli, L.; Wentz, F. Ocean Vector Winds in Storms from the SMAP L-Band Radiometer. Technical Report. In Proceedings of the International Meeting of Measuring High Wind Speeds Over the Ocean, Exeter, UK, 15–17 November 2016. [Google Scholar]
  40. Ricciardulli, L.; Mears, C.; Manaster, A.; Meissner, T. Assessment of CYGNSS Wind Speed Retrievals in Tropical Cyclones. Remote Sens. 2021, 13, 5110. [Google Scholar] [CrossRef]
  41. Manaster, A.; Ricciardulli, L.; Meissner, T. Tropical Cyclone Winds from WindSat, AMSR2, and SMAP: Comparison with the HWRF Model. Remote Sens. 2021, 13, 2347. [Google Scholar] [CrossRef]
  42. Swift, C.; DeHority, D.; Black, P.G.; Chien, J.Z. Microwaveremotesensing of Ocean Surface Wind Speedand Rain Ratesover Tropical Storms; NASA. Marshall Space Flight Center Frontiers of Remote Sensing of the Oceans and Troposphere from Air and Space Platforms: Shoresh, Israel, 1984; pp. 281–286. [Google Scholar]
  43. Uhlhorn, E.W.; Black, P.G.; Franklin, J.L.; Goodberlet, M.; Carswell, J.; Goldstein, A.S. Hurricane Surface Wind Measurements from an Operational Stepped Frequency Microwave Radiometer. Mon. Weather Rev. 2007, 135, 3070–3085. [Google Scholar] [CrossRef]
  44. Gao, Y.; Sun, J.; Zhang, J.; Guan, C. Extreme Wind Speeds Retrieval Using Sentinel-1 IW Mode SAR Data. Remote Sens. 2021, 13, 1867. [Google Scholar] [CrossRef]
  45. Klotz, B.W.; Uhlhorn, E.W. Improved Stepped Frequency Microwave Radiometer Tropical Cyclone Surface Winds in Heavy Precipitation. J. Atmos. Ocean Technol. 2014, 31, 2392–2408. [Google Scholar] [CrossRef]
  46. Rumelhart, D.E.; McClelland, J.L. Parallel Distributed Processing: Explorations in the Microstructure of Cognition; MIT Press: Cambridge, UK, 1986. [Google Scholar]
  47. Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
  48. Chen, K.S.; Tzeng, Y.C.; Chen, P.C. Retrieval of Ocean Winds from Satellite Scatterometer by a Neural Network. IEEE Trans. Geosci. Remote Sens. 2002, 37, 247–256. [Google Scholar] [CrossRef]
  49. Lin, M.; Song, X.; Jiang, X. Neural Network Wind Retrieval from ERS -1/2 Scatterometer Data. Acta Oceanol. Sin. 2006, 25, 35–39. [Google Scholar] [CrossRef]
  50. Xie, X.; Wang, J.; Lin, M. A Neural Network-Based Rain Effect Correction Method for HY-2A Scatterometer Backscatter Measurements. Remote Sens. 2020, 12, 1648. [Google Scholar] [CrossRef]
  51. Cortes, C.; Vapnik, V. Support-vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
  52. Sangitab, P.; Deshmukh, S.R. Use of Support Vector Machine for Wind Speed Prediction. In IEEE 2011 International Conference on Power and Energy Systems (ICPS); International Conference on Power and Energy Systems: Chennai, India, 2011; pp. 1–8. [Google Scholar] [CrossRef]
  53. Sreelakshmi, K.; Ramakanthkumar, P. Performance Evaluation of Short Term Wind Speed Prediction Techniques. IJCSNS Int. J. Comput. Sci. Netw. Secur. 2008, 8, 162–169. [Google Scholar]
  54. Larose, D.; Larose, C. Discovering Knowledge in Data; Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; pp. 96–103. [Google Scholar] [CrossRef]
  55. France, S.; Douglas, C.J.; Xiong, H. Distance Metrics for High Dimensional Nearest Neighborhood Recovery: Compression and Normalization. Inform. Sci. 2012, 184, 92–110. [Google Scholar] [CrossRef]
  56. Yesilbudak, M.; Sagiroglu, S.; Colak, I. A New Approach to Very Short Term Wind Speed Prediction Using K-nearest Neighbor Classification. Energ. Convers. Manag. 2013, 69, 77–86. [Google Scholar] [CrossRef]
  57. Hunt, E. Selection and Reception Conditions in Grammar and Concept Learning. J. Verbal Learn. Verbal Behav. 1966, 4, 211–215. [Google Scholar] [CrossRef]
  58. Gross, D. Induction and ID/3: More Powerful Than We Think. Expert Syst. 1988, 5, 348. [Google Scholar] [CrossRef]
  59. Perner, P.; Zscherpel, U.; Jacobsen, C. A Comparison between Neural Networks and Decision Trees Based on Data from Industrial Radiographic Testing. Pattern Recogn. Lett. 2001, 22, 47–54. [Google Scholar] [CrossRef]
  60. Breiman, L. Random Forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  61. Marwala, T.; Leke, C.A. Decision Trees and Random Forests. In Handbook of Machine Learning; World Scientific: Singapore, 2019; Chapter 11; pp. 199–214. [Google Scholar] [CrossRef]
  62. Dietterich, T. An Experimental Comparison of Three Methods for Constructing Ensembles of Decision Trees: Bagging, Boosting, and Randomization. Mach. Learn. 2000, 40, 139–157. [Google Scholar] [CrossRef]
  63. Liaw, A.; Wiener, M. Classification and Regression by Random Forest. Comput. Sci. 2002, 23, 18–22. [Google Scholar]
  64. Rodriguez-Galiano, V.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J. An Assessment of the Effectiveness of a Random Forest Classifier for Land-cover Classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
  65. Miao, X.; Heaton, J.; Zheng, S.; Charlet, D.; Liu, H. Applying Tree-based Ensemble Algorithms to the Classification of Ecological Zones Using Multi-temporal Multi-source Remote-sensing Data. Int. J. Remote Sens. 2012, 33, 1823–1849. [Google Scholar] [CrossRef]
  66. Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
  67. Denison, D. Contemporary Developments in Bayesian Analysis and Statistical Decision Theory: A Festschrift for William E. Strawderman||Bayesian Prediction with Adaptive Ridge Estimators; Institute of Mathematical Statistics: Hayward, CA, USA, 2012. [Google Scholar] [CrossRef]
  68. Mackay, D. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
  69. Troskie, D.O.; Chalton, C.G. A Bayesian Estimate for the Constants in Ridge Regression. S. Afr. Stat. J. 1996, 30. [Google Scholar] [CrossRef]
  70. Tipping, M. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
  71. Yang, X.; Li, D. Successive Optimization Method via Parametric Monotone Composition Formulation. J. Global Optim. 2000, 16, 355–369. [Google Scholar] [CrossRef]
  72. Arlot, S.; Lerasle, M. Why V=5 is enough in V-fold cross-validation. HAL-INRIA 2012, 17, 7256–7305. [Google Scholar]
  73. Wang, Y. Recent research progress on tropical cyclone structure and intensity. Trop. Cyclone Res. Rev 2012, 1, 254–275. [Google Scholar] [CrossRef]
  74. Wu, L.; Tian, W.; Liu, Q.; Cao, J.; Knaff, J.A. Implications of the Observed Relationship between Tropical Cyclone Size and Intensity over the Western North Pacific. J. Clim. 2015, 28, 9501–9506. [Google Scholar] [CrossRef]
Remotesensing 14 04654 g001 550
Figure 1. Methodology for revising the high wind speed of HY-2B/C/D scatterometers.
Figure 1. Methodology for revising the high wind speed of HY-2B/C/D scatterometers.
Remotesensing 14 04654 g001
Remotesensing 14 04654 g002 550
Figure 2. Global distribution of collocations between HY-2B/C/D series scatterometers and the SMAP radiometer under tropical cyclone conditions during 2019–2021 (0.25 ∘ × 0.25 ∘ grid). (a) Number of collocated HY-2B/C/D scatterometers and the SMAP radiometer; (b–d) are the same for HY-2B, HY-2C, and HY-2D, respectively.
Figure 2. Global distribution of collocations between HY-2B/C/D series scatterometers and the SMAP radiometer under tropical cyclone conditions during 2019–2021 (0.25 ∘ × 0.25 ∘ grid). (a) Number of collocated HY-2B/C/D scatterometers and the SMAP radiometer; (b–d) are the same for HY-2B, HY-2C, and HY-2D, respectively.
Remotesensing 14 04654 g002
Remotesensing 14 04654 g003 550
Figure 3. Two-dimensional scatter comparisons of high wind speed between HY-2B/C/D scatterometers and the SMAP radiometer from July 2019 to December 2021.
Figure 3. Two-dimensional scatter comparisons of high wind speed between HY-2B/C/D scatterometers and the SMAP radiometer from July 2019 to December 2021.
Remotesensing 14 04654 g003
Remotesensing 14 04654 g004 550
Figure 4. Two-dimensional histogram of collocations between HY-2B/C/D and SMAP in the range of 0–50 m/s.
Figure 4. Two-dimensional histogram of collocations between HY-2B/C/D and SMAP in the range of 0–50 m/s.
Remotesensing 14 04654 g004
Remotesensing 14 04654 g005 550
Figure 5. RMSE and bias in wind speed from HY-2B/C/D scatterometers compared to SMAP. The dotted line is marked with triangles to represent RMSE, and the dotted line is marked with circles to represent bias (HY-2–SMAP).
Figure 5. RMSE and bias in wind speed from HY-2B/C/D scatterometers compared to SMAP. The dotted line is marked with triangles to represent RMSE, and the dotted line is marked with circles to represent bias (HY-2–SMAP).
Remotesensing 14 04654 g005
Remotesensing 14 04654 g006a 550Remotesensing 14 04654 g006b 550
Figure 6. Scatterplots of the revised high wind speeds from HY-2B/C/D scatterometers by machine learning with respect to those from the SMAP radiometer. (a) BP-NN algorithm; (b) KNN algorithm; (c) DT algorithm; (d) SVM algorithm; (e) RF algorithm; and (f) BR algorithm.
Figure 6. Scatterplots of the revised high wind speeds from HY-2B/C/D scatterometers by machine learning with respect to those from the SMAP radiometer. (a) BP-NN algorithm; (b) KNN algorithm; (c) DT algorithm; (d) SVM algorithm; (e) RF algorithm; and (f) BR algorithm.
Remotesensing 14 04654 g006aRemotesensing 14 04654 g006b
Remotesensing 14 04654 g007 550
Figure 7. Comparisons before and after revision by the BP-NN algorithm. (a) Two-dimensional histogram of 30% test set in the range 0–35 m/s. (b) RMSE in wind speed before and after revision by the BP-NN algorithm compared to SMAP. (c) Bias in wind speed before and after revision by the BP-NN algorithm compared to SMAP.
Figure 7. Comparisons before and after revision by the BP-NN algorithm. (a) Two-dimensional histogram of 30% test set in the range 0–35 m/s. (b) RMSE in wind speed before and after revision by the BP-NN algorithm compared to SMAP. (c) Bias in wind speed before and after revision by the BP-NN algorithm compared to SMAP.
Remotesensing 14 04654 g007
Remotesensing 14 04654 g008 550
Figure 8. The wind field distribution before and after revision by the BP-NN algorithm in the tropical cyclone eye.
Figure 8. The wind field distribution before and after revision by the BP-NN algorithm in the tropical cyclone eye.
Remotesensing 14 04654 g008
Remotesensing 14 04654 g009 550
Figure 9. Two-dimensional scatter comparisons of high wind speed between HY-2B/C/D and SFMR from July 2019 to December 2021.
Figure 9. Two-dimensional scatter comparisons of high wind speed between HY-2B/C/D and SFMR from July 2019 to December 2021.
Remotesensing 14 04654 g009
Remotesensing 14 04654 g010a 550Remotesensing 14 04654 g010b 550
Figure 10. Scatterplots of the revised high wind speed measurements from HY-2B/C/D scatterometers by machine learning with respect to those from SFMR measurements. (a) BP-NN algorithm; (b) KNN algorithm; (c) DT algorithm; (d) SVM algorithm; (e) RF algorithm; and (f) BR algorithm.
Figure 10. Scatterplots of the revised high wind speed measurements from HY-2B/C/D scatterometers by machine learning with respect to those from SFMR measurements. (a) BP-NN algorithm; (b) KNN algorithm; (c) DT algorithm; (d) SVM algorithm; (e) RF algorithm; and (f) BR algorithm.
Remotesensing 14 04654 g010aRemotesensing 14 04654 g010b
Remotesensing 14 04654 g011 550
Figure 11. Statistical analysis (a) before and (b) after revision by the BP-NN algorithm under rainfall conditions.
Figure 11. Statistical analysis (a) before and (b) after revision by the BP-NN algorithm under rainfall conditions.
Remotesensing 14 04654 g011
Remotesensing 14 04654 g012 550
Figure 12. Comparisons before and after revision by the BP-NN algorithm with respect to SFMR. (a) Two-dimensional histogram of rain rate in the range 0–30 mm/h. (b) RMSE in wind speed before and after revision by the BP-NN algorithm under different rain rate conditions. (c) Bias in wind speed before and after revision by the BP-NN algorithm under different rain rate conditions.
Figure 12. Comparisons before and after revision by the BP-NN algorithm with respect to SFMR. (a) Two-dimensional histogram of rain rate in the range 0–30 mm/h. (b) RMSE in wind speed before and after revision by the BP-NN algorithm under different rain rate conditions. (c) Bias in wind speed before and after revision by the BP-NN algorithm under different rain rate conditions.
Remotesensing 14 04654 g012
Table
Table 1. Basic information of the Haiyang-2 satellite series.
Table 1. Basic information of the Haiyang-2 satellite series.
HY-2AHY-2BHY-2CHY-2D
Launch time16 August 202125 October 201821 September 202019 May 2021
Platform orbitSun-synchronousSun-synchronousSun-synchronousSun-synchronous
Orbit altitude971 km980 km971 km971 km
Revisit period10 day10 day10 day10 day
Frequency13.256 GHz13.256 GHz13.256 GHz13.256 GHz
Bandwidth1 MHz1 MHz1 MHz1 MHz
PolarizationHH + VVHH + VVHH + VVHH + VV
AntennaRotating pencil-beamRotating pencil-beamRotating pencil-beamRotating pencil-beam
Spatial resolution25 km25 km25 km25 km
Swath1700/1350 km1700/1350 km1700/1350 km1700/1350 km
Equator crossing time (local time zone)6 pm ascending /6 am descending6 pm ascending /6 am descending6 pm ascending /6 am descending6 pm ascending /6 am descending
Wind speed precision2 m/s or 10%2 m/s or 10%2 m/s or 10%2 m/s or 10%
Wind direction precision20 ∘ 20 ∘ 20 ∘ 20 ∘
Table
Table 2. Summary of HY-2B/C/D Level 2B wind vector products used for evaluation and calibration.
Table 2. Summary of HY-2B/C/D Level 2B wind vector products used for evaluation and calibration.
HY-2 SatelliteTime Span
HY-2B3 July 2019–31 December 2021
HY-2C25 September 2020–31 December 2021
HY-2D24 June 2021–31 December 2021
Table
Table 3. Summary of tropical cyclones captured by SMAP during the period 2019–2021.
Table 3. Summary of tropical cyclones captured by SMAP during the period 2019–2021.
YearTropical OceanNumber of Captured Tropical Cyclones
SMAPHY-2BHY-2CHY-2D
2019Atlantic Ocean3300
Western Pacific Ocean131100
Eastern Pacific Ocean3200
Northern Indian Ocean4100
Southern hemisphere13200
2020Atlantic Ocean232030
Western Pacific Ocean151140
Eastern Pacific Ocean111000
Northern Indian Ocean3000
Southern hemisphere282150
2021Atlantic Ocean151474
Western Pacific Ocean171148
Eastern Pacific Ocean151365
Northern Indian Ocean4310
Southern hemisphere232071
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Li, X.; Yang, J.; Wang, J.; Han, G. Evaluation and Calibration of Remotely Sensed High Winds from the HY-2B/C/D Scatterometer in Tropical Cyclones. Remote Sens. 2022, 14, 4654. https://doi.org/10.3390/rs14184654

AMA Style

Li X, Yang J, Wang J, Han G. Evaluation and Calibration of Remotely Sensed High Winds from the HY-2B/C/D Scatterometer in Tropical Cyclones. Remote Sensing. 2022; 14(18):4654. https://doi.org/10.3390/rs14184654

Chicago/Turabian Style

Li, Xiaohui, Jingsong Yang, Jiuke Wang, and Guoqi Han. 2022. "Evaluation and Calibration of Remotely Sensed High Winds from the HY-2B/C/D Scatterometer in Tropical Cyclones" Remote Sensing 14, no. 18: 4654. https://doi.org/10.3390/rs14184654

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop