An Advanced Approach to Improve Synchronization Phase Accuracy with Compressive Sensing for LT-1 Bistatic Spaceborne SAR
Abstract
1. Introduction
2. Phase Synchronization Scheme
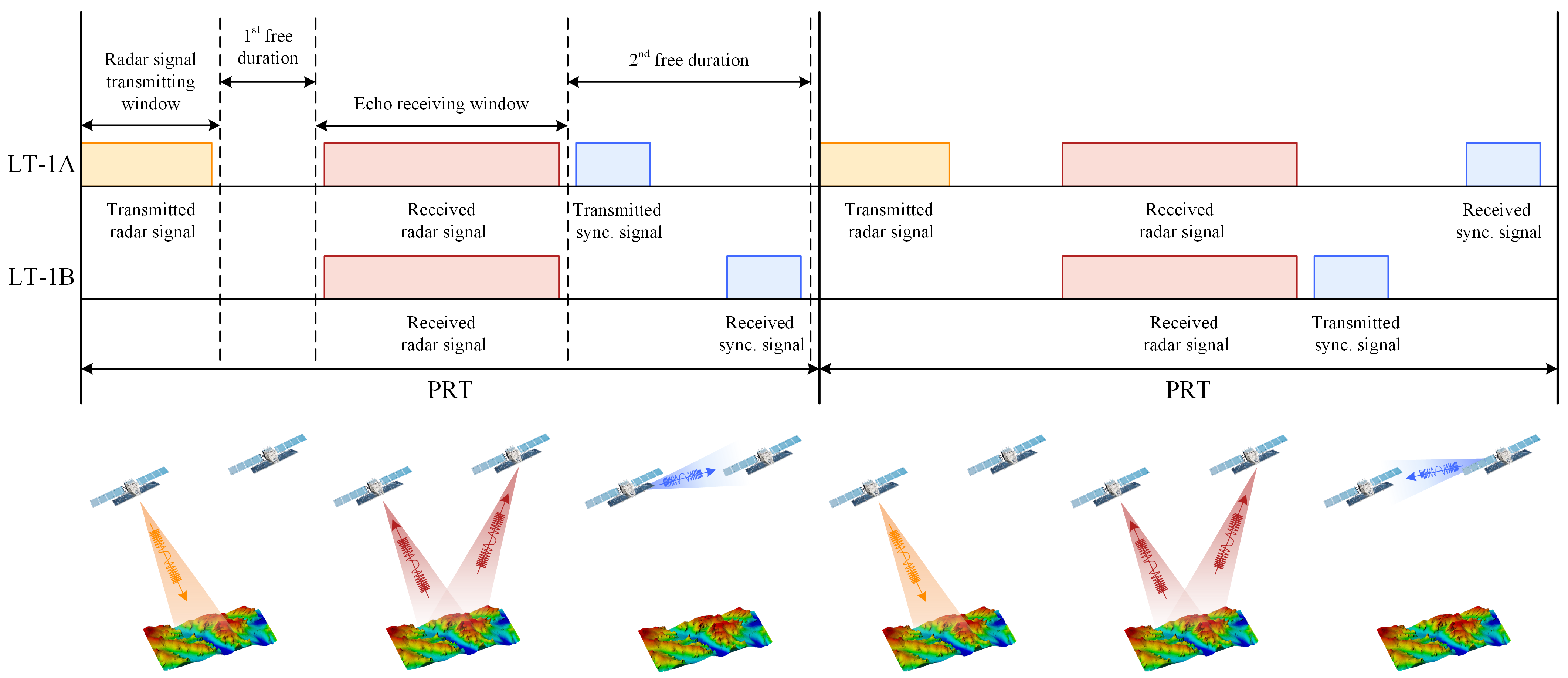
2.1. Synchronization Scheme of LT-1
- (1)
- Timing control: the LT-1 system employs GNSS-disciplined rubidium clock USOs to calibrate time, which combines the excellent short-term stability of high-quality USO and the long-term advantages of GNSS signal. The frequency stability of the rubidium clock can be up to , and such a stable clock source contributes to the high accuracy of timing control.
- (2)
- Spatial coverage: compared with the six horn antennas of TanDEM-X, only four quadrifilar helix antennas as shown in Figure 2 are equipped in LT-1, which are smaller and lighter. Each antenna is designed to be identical and with a wide beam coverage, so the transceiver antenna pair can be selected according to the principle of maximum signal-to-noise ratio (SNR) to realize 360° omnidirectional communication during an orbital period.
- (3)
- Signal selection: linear frequency modulation (LFM) signal with the same carrier frequency as radar signal is transmitted in synchronization link, which reduces the complexity of system design and processing algorithm. After demodulation and pulse compression, the synchronization phase can be extracted from the peak position of the synchronization signal with high SNR.
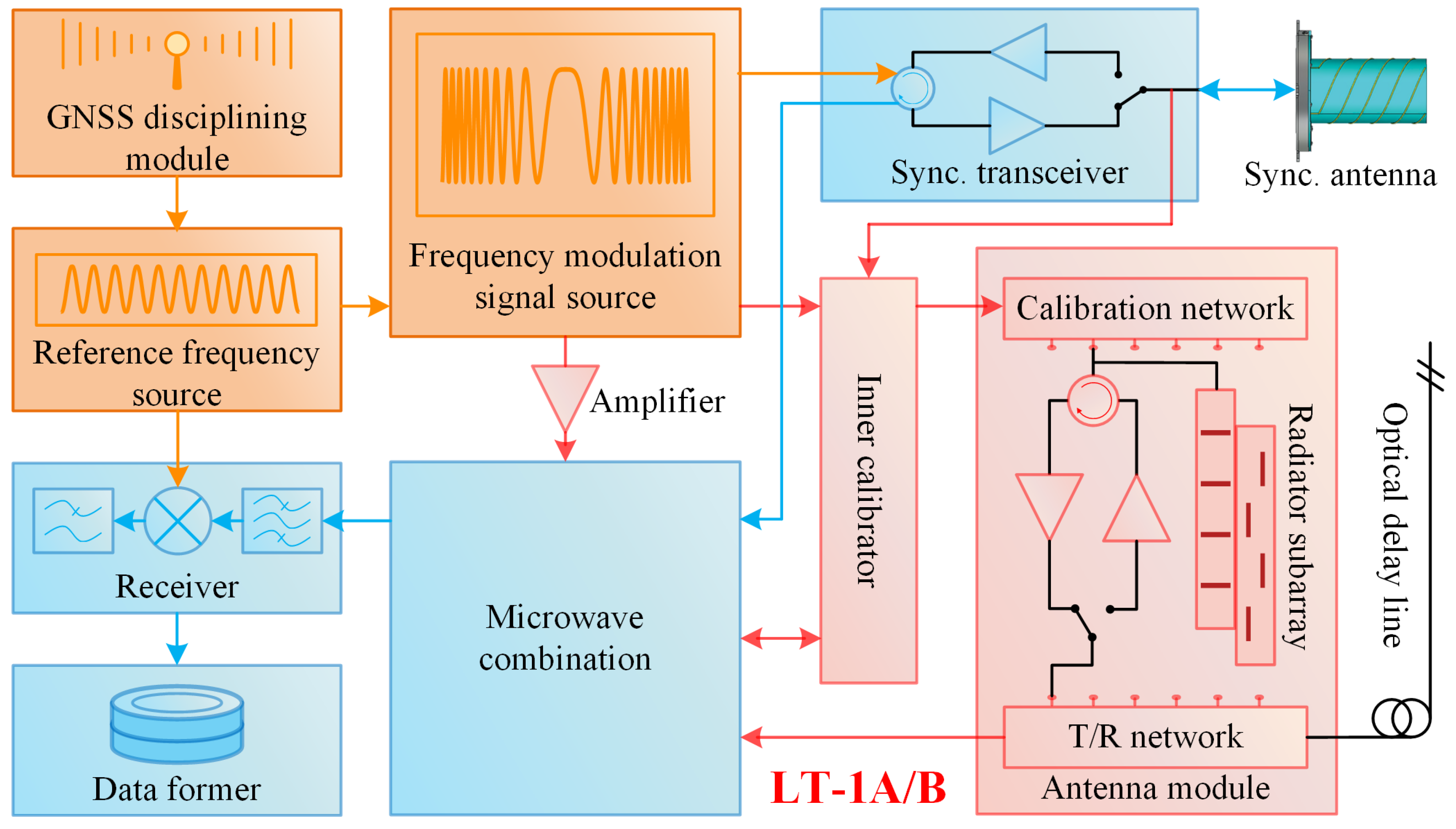
2.2. System Design and Phase Model
- 1.
- Loop CT monitors the phase error caused by the radar transmission link. In this loop, a calibration signal generated by the signal generation unit is sent from the transmitting unit to the antenna calibration network. Then, the signal passes through the internal calibrator and enters the receiving unit.
- 2.
- Loop CR monitors the phase error caused by the radar receiving link. The calibration signal is sent to the internal calibrator, which then passes through the antenna calibration network and antenna receiving channel. After that, the signal enters the receiving unit and is measured.
- 3.
- Loop RE measures the effects of redundant devices in the first two loops. The calibration signal passes through the internal calibrator and reaches the receiving unit for recording.
- 4.
- Loop ST monitors the phase error caused by the synchronization transmission link. The calibration signal enters the internal calibrator through the synchronization transceiver. After that, the signal is collected by the receiving unit.
- 5.
- Loop SR monitors the phase error caused by the synchronization receiving link. the calibration signal is transmitted from the internal calibrator to the synchronization transceiver. Then, the signal is recorded by the radar receiving unit for processing.
3. Processing Flow
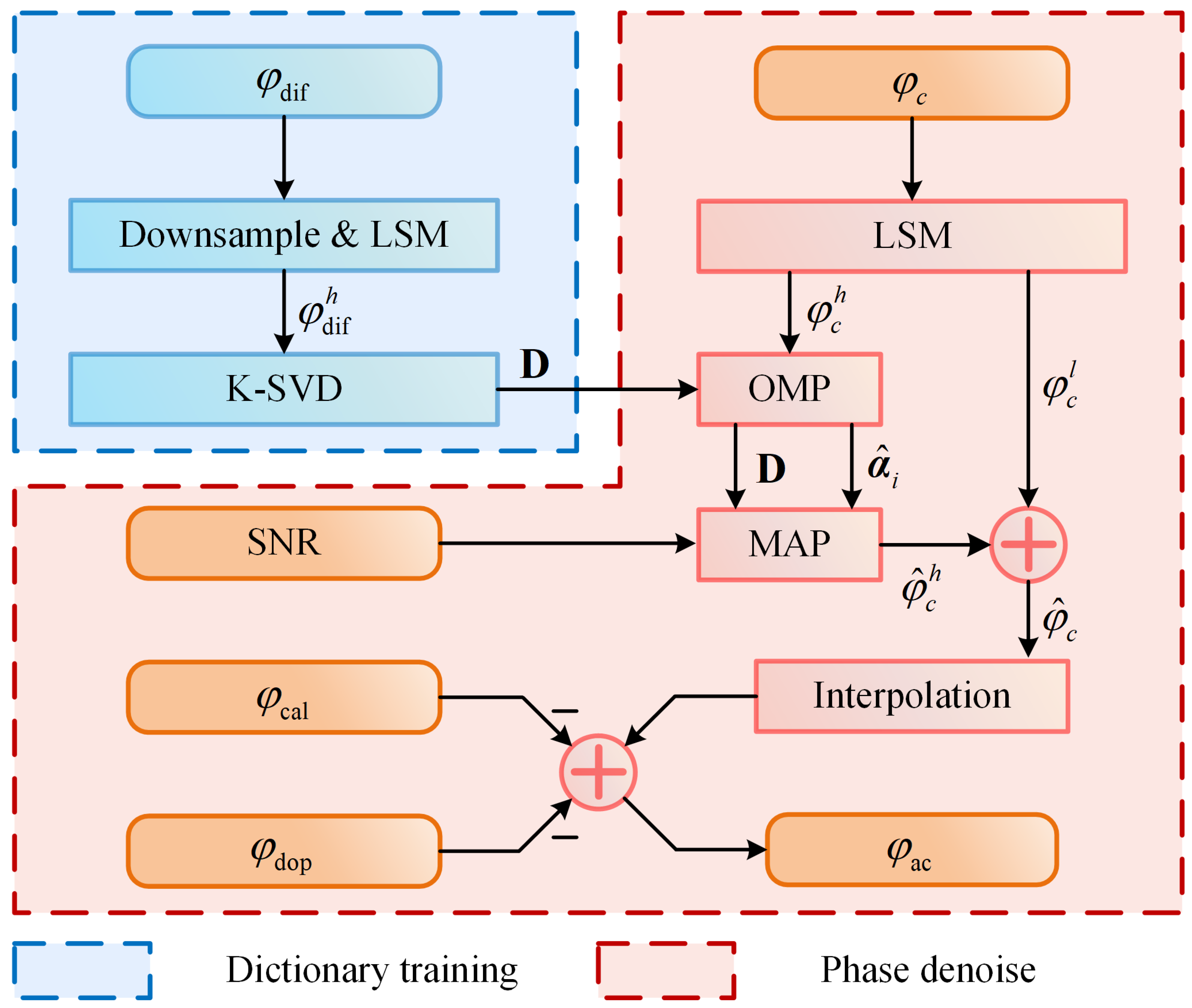
3.1. Phase Denoise Model
3.2. Dictionary Training
4. Phase Denoise Experiment and Result
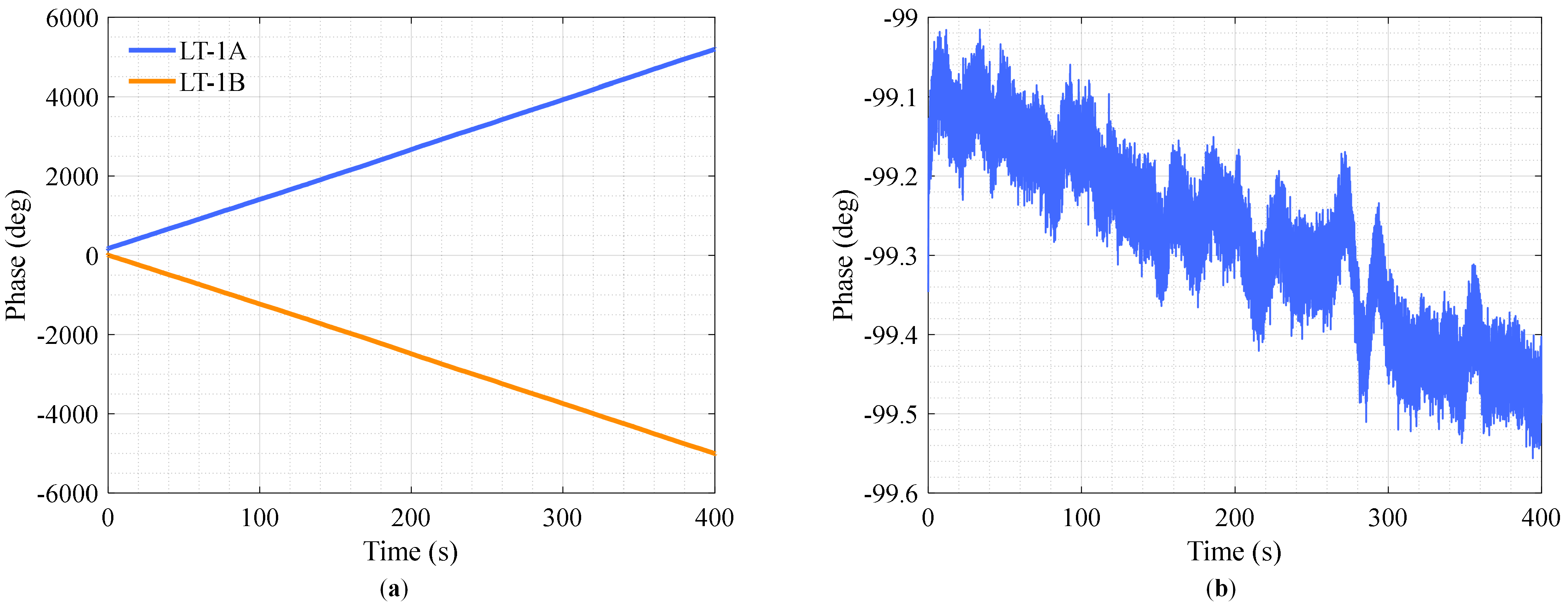
4.1. Data Acquisition and Analysis
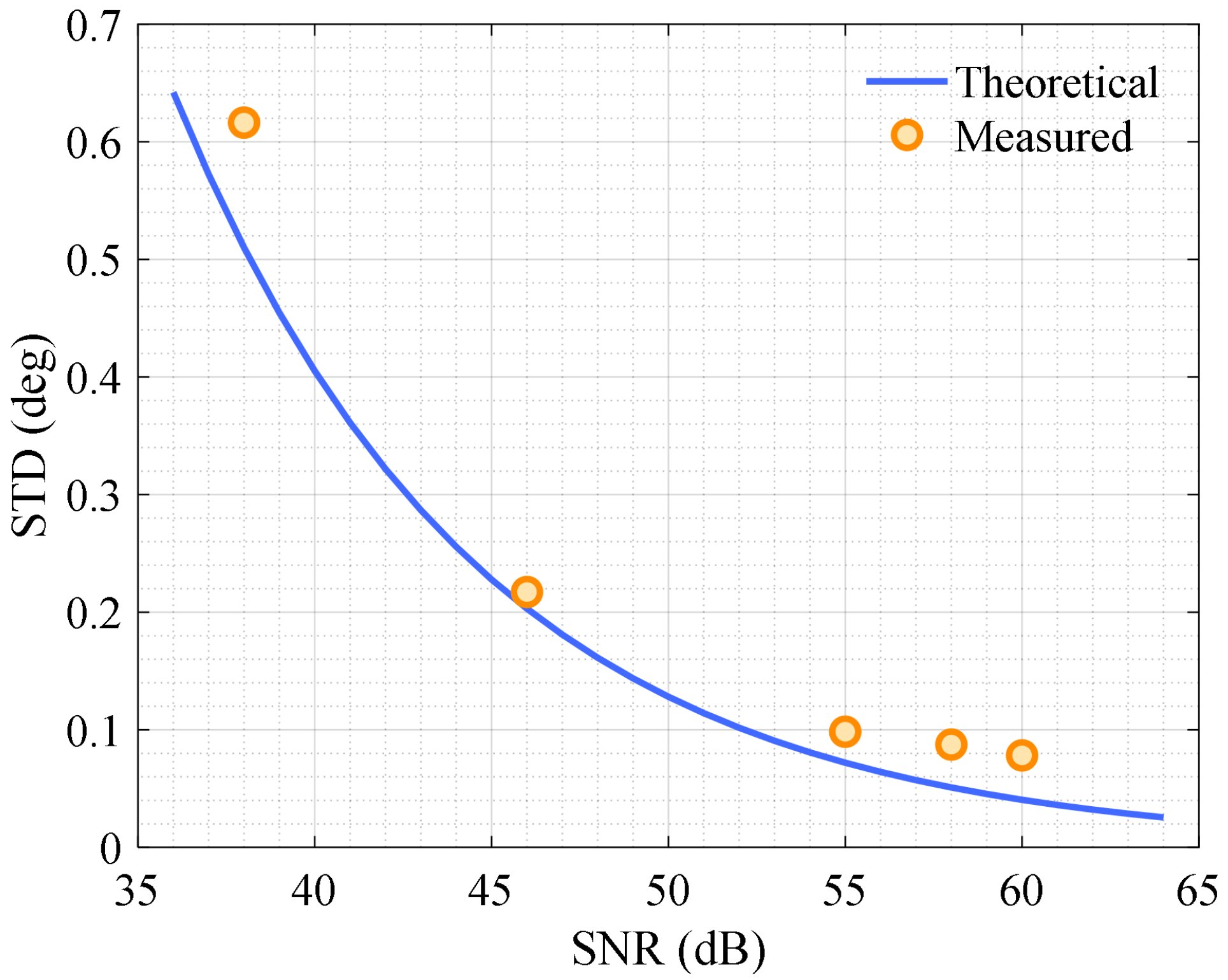
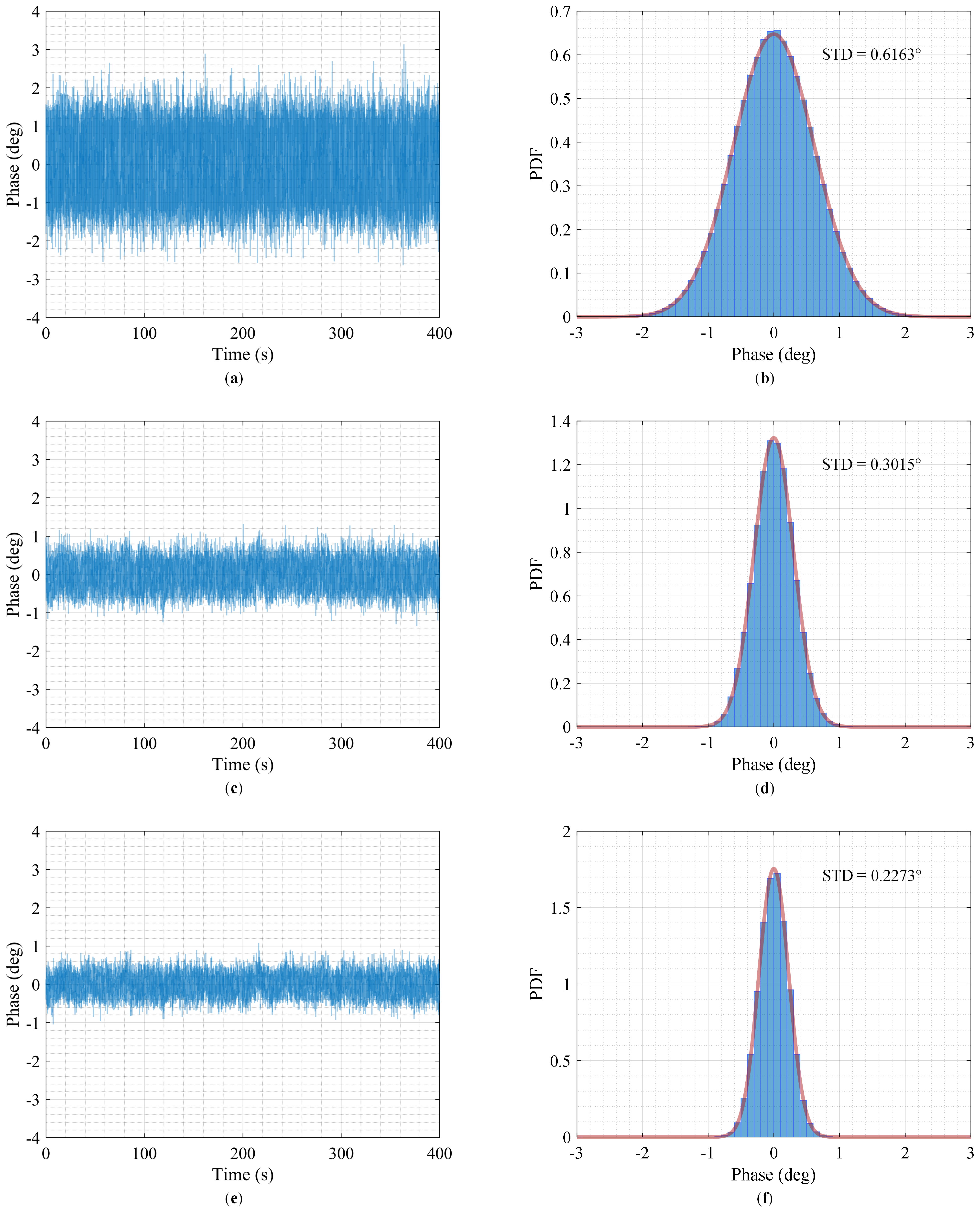
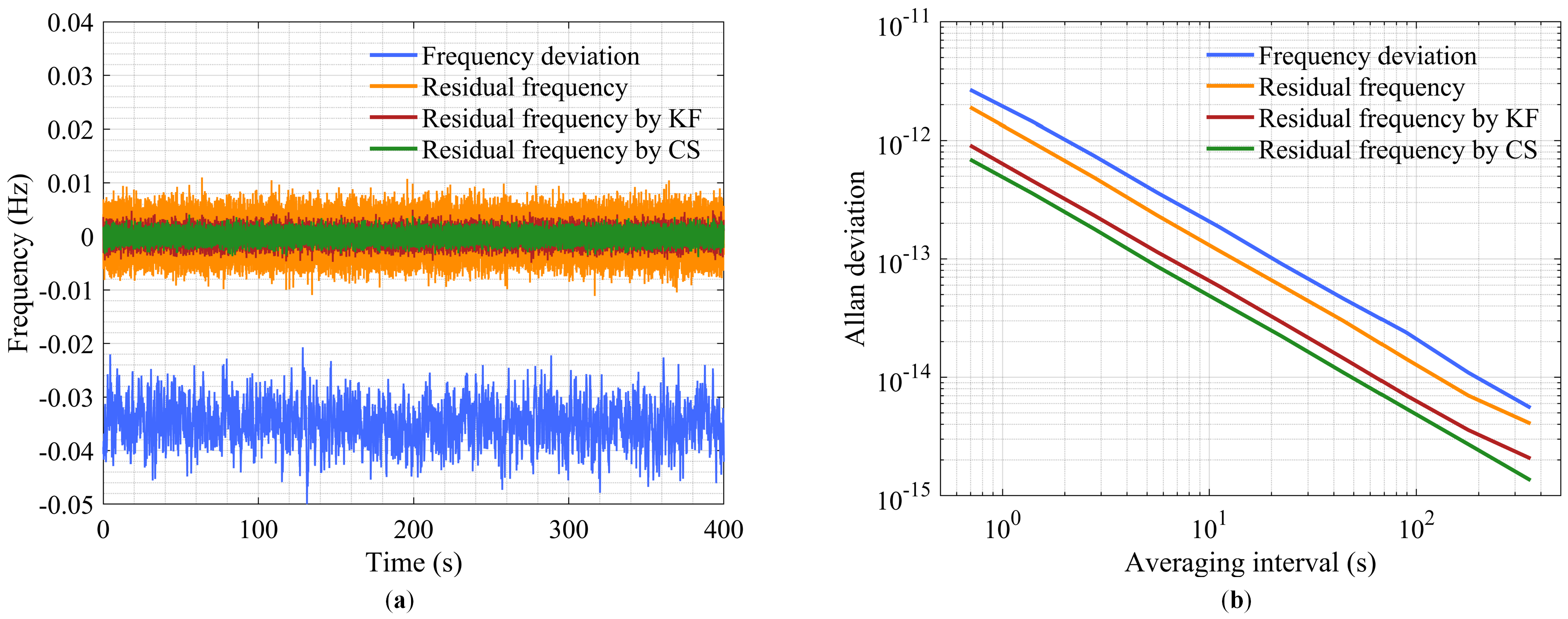
4.2. Result of Synchronization Phase Denoising
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Soumekh, M. Bistatic synthetic aperture radar inversion with application in dynamic object imaging. IEEE Trans. Signal Process. 1991, 39, 2044–2055. [Google Scholar] [CrossRef]
- D’Errico, M. Distributed Space Missions for Earth System Monitoring; Springer Science & Business Media: New York, NY, USA, 2012; Volume 31. [Google Scholar]
- Wang, R.; Deng, Y. Bistatic SAR System and Signal Processing Technology; Springer: Singapore, 2018. [Google Scholar]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Hounam, D.; Werner, M.; Riegger, S.; Settelmeyer, E. TanDEM-X: A TerraSAR-X add-on satellite for single-pass SAR interferometry. In Proceedings of the IGARSS 2004, 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 2, pp. 1000–1003. [Google Scholar] [CrossRef]
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Tridon, D.B.; Bräutigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M.; et al. Generation and performance assessment of the global TanDEM-X digital elevation model. ISPRS J. Photogramm. Remote Sens. 2017, 132, 119–139. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A. Multistatic sar satellite formations: Potentials and challenges. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, IGARSS ’05, Seoul, Korea, 29–29 July 2005; Volume 4, pp. 2680–2684. [Google Scholar] [CrossRef]
- Gebert, N.; Carnicero Dominguez, B.; Davidson, M.W.J.; Diaz Martin, M.; Silvestrin, P. SAOCOM-CS—A passive companion to SAOCOM for single-pass L-band SAR interferometry. In Proceedings of the EUSAR 2014: 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Huber, S.; Villano, M.; Younis, M.; Krieger, G.; Moreira, A.; Grafmueller, B.; Wolters, R. Tandem-L: Design concepts for a next-generation spaceborne SAR system. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016; pp. 1–5. [Google Scholar]
- Jin, G.; Liu, K.; Liu, D.; Liang, D.; Zhang, H.; Ou, N.; Zhang, Y.; Deng, Y.; Li, C.; Wang, R. An Advanced Phase Synchronization Scheme for LT-1. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1735–1746. [Google Scholar] [CrossRef]
- Krieger, G.; Zonno, M.; Rodriguez-Cassola, M.; Lopez-Dekker, P.; Mittermayer, J.; Younis, M.; Huber, S.; Villano, M.; de Almeida, F.Q.; Prats-Iraola, P.; et al. MirrorSAR: A fractionated space radar for bistatic, multistatic and high-resolution wide-swath SAR imaging. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 149–152. [Google Scholar] [CrossRef]
- Rott, H.; López-Dekker, P.; Solberg, S.; Ulander, L.; Nagler, T.; Krieger, G.; Prats, P.; Rodriguez, M.; Zonno, M.; Moreira, A. SESAME: A single-pass interferometric SEntinel-1 companion SAR mission for monitoring GEO-and biosphere dynamics. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 107–110. [Google Scholar]
- Janoth, J.; Jochum, M.; Petrat, L.; Knigge, T. High Resolution wide Swath—The Next Generation X-Band Mission. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3535–3537. [Google Scholar] [CrossRef]
- López-Dekker, P.; Rott, H.; Prats-Iraola, P.; Chapron, B.; Scipal, K.; Witte, E.D. Harmony: An Earth Explorer 10 Mission Candidate to Observe Land, Ice, and Ocean Surface Dynamics. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 8381–8384. [Google Scholar] [CrossRef]
- Jin, G.; Liu, K.; Deng, Y.; Sha, Y.; Wang, R.; Liu, D.; Wang, W.; Long, Y.; Zhang, Y. Nonlinear Frequency Modulation Signal Generator in LT-1. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1570–1574. [Google Scholar] [CrossRef]
- Liang, D.; Liu, K.; Zhang, H.; Chen, Y.; Yue, H.; Liu, D.; Deng, Y.; Lin, H.; Fang, T.; Li, C.; et al. The Processing Framework and Experimental Verification for the Noninterrupted Synchronization Scheme of LuTan-1. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5740–5750. [Google Scholar] [CrossRef]
- Lin, H.; Deng, Y.; Zhang, H.; Liu, D.; Liang, D.; Fang, T.; Wang, R. On the Processing of Dual-Channel Receiving Signals of the LuTan-1 SAR System. Remote Sens. 2022, 14, 515. [Google Scholar] [CrossRef]
- Cai, Y.; Deng, Y.; Zhang, H.; Wang, R.; Wu, Y.; Cheng, S. An Image-Domain Least L1-Norm Method for Channel Error Effect Analysis and Calibration of Azimuth Multi-Channel SAR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Jin, G.; Deng, Y.; Wang, R.; Wang, W.; Wang, P.; Long, Y.; Zhang, Z.M.; Zhang, Y. An advanced nonlinear frequency modulation waveform for radar imaging with low sidelobe. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6155–6168. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A. Spaceborne bi-and multistatic SAR: Potential and challenges. IEE Proc.-Radar Sonar Navig. 2006, 153, 184–198. [Google Scholar] [CrossRef]
- Lopez-Dekker, P.; Mallorqui, J.J.; Serra-Morales, P.; Sanz-Marcos, J. Phase and temporal synchronization in bistatic SAR systems using sources of opportunity. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 97–100. [Google Scholar] [CrossRef]
- Younis, M.; Metzig, R.; Krieger, G. Performance prediction of a phase synchronization link for bistatic SAR. IEEE Geosci. Remote Sens. Lett. 2006, 3, 429–433. [Google Scholar] [CrossRef]
- López-Dekker, P.; Mallorqui, J.J.; Serra-Morales, P.; Sanz-Marcos, J. Phase synchronization and Doppler centroid estimation in fixed receiver bistatic SAR systems. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3459–3471. [Google Scholar] [CrossRef]
- Krieger, G. Advanced bistatic and multistatic SAR concepts and applications. In Proceedings of the European Conference on Synthetic Aperture Radar (EUSAR), Dresden, Germany, 16–18 May 2006; pp. 1–101. [Google Scholar]
- Liang, D.; Zhang, H.; Cai, Y.; Liu, K.; Zhang, K. An Advanced Phase Synchronization Scheme Based on Coherent Integration and Waveform Diversity for Bistatic SAR. Remote Sens. 2021, 13, 981. [Google Scholar] [CrossRef]
- Oelker, E.; Hutson, R.; Kennedy, C.; Sonderhouse, L.; Bothwell, T.; Goban, A.; Kedar, D.; Sanner, C.; Robinson, J.; Marti, G.; et al. Demonstration of 4.8 × 10−17 stability at 1 s for two independent optical clocks. Nat. Photonics 2019, 13, 714–719. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, Y.; Wang, R.; Li, N.; Zhao, S.; Hong, F.; Wu, L.; Loffeld, O. Spaceborne/stationary bistatic SAR imaging with TerraSAR-X as an illuminator in staring-spotlight mode. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5203–5216. [Google Scholar] [CrossRef]
- Rodriguez-Cassola, M.; Prats-Iraola, P.; Lopez-Dekker, P.; Reigber, A.; Krieger, G.; Moreira, A. Autonomous time and phase calibration of spaceborne bistatic SAR systems. In Proceedings of the EUSAR 2014: 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Weib, M. Synchronisation of bistatic radar systems. In Proceedings of the IGARSS 2004, 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 3, pp. 1750–1753. [Google Scholar]
- Zhang, Y.; Wang, R. An Innovative Push-To-Talk (PTT) Synchronization Scheme for Future Distributed SAR. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 8692–8695. [Google Scholar] [CrossRef]
- Zhang, Y.; Chang, S.; Wang, R.; Deng, Y. An Innovative Push-To-Talk (PTT) Synchronization Scheme for Distributed SAR. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar]
- Younis, M.; Metzig, R.; Krieger, G.; Bachmann, M.; Klein, R. Performance prediction and verification for the synchronization link of TanDEM-X. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 5206–5209. [Google Scholar]
- Weigt, M.; Grigorov, C.; Steinbrecher, U.; Schulze, D. Tandem-x mission: Long term in orbit synchronisation link performance analysis. In Proceedings of the EUSAR 2014: 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Pinheiro, M.; Rodriguez-Cassola, M.; Prats-Iraola, P.; Reigber, A.; Krieger, G.; Moreira, A. Reconstruction of Coherent Pairs of Synthetic Aperture Radar Data Acquired in Interrupted Mode. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1876–1893. [Google Scholar] [CrossRef]
- Liang, D.; Liu, K.; Yue, H.; Chen, Y.; Deng, Y.; Zhang, H.; Li, C.; Jin, G.; Wang, R. An Advanced Non-Interrupted Synchronization Scheme for Bistatic Synthetic Aperture Radar. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1116–1119. [Google Scholar] [CrossRef]
- Liang, D.; Liua, K.; Zhang, H.; Liu, D.; Wang, R. An advanced non-interrupted phase synchronization scheme with internal calibration for LuTan-1. In Proceedings of the EUSAR 2021: 13th European Conference on Synthetic Aperture Radar, Online, 29 March–1 April 2021; pp. 1–5. [Google Scholar]
- Zhang, Y.; Zhang, H.; Ou, N.; Liu, K.; Liang, D.; Deng, Y.; Wang, R. First Demonstration of Multipath Effects on Phase Synchronization Scheme for LT-1. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2590–2604. [Google Scholar] [CrossRef]
- Liang, D.; Liu, K.; Zhang, H.; Deng, Y.; Liu, D.; Chen, Y.; Li, C.; Yue, H.; Wang, R. A high-accuracy synchronization phase-compensation method based on Kalman filter for bistatic synthetic aperture radar. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1722–1726. [Google Scholar] [CrossRef]
- Foucart, S.; Rauhut, H. An invitation to compressive sensing. In A Mathematical Introduction to Compressive Sensing; Springer: New York, NY, USA, 2013; pp. 1–39. [Google Scholar]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Krieger, G.; Younis, M. Impact of oscillator noise in bistatic and multistatic SAR. IEEE Geosci. Remote Sens. Lett. 2006, 3, 424–428. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Chen, G.; Krishnan, S.; Bui, T.D. Matrix-based Ramanujan-sums transforms. IEEE Signal Process Lett. 2013, 20, 941–944. [Google Scholar] [CrossRef]




| Parameter | Symbol | Value |
|---|---|---|
| Carrier frequency | 1.26 GHz | |
| Pulse repetition frequency | 1723.05 Hz | |
| Imaging signal pulse duration | 80 s | |
| Imaging signal bandwidth | 150 MHz | |
| Sync. frequency | 143.59 Hz | |
| Sync. signal pulse duration | 10 s | |
| Sync. signal bandwidth | 150 MHz | |
| Acquisition duration | 400 s |
| Parameter | Symbol | Value |
|---|---|---|
| Phase segment length | n | 64 |
| Phase segment overlap rate | r | 50% |
| Number of the atoms | k | 256 |
| Sparsity threshold | m | 4 |
| Error tolerance | 0.1° |
| Parameter | Theoretical | With Phase Error | Before Denoising | Denoising by KF | Denoising by CS |
|---|---|---|---|---|---|
| IRW | 4.90 m | 4.90 m | 4.90 m | 4.90 m | 4.90 m |
| PSLR (L) | −13.26 dB | −13.33 dB | −13.25 dB | −13.25 dB | −13.26 dB |
| PSLR (R) | −13.26 dB | −13.19 dB | −13.27 dB | −13.27 dB | −13.26 dB |
| ISLR | −10.07 dB | −10.07 dB | −10.07 dB | −10.07 dB | −10.07 dB |
| Peak amplitude | 1.0000 | 0.9861 | 0.9999 | 1.0000 | 1.0000 |
| Peak position | 0.0000 m | 0.5441 m | 0.0000 m | 0.0000 m | 0.0000 m |
| Peak phase | 0.0000° | −87.2629° | −0.2182° | −0.2176° | −0.1964° |
| SNR (dB) | Before Denoising | Denoising by KF | Denoising by CS |
|---|---|---|---|
| 38 | 0.6163° | 0.3015° | 0.2273° |
| 46 | 0.2172° | 0.1569° | 0.1287° |
| 55 | 0.0984° | 0.0903° | 0.0851° |
| 58 | 0.0875° | 0.0862° | 0.0861° |
| 60 | 0.0783° | 0.0774° | 0.0774° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Wang, R.; Yu, W.; Liang, D.; Liu, K.; Zhang, H.; Chen, Y. An Advanced Approach to Improve Synchronization Phase Accuracy with Compressive Sensing for LT-1 Bistatic Spaceborne SAR. Remote Sens. 2022, 14, 4621. https://doi.org/10.3390/rs14184621
Cai Y, Wang R, Yu W, Liang D, Liu K, Zhang H, Chen Y. An Advanced Approach to Improve Synchronization Phase Accuracy with Compressive Sensing for LT-1 Bistatic Spaceborne SAR. Remote Sensing. 2022; 14(18):4621. https://doi.org/10.3390/rs14184621
Chicago/Turabian StyleCai, Yonghua, Robert Wang, Weidong Yu, Da Liang, Kaiyu Liu, Heng Zhang, and Yafeng Chen. 2022. "An Advanced Approach to Improve Synchronization Phase Accuracy with Compressive Sensing for LT-1 Bistatic Spaceborne SAR" Remote Sensing 14, no. 18: 4621. https://doi.org/10.3390/rs14184621
APA StyleCai, Y., Wang, R., Yu, W., Liang, D., Liu, K., Zhang, H., & Chen, Y. (2022). An Advanced Approach to Improve Synchronization Phase Accuracy with Compressive Sensing for LT-1 Bistatic Spaceborne SAR. Remote Sensing, 14(18), 4621. https://doi.org/10.3390/rs14184621







