Estimating the Routing Parameter of the Xin’anjiang Hydrological Model Based on Remote Sensing Data and Machine Learning
Abstract
:1. Introduction
2. Data and Methodology
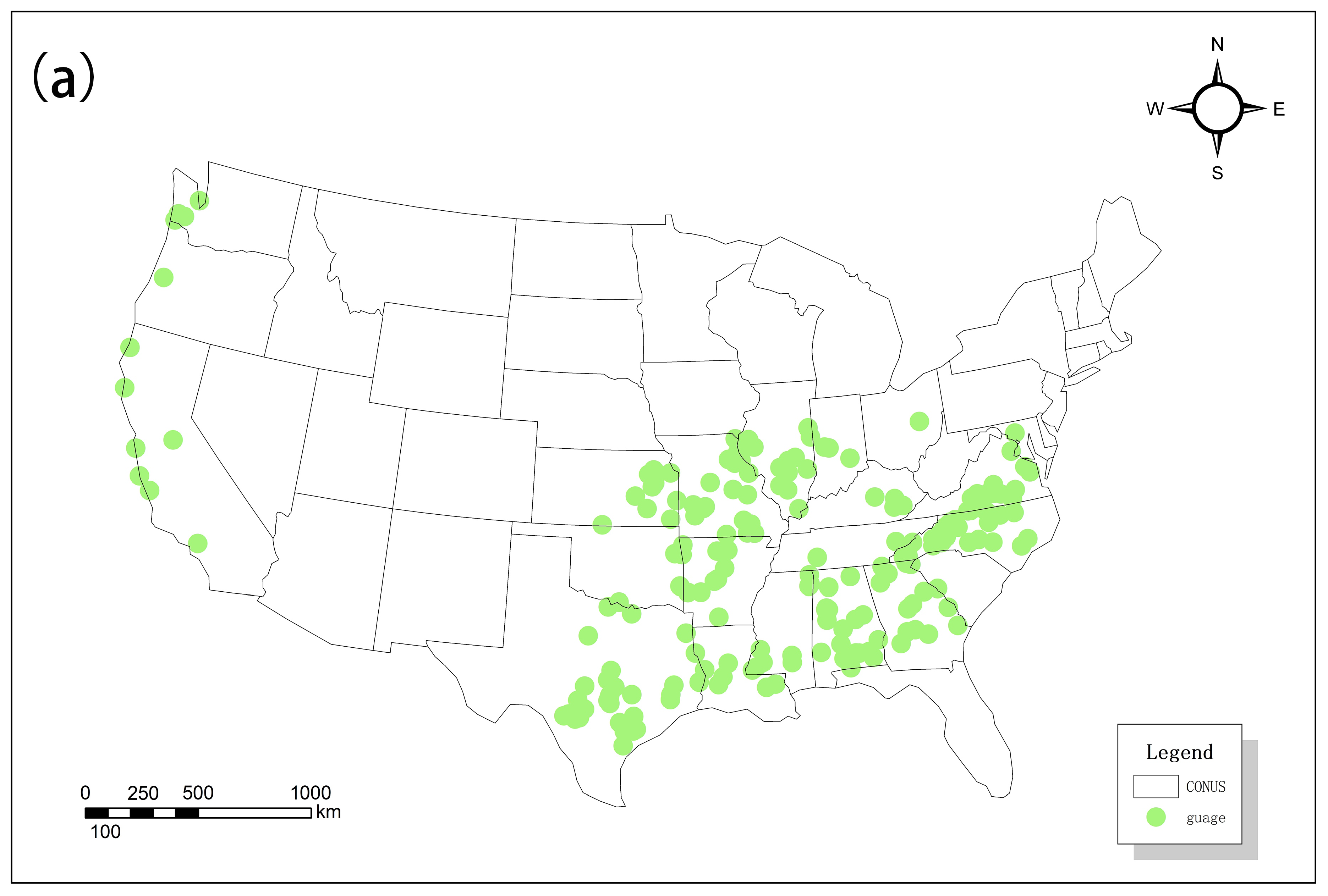
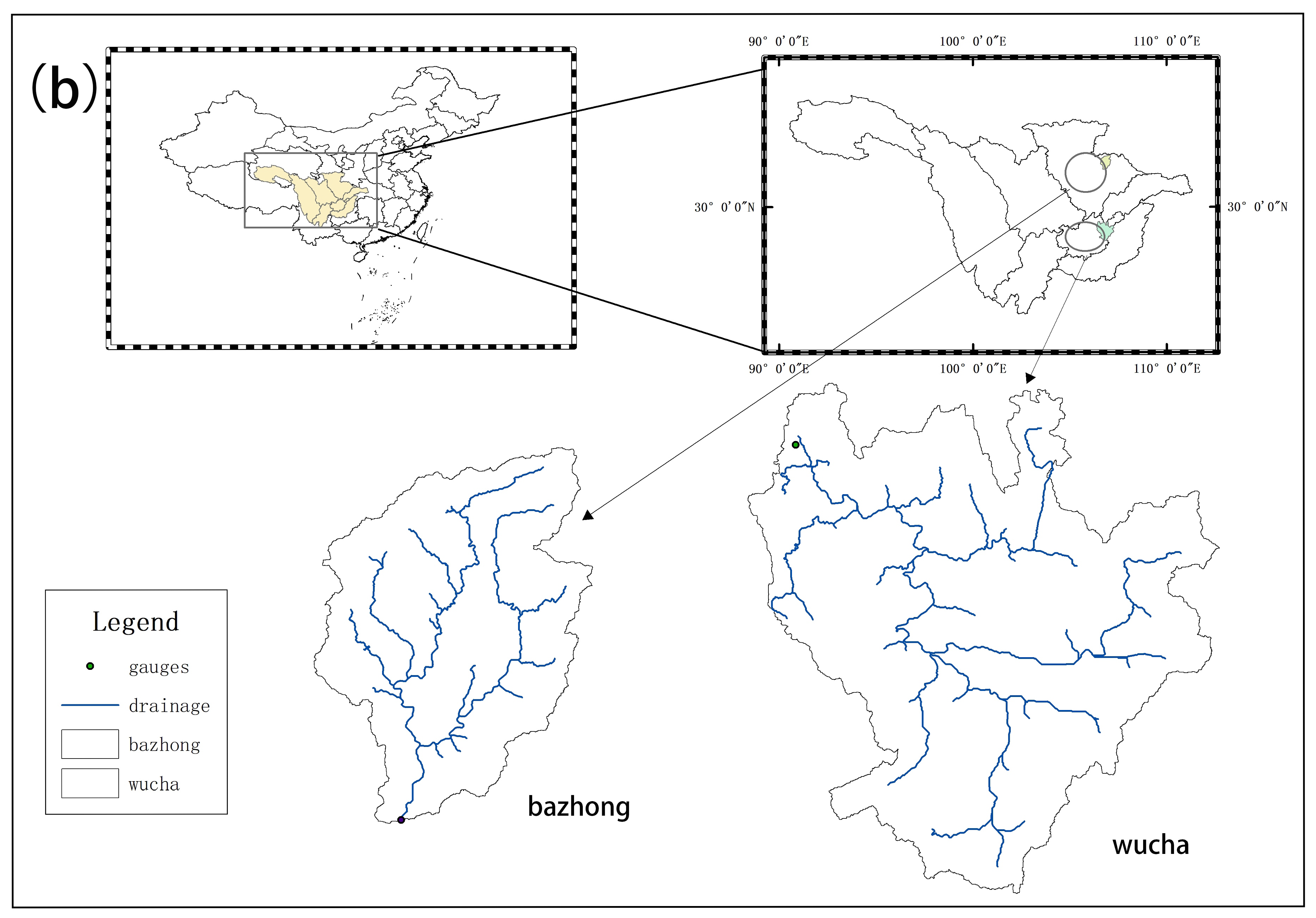
2.1. Study Area and Data
2.2. XAJ Hydrological Model
2.3. Baseline Model Calibration
2.4. Estimating CS Using a Gradient-Boosted Regression Tree (GBRT)
2.4.1. Basic Theory of GBRT
2.4.2. Initial Selection of Independent Predictors
2.4.3. Construction of the GBRT Prediction Model
2.5. Validation of the GBRT-Estimated CS
3. Results
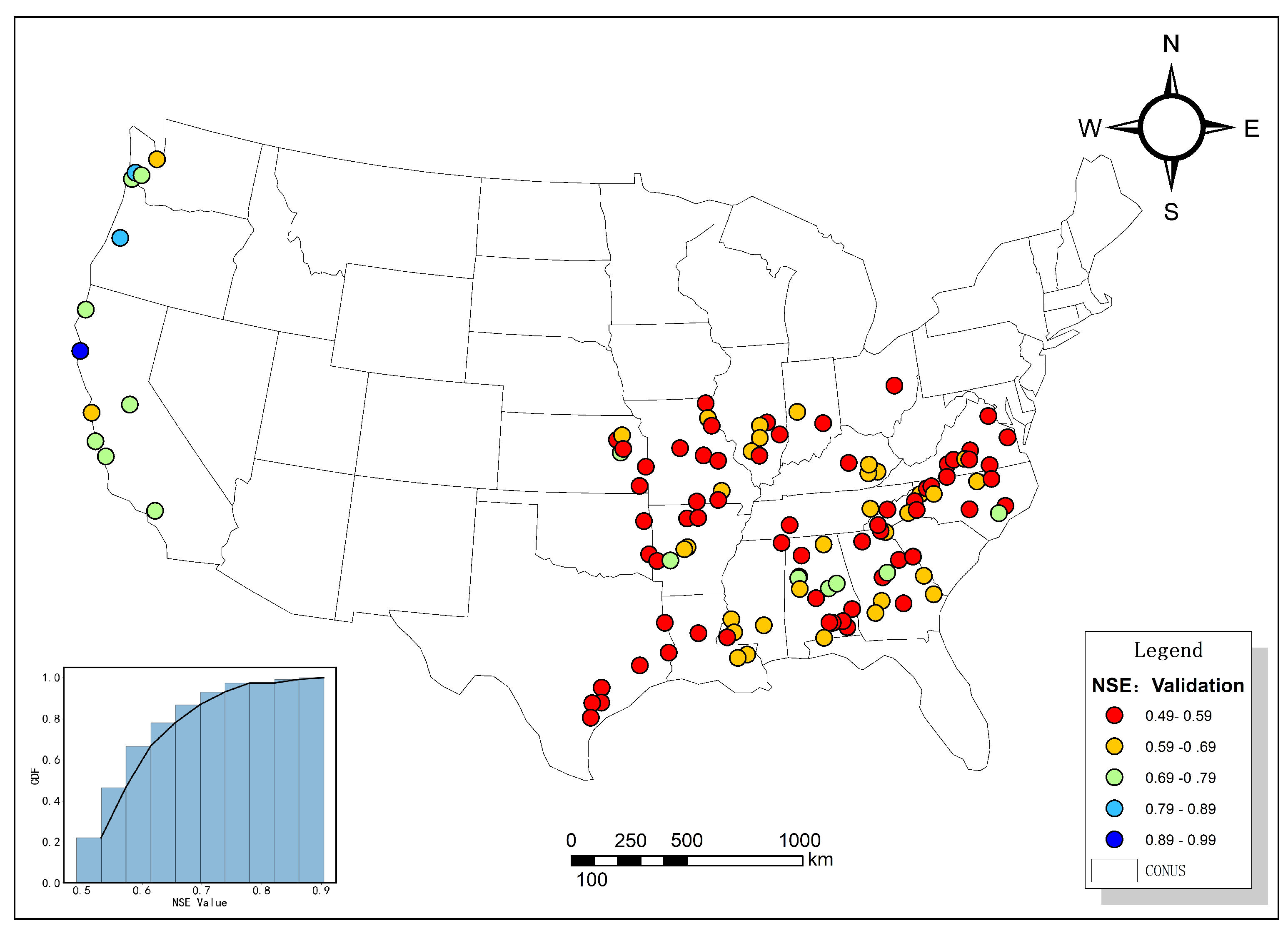
3.1. Calibration of the XAJ Model in the CAMELS Catchments
3.2. Importance of the Selected Predictors
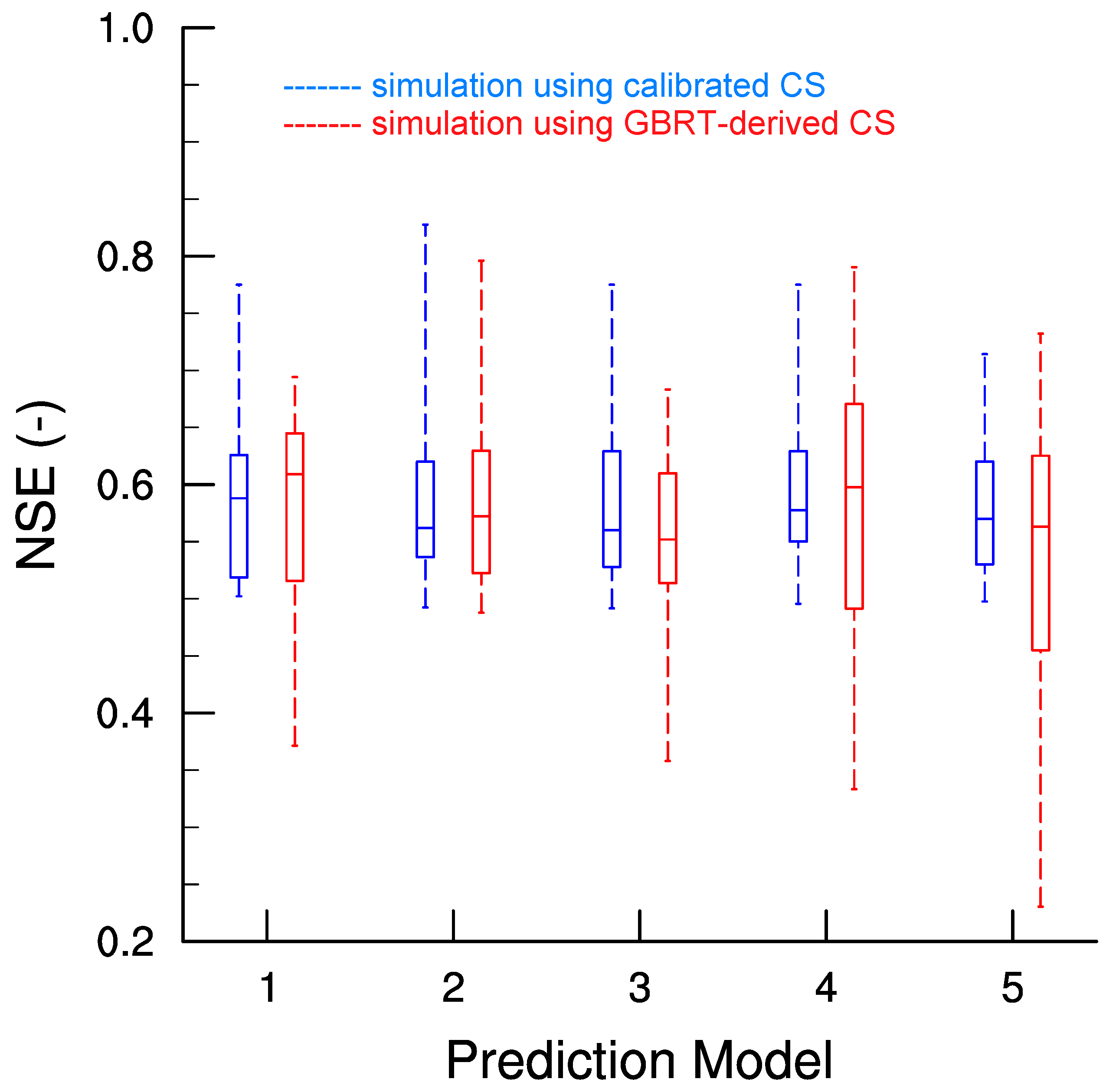
3.3. CS Estimation and Hydrological Simulation
4. Discussion
4.1. Factors Affecting the Routing Process
4.2. Implications of This Study
4.3. Limitations and Future Directions
5. Conclusions
- The drainage density, stream source density and area of the catchment are the three major factors with the most significant impact on CS. This outcome is reasonable based on an examination of the physical discipline of runoff routing.
- Overall, the CS values yielded by the prediction models we developed are comparable to those from the calibration. Considering the values of CS, the best model (Model #1) has a correlation coefficient (r), a root-mean-square error (RMSE) and a mean absolute error (MAE) of 0.96, 0.06 and 0.04, respectively, confirming the good performance of the GBRT for estimating CS.
- Although a bias exists between the GBRT-estimated and calibrated CS, runoff simulations using the GBRT-estimated CS can still achieve results comparable to those using the calibrated CS. Most catchments have a ΔNSE within the ±0.1 limit.
- Validations in two catchments further verify that the GBRT-estimated CS can be used for hydrological simulations and can reflect the spatial patterns of parameters and therefore better exploit the benefits of distributed models.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paniconi, C.; Putti, M. Physically based modeling in catchment hydrology at 50: Survey and outlook. Water Resour. Res. 2015, 51, 7090–7129. [Google Scholar] [CrossRef]
- Fatichi, S.; Vivoni, E.R.; Ogden, F.L.; Ivanov, V.Y.; Mirus, B.; Gochis, D.; Downer, C.W.; Camporese, M.; Davison, J.H.; Ebel, B.; et al. An overview of current applications, challenges, and future trends in distributed process-based models in hydrology. J. Hydrol. 2016, 537, 45–60. [Google Scholar] [CrossRef]
- Niu, G.Y.; Paniconi, C.; Troch, P.A.; Scott, R.L.; Durcik, M.; Zeng, X.; Huxman, T.; Goodrich, D.C. An integrated modelling framework of catchment-scale ecohydrological processes: 1. Model description and tests over an energy-limited watershed. Ecohydrology 2014, 7, 427–439. [Google Scholar] [CrossRef]
- Freeze, R.; Harlan, R. Blueprint for a physically-based, digitally-simulated hydrologic response model. J. Hydrol. 1969, 9, 237–258. [Google Scholar] [CrossRef]
- Nijzink, R.C.; Almeida, S.; Pechlivanidis, I.G.; Capell, R.; Gustafssons, D.; Arheimer, B.; Parajka, J.; Freer, J.; Han, D.; Wagener, T.; et al. Constraining Conceptual Hydrological Models with Multiple Information Sources. Water Resour. Res. 2018, 54, 8332–8362. [Google Scholar] [CrossRef]
- Zhao, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Cheng, C.T.; Zhao, M.Y.; Chau, K.; Wu, X.Y. Using genetic algorithm and TOPSIS for Xinanjiang model calibration with a single procedure. J. Hydrol. 2006, 316, 129–140. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Li, Z.; Wang, S. Application of SCE-UA method for calibrating the Xinanjiang watershed model. J. Lake Sci. 2001, 13, 304–314. [Google Scholar]
- Kan, G.; He, X.; Ding, L.; Li, J.; Hong, Y.; Zuo, D.; Ren, M.; Lei, T.; Liang, K. Fast hydrological model calibration based on the heterogeneous parallel computing accelerated shuffled complex evolution method. Eng. Optim. 2018, 50, 106–119. [Google Scholar] [CrossRef]
- Li, Z.; Xin, P.; Tang, J. Study of the Xinanjiang model parameter calibration. J. Hydrol. Eng. 2013, 18, 1513–1521. [Google Scholar]
- Wu, Q.; Liu, S.; Cai, Y.; Li, X.; Jiang, Y. Improvement of hydrological model calibration by selecting multiple parameter ranges. Hydrol. Earth Syst. Sci. 2017, 21, 393–407. [Google Scholar] [CrossRef]
- Emanuel, R.E.; Hazen, A.G.; McGlynn, B.L.; Jencso, K.G. Vegetation and topographic influences on the connectivity of shallow groundwater between hillslopes and streams. Ecohydrology 2014, 7, 887–895. [Google Scholar] [CrossRef]
- Niu, G.Y.; Pasetto, D.; Scudeler, C.; Paniconi, C.; Putti, M.; Troch, P.A.; Delong, S.B.; Dontsova, K.; Pangle, L.; Breshears, D.D.; et al. Incipient subsurface heterogeneity and its effect on overland flow generation—Insight from a modeling study of the first experiment at the Biosphere 2 Landscape Evolution Observatory. Hydrol. Earth Syst. Sci. 2014, 18, 1873–1883. [Google Scholar] [CrossRef]
- Bárdossy, A.; Singh, S.K. Robust estimation of hydrological model parameters. Hydrol. Earth Syst. Sci. Discuss. 2008, 5, 1641–1675. [Google Scholar] [CrossRef]
- Yao, C.; Li, Z.; Yu, Z.; Zhang, K. A priori parameter estimates for a distributed, grid-based Xinanjiang model using geographically based information. J. Hydrol. 2012, 468–469, 47–62. [Google Scholar] [CrossRef]
- Gong, J.; Yao, C.; Li, Z.; Chen, Y.; Huang, Y.; Tong, B. Improving the Flood Forecasting Capability of the Xinanjiang Model for Small- and Medium-Sized Ungauged Catchments in South China; Number 0123456789; Springer: Dordrecht, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Y.; Zhang, L.; Wang, Z. Regionalization of hydrological modeling for predicting streamflow in ungauged catchments: A comprehensive review. WIREs Water 2021, 8, e1487. [Google Scholar] [CrossRef]
- Bao, Z.; Zhang, J.; Liu, J.; Fu, G.; Wang, G.; He, R.; Yan, X.; Jin, J.; Liu, H. Comparison of regionalization approaches based on regression and similarity for predictions in ungauged catchments under multiple hydro-climatic conditions. J. Hydrol. 2012, 466–467, 37–46. [Google Scholar] [CrossRef]
- Parajka, J.; Merz, R.; Blöschl, G. A comparison of regionalisation methods for catchment model parameters. Hydrol. Earth Syst. Sci. 2005, 9, 157–171. [Google Scholar] [CrossRef]
- Pagliero, L.; Bouraoui, F.; Diels, J.; Willems, P.; McIntyre, N. Investigating regionalization techniques for large-scale hydrological modelling. J. Hydrol. 2019, 570, 220–235. [Google Scholar] [CrossRef]
- Bao, W.; Li, Q. Estimating Selected Parameters for the XAJ Model under Multicollinearity among Watershed Characteristics. J. Hydrol. Eng. 2012, 17, 118–128. [Google Scholar] [CrossRef]
- Lu, M. New approach to synthesization of recession coefficients in Xinanjiang model. J. Hydroelectr. Eng. 2016, 35, 1–6, (In Chinese with English Abstract). [Google Scholar]
- Zang, S.; Li, Z.; Yao, C.; Zhang, K.; Sun, M.; Kong, X. A New Runoff Routing Scheme for Xin’anjiang Model and Its Routing Parameters Estimation Based on Geographical Information. Water 2020, 12, 3429. [Google Scholar] [CrossRef]
- Guo, W.J.; Wang, C.H.; Ma, T.F.; Zeng, X.M.; Yang, H. A distributed Grid-Xinanjiang model with integration of subgrid variability of soil storage capacity. Water Sci. Eng. 2016, 9, 97–105. [Google Scholar] [CrossRef]
- Shi, P.; Rui, X.F.; Qu, S.M.; Chen, X. Calculating storage capacity with topographic index. Adv. Water Sci. 2008, 19, 264, (In Chinese with English Abstract). [Google Scholar]
- Cao, X.; Ni, G.; Qi, Y.; Liu, B. Does Subgrid Routing Information Matter for Urban Flood Forecasting? A Multiscenario Analysis at the Land Parcel Scale. J. Hydrometeorol. 2020, 21, 2083–2099. [Google Scholar] [CrossRef]
- Meng, S.; Xie, X.; Liang, S. Assimilation of soil moisture and streamflow observations to improve flood forecasting with considering runoff routing lags. J. Hydrol. 2017, 550, 568–579. [Google Scholar] [CrossRef]
- Zhang, X.N.; Fang, Y.H.; Qu, B.; Ma, L.J.; Wu, M. Study on Parameters Estimation of the Xaj Model Based on Underlying Surface Characteristics. In Proceedings of the 37th IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017. [Google Scholar]
- Heuvelmans, G.; Muys, B.; Feyen, J. Regionalisation of the parameters of a hydrological model: Comparison of linear regression models with artificial neural nets. J. Hydrol. 2006, 319, 245–265. [Google Scholar] [CrossRef]
- Schmidt, L.; Heße, F.; Attinger, S.; Kumar, R. Challenges in Applying Machine Learning Models for Hydrological Inference: A Case Study for Flooding Events Across Germany. Water Resour. Res. 2020, 56, e2019WR025924. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef]
- Xu, T.; Liang, F. Machine learning for hydrologic sciences: An introductory overview. Wiley Interdiscip. Rev. Water 2021, 8, 1–29. [Google Scholar] [CrossRef]
- Abrahart, R.J.; See, L.M. Neural network modelling of non-linear hydrological relationships. Hydrol. Earth Syst. Sci. 2007, 11, 1563–1579. [Google Scholar] [CrossRef]
- Choubin, B.; Khalighi-Sigaroodi, S.; Malekian, A.; Kişi, Ö. Multiple linear regression, multi-layer perceptron network and adaptive neuro-fuzzy inference system for forecasting precipitation based on large-scale climate signals. Hydrol. Sci. J. 2016, 61, 1001–1009. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; El-shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S.; Li, M.; Post, D. Predicting Runoff Signatures Using Regression and Hydrological Modeling Approaches. Water Resour. Res. 2018, 54, 7859–7878. [Google Scholar] [CrossRef]
- Oppel, H.; Schumann, A.H. Machine learning based identification of dominant controls on runoff dynamics. Hydrol. Process. 2020, 34, 2450–2465. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Song, J.; Cheng, L.; Kumar Paul, P.; Gan, R.; Shi, X.; Luo, Z.; Zhao, P. Large-scale baseflow index prediction using hydrological modelling, linear and multilevel regression approaches. J. Hydrol. 2020, 585, 124780. [Google Scholar] [CrossRef]
- Iqbal, U.; Bin Riaz, M.Z.; Barthelemy, J.; Perez, P. Prediction of Hydraulic Blockage at Culverts using Lab Scale Simulated Hydraulic Data. Urban Water J. 2022, 19, 686–699. [Google Scholar] [CrossRef]
- Abowarda, A.S.; Bai, L.; Zhang, C.; Long, D.; Li, X.; Huang, Q.; Sun, Z. Generating surface soil moisture at 30 m spatial resolution using both data fusion and machine learning toward better water resources management at the field scale. Remote Sens. Environ. 2021, 255, 112301. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Mishra, A.K. Multi-layer high-resolution soil moisture estimation using machine learning over the United States. Remote Sens. Environ. 2021, 266, 112706. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, Z.; Jiang, H.; Sun, S. Estimating daily reference evapotranspiration based on limited meteorological data using deep learning and classical machine learning methods. J. Hydrol. 2020, 591, 125286. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G.; Merz, R. Regional calibration of catchment models: Potential for ungauged catchments. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Zhang, X.N.; Jing, L.Y.; Ye, L.H.; Guo, H.B. Study of hydrological simulation on the basis of digital elevation model. Shuili Xuebao J. Hydraul. Eng. 2005, 36, 759–763. [Google Scholar]
- Velásquez, N.; Mantilla, R.; Krajewski, W.; Quintero, F.; Zanchetta, A.D.L. Identification and Regionalization of Streamflow Routing Parameters Using Machine Learning for the HLM Hydrological Model in Iowa. J. Adv. Model. Earth Syst. 2022, 14, e2021MS002855. [Google Scholar] [CrossRef]
- Salehi, H.; Sadeghi, M.; Golian, S.; Nguyen, P.; Murphy, C.; Sorooshian, S. The Application of PERSIANN Family Datasets for Hydrological Modeling. Remote Sens. 2022, 14, 3675. [Google Scholar] [CrossRef]
- Gehring, J.; Duvvuri, B.; Beighley, E. Deriving River Discharge Using Remotely Sensed Water Surface Characteristics and Satellite Altimetry in the Mississippi River Basin. Remote Sens. 2022, 14, 3541. [Google Scholar] [CrossRef]
- Ye, X.; Guo, Y.; Wang, Z.; Liang, L.; Tian, J. Extensive Evaluation of Four Satellite Precipitation Products and Their Hydrologic Applications over the Yarlung Zangbo River. Remote Sens. 2022, 14, 3350. [Google Scholar] [CrossRef]
- Jamali, A.A.; Montazeri Naeeni, M.A.; Zarei, G. Assessing the expansion of saline lands through vegetation and wetland loss using remote sensing and GIS. Remote Sens. Appl. Soc. Environ. 2020, 20, 100428. [Google Scholar] [CrossRef]
- Addor, N.; Newman, A.J.; Mizukami, N.; Clark, M.P. The CAMELS data set: Catchment attributes and meteorology for large-sample studies. Hydrol. Earth Syst. Sci. 2017, 21, 5293–5313. [Google Scholar] [CrossRef]
- Broxton, P.D.; Zeng, X.; Sulla-Menashe, D.; Troch, P.A. A Global Land Cover Climatology Using MODIS Data. J. Appl. Meteorol. Climatol. 2014, 53, 1593–1605. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G.; Zha, Y. A High-Resolution Global Map of Soil Hydraulic Properties Produced by a Hierarchical Parameterization of a Physically Based Water Retention Model. Water Resour. Res. 2018, 54, 9774–9790. [Google Scholar] [CrossRef]
- Fang, Y.H.; Zhang, X.; Corbari, C.; Mancini, M.; Niu, G.Y.; Zeng, W. Improving the Xin’anjiang hydrological model based on mass–energy balance. Hydrol. Earth Syst. Sci. 2017, 21, 3359–3375. [Google Scholar] [CrossRef]
- Doherty, J. Model-Independent Parameter Estimation. Watermark Numer. Comput. 2002, 2005, 279. [Google Scholar]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble machine learning paradigms in hydrology: A review. J. Hydrol. 2021, 598, 126266. [Google Scholar] [CrossRef]
- Erdal, H.I.; Karakurt, O. Advancing monthly streamflow prediction accuracy of CART models using ensemble learning paradigms. J. Hydrol. 2013, 477, 119–128. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Arabameri, A.; Yamani, M.; Pradhan, B.; Melesse, A.; Shirani, K.; Tien Bui, D. Novel ensembles of COPRAS multi-criteria decision-making with logistic regression, boosted regression tree, and random forest for spatial prediction of gully erosion susceptibility. Sci. Total Environ. 2019, 688, 903–916. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bhat, S.A.; Huang, N.F.; Hussain, I.; Bibi, F.; Sajjad, U.; Sultan, M.; Alsubaie, A.S.; Mahmoud, K.H. On the classification of a greenhouse environment for a rose crop based on ai-based surrogate models. Sustainability 2021, 13, 12166. [Google Scholar] [CrossRef]
- Hopson, T.; Wood, A.; Hay, L.E.; Sampson, K.; Arnold, J.R.; Clark, M.P.; Bock, A.; Brekke, L.; Blodgett, D.; Duan, Q.; et al. Development of a large-sample watershed-scale hydrometeorological data set for the contiguous USA: Data set characteristics and assessment of regional variability in hydrologic model performance. Hydrol. Earth Syst. Sci. 2015, 19, 209–223. [Google Scholar] [CrossRef]
- Burnash, R.J.C.; Ferral, R.L.; McGuire, R.A. A Generalized Streamflow Simulation System, Conceptual Modeling for Digital Computers; US Department of Commerce, National Weather Service, and State of California, Department of Water Resources: Sacramento, CA, USA, 1973.
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Technical report; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Dingman, S.L. Drainage density and streamflow: A closer look. Water Resour. Res. 1978, 14, 1183–1187. [Google Scholar] [CrossRef]
- Di Lazzaro, M.; Zarlenga, A.; Volpi, E. Hydrological effects of within-catchment heterogeneity of drainage density. Adv. Water Resour. 2015, 76, 157–167. [Google Scholar] [CrossRef]
- Horton, R.E. Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology. GSA Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Pallard, B.; Castellarin, A.; Montanari, A. A look at the links between drainage density and flood statistics. Hydrol. Earth Syst. Sci. 2009, 13, 1019–1029. [Google Scholar] [CrossRef]
- Clubb, F.J.; Mudd, S.M.; Attal, M.; Milodowski, D.T.; Grieve, S.W. The relationship between drainage density, erosion rate, and hilltop curvature: Implications for sediment transport processes. J. Geophys. Res. Earth Surf. 2016, 121, 1724–1745. [Google Scholar] [CrossRef]
- Mwakalila, S.; Feyen, J.; Wyseure, G. The influence of physical catchment properties on baseflow in semi-arid environments. J. Arid Environ. 2002, 52, 245–258. [Google Scholar] [CrossRef]
- Hallema, D.W.; Moussa, R. A model for distributed GIUH-based flow routing on natural and anthropogenic hillslopes. Hydrol. Process. 2014, 28, 4877–4895. [Google Scholar] [CrossRef]
- D’Odorico, P.; Rigon, R. Hillslope and channel contributions to the hydrologic response. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Qi, M.J.; Zhang, X.F. Selection of appropriate topographic data for 1D hydraulic models based on impact of morphometric variables on hydrologic process. J. Hydrol. 2019, 571, 585–592. [Google Scholar] [CrossRef]
- Fujisada, H.; Urai, M.; Iwasaki, A. Technical Methodology for ASTER Global DEM. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3725–3736. [Google Scholar] [CrossRef]
- Corbari, C.; Mancini, M.; Li, J.; Su, Z. Les données satellitaires de température de surface peuvent-elles être utilisées de la même manière que les mesures de débit au sol pour le calage de modèles hydrologiques distribués? Hydrol. Sci. J. 2015, 60, 202–217. [Google Scholar] [CrossRef]
- Immerzeel, W.; Droogers, P. Calibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Birkett, C.M.; Jones, J.W.; Carabajal, C.; Rover, J.A.; Fulton, J.W.; Garambois, P.A. Satellite remote sensing estimation of river discharge: Application to the Yukon River Alaska. J. Hydrol. 2018, 561, 1000–1018. [Google Scholar] [CrossRef]
- Durand, M.; Gleason, C.J.; Garambois, P.A.; Bjerklie, D.; Smith, L.C.; Roux, H.; Rodriguez, E.; Bates, P.D.; Pavelsky, T.M.; Monnier, J.; et al. An intercomparison of remote sensing river discharge estimation algorithms from measurements of river height, width, and slope. Water Resour. Res. 2016, 52, 4527–4549. [Google Scholar] [CrossRef]
- Ni, Y.; Cao, Z.; Liu, Q. Mathematical modeling of shallow-water flows on steep slopes. J. Hydrol. Hydromech. 2019, 67, 252–259. [Google Scholar] [CrossRef] [Green Version]
- Ajmal, M.; Waseem, M.; Kim, D.; Kim, T.W. A Pragmatic Slope-Adjusted Curve Number Model to Reduce Uncertainty in Predicting Flood Runoff from Steep Watersheds. Water 2020, 12, 1469. [Google Scholar] [CrossRef]








| Predictor | Definition |
|---|---|
| Area (A) | Total area of the subcatchment |
| Slope () | Average slope of the stream network |
| Coefficient of variation of the terrain (CVter) | |
| Drainage density (Dd) | |
| Stream source density (Dss) | |
| Roundness (RN) | |
| Shape factor (SF) |
| n_estimators (-) | learning_rate (-) | max_depth (-) | |
|---|---|---|---|
| Parameter ranges | [50, 300] | [0.01, 0.05] | [2, 4] |
| Optimization step size | 50 | 0.005 | 1 |
| Model #1 | Model #2 | Model #3 | Model #4 | Model #5 | |
|---|---|---|---|---|---|
| n_estimators (-) | 100 | 50 | 150 | 100 | 150 |
| learing_rate (-) | 0.03 | 0.045 | 0.025 | 0.035 | 0.02 |
| max_depth (-) | 3 | 2 | 2 | 2 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Huang, Y.; Qu, B.; Zhang, X.; Zhang, T.; Xia, D. Estimating the Routing Parameter of the Xin’anjiang Hydrological Model Based on Remote Sensing Data and Machine Learning. Remote Sens. 2022, 14, 4609. https://doi.org/10.3390/rs14184609
Fang Y, Huang Y, Qu B, Zhang X, Zhang T, Xia D. Estimating the Routing Parameter of the Xin’anjiang Hydrological Model Based on Remote Sensing Data and Machine Learning. Remote Sensing. 2022; 14(18):4609. https://doi.org/10.3390/rs14184609
Chicago/Turabian StyleFang, Yuanhao, Yizhi Huang, Bo Qu, Xingnan Zhang, Tao Zhang, and Dazhong Xia. 2022. "Estimating the Routing Parameter of the Xin’anjiang Hydrological Model Based on Remote Sensing Data and Machine Learning" Remote Sensing 14, no. 18: 4609. https://doi.org/10.3390/rs14184609
APA StyleFang, Y., Huang, Y., Qu, B., Zhang, X., Zhang, T., & Xia, D. (2022). Estimating the Routing Parameter of the Xin’anjiang Hydrological Model Based on Remote Sensing Data and Machine Learning. Remote Sensing, 14(18), 4609. https://doi.org/10.3390/rs14184609





