New Orbit Determination Method for GEO Satellites Based on BeiDou Short-Message Communication Ranging
Abstract
:1. Introduction
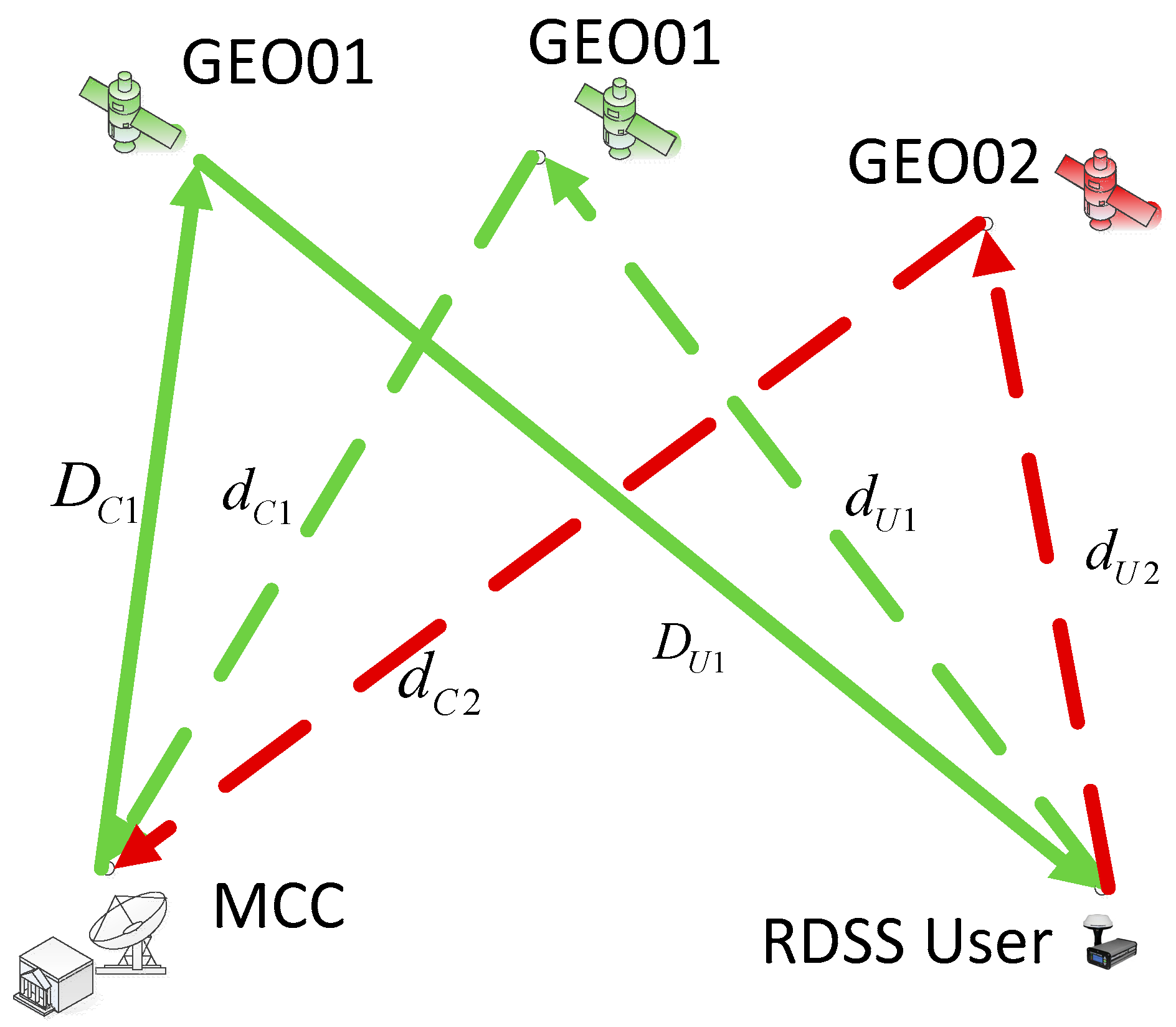
2. Measurement Model of RDSS
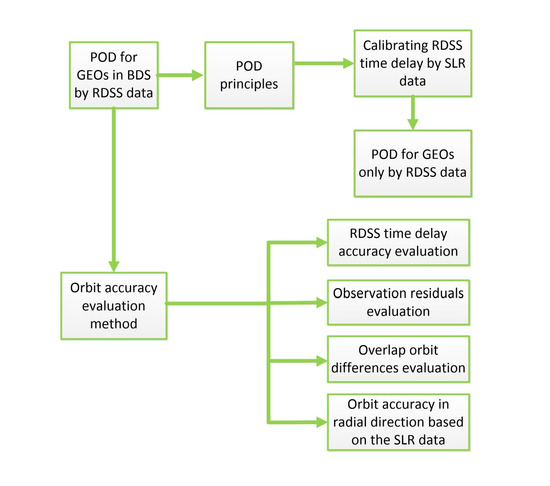
3. Orbit Determination Method for GEO Satellite Based on RDSS Data
3.1. Principles of Orbit Determination
3.2. Principles of Calibrating Time Delay for RDSS Equipments Based on SLR Data
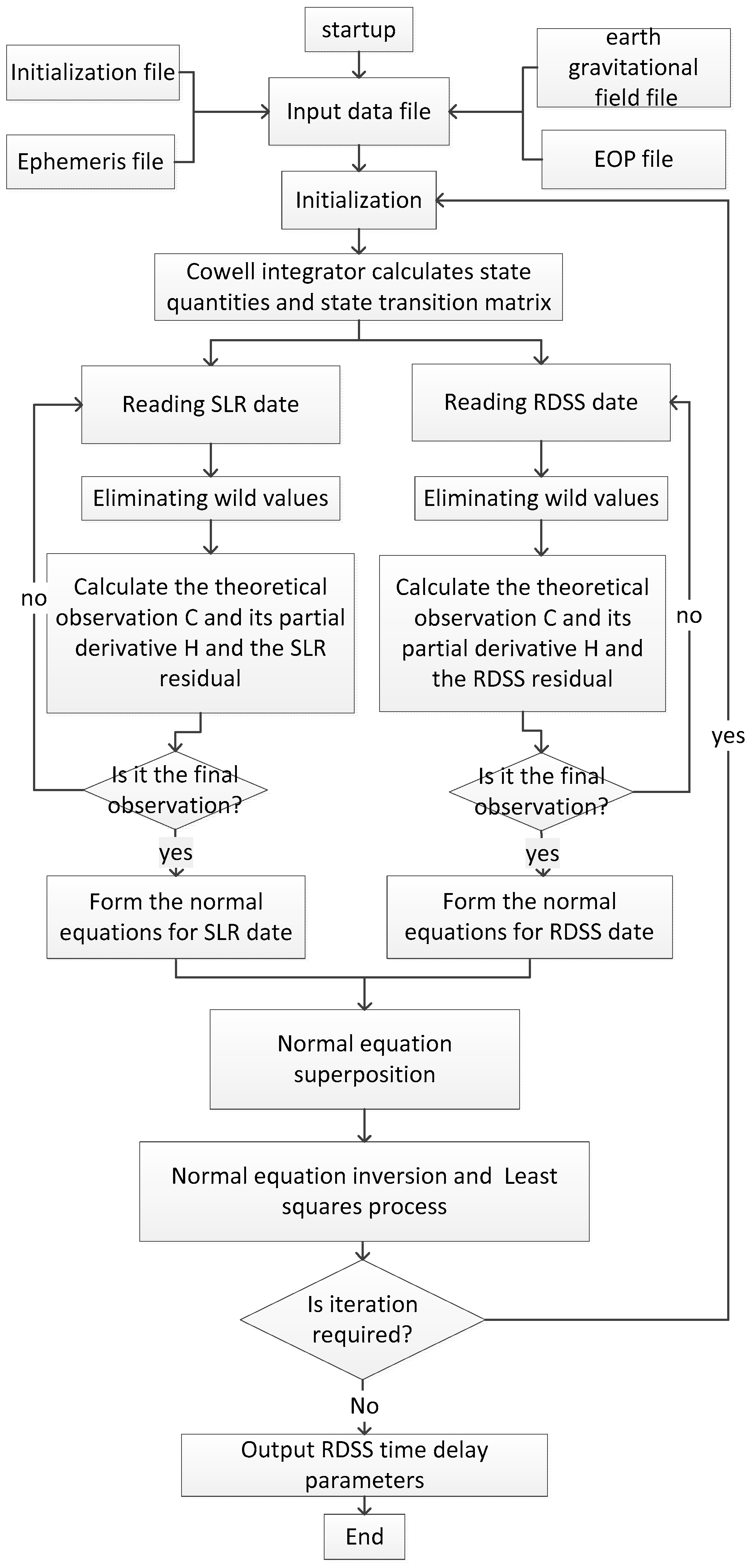
3.3. Program Design
4. Experiment and Analysis
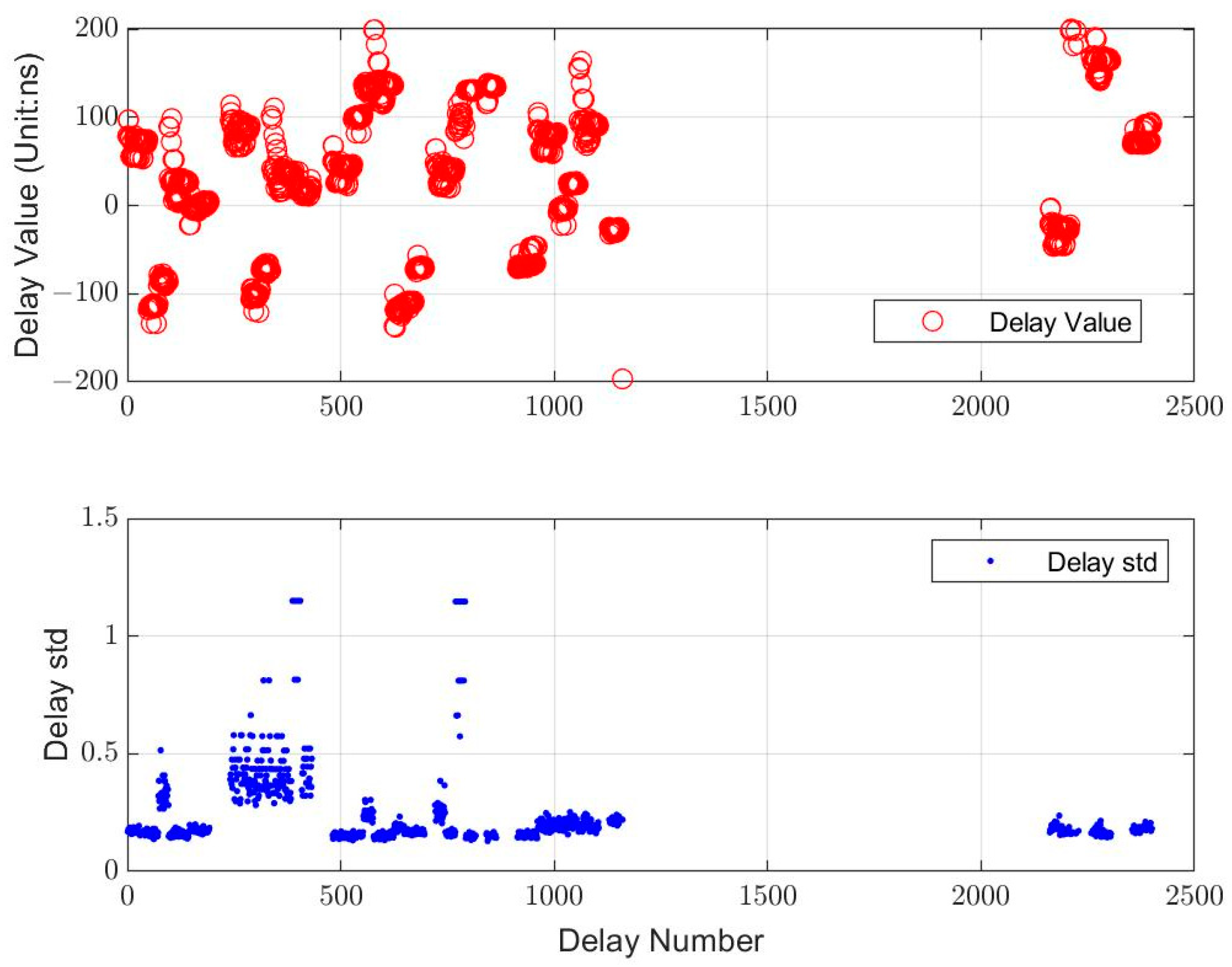
4.1. Accuracy Analysis of RDSS Time Delay
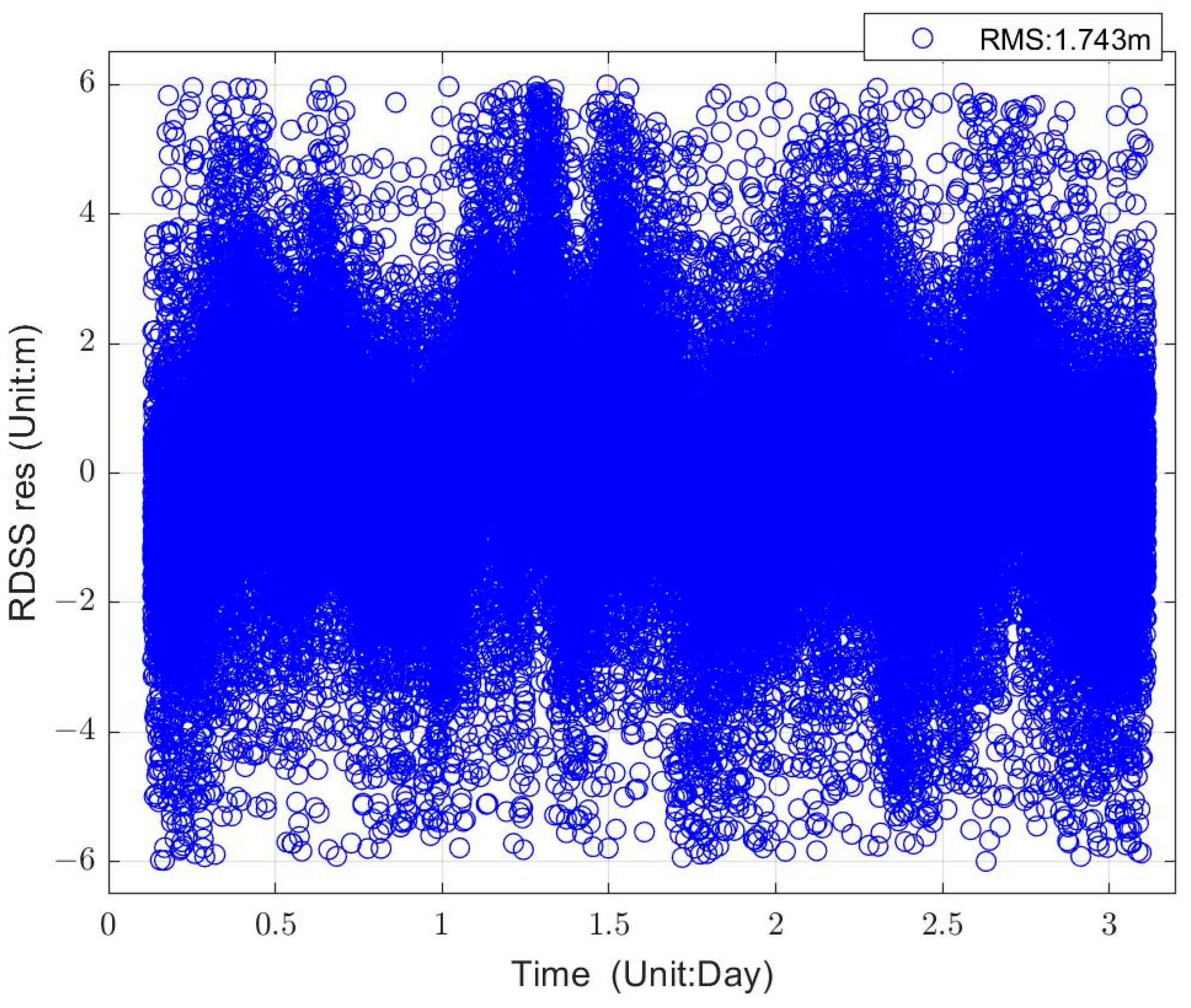
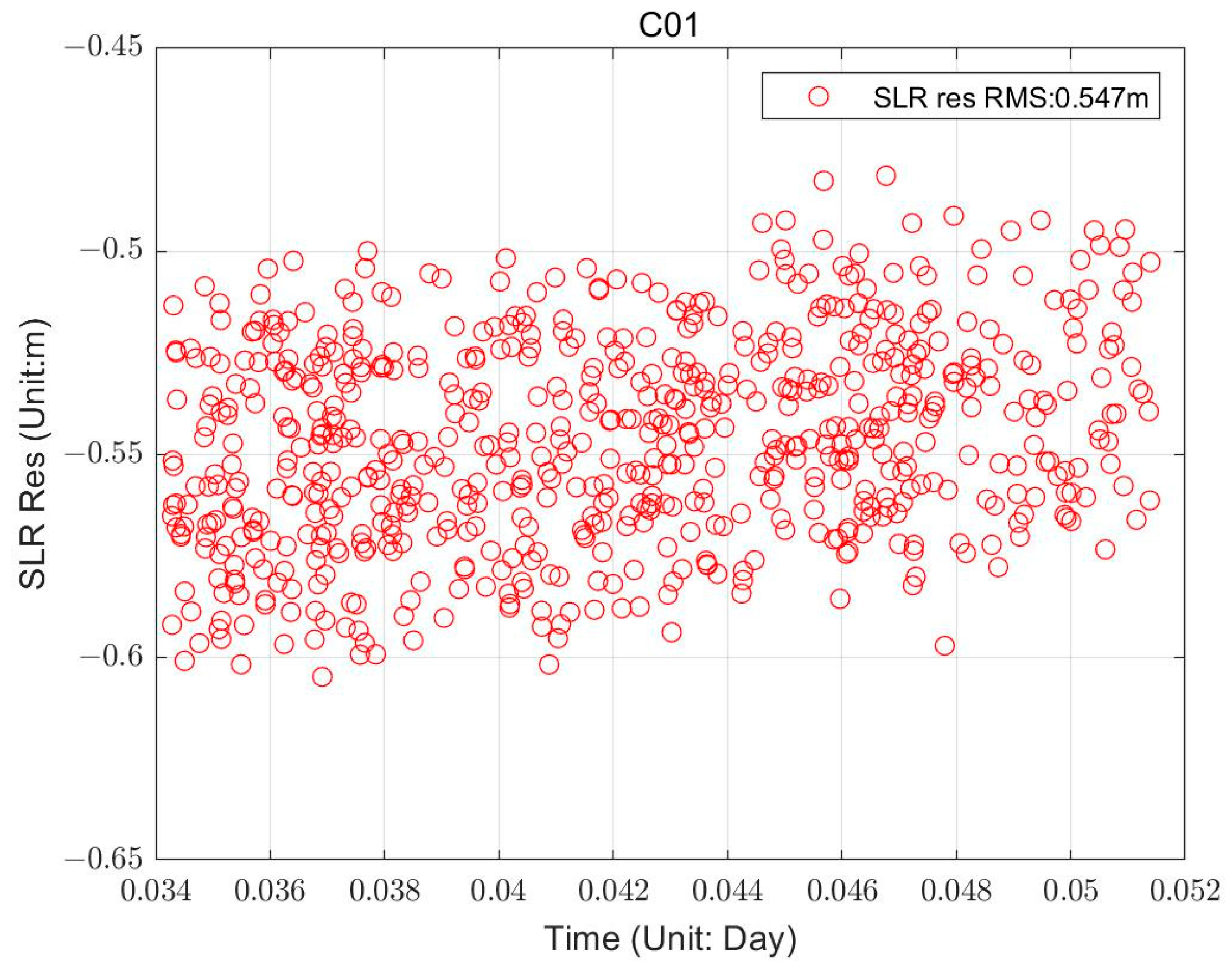
4.2. Observation Residuals of RDSS Data
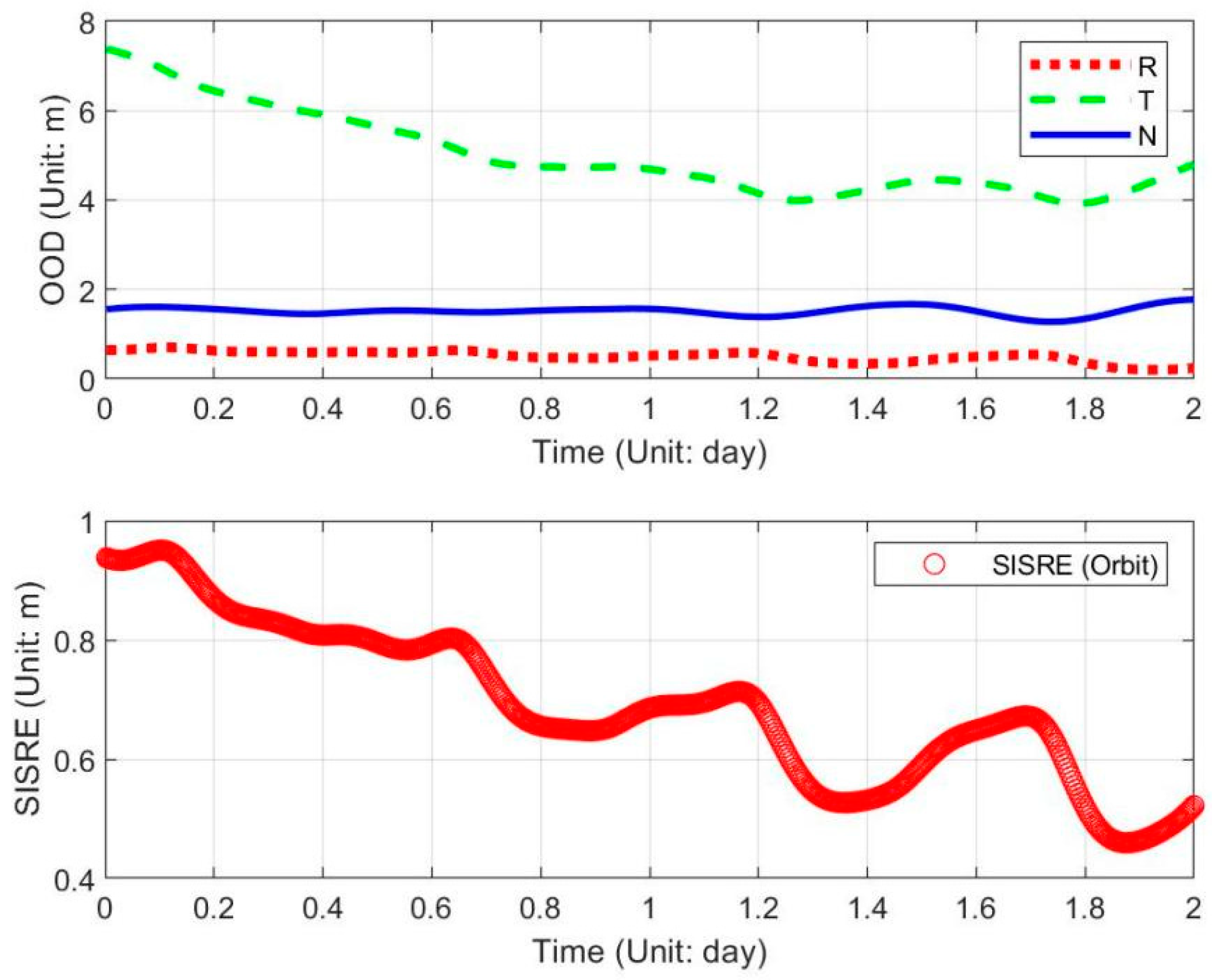
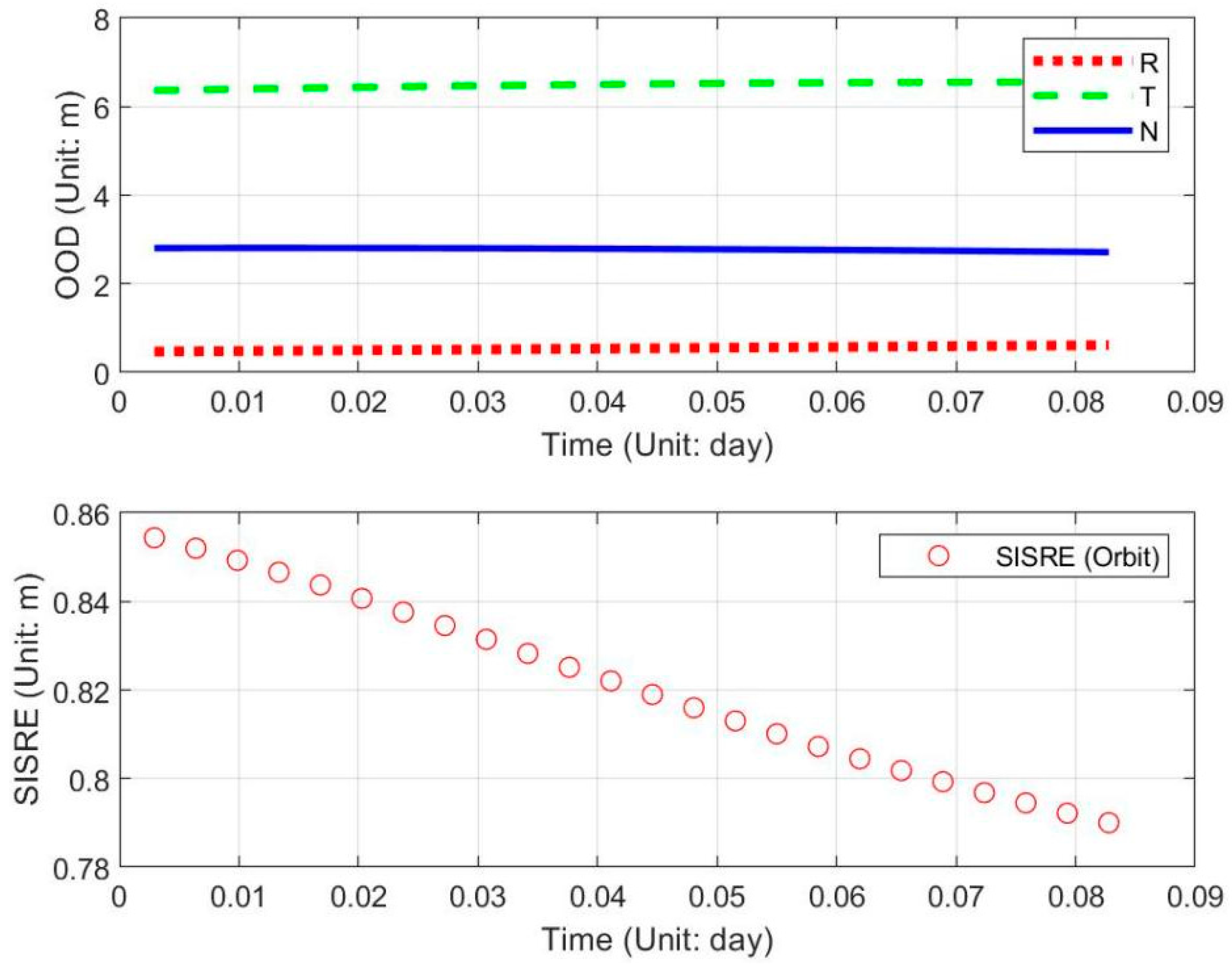
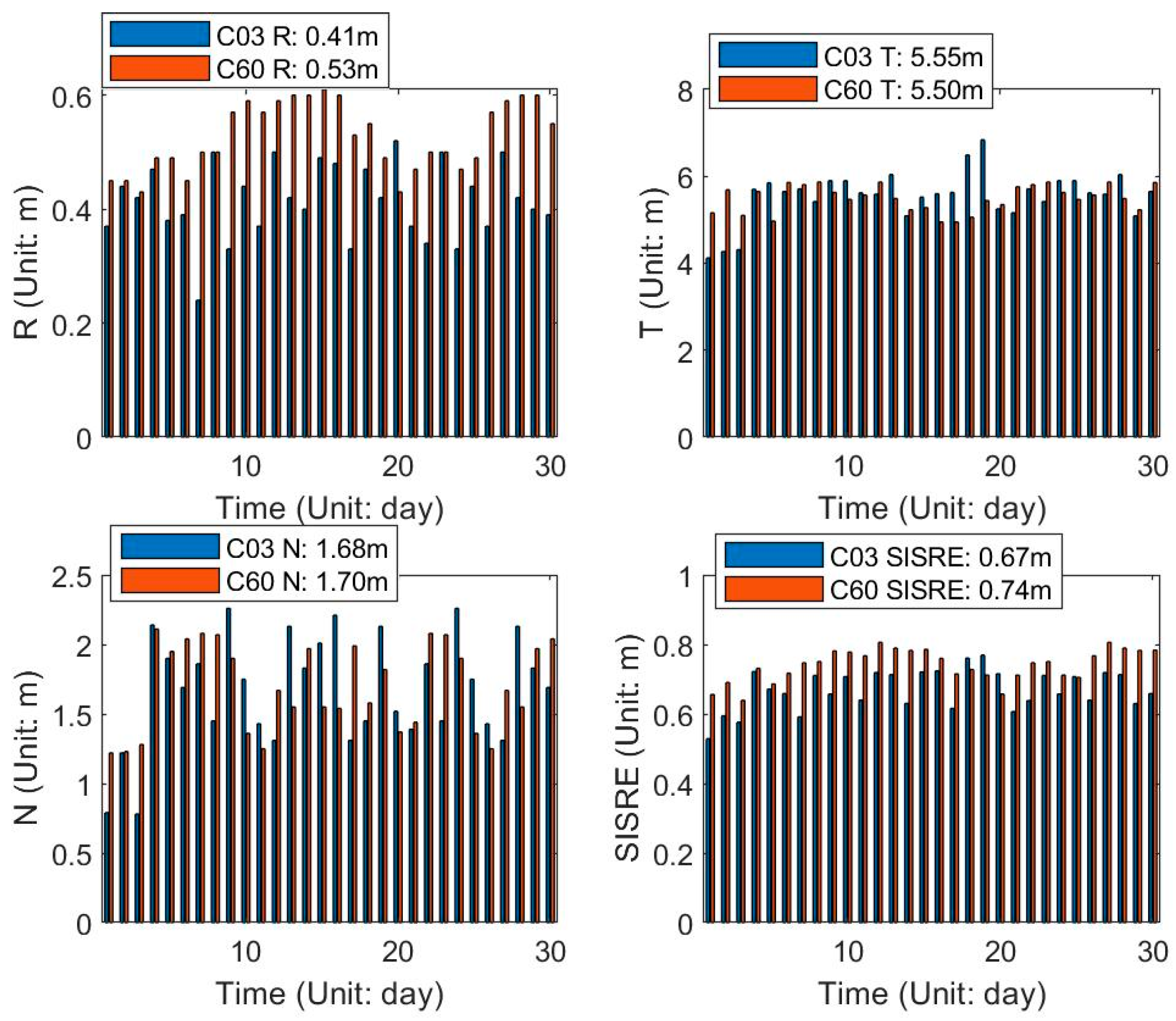
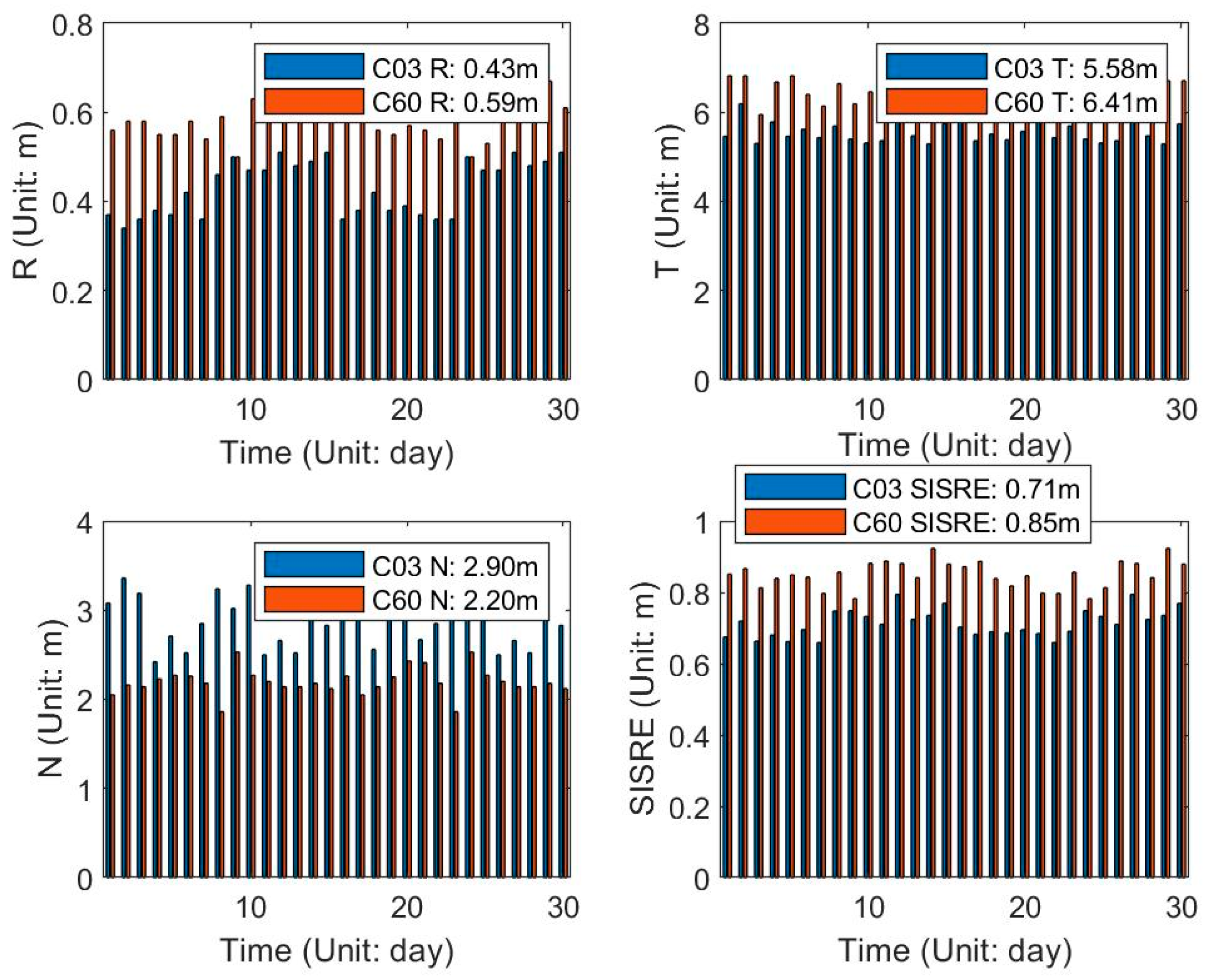
4.3. Overlap Orbit Differences (OOD)
The OOD Comparisons in the Orbital Arc
4.4. Orbit Accuracy Analysis in Radial Direction Based on the SLR Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Mao, Y.; Sun, B. Basic performance and future developments of BeiDou global navigation satellite system. Satell. Navig. 2020, 1, 1–8. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Y.; Hu, X.; Tang, C.; Zhao, L.; Xu, J. Comparison and analysis of two orbit determination methods for BDS-3 satellites. Acta Geod. Cartogr. Sin. 2019, 48, 831–839. [Google Scholar]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navig. J. Inst. Navig. 2019, 66, 7–18. [Google Scholar] [CrossRef]
- Tan, S. Innovative development and forecast of BeiDou system. Acta Geod. Et Cartogr. Sin. 2017, 46, 1284–1289. [Google Scholar]
- Tan, S. The Engineering of Satellite Navigation and Positioning; National Defense Industry Press: Arlington, VA, USA, 2011; Volume 1, pp. 12–27. [Google Scholar]
- Tan, S. The Comprehensive RDSS Global Position and Report System; National Defense Industry Press: Arlington, VA, USA, 2011; Volume 1, pp. 26–32. [Google Scholar]
- Tan, S. Theory and application of comprehensive RDSS position and report. Acta Geod. Cartogr. Sin. 2009, 38, 1–5. [Google Scholar]
- Zheng, J. Design of general aviation emergency communication, surveillance and rescue service system based on RDSS. Mod. Navig. 2016, 1, 1–5. [Google Scholar]
- Li, X.; Zhou, J.; Hu, X.; Liu, L.; Guo, R.; Zhou, S. Orbit determination and prediction for Beidou GEO satellites at the time of the spring/autumn equinox. Sci. China Phys. Mech. Astron. 2015, 58, 089501. [Google Scholar] [CrossRef]
- Li, X.; Guo, R.; Hu, X.; Tang, C.; Wu, S.; Chang, Z.; Liu, S. Construction of a BDSPHERE solar radiation pressure model for BeiDou GEOs at vernal and autumn equinox periods. Adv. Space Res. 2018, 62, 1717–1727. [Google Scholar] [CrossRef]
- Zhou, S.; Hu, X.; Wu, B. Orbit Determination and Time Synchronization for a GEO/IGSO Satellite Navigation Constellation with Regional Tracking Network. Sci. China Phys. Mech. Astron. 2011, 54, 1089–1097. [Google Scholar] [CrossRef]
- Tang, C.; Hu, X.; Zhou, S.; Guo, R.; He, F.; Liu, L.; Zhu, L.; Li, X.; Wu, S.; Zhao, G.; et al. Improvement of orbit determination accuracy for Beidou Navigation Satellite System with Two-way Satellite Time Frequency Transfer. Adv. Space Res. 2016, 58, 1390–1400. [Google Scholar] [CrossRef]
- Chen, J.; Hu, X.; Tang, C.; Zhou, S.; Yang, Y.; Pan, J.; Ren, H.; Ma, Y.; Tian, Q.; Wu, B.; et al. SIS accuracy and service performance of the BDS-3 basic system. Sci. China Phys. Mech. Astron. 2020, 63, 269511. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Y.; Hu, X.; Chen, J.; Guo, R.; Tang, C.; Zhou, S.; Zhao, L.; Xu, J. Inter-Satellite Link Enhanced Orbit Determination for BeiDou-3. J. Navig. 2020, 73, 115–130. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Y.; Zheng, K.; Yuan, Y.; Liu, G.; Xiong, Y. Precise orbit and clock products of Galileo, BDS and QZSS from MGEX since 2018: Comparison and PPP validation. Remote Sens. 2020, 12, 1415. [Google Scholar] [CrossRef]
- Lv, Y.; Geng, T.; Zhao, Q.; Xie, X.; Zhou, R. Initial assessment of BDS-3 preliminary system signal-in-space range error. GPS Solut. 2020, 24, 16. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, Q.; Guo, J.; Liu, J.; Chen, G. The contribution of intersatellite links to BDS-3 orbit determination: Model refinement and comparisons. Navigation 2019, 66, 71–82. [Google Scholar] [CrossRef]
- Li, X.; Zhou, J.; Guo, R. High-precision orbit prediction and error control techniques for COMPASS navigation satellite. Chin. Sci. Bull. 2014, 59, 2841–2849. [Google Scholar] [CrossRef]
- Xing, N.; Tang, C.; Li, X.; Zhang, T.; Ren, H.; Guo, R.; Hu, X. Precision analysis of BDS-3 GEO satellite orbit determination using RDSS. Sci. China Phys. Mech. Astron. 2021, 51, 019510. [Google Scholar]
- Li, X.; Hu, X.; Guo, R.; Tang, C.; Zhou, S.; Liu, S.; Chen, J. Orbit and Positioning Accuracy for the New Generation Beidou Satellites during the Earth Eclipsing Period. J. Navig. 2018, 71, 1069–1087. [Google Scholar] [CrossRef]
- Xing, N.; Su, R.; Zhou, J.; Hu, X.; Gong, X.; Liu, L.; He, F.; Guo, R.; Ren, H.; Hu, G. Analysis of RDSS positioning accuracy based on RNSS wide area differential technique. Sci. China Phys. Mech. Astron. 2013, 56, 1995–2001. [Google Scholar] [CrossRef]
- Yuan, Y.; Huang, J.; Wu, P. Research on the method of satellite selecting in BDS TDOA position reporting. J. Navig. Position. 2014, 2, 15. [Google Scholar]
- Yuan, Y.; Huang, J.; Tao, J. A Beidou RDSS positioning model and its error analysis without elevation. Comput. Appl. Softw. 2017, 34, 114–118. [Google Scholar]
- Li, X.; Hu, X.; Guo, R.; Tang, C.; Liu, S.; Huang, S.; Xin, J.; Pu, J.; Chen, J. A new time delay calibration method to improve the service performance of RDSS in the BDS. Adv. Space Res. 2020, 66, 2365–2377. [Google Scholar] [CrossRef]
- Pang, J.; Zhang, Y.; Zhan, J.; Ou, G. Research on key techniques of the Beidou RDSS receiver test system. J. Astronaut. Metrol. Meas. 2016, 36, 95–100. [Google Scholar]
- Liang, G. Research on EIRP calibration method of RDSS closed-loop test system. Foreign Electron. Meas. Technol. 2017, 36, 18–20. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Broadcast versus precise ephemerides: A multi-GNSS perspective. GPS Solut. 2015, 19, 321–333. [Google Scholar] [CrossRef]
- Steigenberger, P.; Hugentobler, U.; Hauschild, A.; Montenbruck, O. Orbit and clock analysis of Compass GEO and IGSO satellites. J. Geod. 2013, 87, 515–525. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)–achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
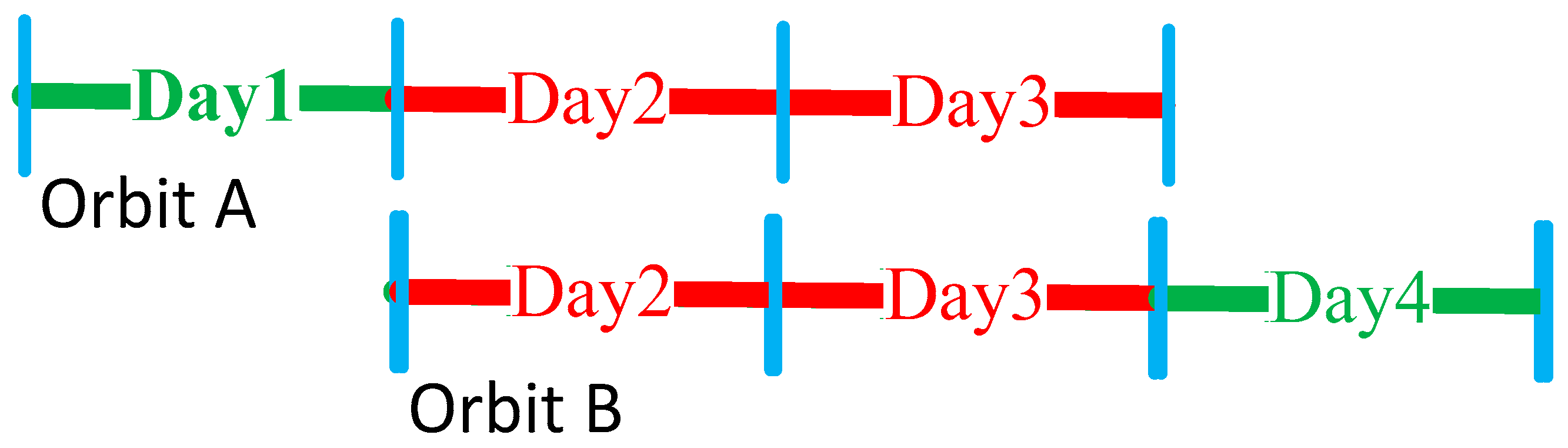
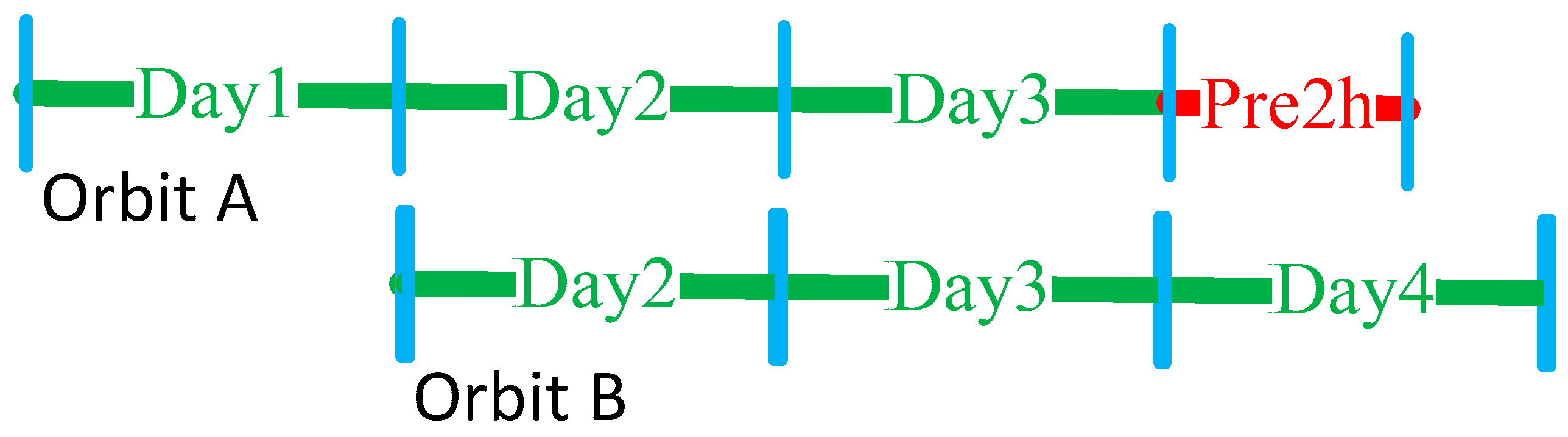
| POD Methods by RDSS and SLR Data | |
|---|---|
| Satellite | 8 GEO: C01, C02, C03, C04, C05 in BDS-2 system C59, C60, C61 in BDS-3 system |
| Stations | Seven RDSS calibration stations deployed in Beijing, Sichuan, Hainan, Southeast China, and Northeast China, and two in Xinjiang One SLR station: Beijing |
| Arc length | 3 days, sampling interval: RDSS data: 60 s SLR data: 1 s |
| observation | RDSS data in Seven RDSS calibration stations SLR data in Beijing station |
| Estimated parameter | GEO Initial orbit of the satellite, solar radiation pressure parameters and RDSS equipment time delay parameters |
| Parameter estimation method | Least squares algorithm |
| Gravitational field model | EGM 2008 12 × 12 |
| Sun, Moon gravity and the gravitational force of the other planets | Jet Propulsion Laboratory Development Ephemeris 405 (JPL DE405) |
| Solar radiation pressure (SRP) | An empirical SRP model which is similar to BERNESE ECOM 9 parameter model |
| Solid tides, ocean tide perturbation | IERS Convention 2003 |
| Precession and nutation | IAU2000R06 |
| EOP parameters | Constraints to the International Earth Rotation and Reference Systems Service (IERS) C04 model |
| Satellites | R | T | N | Positions | SISRE (Orbit) |
|---|---|---|---|---|---|
| C01 | 0.47 | 6.05 | 1.81 | 6.33 | 0.74 |
| C02 | 0.41 | 5.35 | 1.74 | 5.64 | 0.65 |
| C03 | 0.38 | 5.37 | 1.62 | 5.63 | 0.63 |
| C05 | 0.43 | 6.97 | 0.63 | 7.01 | 0.76 |
| C59 | 0.48 | 5.99 | 1.86 | 6.29 | 0.74 |
| C60 | 0.39 | 5.32 | 1.77 | 5.62 | 0.64 |
| C61 | 0.34 | 5.30 | 1.59 | 5.54 | 0.60 |
| Mean Values | 0.41 | 5.76 | 1.57 | 6.01 | 0.68 |
| Satellites | R | T | N | Positions | SISRE (Orbit) |
|---|---|---|---|---|---|
| C01 | 0.56 | 6.73 | 2.25 | 7.12 | 0.85 |
| C02 | 0.53 | 6.49 | 2.78 | 7.09 | 0.82 |
| C03 | 0.40 | 5.55 | 2.54 | 6.12 | 0.68 |
| C05 | 0.58 | 7.91 | 2.56 | 8.34 | 0.94 |
| C59 | 0.57 | 6.77 | 2.28 | 7.17 | 0.86 |
| C60 | 0.51 | 6.46 | 2.74 | 7.03 | 0.81 |
| C61 | 0.36 | 5.47 | 2.5 | 6.03 | 0.65 |
| Mean Values | 0.50 | 6.48 | 2.52 | 6.99 | 0.80 |
| Satellites | R | T | N | Positions | SISRE (Orbit) |
|---|---|---|---|---|---|
| C01 | 1.95 | 8.76 | 5.33 | 10.44 | 2.16 |
| C02 | 2.21 | 9.78 | 6.05 | 11.71 | 2.44 |
| C03 | 2.14 | 9.32 | 6.14 | 11.29 | 2.36 |
| C04 | 2.80 | 10.14 | 7.60 | 12.98 | 3.02 |
| C05 | 2.78 | 10.06 | 7.55 | 12.88 | 3.00 |
| C59 | 1.90 | 8.65 | 5.13 | 10.23 | 2.10 |
| C60 | 1.78 | 8.14 | 4.89 | 9.66 | 1.97 |
| C61 | 1.67 | 8.13 | 5.03 | 9.71 | 1.88 |
| Mean values | 2.15 | 9.12 | 5.97 | 11.11 | 2.37 |
| Satellites | 2 July 2019 | 1 June to 31 July 2021 |
|---|---|---|
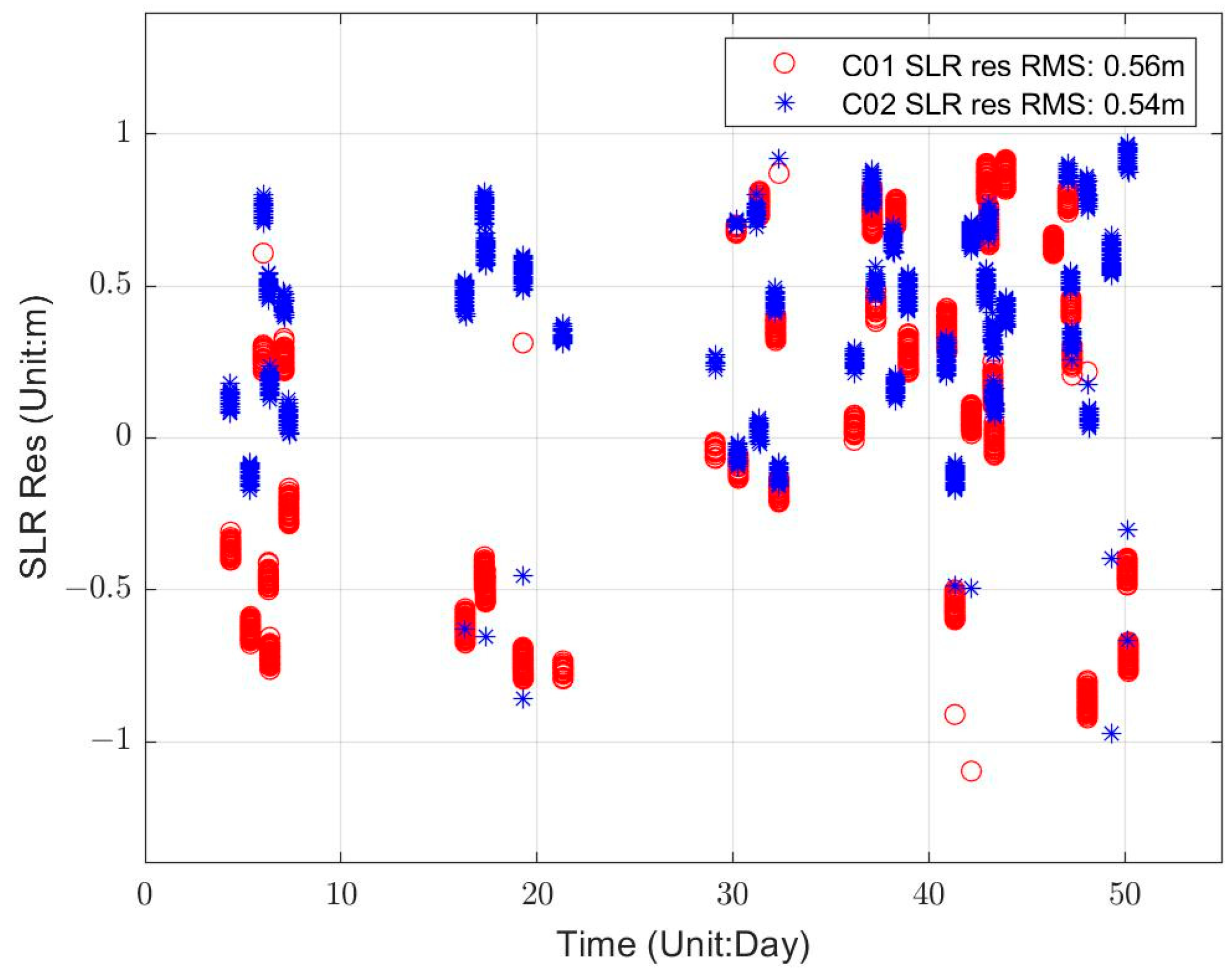
| C01 | 0.55 | 0.56 |
| C02 | 0.57 | 0.54 |
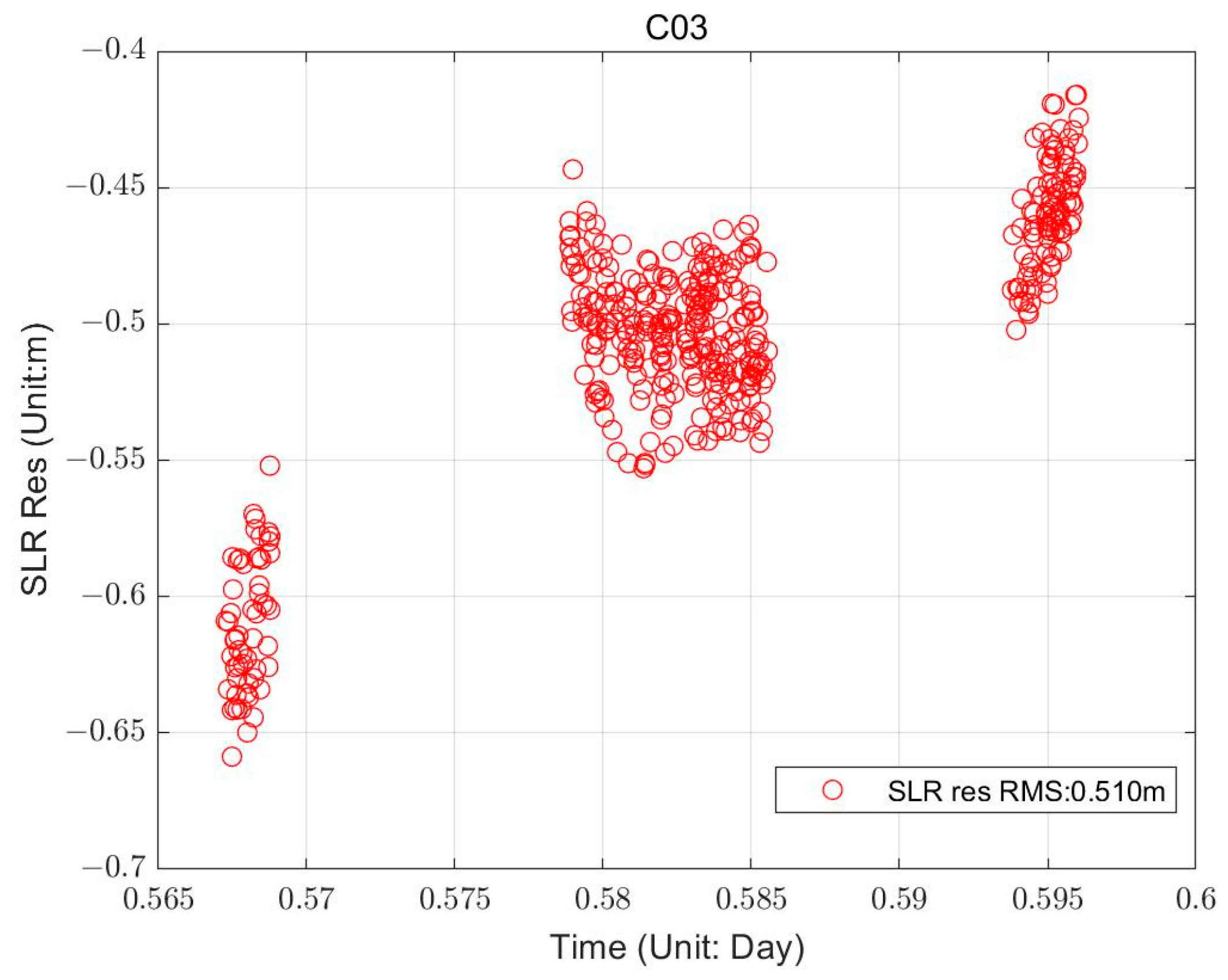
| C03 | 0.51 | 0.50 |
| C04 | - | 0.55 |
| C05 | 0.62 | 0.57 |
| Mean values | 0.56 | 0.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Guo, R.; Chen, J.; Liu, S.; Chang, Z.; Xin, J.; Guo, J.; Tian, Y. New Orbit Determination Method for GEO Satellites Based on BeiDou Short-Message Communication Ranging. Remote Sens. 2022, 14, 4602. https://doi.org/10.3390/rs14184602
Li X, Guo R, Chen J, Liu S, Chang Z, Xin J, Guo J, Tian Y. New Orbit Determination Method for GEO Satellites Based on BeiDou Short-Message Communication Ranging. Remote Sensing. 2022; 14(18):4602. https://doi.org/10.3390/rs14184602
Chicago/Turabian StyleLi, Xiaojie, Rui Guo, Jianbing Chen, Shuai Liu, Zhiqiao Chang, Jie Xin, Jinglei Guo, and Yijun Tian. 2022. "New Orbit Determination Method for GEO Satellites Based on BeiDou Short-Message Communication Ranging" Remote Sensing 14, no. 18: 4602. https://doi.org/10.3390/rs14184602
APA StyleLi, X., Guo, R., Chen, J., Liu, S., Chang, Z., Xin, J., Guo, J., & Tian, Y. (2022). New Orbit Determination Method for GEO Satellites Based on BeiDou Short-Message Communication Ranging. Remote Sensing, 14(18), 4602. https://doi.org/10.3390/rs14184602