Auto-Weighted Structured Graph-Based Regression Method for Heterogeneous Change Detection
Abstract
:1. Introduction
1.1. Background
1.2. Related Work
1.3. Motivation and Contribution
- We learn an auto-weighted structured graph to represent the image structure by using a self-conducted weight learning;
- We combine the local and global structure information in the graph learning process to obtain a more informative graph;
- We exploit the high-order neighbor information of the graph in the structure regression process;
- We conduct comprehensive experiments on different real datasets to demonstrate the effectiveness of the proposed method.
1.4. Outline
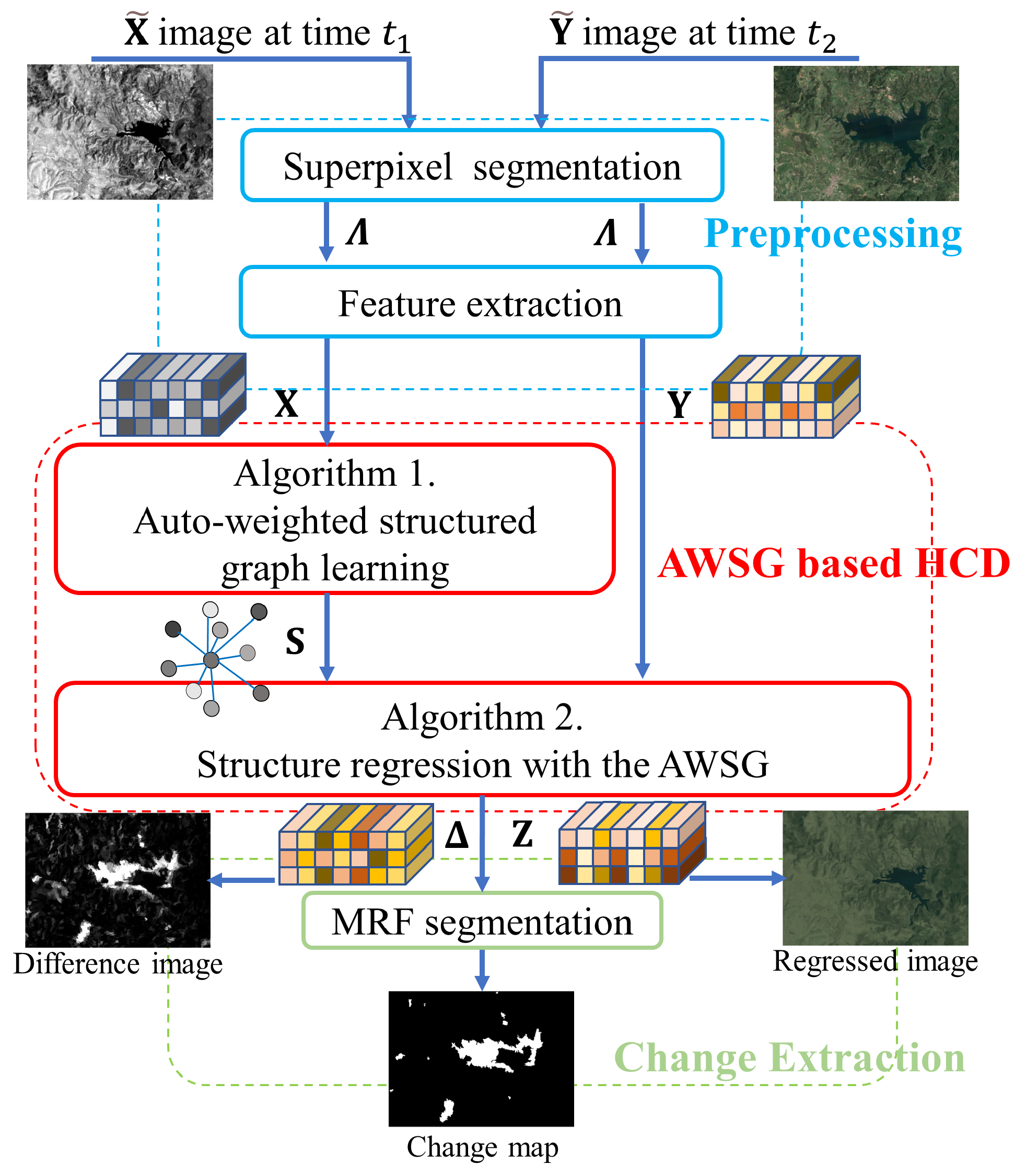
2. Auto-Weighted Structured Graph Learning
2.1. Pre-Processing
2.2. Graph Learning
2.3. Structured Graph Learning Model
2.4. Weighted Graph Learning Model
2.5. Auto-Weighted Structured Graph Learning
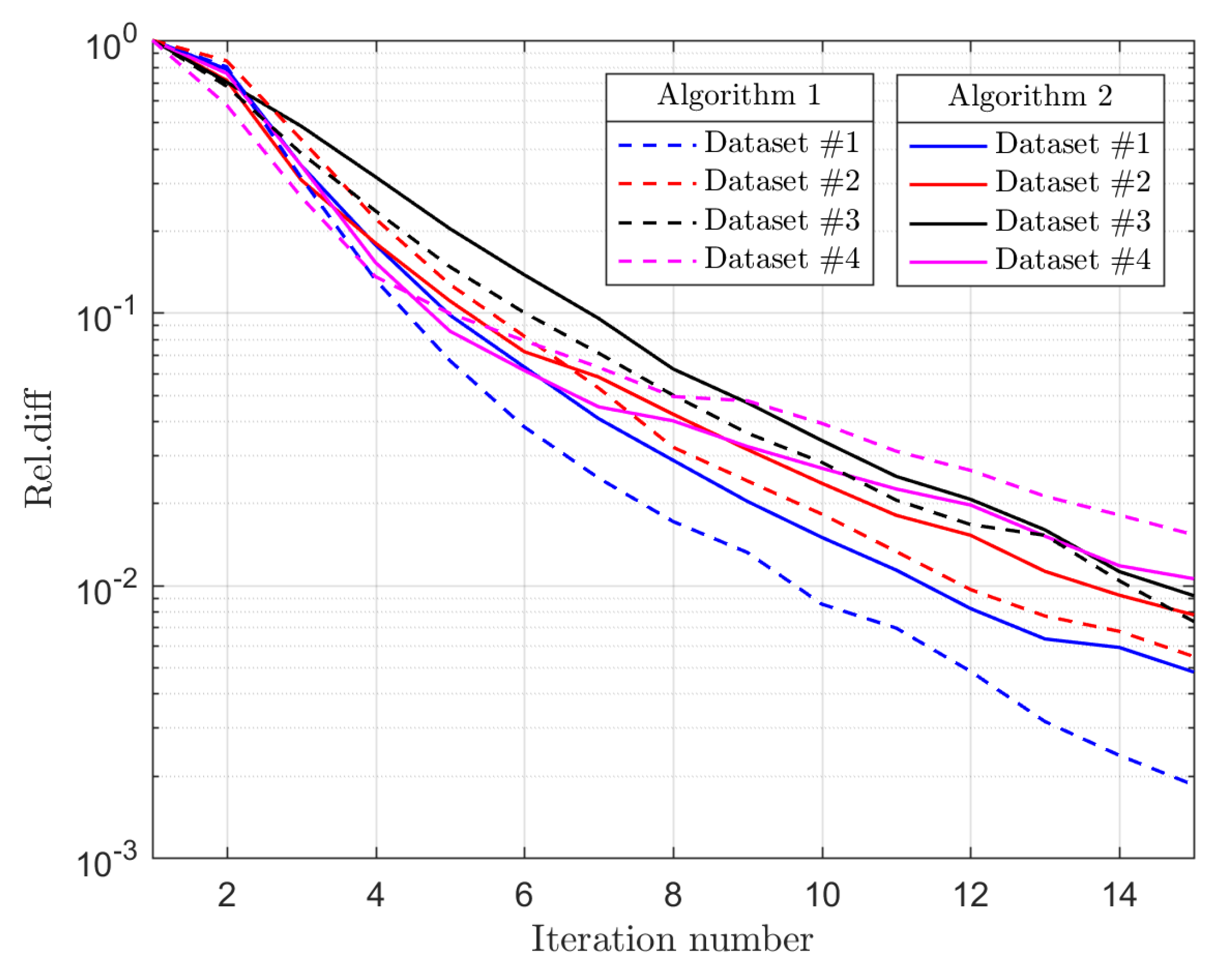
2.6. Optimization
| Algorithm 1: AWSG learning. |
Input: The feature matrix , parameter . Initialize: Set , , and , and adaptively select . Repeat: 1: Update through (14) according to different . 2: Update through (19). 3: Update through (22). 4: Update through (24). 5: Update and through (25). Until stopping criterion is met. Output: The learned graph . |
3. Structure Regression
3.1. Structure Consistency-Based Regularization
3.2. Structure Regression Model
3.3. Optimization
| Algorithm 2: Structure regression. |
Input: The matrices of , and , parameters . Initialize: Set , and . Repeat: 1: Update through (31a) according to different . 2: Update through (31b). 3: Update through (31c). 4: Update through (31d). 5: Update and through (31e) and (31f). Until stopping criterion is met. Output: The feature matrices of and . |
3.4. Change Extraction
4. Experimental Results and Discussions
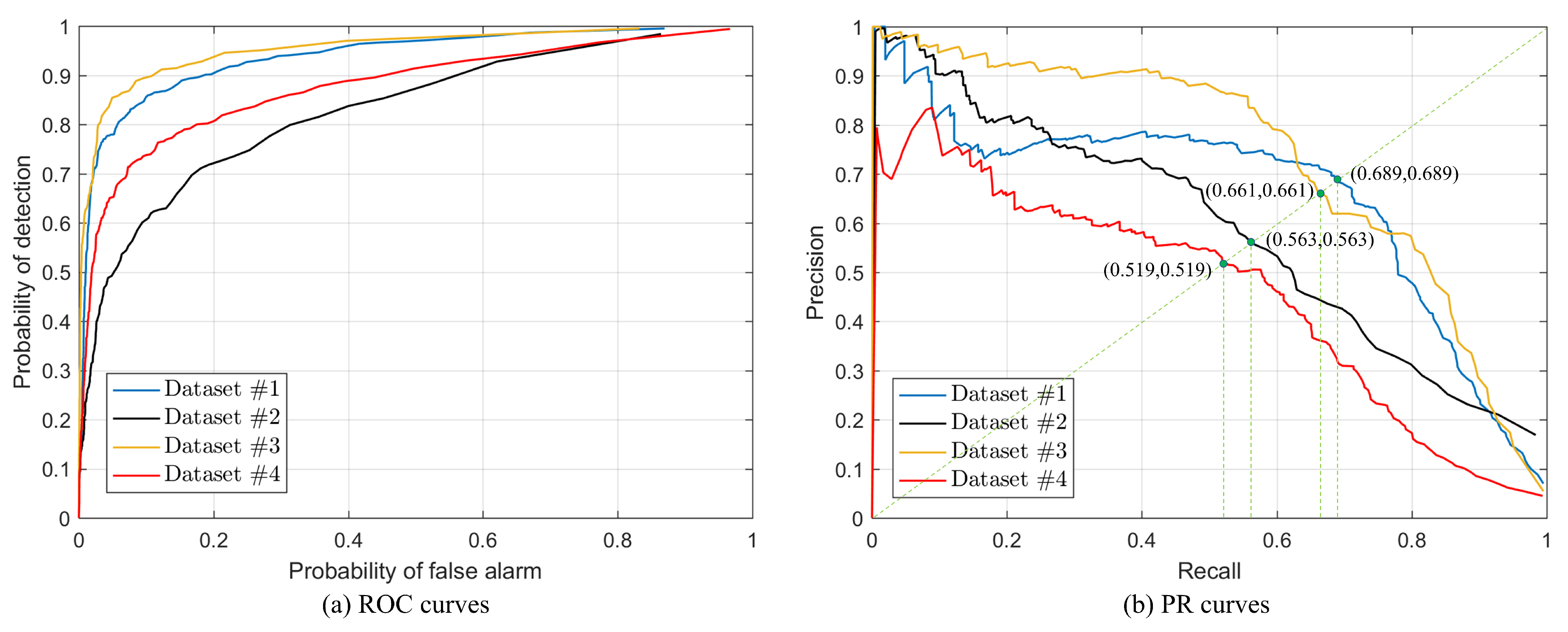
4.1. Datasets and Evaluation Metrics
4.2. Regression Images and Difference Images
4.3. Change Maps
4.4. Discussion
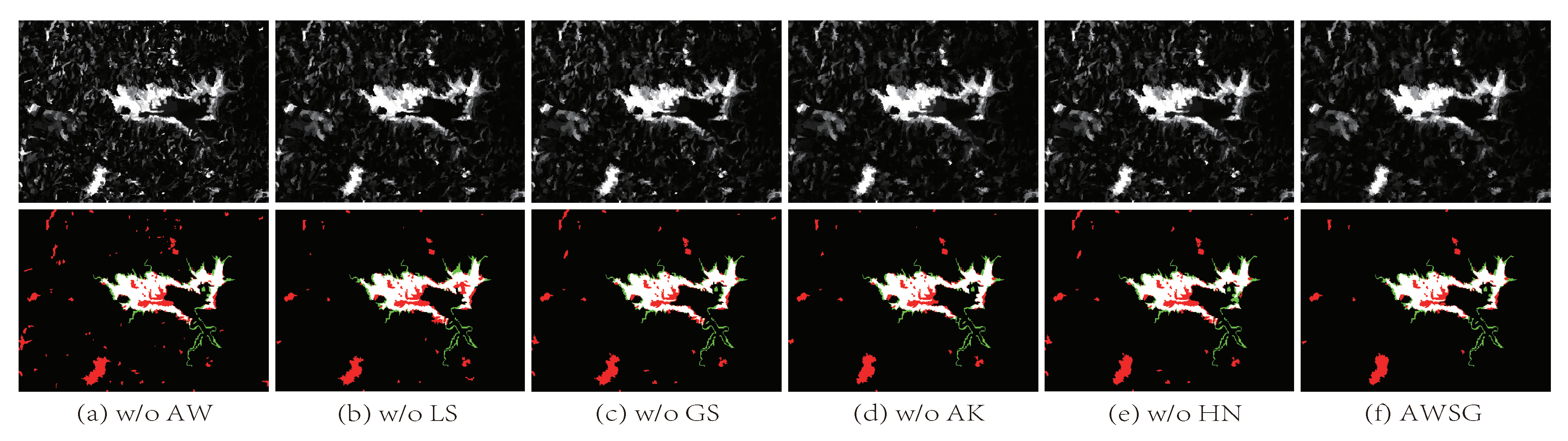
4.4.1. Ablation Study
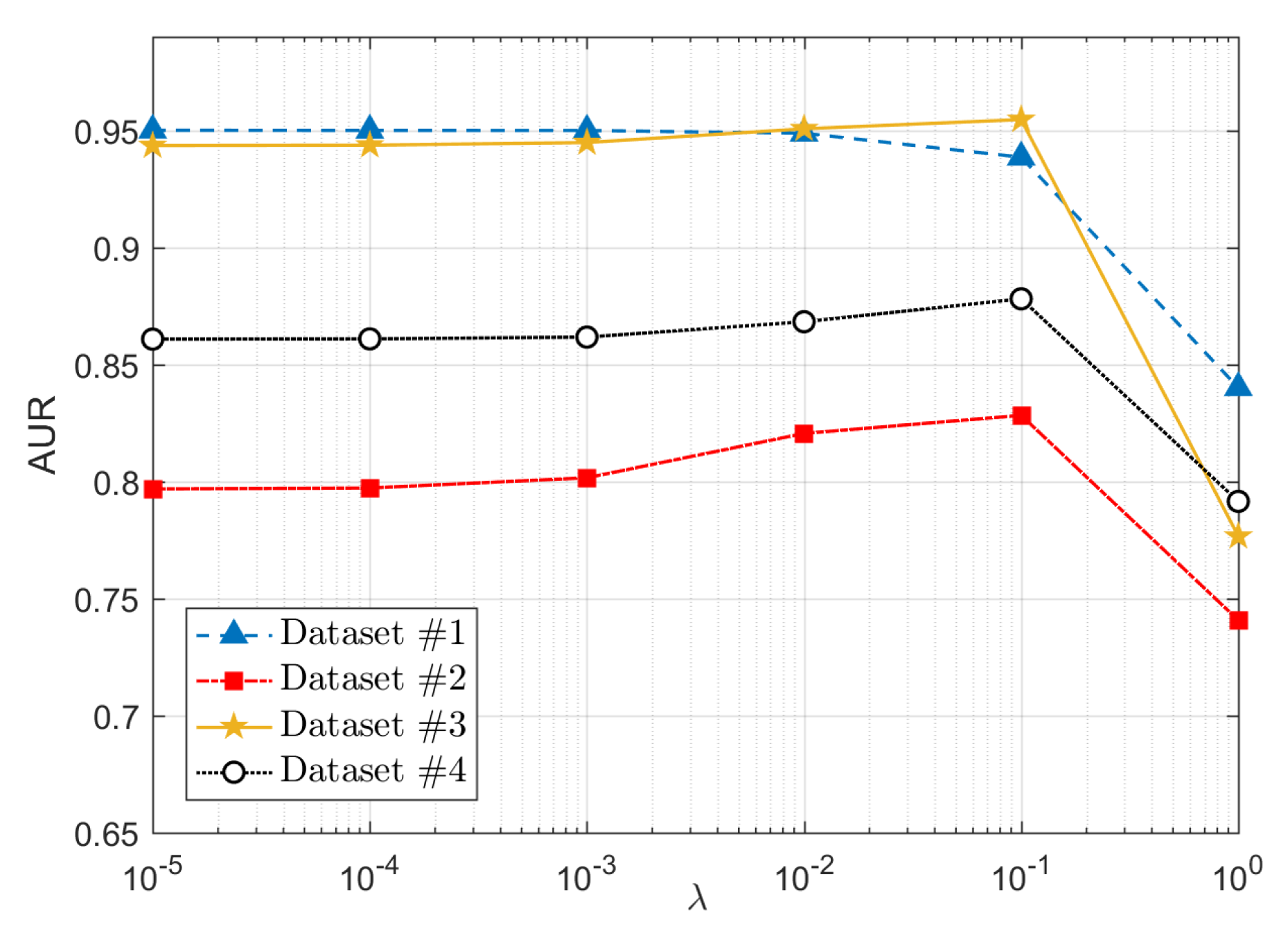
4.4.2. Parameter Analysis
4.4.3. Complexity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Singh, A. Review Article Digital change detection techniques using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef]
- Liu, S.; Marinelli, D.; Bruzzone, L.; Bovolo, F. A Review of Change Detection in Multitemporal Hyperspectral Images: Current Techniques, Applications, and Challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 140–158. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, T.; Benediktsson, J.A.; Falco, N. Land Cover Change Detection Techniques: Very-High-Resolution Optical Images: A Review. IEEE Geosci. Remote Sens. Mag. 2021, 10, 2–21. [Google Scholar] [CrossRef]
- Wen, D.; Huang, X.; Bovolo, F.; Li, J.; Ke, X.; Zhang, A.; Benediktsson, J.A. Change Detection From Very-High-Spatial-Resolution Optical Remote Sensing Images: Methods, applications, and future directions. IEEE Geosci. Remote Sens. Mag. 2021, 9, 68–101. [Google Scholar] [CrossRef]
- Moser, G.; Serpico, S. Generalized minimum-error thresholding for unsupervised change detection from SAR amplitude imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2972–2982. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, T.; Shi, C.; Benediktsson, J.A. Local Histogram-Based Analysis for Detecting Land Cover Change Using VHR Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1284–1287. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, F.; Cui, G.; Benediktsson, J.A.; Lei, T.; Sun, W. Spatial-Spectral Attention Network Guided with Change Magnitude Image for Land Cover Change Detection Using Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1. [Google Scholar] [CrossRef]
- Wang, Q.; Yuan, Z.; Du, Q.; Li, X. GETNET: A General End-to-End 2-D CNN Framework for Hyperspectral Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3–13. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Guan, D.; Wu, J.; Kuang, G.; Liu, L. Image Regression With Structure Cycle Consistency for Heterogeneous Change Detection. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–15. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Guan, D.; Li, M.; Kuang, G. Sparse-Constrained Adaptive Structure Consistency-Based Unsupervised Image Regression for Heterogeneous Remote Sensing Change Detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Deng, W.; Liao, Q.; Zhao, L.; Guo, D.; Kuang, G.; Hu, D.; Liu, L. Joint Clustering and Discriminative Feature Alignment for Unsupervised Domain Adaptation. IEEE Trans. Image Process. 2021, 30, 7842–7855. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Zhao, L.; Kuang, G.; Hu, D.; Pietikäinen, M.; Liu, L. Deep Ladder-Suppression Network for Unsupervised Domain Adaptation. IEEE Trans. Cybern. 2021, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Cui, Y.; Liu, Z.; Kuang, G.; Hu, D.; Pietikäinen, M.; Liu, L. Informative Class-Conditioned Feature Alignment for Unsupervised Domain Adaptation. In Proceedings of the 29th ACM International Conference on Multimedia, Nice, France, 21–25 October 2021; pp. 1303–1312. [Google Scholar]
- Luppino, L.T.; Bianchi, F.M.; Moser, G.; Anfinsen, S.N. Unsupervised Image Regression for Heterogeneous Change Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9960–9975. [Google Scholar] [CrossRef]
- Mignotte, M. A Fractal Projection and Markovian Segmentation-Based Approach for Multimodal Change Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8046–8058. [Google Scholar] [CrossRef]
- Touati, R.; Mignotte, M.; Dahmane, M. Multimodal Change Detection in Remote Sensing Images Using an Unsupervised Pixel Pairwise-Based Markov Random Field Model. IEEE Trans. Image Process. 2020, 29, 757–767. [Google Scholar] [CrossRef]
- Liu, Z.; Li, G.; Mercier, G.; He, Y.; Pan, Q. Change Detection in Heterogenous Remote Sensing Images via Homogeneous Pixel Transformation. IEEE Trans. Image Process. 2018, 27, 1822–1834. [Google Scholar] [CrossRef]
- Li, X.; Du, Z.; Huang, Y.; Tan, Z. A deep translation (GAN) based change detection network for optical and SAR remote sensing images. ISPRS J. Photogramm. Remote Sens. 2021, 179, 14–34. [Google Scholar] [CrossRef]
- Lv, Z.; Huang, H.; Gao, L.; Benediktsson, J.A.; Zhao, M.; Shi, C. Simple Multiscale UNet for Change Detection With Heterogeneous Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Lv, Z.; Li, G.; Jin, Z.; Benediktsson, J.A.; Foody, G.M. Iterative Training Sample Expansion to Increase and Balance the Accuracy of Land Classification From VHR Imagery. IEEE Trans. Geosci. Remote Sens. 2021, 59, 139–150. [Google Scholar] [CrossRef]
- Luppino, L.T.; Kampffmeyer, M.; Bianchi, F.M.; Moser, G.; Serpico, S.B.; Jenssen, R.; Anfinsen, S.N. Deep Image Translation With an Affinity-Based Change Prior for Unsupervised Multimodal Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–22. [Google Scholar] [CrossRef]
- Liu, J.; Gong, M.; Qin, K.; Zhang, P. A Deep Convolutional Coupling Network for Change Detection Based on Heterogeneous Optical and Radar Images. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 545–559. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Lei, L.; Guan, D.; Kuang, G. Iterative Robust Graph for Unsupervised Change Detection of Heterogeneous Remote Sensing Images. IEEE Trans. Image Process. 2021, 30, 6277–6291. [Google Scholar] [CrossRef] [PubMed]
- Touati, R.; Mignotte, M. An Energy-Based Model Encoding Nonlocal Pairwise Pixel Interactions for Multisensor Change Detection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1046–1058. [Google Scholar] [CrossRef]
- Gong, M.; Zhang, P.; Su, L.; Liu, J. Coupled Dictionary Learning for Change Detection From Multisource Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7077–7091. [Google Scholar] [CrossRef]
- Mercier, G.; Moser, G.; Serpico, S.B. Conditional Copulas for Change Detection in Heterogeneous Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1428–1441. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Li, X.; Tan, X.; Kuang, G. Patch Similarity Graph Matrix-Based Unsupervised Remote Sensing Change Detection With Homogeneous and Heterogeneous Sensors. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4841–4861. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Li, X.; Tan, X.; Kuang, G. Structure Consistency-Based Graph for Unsupervised Change Detection With Homogeneous and Heterogeneous Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–21. [Google Scholar] [CrossRef]
- Prendes, J.; Chabert, M.; Pascal, F.; Giros, A.; Tourneret, J.Y. A New Multivariate Statistical Model for Change Detection in Images Acquired by Homogeneous and Heterogeneous Sensors. IEEE Trans. Image Process. 2015, 24, 799–812. [Google Scholar] [CrossRef]
- Volpi, M.; Camps-Valls, G.; Tuia, D. Spectral alignment of multi-temporal cross-sensor images with automated kernel canonical correlation analysis. ISPRS J. Photogramm. Remote Sens. 2015, 107, 50–63. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Tan, X.; Guan, D.; Wu, J.; Kuang, G. Structured graph based image regression for unsupervised multimodal change detection. ISPRS J. Photogramm. Remote Sens. 2022, 185, 16–31. [Google Scholar] [CrossRef]
- Jiang, X.; Li, G.; Liu, Y.; Zhang, X.P.; He, Y. Change Detection in Heterogeneous Optical and SAR Remote Sensing Images Via Deep Homogeneous Feature Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1551–1566. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Pan, Q.; Ning, L. Unsupervised Change Detection From Heterogeneous Data Based on Image Translation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Wu, Y.; Li, J.; Yuan, Y.; Qin, A.K.; Miao, Q.G.; Gong, M.G. Commonality Autoencoder: Learning Common Features for Change Detection From Heterogeneous Images. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 1–14. [Google Scholar] [CrossRef]
- Saha, S.; Ebel, P.; Zhu, X.X. Self-Supervised Multisensor Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Chen, Y.; Bruzzone, L. Self-Supervised Change Detection in Multiview Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Wu, J.; Li, B.; Qin, Y.; Ni, W.; Zhang, H.; Fu, R.; Sun, Y. A multiscale graph convolutional network for change detection in homogeneous and heterogeneous remote sensing images. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102615. [Google Scholar] [CrossRef]
- Jimenez-Sierra, D.A.; Benítez-Restrepo, H.D.; Vargas-Cardona, H.D.; Chanussot, J. Graph-Based Data Fusion Applied to: Change Detection and Biomass Estimation in Rice Crops. Remote Sens. 2020, 12, 2683. [Google Scholar] [CrossRef]
- Jimenez-Sierra, D.A.; Quintero-Olaya, D.A.; Alvear-Muñoz, J.C.; Benítez-Restrepo, H.D.; Florez-Ospina, J.F.; Chanussot, J. Graph Learning Based on Signal Smoothness Representation for Homogeneous and Heterogeneous Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Li, X.; Sun, H.; Kuang, G. Nonlocal patch similarity based heterogeneous remote sensing change detection. Pattern Recognit. 2021, 109, 107598. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Guan, D.; Kuang, G.; Liu, L. Graph Signal Processing for Heterogeneous Change Detection–Part I: Vertex Domain Filtering. arXiv 2022, arXiv:2208.01881. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Guan, D.; Kuang, G.; Liu, L. Graph Signal Processing for Heterogeneous Change Detection–Part II: Spectral Domain Analysis. arXiv 2022, arXiv:2208.01905. [Google Scholar] [CrossRef]
- Baatz, M. Multi resolution segmentation: An optimum approach for high quality multi scale image segmentation. In Proceedings of the Beutrage zum AGIT-Symposium; Springer: Salzburg, Germany, 2000; pp. 12–23. [Google Scholar]
- Zhou, D.; Bousquet, O.; Lal, T.N.; Weston, J.; Schölkopf, B. Learning with local and global consistency. Adv. Neural Inf. Process. Syst. 2004, 16, 321–328. [Google Scholar]
- Wang, F.; Zhang, C.; Li, T. Clustering with local and global regularization. IEEE Trans. Knowl. Data Eng. 2009, 21, 1665–1678. [Google Scholar] [CrossRef]
- Kang, Z.; Peng, C.; Cheng, Q.; Liu, X.; Peng, X.; Xu, Z.; Tian, L. Structured graph learning for clustering and semi-supervised classification. Pattern Recognit. 2021, 110, 107627. [Google Scholar] [CrossRef]
- Zhu, X.; Li, X.; Zhang, S.; Ju, C.; Wu, X. Robust joint graph sparse coding for unsupervised spectral feature selection. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 1263–1275. [Google Scholar] [CrossRef]
- Nie, F.; Li, J.; Li, X. Parameter-free auto-weighted multiple graph learning: A framework for multiview clustering and semi-supervised classification. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016; pp. 1881–1887. [Google Scholar]
- Yang, J.; Yin, W.; Zhang, Y.; Wang, Y. A fast algorithm for edge-preserving variational multichannel image restoration. SIAM J. Imaging Sci. 2009, 2, 569–592. [Google Scholar] [CrossRef]
- Zhang, X.; Ying, W.; Yang, P.; Sun, M. Parameter estimation of underwater impulsive noise with the Class B model. IET Radar Sonar Navig. 2020, 14, 1055–1060. [Google Scholar] [CrossRef]
- Mahmood, A.; Chitre, M. Modeling colored impulsive noise by Markov chains and alpha-stable processes. In Proceedings of the OCEANS 2015, Genova, Italy, 18–21 May 2015; pp. 1–7. [Google Scholar]
- Nie, F.; Wang, X.; Huang, H. Clustering and projected clustering with adaptive neighbors. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 977–986. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A k-means clustering algorithm. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Touati, R. Détection de Changement en Imagerie Satellitaire Multimodale. Ph.D. Thesis, Université de Montréal, Montréal, QC, Canada, 2019. [Google Scholar]
- Nar, F.; Özgür, A.; Saran, A.N. Sparsity-Driven Change Detection in Multitemporal SAR Images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1032–1036. [Google Scholar] [CrossRef]


| Dataset | Location | Event (& Spatial Resolution) | Sensing Date | Collection Sensor | Image Size (Pixels) |
|---|---|---|---|---|---|
| #1 | Sardinia, Italy | Lake expansion (30 m) | Sept. 1995 July 1996 | Landsat-5 Google Earth | |
| #2 | Toulouse, France | Construction (0.52 m) | May 2012 July 2013 | Pleiades WorldView2 | |
| #3 | Shuguang Village, China | Building construction (8 m) | June 2008 Sept. 2012 | Radarsat-2 Google Earth | |
| #4 | Sutter County, CA, USA | Flooding (≈15 m) | Jan. 2017 Feb. 2017 | Landsat-8 Sentinel-1A |
| Methods | Dataset #1 | Dataset #2 | Dataset #3 | Dataset #4 | Average | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OA | F1 | OA | F1 | OA | F1 | OA | F1 | OA | F1 | ||||||
| M3CD | 0.963 | 0.669 | 0.689 | 0.863 | 0.405 | 0.481 | 0.962 | 0.602 | 0.622 | 0.575 | 0.021 | 0.077 | 0.841 | 0.424 | 0.467 |
| FPMS | 0.925 | 0.552 | 0.588 | 0.838 | 0.215 | 0.296 | 0.938 | 0.569 | 0.597 | 0.947 | 0.329 | 0.356 | 0.912 | 0.416 | 0.459 |
| CICM | 0.943 | 0.451 | 0.481 | 0.867 | 0.270 | 0.321 | 0.974 | 0.745 | 0.759 | 0.899 | 0.081 | 0.131 | 0.921 | 0.387 | 0.423 |
| SCASC | 0.947 | 0.593 | 0.621 | 0.892 | 0.464 | 0.516 | 0.979 | 0.741 | 0.751 | 0.961 | 0.479 | 0.500 | 0.945 | 0.569 | 0.597 |
| AGSCC | 0.959 | 0.658 | 0.680 | 0.897 | 0.490 | 0.540 | 0.983 | 0.773 | 0.782 | 0.960 | 0.486 | 0.506 | 0.950 | 0.602 | 0.627 |
| SCCN | 0.900 | 0.478 | 0.524 | 0.848 | 0.417 | 0.507 | 0.908 | 0.344 | 0.386 | 0.906 | 0.392 | 0.431 | 0.891 | 0.408 | 0.462 |
| ACE-Net | 0.964 | 0.718 | 0.737 | 0.886 | 0.480 | 0.541 | 0.981 | 0.788 | 0.798 | 0.940 | 0.468 | 0.497 | 0.943 | 0.614 | 0.643 |
| AWSG | 0.963 | 0.690 | 0.711 | 0.896 | 0.524 | 0.581 | 0.984 | 0.775 | 0.783 | 0.962 | 0.524 | 0.547 | 0.951 | 0.628 | 0.656 |
| Methods | Heterogeneous Datasets | Average | |||
|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | ||
| AWSG w/o AW | 0.665 | 0.549 | 0.751 | 0.513 | 0.620 |
| AWSG w/o LS | 0.682 | 0.564 | 0.761 | 0.525 | 0.633 |
| AWSG w/o GS | 0.695 | 0.558 | 0.752 | 0.540 | 0.636 |
| AWSG w/o AK | 0.703 | 0.570 | 0.772 | 0.521 | 0.642 |
| AWSG w/o HN | 0.677 | 0.565 | 0.760 | 0.539 | 0.635 |
| AWSG | 0.711 | 0.581 | 0.783 | 0.547 | 0.656 |
| Datasets | N | |||
|---|---|---|---|---|
| Dataset #2 | 2500 | 3.8 | 2.0 | 9.1 |
| 5000 | 12.1 | 5.9 | 29.3 | |
| 10,000 | 69.8 | 28.7 | 127.5 | |
| Dataset #3 | 2500 | 3.5 | 1.8 | 8.4 |
| 5000 | 10.4 | 5.1 | 24.2 | |
| 10,000 | 65.9 | 26.6 | 120.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Sun, Y.; Lei, L.; Zhang, S. Auto-Weighted Structured Graph-Based Regression Method for Heterogeneous Change Detection. Remote Sens. 2022, 14, 4570. https://doi.org/10.3390/rs14184570
Zhao L, Sun Y, Lei L, Zhang S. Auto-Weighted Structured Graph-Based Regression Method for Heterogeneous Change Detection. Remote Sensing. 2022; 14(18):4570. https://doi.org/10.3390/rs14184570
Chicago/Turabian StyleZhao, Lingjun, Yuli Sun, Lin Lei, and Siqian Zhang. 2022. "Auto-Weighted Structured Graph-Based Regression Method for Heterogeneous Change Detection" Remote Sensing 14, no. 18: 4570. https://doi.org/10.3390/rs14184570
APA StyleZhao, L., Sun, Y., Lei, L., & Zhang, S. (2022). Auto-Weighted Structured Graph-Based Regression Method for Heterogeneous Change Detection. Remote Sensing, 14(18), 4570. https://doi.org/10.3390/rs14184570







