Abstract
It has been demonstrated that deep neural network (DNN)-based synthetic aperture radar (SAR) automatic target recognition (ATR) techniques are extremely susceptible to adversarial intrusions, that is, malicious SAR images including deliberately generated perturbations that are imperceptible to the human eye but can deflect DNN inference. Attack algorithms in previous studies are based on direct access to a ATR model such as gradients or training data to generate adversarial examples for a target SAR image, which is against the non-cooperative nature of ATR applications. In this article, we establish a fully black-box universal attack (FBUA) framework to craft one single universal adversarial perturbation (UAP) against a wide range of DNN architectures as well as a large fraction of target images. It is of both high practical relevance for an attacker and a risk for ATR systems that the UAP can be designed by an FBUA in advance and without any access to the victim DNN. The proposed FBUA can be decomposed to three main phases: (1) SAR images simulation, (2) substitute model training, and (3) UAP generation. Comprehensive evaluations on the MSTAR and SARSIM datasets demonstrate the efficacy of the FBUA, i.e., can achieve an average fooling ratio of 64.6% on eight cutting-edge DNNs (when the magnitude of the UAP is set to 16/255). Furthermore, we empirically find that the black-box UAP mainly functions by activating spurious features which can effectively couple with clean features to force the ATR models to concentrate on several categories and exhibit a class-wise vulnerability. The proposed FBUA aligns with the non-cooperative nature and reveals the access-free adversarial vulnerability of DNN-based SAR ATR techniques, providing a foundation for future defense against black-box threats.
1. Introduction
Synthetic aperture radar (SAR) can actively emit microwaves and utilize the notion of synthetic aperture to improve azimuth resolution and eventually obtain high-resolution radar images of ground targets. Due to its all-weather as well as day-and-night working capabilities, SAR has various applications, including resource mapping, military surveillance, post-disaster assessment, and environment monitoring, etc. [1]. With the eye-catching advances of deep neural networks (DNNs) over the past decade [2,3], they have been widely implemented into remote sensing image processing tasks. Although the applications of DNNs are largely limited to optical imagery interpretation, they have also been introduced in SAR imagery interpretations such as automatic target recognition (ATR) [4,5,6] and terrain classification [7], attaining spectacular progress and gaining increasing interest [8].
SAR ATR is of great importance for homeland security and military applications. Therefore, SAR ATR techniques are required to be both highly accurate yet trustworthy. However, it has been demonstrated that DNN-based SAR ATR techniques are highly susceptible to adversarial intrusions in the form of clean inputs added with malicious perturbations [9,10]. These perturbations are intentionally designed to be invisible to human eyes but can dramatically manipulate DNNs’ prediction, which is what makes this adversarial vulnerability of DNNs so significant and striking. The lack of robustness of DNNs was initially reported in the field of optical image processing [11] back into 2014. Throughout the past decade, many attempts have been made to find mathematical, empirical, or geometrical explanations. Szegedy et al. noted that adversarial examples are located in low-probability pockets where regular data is unlikely to be sampled [11]. This intriguing vulnerability, according to Goodfellow et al., may be induced by the local linearity of DNNs [12]. Tanay et al. proposed that the non-robust behavior occurs when a tilting decision boundary in high-dimensional space permits a small vertical step to lead a data point past the boundary [13]. Fawzi et al. advocated utilizing adversarial perturbations to investigate the geometric properties of the DNNs’ high-dimensional feature space, having generated a large number of discoveries regarding high-dimensional classification [14]. Although the adversarial vulnerability has not been tackled yet, several studies focusing on finding, defending, and understanding adversarial examples have provided insights into robust and trustworthy DNNs [15].
It is important to find novel (or potential) attacks to further facilitate the defense and robustness in a corresponding threat scenario. In optical image processing, adversarial attacks can be classified as white-box or black-box, depending on whether the attacker has direct access to the victim model. White-box attacks allow attackers to gain full access to detailed information about the target model, such as gradient, training data, architecture, parameters, and so on [16]. Straightforward examples of the white-box attacks are the first-order methods such as the fast gradient sign method (FGSM) [12], which is basically a classification loss magnifier. In the more practical black-box scenario, attackers a have limited (query-based framework [17,18,19]) or no (transfer-based framework [20,21,22,23]) access to the victim model. Adversarial attack frameworks can also be decomposed to image-dependent and image-agnostic, depending on whether the generated perturbation is just sensitive to a specific target image or a set of images. The image-agnostic adversarial perturbation, i.e., universal adversarial perturbation (UAP) was first proposed by Moosavi–Dezfooli et al. [24], which iteratively updates the perturbation for fooling most of data points in the input space. Afterward, several attempts were made to utilize generative models for crafting UAPs [25,26]. The UAPs can also be crafted by manipulating the intermediate features [27,28,29,30]. Compared to image-dependent perturbation, the UAP is highly feasible because it can be crafted and deployed in advance. Both the black-box and universal adversarial attacks are arguably the most practical yet challenging attack scenarios and also the best surrogates to study the non-cooperative threats of DNN-based SAR ATR systems.
Recently, the adversarial vulnerability of DNNs has received increasing attention in the SAR ATR community. Huang et al. revealed that the DNN-based SAR ATR techniques are also vulnerable to adversarial examples [31]. Following studies made comprehensive examinations of various DNN structures and different databases, providing several conclusions. For instance, Chen et al. demonstrated that the data-dependent adversarial examples generalize well across different DNN models [9]. Li et al. concluded that network structure has a significant impact on robustness [10]. Specifically, simpler network structures result in more robustness against adversarial attacks. Further, Du et al. introduced generative models to accelerate the attack process and to refine the scattering features [32,33]. Most recently, Liu et al. illustrated the physical feasibility of the digital adversarial examples by exploiting the phase modulation jamming metasurface [34,35,36]. Meanwhile, Peng et al. proposed that regional restricted design also potential to be implemented in real-world [37]. It is worth noting that all the current studies comply with a default setting with which the attacker can access the same training data of the victim model. Such a setting is undoubtedly against the intrinsic nature of SAR ATR being extremely non-cooperative and leaves the question whether the SAR ATR needs to worry about adversarial examples.
By contrast, this article explores the adversarial vulnerability of DNN-based SAR ATR in the fully black-box and non-cooperative operational circumstance. With the specific intention of shedding light on the threat in the practical scenario, we take into consideration an appropriate yet also the most challenging setting in which the SAR ATR systems would deny any of the queries, requests or access to the model and training data. Thus, the attacker may just have very limited intelligence or public information about the SAR system such as the radar frequency, imaging modes or resolution, etc. Meanwhile, we purse a universal attack capability that a fixed and pre-calculated UAP can bias most of the target models and target images. Figure 1 depicts the proposed fully black-box universal attack (FBUA) framework, which can be decomposed into three stages. Firstly, we need to obtain a simulated SAR dataset that carries enough information and knowledge to train a substitute model. The generation process in Figure 1 refers to the generation process of [38] and simulates the real imaging results with CAD models and electromagnetic calculation. Secondly, we train the substitute model with the synthesized dataset. Finally, the existing universal attack algorithms are utilized to craft the UAP and attack the black-box ATR models.
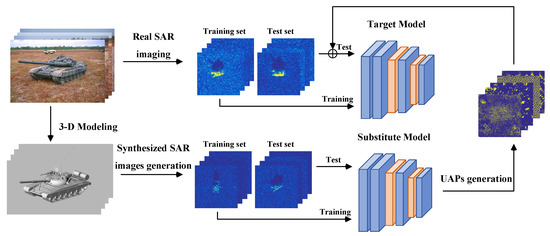
Figure 1.
Workflow of the proposed FBUA for the SAR ATR. The simulated SAR images are from the publically accessible SARSIM dataset [38,39], and the real SAR images are from the MSTAR dataset. Please notice that the Parula color map is employed in this article to visualize the gray-scale SAR images.
Utilizing the proposed FBUA framework, we empirically investigated the non-cooperative adversarial threats of a DNN-based SAR ATR with eight cutting-edge DNN architectures and five state-of-the-art (SOTA) UAP generation algorithms based on the publically accessible MSTAR and SARSIM datasets. The main contributions and experimental results of this study are summarized as follows.
- 1.
- We propose a novel FBUA framework that can effectively attack a DNN-based SAR ATR without any access to the model’s gradient, parameters, architecture, or even training data. In addition, the generated single adversarial perturbation is universal to attack a variety of models and a large fraction of target images. Comprehensive experimental evaluations on the MSTAR and SARSIM datasets prove the efficacy of our proposal.
- 2.
- This article conducts a comprehensive evaluation to reveal the black-box adversarial threats of ATR systems using the proposed FBUA method. We find that popular DNN-based SAR ATR models are vulnerable to UAPs generated by an FBUA. Specifically, with a relatively small magnitude (16 out of 255), a single UAP is capable of achieving a fooling ratio of 64.6% averaged on eight DNN models.
- 3.
- We find that the vulnerability of the target DNN model exhibits a high degree of class-wise variability; that is, data points within a class share the similar robustness to the UAP generated by an FBUA.
- 4.
- We empirically demonstrate that the UAPs created by an FBUA primarily function by activating spurious features, which are then coupled with clean features to form robust features that support several dominant labels. Therefore, DNNs demonstrate class-wise vulnerability to UAPs; that is, classes that do not conform to dominant labels are easily induced, whilst other classes show robustness to UAPs.
2. Preliminaries and Experimental Settings
In this section, we provide details about the problem description, the studied UAP generation algorithms, datasets, DNN models, and implementation details.
2.1. Problem Description of Universal Adversarial Attack to SAR ATR
Let represent a SAR ATR classifier with a set of trained parameters (weights) . General adversarial attacks aim at finding a perturbation for each SAR target image and its corresponding ground truth label that bias the DNN inference: (untargeted attack) or (targeted attack). At this time, we call the perturbed input as adversarial example, which is denoted by . The goal of untargeted attacks is to interfere with the correct predictions, while the targeted attacks are calculated to force the predictions to concentrate on a specific target class . Unless otherwise specified, the UAP in this article is by default untargeted. An adversarial example is commonly restricted by a distance measurement function to satisfy that of being imperceptible to the human visual system. In this framework, different attack methods can be summarized as diverse solutions for the following optimization problem [24]:
where cooperates with serve as a distance constraint. We follow most studied cases that adopt the -norm with radius as the constraint. Then, in our context, i.e., the universal attack scenario, the goal is to seek a single UAP such that
2.2. UAP Generation Algorithms
Various UAP generation algorithms were proposed to provide solutions to Equation (2) from different perspectives. In this section, five SOTA UAP generation algorithms will be studied in the experiments introduced.
2.2.1. DeepFool-UAP
DeepFool-UAP [24] runs over the available training images for several iterations until achieving a desired fooling ratio on the test images. Specifically, the minimum data-dependent perturbation for the i-th data point in the m-th iteration will be accumulated to the total perturbation
The whole process stops when the specific fooling ratio is achieved. The perturbation calculation operator [40] is an attack algorithm that generates the perturbation with minimum Euclidean distance away from the original data to fool the classifier. Across the DeepFool-UAP iterations, the accumulated UAP will be projected back to the -norm ball of radius when , where the projection function is defined as [24]
2.2.2. Dominant Feature-UAP (DF-UAP)
DF-UAP [41] applies the general DNN training framework to optimize the UAP. Suppose a perturbation is zero-initialized: , and then it will be progressively modified to maximize the classification loss of each m mini-batch data points:
Optimization in batch training is essential to obtain the universal perturbation, and can be conveniently optimized by common out-of-the-box optimizers, such as Adam [42] and stochastic gradient descent (SGD) [43], when training DNNs. Consistent with the DeepFool-UAP, the perturbation also should be projected back into the given norm ball. Following the original paper, we utilize the cross-entropy loss function as the classification loss item in Equation (5).
2.2.3. CosSim-UAP
Zhang et al. propose to maximize the cosine similarity (CosSim) between the model output of clean input and adversarial examples [44]. The objective is simply formulated as
The solution is similar to Equation (5). With the network parameters frozen, the perturbation is updated by batch gradient descent.
2.2.4. Fast Feature Fool (FFF) and Generalizable Data-Free UAP (GD-UAP)
Mopuri et al. propose to generate a UAP in data-free condition [27], i.e., the attacker has no access to training data to craft any data-dependent sub-perturbation. They propose an efficient objective to maximize spurious activations at each of the convolution layers. The objective is formulated as
where is the mean value of the output at layer i after non-linear activation such as error. The aim at maximizing the total activation of that ignited by . In their later published work GD-UAP [29], the loss is changed to calculate a Euclidean norm of each activation:
FFF and GD-UAP intentionally cause over-fitting of the neurons to deteriorate the features that derived from normal inputs. The mathematical significance of and is comparable. In practice, we find that the performance of the later objective is marginally superior to that of the former; hence the remainder of this work focuses primarily on the .
2.3. Database
Recall the condition that the attacker does not have any data; thus, the substitute models are expected to be trained by the images that are similar enough to the target SAR system. In this article, we focus on the most studied MSTAR recognition task. Taking the public setting of the MSTAR measured data as the only information we could know, e.g., the frequency, resolution, spotlight imaging mode, and so on. We propose to generate spurious data to obtain the informative and cognitive substitute models. To encourage reproducible research, a publicly accessible simulated MSTAR-like SAR dataset, namely SARSIM, was selected to train the substitute models [38].
2.3.1. MSTAR Dataset
MSTAR dataset for the public research of SAR ATR was made available by the moving and stationary target acquisition and recognition (MSTAR) program, which was funded by the defense advanced research projects agency (DARPA) and the Air Force Research Laboratory (AFRL). The Sandia National Laboratory SAR sensor platform with X-Band imaging capability and 1-foot resolution was utilized to gather the SAR data. The resulting measured data consists of 128 × 128 pixel size images with 360° articulation, 1° spacing, and several depression angles. A total of 10 different types of ground vehicle targets are included in the MSTAR dataset. We follow the standard operation condition (SOC) that use the 17° data to train and 15° data to test the models. More details of the SOC subset are specified in Figure 2 and Table 1.
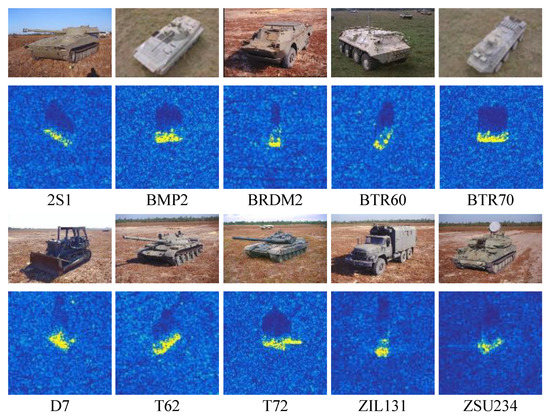
Figure 2.
Examples of the targets in the MSTAR dataset: (top) optical images; and (bottom) the corresponding SAR images.

Table 1.
Details of the SOC subset of MSTAR dataset.
2.3.2. SARSIM Dataset
SARSIM data were calculated specifically with the public information about the MSTAR dataset [38,39]. Initially, the far-field radar cross section (RCS) in corresponding frequency, azimuth, and depression angle was calculated utilizing the CST Microwave Studio Asymptotic Solver. Then, three types of terrain clutter (grass, roads, and the mix of them) and thermal noise were statistically provided. Meanwhile, the electromagnetic shadowing was well-estimated by ray projection from the sensor position to each scatterer. The focusing of the simulated radar data was performed by a time-domain back-projection algorithm. The SARSIM dataset consists of seven types of ground targets, and two sub-objects are included in each of the seven types of targets. The whole dataset contains seven depression angles (15°, 17°, 25°, 30°, 40°, and 45°), and the granularity in azimuth angle is 5°. It should be noted that the SARSIM dataset has shown to be effective in providing valid knowledge about the MSTAR targets in recent works [5,39].
In the experiments, we selected 10 objects and followed the MSTAR SOC setting that 17° images are for training. All the three terrain clutters were included in our setting. Figure 3 and Table 2 display the specifics of the SARSIM setting in our experiment.

Figure 3.
Examples of the targets in the SARSIM dataset.

Table 2.
Details of the training set of the SARSIM dataset used in this work.
2.4. Implementation Details
2.4.1. Environment
The Python programming language (v3.6) and Pytorch deep learning framework (v1.10.1) were used to implement all the software parts of the evaluations, including the data processing, DNN, and attack implementations. All the evaluations were supported by a NVIDIA DGX-1 server which is equipped with eight Tesla-V100 GPUs and powered by a dual 20-core Intel Xeon E5-2698 v4 CPU.
2.4.2. DNN Models and Training Details
The evaluations included eight DNN models: AlexNet [2], VGG11 [45], ResNet50 [46], DenseNet121 [47], MobileNetV2 [48], AConvNet [4], ShuffleNetV2 [49], and SqueezeNet [50]. The first four are typical structures that serve as backbone in various deep learning applications, and the last four are lightweight designs. Note that the AConvNet was especially proposed to be applied for the SAR ATR. The well-known procedure in [4] was followed to train these models. Specifically, the images were randomly cropped to 88 × 88 for training and center-cropped for testing. The single-channel SAR images were treated as gray-scale images and normalized to [0, 1] for faster convergence. With an SGD optimizer [43] and multi-step learning rate adjustment strategy, the models were, respectively, trained on the two studied datasets. Details of the models can be found in Table 3. It is shown that with far fewer parameters and computational resource requirements, the lightweight models can achieve competitive performance on both the studied datasets, which are of value for the on-board or edge-device ATR scenarios such as the drone-borne SAR.

Table 3.
Details of the studied models.
2.4.3. Implementation Details
All the aforementioned UAP generation algorithms were re-implemented using Pytorch according to the original papers. Each of the images in the SARSIM training set are available for DeepFool-UAP, DF-UAP, and CosSim-UAP, and the perturbation was generated for five epochs of the whole training set. For DF-UAP, CosSim-UAP, and GD-UAP, the Adam [42] algorithm was provided to optimize the perturbation with respect to their loss functions. The learning rate was set to 0.1, and maximum iterations were set to 300 (GD-UAP); other parameters were set by default. and were selected as constraint unless otherwise stated, e.g., the pixels’ absolute value of perturbation was not allowed to exceed (for ). The -norm is defined as
where are the pixel index of the perturbation image (matrix) with a pixel size of . When the UAP transfers across models that have different input size requirements, it will be scaled by bilinear interpolation to fit the target size.
2.4.4. Metric
In light of the aforementioned definition of UAPs, the fooling ratio is the most frequently used metric for assessing the effectiveness of UAPs. Specifically, the fooling ratio is defined as the percentage of samples whose prediction changes after the UAP is applied:
Herein, denotes the indicator function, and is the capacity of the test set to evaluate the attack performance. In the experiments, this test set is a uniformly extracted subset from the MSTAR test set and . These 1000 images can be correctly classified by all the eight MSTAR models and contain 100 images for each of the classes.
3. Results
3.1. Quantitative Results
We first investigate the overall attack performance of the studied UAP generation algorithms. The fooling ratios under 256 attack scenarios, that is, diverse UAP generation algorithms and substitute model architectures versus different black-box target models, are available in Figure 4. Each element of these matrices indicates the fooling ratio against the target MSTAR model (column index) achieved by the UAP (caption) generated based on the substitute SARSIM model (row index). We observe that the DeepFool-UAP algorithm is unable to carry out a successful cross-dataset universal attack, while the other algorithms exhibit considerable attack capability. The DF-UAP, CosSim-UAP, and GD-UAP, respectively, achieve 58.4%, 62.4%, and 49.8% overall average fooling ratios. The MobileNetV2 is shown to be the most effective substitute model for DF-UAP and CosSim-UAP, and VGG11 is for GD-UAP, respectively, achieving 62.4%, 64.6%, and 61.3% fooling ratios. Therefore, these three attack settings are further investigated in the following experiments. To conclude, the CosSim-UAP algorithm exhibits the most robust and effective attack performance against a variety of target models with different substitute models. In the subsequent sections of this article, we will report the results of the CosSim-UAP algorithm. The results of DF-UAP and GD-UAP will be listed in the Appendix A.
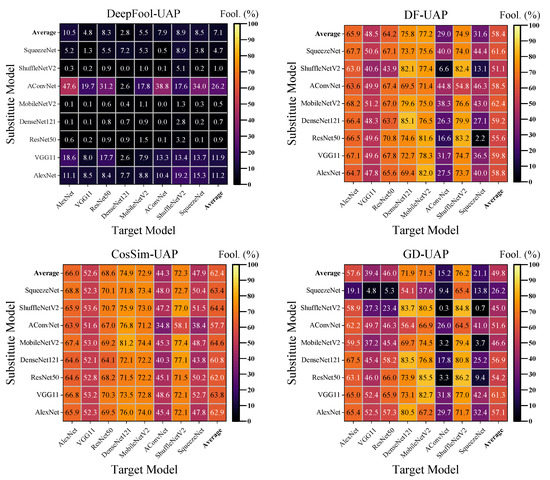
Figure 4.
Transferability of UAPs generated by the studied attack algorithms. The fooling ratio is evaluated by using the UAPs generated by substitute SARSIM models to attack the target MSTAR models.
At the same time, the vulnerability of different target models is less related to the choice of substitute model. Each column shows an approximate fooling ratio, indicating that the remained accuracy of the target model is mostly influenced by itself and the attack algorithm other than the substitute model. Moreover, several cases reveal that the UAP performs badly to specific target models, such as the DF-UAP and GD-UAP achieving worse fooling ratios against AConvNet and SqueezeNet. Among all the target models, AConvNet exhibits the best resistance to UAPs in the face of DF-UAP, CosSim-UAP, and GD-UAP attacks, which may be due to the rescaling of UAPs losing their aggressiveness.
3.2. Qualitative Results
The UAPs generated in all the aforementioned attack scenarios are visualized in Figure 5. Since the magnitude of the UAPs is relatively small, we amplify them for better observation. The generated perturbation patterns are observed to link to the generation algorithm and model architecture, which, however, is not interpretable by a human observer. Nonetheless, we report the perturbed images along with the UAP that constrained by various magnitude in Figure 6. It can be observed that the perturbed images are not easy to discriminate with naked eyes and without original images as reference.
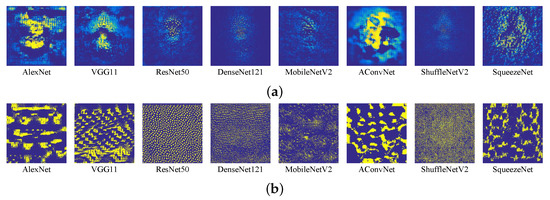

Figure 5.
UAPs generated by different algorithms for the studied DNN models: (a) DeepFool-UAP; (b) DF-UAP; (c) CosSim-UAP; and (d) GD-UAP. All the UAPs are enlarged to for observation.
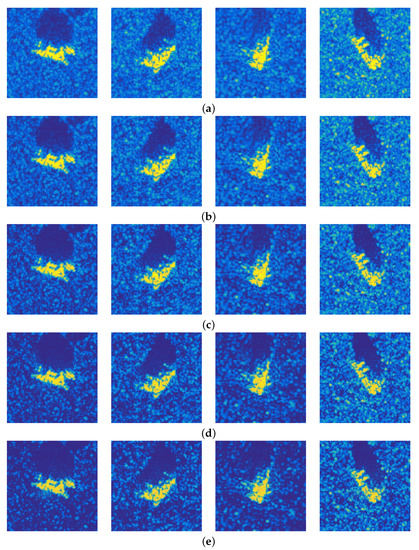
Figure 6.
Adversarial examples with various constraint . (a) Ori. (b) = 8/255. (c) = 16/255. (d) = 24/255. (e) = 32/255.
3.3. Comparison to Random Noise
We further compare the UAP generated by an FBUA with random noise to study its efficacy. The UAPs, uniform noise, and Gaussian noise are generated with the same -norm constraints. Please notice that we set the deviation of Gaussian noise as to make most of the pixel modifications lie in the range section of . Table 4, Table A1, and Table A2 detail the attack performances of all the studied noise from which the following observations can be summarized. Firstly, with larger , the UAPs exhibit more powerful universal aggressivity. It achieves an average fooling ratio of with . Secondly, some models are sensitive to random noise, such as the DenseNet121, MobileNetV2, and ShuffleNetV2. However, compared to the universal nature of UAPs, the random noise exhibits severe particularity and failed to attack all the target models. The results of this comparison are aligned with the aforementioned efficacy of the UAPs.
3.4. Robustness of the UAP
Well-designed perturbations are challenged by many factors in the SAR imaging thread, such as the velocity shake of the airborne platform, atmospheric factors of the space-borne platform, as well as the speckle noise, among many others. Therefore, we conduct several perturbations to test the UAPs’ robustness, including additive white noise, multiplicative exponential noise, Gaussian filtering, and median filtering. Details and results are elaborated in Table 5, Table A3, and Table A4. The most destructive perturbation to UAPs is the multiplicative noise which generally models the speckle noise in SAR imagery. There are cases in which extra perturbation enhances the fooling ratio for particular models, such as median filtering for AConvNet and SqueezeNet. Overall, the UAPs exhibit impressive robustness against these perturbations when , and when become larger, the perturbations would have less influence on the attack performance.

Table 5.
Fooling ratio (%) against various perturbations. The additive noise is white noise with a deviation of , the multiplicative noise is truncated exponential noise with a tail of 2, the deviation of Gaussian filtering is 1. Kernel size of the filters is 7 × 7. The results of random noise are averaged on 10 runs. Results of DF-UAP and GD-UAP can be found in Table A3 and Table A4.
3.5. Analysis of the Class-Wise Vulnerability
In this section, we focus on investigating the vulnerability gap between different target models. Table 6, Table A5 and Table A6 elaborate the detailed fooling ratios, showing that the difference in fooling ratio between models is mainly determined by whether certain classes are effectively attacked. For example, the total difference between AlexNet and VGG 11 is 14.4%, mainly composed of the difference 8.8% for the ZSU234. Figure 7, Figure A1 and Figure A2 exhibit more specifics of the class transfer. In these figures, each element expresses the number of samples transferred to the adversarial category from the original category after being added with the UAP. Take the first matrix of Figure 7 as an example. The first row (index 9) indicates that there were 88 (out of 100) ZSU234 samples misclassified as 4 BMP2, 62 T72, and 22 ZIL131 after being attacked. It is shown that the UAP transfers most images to several dominant labels represented by bright cells in the vertical direction. There is shown a class-wise vulnerability across all the studied models that images of a single class are similarly vulnerable or robust to the UAP. The main properties of this class-wise vulnerability are summarized as follows.

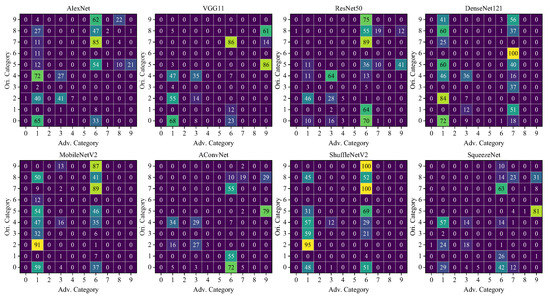
Figure 7.
Distribution of adversarial label: Ori category refers to the ground truth category of targets; Adv. category denotes the misclassified category of the universal adversarial examples. The numbers from 0 to 9, respectively, indicate the following classes: 2S1, BMP2, BRDM2, BTR70, BTR60, D7, T72, T62, ZIL131, and ZSU234. Results of DF-UAP and GD-UAP can be found in Figure A1 and Figure A2.
- The dominant labels where the misclassified data concentrate are meanwhile the robust classes where the clean data are not easy to be successfully attacked. Additionally, data within the robust classes also tend to transfer to one of the dominant labels, such as for DenseNet121, the BMP2 data is easy to be induced to T62.
- The dominant labels of diverse models share a certain similarity, although they are caused by a single substitute model. For instance, BMP2 is shown as a dominant label for all eight models and T72 for seven models (except DenseNet121). It demonstrates a universal representation of all the target models
- The class-wise vulnerability to UAPs is more universal than the attack selectivity reported in previous image-dependent attack studies [9,10]. When facing the data-dependent adversarial examples, dominant labels are highly class-dependent. For example, most of the adversarial examples of D7 would be recognized as ZIL131, ZSU234, and T62, while examples of other classes are misclassified to different labels. It also behaves differently from the universal attack for optical image classifiers which trained on 1000 categories of images that the adversarial images would classify as a single dominant class [24,44].
Based on the aforementioned facts, we hypothesize that the UAP gives rise to robust features when flowing through the DNNs. These spurious features tend to merge with the normal features to generate dominant evidence and further deflect the DNN reference. Composite features may not support a single normal label or the predicted label of the UAP itself but may support other labels which we call dominant labels. As a result, when the clean features do not comply with the UAP features, data of the entire class tend to be misclassified to the dominant labels, whereas the data are resilient when the class features conform to the UAP features.
3.6. Summary
In this section, the proposed FBUA framework was evaluated by comprehensive experiments involving eight cutting-edge DNNs, five SOTA UAP generation algorithms, and a pair of synthetic-real SAR datasets (SARSIM and MSTAR). The results show that the FBUA is of considerable efficacy in attacking DNN-based SAR ATR models. The UAPs generated by an FBUA also represent certain robustness against various interference, illustrating the potential threats from invisible adversaries. Furthermore, we demonstrated and analyzed the class-wise vulnerability of the ATR models when attacked by the black-box UAPs. The hypothesis of how the UAPs work was provided, that is, by igniting strong spurious features to destruct the original discriminative evidence.
4. Conclusions and Discussion
In this article, we have proposed the FBUA framework to fool various DNN-based SAR ATR models and SAR target images with a single UAP, in which scenario the attacker has no direct access to any of the target models’ information, including architecture, parameters, gradients, and training data. With extensive evaluations on the MSTAR and SARSIM datasets, we found that the substitute models trained with simulated SAR images could be utilized to craft UAPs that are very sensitive to the target models trained with real SAR data. This cross-dataset universal attack results in vigorous and spurious features for the target models which manifest as class-wise vulnerability; that is, there exist several dominant labels of which the attacked images are highly clustered and the original images are robust to the UAP. The class-wise vulnerability behaves differently from the hypothesis of dominant features reported in the intra-dataset universal attack for optical image classifiers. It may be caused by the different representations for SAR targets learned by models from the simulated data and real measured data.
This study demonstrates the existence of an access-free adversarial threat against DNN-based SAR ATR techniques. Due to the high stakes and the intrinsic non-cooperative nature of SAR ATR applications, the proposed FBUA is worth being further investigated in many aspects. For example, the key to a cross-dataset attack may be to model the knowledge of the structures and electromagnetic scattering behavior so perhaps this physical knowledge can be utilized directly to obtain efficient substitute models or directly to obtain aggressive adversarial examples. For another example, the UAP fools the target ATR system for SAR target images from all classes, which can lead to severe system misbehavior and raise suspicion for a human co-operator [51]. Therefore, a class-discriminative UAP may further facilitate the practical relevance that allows the attacker to have control over the classes to attack, such as a discriminative UAP may only deflect the tank targets to air defense units but has minimal influence on other types of targets [52]. In addition, the proposed framework can be directly exploited to improve the robustness of the ATR models against the black-box universal attacks. Specifically, current research has demonstrated that the UAP generation algorithm can be conventionally combined with the neural network training process to pursue the low-cost robustness against UAPs [53].
In future work, we plan to further facilitate the current attack with physical feasibility, such as by using electromagnetic metasurface [34]. We would also like to utilize the proposed method to construct robust SAR ATR models against black-box universal perturbations.
Author Contributions
Conceptualization, B.P. (Bowen Peng) and B.P. (Bo Peng); methodology, B.P. (Bowen Peng); software, B.P. (Bowen Peng); validation, B.P. (Bowen Peng), B.P. (Bo Peng) and L.L.; resources, B.P. (Bo Peng) and S.Y.; writing—original draft preparation, B.P. (Bowen Peng); writing—review and editing, B.P. (Bo Peng) and L.L.; supervision, S.Y.; funding acquisition, B.P. (Bo Peng) and L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported partially by the National Key Research and Development Program of China under Grant 2021YFB3100800, National Natural Science Foundation of China under Grant 61921001, 62022091, and the Changsha Outstanding Innovative Youth Training Program under Grant kq2107002.
Data Availability Statement
The MSTAR dataset is available at https://www.sdms.afrl.af.mil/datasets/mstar/ (accessed on 29 October 2020). The SARSIM dataset is available at https://zenodo.org/record/573750 (accessed on 1 May 2022).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ATR | Automatic Target Recognition |
| BIM | Basic Iterative Method |
| CosSim | Cosine Similarity |
| DF | Dominant Feature |
| DNN | Deep Neural Network |
| FFF | Fast Feature Fool |
| FGSM | Fast Gradient Sign Method |
| GD | Generalizable Date-Free |
| MSTAR | Moving and Stationary Target Acquisition and Recognition |
| SAR | Synthetic Aperture Radar |
| UAP | Universal Adversarial Perturbation |
Appendix A

Table A1.
Fooling ratio (%) of DF-UAP with MobileNetV2 as substitute model and various . The deviation of Gaussian noise is set to and the results of random noise are averaged on 10 runs.
Table A1.
Fooling ratio (%) of DF-UAP with MobileNetV2 as substitute model and various . The deviation of Gaussian noise is set to and the results of random noise are averaged on 10 runs.
| Noise | AlexNet | VGG11 | ResNet50 | Dense | Mobile | AConvNet | Shuffle | Squeeze | |
|---|---|---|---|---|---|---|---|---|---|
| Uniform | 3.6 | 0.2 | 0.4 | 27.5 | 7.4 | 0 | 29.7 | 0.2 | |
| Gaussian | 0.6 | 0.1 | 0.3 | 1.0 | 1.3 | 0 | 4.0 | 0.1 | |
| UAP | 47.7 | 24.7 | 32.5 | 55.8 | 47.3 | 10.4 | 57.2 | 12.7 | |
| Uniform | 24.5 | 6.4 | 2.6 | 62.9 | 44.4 | 0 | 72.9 | 0.2 | |
| Gaussian | 5.2 | 0.4 | 0.6 | 37.0 | 12.3 | 0 | 38.6 | 0.2 | |
| UAP | 68.2 | 51.2 | 67.0 | 79.6 | 75.0 | 38.3 | 76.6 | 43.0 | |
| Uniform | 42.0 | 17.7 | 9.2 | 77.5 | 70.4 | 0.1 | 85.1 | 0.7 | |
| Gaussian | 16.7 | 28.3 | 1.4 | 59.0 | 36.2 | 0 | 65.7 | 0.2 | |
| UAP | 74.5 | 58.7 | 77.9 | 89.9 | 80.7 | 57.3 | 82.2 | 60.6 | |
| Uniform | 52.8 | 27.2 | 18.8 | 85.9 | 84.2 | 2.1 | 89.3 | 6.3 | |
| Gaussian | 29.1 | 9.2 | 3.8 | 67.3 | 53.4 | 0 | 78.1 | 0.2 | |
| UAP | 80.4 | 68.2 | 81.4 | 90.1 | 88.6 | 64.0 | 89.1 | 66.2 |

Table A2.
Fooling ratio (%) of GD-UAP with VGG11 as substitute model and various . The deviation of Gaussian noise is set to and the results of random noise are averaged on 10 runs.
Table A2.
Fooling ratio (%) of GD-UAP with VGG11 as substitute model and various . The deviation of Gaussian noise is set to and the results of random noise are averaged on 10 runs.
| Noise | AlexNet | VGG11 | ResNet50 | Dense | Mobile | AConvNet | Shuffle | Squeeze | |
|---|---|---|---|---|---|---|---|---|---|
| Uniform | 3.6 | 0.2 | 0.4 | 27.5 | 7.4 | 0 | 29.7 | 0.2 | |
| Gaussian | 0.6 | 0.1 | 0.3 | 1.0 | 1.3 | 0 | 4.0 | 0.1 | |
| UAP | 44.9 | 24.9 | 34.8 | 35.4 | 48.6 | 16.2 | 40.4 | 17.9 | |
| Uniform | 24.5 | 6.4 | 2.6 | 62.9 | 44.4 | 0 | 72.9 | 0.2 | |
| Gaussian | 5.2 | 0.4 | 0.6 | 37.0 | 12.3 | 0 | 38.6 | 0.2 | |
| UAP | 65.0 | 52.4 | 65.9 | 73.1 | 82.7 | 31.8 | 77.0 | 42.4 | |
| Uniform | 42.0 | 17.7 | 9.2 | 77.5 | 70.4 | 0.1 | 85.1 | 0.7 | |
| Gaussian | 16.7 | 28.3 | 1.4 | 59.0 | 36.2 | 0 | 65.7 | 0.2 | |
| UAP | 72.9 | 62.9 | 83.0 | 89.1 | 86.0 | 50.8 | 80.9 | 64.9 | |
| Uniform | 52.8 | 27.2 | 18.8 | 85.9 | 84.2 | 2.1 | 89.3 | 6.3 | |
| Gaussian | 29.1 | 9.2 | 3.8 | 67.3 | 53.4 | 0 | 78.1 | 0.2 | |
| UAP | 80.9 | 70.5 | 87.4 | 90.0 | 87.4 | 61.1 | 82.5 | 76.1 |

Table A3.
Robustness test of DF-UAP with MobileNetV2 as substitute model.
Table A3.
Robustness test of DF-UAP with MobileNetV2 as substitute model.
| Interference | AlexNet | VGG11 | ResNet50 | Dense | Mobile | AConvNet | Shuffle | Squeeze | |
|---|---|---|---|---|---|---|---|---|---|
| Clean | 47.7 | 24.7 | 32.5 | 55.8 | 47.3 | 10.4 | 57.2 | 12.7 | |
| Additive | 49.2 | 26.2 | 32.7 | 59.1 | 50.3 | 10.1 | 61.2 | 12.9 | |
| Multiplicative | 35.6 | 13.6 | 16.7 | 53.8 | 37.7 | 3.6 | 52.6 | 6.0 | |
| Gaussian | 40.5 | 18.2 | 28.1 | 17.7 | 26.5 | 11.1 | 22.6 | 11.3 | |
| Median | 48.4 | 33.9 | 43.1 | 36.9 | 43.6 | 20.8 | 38.4 | 21.5 | |
| Clean | 68.2 | 51.2 | 67.0 | 79.6 | 75.0 | 38.3 | 76.6 | 43.0 | |
| Additive | 67.1 | 50.2 | 65.6 | 77.1 | 73.6 | 35.7 | 76.1 | 40.5 | |
| Multiplicative | 56.8 | 38.7 | 42.6 | 70.1 | 63.1 | 15.2 | 73.2 | 19.7 | |
| Gaussian | 64.8 | 49.8 | 66.0 | 66.9 | 66.3 | 40.7 | 54.6 | 41.5 | |
| Median | 66.7 | 54.4 | 72.6 | 73.3 | 70.9 | 55.0 | 63.3 | 55.3 | |
| Clean | 74.5 | 58.7 | 77.9 | 89.9 | 80.7 | 57.3 | 82.2 | 60.6 | |
| Additive | 73.0 | 58.0 | 77.8 | 89.7 | 79.6 | 55.9 | 81.2 | 59.8 | |
| Multiplicative | 66.9 | 49.9 | 62.6 | 75.5 | 74.8 | 30.6 | 78.7 | 40.5 | |
| Gaussian | 68.5 | 58.4 | 75.4 | 78.9 | 75.3 | 59.5 | 70.7 | 60.8 | |
| Median | 74.1 | 62.8 | 77.8 | 77.7 | 79.3 | 66.6 | 73.5 | 66.2 | |
| Clean | 80.4 | 68.2 | 81.4 | 90.1 | 88.6 | 64.0 | 89.1 | 66.2 | |
| Additive | 80.1 | 67.0 | 81.3 | 90.1 | 87.7 | 63.5 | 88.9 | 66.3 | |
| Multiplicative | 69.5 | 55.0 | 68.9 | 87.3 | 79.4 | 41.6 | 80.1 | 50.8 | |
| Gaussian | 75.3 | 66.3 | 79.5 | 84.0 | 82.1 | 66.1 | 78.3 | 67.4 | |
| Median | 77.2 | 69.5 | 81.4 | 87.3 | 84.7 | 70.7 | 80.8 | 73.8 |

Table A4.
Robustness test of of GD-UAP with VGG11 as substitute model.
Table A4.
Robustness test of of GD-UAP with VGG11 as substitute model.
| Interference | AlexNet | VGG11 | ResNet50 | Dense | Mobile | AConvNet | Shuffle | Squeeze | |
|---|---|---|---|---|---|---|---|---|---|
| Clean | 44.9 | 24.9 | 34.8 | 35.4 | 48.6 | 16.2 | 40.4 | 17.9 | |
| Additive | 40.0 | 20.0 | 28.0 | 31.6 | 42.4 | 11.5 | 35.3 | 13.3 | |
| Multiplicative | 26.0 | 5.1 | 12.5 | 22.1 | 21.3 | 4.1 | 26.4 | 6.1 | |
| Gaussian | 42.1 | 19.8 | 31.1 | 20.3 | 30.2 | 15.1 | 25.1 | 14.8 | |
| Median | 48.8 | 26.6 | 40.1 | 28.6 | 37.7 | 23.2 | 32.2 | 21.5 | |
| Clean | 65.0 | 52.4 | 65.9 | 73.1 | 82.7 | 31.8 | 77.0 | 42.4 | |
| Additive | 63.6 | 50.4 | 62.0 | 70.0 | 80.7 | 27.9 | 75.9 | 39.5 | |
| Multiplicative | 51.2 | 34.4 | 31.4 | 67.3 | 64.0 | 8.0 | 69.1 | 17.7 | |
| Gaussian | 62.4 | 48.7 | 58.6 | 63.3 | 65.9 | 31.4 | 52.9 | 37.3 | |
| Median | 67.7 | 54.6 | 68.1 | 76.0 | 71.1 | 42.7 | 56.5 | 48.1 | |
| Clean | 72.9 | 62.9 | 83.0 | 89.1 | 86.0 | 50.8 | 80.9 | 64.9 | |
| Additive | 72.2 | 61.8 | 82.3 | 88.8 | 85.7 | 49.3 | 81.1 | 63.2 | |
| Multiplicative | 64.2 | 47.3 | 54.2 | 71.6 | 82.4 | 17.8 | 80.4 | 34.5 | |
| Gaussian | 69.8 | 60.7 | 79.4 | 81.5 | 78.5 | 51.9 | 63.2 | 59.0 | |
| Median | 73.5 | 65.5 | 85.0 | 81.7 | 77.9 | 62.6 | 71.6 | 68.9 | |
| Clean | 80.9 | 70.5 | 87.4 | 90.0 | 87.4 | 61.1 | 82.5 | 76.1 | |
| Additive | 80.6 | 69.4 | 87.3 | 90.0 | 87.0 | 59.4 | 81.6 | 75.1 | |
| Multiplicative | 70.0 | 55.4 | 67.0 | 85.9 | 87.2 | 27.4 | 83.3 | 47.7 | |
| Gaussian | 76.9 | 69.5 | 86.6 | 82.0 | 83.0 | 64.9 | 75.3 | 72.9 | |
| Median | 79.9 | 76.8 | 88.3 | 89.0 | 85.4 | 75.3 | 82.8 | 79.4 |

Table A5.
Robustness test of DF-UAP with MobileNetV2 as substitute model.
Table A5.
Robustness test of DF-UAP with MobileNetV2 as substitute model.
| Class | AlexNet | VGG11 | ResNet50 | DenseNet121 | MobileNetV2 | AConvNet | ShuffleNetV2 | SqueezeNet |
|---|---|---|---|---|---|---|---|---|
| 2S1 | 100 | 99 | 100 | 100 | 100 | 78 | 100 | 85 |
| BMP2 | 9 | 5 | 48 | 48 | 5 | 26 | 2 | 7 |
| BRDM2 | 89 | 68 | 77 | 89 | 92 | 43 | 91 | 37 |
| BTR70 | 1 | 3 | 7 | 31 | 39 | 0 | 77 | 2 |
| BTR60 | 99 | 88 | 87 | 98 | 98 | 67 | 98 | 82 |
| D7 | 98 | 87 | 98 | 100 | 100 | 76 | 100 | 85 |
| T72 | 14 | 0 | 1 | 100 | 24 | 0 | 2 | 0 |
| T62 | 100 | 100 | 91 | 32 | 100 | 57 | 100 | 64 |
| ZIL131 | 78 | 62 | 83 | 98 | 92 | 34 | 96 | 58 |
| ZSU234 | 94 | 0 | 78 | 100 | 100 | 2 | 100 | 10 |
| Total | 682 | 512 | 670 | 796 | 750 | 383 | 766 | 430 |

Table A6.
Detailed fooling ratio (%) on each class. The attack is GD-UAP with VGG11 as substitute model.
Table A6.
Detailed fooling ratio (%) on each class. The attack is GD-UAP with VGG11 as substitute model.
| Class | AlexNet | VGG11 | ResNet50 | DenseNet121 | MobileNetV2 | AConvNet | ShuffleNetV2 | SqueezeNet |
|---|---|---|---|---|---|---|---|---|
| 2S1 | 100 | 99 | 100 | 100 | 100 | 71 | 100 | 82 |
| BMP2 | 17 | 5 | 60 | 29 | 2 | 26 | 0 | 9 |
| BRDM2 | 85 | 54 | 67 | 80 | 88 | 19 | 82 | 28 |
| BTR70 | 22 | 34 | 11 | 43 | 80 | 8 | 90 | 14 |
| BTR60 | 94 | 89 | 79 | 92 | 98 | 59 | 98 | 90 |
| D7 | 93 | 85 | 95 | 100 | 99 | 75 | 100 | 83 |
| T72 | 9 | 0 | 4 | 100 | 76 | 0 | 9 | 0 |
| T62 | 99 | 100 | 86 | 2 | 100 | 42 | 100 | 51 |
| ZIL131 | 69 | 58 | 82 | 87 | 85 | 18 | 91 | 49 |
| ZSU234 | 62 | 0 | 75 | 98 | 99 | 0 | 100 | 18 |
| Total | 650 | 524 | 659 | 731 | 827 | 318 | 770 | 424 |
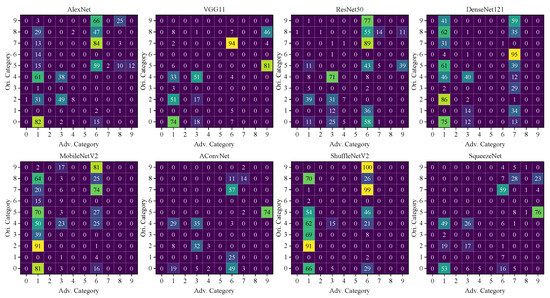
Figure A1.
Distribution of adversarial labels. The attack is DF-UAP with MobileNetV2 as substitute model. Ori. Category refers to the ground truth category of targets, Adv. Category denotes the misclassified category of the universal adversarial examples. The number from 0 to 9 respectively indicates the following classes: 2S1, BMP2, BRDM2, BTR70, BTR60, D7, T72, T62, ZIL131, ZSU234.
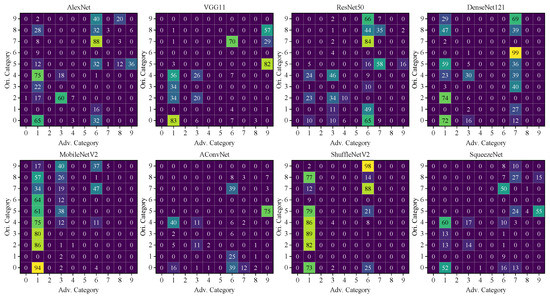
Figure A2.
Distribution of adversarial labels. The attack is GD-UAP with VGG11 as substitute model. Ori. Category refers to the ground truth category of targets, Adv. Category denotes the misclassified category of the universal adversarial examples. The number from 0 to 9 respectively indicates the following classes: 2S1, BMP2, BRDM2, BTR70, BTR60, D7, T72, T62, ZIL131, ZSU234.
References
- Yue, D.; Xu, F.; Frery, A.C.; Jin, Y. Synthetic Aperture Radar Image Statistical Modeling: Part One-Single-Pixel Statistical Models. IEEE Geosci. Remote Sens. Mag. 2021, 9, 82–114. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Conference and Workshop on Neural Information Processing Systems (NeurIPS); NIPS: Lake Tahoe, NV, USA, 2012; pp. 1097–1105. [Google Scholar]
- Liu, L.; Chen, J.; Zhao, G.; Fieguth, P.; Chen, X.; Pietikäinen, M. Texture Classification in Extreme Scale Variations Using GANet. IEEE Trans. Image Proces. 2019, 18, 3910–3922. [Google Scholar] [CrossRef]
- Chen, S.; Wang, H.; Xu, F.; Jin, Y.Q. Target Classification Using the Deep Convolutional Networks for SAR Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4806–4817. [Google Scholar] [CrossRef]
- Zhang, L.; Leng, X.; Feng, S.; Ma, X.; Ji, K.; Kuang, G.; Liu, L. Domain Knowledge Powered Two-Stream Deep Network for Few-Shot SAR Vehicle Recognition. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Li, Y.; Du, L.; Wei, D. Multiscale CNN Based on Component Analysis for SAR ATR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Ai, J.; Wang, F.; Mao, Y.; Luo, Q.; Yao, B.; Yan, H.; Xing, M.; Wu, Y. A Fine PolSAR Terrain Classification Algorithm Using the Texture Feature Fusion Based Improved Convolutional Autoencoder. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1. [Google Scholar] [CrossRef]
- Zhu, X.; Montazeri, S.; Ali, M.; Hua, Y.; Wang, Y.; Mou, L.; Shi, Y.; Xu, F.; Bamler, R. Deep Learning Meets SAR: Concepts, Models, Pitfalls, and Perspectives. IEEE Geosci. Remote Sens. Mag. 2021, 9, 143–172. [Google Scholar] [CrossRef]
- Chen, L.; Xu, Z.; Li, Q.; Peng, J.; Wang, S.; Li, H. An Empirical Study of Adversarial Examples on Remote Sensing Image Scene Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7419–7433. [Google Scholar] [CrossRef]
- Li, H.; Huang, H.; Chen, L.; Peng, J.; Huang, H.; Cui, Z.; Mei, X.; Wu, G. Adversarial Examples for CNN-Based SAR Image Classification: An Experience Study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1333–1347. [Google Scholar] [CrossRef]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing Properties of Neural Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Tanay, T.; Griffin, L. A Boundary Tilting Persepective on the Phenomenon of Adversarial Examples; Cornell University: Ithaca, NY, USA, 2016. [Google Scholar] [CrossRef]
- Fawzi, A.; Moosavi-Dezfooli, S.M.; Frossard, P. The Robustness of Deep Networks: A Geometrical Perspective. IEEE Signal Process. Mag. 2017, 34, 50–62. [Google Scholar] [CrossRef]
- Ortiz-Jiménez, G.; Modas, A.; Moosavi-Dezfooli, S.M.; Frossard, P. Optimism in the Face of Adversity: Understanding and Improving Deep Learning through Adversarial Robustness. Proc. IEEE 2021, 109, 635–659. [Google Scholar] [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Ma, C.; Chen, L.; Yong, J.H. Simulating Unknown Target Models for Query-Efficient Black-Box Attacks. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Online, 21–25 June 2021; pp. 11835–11844. [Google Scholar]
- Chen, W.; Zhang, Z.; Hu, X.; Wu, B. Boosting Decision-Based Black-Box Adversarial Attacks with Random Sign Flip. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 276–293. [Google Scholar]
- Shi, Y.; Han, Y.; Hu, Q.; Yang, Y.; Tian, Q. Query-efficient Black-box Adversarial Attack with Customized Iteration and Sampling. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 1. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Pang, T.; Su, H.; Zhu, J. Evading Defenses to Transferable Adversarial Examples by Translation-Invariant Attacks. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4312–4321. [Google Scholar]
- Lin, J.; Song, C.; He, K.; Wang, L.; Hopcroft, J. Nesterov Accelerated Gradient and Scale Invariance for Adversarial Attacks. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Xie, C.; Zhang, Z.; Zhou, Y.; Bai, S.; Wang, J.; Ren, Z.; Yuille, A.L. Improving Transferability of Adversarial Examples With Input Diversity. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Wang, X.; He, K. Enhancing the Transferability of Adversarial Attacks Through Variance Tuning. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 1924–1933. [Google Scholar]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Fawzi, O.; Frossard, P. Universal Adversarial Perturbations. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Poursaeed, O.; Katsman, I.; Gao, B.; Belongie, S. Generative Adversarial Perturbations. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Mopuri, K.R.; Ojha, U.; Garg, U.; Babu, R.V. NAG: Network for Adversary Generation. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Mopuri, K.R.; Garg, U.; Babu, R.V. Fast Feature Fool: A Data Independent Approach to Universal Adversarial Perturbations. arXiv 2017, arXiv:1707.05572. [Google Scholar]
- Khrulkov, V.; Oseledets, I. Art of Singular Vectors and Universal Adversarial Perturbations. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Mopuri, K.R.; Ganeshan, A.; Babu, R.V. Generalizable Data-Free Objective for Crafting Universal Adversarial Perturbations. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 2452–2465. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Benz, P.; Lin, C.; Karjauv, A.; Wu, J.; Kweon, I.S. A Survey on Universal Adversarial Attack. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Online, 19–26 August 2021; pp. 4687–4694. [Google Scholar]
- Huang, T.; Zhang, Q.; Liu, J.; Hou, R.; Wang, X.; Li, Y. Adversarial Attacks on Deep-Learning-Based SAR Image Target Recognition. J. Netw. Comput. Appl. 2020, 162, 102632. [Google Scholar] [CrossRef]
- Du, C.; Zhang, L. Adversarial Attack for SAR Target Recognition Based on UNet-Generative Adversarial Network. Remote Sens. 2021, 13, 4358. [Google Scholar] [CrossRef]
- Du, C.; Huo, C.; Zhang, L.; Chen, B.; Yuan, Y. Fast C&W: A Fast Adversarial Attack Algorithm to Fool SAR Target Recognition With Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Liu, Z.; Xia, W.; Lei, Y. SAR-GPA: SAR Generation Perturbation Algorithm. In Proceedings of the 2021 3rd International Conference on Advanced Information Science and System (AISS 2021), Sanya, China, 26–28 November 2021; pp. 1–6. [Google Scholar]
- Xu, L.; Feng, D.; Zhang, R.; Wang, X. High-Resolution Range Profile Deception Method Based on Phase-Switched Screen. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1665–1668. [Google Scholar] [CrossRef]
- Xu, H.; Guan, D.F.; Peng, B.; Liu, Z.; Yong, S.; Liu, Y. Radar One-Dimensional Range Profile Dynamic Jamming Based on Programmable Metasurface. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 1883. [Google Scholar] [CrossRef]
- Peng, B.; Peng, B.; Zhou, J.; Xia, J.; Liu, L. Speckle-Variant Attack: Towards Transferable Adversarial Attack to SAR Target Recognition. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4509805. [Google Scholar] [CrossRef]
- Kusk, A.; Abulaitijiang, A.; Dall, J. Synthetic SAR Image Generation Using Sensor, Terrain and Target Models. In Proceedings of the 11th European Conference on Synthetic Aperture Radar (VDE), Hamburg, Germany, 6–9 June 2016; pp. 1–5. [Google Scholar]
- Malmgren-Hansen, D.; Kusk, A.; Dall, J.; Nielsen, A.A.; Engholm, R.; Skriver, H. Improving SAR Automatic Target Recognition Models with Transfer Learning from Simulated Data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1484–1488. [Google Scholar] [CrossRef]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Frossard, P. Deepfool: A Simple and Accurate Method to Fool Deep Neural Networks. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Las Vegas, NV, USA, 26–30 June 2016; pp. 2574–2582. [Google Scholar]
- Zhang, C.; Benz, P.; Imtiaz, T.; Kweon, I.S. Understanding Adversarial Examples From the Mutual Influence of Images and Perturbations. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Seoul, Korea, 14–19 June 2020. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the Importance of Initialization and Momentum in Deep Learning. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; pp. 1139–1147. [Google Scholar]
- Zhang, C.; Benz, P.; Karjauv, A.; Kweon, I.S. Data-Free Universal Adversarial Perturbation and Black-Box Attack. In Proceedings of the International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 7868–7877. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K. Densely Connected Convolutional Networks. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the Computer Vision and Pattern Recognition Conference (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.T.; Sun, J. ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-Level Accuracy with 50× Fewer Parameters and <0.5 MB Model Size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Zhang, C.; Benz, P.; Imtiaz, T.; Kweon, I.S. CD-UAP: Class Discriminative Universal Adversarial Perturbation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 6754–6761. [Google Scholar]
- Benz, P.; Zhang, C.; Imtiaz, T.; Kweon, I.S. Double Targeted Universal Adversarial Perturbations. In Proceedings of the Asian Conference on Computer Vision (ACCV), Kyoto, Japan, 30 November–4 December 2020. [Google Scholar]
- Shafahi, A.; Najibi, M.; Xu, Z.; Dickerson, J.; Davis, L.S.; Goldstein, T. Universal Adversarial Training. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5636–5643. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).