Debris-Flow Susceptibility Assessment in China: A Comparison between Traditional Statistical and Machine Learning Methods
Abstract
:1. Introduction
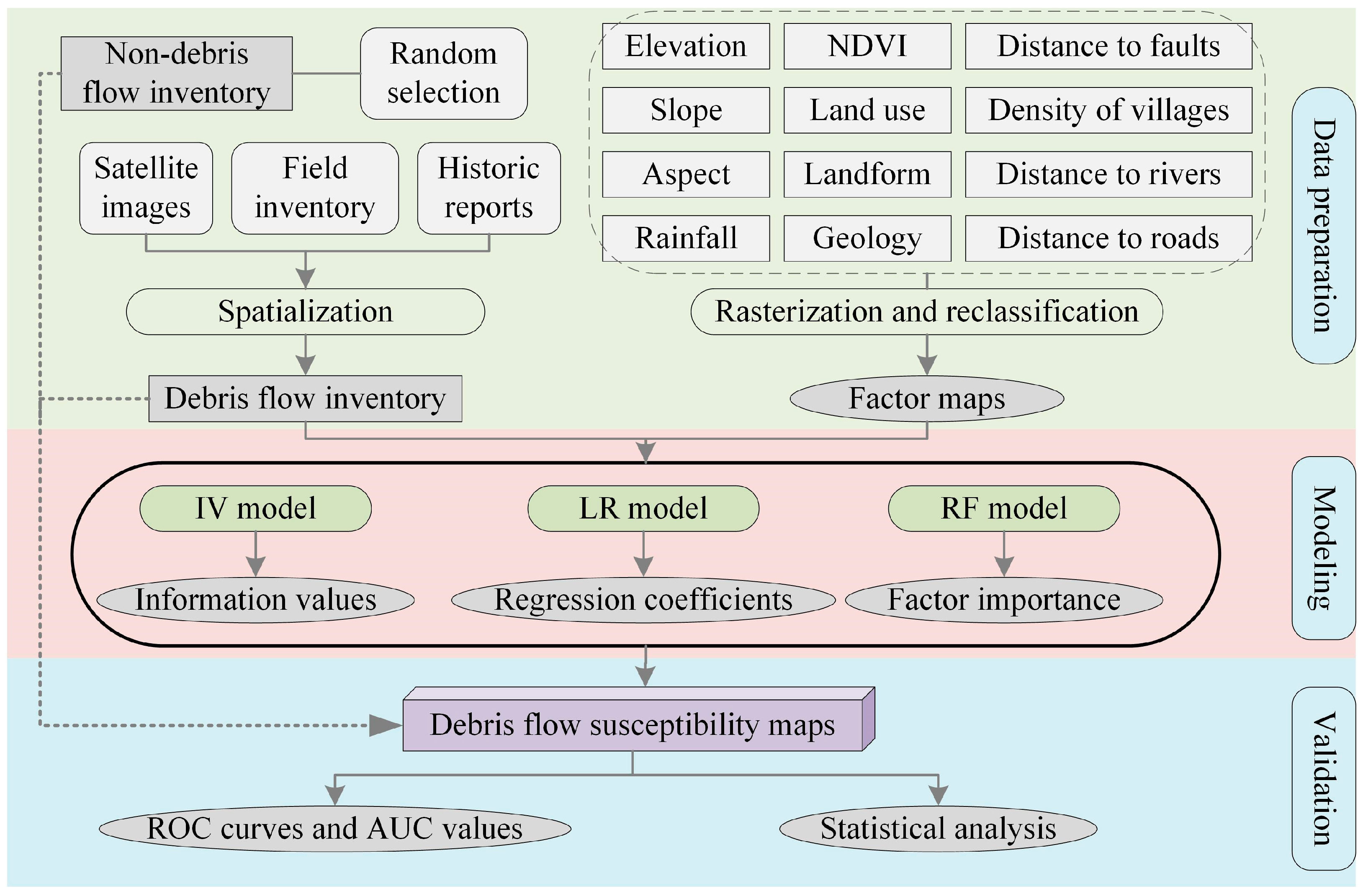
2. Materials and Methods
2.1. Data Sources and Processing
2.1.1. Debris-Flow Inventory
2.1.2. Causative Factors
2.2. Methods
2.2.1. Information Value
2.2.2. Logistic Regression
2.2.3. Random Forest
3. Results
3.1. Application of the IV Model
3.2. Application of the LR Model
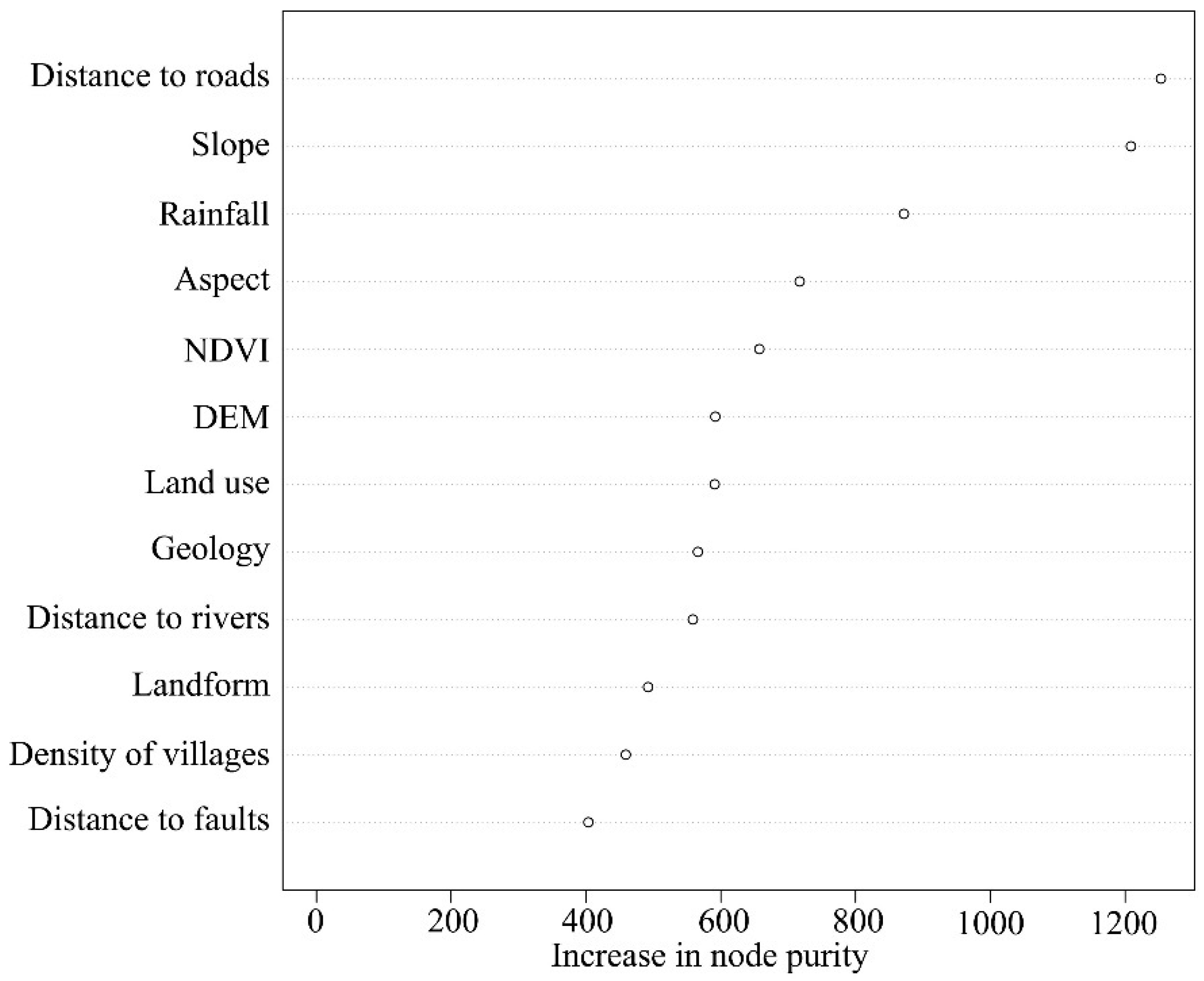
3.3. Application of the RF Model
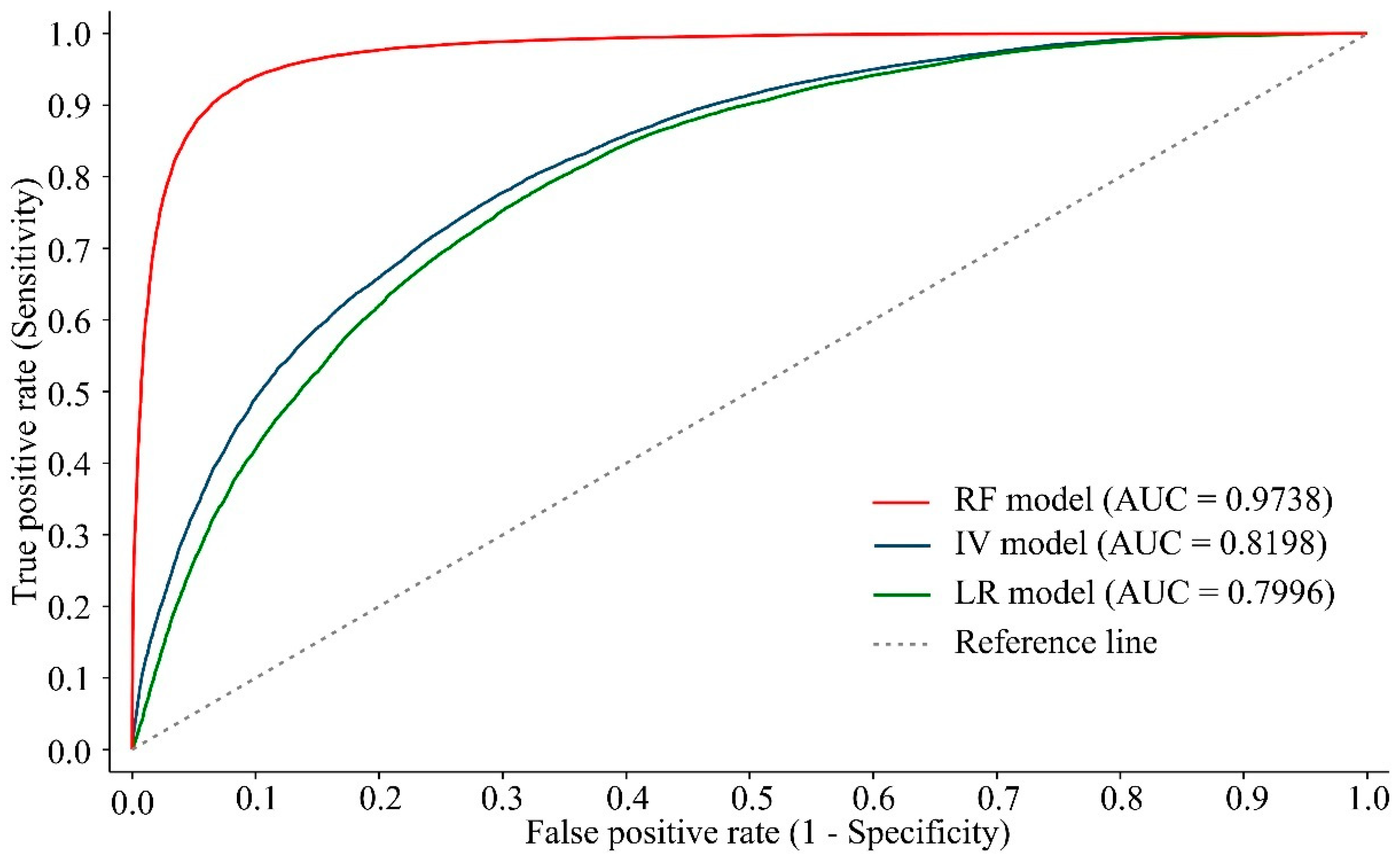
3.4. Validation of the DFS Maps
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, C.W.; Woo, C.; Kim, D.Y.; Jeong, S.H.; Koo, G.S. Knowing Landslide Right for Public Safety and Territorial Integrity. Research Report; Korea Forest Research Institute: Songdo, Korea, 2014. [Google Scholar]
- Xu, W.; Yu, W.; Jing, S.; Zhang, G.; Huang, J. Debris flow susceptibility assessment by GIS and information value model in a large-scale region, Sichuan Province (China). Nat. Hazards 2013, 65, 1379–1392. [Google Scholar] [CrossRef]
- Fan, X.; Yunus, A.P.; Scaringi, G.; Catani, F.; Subramanian, S.S.; Xu, Q.; Huang, R. Rapidly evolving controls of landslides after a strong earthquake and implications for hazard assessments. Geophys. Res. Lett. 2021, 48, e2020GL090509. [Google Scholar] [CrossRef]
- Kang, S.; Lee, S.R. Debris flow susceptibility assessment based on an empirical approach in the central region of South Korea. Geomorphology 2018, 308, 1–12. [Google Scholar] [CrossRef]
- Kappes, M.; Malet, J.; Remeître, A.; Horton, P.; Jaboyedoff, M.; Bell, R. Assessment of debris-flow susceptibility at medium-scale in the Barcelonnette Basin, France. Nat. Hazards Earth Syst. Sci. 2011, 11, 627–641. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, C.; Zhang, Z.; Khan, K.U.J. A comparison of statistical and machine learning methods for debris flow susceptibility mapping. Stoch. Env. Res. Risk A 2020, 34, 1887–1907. [Google Scholar] [CrossRef]
- Wang, D.; Hao, M.; Chen, S.; Meng, Z.; Jiang, D.; Ding, F. Assessment of landslide susceptibility and risk factors in China. Nat. Hazards 2021, 108, 3045–3059. [Google Scholar] [CrossRef]
- Fan, X.; Scaringi, G.; Domènech, G.; Yang, F.; Guo, X.; Dai, L.; He, C.; Xu, Q.; Huang, R. Two multi-temporal datasets that track the enhanced landsliding after the 2008 Wenchuan earthquake. Earth Syst. Sci. Data 2019, 11, 35–55. [Google Scholar] [CrossRef]
- Kang, S.; Lee, S.R.; Vasu, N.N.; Park, J.Y.; Lee, D.H. Development of an initiation criterion for debris flows based on local topographic properties and applicability assessment at a regional scale. Eng. Geol. 2017, 230, 64–76. [Google Scholar] [CrossRef]
- Du, G.; Zhang, Y.; Yang, Z.; Guo, C.; Yao, X.; Sun, D. Landslide susceptibility mapping in the region of eastern Himalayan syntaxis, Tibetan Plateau, China: A comparison between analytical hierarchy process information value and logistic regression-information value methods. Bull. Eng. Geol. Environ. 2019, 78, 4201–4215. [Google Scholar] [CrossRef]
- Dash, R.K.; Falae, P.O.; Kanungo, D.P. Debris flow susceptibility zonation using statistical models in parts of Northwest Indian Himalayas—implementation, validation and comparative evaluation. Nat. Hazards 2022, 111, 2011–2058. [Google Scholar] [CrossRef]
- Yalcin, A.; Reis, S.; Aydinoglu, A.C.; Yomralioglu, T. A GIS-based comparative study of frequency ratio, analytical hierarchy process, bivariate statistics and logistics regression methods for landslide susceptibility mapping in Trabzon, NE Turkey. Catena 2011, 85, 274–287. [Google Scholar] [CrossRef]
- Michelini, T.; Bettella, F.; D’Agostino, V. Field investigations of the interaction between debris flows and forest vegetation in two Alpine fans. Geomorphology 2017, 279, 150–164. [Google Scholar] [CrossRef]
- Sharma, S.; Mahajan, A.K. A comparative assessment of information value, frequency ratio and analytical hierarchy process models for landslide susceptibility mapping of a Himalayan watershed, India. Bull. Eng. Geol. Environ. 2019, 78, 2431–2448. [Google Scholar] [CrossRef]
- Melo, R.; Zêzere, J.L. Modeling debris flow initiation and run-out in recently burned areas using data-driven methods. Nat. Hazards 2017, 88, 1373–1407. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.; Tan, C.; Li, Y.; Gu, F.; Zhang, Y.; Mehmood, Q. Application of the borderline-SMOTE method in susceptibility assessments of debris flows in Pinggu District, Beijing, China. Nat. Hazards 2021, 105, 2499–2522. [Google Scholar] [CrossRef]
- Cama, M.; Conoscenti, C.; Lombardo, L.; Rotigliano, E. Exploring relationships between grid cell size and accuracy for debris-flow susceptibility models: A test in the Giampilieri catchment (Sicily, Italy). Environ. Earth Sci. 2016, 75, 1–21. [Google Scholar] [CrossRef]
- Du, G.; Zhang, Y.; Iqbal, J.; Yang, Z.; Yao, X. Landslide susceptibility mapping using an integrated model of information value method and logistic regression in the Bailongjiang watershed, Gansu Province, China. J. Mt. Sci. 2017, 14, 249–268. [Google Scholar] [CrossRef]
- Xiong, K.; Adhikari, B.R.; Stamatopoulos, C.A.; Zhan, Y.; Wu, S.; Dong, Z.; Di, B. Comparison of different machine learning methods for debris flow susceptibility mapping: A case study in the Sichuan Province, China. Remote Sens. 2020, 12, 295. [Google Scholar] [CrossRef]
- Qin, S.; Lv, J.; Cao, C.; Ma, Z.; Hu, X.; Liu, F.; Qiao, S.; Dou, Q. Mapping debris flow susceptibility based on watershed unit and grid cell unit: A comparison study. Geomat. Nat. Haz. Risk 2019, 10, 1648–1666. [Google Scholar] [CrossRef]
- Esper Angillieri, M.Y. Debris flow susceptibility mapping using frequency ratio and seed cells, in a portion of a mountain international route, Dry Central Andes of Argentina. Catena 2020, 189, 104504. [Google Scholar] [CrossRef]
- Chen, X.; Chen, H.; You, Y.; Chen, X.; Liu, J. Weights-of-evidence method based on GIS for assessing susceptibility to debris flows in Kangding County, Sichuan Province, China. Environ. Earth Sci. 2016, 75, 70. [Google Scholar] [CrossRef]
- Qing, F.; Zhao, Y.; Meng, X.; Su, X.; Qi, T.; Yue, D. Application of machine learning to debris flow susceptibility mapping along the China–Pakistan Karakoram Highway. Remote Sens. 2020, 12, 2933. [Google Scholar] [CrossRef]
- Gao, R.; Wang, C.; Liang, Z. Comparison of different sampling strategies for debris flow susceptibility mapping: A case study using the centroids of the scarp area, flowing area and accumulation area of debris flow watersheds. J. Mt. Sci. 2021, 18, 1476–1488. [Google Scholar] [CrossRef]
- Lin, J.; He, X.; Lu, S.; Liu, D.; He, P. Investigating the influence of three-dimensional building configuration on urban pluvial flooding using random forest algorithm. Environ. Res. 2021, 196, 110438. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ge, T.; Tian, W.; Liou, Y. Debris flow susceptibility mapping using machine-learning techniques in Shigatse area, China. Remote Sens. 2019, 11, 2801. [Google Scholar] [CrossRef]
- Zhou, Y.; Yue, D.; Liang, G.; Li, S.; Zhao, Y.; Chao, Z.; Meng, X. Risk assessment of debris flow in a mountain-basin area, western China. Remote Sens. 2022, 14, 2942. [Google Scholar] [CrossRef]
- Chen, Y.; Qin, S.; Qiao, S.; Dou, Q.; Che, W.; Su, G.; Yao, J.; Nnanwuba, U.E. Spatial predictions of debris flow susceptibility mapping using convolutional neural networks in Jilin Province, China. Water 2020, 12, 2079. [Google Scholar] [CrossRef]
- Di, B.; Zhang, H.; Liu, Y.; Li, J.; Chen, N.; Stamatopoulos, C.A.; Luo, Y.; Zhan, Y. Assessing susceptibility of debris flow in southwest China using gradient boosting machine. Sci. Rep. 2019, 9, 12532. [Google Scholar] [CrossRef]
- Chen, W.; Li, W.; Hou, E.; Zhao, Z.; Deng, N.; Bai, H.; Wang, D. Landslide susceptibility mapping based on GIS and information value model for the Chencang District of Baoji, China. Arab. J. Geosci. 2014, 7, 4499–4511. [Google Scholar] [CrossRef]
- Huang, F.; Yan, J.; Fan, X.; Yao, C.; Huang, J.; Chen, W.; Hong, H. Uncertainty pattern in landslide susceptibility prediction modeling: Effects of different landslide boundaries and spatial shape expressions. Geosci. Front. 2022, 13, 101317. [Google Scholar] [CrossRef]
- Lin, J.; He, P.; Yang, L.; He, X.; Lu, S.; Liu, D. Predicting future urban waterlogging-prone areas by coupling the maximum entropy and FLUS model. Sustain. Cities Soc. 2022, 80, 103812. [Google Scholar] [CrossRef]
- Rahmati, O.; Golkarian, A.; Biggs, T.; Keesstra, S.; Mohammadi, F.; Daliakopoulos, I.N. Land subsidence hazard modeling: Machine learning to identify predictors and the role of human activities. J. Environ. Manag. 2019, 236, 466–480. [Google Scholar] [CrossRef]
- Elkadiri, R.; Sultan, M.; Youssef, A.M.; Elbayoumi, T.; Chase, R.; Bulkhi, A.B.; Al-Katheeri, M.M. A remote sensing-based approach for debris-flow susceptibility assessment using artificial neural networks and logistic regression modeling. Ieee. J. Stars 2014, 7, 4818–4835. [Google Scholar] [CrossRef]
- Lin, J.; Wan, H.; Cui, Y. Analyzing the spatial factors related to the distributions of building heights in urban areas: A comparative case study in Guangzhou and Shenzhen. Sustain. Cities Soc. 2020, 52, 101854. [Google Scholar] [CrossRef]
- Marino, P.; Subramanian, S.S.; Fan, X.; Greco, R. Changes in debris-flow susceptibility after the Wenchuan earthquake revealed by meteorological and hydro-meteorological thresholds. Catena 2022, 210, 105929. [Google Scholar] [CrossRef]
- Huang, F.; Pan, L.; Fan, X.; Jiang, S.; Huang, J.; Zhou, C. The uncertainty of landslide susceptibility prediction modeling: Suitability of linear conditioning factors. Bull. Eng. Geol. Environ. 2022, 81, 182. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Yang, S.R. Probability of road interruption due to landslides under different rainfall-return periods using remote sensing techniques. J. Perform. Constr. Facil. 2016, 30, C4015002. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall thresholds for possible landslide occurrence in Italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z.; Wang, R.; Zhang, X.; Liu, X.; Yao, Z. Analysis of debris flow triggering conditions for different rainfall patterns based on satellite rainfall products in Hengduan mountain region, China. Remote Sens. 2022, 14, 2731. [Google Scholar] [CrossRef]
- Ekinci, Y.L.; Turkes, M.; Demirci, A.; Erginal, A.E. Shallow and deep-seated regolith slides on deforested slopes in Canakkale, NW Turkey. Geomorphology 2013, 201, 70–79. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Tien Bui, D. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Peng, L.; Xu, S.; Hou, J.; Peng, J. Quantitative risk analysis for landslides: The case of the Three Gorges area, China. Landslides 2015, 12, 943–960. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2015, 13, 839–856. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, H.; Liu, Y. The spatial distribution characteristics and influencing factors of Chinese villages. Acta. Geogra. Sin. 2020, 75, 2206–2223. [Google Scholar]
- Yin, K.L.; Yan, T.Z. Statistical prediction model for slope instability of metamorphosed rocks. In Proceedings of the 5th International Symposium on Landslides, Lausanne, Switzerland, 10–15 July 1988; Volume 2, pp. 1269–1272. [Google Scholar]
- Sarkar, S.; Kanungo, D.; Patra, A. GIS Based Landslide Susceptibility Mapping—A Case Study in Indian Himalaya in Disaster Mitigation of Debris Flows, Slope Failures and Landslides; Universal Academic Press: Tokyo, Japan, 2006; pp. 617–624. [Google Scholar]
- Sarkar, S.; Roy, A.T.; Martha, T.R. Landslide susceptibility assessment using information value method in parts of the Darjeeling Himalayas. Geol. Soc. India 2013, 82, 351–362. [Google Scholar] [CrossRef]
- Piedade, A.; Zêzere, J.; Garcia, R.; Oliveira, S. Modelos de susceptibilidade a deslizamentos superficiais translacionais na Região a Norte de Lisboa. Finisterra 2011, 46, 9–26. [Google Scholar] [CrossRef]
- Dias, H.; Gramani, M.F.; Grohmann, C.H.; Bateira, C.; Vieira, B.C. Statistical-based shallow landslide susceptibility assessment for a tropical environment: A case study in the southeastern Brazilian coast. Nat. Hazards 2021, 108, 205–223. [Google Scholar] [CrossRef]
- Chang, T.; Chiang, S.H.; Hsu, M.L. Modeling typhoon- and earthquake-induced landslides in a mountainous watershed using logistic regression. Geomorphology 2007, 89, 335–347. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Massari, R. Autologistic modelling of susceptibility to landsliding in the Central Apennines, Italy. Geomorphology 2011, 130, 55–64. [Google Scholar] [CrossRef]
- Budimir, M.E.A.; Atkinson, P.M.; Lewis, H.G. A systematic review of landslide probability mapping using logistic regression. Landslides 2015, 12, 419–436. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we need hundreds of classifiers to solve real world classification problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.; Pei, X.; Duan, Z. Landslide susceptibility modelling using GIS-based machine learning techniques for Chongren County, Jiangxi Province, China. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef]
- Kausar, N.; Majid, A. Random forest-based scheme using feature and decision levels information for multi-focus image fusion. Pattern Anal. Appl. 2016, 19, 221–236. [Google Scholar] [CrossRef]
- Lombardo, L.; Mai, P.M. Presenting logistic regression-based landslide susceptibility results. Eng. Geol. 2018, 244, 14–24. [Google Scholar] [CrossRef]
- Sun, D.; Wen, H.; Wang, D.; Xu, J. A random forest model of landslide susceptibility mapping based on hyperparameter optimization using Bayes algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
- Che, V.B.; Kervyn, M.; Suh, C.E.; Fontijn, K.; Ernst, G.G.J.; del Marmol, M.A.; Trefois, P.; Jacobs, P. Landslide susceptibility assessment in Limbe (SW Cameroon): A field calibrated seed cell and information value method. Catena 2012, 92, 83–98. [Google Scholar] [CrossRef]
- Dai, F.; Lee, C.F. Landslide characteristics and slope instability modeling using GIS, Lantau Island, Hong Kong. Geomorphology 2002, 42, 213–228. [Google Scholar] [CrossRef]
- Ni, S.; Ma, C.; Yang, H.; Zhang, Y. Spatial distribution and susceptibility analysis of avalanche, landslide and debris flow in Beijing mountain region. J. Beijing Univ. 2018, 40, 81–91. [Google Scholar]
- Youssef, A.M.; Pradhan, B.; Jebur, M.N.; El-Harbi, H.M. Landslide susceptibility mapping using ensemble bivariate and multivariate statistical models in Fayfa area, Saudi Arabia. Environ. Earth Sci. 2015, 73, 3745–3761. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.; Pourtaghi, Z. Landslide susceptibility assessment in Lianhua County (China): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Cheng, J.; Dai, X.; Wang, Z.; Li, J.; Qu, G.; Li, W.; She, J.; Wang, Y. Landslide susceptibility assessment model construction using typical machine learning for the Three Gorges Reservoir Area in China. Remote Sens. 2022, 14, 2257. [Google Scholar] [CrossRef]
- Kanungo, D.P.; Arora, M.K.; Sarkar, S.; Gupta, R.P. Landslide susceptibility zonation (LSZ) mapping—A review. J. South Asia Disaster Stud. 2009, 2, 81–105. [Google Scholar]
- Ließ, M.; Glaser, B.; Huwe, B. Uncertainty in the spatial prediction of soil texture: Comparison of regression tree and Random Forest models. Geoderma 2012, 170, 70–79. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Tien Bui, D.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]



| Data | Source of Data | Year | Data Type | Definition/Data Processing |
|---|---|---|---|---|
| Debris flow inventory | RESDC, available at https://www.resdc.cn (accessed on 1 July 2021) | By the end of 2018 | Point | Each point located in the centroid of the area for each debris flow. |
| Elevation | Shuttle Radar Topography Mission images, available at http://www.gscloud.cn (accessed on 1 June 2020) | - | Grid (90 m) | Resampling (the nearest neighbor interpolation) |
| Slope | Shuttle Radar Topography Mission images, available at http://www.gscloud.cn (accessed on 1 June 2020) | - | Grid (90 m) | Slope gradient, resampling (the nearest neighbor interpolation) |
| Aspect | Shuttle Radar Topography Mission images, available at http://www.gscloud.cn (accessed on 1 June 2020) | - | Grid (90 m) | Slope orientation, resampling (the nearest neighbor interpolation) |
| Rainfall | Annual average precipitation from 613 basic stations, available at http://data.cma.cn (accessed on 1 Septemper 2021) | 1978–2018 | Point | Averaging, spatial interpolation (Ordinary Kriging) |
| NDVI | Landsat ETM+ satellite images, available at http://www.gscloud.cn (accessed on 1 August 2021) | 2001–2018 | Grid (500 m) | Resampling (the nearest neighbor interpolation) |
| Land use | RESDC, available at https://www.resdc.cn (accessed on 1 June 2020) | 2015 | Grid (100 m) | Reclassification, resampling (the nearest neighbor interpolation) |
| Landform | Geomorphological of China 1:4,000,000 | - | Polygon | Reclassification and rasterizing (Feature to raster) |
| Geology | The 1:2,500,000 geological map of China | - | Polygon | Reclassification and rasterizing (Feature to raster) |
| Distance to faults | The 1:2,500,000 geological map of China | - | Line | Euclidean distance |
| Density of villages | China Electronic Map 2012 | 2012 | Point | Kernel density |
| Distance to rivers | NESSDC, available at http://www.geodata.cn (accessed on 1 June 2020) | 2018 | Polygon | Euclidean distance |
| Distance to roads | NESSDC, available at http://www.geodata.cn (accessed on 1 June 2020) | 2018 | Line | Euclidean distance |
| Factor | Class | Code | %Site | %Class | IV |
|---|---|---|---|---|---|
| Elevation | <500 m | 1 | 20.64 | 27.60 | −0.2906 |
| 500–1500 m | 2 | 31.73 | 33.45 | −0.0529 | |
| 1500–3500 m | 3 | 30.27 | 15.41 | 0.6752 | |
| 3500–5500 m | 4 | 17.34 | 22.34 | −0.2533 | |
| >5500 m | 5 | 0.02 | 1.19 | −4.0393 | |
| Slope | 0–2° | 1 | 8.33 | 36.88 | −1.4881 |
| 2–5° | 2 | 18.13 | 15.37 | 0.1653 | |
| 5–15° | 3 | 43.86 | 24.15 | 0.5967 | |
| 15–25° | 4 | 20.16 | 14.14 | 0.3547 | |
| 25–35° | 5 | 7.61 | 7.17 | 0.0594 | |
| >35° | 6 | 1.91 | 2.30 | −0.1814 | |
| Aspect | Flat | 1 | 0.30 | 2.06 | −1.9320 |
| North | 2 | 10.77 | 11.74 | −0.0869 | |
| Northeast | 3 | 13.30 | 13.00 | 0.0224 | |
| East | 4 | 15.06 | 12.38 | 0.1957 | |
| Southeast | 5 | 14.42 | 12.26 | 0.1623 | |
| South | 6 | 13.47 | 12.23 | 0.0963 | |
| Southwest | 7 | 11.93 | 12.37 | −0.0360 | |
| West | 8 | 10.83 | 11.80 | −0.0862 | |
| Northwest | 9 | 9.94 | 12.15 | −0.2016 | |
| Rainfall | <200 mm | 1 | 7.74 | 29.85 | −1.3504 |
| 200–400 mm | 2 | 11.36 | 14.54 | −0.2468 | |
| 400–600 mm | 3 | 30.48 | 20.77 | 0.3838 | |
| 600–800 mm | 4 | 22.58 | 8.25 | 1.0065 | |
| 800–1200 mm | 5 | 18.19 | 10.72 | 0.5287 | |
| 1200–1600 mm | 6 | 6.13 | 9.41 | −0.4287 | |
| >1600 mm | 7 | 3.52 | 6.46 | −0.6068 | |
| NDVI | <0.2 | 1 | 4.58 | 26.67 | −1.7611 |
| 0.2–0.4 | 2 | 9.70 | 10.60 | −0.0880 | |
| 0.4–0.6 | 3 | 18.22 | 9.62 | 0.6390 | |
| 0.6–0.8 | 4 | 37.23 | 22.51 | 0.5030 | |
| >0.8 | 5 | 30.26 | 30.60 | −0.0112 | |
| Land use | Cropland | 1 | 32.23 | 18.77 | 0.5406 |
| Forest land | 2 | 23.40 | 24.07 | −0.0282 | |
| Grassland | 3 | 30.82 | 28.02 | 0.0953 | |
| Water | 4 | 3.38 | 3.02 | 0.1110 | |
| Built-up land | 5 | 5.54 | 2.65 | 0.7375 | |
| Unused land | 6 | 4.63 | 23.47 | −1.6226 | |
| Landform | Plain | 1 | 12.87 | 29.52 | −0.8301 |
| Mountain | 2 | 73.07 | 45.19 | 0.4805 | |
| Hill | 3 | 9.54 | 12.64 | −0.2816 | |
| Platform | 4 | 4.39 | 5.99 | −0.3115 | |
| Dune | 5 | 0.02 | 5.63 | −5.4340 | |
| Lake | 6 | 0.08 | 0.56 | −1.8987 | |
| Glacier | 7 | 0.03 | 0.47 | −2.8099 | |
| Geology | Cenozoic | 1 | 18.42 | 37.21 | −0.7031 |
| Mesozoic | 2 | 38.61 | 29.84 | 0.2577 | |
| Proterozoic | 3 | 14.41 | 8.65 | 0.5109 | |
| Paleozoic | 4 | 23.41 | 20.80 | 0.1179 | |
| Undated | 5 | 0.16 | 2.05 | −2.5228 | |
| Archaean | 6 | 4.98 | 1.45 | 1.2375 | |
| Distance to faults | <5 km | 1 | 60.71 | 41.39 | 0.3829 |
| 5–10 km | 2 | 20.55 | 21.25 | −0.0334 | |
| 10–40 km | 3 | 17.96 | 31.22 | −0.5527 | |
| 40–100 km | 4 | 0.78 | 4.84 | −1.8264 | |
| 100–200 km | 5 | 0.00 | 1.29 | −1.8264 | |
| >200 km | 6 | 0.00 | 0.01 | −1.8264 | |
| Density of villages | <0.2 per km2 | 1 | 43.59 | 61.91 | −0.3509 |
| 0.2–0.6 per km2 | 2 | 31.24 | 15.55 | 0.6977 | |
| 0.6–1.0 per km2 | 3 | 15.08 | 9.04 | 0.5121 | |
| 1.0–1.6 per km2 | 4 | 7.80 | 8.37 | −0.0712 | |
| 1.6–2.2 per km2 | 5 | 1.73 | 3.57 | −0.7219 | |
| >2.2 per km2 | 6 | 0.57 | 1.57 | −1.0127 | |
| Distance to rivers | <2 km | 1 | 21.27 | 16.23 | 0.2707 |
| 2–5 km | 2 | 15.50 | 17.40 | −0.1157 | |
| 5–10 km | 3 | 19.70 | 20.76 | −0.0524 | |
| 10–30 km | 4 | 35.04 | 34.64 | 0.0114 | |
| 30–50 km | 5 | 7.01 | 7.56 | −0.0762 | |
| >50 km | 6 | 1.48 | 3.41 | −0.8345 | |
| Distance to roads | <2 km | 1 | 71.68 | 38.07 | 0.6329 |
| 2–5 km | 2 | 14.23 | 17.25 | −0.1923 | |
| 5–10 km | 3 | 6.24 | 11.50 | −0.6109 | |
| 10–20 km | 4 | 4.24 | 10.51 | −0.9089 | |
| 20–50 km | 5 | 2.89 | 11.66 | −1.3953 | |
| >50 km | 6 | 0.72 | 11.01 | −2.7337 |
| Factor | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) Elevation | 1.000 | |||||||||||
| (2) Slope | 0.074 | 1.000 | ||||||||||
| (3) Aspect | 0.025 | −0.008 | 1.000 | |||||||||
| (4) Rainfall | −0.423 | 0.213 | 0.005 | 1.000 | ||||||||
| (5) NDVI | −0.518 | 0.163 | −0.012 | 0.637 | 1.000 | |||||||
| (6) Land use | 0.275 | −0.052 | 0.031 | −0.387 | −0.483 | 1.000 | ||||||
| (7) Landform | −0.158 | −0.039 | 0.004 | 0.044 | 0.091 | −0.090 | 1.000 | |||||
| (8) Geology | −0.289 | 0.159 | −0.007 | 0.154 | 0.240 | −0.069 | 0.005 | 1.000 | ||||
| (9) Distance to faults | −0.033 | −0.096 | −0.002 | −0.100 | −0.048 | 0.019 | 0.086 | −0.187 | 1.000 | |||
| (10) Density of villages | −0.484 | 0.067 | −0.024 | 0.522 | 0.342 | −0.245 | 0.148 | 0.127 | 0.039 | 1.000 | ||
| (11) Distance to rivers | 0.194 | 0.002 | −0.010 | −0.166 | −0.081 | 0.049 | 0.055 | −0.007 | 0.022 | −0.059 | 1.000 | |
| (12) Distance to roads | 0.339 | 0.039 | −0.003 | −0.283 | −0.263 | 0.220 | −0.032 | −0.013 | 0.005 | −0.264 | 0.158 | 1.000 |
| Factor | Coef. | SD | t-Value | p-Value | Sig. | VIF |
|---|---|---|---|---|---|---|
| Elevation | 0.533 | 0.013 | 39.65 | 0.000 | *** | 1.96 |
| Slope | 0.237 | 0.009 | 25.36 | 0.000 | *** | 1.49 |
| Aspect | −0.023 | 0.004 | −5.37 | 0.000 | *** | 1.00 |
| Rainfall | −0.082 | 0.009 | −8.75 | 0.000 | *** | 3.01 |
| NDVI | 0.035 | 0.012 | 2.91 | 0.004 | *** | 3.10 |
| Land use | −0.208 | 0.009 | −23.00 | 0.000 | *** | 1.96 |
| Landform | 0.026 | 0.012 | 2.22 | 0.026 | ** | 1.07 |
| Geology | 0.171 | 0.008 | 20.31 | 0.000 | *** | 1.20 |
| Distance to faults | −0.34 | 0.012 | −29.34 | 0.000 | *** | 1.21 |
| Density of villages | −0.118 | 0.011 | −10.73 | 0.000 | *** | 1.89 |
| Distance to rivers | −0.033 | 0.008 | −4.00 | 0.000 | *** | 1.16 |
| Distance to roads | −0.783 | 0.009 | −82.97 | 0.000 | *** | 1.64 |
| Constant | 0.966 | 0.086 | 11.22 | 0.000 | *** | |
| Pseudo r2 | 0.219 | No. of observations | 56,970 | |||
| χ2 | 17,334.713 | Prob. > χ2 | 0.000 | |||
| Akaike crit. (AIC) | 61,668.477 | Bayesian crit. (BIC) | 61,784.830 | |||
| Grade | Information Value Model | Logistic Regression Model | Random Forest Model | ||||||
|---|---|---|---|---|---|---|---|---|---|
| %Debris Flow | %Predicted Area | Density of Debris Flow | %Debris Flow | %Predicted Area | Density of Debris Flow | %Debris Flow | %Predicted Area | Density of Debris Flow | |
| Very low | 0.0246 | 4.8651 | 0.0051 | 1.9940 | 25.7552 | 0.0774 | 0.2808 | 42.2923 | 0.0066 |
| Low | 0.7479 | 13.7304 | 0.0545 | 6.3437 | 20.7454 | 0.3058 | 1.2954 | 20.8209 | 0.0622 |
| Moderate | 3.2303 | 17.0246 | 0.1897 | 13.8108 | 20.7658 | 0.6651 | 4.4760 | 16.2221 | 0.2759 |
| High | 15.3125 | 30.4536 | 0.5028 | 28.1552 | 19.0359 | 1.4791 | 15.5731 | 12.2040 | 1.2761 |
| Very high | 80.6847 | 33.9263 | 2.3782 | 49.6963 | 13.6976 | 3.6281 | 78.3746 | 8.4607 | 9.2634 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Wang, Y.; Li, Y.; Zhou, Y.; Zeng, Z. Debris-Flow Susceptibility Assessment in China: A Comparison between Traditional Statistical and Machine Learning Methods. Remote Sens. 2022, 14, 4475. https://doi.org/10.3390/rs14184475
Huang H, Wang Y, Li Y, Zhou Y, Zeng Z. Debris-Flow Susceptibility Assessment in China: A Comparison between Traditional Statistical and Machine Learning Methods. Remote Sensing. 2022; 14(18):4475. https://doi.org/10.3390/rs14184475
Chicago/Turabian StyleHuang, Han, Yongsheng Wang, Yamei Li, Yang Zhou, and Zhaoqi Zeng. 2022. "Debris-Flow Susceptibility Assessment in China: A Comparison between Traditional Statistical and Machine Learning Methods" Remote Sensing 14, no. 18: 4475. https://doi.org/10.3390/rs14184475
APA StyleHuang, H., Wang, Y., Li, Y., Zhou, Y., & Zeng, Z. (2022). Debris-Flow Susceptibility Assessment in China: A Comparison between Traditional Statistical and Machine Learning Methods. Remote Sensing, 14(18), 4475. https://doi.org/10.3390/rs14184475









