Abstract
Due to the virtues of low-cost and high positioning accuracy, Single-Frequency Precise Point Positioning (SF-PPP) is becoming a prospective technique. However, SF-PPP is not as widely used as dual-frequency and triple-frequency PPP at present, owing to the effect of ionospheric delay residuals after model rectification. In recent years, with the evolution of multi-constellation Global Navigation Satellite Systems (multi-GNSS, i.e., GPS, BDS-2, and BDS-3), it has become possible to obtain credible and continuous positioning results using SF-PPP. However, such performance would be significantly degraded in challenging environments (i.e., boulevards, tunnels, and tall buildings). Under these circumstances, GNSS signals are obstructed, and it is difficult to provide sufficient observations for SF-PPP. Therefore, the Inertial Navigation System (INS) is employed to promote the positioning performance of SF-PPP. The PPP/INS integration is regarded as one of the most efficient approaches in GNSS-denied environments. To satisfy the request of supplying real-time positioning information, the Real-Time Services (RTS) of the International GNSS Service (IGS) provide real-time precise orbit and clock products for globally distributed users through the internet. In this paper, a real-time GPS/BDS-2/BDS-3 SF-PPP and INS tight integration model is proposed, and it is assessed using the data gathered by vehicle and real-time products afforded by CAS (Chinese Academy of Sciences), GFZ (Deutsche GeoForschungsZentrum), and WHU (Wuhan University). The outcomes illustrate the following: (1) GPS + BDS SF-PPP/INS can provide more accurate and continuous positioning solutions compared with those of GPS + BDS SF-PPP, with improvements of 52.8%, 31.1%, and 42.8% in the north, east, and vertical components, respectively. (2) In general, the orbit and clock products’ accuracies in terms of GPS afforded by the three analysis centers are consistent with each other. For BDS, the orbit product from WHU is more accurate compared to those of CAS and GFZ. However, the accuracy of the clock product afforded by WHU is lower compared with those provided by the other two centers, especially for BDS-2 satellites. (3) The positioning accuracy in terms of Root Mean Square (RMS) values based on GFZ products are much higher than the results based on CAS and WHU products in the three directions.
1. Introduction
Since Precise Point Positioning (PPP) was first introduced [1,2], it has been a popular tool in numerous applications, for instance, GNSS (Global Navigation Satellite System) seismology [3,4], GNSS meteorology [5,6], deformation monitoring [7,8], etc. PPP utilizes only single-station GNSS data and orbit/clock products with high precision supplied via the International GNSS Service (IGS) centers to provide users with centimeter-level positioning solutions, and the errors contained in observations are remedied by appointed models, treated as unknown parameters, or parameterized after model correction. The research presented in [9,10,11] has proved the advantages of PPP, especially after applying the ambiguity fixing model [12,13] and the slant ionospheric delay and receiver Differential Code Bias (DCB) constraint models [14,15]. However, most of the works conducted thus far mainly consider conditions of dual-frequency observations. In contrast, Single-Frequency PPP (SF-PPP) is not as widely applied as dual-/triple-frequency PPP [16]. This is chiefly owing to the fact that no effective model can be utilized in SF-PPP to decrease or eliminate the effect of the ionospheric delay. Hence, this may directly lead to low positioning accuracy and long convergence time, especially in kinematic conditions.
Recently, GNSS satellite availability has significantly improved, along with the evolution of multi-constellation GNSS, and obtaining reliable and continuous positioning solutions using SF-PPP has become possible. The performance of three SF-PPP models, namely the GRoup And PHase Ionosphere Correction (GRAPHIC) model, GRAPHIC with code observation model, and an ionosphere-constrained model were analyzed in [17]. The contribution of the QZSS (Quasi-Zenith Satellite System) to GPS/BDS/GLONASS/Galileo SF-PPP was also presented. The outcomes proved that QZSS significantly increased the positioning accuracy of BDS and GLONASS when using simulated dynamic data. Such improvement was invisible while using the GPS-only, Galileo-only, and GPS/BDS/GLONASS/Galileo data. Furthermore, in the work of [17], the SF-PPP with ionosphere constraints presented a superior convergence performance, while the positioning accuracies supplied by the three SF-PPP models were close to each other. Moreover, with the completion of the BDS-3 constellation [18] on 23 June 2020, the modeling and performance provided by BDS-2/BDS-3 SF-PPP have become a new topic. Based on data from global distribution stations, Shi et al. [18] presented a BDS-2/BDS-3 SF-PPP model and studied the improvement of the combination based on BDS-2 and BDS-3 in precise positioning. The results indicated that the positioning accuracy was relevant to the receiver type adopted in different GNSS networks. The positioning performance based on the B1I signal is superior to that based on the B1C signal from the stations of the international GNSS Monitoring and Assessment System (iGMAS), while it is opposite at the stations of the Multi-GNSS EXperiment (MGEX). Contrasted with BDS-2 SF-PPP and BDS-3 SF-PPP, the convergence performance of BDS-2 + BDS-3 SF-PPP is significantly increased. As a major error in SF-PPP, ionospheric delay must be considered carefully. For ionospheric studies, Su et al. [19] proposed a novel single-frequency ionospheric-free-half PPP technique. To validate the reliability of the method, the performances of two conventional PPP models, and the proposed method, were evaluated. Results showed that slant ionospheric observables can be extracted with submeter-level accuracy towards the proposed novel method.
However, the continuous satellite availability will decrease in most dynamic applications when the receiver passes through overbridges, tunnels, and near towering constructions. Under these circumstances, the availability of GNSS satellites will be obstructed, and it is difficult to provide sufficient observations for PPP calculation. Therefore, high positioning accuracy with SF-PPP is difficult to achieve. Fortunately, according to [20], GPS positioning performance can be improved by fusing GPS with an Inertial Navigation System (INS), especially in challenging environments. In the last few years, profiting from the rapid development of PPP, PPP/INS integration has been regarded as one of the most efficient approaches to provide positions and attitudes. However, there are just a small number of works on SF-PPP/INS tight integration. Gao et al. [21] presented a multi-GNSS tight integration technique for single-frequency measurements and IMU outputs, by which the performance supplied by the ionospheric-delay- and receiver-DCB-constrained model was ameliorated significantly. The results indicated that the proposed model can obtain more accurate, continuous, and credible solutions in open-sky and GNSS-denied environments compared with traditional SF-PPP. The work in [22] presented a GNSS/INS tight integration with augmentations on ionospheric delay and tropospheric delay. Results illustrated that tight integration has a great effect in urban environments. Regional atmospheric augmentation increases the positioning accuracy of SF-PPP significantly on account of the sensibility of single-frequency signals to the ionospheric delay.
With the development of society, the requirement for real-time positioning is becoming urgent. To satisfy this demand, the Real-Time Services (RTS) of the IGS afford precise orbit and clock products to global users through the internet. The work in [23] verified that the RTS products are, with high accuracy, comparing with the final products of the ESA (European Space Agency, Paris, France). Subsequently, the work in [24] appraised the positioning performance of BDS-2-only real-time PPP based on RTS products (CLK93) and MGEX stations. Results showed that the positioning accuracy acquired can be centimeter-/decimeter-level in static/kinematic environments. Kazmierski et al. [25] further investigated the quality of real-time products of CNES (Centre National d’Etudes Spatiales) for GPS, GLONASS, Galileo, and BDS-2. Results illustrated that the orbits and clocks of the GPS are the most accurate currently. Based on these backgrounds, this paper introduces a real-time GPS/BDS-2/BDS-3 SF-PPP/INS tight integration model. It is assessed via a set of vehicle-borne data and real-time orbit and clock products afforded by the IGS centers of CAS (Chinese Academy of Sciences), GFZ (Deutsche GeoForschungsZentrum), and WHU (Wuhan University). The paper is organized as follows: The methodology of the GPS/BDS-2/BDS-3 SF-PPP/INS tight integration model is described in Section 2. Then, the evaluations and the conclusions are presented in Section 3 and Section 4.
2. Methodology
In this section, the methods of undifferenced and uncombined GPS/BDS-2/BDS-3 SF-PPP, recovery of real-time orbit and clock products, GPS/BDS-2/BDS-3 SF-PPP/INS tight integration, and parameter adjustments are described in detail.
2.1. Real-Time SF-PPP Model
The linearized observation functions for the undifferenced and uncombined pseudorange and carrier phase are expressed as [21]
where and refer to observed minus computed values of the original pseudorange and carrier phase observations; represents satellite, is the receiver, and is signal frequency; is the receiver position increments vector; is the direction cosine between receiver and satellite; is the receiver clock offset; and are the residual of tropospheric delay and the relevant mapping function; is the ionospheric delay at frequency 1 when the signal is passing through the propagation path; is the multiplier factor dependent on signal frequency; represents receiver hardware time delay; is the velocity of light; is the wavelength and is integer ambiguity; and represent multipath biases, which are unmodeled, and the observation noise from the pseudorange and carrier phase, respectively.
The ionospheric delay is a key section that influences the performance of SF-PPP. Therefore, several models, for instance, the GIM (Global Ionosphere Map) data correction model [26], the single-frequency GRAPHIC model [27], and the single-frequency ZIDE (Zenith Ionospheric Delay Estimation) PPP model [28], have been proposed to limit such influence. For example, Øvstedal [26] recommended using the GIM to amend the ionospheric delay of the pseudorange and carrier phase. However, the drawback of the GIM-correction-based SF-PPP is that the residual of each satellite’s ionospheric delay and the undisposed receiver DCB will degrade the performance of SF-PPP. To overcome this drawback, Montenbruck [29] tried to use the GRAPHIC model [27] instead of GIM data to eliminate the ionospheric delay in the carrier phase. In the GRAPHIC model, the characteristic that the ionospheric delays on pseudorange and carrier phase are equal in magnitude and opposite in sign for the same satellite is utilized. Hence, a linear ionospheric-free combination between pseudorange and carrier phase is adopted to form a new ionospheric-free carrier phase observation. Even so, the SF-PPP positioning accuracy still cannot satisfy the accuracy requirement because of the large noise of the new carrier phase [30]. Therefore, based on the GRAPHIC model, Beran et al. [28,31] proposed the ZIDE model to estimate the zenith ionospheric delay of each satellite as a parameter, which has been verified to be effective to increase the performance of SF-PPP [30]. According to the works of [32,33,34], the position accuracy and convergence time of ZIDE SF-PPP can be ameliorated by adopting precise global and regional ionospheric models. However, the receiver DCB on pseudorange is ignored in the ZIDE model. Hence, the SF-PPP model based on Ionospheric delay and Receiver DCB Constraint (IRC) [21] is applied in this contribution. Here, to separate the receiver DCB from the ionospheric delay [14], the real-time ionospheric product provided by Wuhan University is utilized to generate a virtual external observation for each ionospheric delay. The basic observation equation can be written as
where and stand for vertical total electron content acquired from the WHU’s real-time ionospheric product and the zenith angle at the Ionospheric Punctuation Point (IPP); is the accuracy of the real-time ionospheric product with prior variance of ; is the DCB between pseudoranges and in the same GNSS system; and are signal frequencies; and are hardware time delays in frequencies 1 and 2; the meanings of other parameters are the same as those in Equations (1) and (2).
In real-time data processing, products from IGS are transmitted into the RTCM-SSR (Radio Technical Commission for Maritime Services State Space Representation) form. The real-time corrections are the differences between precise products and broadcast products. The real-time products cannot be applied in positioning directly. Therefore, the products must be recovered to satisfy the requirement of PPP. SSR corrections for real-time orbit at the present epoch can be calculated by corrections at the reference epoch using [35]
where , , and are satellite position corrections in radial, along, and cross directions; , , and are the corresponding velocities.
The rotation matrix between the orbital coordinate system and Earth-Centered Earth-Fixed (ECEF) frame can be expressed as
where and stand for position and velocity vector for satellites calculated from the broadcast ephemeris, respectively.
The orbit corrections can be transferred from the orbital coordinate system to the ECEF frame via
where , , and are satellite orbit corrections in the ECEF frame.
Then, the precise products can be recovered by combining orbit corrections with satellite positions calculated by broadcast ephemeris
where , , and are satellite coordinates in ECEF frame at the time after SSR corrections; , , and are satellite coordinates calculated from broadcast ephemeris.
For real-time clock offset, the SSR corrections at the present epoch can be calculated by corrections at the reference epoch by [35]
where is the real-time clock correction in distance form calculated from SSR clock offsets. Then, the real-time precise clock can be obtained by
where is the satellite offset at epoch after SSR corrections.
The signal–noise ratio, GNSS satellite elevation, as well as GNSS measurement environment are chiefly factors to influence the observation quality. Considering these terms, the conventional satellite elevation-dependent weight function is utilized here to figure out the prior variance [36]
where and are the elevation of satellites and the corresponding prior variance.
2.2. GPS/BDS-2/BDS-3 SF-PPP/INS Tight Integration Model
In the GPS/BDS-2/BDS-3 SF-PPP/INS tight integration model, the theoretical geometrical distance in SF-PPP can be replaced by the INS-predicted values. Meanwhile, the doppler observation was proved to be effective to estimate the INS sensor errors [21]. Hence, the corresponding functions can be expressed as:
where and are the lever arms on position and velocity; stands for the doppler observations with the unit of m/s.
In general, the mathematical model of INS mechanization can be written as [21]
where and are the angular rate and specific force that measured by accelerometer and gyroscope; and represent the position and velocity, computed via INS; is the transform matrix for attitude from body frame () to navigation frame (); is the direction cosine matrix of attitude, which can be described based on the Euler angle; is the integral operation from epoch to ; and are the rotation angular rate of the frame and ECEF frame in terms of inertial frame () projected in the frame; is the gravity in the frame. Then, the basic observational functions for SF-PPP/INS tight integration can be expressed as
where and refer to position and velocity of a satellite in the frame computed by the real-time satellite orbit and clock products; and stand for the position at the IMU center in the geodetic coordinate system and velocity at the IMU center in frame, which can be obtained from and ; is the transform matrix from the frame to the frame; is the lever arm measured from the IMU center to the GNSS receiver antenna phase center in frame; , , and represent the sum of the error corrections of the pseudorange, carrier phase, and doppler.
As illustrated above, the INS solutions and GNSS observations are in different frames ( frame for INS and frame for GNSS). Therefore, to utilize the information on the same foundation, the following corrections on position and velocity can be introduced:
where is the transform matrix between the geodetic coordinate frame and the frame of the position increments; stands for the coefficient relevant to position derived from [21]; is the coefficient related to attitude; denotes the gyroscope errors (bias and scale factor). In general, this parameter can be expressed as [37]
where indicates the IMU observations interval.
The state vector of the multi-GNSS SF-PPP/INS model can be described as
where and refer to the parameters related to receiver clock error and receiver DCB errors; and denote the ambiguities and ionospheric delays in the slant propagation path.
The PSI angle model [21] is adopted to describe the variations of position, velocity, and attitude in the temporal domain, which can be described as
where the meanings of the parameters are the same as those mentioned above. The variation of IMU errors can be described by the first-order Gauss–Markov process. Meanwhile, the random constant process is adopted to express the variation of float ambiguities. The random walk process is chosen as the dynamic model for the receiver-clock-related parameters and the atmosphere-related parameters.
Finally, the parameterized elements can be estimated by the Extended Kalman Filter (EKF) [38]
where is the unit matrix. The elements in can be acquired from the state models mentioned above; refers to the gain matrix; is the state noise variance.
2.3. Implementation of SF-PPP/INS Tight Integration Model
Based on the descriptions above, the structure of the proposed real-time multi-GNSS SF-PPP/INS tight integration model is presented in Figure 1. Velocity and angular increments are provided by IMU sensors. After initializing the system, the compensated IMU outputs are processed in the INS mechanization to supply position, velocity, and attitude information. Then, the information, along with real-time GNSS products, is utilized to obtain the GNSS observation predictions (pseudorange, carrier phase, and doppler). After this, the INS-predicted observations are fused with the original observations provided by GNSS in the EKF. Finally, the estimated IMU errors are fed back to the IMU outputs before INS mechanization. Meanwhile, the navigation information is corrected.
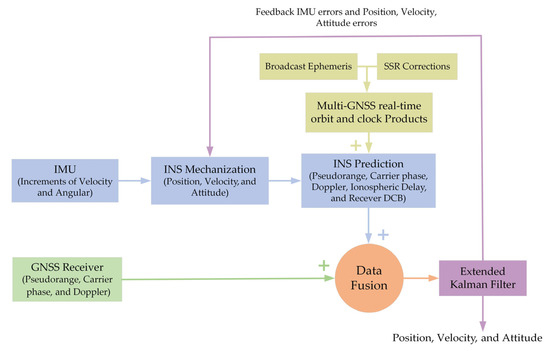
Figure 1.
Implementation of real-time multi-GNSS SF-PPP/INS tight integration model.
3. Tests, Results, and Discussions
To validate the performance of the presented real-time GPS/BDS-2/BDS-3 SF-PPP/INS tight integration, the data of the GNSS original observations and IMU outputs were processed and analyzed. The first subsection demonstrates the positioning performance of GPS + BDS (G + B) SF-PPP and SF-PPP/INS tight integration based on IGS’ final precise products under kinematic conditions. The second subsection is to evaluate the performance while using real-time orbit and clock products from CAS, GFZ, and WHU.
3.1. Data Collection
The original test data for GPS (L1) and BDS-2/BDS-3 (B1I) were gathered on 21 December 2021, at China University of Geosciences Beijing. Figure 2 (top left and top right) shows the typical scenery in data collection areas, which were mainly around large buildings and boulevards. In these environments, the GNSS signal is heavily blocked. Figure 2 (bottom left) shows the test platform and equipment. Figure 2 (bottom right) presents the mission route. The multi-GNSS multi-frequency PANDA PD318 receiver was adopted in this mission, the sampling rate of which was 1 Hz. IMU outputs were provided by POS320, and the output rate was 200 Hz. Table 1 presents the details of POS320.


Figure 2.
Mission details of vehicle test on 21 December 2021, in Beijing, China. Typical scenery in data collection areas (top left and top right); test platform and equipment (bottom left); and mission trajectory (bottom right).

Table 1.
Technical parameters of POS320.
For data processing, the final precise orbit and clock products were afforded by Wuhan University, and the real-time products were provided by CAS, GFZ, and WHU. The DCB product was from CAS. The satellite cutoff elevation was intercalated as 10°. The satellite antenna phase center offsets were rectified by adopting igs14_2076_plus.atx. The slant ionospheric delay was corrected first using WHU’s GIM data. Afterward, the residuals were parameterized as random walks. Receiver DCB, drifts and offsets of the receiver clock, and ISB were also modeled as random walk processes. Moreover, float ambiguities were parameterized as random constants. In INS data processing, coning offsets, rotational, and sculling effect engendered from inertial axes motion were rectified using the INS mechanization [39]. According to the research in [40], to reduce the impact of receiver Time Delay Bias (TDB) between BDS-2 and BDS-3, the weight ratio of BDS-2 and BDS-3 MEOs was set to 1:3. The weight ratio of BDS-2 GEOs and MEOs/IGSOs was set to 1:10. In the validation stage, the results provided by the smoothed RTK/INS tight integration were utilized as reference values.
Figure 3 describes the numbers of available satellites and relevant Position Dilution of Precision (PDOP) of GPS-only, BDS-only, and G + B modes. The numbers of satellites on average were 5.1, 12.4, and 16.2, respectively. The corresponding PDOPs on average were 3.35, 4.27, and 2.99, respectively. These results illustrate that frequent signal blocks occurred under the GPS-only mode. BDS satellites could remedy the loss of GPS satellites in most of these periods, but there was still a GNSS outage for the partially obstructed observation environment. According to the statistics, about 24 s satellite outages (from 2048 s to 2072 s) occurred during the test (the black rectangle in Figure 3); therefore, the effect of INS is mainly focused on this section.
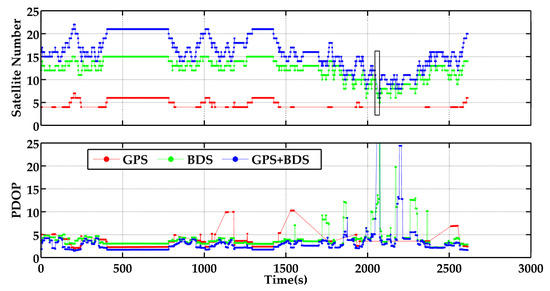
Figure 3.
Satellite number and PDOP of GPS-only, BDS-only, and G + B (the start time is 195,453 s (GPS time)); the black rectangle represents the GNSS outage period under G + B mode.
3.2. Positioning Performance of PPP and PPP/INS Tight Integration
Figure 4 presents the position differences of G + B SF-PPP and G + B SF-PPP/INS in terms of the reference solutions, and the relevant RMS (Root Mean Square) values of the position differences are shown in Table 2. According to Figure 4, the performance of SF-PPP/INS was obviously higher than that of SF-PPP in both horizontal and vertical directions. The position RMS in the three directions is enhanced from 0.642 m, 0.649 m, and 1.331 m with SF-PPP to 0.303 m, 0.447 m, and 0.761 m with SF-PPP/INS tight integration, with improvements of 52.8%, 31.1%, and 42.8%, respectively. Figure 5 portrays the distributions of position differences of SF-PPP and SF-PPP/INS tight integration in the horizontal direction and vertical direction. Relevant statistics indicate that the horizontal position differences percentages within 0.3 m were 18.22% and 2.05% for SF-PPP/INS and SF-PPP, respectively. The vertical position differences percentages within 0.3 m were 12.90% and 2.08% for SF-PPP/INS tight integration and SF-PPP, respectively. The results also indicate that the percentage of the horizontal position differences from the SF-PPP/INS tight integration within 0.6 m reached 86.11%. However, for SF-PPP only, this percentage was 59.19%. After about 1800 s, the position accuracy of SF-PPP was strongly influenced by the surrounding observation environment. Nevertheless, the position accuracy of SF-PPP/INS tight integration was hardly influenced. Moreover, the SF-PPP/INS tight integration could still provide navigation solutions during GNSS outage periods. Therefore, INS can significantly increase position accuracy and continuity.
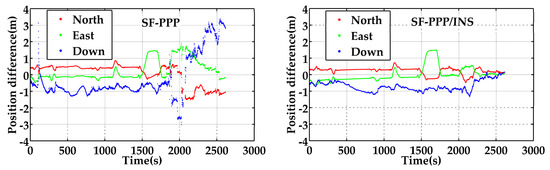
Figure 4.
Position differences provided by G + B SF-PPP (left) and G + B SF-PPP/INS tight integration (right) in the three directions, in terms of the reference solution provided by RTK/INS tight integration (the start time is 195,453 s).

Table 2.
RMS of position differences in the three directions of SF-PPP and SF-PPP/INS tight integration.
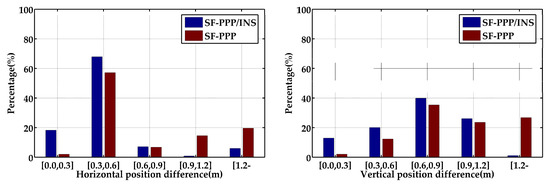
Figure 5.
Distribution of position differences of G + B SF-PPP and G + B SF-PPP/INS tight integration in the horizontal direction (left) and vertical direction (right).
3.3. Evaluation of Real-Time Orbit and Clock Products
In this section, the accuracy of the real-time orbit and clock products provided by CAS, GFZ, and WHU are evaluated. Firstly, to validate the performance of each IGS center’s products, the final orbit and clock products supplied by Wuhan University were adopted as reference values. Figure 6 presents the RMS of real-time orbit products compared to reference values. Relevant mean RMS values are enumerated in Table 3. According to the statistics, the accuracy of GPS real-time orbits provided by the three analysis centers were generally consistent with each other. For the products from WHU, the orbit accuracies of GPS satellites were 1.7 cm, 4.6 cm, and 3.6 cm, with improvements of 81.3%, 65.7%, and 78.7% compared to those of BDS satellites in the three directions. For BDS satellites, the orbit accuracy of WHU was higher than that of CAS and GFZ, with improvements of 32.1%, 51.8%, and 31.9% compared to that of CAS, respectively. Such improvements were up to 78.3%, 71.1%, and 73.1% compared to that of GFZ in radial, along, and cross directions. The orbit accuracies of the BDS MEO satellites were significantly higher than those of the GEO and IGSO satellites. When the GEO and IGSO satellites were detached, the RMSs of MEO-only in the three directions obtained about 45.1%, 31.3%, and 62.1% accuracy upgradation for the products from WHU. According to the work in [35], the accuracy of final precise orbits is 2.5 cm. Therefore, the orbit accuracies of the GPS real-time products were comparable, but those of the BDS MEO orbits were marginally lower.
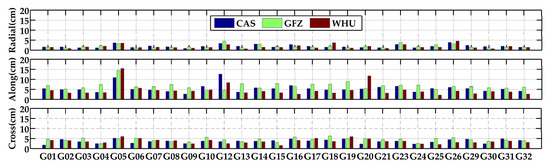
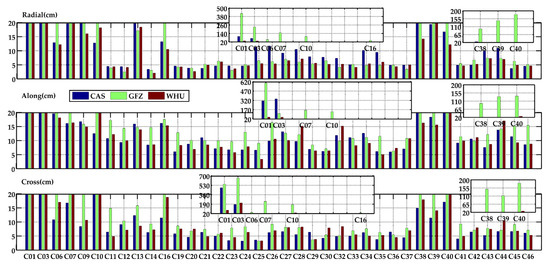
Figure 6.
Orbit RMS of real-time products of GPS satellites (top) and BDS satellites (bottom) from the three IGS analysis centers.

Table 3.
Mean orbit RMS of GPS and BDS satellites in radial, along, and cross directions of each analysis center.
Figure 7 presents the RMS and STD of the real-time clock offsets from three IGS analysis centers with respect to the reference products. Table 4 illustrates the average values of RMS and STD for GPS and BDS satellite clock offsets. The results shows that the accuracies of the GPS clock offset products supported via the three centers were basically consistent with each other. The accuracies of the products provided by WHU were slightly higher than those for the other analysis centers. For the BDS satellites, the accuracy of WHU was lower compared to the others, especially for the BDS-2 satellites. The maximum clock offset RMS achieved 46.10 ns, which directly led to a larger RMS value, on average, for WHU. For the CAS and GFZ products, the accuracies of the BDS GEO and IGSO satellite clock offsets were significantly lower than those of BDS MEO satellites. When GEO and IGSO satellites were detached, the RMS of MEO-only was improved by 12.6% for the products from CAS, whereas such improvement was 43.1% for the products from GFZ.
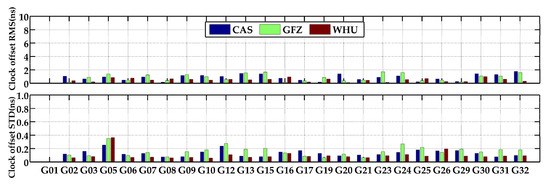
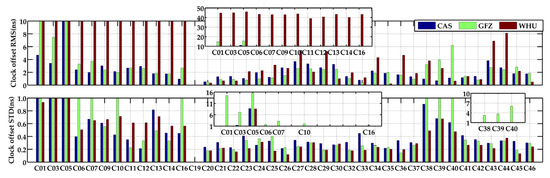
Figure 7.
Clock offset RMS and STD of real-time products of GPS satellites (top) and BDS satellites (bottom) from each analysis center.

Table 4.
Average values of clock offset RMS and STD of GPS and BDS satellites of each analysis center.
3.4. Performance of Real-Time PPP/INS Tight Integration
To analyze the positioning and navigation performance of the presented real-time SF-PPP/INS tight integration, in addition to the real-time orbit/clock products, the real-time ionospheric data provided by Wuhan University (ftp address: igs.gnsswhu.cn), with an interval of 5 min, were also used.
Figure 8 reveals the position differences of real-time G + B PPP/INS tight integration in terms of the reference solutions provided by the smoothed RTK/INS tight integration. The RMS and STD are illustrated in Table 5. According to the results of STD, the real-time SF-PPP/INS tight integration could also provide stable and continuous positioning solutions. The position accuracies based on the real-time products from GFZ were higher in the horizontal and vertical directions compared with the results based on the products of CAS and WHU. The position RMSs of the GFZ-product-based solutions were 0.206 m, 0.542 m, and 0.368 m, which is about 65.5%, 14.9%, and 68.7% more accurate than those based on CAS products in the three directions. Compared to the solutions based on WHU products, the position improvements were more obvious, at about 50.1% and 73.1% in east and vertical directions. This is chiefly owing to the lower accuracies of the clock products from WHU, especially for BDS-2. Moreover, compared with the results based on WHU final products, the accuracies of the results based on GFZ’s real-time products still present about 32.0% and 51.6% improvements in the north and vertical directions. This may be on account of a high rate of real-time products (orbit, clock offset, and ionospheric data). Figure 9 illustrates the distributions of position differences for G + B SF-PPP/INS tight integration adopting real-time products from CAS, GFZ, and WHU in horizontal and vertical directions. The statistics indicate that the horizontal position differences percentages within 0.3 m were 0.61%, 57.48%, and 0.15% for the results based on the products of CAS, GFZ, and WHU, respectively. The corresponding percentages of the vertical position differences within 0.3 m were 0.00%, 52.62%, and 3.36%, respectively. Accordingly, the positioning accuracy was principally affected by the real-time product quality of BDS MEO. The analysis of positioning performance and the accuracies of real-time products infer that the positioning accuracy is greatly impacted by the quality of the clock products under the premise of consistent orbit accuracy. When using higher-accuracy clock products, it will be easier to obtain positioning solutions with high accuracy.
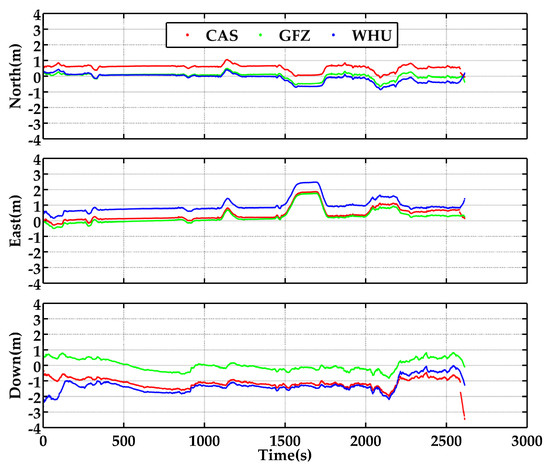
Figure 8.
Position differences of G + B SF-PPP/INS tight integration in the three directions using the real-time products from CAS, GFZ, and WHU (the start time is 195,453 s).

Table 5.
Position RMS and STD in the three directions of SF-PPP/INS tight integration using real-time products from CAS, GFZ, and WHU.
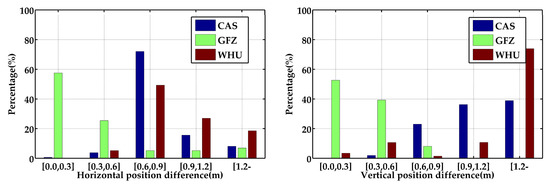
Figure 9.
Distribution of position differences of G + B SF-PPP/INS tight integration in the horizontal direction (left) and vertical direction (right) using real-time products from CAS, GFZ, and WHU.
Other than the positioning solutions, the G + B SF-PPP/INS tight integration can also support real-time attitudes with regard to roll, pitch, and heading. The attitude offsets via comparing the attitude solutions with the reference values are portrayed in Figure 10. In the light of the RMSs enumerated in Table 6, attitude accuracy also illustrates a certain relationship to the accuracy of orbit/clock products. The attitude RMSs based on WHU’s real-time products were 0.020°, 0.019°, and 0.523° in roll, pitch, and heading, with improvements of 37.5%, 40.6%, and 46.4% compared to the solutions based on CAS’s products. Similarly, there were about 25.9% and 29.6% enhancements in roll and pitch compared to the results supplied by GFZ’s products. Figure 11 presents the distributions of attitude offsets of the G + B SF-PPP/INS tight integration using the real-time products from CAS, GFZ, and WHU in roll, pitch, and heading. Relevant statistics indicate that the percentages of roll attitude offsets within 0.03° were 65.98%, 69.42%, and 91.20% for the results based on the products of CAS, GFZ, and WHU, respectively. The percentages of pitch attitude offsets within 0.03° were 62.23%, 66.93%, and 92.34%, respectively. In general, the offset distribution in roll and pitch was consistent for solutions based on CAS and GFZ. Additionally the percentages of heading attitude offsets within 0.5° were 32.99%, 66.32%, and 83.16%, respectively.
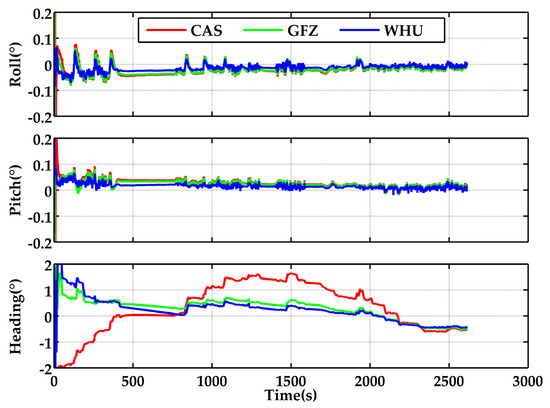
Figure 10.
Attitude offsets of G + B SF-PPP/INS tight integration in roll, pitch, and heading directions using the real-time products from CAS, GFZ, and WHU, in terms of reference solutions (the start time is 195,453 s).

Table 6.
RMS of attitude and velocity offsets of SF-PPP/INS tight integration using the real-time products from CAS, GFZ, and WHU.
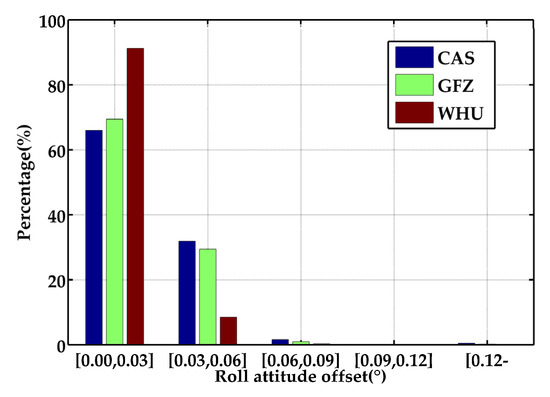
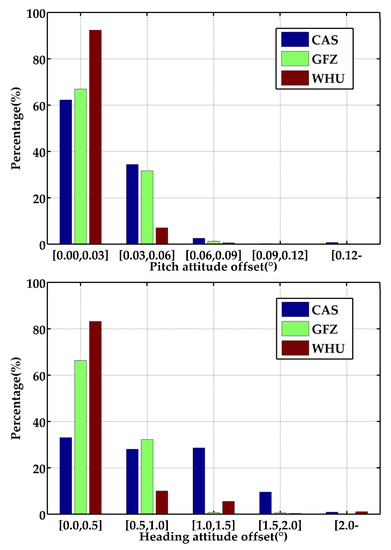
Figure 11.
Distribution of the offsets in roll (top), pitch (middle), and heading (bottom) of the G + B SF-PPP/INS tight integration using the real-time products from CAS, GFZ, and WHU.
Theoretically, in GNSS/INS tight integration, attitudes are discernible when the vehicle makes maneuvers. In this condition, the accuracy of attitude estimation will be marginally affected by the positioning information change. In addition, the estimation accuracy of other parameters in the Kalman filtering could also slightly influence the estimation accuracy of attitude [21]. Therefore, the GNSS/INS tight integration based on different real-time products will make the attitude solutions a little different. Figure 12 illustrates the velocity differences of G + B SF-PPP/INS tight integration. The distributions of velocity offsets of the G + B SF-PPP/INS tight integration using real-time products from CAS, GFZ, and WHU in horizontal and vertical directions are presented in Figure 13. The statistics indicate that percentages of the horizontal velocity offsets within 0.03 m/s were 61.23%, 62.04%, and 62.11% for the results based on the products of CAS, GFZ, and WHU, respectively. The corresponding percentages of the vertical velocity differences within 0.03 m/s were 98.09%, 99.89%, and 99.85%, respectively. In general, the distribution of velocity offsets based on the real-time products from three centers were consistent in horizontal and vertical directions. In terms of the statistics in Table 6, the velocity offset RMS was almost equivalent when adopting the real-time products from different centers (CAS, GFZ, and WHU). This is because (1) the velocity accuracy of GNSS/INS tight integration chiefly relies on the quality of doppler observations and the performance of IMU sensors, and (2) it has a weak relationship with positioning accuracy. Plotted in Figure 14 are the estimated biases and scale factors of the accelerometer and gyroscope of POS320 in the body frame. Additionally, the estimations present a visible relationship with the quality of real-time satellite orbit/clock products.
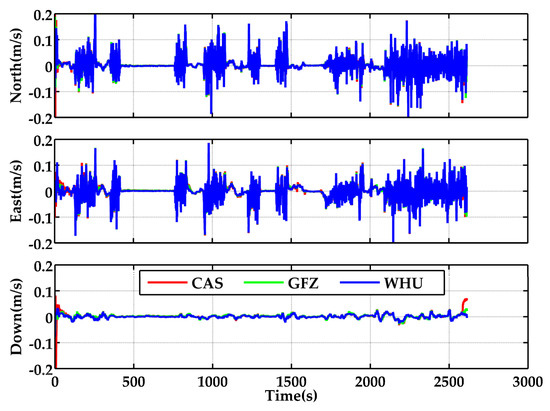
Figure 12.
Velocity offsets of G + B SF-PPP/INS tight integration in the three directions using the real-time products from CAS, GFZ, and WHU, in terms of reference solutions (the start time is 195,453 s).
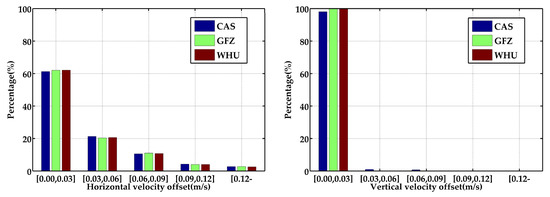
Figure 13.
Distribution of velocity offsets in horizontal (left) and vertical (right) directions of G + B SF-PPP/INS tight integration using the real-time products from CAS, GFZ, and WHU.
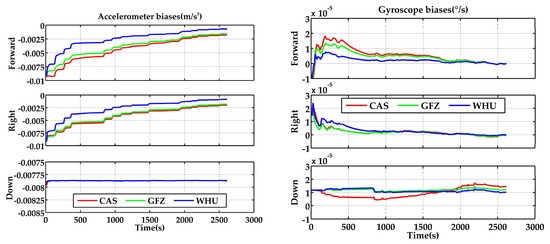
Figure 14.
Accelerometer (left) and gyroscope (right) biases and scale factors in the body frame (Forward–Right–Down) by utilizing real-time products from CAS, GFZ, and WHU (the start time is 195,453 s).
4. Conclusions
In this contribution, a real-time GPS/BDS-2/BDS-3 SF-PPP/INS tight integration model is introduced. To assess its performance, we firstly dissect the positioning performance of SF-PPP and SF-PPP/INS tight integration. Then, the accuracy of real-time products afforded by CAS, GFZ, and WHU are evaluated. To present the performance using orbit and clock products from different analysis centers, a set of vehicle-borne data was processed using the same strategy. According to the results, it can be concluded that: (1) GPS + BDS SF-PPP/INS tight integration can obtain more accurate and continuous positioning solutions, especially during GNSS outage, compared to the solutions of the GPS + BDS SF-PPP. (2) The accuracy of GPS orbit and clock products provided by the three analysis centers are consistent with each other. For BDS satellites, the accuracy of orbits provided by WHU is higher, but the accuracy of the clocks is lower than the others, especially for BDS-2 satellites. The accuracy of BDS MEO satellite products is significantly superior to that of GEO and IGSO satellites. (3) The positioning RMS values based on GFZ’s real-time products are better than those based on the products of CAS and WHU. (4) Owing to the high rate of real-time products, the positioning accuracies in north and vertical directions based on GFZ real-time products are even higher compared to the solutions based on the IGS final products. In addition, the accuracy of attitude and the convergence of IMU sensor errors also present a visible relationship with the real-time orbit/clock products’ accuracy.
With the development of multi-sensor fusion, other sensors such as LiDAR, camera, odometer, and Ultra Wide Band (UWB) can be utilized for positioning and navigation in a GNSS challenging environment.
Author Contributions
Conceptualization, J.L. and Z.G.; data curation, J.L., Q.X. and R.L.; funding acquisition, C.Y. and J.P.; investigation, J.L. and Z.G.; software, Z.G.; visualization, C.Y. and J.P.; writing—original draft preparation, J.L.; writing—review and editing, J.L. and Z.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly supported by the National Key Research and Development Program of China (Grant No. 2020YFB0505802) and the National Natural Science Foundation of China (NSFC) (Grants No. 42074004).
Data Availability Statement
The datasets adopted in this paper are managed by the School of Land Science and Technology, China University of Geosciences, Beijing, and are available on request from the corresponding author.
Acknowledgments
The authors would like to thank anonymous reviewers who provided valuable suggestions that have helped to improve the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Malys, S.; Jensen, P.A. Geodetic point positioning with GPS carrier beat phase data from the CASA UNO experiment. Geophys. Res. Lett. 1990, 17, 651–654. [Google Scholar] [CrossRef]
- Larson, K.M.; Bodin, P.; Gomberg, J. Using 1-Hz GPS data to measure deformations caused by the Denali fault earthquake. Science 2003, 300, 1421–1424. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ge, M.; Lu, C.; Zhang, Y.; Wang, R.; Wickert, J.; Schuh, H. High-Rate GPS Seismology Using Real-Time Precise Point Positioning with Ambiguity Resolution. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6165–6180. [Google Scholar]
- Yao, Y.; Liu, C.; Xu, C. A New GNSS-Derived Water Vapor Tomography Method Based on Optimized Voxel for Large GNSS Network. Remote Sens. 2020, 12, 2306. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Guo, F. Predicting atmospheric delays for rapid ambiguity resolution in precise point positioning. Adv. Space Res. 2014, 54, 840–850. [Google Scholar] [CrossRef]
- Zhang, K.; Liang, S.; Gan, W. Crustal strain rates of southeastern Tibetan Plateau derived from GPS measurements and implications to lithospheric deformation of the Shan-Thai terrane. Earth Planet. Phys. 2019, 3, 45–52. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Y.; Gan, W.; Liang, S. Impacts of Local Effects and Surface Loads on the Common Mode Error Filtering in Continuous GPS Measurements in the Northwest of Yunnan Province, China. Sensors 2020, 20, 5408. [Google Scholar] [CrossRef]
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2016, 20, 849–862. [Google Scholar] [CrossRef]
- Ge, Y.; Dai, P.; Qin, W.; Yang, X.; Zhou, F.; Wang, S.; Zhao, X. Performance of Multi-GNSS Precise Point Positioning Time and Frequency Transfer with Clock Modeling. Remote Sens. 2019, 11, 347. [Google Scholar] [CrossRef]
- Lv, J.; Gao, Z.; Kan, J.; Lan, R.; Li, Y.; Lou, Y.; Yang, H.; Peng, J. Modeling and assessment of multi-frequency GPS/BDS-2/BDS-3 kinematic precise point positioning based on vehicle-borne data. Measurement 2022, 189, 110453. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Ma, F.; Yuan, Y.; Zhang, K.; Zhou, F.; Zhang, X. Improved PPP Ambiguity Resolution with the Assistance of Multiple LEO Constellations and Signals. Remote Sens. 2019, 11, 408. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Dodson, A.H.; Ge, M.; Teferle, F.N. Rapid re-convergences to ambiguity-fixed solutions in precise point positioning. J. Geod. 2010, 84, 705–714. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, Z.; Ge, M.; Niu, X.; Huang, L.; Tu, R.; Li, X. On the convergence of ionospheric constrained precise point positioning (IC-PPP) based on undifferential uncombined raw GNSS observations. Sensors 2013, 13, 15708–15725. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G.; Yuan, Y.; Zhang, X.; Li, M. A modified carrier-to-code leveling method for retrieving ionospheric observables and detecting short-term temporal variability of receiver differential code biases. J. Geod. 2019, 93, 19–28. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, X.; Wang, J.; Ren, X. Modeling and assessment of triple-frequency BDS precise point positioning. J. Geod. 2016, 90, 1223–1235. [Google Scholar] [CrossRef]
- Hong, J.; Tu, R.; Zhang, R.; Fan, L.; Zhang, P.; Han, J. Contribution analysis of QZSS to single-frequency PPP of GPS/BDS/GLONASS/Galileo. Adv. Space Res. 2020, 65, 1803–1817. [Google Scholar] [CrossRef]
- Shi, C.; Wu, X.; Zheng, F.; Wang, X.; Wang, J. Modeling of BDS-2/BDS-3 single-frequency PPP with B1I and B1C signals and positioning performance analysis. Measurement 2021, 178, 109355. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. A novel GNSS single-frequency PPP approach to estimate the ionospheric TEC and satellite pseudorange observable-specific signal bias. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5801712. [Google Scholar] [CrossRef]
- Cox, D.B. Integration of GPS with Inertial Navigation Systems. Navig. J. Inst. Navig. 1978, 25, 236–245. [Google Scholar] [CrossRef]
- Gao, Z.; Ge, M.; Shen, W.; Zhang, H.; Niu, X. Ionospheric and receiver DCB-constrained multi-GNSS single-frequency PPP integrated with MEMS inertial measurements. J. Geod. 2017, 91, 1351–1366. [Google Scholar] [CrossRef]
- Gu, S.; Dai, C.; Fang, W.; Zheng, F.; Wang, Y.; Zhang, Q.; Lou, Y.; Niu, X. Multi-GNSS PPP/INS tightly coupled integration with atmospheric augmentation and its application in urban vehicle navigation. J. Geod. 2021, 95, 1–15. [Google Scholar] [CrossRef]
- Hadas, T.; Bosy, J. IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Solut. 2015, 19, 93–105. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.; Ge, M.; Neitzel, F.; Wang, X.; Yuan, H. Investigation of the performance of real-time BDS-only precise point positioning using the IGS real-time service. GPS Solut. 2019, 23, 1–12. [Google Scholar] [CrossRef]
- Kazmierski, K.; Zajdel, R.; Sośnica, K. Evolution of orbit and clock quality for real-time multi-GNSS solutions. GPS Solut. 2020, 24, 1–12. [Google Scholar] [CrossRef]
- Øvstedal, O. Absolute positioning with single-frequency GPS receivers. GPS Solut. 2002, 5, 33–44. [Google Scholar] [CrossRef]
- Yunck, T.P. Orbit determination. In Global Positioning System-Theory and Applications; Parkinson, B.W., Spilker, J.J., Eds.; AIAA: Washington, DC, USA, 1996. [Google Scholar]
- Beran, T.; Kim, D.; Langley, R.B. High-precision single-frequency GPS point positioning. In Proceedings of the 16th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS/GNSS 2003), Portland, OR, USA, 9–12 September 2003; pp. 1192–1200. [Google Scholar]
- Montenbruck, O. Kinematic GPS positioning of LEO satellites using ionosphere-free single frequency measurements. Aerosp. Sci. Technol. 2003, 7, 396–405. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Y.; Chen, K. Development of a real-time single frequency precise point positioning system and test results. In Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2006), Fort Worth, TX, USA, 26–29 September 2006; pp. 2297–2303. [Google Scholar]
- Beran, T.; Bisnath, S.B.; Langley, R.B. Evaluation of high-precision, single-frequency GPS point positioning models. In Proceedings of the 17th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2004), Long Beach, CA, USA, 21–24 September 2004; pp. 1893–1901. [Google Scholar]
- Le, A.Q.; Tiberius, C.C.J.M.; Van der Marel, H.; Jakowski, N. Use of global and regional ionosphere maps for single-frequency precise point positioning. In Observing Our Changing Earth; Springer: Berlin, Germany, 2009; pp. 759–769. [Google Scholar]
- Shi, C.; Gu, S.; Lou, Y.; Ge, M. An improved approach to model ionospheric delays for single-frequency precise point positioning. Adv. Space Res. 2012, 49, 1698–1708. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, R.; Song, W.; Shi, C.; Lou, Y. An improved approach to model regional ionosphere and accelerate convergence for precise point positioning. Adv. Space Res. 2013, 52, 1406–1415. [Google Scholar] [CrossRef]
- Di, M.; Zhang, A.; Guo, B.; Zhang, J.; Liu, R.; Li, M. Evaluation of Real-Time PPP-Based Tide Measurement Using IGS Real-Time Service. Sensors 2020, 20, 2968. [Google Scholar] [CrossRef]
- Gendt, G.; Dick, G.; Reigber, C.H.; Tomassini, M.; Liu, Y. Demonstration of NRT GPS water vapor monitoring for numerical weather prediction in Germany. J. Meteorol. Soc. Jpn. 2003, 82, 360–370. [Google Scholar]
- Niu, X.; Goodall, C.; Nassar, S.; El-Sheimy, N. An efficient method for evaluating the performance of MEMS IMUs. In Proceedings of the Position Location and Navigation Symposium, 2006 IEEE/ION, San Diego, CA, USA, 25–27 April 2006; pp. 766–771. [Google Scholar]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering; Willey: New York, NY, USA, 1992. [Google Scholar]
- Shin, E.H. Estimation Techniques for Low-Cost Inertial Navigation; Library and Archives Canada: Ottawa, ON, Canada, 2006. [Google Scholar]
- Su, K.; Jin, S. Analysis and comparisons of the BDS/Galileo quad-frequency PPP models performances. Acta Geod. Cartogr. Sin. 2020, 49, 1189–1201. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).