Trajectory Optimization of Autonomous Surface Vehicles with Outliers for Underwater Target Localization
Abstract
:1. Introduction
- (1)
- The closed-form expression of the function under outliers is obtained using D-optimality combined with a Monte Carlo approach.
- (2)
- Two methodologies for obtaining the optimal configuration in the absence of a target location are provided. In the case of a single or two ASVs, the target position is supposed to be in an unclear zone, and a worst-case-scenario-based min–max method is provided. For the three ASVs scheme, a novel localization approach, TPLA, for determining the target position at each time slot is provided.
- (3)
- Optimal ASV trajectories are determined by obtaining a sequence of optimal waypoints at each time slot.
2. Methods
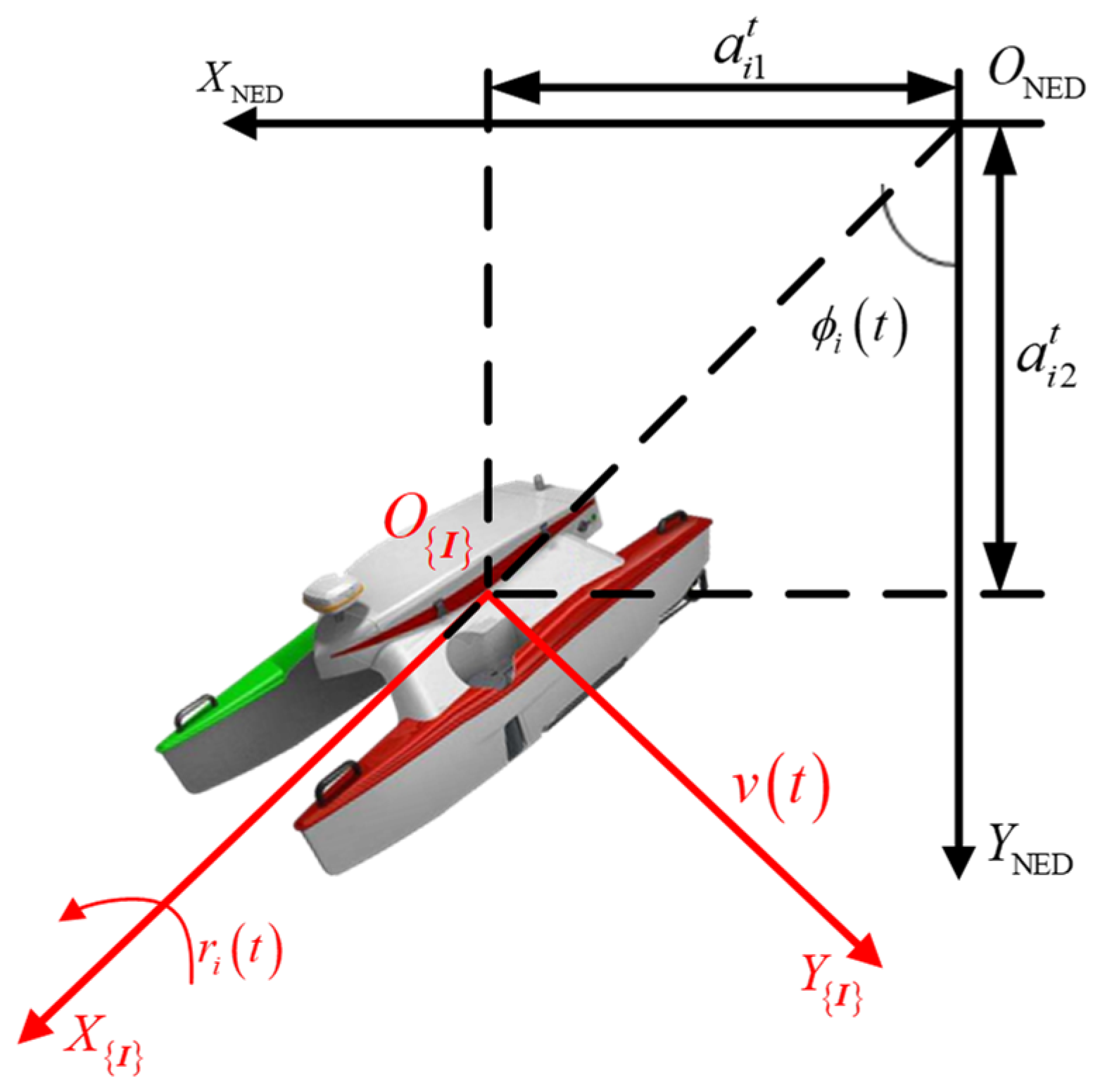
2.1. Kinematic Model of ASVs
2.2. Observation Model
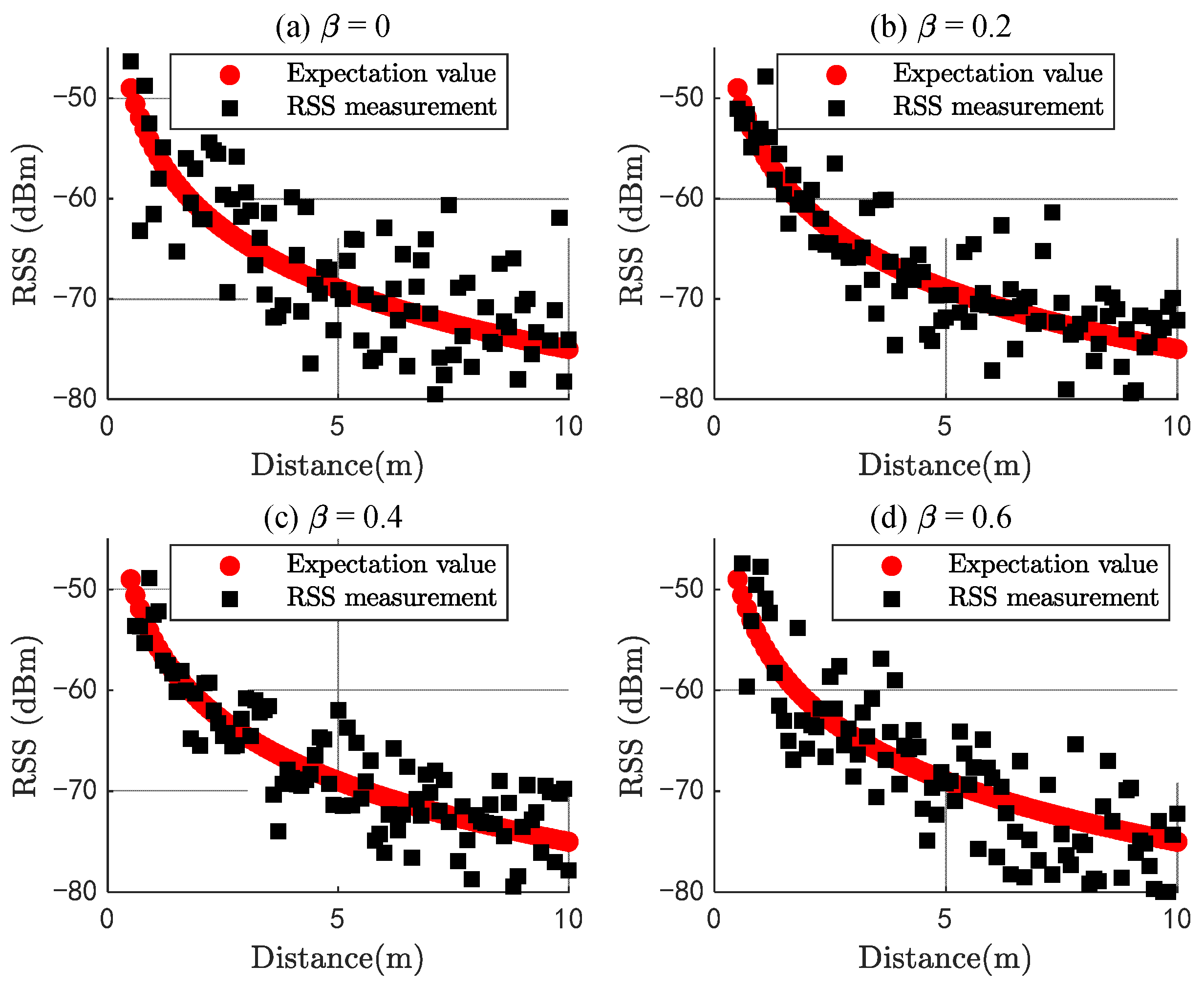
2.3. Optimal Configuration Analysis Using RSS
2.4. Closed-Form Expression and Objective Function
2.5. Optimal Configuration under Outliers
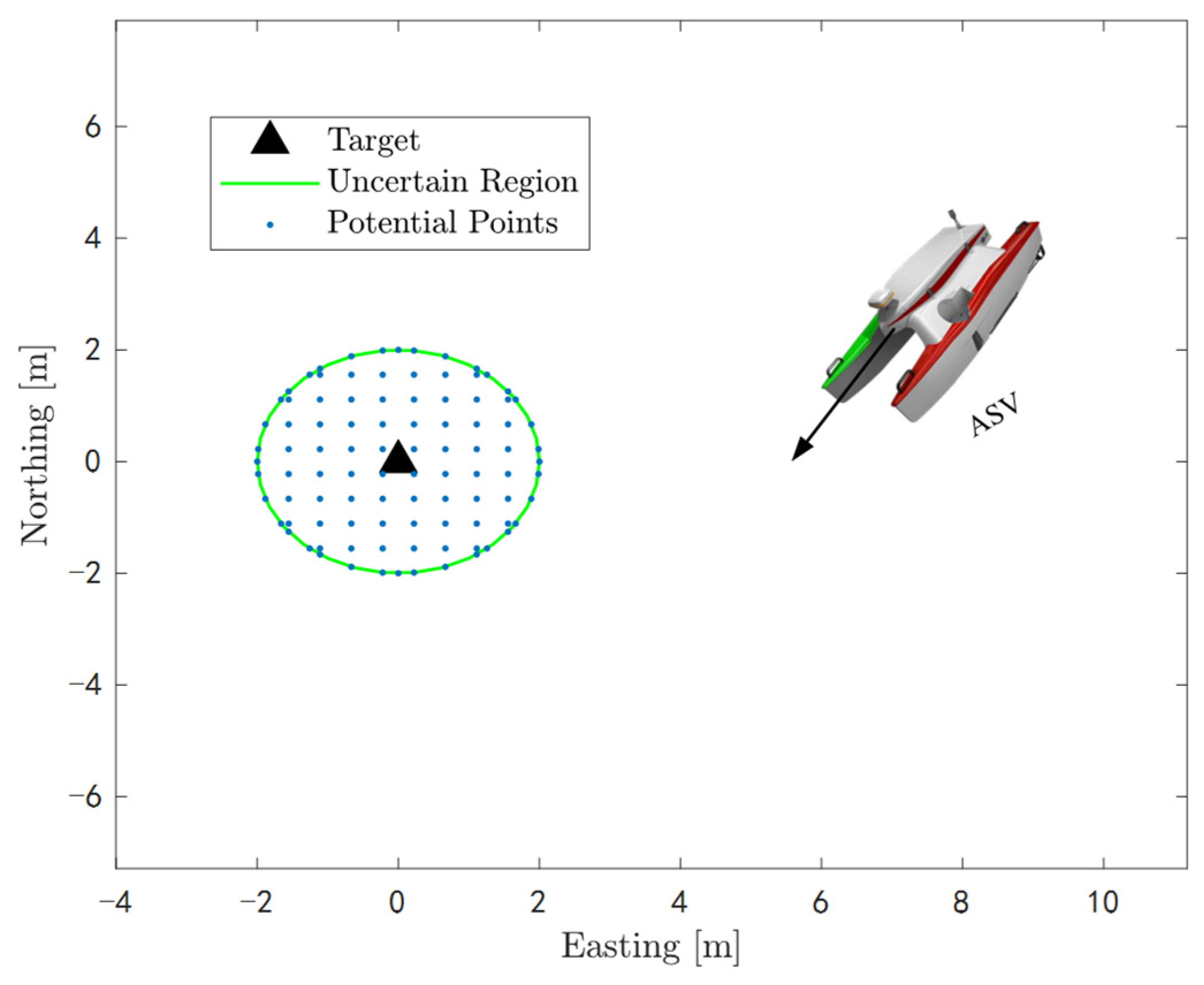
2.5.1. Optimal Trajectory for a Single ASV
- 1.
- Input the initial parameters including , , , , and potential points in the uncertain area.
- 2.
- Figure out according to (16) at each time slot.
- 3.
- Find the point to make the logarithm of the determinant of the FIM minimum.
- 4.
- Calculate according to (22) with the point .
- 5.
- Calculate according to and .
- 6.
- Compute using (3) with .
- 7.
- Output .
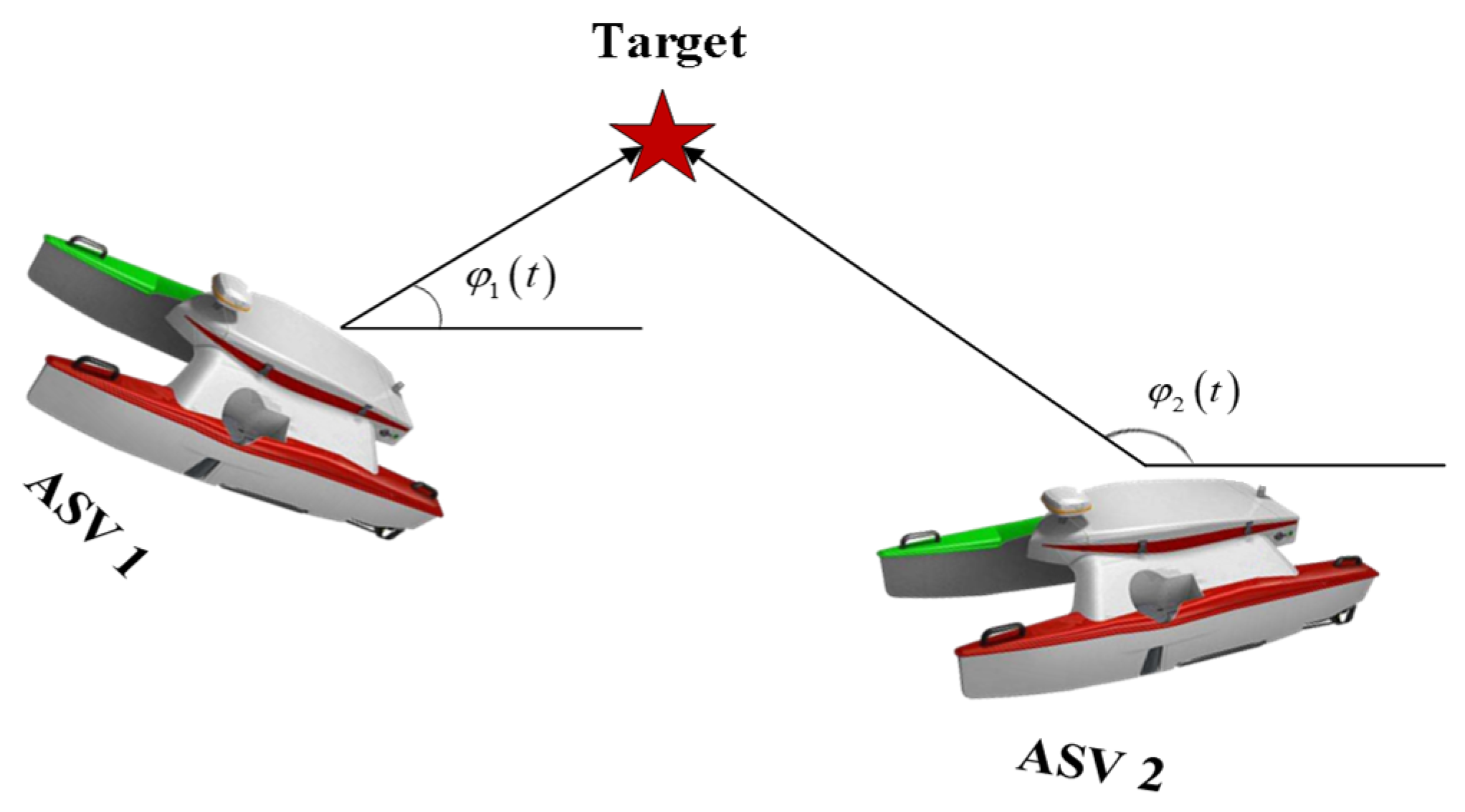
2.5.2. Optimal Trajectories for Two ASVs
2.5.3. Optimal Trajectories for Three ASVs
Optimal Initial Geometry of Three ASVs
TPLA
| Algorithm 1. TPLA |
| 1. Input: , , , total number of iterations at the first phase , and the second phase . |
| 2. Calculate the RSS measurements |
| 3. Reshape the problem to a GTRS problem as (35). |
| 4. While do |
| 5. Determine the multiplier λ at each iteration according to |
| 6. |
| 7. Determine the optimal at each iteration according to |
| 8. If |
| 9. Break |
| 10. End if |
| 11. |
| 12. End while |
| 13. Output (as the input to the second phase) |
| 14. |
| 15. While do |
| 16. Update according to (40) |
| 17. End while |
| 18. Output: |
Convergence Analysis of TPLA
Optimal Trajectories of Three ASVs
3. Results and Discussion
3.1. Parameters Setup
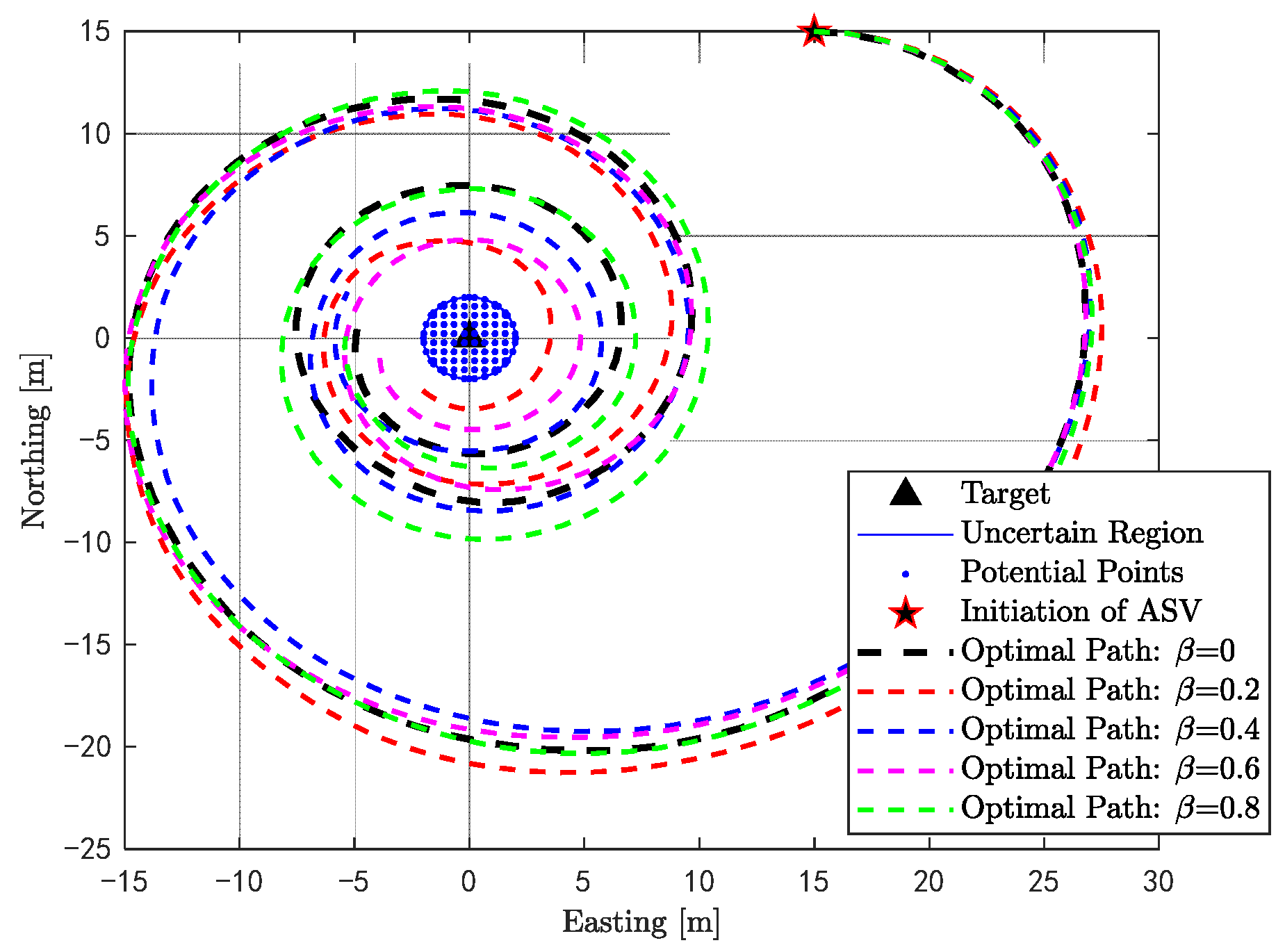
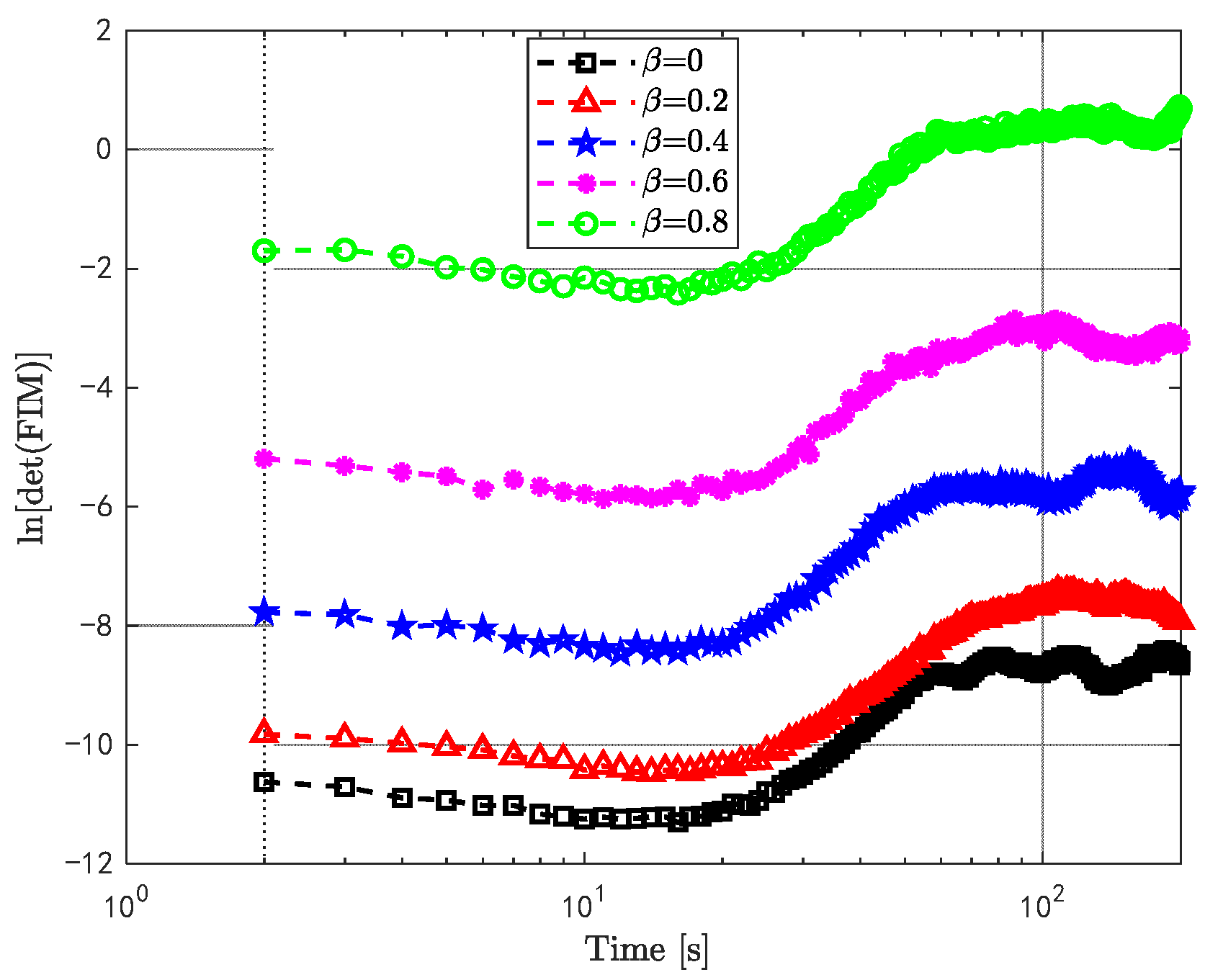
3.2. Optimal Trajectory of a Single ASV
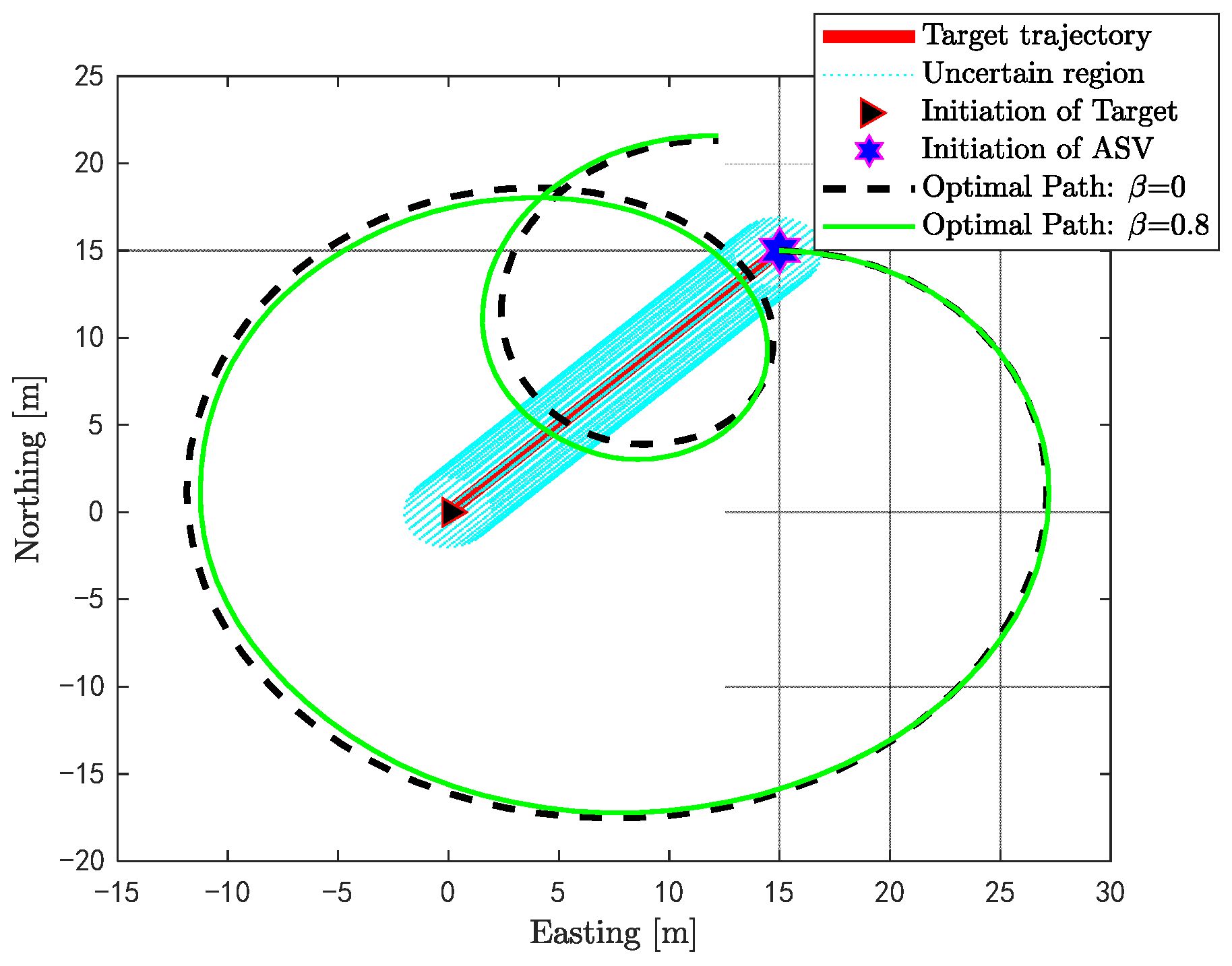
3.3. Optimal Trajectories of Two ASVs
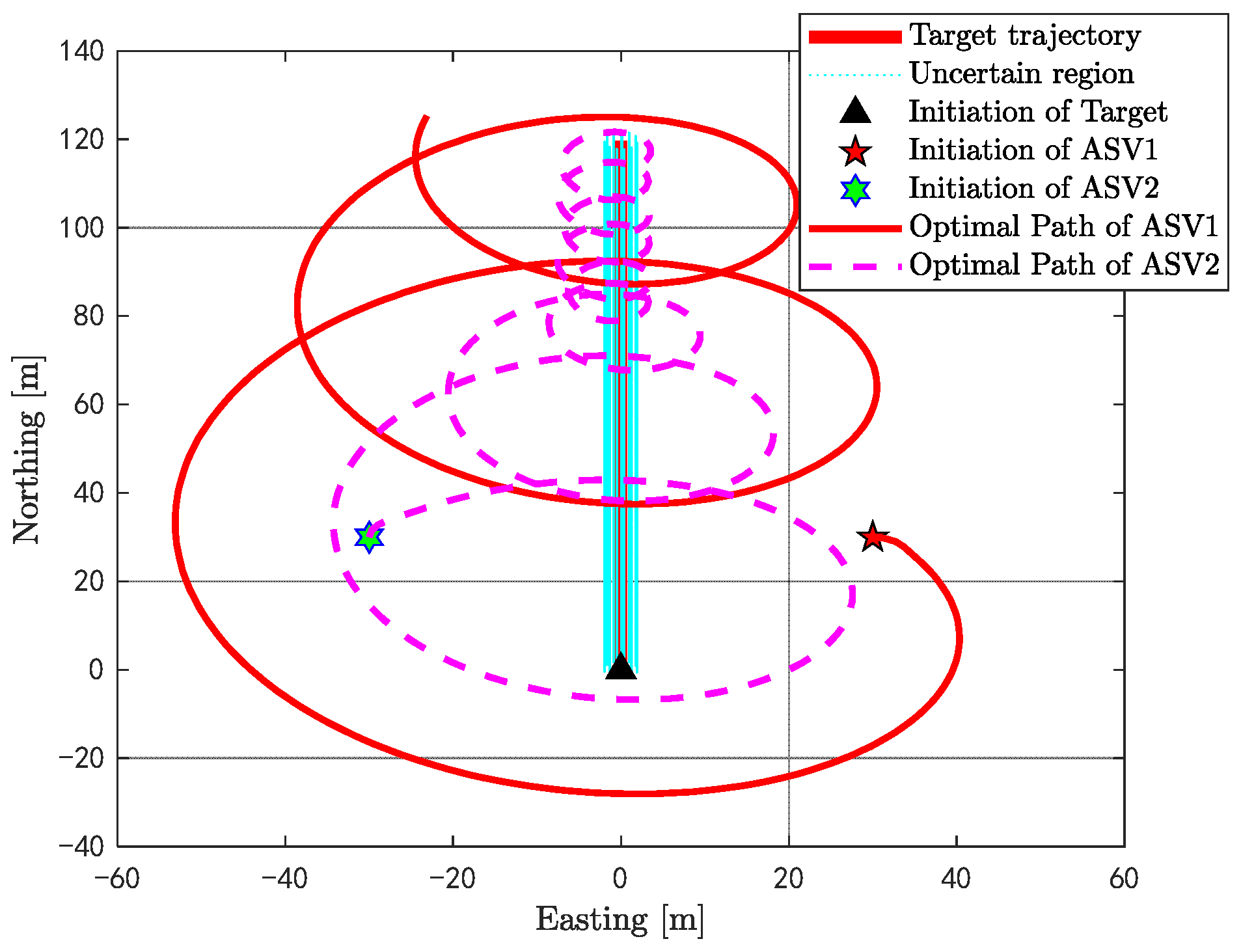
3.4. Optimal Trajectories of Three ASVs
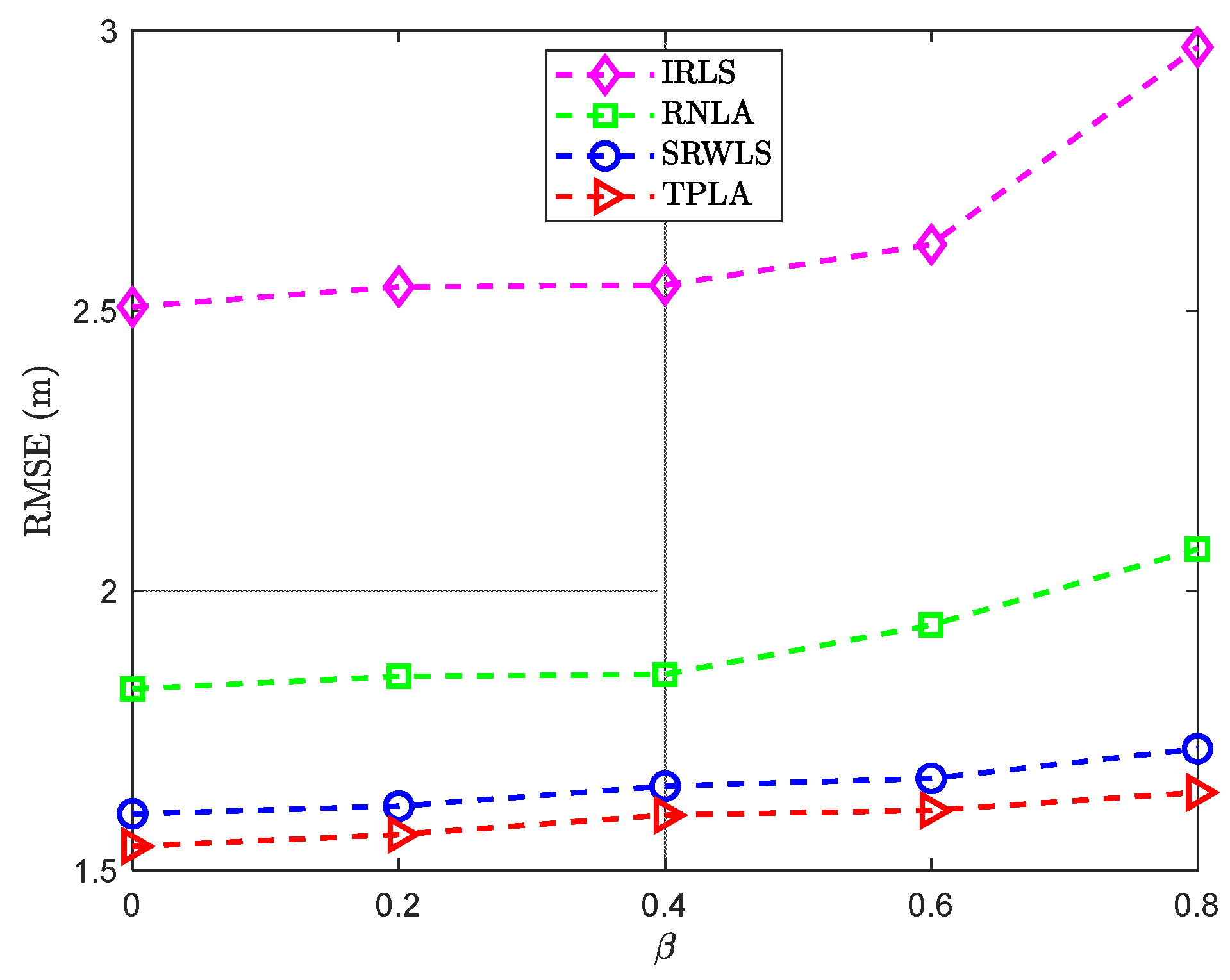
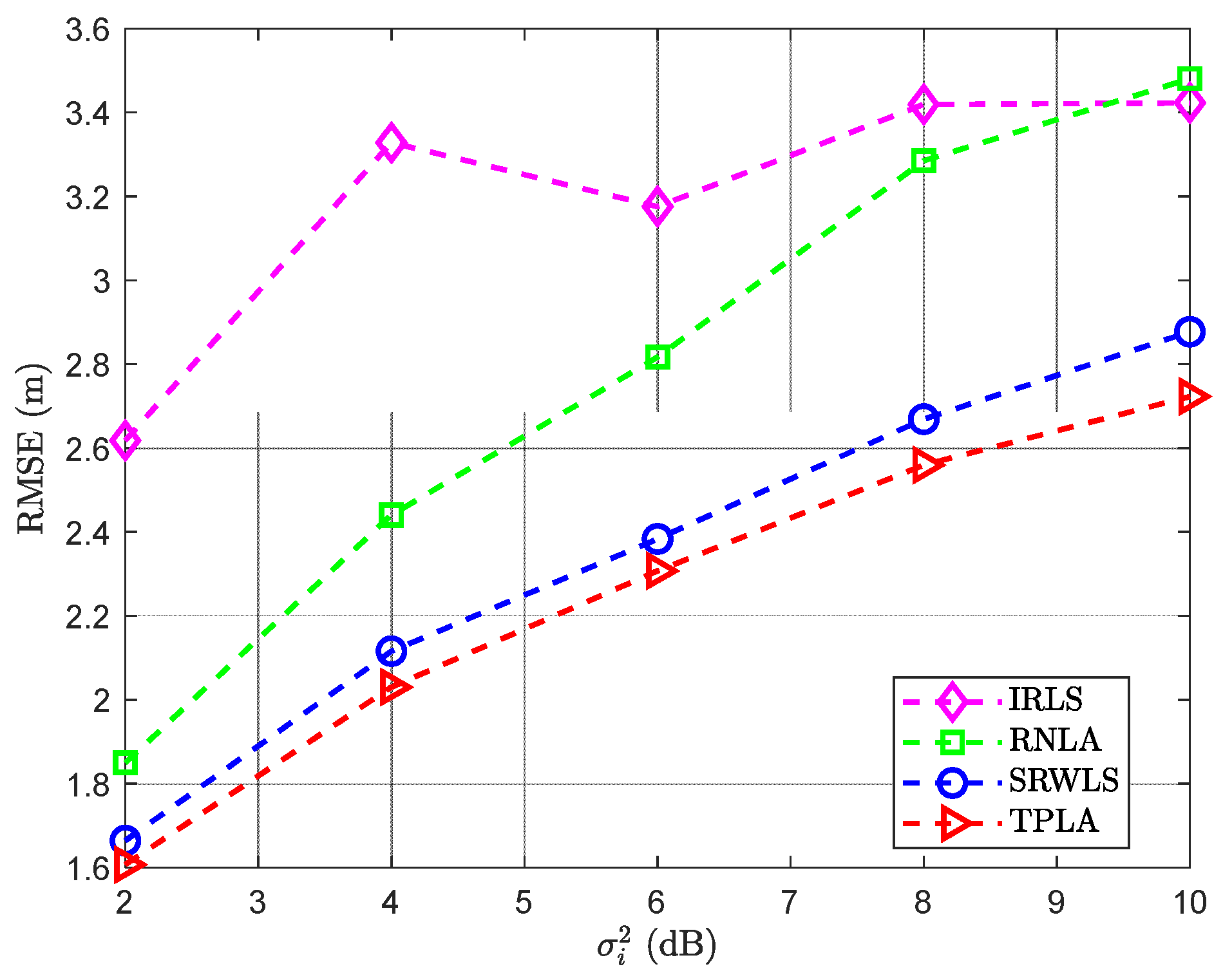
3.4.1. Localization Method Comparison
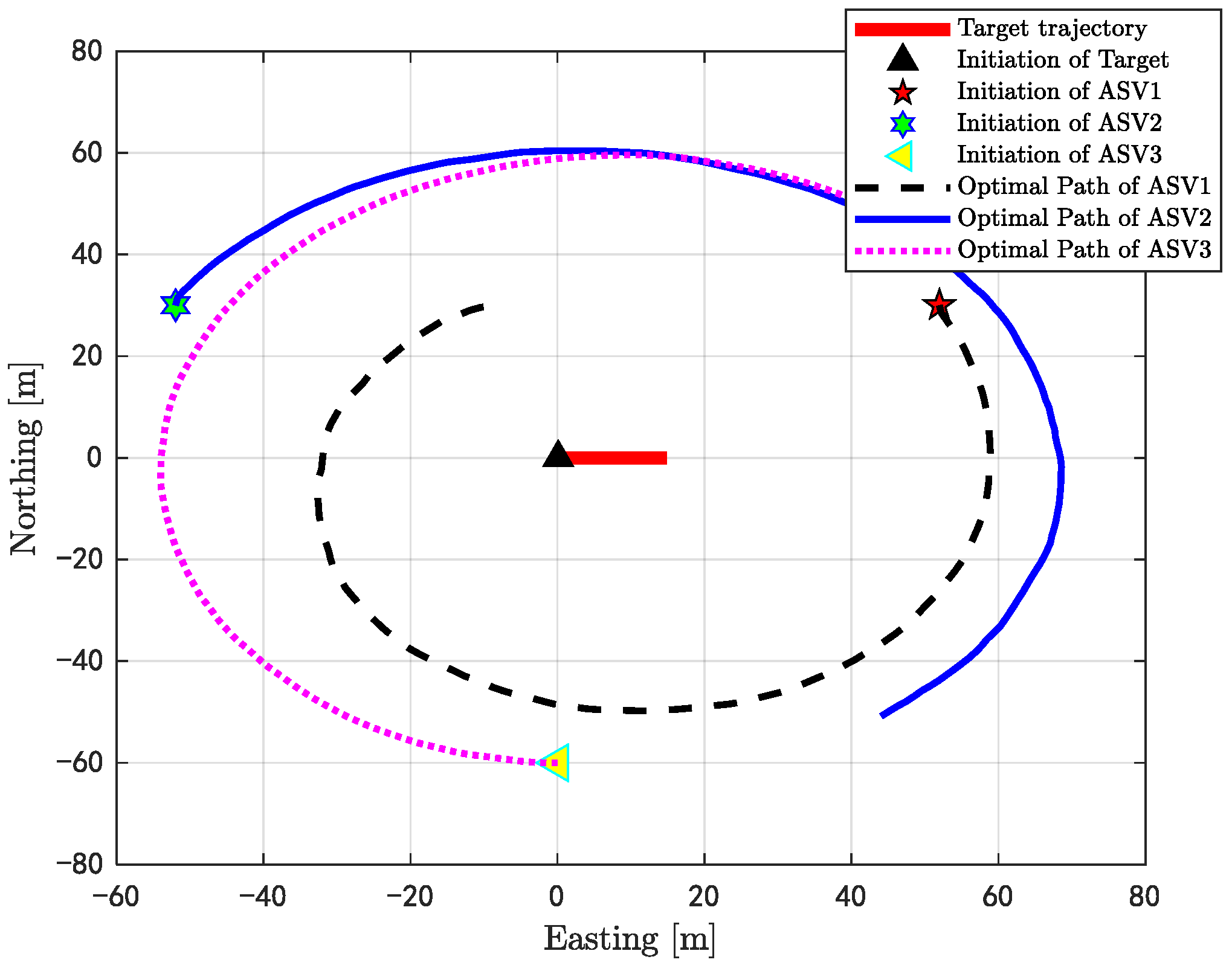
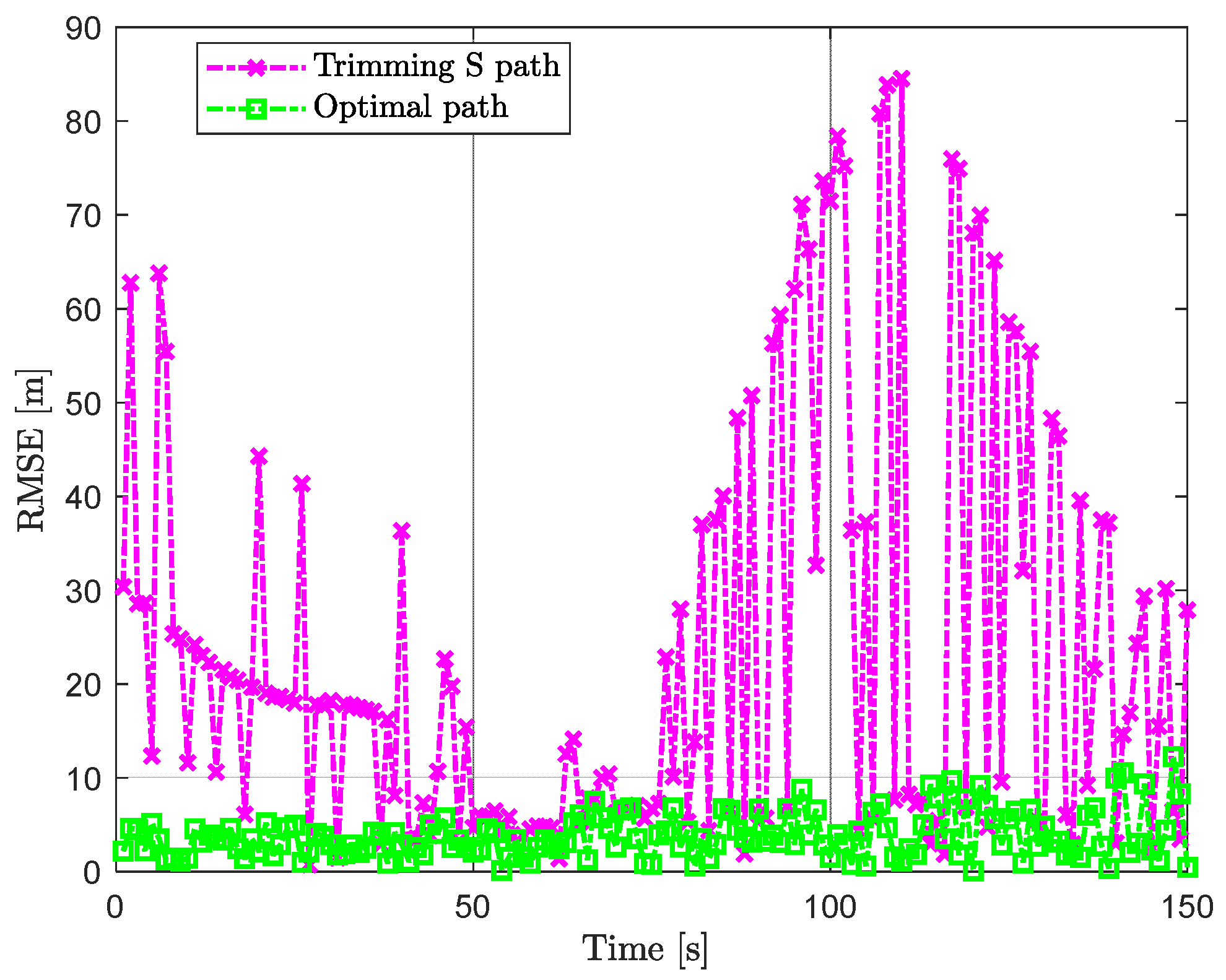
3.4.2. Optimal Trajectories
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, G.; Long, X.; Zhu, C.; Guizani, M.; Bi, Y.; Zhang, W. An AUV Location Prediction-Based Data Collection Scheme for Underwater Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2019, 68, 6037–6049. [Google Scholar] [CrossRef]
- Zhuo, X.; Liu, M.; Wei, Y.; Yu, G.; Qu, F.; Sun, R. AUV-aided Energy-Efficient Data Collection in Underwater Acoustic Sensor Networks. IEEE Internet Things J. 2020, 7, 10010–10022. [Google Scholar] [CrossRef]
- Jing, P.; Xu, G.; Chen, Y.; Shi, Y.; Zhan, F. The Determinants behind the Acceptance of Autonomous Vehicles: A Systematic Review. Sustainability 2020, 12, 1719. [Google Scholar] [CrossRef]
- Mei, X.; Wu, H.; Xian, J.; Chen, B.; Zhang, H.; Liu, X. A Robust, Non-Cooperative Localization Algorithm in the Presence of Outlier Measurements in Ocean Sensor Networks. Sensors 2019, 19, 2708. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Mei, X.; Chen, X.; Li, J.; Wang, J.; Mohapatra, P. A novel cooperative localization algorithm using enhanced particle filter technique in maritime search and rescue wireless sensor network. ISA Trans. 2018, 78, 39–46. [Google Scholar] [CrossRef]
- Chen, X.; Ling, J.; Wang, S.; Yang, Y.; Luo, L.; Yan, Y. Ship detection from coastal surveillance videos via an ensemble Canny-Gaussian-morphology framework. J. Navig. 2021, 74, 1252–1266. [Google Scholar] [CrossRef]
- Bayat, M.; Crasta, N.; Aguiar, A.P.; Pascoal, A.M. Range-Based Underwater Vehicle Localization in the Presence of Unknown Ocean Currents: Theory and Experiments. IEEE Trans. Control Syst. Technol. 2016, 24, 122–139. [Google Scholar] [CrossRef]
- Su, R.; Zhang, D.; Li, C.; Gong, Z.; Venkatesan, R.; Jiang, F. Localization and Data Collection in AUV-Aided Underwater Sensor Networks: Challenges and Opportunities. IEEE Netw. 2019, 33, 86–93. [Google Scholar] [CrossRef]
- Ma, T.; Li, Y.; Zhao, Y.; Jiang, Y.; Cong, Z.; Zhao, Q.; Xu, S. An AUV localization and path planning algorithm for terrain-aided navigation. ISA Trans. 2020, 103, 215–227. [Google Scholar] [CrossRef]
- Mei, X.; Han, D.; Saeed, N.; Wu, H.; Ma, T.; Xian, J. Range Difference-based Target Localization under Stratification Effect and NLOS bias in UWSNs. IEEE Wirel. Commun. Lett. 2022; early access. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Cai, L.; Shen, X.; Zhao, R. Fundamentals and Advancements of Topology Discovery in Underwater Acoustic Sensor Networks: A Review. IEEE Sens. J. 2021, 21, 21159–21174. [Google Scholar] [CrossRef]
- Sozer, E.M.; Stojanovic, M.; Proakis, J.G. Underwater acoustic networks. IEEE J. Ocean. Eng. 2000, 25, 72–83. [Google Scholar] [CrossRef]
- Crasta, N.; Moreno-Salinas, D.; Pascoal, A.M.; Aranda, J. Multiple autonomous surface vehicle motion planning for cooperative range-based underwater target localization. Annu. Rev. Control 2018, 46, 326–342. [Google Scholar] [CrossRef]
- Marie, T.F.B.; Yang, B.; Han, D.; An, B. A Hybrid Model Integrating MPSE and IGNN for Events Recognition along Submarine Cables. IEEE Trans. Instrum. Meas. 2022; early access. [Google Scholar] [CrossRef]
- Chen, P.; Han, D. Effective wind speed estimation study of the wind turbine based on deep learning. Energy 2022, 247, 123491. [Google Scholar] [CrossRef]
- Moreno-Salinas, D.; Pascoal, A.M.; Aranda, J. Optimal Sensor Trajectories for Mobile Underwater Target Positioning with Noisy Range Measurements. IFAC Proc. Vol. 2014, 47, 5139–5144. [Google Scholar] [CrossRef]
- Mei, X.; Wu, H.; Xian, J.; Chen, B. RSS-based Byzantine Fault-tolerant Localization Algorithm under NLOS Environment. IEEE Commun. Lett. 2021, 25, 474–478. [Google Scholar] [CrossRef]
- Mei, X.; Wu, H.; Xian, J. Matrix Factorization based Target Localization via Range Measurements with Uncertainty in Transmit Power. IEEE Wirel. Commun. Lett. 2020, 9, 1611–1615. [Google Scholar] [CrossRef]
- Mei, X.; Wu, H.; Saeed, N.; Ma, T.; Xian, J.; Chen, Y. An Absorption Mitigation Technique for Received Signal Strength-Based Target Localization in Underwater Wireless Sensor Networks. Sensors 2020, 20, 4698. [Google Scholar] [CrossRef]
- Moreno-Salinas, D.; Pascoal, A.M.; Aranda, J. Surface sensor networks for Underwater Vehicle positioning with bearings-only measurements. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 208–214. [Google Scholar]
- Moreno-Salinas, D.; Pascoal, A.; Aranda, J. Sensor Networks for Optimal Target Localization with Bearings-Only Measurements in Constrained Three-Dimensional Scenarios. Sensors 2013, 13, 10386–10417. [Google Scholar] [CrossRef] [Green Version]
- Moreno-Salinas, D.; Pascoal, A.; Aranda, J. Optimal Sensor Placement for Acoustic Underwater Target Positioning with Range-Only Measurements. IEEE J. Ocean. Eng. 2016, 41, 620–643. [Google Scholar] [CrossRef]
- Moreno-Salinas, D.; Crasta, N.; Pascoal, A.; Aranda, J. Optimal multiple underwater target localization and tracking using two surface acoustic ranging sensors. IFAC-Pap. 2018, 51, 177–182. [Google Scholar] [CrossRef]
- Bo, X.; Razzaqi, A.A.; Wang, X. Optimal Sensor Formation for 3D Cooperative Localization of AUVs Using Time Difference of Arrival (TDOA) Method. Sensors 2018, 18, 4442. [Google Scholar] [CrossRef] [PubMed]
- Duecker, D.-A.; Geist, R.A.; Hengeler, M.; Kreuzer, E.; Pick, M.-A.; Rausch, V.; Solowjow, E. Embedded Spherical Localization for Micro Underwater Vehicles Based on Attenuation of Electro-Magnetic Carrier Signals. Sensors 2017, 17, 959. [Google Scholar] [CrossRef]
- Cario, G.; Casavola, A.; Gagliardi, G.; Lupia, M.; Severino, U.; Bruno, F. Analysis of error sources in underwater localization systems. In Proceedings of the OCEANS 2019, Marseille, France, 17–20 June 2019; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar]
- Ullah, I.; Gao, M.-S.; Kamal, M.M.; Khan, Z. A Survey on Underwater Localization, Localization Techniques and Its Algorithms BT. In Proceedings of the 3rd Annual International Conference on Electronics, Electrical Engineering and Information Science (EEEIS 2017), Guangzhou, China, 8–10 September 2017; Atlantis Press: Amsterdam, The Netherlands, 2017; pp. 252–259. [Google Scholar]
- Nguyen, L.N.T.; Shin, Y. An Efficient RSS Localization for Underwater Wireless Sensor Networks. Sensors 2019, 19, 3105. [Google Scholar] [CrossRef]
- Mei, X.; Chen, Y.; Xu, X.; Wu, H. RSS Localization Using Multistep Linearization in the Presence of Unknown Path Loss Exponent. IEEE Sens. Lett. 2022, 6, 1–4. [Google Scholar] [CrossRef]
- Saleheh, P.; Hossein, Z.J. Received Signal Strength Based Localization in Inhomogeneous Underwater Medium. Signal Process. 2019, 154, 45–56. [Google Scholar]
- Xu, T.; Hu, Y.; Zhang, B.; Leus, G. RSS-based sensor localization in underwater acoustic sensor networks. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; IEEE: New York, NY, USA; pp. 3906–3910. [Google Scholar]
- Poursheikhali, S.; Zamiri-Jafarian, H. Source localization in inhomogeneous underwater medium using sensor arrays: Received signal strength approach. Signal Process. 2021, 183, 108047. [Google Scholar] [CrossRef]
- Bishop, A.N.; Fidan, B.; Anderson, B.D.O.; Doğançay, K.; Pathirana, P.N. Optimality analysis of sensor-target localization geometries. Automatica 2010, 46, 479–492. [Google Scholar] [CrossRef]
- Han, G.; Zhang, C.; Shu, L.; Rodrigues, J.J.P.C. Impacts of Deployment Strategies on Localization Performance in Underwater Acoustic Sensor Networks. IEEE Trans. Ind. Electron. 2015, 62, 1725–1733. [Google Scholar] [CrossRef]
- Xu, B.; Razzaqi, A.A.; Farid, G. A Review on Optimal Placement of Sensors for Cooperative Localization of AUVs. J. Sens. 2019, 2019, 4276987. [Google Scholar]
- Li, H.; Han, D.; Tang, M. A Privacy-Preserving Storage Scheme for Logistics Data With Assistance of Blockchain. IEEE Internet Things J. 2022, 9, 4704–4720. [Google Scholar] [CrossRef]
- Cui, M.; Han, D.; Wang, J.; Li, K.-C.; Chang, C.-C. ARFV: An Efficient Shared Data Auditing Scheme Supporting Revocation for Fog-Assisted Vehicular Ad-Hoc Networks. IEEE Trans. Veh. Technol. 2020, 69, 15815–15827. [Google Scholar] [CrossRef]
- Xu, S.; Ou, Y.; Wu, X. Optimal Sensor Placement for 3-D Time-of-Arrival Target Localization. IEEE Trans. Signal Process. 2019, 67, 5018–5031. [Google Scholar] [CrossRef]
- Xu, S.; Ou, Y.; Zheng, W. Optimal Sensor-Target Geometries for 3-D Static Target Localization Using Received-Signal-Strength Measurements. IEEE Signal Process. Lett. 2019, 26, 966–970. [Google Scholar] [CrossRef]
- Moreno-Salinas, D.; Pascoal, A.M.; Aranda, J. Multiple underwater target positioning with optimally placed acoustic surface sensor networks. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718773234. [Google Scholar] [CrossRef]
- Mei, X.; Wu, H.; Xian, J.; Ma, T. Information-driven optimal placement strategy for target localization in ocean sensor networks. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2021, 49, 23–29. [Google Scholar]
- Masmitja, I.; Gomariz, S.; Del-Rio, J.; Kieft, B.; O’Reilly, T.; Bouvet, P.; Aguzzi, J. Range-Only Single-Beacon Tracking of Underwater Targets From an Autonomous Vehicle: From Theory to Practice. IEEE Access 2019, 7, 86946–86963. [Google Scholar] [CrossRef]
- Crasta, N.; Moreno-Salinas, D.; Bayat, B.; Pascoal, A.M.; Aranda, J. Range-based underwater target localization using an autonomous surface vehicle: Observability analysis. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; IEEE: New York, NY, USA, 2018; pp. 487–496. [Google Scholar]
- Chen, C.; Han, D.; Chang, C.-C. CAAN: Context-Aware attention network for visual question answering. Pattern Recognit. 2022, 132, 108980. [Google Scholar] [CrossRef]
- Saeed, N.; Al-Naffouri, T.Y.; Alouini, M.S. Outlier Detection and Optimal Anchor Placement for 3-D Underwater Optical Wireless Sensor Network Localization. IEEE Trans. Commun. 2019, 67, 611–622. [Google Scholar] [CrossRef]
- Boyles, C.A.; Rosenberg, A.P.; Zhang, Q. Underwater acoustic communication channel characterization in the presence of bubbles and rough sea surfaces. In Proceedings of the OCEANS 2011 IEEE—Spain, Santander, Spain, 6–9 June 2011; IEEE: New York, NY, USA, 2011; pp. 1–8. [Google Scholar]
- Chua, G.; Chitre, M.; Deane, G. Impact of Persistent Bubbles on Underwater Acoustic Communication. In Proceedings of the 2018 Fourth Underwater Communications and Networking Conference (UComms), Lerici, Italy, 28–30 August 2018; IEEE: New York, NY, USA, 2018; pp. 1–5. [Google Scholar]
- Jouhari, M.; Ibrahimi, K.; Tembine, H.; Ben-Othman, J. Underwater Wireless Sensor Networks: A Survey on Enabling Technologies, Localization Protocols, and Internet of Underwater Things. IEEE Access 2019, 7, 96879–96899. [Google Scholar] [CrossRef]
- Dogancay, K. UAV Path Planning for Passive Emitter Localization. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1150–1166. [Google Scholar] [CrossRef]
- Jimenez-Martinez, M. Harbor and coastal structures: A review of mechanical fatigue under random wave loading. Heliyon 2021, 7, e08241. [Google Scholar] [CrossRef] [PubMed]
- Mahmutoglu, Y.; Turk, K. Received signal strength difference based leakage localization for the underwater natural gas pipelines. Appl. Acoust. 2019, 153, 14–19. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1993; ISBN 0133457117. [Google Scholar]
- Nguyen, N.H.; Doğançay, K. Optimal Geometry Analysis for Multistatic TOA Localization. IEEE Trans. Signal Process. 2016, 64, 4180–4193. [Google Scholar] [CrossRef]
- Kitagawa, G. Monte Carlo Filter and Smoother for Non-Gaussian Nonlinear State Space Models. J. Comput. Graph. Stat. 1996, 5, 1–25. [Google Scholar]
- Boggs, P.T.; Tolle, J.W. Sequential quadratic programming for large-scale nonlinear optimization. J. Comput. Appl. Math. 2000, 124, 123–137. [Google Scholar] [CrossRef]
- Doğançay, K.; Hmam, H. Optimal angular sensor separation for AOA localization. Signal Process. 2008, 88, 1248–1260. [Google Scholar] [CrossRef]
- Chang, S.; Li, Y.; He, Y.; Hui, W. Target Localization in Underwater Acoustic Sensor Networks Using RSS Measurements. Appl. Sci. 2018, 8, 225. [Google Scholar] [CrossRef]
- Chang, S.; Li, Y.; He, Y.; Wu, Y. RSS-Based Target Localization in Underwater Acoustic Sensor Networks via Convex Relaxation. Sensors 2019, 19, 2323. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Dinis, R. 3-D Target Localization in Wireless Sensor Networks Using RSS and AoA Measurements. IEEE Trans. Veh. Technol. 2017, 66, 3197–3210. [Google Scholar] [CrossRef]
- Sun, Y.; Babu, P.; Palomar, D.P. Majorization-Minimization Algorithms in Signal Processing, Communications, and Machine Learning. IEEE Trans. Signal Process. 2017, 65, 794–816. [Google Scholar] [CrossRef]
- De Angelis, A.; De Angelis, G.; Carbone, P. Using Gaussian-Uniform Mixture Models for Robust Time-Interval Measurement. IEEE Trans. Instrum. Meas. 2015, 64, 3545–3554. [Google Scholar] [CrossRef]
- Helmberg, C.; Rendl, F.; Vanderbei, R.J.; Wolkowicz, H. An Interior-Point Method for Semidefinite Programming. SIAM J. Optim. 1996, 6, 342–361. [Google Scholar] [CrossRef]
- Zaeemzadeh, A.; Joneidi, M.; Shahrasbi, B.; Rahnavard, N. Robust Target Localization Based on Squared Range Iterative Reweighted Least Squares. In Proceedings of the 2017 IEEE 14th International Conference on Mobile Ad Hoc and Sensor Systems (MASS), Orlando, FL, USA, 22–25 October 2017; IEEE: New York, NY, USA, 2017; pp. 380–388. [Google Scholar]
- Crasta, N.; Bayat, M.; Aguiar, A.P.; Pascoal, A.M. Observability analysis of 3D AUV trimming trajectories in the presence of ocean currents using range and depth measurements. Annu. Rev. Control 2015, 40, 142–156. [Google Scholar] [CrossRef]
- Sadeghi, M.; Behnia, F.; Amiri, R. Optimal Geometry Analysis for TDOA-Based Localization Under Communication Constraints. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3096–3106. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, J.; Liu, H.; Ho, K.C.; Chen, Y.; Yang, Z. Optimal sensor placement for source tracking under synchronization offsets and sensor location errors with distance-dependent noises. Signal Process. 2022, 193, 108399. [Google Scholar] [CrossRef]
- Han, D.; Pan, N.; Li, K.-C. A Traceable and Revocable Ciphertext-Policy Attribute-based Encryption Scheme Based on Privacy Protection. IEEE Trans. Dependable Secur. Comput. 2022, 19, 316–327. [Google Scholar] [CrossRef]
- Han, D.; Zhu, Y.; Li, D.; Liang, W.; Souri, A.; Li, K.-C. A Blockchain-Based Auditable Access Control System for Private Data in Service-Centric IoT Environments. IEEE Trans. Ind. Inform. 2022, 18, 3530–3540. [Google Scholar] [CrossRef]
- Li, H.; Han, D.; Tang, M. A Privacy-Preserving Charging Scheme for Electric Vehicles Using Blockchain and Fog Computing. IEEE Syst. J. 2021, 15, 3189–3200. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, X.; Han, D.; Saeed, N.; Wu, H.; Chang, C.-C.; Han, B.; Ma, T.; Xian, J. Trajectory Optimization of Autonomous Surface Vehicles with Outliers for Underwater Target Localization. Remote Sens. 2022, 14, 4343. https://doi.org/10.3390/rs14174343
Mei X, Han D, Saeed N, Wu H, Chang C-C, Han B, Ma T, Xian J. Trajectory Optimization of Autonomous Surface Vehicles with Outliers for Underwater Target Localization. Remote Sensing. 2022; 14(17):4343. https://doi.org/10.3390/rs14174343
Chicago/Turabian StyleMei, Xiaojun, Dezhi Han, Nasir Saeed, Huafeng Wu, Chin-Chen Chang, Bin Han, Teng Ma, and Jiangfeng Xian. 2022. "Trajectory Optimization of Autonomous Surface Vehicles with Outliers for Underwater Target Localization" Remote Sensing 14, no. 17: 4343. https://doi.org/10.3390/rs14174343
APA StyleMei, X., Han, D., Saeed, N., Wu, H., Chang, C.-C., Han, B., Ma, T., & Xian, J. (2022). Trajectory Optimization of Autonomous Surface Vehicles with Outliers for Underwater Target Localization. Remote Sensing, 14(17), 4343. https://doi.org/10.3390/rs14174343









