A Beacons Selection Method under Random Interference for Indoor Positioning

Abstract

GNSS is still not well applied in indoor environments. This is an important challenge for seamless positioning and navigation. Using other sensors to replace and connect is the mainstream practice at present. No matter what technology is used, the problem of real-time optimal station selection is faced in complex indoor environments. In this paper, we first verified the impact of random interference from walkers on positioning signals in an indoor environment. Based on this phenomenon, we proposed a novel real-time dynamic Beacons selection method (RD) in the field of indoor positioning. First, we introduced a machine learning algorithm for real-time anomaly detection of received signals from different Beacons. Then the Beacon selection is completed based on the real-time anomaly detection results and RSSI. In an indoor scene, we verified the positioning accuracy of three other methods when selecting various numbers of Beacons. Then we used the best selection strategies to compare with the RD method. Experiments showed that the RD method can use the least Beacons to obtain higher accuracy and stable positioning results. This paper provides a new idea for real-time optimal selection of signal sources in a complex indoor environment.

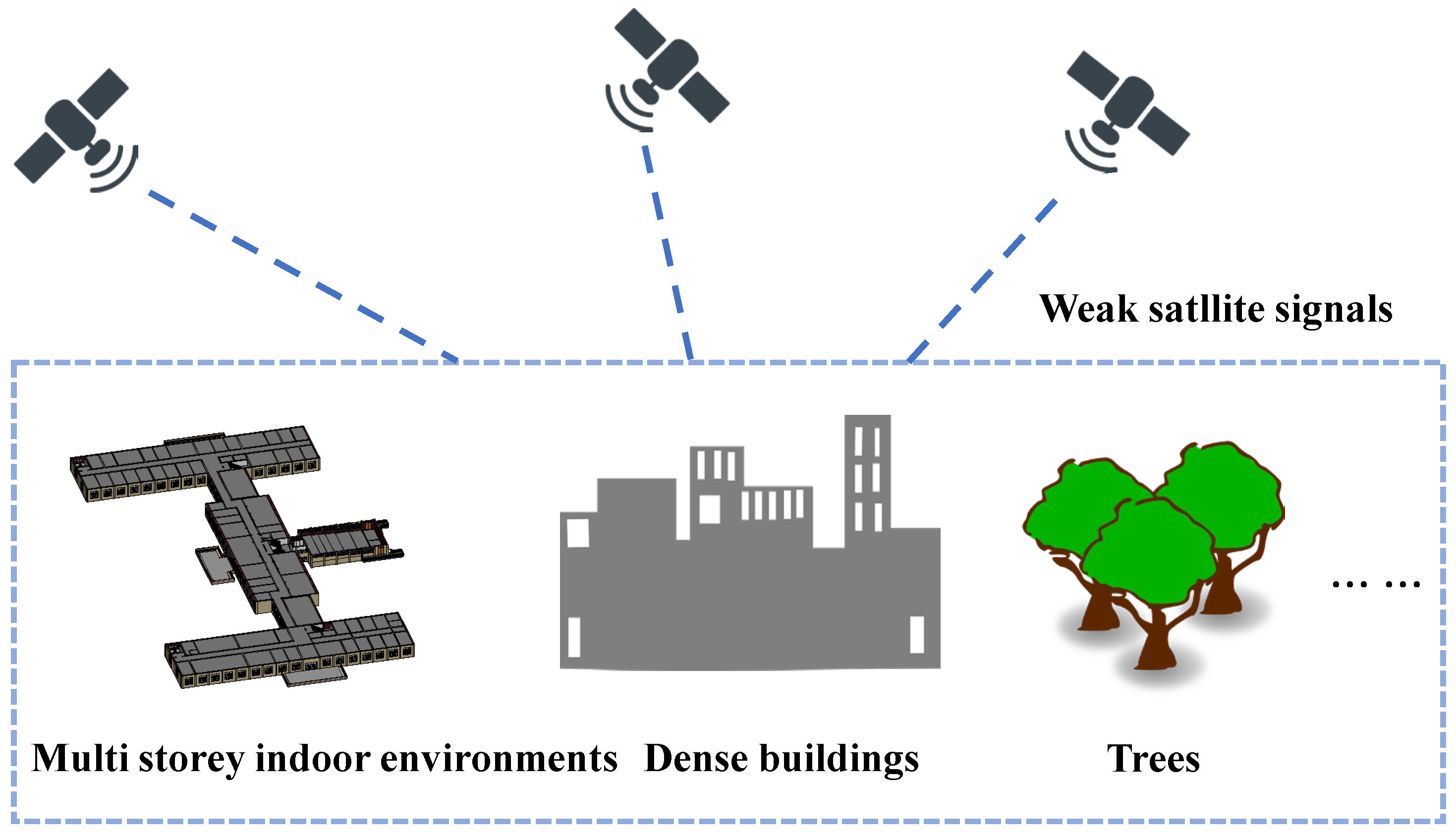
1. Introduction

In recent years, location-based services (LBS) have gradually become a research hotspot [1,2]. In outdoor scenarios, the GNSS has been able to provide accurate and stable real-time positioning and navigation services [3,4]. Delivering effective location services in indoor scenarios is challenging because satellite signals are difficult to be obtained in indoor environments [5,6]. The main challenges faced by GNSS are shown in Figure 1. Therefore, it is urgent to find a reliable and simple alternative technology in the indoor positioning and navigation stage. Now, the realization of efficient indoor positioning and navigation is inseparable from the use of sensors such as Wireless Local Area Network (WLAN) [7,8], Bluetooth [9,10], Ultra Wide Band (UWB) [11,12], etc. The basic technologies these rely on Time of Arrival (TOA) [13], Time Difference of Arrival (TDOA) [14], Angle of Arrival (AOA) [15], Received Signal Strength Indication (RSSI) [16], etc. Of these, the RSSI technology based on Bluetooth Low Energy (BLE) [9] has many advantages, such as low cost and easy implementation, and has thus attracted the attention of many scholars and enterprises.

There are two mainstream technologies for RSSI-based indoor positioning: trilateration and fingerprinting [17,18]. Regardless of the basic technology used, however, choosing an optimal station may be challenging in an indoor environment. Some research results showed that it is not that more stations used can achieve higher positioning accuracy and stability [19,20]. The current choices for real-time Beacons mainly include Max Mean RSSI (MM) [21], Loss Rate (LR) [22], Minimum Variance (MV) [23], etc.

In the fingerprinting technology for indoor positioning, the selection methods of Access Points (AP) or Beacons are often static [24,25,26]. This is because the RSSI map needs to be generated in the offline stage in advance for positioning based on the database. And then perform positioning based on KNN and other methods in the online stage [27,28]. This means that some fixed signal base stations must be selected before positioning for RSSI map generation. In recent years, in addition to the above-mentioned methods (MM, MV, LR), base station selection methods based on information theory (InfoGain) and machine learning (PCA) have also been proposed by many scholars for fingerprinting [24,29]. However, these methods can’t achieve a real-time selection of APs or Beacons. On the other hand, fingerprinting needs to make RSSI maps in advance, which increases the cost and makes it difficult to deploy applications quickly. In contrast, trilateration can achieve rapid and low-cost deployment and application. Now, there are few published works on real-time APs/Beacons selection for trilateration.

At present, the methods for selecting the best Beacons are mostly based on the absolute value of RSSI or the distribution of Beacons’ positions (whether it is fingerprinting or trilateration). The RSSI value transmitted by BLE is extremely susceptible to the influence of pedestrians and other environmental factors, and these influences often are volatile and unpredictable [30]. Simply using the RSSI value or spatial distribution to select Beacons, therefore, means that it is nearly impossible to avoid these random influences. In the literature [30], a method of weighting based on real-time abnormal ratios was proposed. However, it did not discuss Beacons selection in detail.

In this paper, we focused on the real-time Beacons selection problem when the number of base stations in the scene is large. To address the phenomenon that the RSSI of the signal is easily affected by environmental factors, an automatic anomaly detection algorithm (isolation forest [31]) is used to detect anomalies in each Beacon’s signals in the scene in real-time. The anomaly detection results and RSSI values are used to select the optimal Beacons in real-time. Finally, in order to verify the positioning accuracy of the RD method, these optimal Beacons selected are used to calculate indoor coordinates based on nonlinear least squares. The main differences between the proposed work are as follows:

(1)

the effect of pedestrian random walking on real-time indoor positioning was verified;

(2)

a fast and real-time Beacons selection method was proposed and verified.

2. Materials and Methods

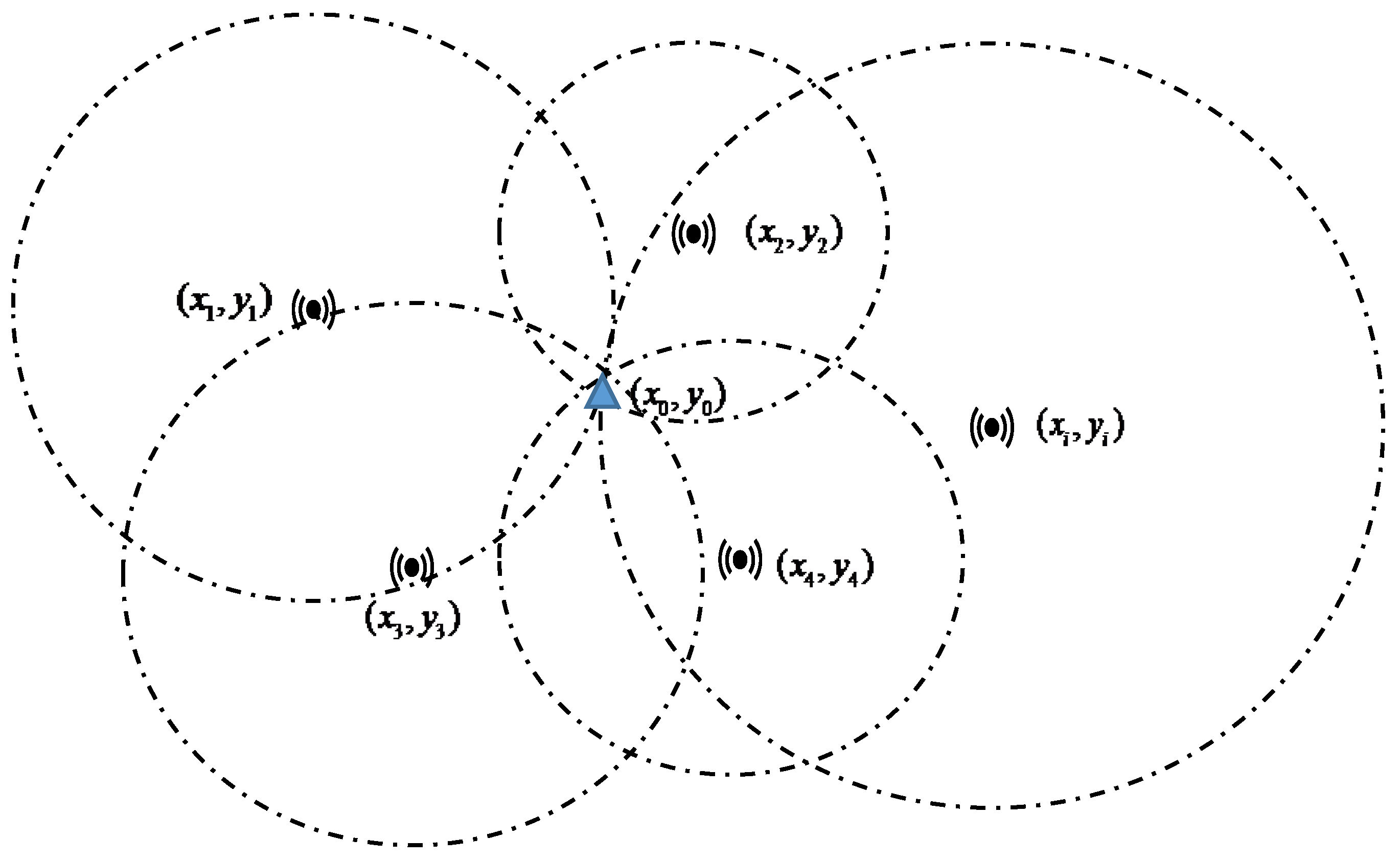
2.1. Indoor Positioning Based on BLE Technology and RSSI

Since this paper uses RSSI for indoor positioning, a proper signal path attenuation model is essential. The widely used logarithmic decay factor model is used for this, as shown in Equation (1) [32]:

$$d={10}^{\frac{A - RSSI}{10n}}$$

(1)

where, the parameters $A$ and $n$ are variables that need to be fitted and calculated according to the current indoor environment, and $A$ is the RSSI at 1 m from the base station, $n$ is the signal attenuation parameter in the current indoor scene, $d$ is the distance from the base station.

The distance between an unknown point and the BLE base station based on RSSI can be used to calculate indoor coordinates. In theory, only three BLE stations ($(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$) are required to solve the spatial plane coordinates of unknown points, but, in practice, this makes it difficult to obtain the most accurate coordinates. In actual situations, RSSI signals from several base stations are often required to participate in the final coordinate calculation, so as to improve the accuracy and stability of indoor positioning. Equation (2) is the calculation to solve the unknown point, and this is further represented in the schematic diagram shown in Figure 2:

$$\left\{\begin{array}{l}(x_0-x_1{)}^2+(y_0-y_1{)}^2=d_1^2\\ (x_0-x_2{)}^2+(y_0-y_2{)}^2=d_2^2\\ ⋮\\ (x_0-x_i{)}^2+(y_0-y_i{)}^2=d_i^2\end{array}\right.$$

(2)

This paper used the nonlinear least squares Gauss-Newton (GN) [33] algorithm for the coordinate calculation (Equation (2)), the iterative solution of which is shown in Equation (3):

$$F^{s+1}=F^s+\mathsf{\Delta }$$

(3)

where, $F$ is the coordinate $[x,y]$ to be solved, $s$ is the number of iterations, and $\mathsf{\Delta }$ is as in Equation (4):

$$\mathsf{\Delta }=-{(J^{T}J)}^{-1}{J}^T\epsilon$$

(4)

where, $J$ is as in Equation (5), $\epsilon$ is the residual vector calculated previously, as in Equation (6):

$$J=\left. [\begin{array}{l}\frac{\partial f_1}{\partial x},\frac{\partial f_1}{\partial y}\\ \frac{\partial f_2}{\partial x},\frac{\partial f_2}{\partial y}\\ ⋮\ddots ⋮\\ \frac{\partial f_i}{\partial x},\frac{\partial f_i}{\partial y}\end{array}\right]$$

(5)

$${\epsilon }_i=d_i-f_i(x_0,y_0)$$

(6)

The $f$ in Equations (5) and (6) is as Equation (7):

$$f_i(x_0,y_0)=\sqrt{{(x_0-x_i)}^2+{(y_0-y_i)}^2}$$

(7)

We then carried out iterative calculations according to Equation (3), and the final optimal coordinates are calculated as in Equation (8):

$$(x_0,y_0)=\arg \min (\left|\right|{\epsilon }^T\epsilon \left|\right|)$$

(8)

As shown in Equation (2), when using the GN algorithm, a selection of base stations must be used in the iterative solution. The choice of base stations affects the exact coordinates that are calculated as a result. Furthermore, as Xue et al. [19] and Zhang et al. [20] have shown, when undertaking indoor positioning based on RSSI, using more BLE base stations does not deliver greater positioning accuracy. This means that it is very important to choose suitable Beacons to participate in the coordinate calculation.

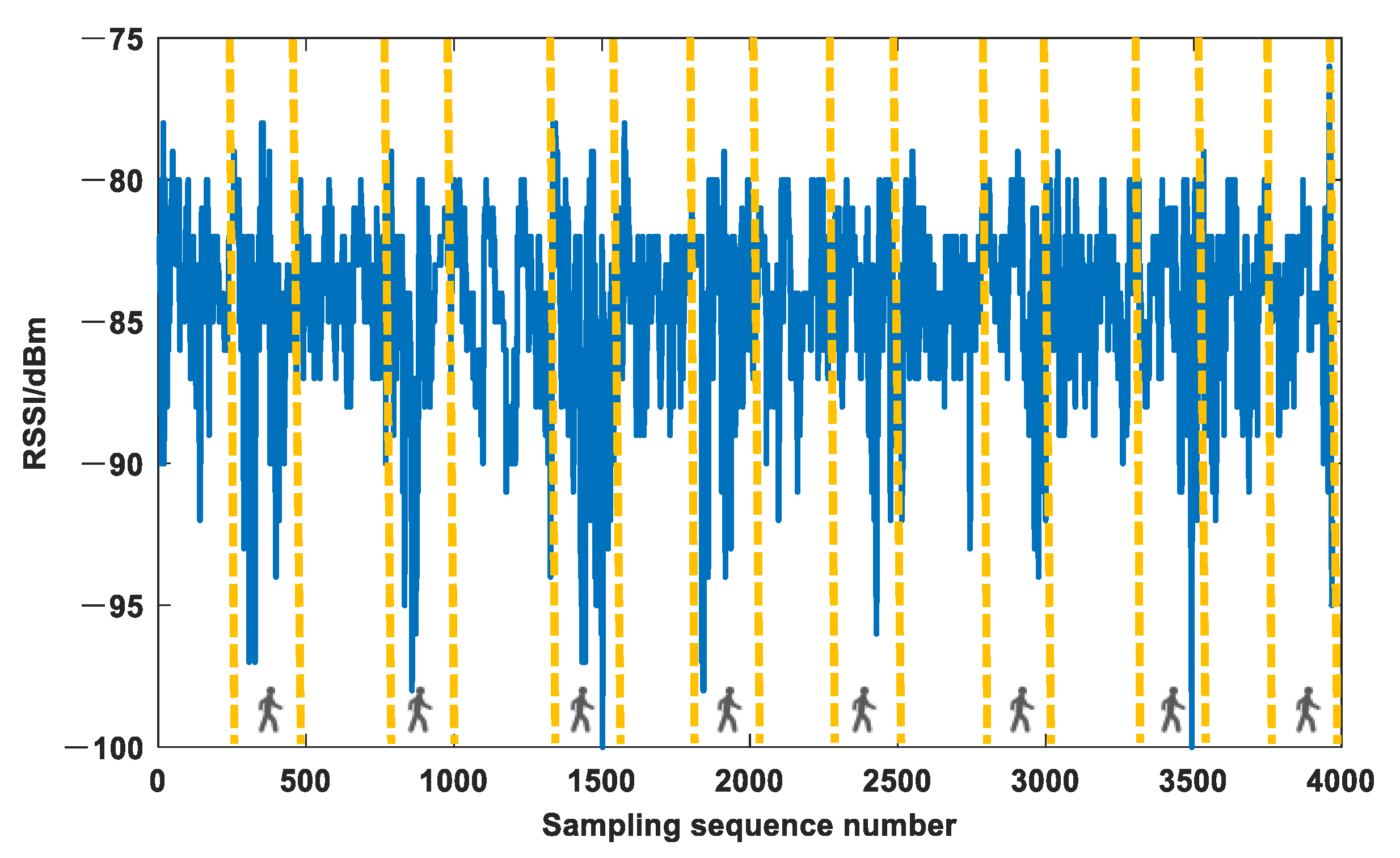
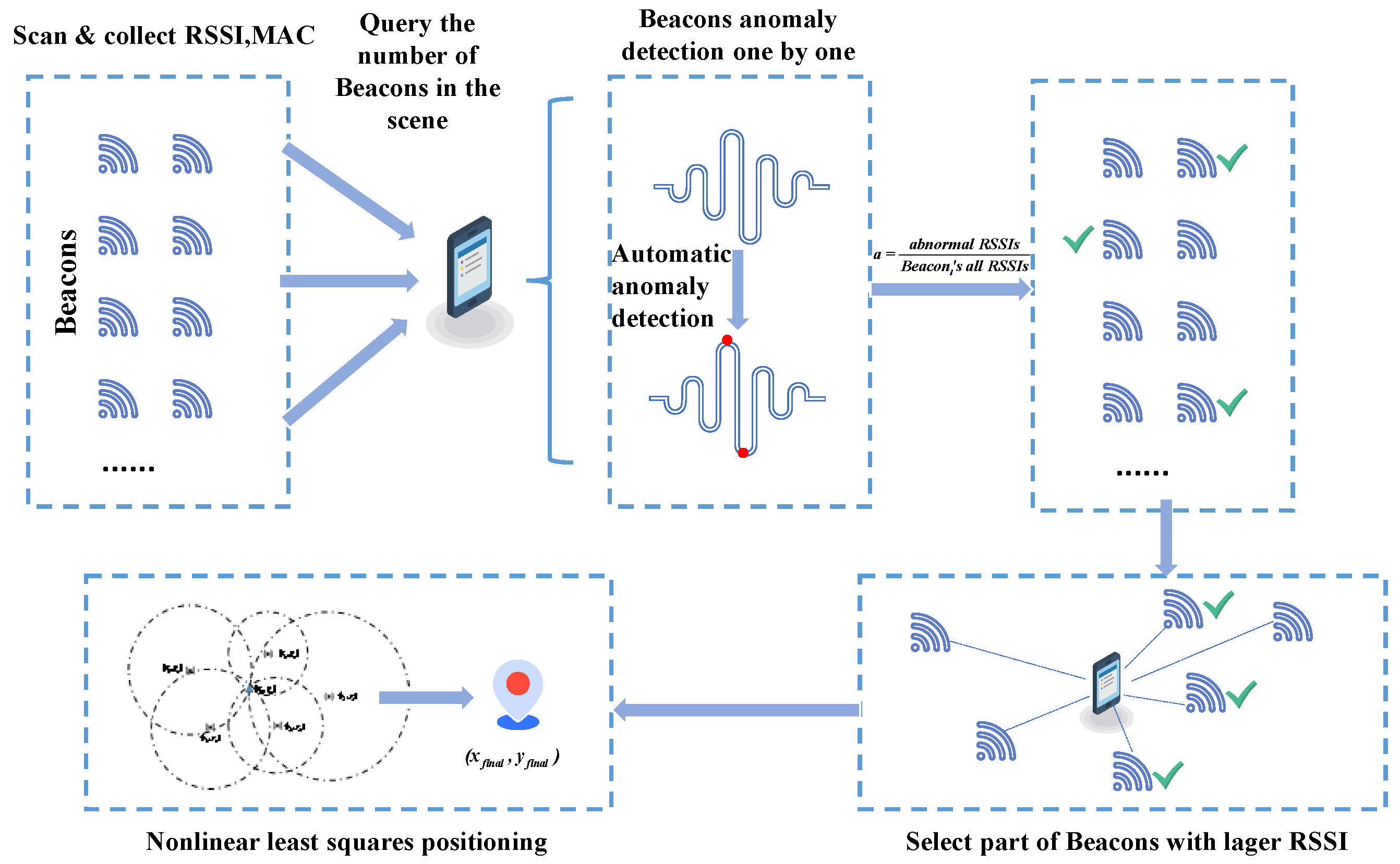
2.2. Signal Real-Time Anomaly Detection and Beacons Selection

As discussed in the Introduction section, however, most of these Beacons selection strategies do not take into account the real-time fluctuations of the base station for example, due to the influence of pedestrians. In the experimental scenario in this paper, the influence of a pedestrian on the RSSI is shown in Figure 3 (a real experiment in the scene). Thus, it is unreasonable to select a Beacon based solely on the absolute value of the RSSI or the position of the BLE base station.

As shown in Figure 3, this paper showed through experiments that the influence of pedestrians will have a great impact on the RSSI transmitted by the BLE base station. Specifically, we collected RSSI signals at a distance of 3m from a Beacon station. Taking 60 s as the time unit, there is no interference between the mobile phone and the Beacon in about 40 s, and pedestrians are arranged to walk randomly between the mobile phone and the Beacon in about 20 s. Experiments showed that the random interference of pedestrians can have a strong impact on RSSI signals. Compared with the case without interference, the attenuation of the RSSI signals can exceed 20%. In turn, this will affect the subsequent calculation of indoor coordinates, causing fluctuations in positioning accuracy. This paper addressed the shortcomings of relying only on the value of RSSI for Beacons selection by detecting anomalies in the RSSI of Beacons and then using these anomaly results to inform the selection of the optimum Beacons. We proposed the selection method that considered the real-time status of the RSSI for the situation where there are many Beacons in the scene. The RD method proposed in this paper mainly includes the following steps: (a) calculate the number of all Beacons in the scene by the Media Access Control Address (MAC); (b) implement real-time anomaly detection for each Beacon based on a machine learning method; (c) select some of the Beacons with lower real-time abnormal ratios; (d) on the basis of the third step, selecting some of the Beacons with the larger RSSI as the best optimal strategy. The detailed flow chart is shown in Figure 4.

As shown in Figure 4, we need to choose a suitable and convenient real-time RSSI anomaly detection method. Thus, an unsupervised machine learning algorithm is used to detect abnormality in RSSI fluctuations over a period of time. The commonly used and effective methods for signal fluctuation anomaly detection include isolation forest, Support Vector Machine (SVM), etc. In this paper, we chose the one-dimensional isolation forest algorithm for RSSI real-time fluctuation detection. The main steps of the isolation forest used in this paper include: (a) generating 100 isolated binary trees to form an isolation forest; (b) then, the RSSIs are segmented using the isolation trees until each RSSI is in a separate space; (c) calculate the anomaly score for each RSSI using Equation (9) ($A(h(x))$ is the average depth of an RSSI signal in 100 isolated trees, and $C(\psi )$ is the average path length of isolated trees generated); (d) obtain abnormal signals (the closer $Q$ is to 1, the greater the probability the signal is an abnormal value, the threshold set in this paper is 0.7). As Liu et al. [31] have shown in their detailed account of the specific principles and implementation process of isolation forests, this algorithm can ensure a good anomaly detection result when the data is limited.

$$Q=2^{-\frac{A(h(x))}{C(\psi )}}$$

(9)

Given the scenario of RSSIs received from different Beacons stations at a certain point, this paper implemented the isolation forest algorithm to conduct real-time outlier detection in turn. Firstly, generate a hyper-plane segmented isolation forest of the one-dimensional space where each group of RSSI is located. Secondly, to get the real-time abnormal RSSI of each Beacon, we used the generated isolation forest hyper-plane to perform anomaly detection on each Beacon and then judged abnormal points based on ensemble theory. Thirdly, the signal anomaly rate $a$ is calculated in the current time period. The calculation method of $a$ can be expressed as Equation (10)

$$a=\frac{abnormalRSSIs}{Beaco{n}_i’sallRSSIs}$$

(10)

The non-abnormal rate is calculated as $b=1-a$ (that is, the non-volatile RSSI ratio). Finally, the Beacons are sorted for selection based on $b$. The pseudo-code for Beacons selection is given in Algorithm 1.

Algorithm 1 Beacons selection based on isolation forest

Require: RSSI signals and MACs by Beacons.

Ensure: Beacons are real coordinates. 1: Match and group all RSSIs according to MACs:  $R=\{RSS{I}_{Beacon1},RSS{I}_{Beacon2},\dots ,RSS{I}_{Beaconi}\}$; 2: Set to generate isolation forest $T_i$ 3: Use $T_i$ to perform anomaly detection on each grouped $R$ in turn; 4: Calculate Beacon’s non-abnormal rate $b$; 5: Beacons are sorted by $b$ and push Beacons’ MAC into $F$; 6: Return: $F$ and $R$.

We first selected part of the Beacons with smaller abnormal fluctuations (60%, 50%, 40%, etc.). Then, we selected part of the Beacons with a larger average RSSI in the first selection result (60%, 50%, 40%, etc.). Each spatial distance is calculated according to Equation (1). Then we take $1/RSS{I}^2$ as the weighted matrix and the coordinates are calculated in the experimental scene by using Equation (8). The experiment proves the feasibility and effectiveness of Beacons selection based on the RD method. The results will be explained in detail in the experimental section.

In order to prove the phenomenon (that indoor positioning accuracy is affected by real-time pedestrian movement) and the effectiveness, rationality and superiority of the RD method, an experiment was devised to compare the results from several other methods. We set up three other comparison methods as follows:

(A)

Max Mean RSSI (MM): Beacons selection based on the mean maximum RSSI over a period of time.

(B)

Loss Rate (LR): The basic idea of the LR method is that we should choose the Beacons with the lowest RSSI loss rate within a period of time. It can be calculated by Beacon transmit frequency and acquisition time. It can be expressed as Equation (11):

$$L{R}_{B{\mathrm{eacons}}_i}=(s-s_i)/s$$

(11)

where, $Beaco{n}_i$ represents the $i$th Beacon, $s$ represents the maximum number of RSSIs that can be received during this period, and $s_i$ represents the actual number of RSSIs received by this Beacon.

(C)

Minimum Variance (MV): Use the collected RSSI variance as the basis for selecting Beacons.

In the experimental stage of this paper, a comparison was set up between the use of MM, LR, MV and our RD method. Because the three comparison methods are difficult to directly determine the optimal Beacons number selection strategy. Therefore, we first calculated the positioning accuracy of 42 experimental points when selecting 3~18 Beacons (MM, LR, MV). Then choose the optimal number of Beacons among them to compare with the RD method in this paper.

3. Experiment and Discussion

The experiment was conducted in an indoor scene with an area of about 8 × 20 m, and in which we deployed 18 BLE base stations. We then used a mobile phone (HUAWEI P20, Shenzhen, China) along the routes shown in Figure 4 to collect the RSSIs data at 42 fixed points (their coordinates gotten by the traditional measurement method (the errors are in millimeters)). As shown in Figure 5 and Figure 6, we engaged researchers to walk completely randomly and irregularly across the scene, allowing us to simulate the presence of pedestrians and their influence on the collected RSSI.

As shown in Equation (1), in order to calculate the collected RSSI value as a spatial distance, it is necessary to obtain the parameters $A$ and $n$. Accordingly, the RSSI values were collected between 0.6 m and 9.6 m from the base stations at 0.6 m intervals. From this, we found that $A=-66.25 dBm$ and $n=2.877$. The RSSI attenuation curve is shown in Figure 7.

After completing the above preparatory work, we collected the RSSIs of 42 fixed positions in the scene and calculated the coordinates of each position using Equation (8).

4. Results

Equation (12) (RMSE) and Equation (13) (ME) are used to calculate the overall accuracy of the 42 positioning points.

$$RMSE=\sqrt{\frac{{\displaystyle \sum _{i=1}^M[{(x_i-x_i^{*})}^2+{(y_i-y_i^{*})}^2]}}{M}}$$

(12)

$$ME=\frac{{\displaystyle \sum _{i=1}^M\sqrt{{(x_i-x_i^{*})}^2+{(y_i-y_i^{*})}^2}}}{M}$$

(13)

where, $(x_i,y_i)$ is the true value of the coordinate, $(x_i^{*},y_i^{*})$ is the positioning results, and $M$ is the number of measurement points (42). We first calculated the positioning accuracy when selecting 3~18 Beacons by three comparison methods (Figure 8,

Table 1. Comparison of method positioning accuracy.

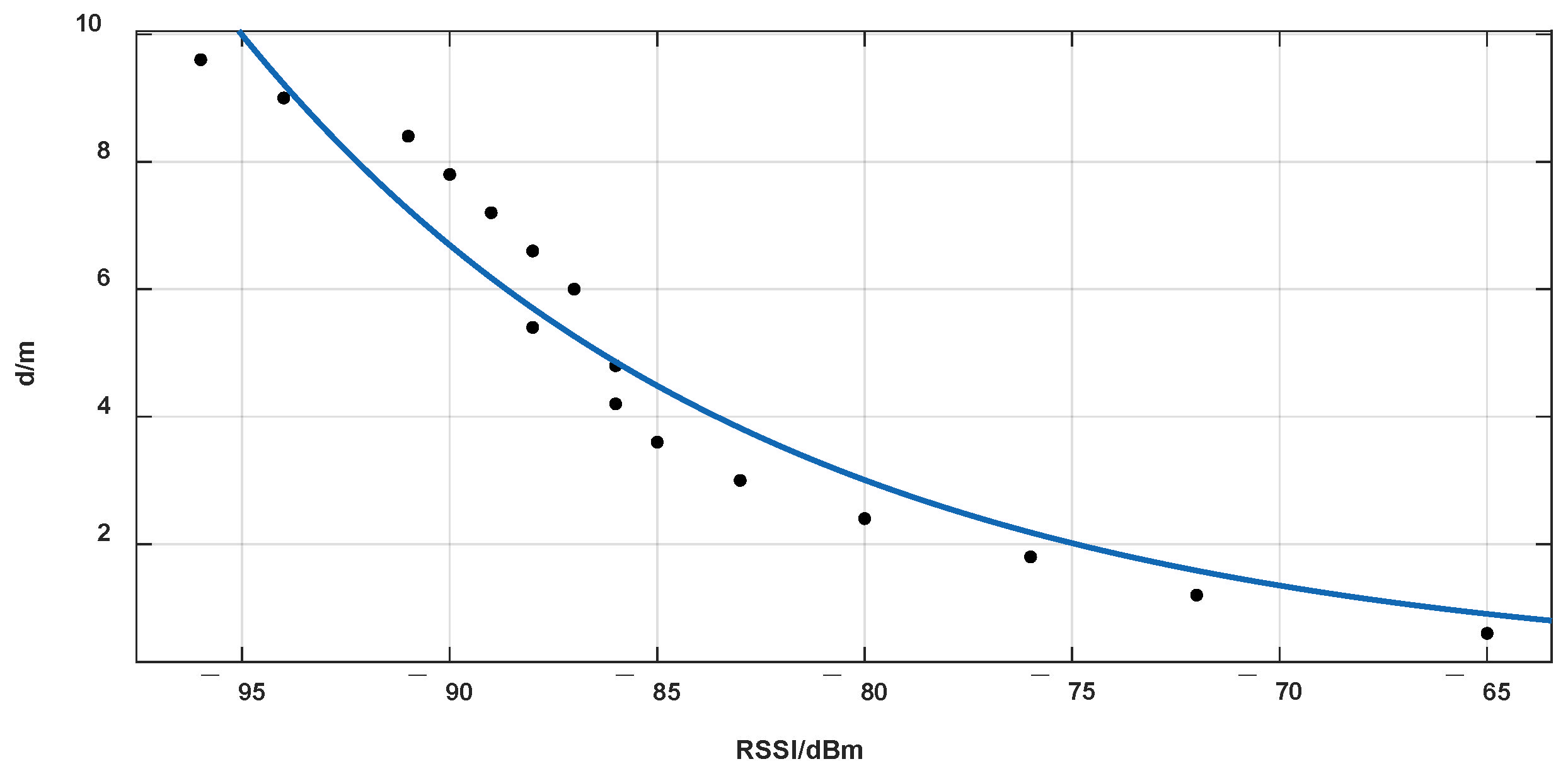
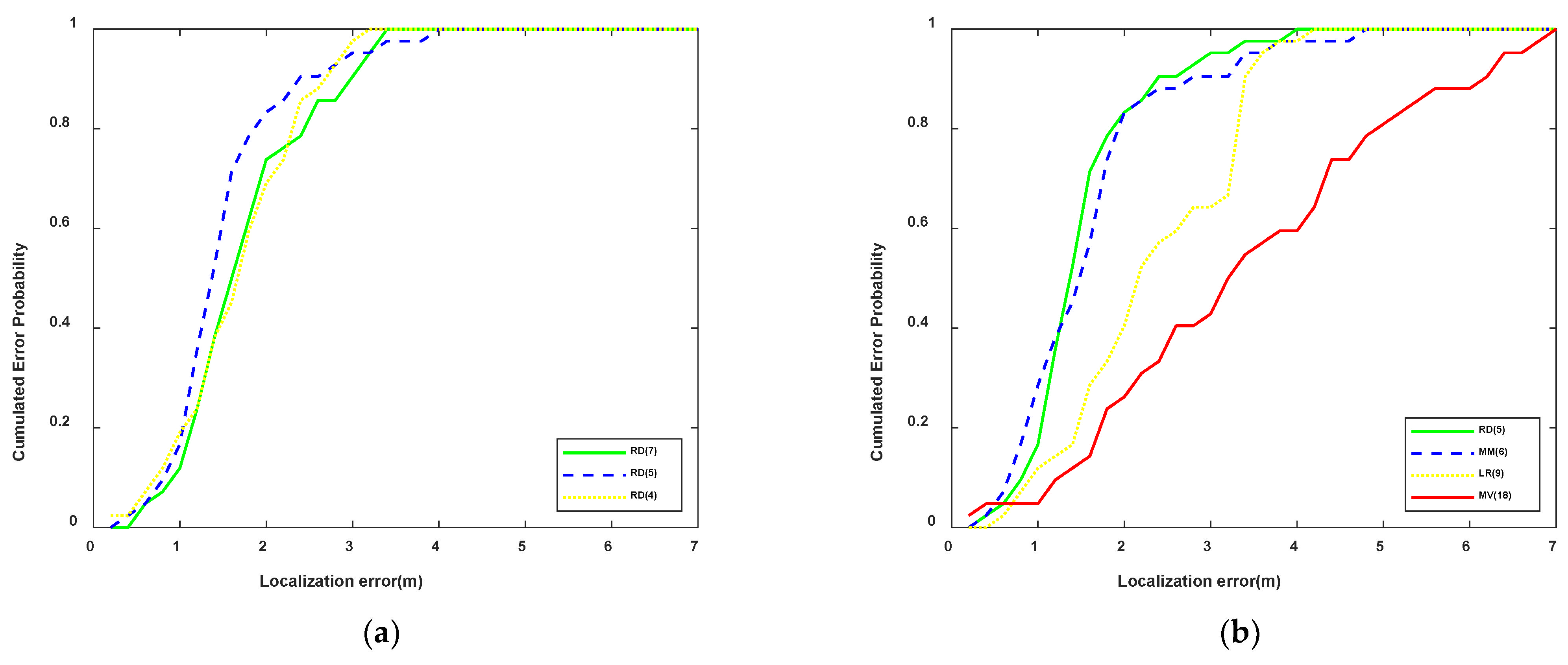
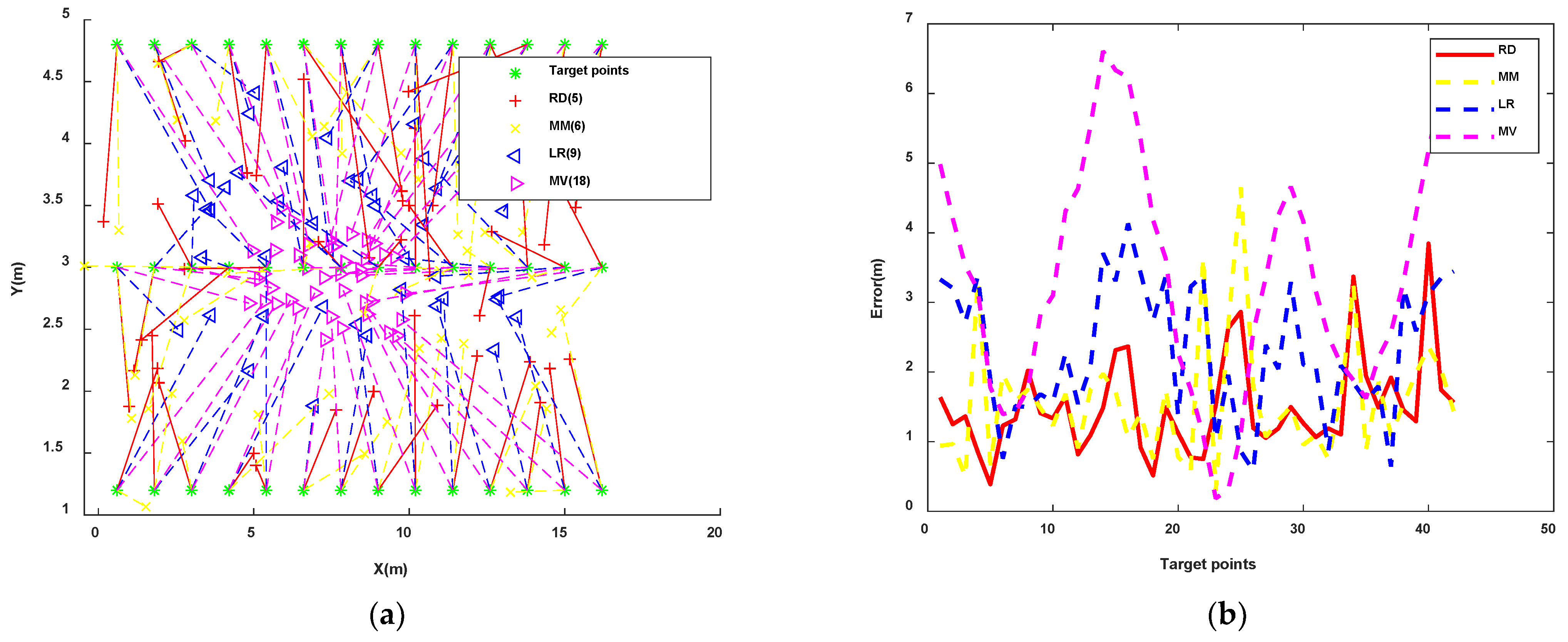
Errors (m)	3Beacons	4Beacons	5Beacons	6Beacons	7Beacons	8Beacons	9Beacons	10Beacons
RMSE (MM)	2.07	2.08	1.82	1.81	1.85	1.90	1.90	1.98
RMSE (LR)	2.99	3.27	2.80	2.61	2.55	2.52	2.50	2.53
RMSE (MV)	8.70	7.78	7.89	6.82	6.59	6.26	6.00	5.76
ME (MM)	1.70	1.74	1.51	1.59	1.61	1.67	1.72	1.81
ME (LR)	2.71	2.97	2.51	2.37	2.34	2.32	2.31	2.36
ME (MV)	7.37	6.79	6.77	5.99	5.80	5.50	5.27	5.03
Errors (m)	11Beacons	12Beacons	13Beacons	14Beacons	15Beacons	16Beacons	17Beacons	18Beacons
RMSE (MM)	2.25	2.47	2.72	2.96	3.13	3.35	3.59	3.81
RMSE (LR)	2.57	2.66	2.82	2.92	3.12	3.35	3.59	3.81
RMSE (MV)	5.32	5.14	4.95	4.70	4.51	4.35	4.07	3.81
ME (MM)	2.07	2.26	2.46	2.67	2.78	2.96	3.18	3.39
ME (LR)	2.41	2.47	2.60	2.65	2.77	2.99	3.19	3.39
ME (MV)	4.68	4.50	4.29	4.10	3.93	3.81	3.58	3.39

).

For the RD method, we set up three different selection ratios for verification. The optimal selection strategies of the above three comparison methods and the results of the RD method are shown in

Table 2. Comparison methods positioning accuracy.

Errors (m)	RMSE	ME
MM (Beacons = 6)	1.81	1.59
LR (Beacons = 9)	2.50	2.31
MV (Beacons = 18)	3.81	3.39
RD (Beacons = 7 (60%, 60%))	1.88	1.73
RD (Beacons = 5 (50%, 50%))	1.66	1.51
RD (Beacons = 4 (40%, 40%))	1.82	1.68

.

From Table 1 and Table 2, it can be seen that the RD method delivers the most accurate positioning when 5 Beacons are selected (an RMSE of 1.66 m and a ME of 1.51 m). Meanwhile, the MM, LR and MV methods deliver their most accurate positioning when 6, 9 and 18 Beacons are selected. The other two ratio choices (Beacons = 4, 7) verified in this paper are similar to the optimal choice of MM. Thus, using the method proposed in this paper for Beacons selection and positioning can reduce RMSE by 8.3%, 33.6% and 56.4% compared with MM, LR and MV. We also calculated the cumulative distribution of errors (Figure 9) and error frequency (Figure 10) for the RD method, the best case with the MM method (Beacons = 6), the LR method (Beacons = 9) and the MV method (Beacons = 18). The results showed that the RD method achieved a better positioning accuracy with a smaller number of Beacons. Using the RD method showed a more significant improvement compared with the other three methods, especially in reducing the occurrence of fluctuation errors (Figure 9). Specifically, 95.24% of the 42 points were located with an error of less than 3 m (Beacons = 5).

In order to show the error of each target point more clearly, we draw the plane distance graph between the results of the four methods and the target points, as well as the RMSE of each point (Figure 11). It is not difficult to see that the method RD in this paper shows more accurate results in both in-plane distribution and RMSE. Especially when the Beacon’s performance selected by other methods fluctuates violently, it still maintains high robustness.

The main contributions of this paper are as follows: (1) We verified that the choice of Beacons in a complex indoor environment will affect the positioning accuracy; (2) using more Beacons does not straightforwardly deliver more accurate indoor positioning; (3) relying solely on the absolute RSSI cannot avoid the influence of pedestrians on the signals; (4) we proposed a Beacons selection strategy that takes into account the real-time abnormal states of the stations, and verified its superiority and reliability through experiments.

5. Conclusions

In order to solve the problem of fast selection of positioning signals in a complex indoor environment, we proposed a novel method to dynamically select Beacons based on real-time signal anomaly detection results and RSSI (RD). The GN nonlinear least squares algorithm was then used for indoor positioning. Experiments showed that the method proposed in this paper can effectively overcome the interference of pedestrians on signals, and select the best Beacons for indoor positioning in real-time. Compared with MM, LR, and MV methods, the RD method can greatly improve positioning accuracy and stability. Further, the number of Beacons required can be greatly decreased.