Preliminary Assessment and Verification of the Langley Plots Calibration of the Sun Photometer at Mt Foyeding Observatory, Beijing
Abstract
1. Introduction
2. Instruments, Sites and Methods
2.1. Instrument
2.2. Site Information
2.3. Calibration Method
2.4. Data Processing
3. Results and Discussion
3.1. Aerosol Climatology
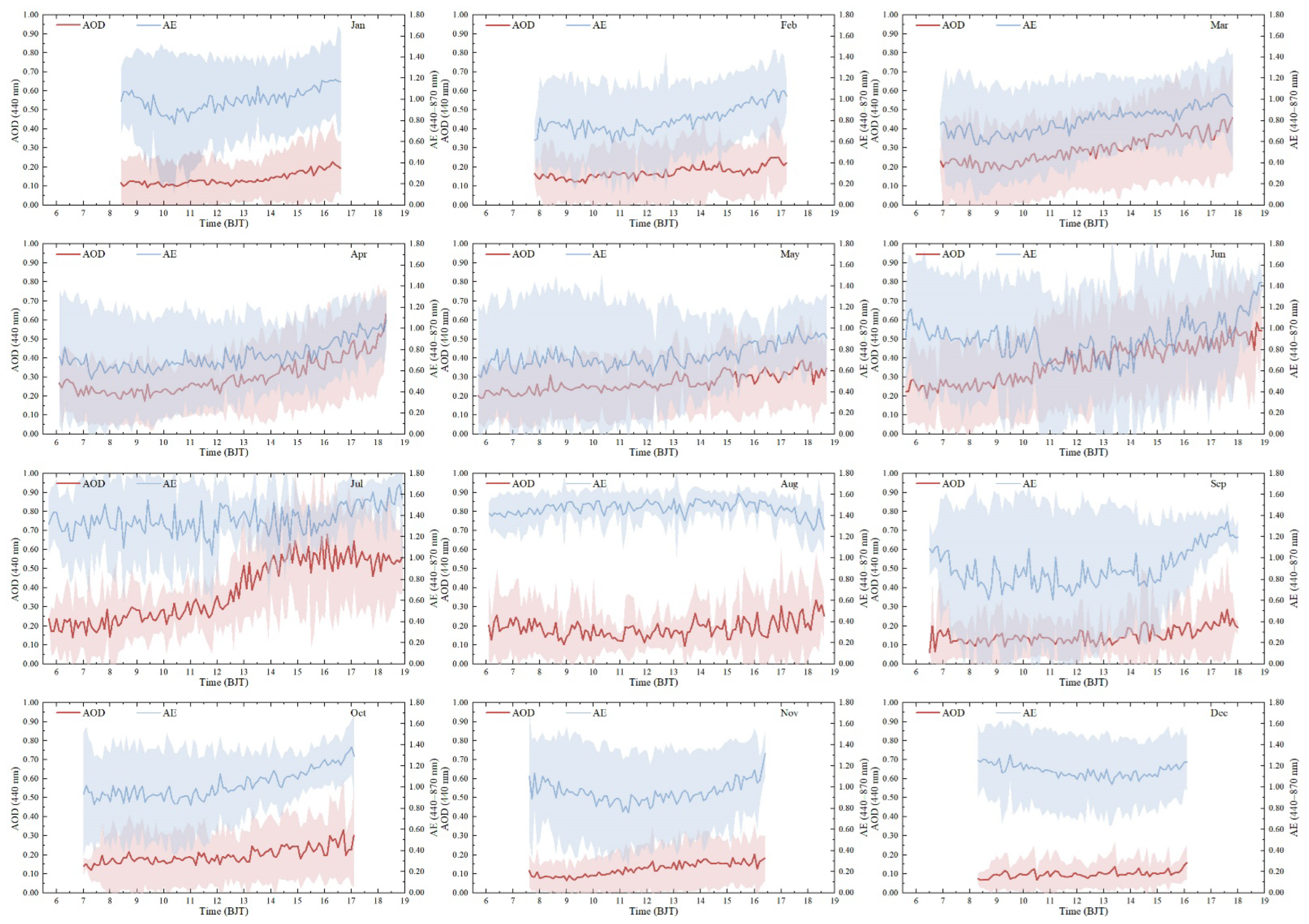
3.2. Meteorological Conditions
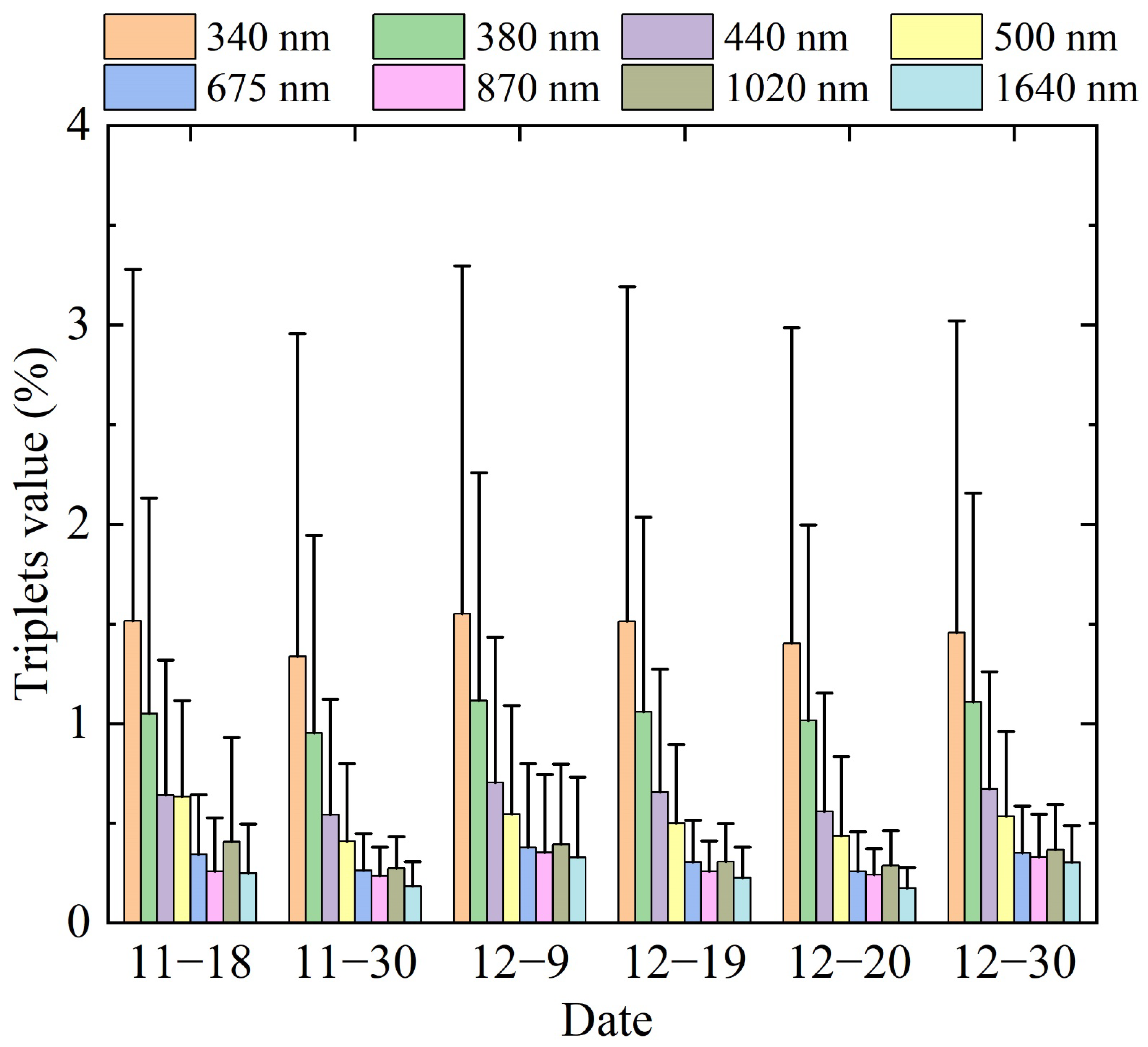
3.3. Evaluation of the Raw Digital Count
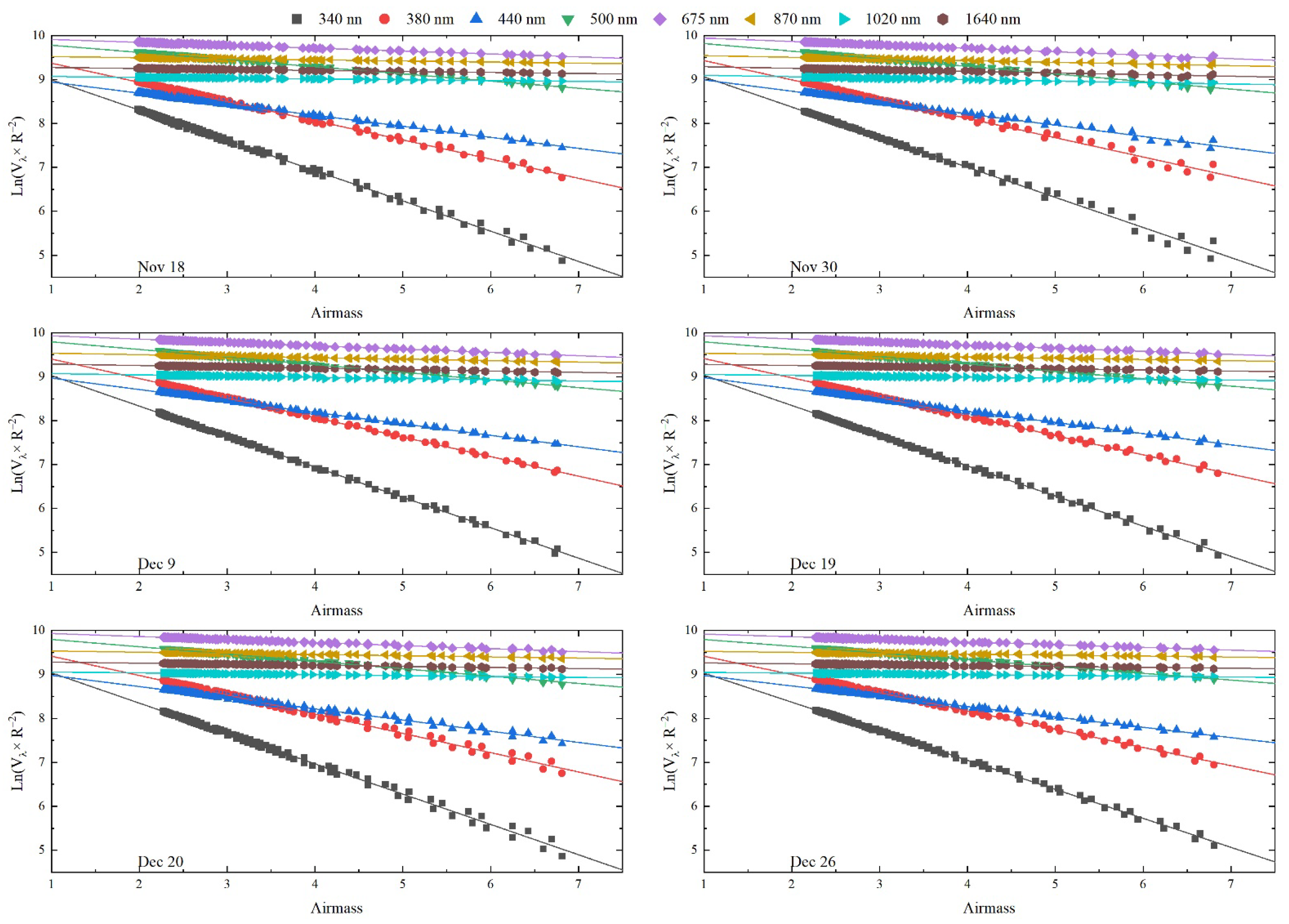
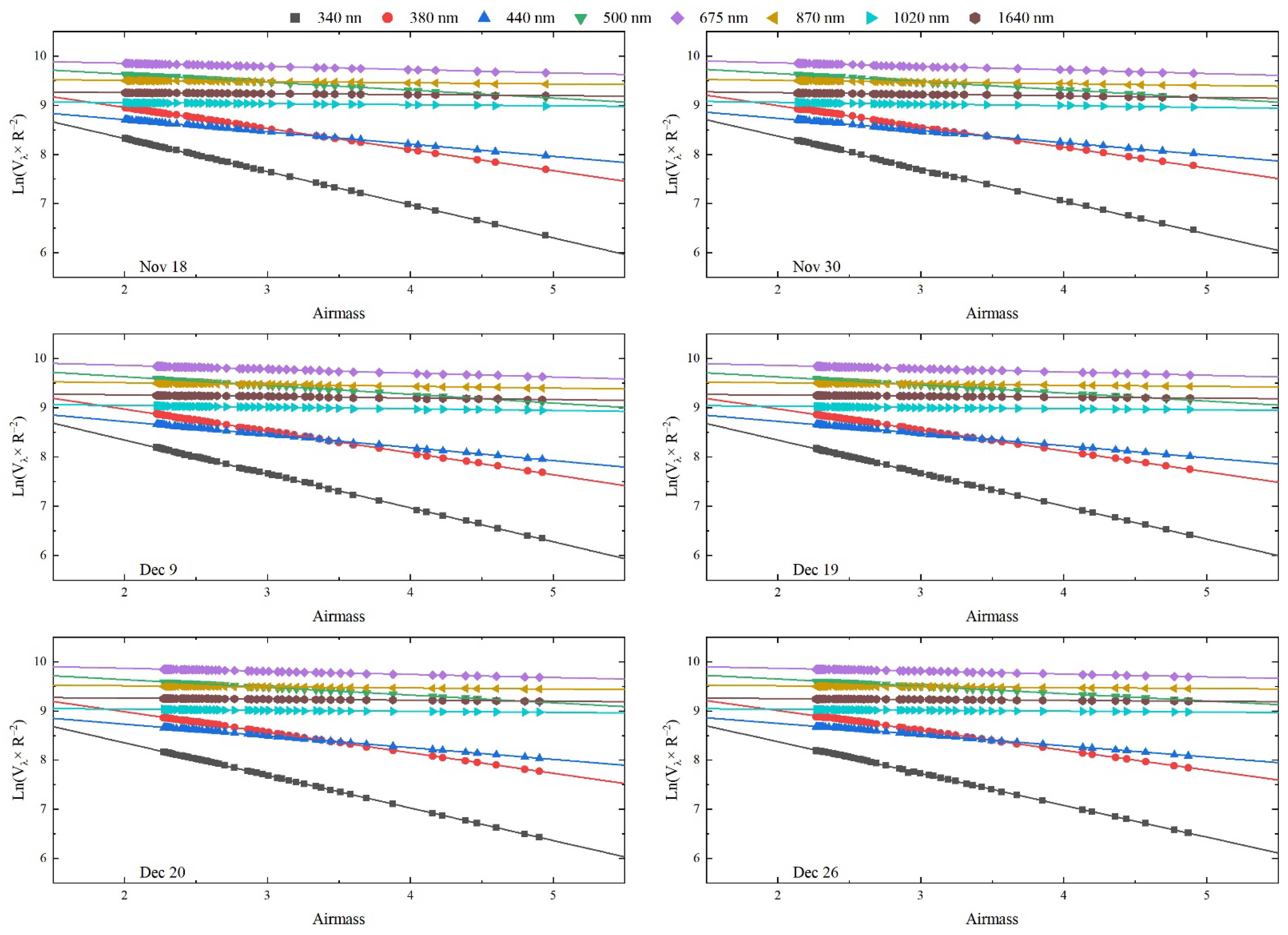
3.4. Langley Plot Calibration
3.5. Assessment of Calibration Results
4. Conclusions
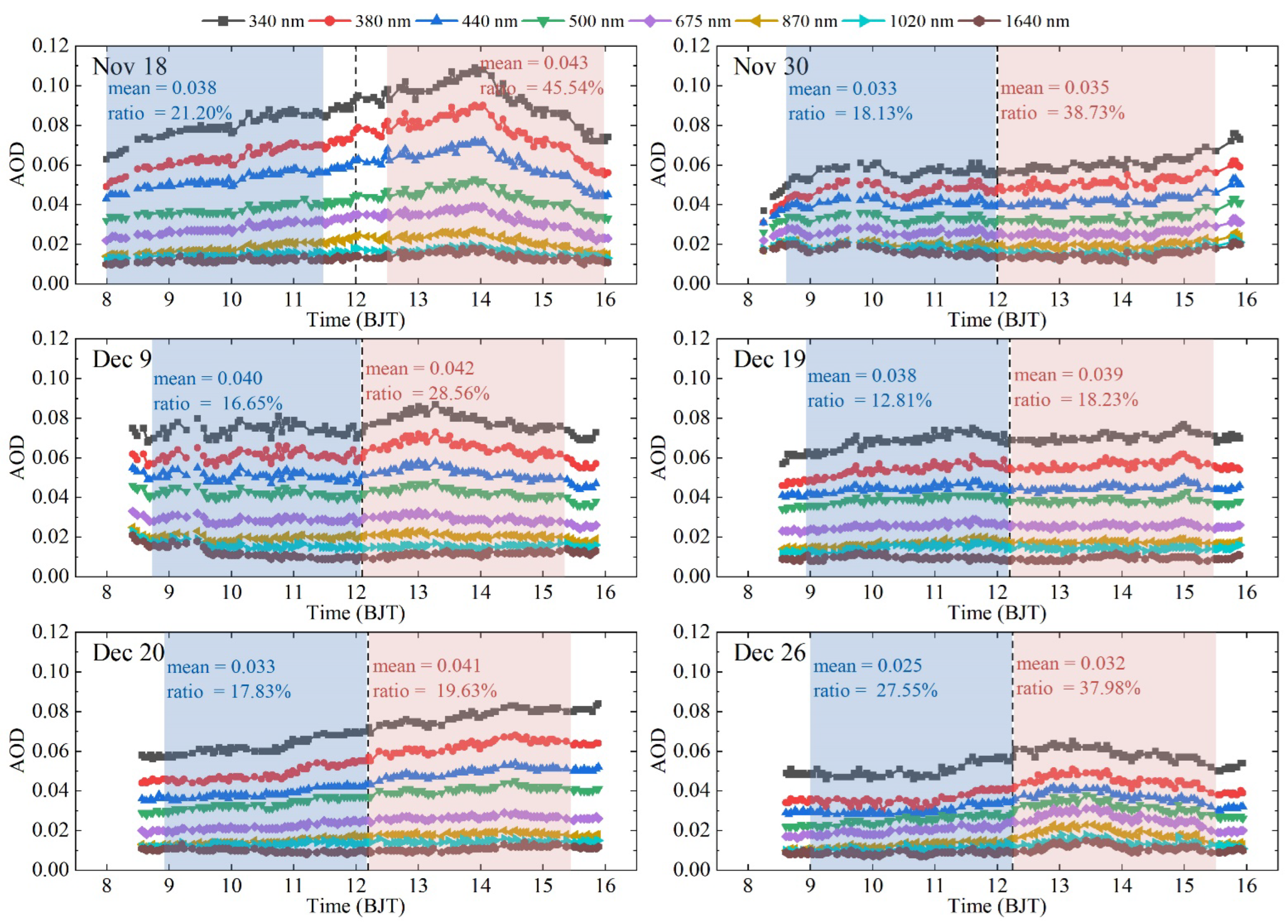
- The winter season may be more suitable for the application of the Langley calibration method at the MFYD Observatory, especially in the morning. Based on long-term observations, the monthly mean AOD440 nm over the MFYD Observatory peaked in spring (March–May) at ~0.26 ± 0.21, followed by ~0.25 ± 0.23 in summer (June–August), ~0.15 ± 0.16 in autumn (September–November) and ~0.13 ± 0.11 in winter (December–February). In addition, the 50th percentile of the AOD in winter, was <0.10, demonstrating the very clean atmospheric conditions over the MFYD Observatory. Although the atmospheric conditions were influenced by vertical diffusion caused by the deepened PBLH (as revealed by the diurnal variation of the AOD), relatively clean and stable atmospheric conditions were present in the morning, characterized by a smaller average AOD (~0.09–0.14) and lower ratio (~36.97–63.38%) compared with the values in the afternoon and over the whole day.
- The six selected study days had stable atmospheric conditions and the final values from the morning observations were consistent with the reference . The daily average triplets were all <2% at all wavelengths; when the air mass was 2–5 in the morning (about 09:00–12:00 BJT), the triplets for the instantaneous observations were mostly <1% (with some outliers in the 340 and 380 nm bands). The RSS for the final at all wavelengths were <0.0002 and the RSD was <0.2%, indicating the precise results of the linear regression in these Langley plots. The results showed a great improvement was found in the linear regression at morning relative to the statistics obtained over the whole day, when the coefficient of determination and residual standard deviation were promoted by 0.22–2.90% and ~2.76–23.32, respectively. The final value was derived from 31 days of observation and the deviations from the reference of the were about −1.69, −1.29, −0.81, −0.42, −0.34, −0.22, −0.63 and −0.36% at 340, 380, 440, 500, 675, 870, 1020 and 1640 nm, respectively.
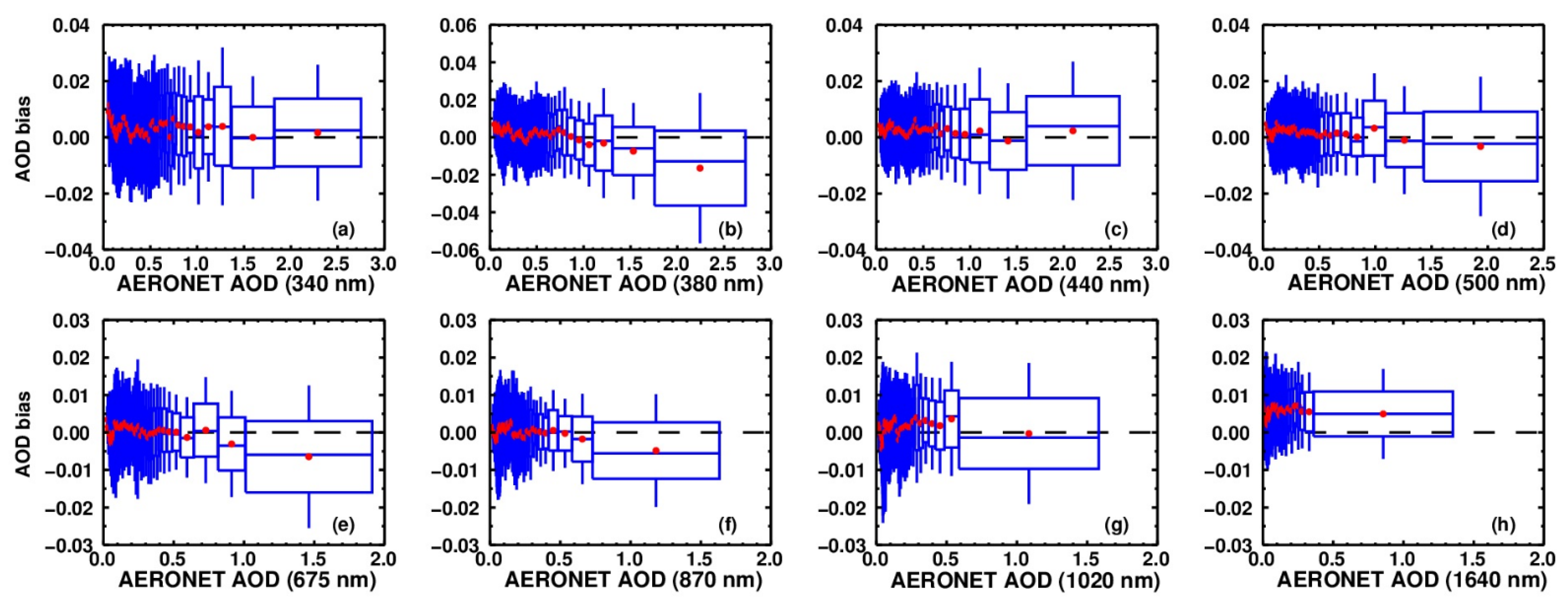
- The AOD validation indicated the high accuracy of the final value compared with the reference AOD from AERONET. The regression analysis showed a perfect AOD performance, with 100% of the retrievals lying within the expected error (0.05 ± 10%) from 380 to 1640 nm and 99.99% for the 340 nm band. Good AOD agreement (R > 0.998) and RSD values ranging from ~0.006 to 0.011 were observed, with the RMB varying from 0.999 to 1.066. The AOD bias analysis showed an overall deviation for the visible and near-infrared wavelengths of −0.02 to 0.02, and −0.02 to 0.03 and −0.05 to 0.03 for 340 and 380 nm, respectively. The mean biases for the ultraviolet bands were concentrated within ±0.02 and ±0.01 for the other bands.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Charlson, R.J.; Schwartz, S.E.; Hales, J.M.; Cess, R.D.; Coakley, J.A., Jr.; Hansen, J.E.; Hofmann, D.J. Climate forcing by anthropogenic aerosols. Science 1992, 255, 423–430. [Google Scholar] [CrossRef] [PubMed]
- Letu, H.; Shi, J.; Li, M.; Wang, T.; Shang, H.; Lei, Y.; Ji, D.; Wen, J.; Yang, K.; Chen, L. A review of the estimation of downward surface shortwave radiation based on satellite data: Methods, progress and problems. Sci. China Earth Sci. 2020, 63, 774–789. [Google Scholar] [CrossRef]
- Zhao, H.; Gui, K.; Ma, Y.; Wang, Y.; Wang, Y.; Wang, H.; Zheng, Y.; Li, L.; Zhang, L.; Che, H.; et al. Climatological variations in aerosol optical depth and aerosol type identification in Liaoning of Northeast China based on MODIS data from 2002 to 2019. Sci. Total Environ. 2021, 781, 146810. [Google Scholar] [CrossRef]
- Li, L.; Che, H.; Derimian, Y.; Dubovik, O.; Luan, Q.; Li, Q.; Huang, X.; Zhao, H.; Gui, K.; Zheng, Y.; et al. Climatology of fine and coarse mode aerosol optical thickness over East and South Asia derived from POLDER/PARASOL satellite. J. Geophys. Res. Atmos. 2020, 125, e2020JD032665. [Google Scholar] [CrossRef]
- Zhuang, B.; Wang, T.; Liu, J.; Li, S.; Xie, M.; Han, Y.; Chen, P.; Hu, Q.; Yang, X.Q.; Fu, C.; et al. The surface aerosol optical properties in the urban area of Nanjing, west Yangtze River Delta, China. Atmos. Chem. Phys. 2017, 17, 1143–1160. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, M.; Jin, S.; Gong, W.; Chen, N.; Chen, Z.; Jin, Y.; Shi, Y. Long-term investigation of aerosol optical and radiative characteristics in a typical megacity of central China during winter haze periods. J. Geophys. Res. Atmos. 2019, 124, 12093–12106. [Google Scholar] [CrossRef]
- Bi, J.; Huang, J.; Hu, Z.; Holben, B.N.; Guo, Z. Investigating the aerosol optical and radiative characteristics of heavy haze episodes in Beijing during January of 2013. J. Geophys. Res. Atmos. 2014, 119, 9884–9900. [Google Scholar] [CrossRef]
- Ningombam, S.S.; Song, H.J.; Mugil, S.K.; Dumka, U.C.; Larson, E.J.L.; Kumar, B.; Sagar, R. Evaluation of fractional clear sky over potential astronomical sites. Mon. Not. R. Astron. Soc. 2021, 507, 3745–3760. [Google Scholar] [CrossRef]
- Bréon, F.-M.; Tanré, D.; Generoso, S. Aerosol effect on cloud droplet size monitored from satellite. Science 2002, 295, 834–838. [Google Scholar] [CrossRef]
- Letu, H.; Yang, K.; Nakajima, T.Y.; Ishimoto, H.; Nagao, T.M.; Riedi, J.; Baran, A.J.; Ma, R.; Wang, T.; Shang, H.; et al. High-resolution retrieval of cloud microphysical properties and surface solar radiation using Himawari-8/AHI next-generation geostationary satellite. Remote Sens. Environ. 2020, 239, 111583. [Google Scholar] [CrossRef]
- Li, L.; Che, H.; Derimian, Y.; Dubovik, O.; Schuster, G.L.; Chen, C.; Li, Q.; Wang, Y.; Guo, B.; Zhang, X. Retrievals of fine mode light-absorbing carbonaceous aerosols from POLDER/PARASOL observations over East and South Asia. Remote Sens. Environ. 2020, 247, 111913. [Google Scholar] [CrossRef]
- Zhang, X.; Li, L.; Chen, C.; Chen, X.; Dubovik, O.; Derimian, Y.; Gui, K.; Zheng, Y.; Zhao, H.; Zhang, L.; et al. Validation of the aerosol optical property products derived by the GRASP/component approach from multi-angular polarimetric observations. Atmos. Res. 2021, 263, 105802. [Google Scholar] [CrossRef]
- Miao, Y.; Liu, S.; Zheng, Y.; Wang, S.; Chen, B.; Zheng, H.; Zhao, J. Numerical study of the effects of local atmospheric circulations on a pollution event over Beijing–Tianjin–Hebei, China. J. Environ. Sci. 2015, 30, 9–20. [Google Scholar] [CrossRef] [PubMed]
- Xing, C.; Liu, C.; Hu, Q.; Fu, Q.; Wang, S.; Lin, H.; Zhu, Y.; Wang, S.; Wang, W.; Javed, Z.; et al. Vertical distributions of wintertime atmospheric nitrogenous compounds and the corresponding OH radicals production in Leshan, southwest China. J. Environ. Sci. 2021, 105, 44–55. [Google Scholar] [CrossRef]
- Gui, K.; Che, H.; Li, L.; Zheng, Y.; Zhang, L.; Zhao, H.; Zhong, J.; Yao, W.; Liang, Y.; Wang, Y.; et al. The significant contribution of small-sized and spherical aerosol particles to the decreasing trend in total aerosol optical depth over land from 2003 to 2018. Engineering, 2021, in press. [CrossRef]
- Liang, Y.; Che, H.; Gui, K.; Zheng, Y.; Yang, X.; Li, X.; Liu, C.; Sheng, Z.; Sun, T.; Zhang, X. Impact of biomass burning in South and Southeast Asia on background aerosol in southwest China. Aerosol Air Qual. Res. 2019, 19, 1188–1204. [Google Scholar] [CrossRef]
- Xing, C.; Liu, C.; Hu, Q.; Fu, Q.; Lin, H.; Wang, S.; Su, W.; Wang, W.; Javed, Z.; Liu, J. Identifying the wintertime sources of volatile organic compounds (VOCs) from MAX-DOAS measured formaldehyde and glyoxal in Chongqing, southwest China. Sci. Total Environ. 2020, 715, 136258. [Google Scholar] [CrossRef]
- Li, L.; Che, H.; Zhang, X.; Chen, C.; Chen, X.; Gui, K.; Liang, Y.; Wang, F.; Derimian, Y.; Fuertes, D.; et al. A satellite-measured view of aerosol component content and optical property in a haze-polluted case over North China Plain. Atmos. Res. 2022, 266, 105958. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J.; King, M.D.; Tanré, D.; Slutsker, I. Variability of absorption and optical properties of key aerosol types observed in worldwide locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar] [CrossRef]
- Che, H.; Xia, X.; Zhao, H.; Dubovik, O.; Holben, B.N.; Goloub, P.; Cuevas-Agulló, E.; Estelles, V.; Wang, Y.; Zhu, J.; et al. Spatial distribution of aerosol microphysical and optical properties and direct radiative effect from the China aerosol remote sensing network. Atmos. Chem. Phys. 2019, 19, 11843–11864. [Google Scholar] [CrossRef]
- Huang, R.-J.; Zhang, Y.; Bozzetti, C.; Ho, K.-F.; Cao, J.-J.; Han, Y.; Daellenbach, K.R.; Slowik, J.G.; Platt, S.M.; Canonaco, F.; et al. High secondary aerosol contribution to particulate pollution during haze events in China. Nature 2014, 514, 218–222. [Google Scholar] [CrossRef]
- Xing, C.; Liu, C.; Wang, S.; Lok Chan, K.; Gao, Y.; Huang, X.; Su, W.; Zhang, C.; Dong, Y.; Fan, G.; et al. Observations of the vertical distributions of summertime atmospheric pollutants and the corresponding ozone production in Shanghai, China. Atmos. Chem. Phys. 2017, 17, 14275–14289. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Wang, Y.Q.; Niu, T.; Zhang, X.C.; Gong, S.L.; Zhang, Y.M.; Sun, J.Y. Atmospheric aerosol compositions in China: Spatial/temporal variability, chemical signature, regional haze distribution and comparisons with global aerosols. Atmos. Chem. Phys. 2012, 12, 779–799. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Z.; Ding, A. Impact of aerosol-PBL interaction on haze pollution: Multiyear observational evidences in North China. Geophys. Res. Lett. 2018, 45, 8596–8603. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, L.; Wang, Y.; Ren, Y.; Wang, X.; Shi, Z.; Zhang, D.; Che, H.; Zhao, H.; Liu, Y.; et al. Chemical composition, source, and process of urban aerosols during winter haze formation in Northeast China. Environ. Pollut. 2017, 231, 357–366. [Google Scholar] [CrossRef] [PubMed]
- Gui, K.; Che, H.; Zheng, Y.; Zhao, H.; Yao, W.; Li, L.; Zhang, L.; Wang, H.; Wang, Y.; Zhang, X. Three-dimensional climatology, trends, and meteorological drivers of global and regional tropospheric type-dependent aerosols: Insights from 13 years (2007–2019) of CALIOP observations. Atmos. Chem. Phys. 2021, 21, 15309–15336. [Google Scholar] [CrossRef]
- Kazadzis, S.; Kouremeti, N.; Nyeki, S.; Gröbner, J.; Wehrli, C. The world optical depth research and calibration center (WORCC) quality assurance and quality control of GAW-PFR AOD measurements. Geosci. Instrum. Methods Data Syst. 2018, 7, 39–53. [Google Scholar] [CrossRef]
- Gui, K.; Yao, W.; Che, H.; An, L.; Zheng, Y.; Li, L.; Zhao, H.; Zhang, L.; Zhong, J.; Wang, Y.; et al. Record-breaking dust loading during two mega dust storm events over northern China in March 2021: Aerosol optical and radiative properties and meteorological drivers. Atmos. Chem. Phys. 2022, 22, 7905–7932. [Google Scholar] [CrossRef]
- Li, L.; Derimian, Y.; Chen, C.; Zhang, X.; Che, H.; Schuster, G.L.; Fuertes, D.; Litvinov, P.; Lapyonok, T.; Lopatin, A.; et al. Climatology of aerosol component concentrations derived from multi-angular polarimetric POLDER-3 observations using GRASP algorithm. Earth Syst. Sci. Data 2022, 14, 3439–3469. [Google Scholar] [CrossRef]
- Sayer, A.M.; Hsu, N.C.; Bettenhausen, C.; Jeong, M.J.; Holben, B.N.; Zhang, J. Global and regional evaluation of over-land spectral aerosol optical depth retrievals from SeaWiFS. Atmos. Meas. Tech. 2012, 5, 1761–1778. [Google Scholar] [CrossRef]
- Che, H.; Yang, L.; Liu, C.; Xia, X.; Wang, Y.; Wang, H.; Wang, H.; Lu, X.; Zhang, X. Long-term validation of MODIS C6 and C6.1 dark target aerosol products over China using CARSNET and AERONET. Chemosphere 2019, 236, 124268. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Peng, Y.; Sun, L. MODIS Collection 6.1 aerosol optical depth products over land and ocean: Validation and comparison. Atmos. Environ. 2019, 201, 428–440. [Google Scholar] [CrossRef]
- Shahid, M.Z.; Shahid, I.; Chishtie, F.; Shahzad, M.I.; Bulbul, G. Analysis of a dense haze event over North-eastern Pakistan using WRF-Chem model and remote sensing. J. Atmos. Sol.-Terr. Phys. 2019, 182, 229–241. [Google Scholar] [CrossRef]
- Kim, M.H.; Omar, A.H.; Tackett, J.L.; Vaughan, M.A.; Winker, D.M.; Trepte, C.R.; Hu, Y.; Liu, Z.; Poole, L.R.; Pitts, M.C.; et al. The CALIPSO version 4 automated aerosol classification and lidar ratio selection algorithm. Atmos. Meas. Tech. 2018, 11, 6107–6135. [Google Scholar] [CrossRef] [PubMed]
- Eck, T.F.; Holben, B.N.; Reid, J.S.; Dubovik, O.; Smirnov, A.; O’Neill, N.T.; Slutsker, I.; Kinne, S. Wavelength dependence of the optical depth of biomass burning, urban, and desert dust aerosols. J. Geophys. Res. Atmos. 1999, 104, 31333–31349. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Che, H.Z.; Tan, S.C.; Shi, G.Y.; Yao, X.P.; Zhao, H.J. Improvement of snow/haze confusion data gaps in MODIS dark target aerosol retrievals in East China. Atmos. Res. 2020, 245, 105063. [Google Scholar] [CrossRef]
- Toledano, C.; Torres, B.; Velasco-Merino, C.; Althausen, D.; Groß, S.; Wiegner, M.; Weinzierl, B.; Gasteiger, J.; Ansmann, A.; González, R.; et al. Sun photometer retrievals of Saharan dust properties over Barbados during SALTRACE. Atmos. Chem. Phys. 2019, 19, 14571–14583. [Google Scholar] [CrossRef]
- Xia, X.; Che, H.; Shi, H.; Chen, H.; Zhang, X.; Wang, P.; Goloub, P.; Holben, B. Advances in sunphotometer-measured aerosol optical properties and related topics in China: Impetus and perspectives. Atmos. Res. 2021, 249, 105286. [Google Scholar] [CrossRef] [PubMed]
- Che, H.; Zhang, X.Y.; Xia, X.; Goloub, P.; Holben, B.; Zhao, H.; Wang, Y.; Zhang, X.C.; Wang, H.; Blarel, L.; et al. Ground-based aerosol climatology of China: Aerosol optical depths from the China aerosol remote sensing network (CARSNET) 2002–2013. Atmos. Chem. Phys. 2015, 15, 7619–7652. [Google Scholar] [CrossRef]
- Nakajima, T.; Campanelli, M.; Che, H.; Estellés, V.; Irie, H.; Kim, S.W.; Kim, J.; Liu, D.; Nishizawa, T.; Pandithurai, G.; et al. An overview of and issues with sky radiometer technology and SKYNET. Atmos. Meas. Tech. 2020, 13, 4195–4218. [Google Scholar] [CrossRef]
- Cuevas, E.; Romero-Campos, P.M.; Kouremeti, N.; Kazadzis, S.; Räisänen, P.; García, R.D.; Barreto, A.; Guirado-Fuentes, C.; Ramos, R.; Toledano, C.; et al. Aerosol optical depth comparison between GAW-PFR and AERONET-Cimel radiometers from long-term (2005–2015) 1 min synchronous measurements. Atmos. Meas. Tech. 2019, 12, 4309–4337. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Goloub, P.; Li, Z.; Dubovik, O.; Blarel, L.; Podvin, T.; Jankowiak, I.; Lecoq, R.; Deroo, C.; Chatenet, B.; Morel, J.P.; et al. PHOTONS/AERONET sunphotometer network overview: Description, activities, results. In Proc. SPIE, Proceedings of the Fourteenth International Symposium on Atmospheric and Ocean Optics/Atmospheric Physics, Buryatia, Russian, 24–30 June 2007; SPIE: Bellingham, WA, USA, 2008; Volume 6936, pp. 218–232. [Google Scholar] [CrossRef]
- Che, H.; Xia, X.; Zhu, J.; Li, Z.; Dubovik, O.; Holben, B.; Goloub, P.; Chen, H.; Estelles, V.; Cuevas-Agulló, E.; et al. Column aerosol optical properties and aerosol radiative forcing during a serious haze-fog month over North China Plain in 2013 based on ground-based sunphotometer measurements. Atmos. Chem. Phys. 2014, 14, 2125–2138. [Google Scholar] [CrossRef]
- Kazadzis, S.; Kouremeti, N.; Diémoz, H.; Gröbner, J.; Forgan, B.W.; Campanelli, M.; Estellés, V.; Lantz, K.; Michalsky, J.; Carlund, T.; et al. Results from the fourth WMO filter radiometer comparison for aerosol optical depth measurements. Atmos. Chem. Phys. 2018, 18, 3185–3201. [Google Scholar] [CrossRef]
- Che, H.; Wang, Y.; Sun, J.; Zhang, X. Assessment of in-situ Langley calibration of CE-318 sunphotometer at Mt. Waliguan observatory, China. Sola 2011, 7, 89–92. [Google Scholar] [CrossRef][Green Version]
- Campanelli, M.; Estellés, V.; Tomasi, C.; Nakajima, T.; Malvestuto, V.; Martínez-Lozano, J.A. Application of the SKYRAD improved Langley plot method for the in situ calibration of CIMEL sun-sky photometers. Appl. Opt. 2007, 46, 2688–2702. [Google Scholar] [CrossRef]
- Tao, R.; Che, H.; Chen, Q.; Wang, Y.; Sun, J.; Zhang, X.; Lu, S.; Guo, J.; Wang, H.; Zhang, X. Development of an integrating sphere calibration method for Cimel sunphotometers in China aerosol remote sensing network. Particuology 2014, 13, 88–99. [Google Scholar] [CrossRef]
- Toledano, C.; González, R.; Fuertes, D.; Cuevas, E.; Eck, T.F.; Kazadzis, S.; Kouremeti, N.; Gröbner, J.; Goloub, P.; Blarel, L.; et al. Assessment of sun photometer Langley calibration at the high-elevation sites Mauna Loa and Izaña. Atmos. Chem. Phys. 2018, 18, 14555–14567. [Google Scholar] [CrossRef]
- Zheng, Y.; Che, H.; Xia, X.; Wang, Y.; Yang, L.; Chen, J.; Wang, H.; Zhao, H.; Li, L.; Zhang, L.; et al. Aerosol optical properties and its type classification based on multiyear joint observation campaign in north China plain megalopolis. Chemosphere 2021, 273, 128560. [Google Scholar] [CrossRef]
- Zheng, Y.; Che, H.; Xia, X.; Wang, Y.; Wang, H.; Wu, Y.; Tao, J.; Zhao, H.; An, L.; Li, L.; et al. Five-year observation of aerosol optical properties and its radiative effects to planetary boundary layer during air pollution episodes in North China: Intercomparison of a plain site and a mountainous site in Beijing. Sci. Total Environ. 2019, 674, 140–158. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z.; Lv, Y.; Xu, H.; Li, K.; Li, D.; Hou, W.; Zheng, F.; Wei, Y.; Ge, B. Observational study of aerosol-induced impact on planetary boundary layer based on lidar and sunphotometer in Beijing. Environ. Pollut. 2019, 252, 897–906. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, X.; Wang, Y.; Wang, J.; Shen, X.; Zhang, H.; Wang, T.; Xie, Z.; Liu, C.; Zhang, H.; et al. The two-way feedback mechanism between unfavorable meteorological conditions and cumulative aerosol pollution in various haze regions of China. Atmos. Chem. Phys. 2019, 19, 3287–3306. [Google Scholar] [CrossRef]
- Miao, Y.; Che, H.; Zhang, X.; Liu, S. Integrated impacts of synoptic forcing and aerosol radiative effect on boundary layer and pollution in the Beijing-Tianjin-Hebei region, China. Atmos. Chem. Phys. 2020, 20, 5899–5909. [Google Scholar] [CrossRef]
- Schmid, B.; Wehrli, C. Comparison of Sun photometer calibration by use of the Langley technique and the standard lamp. Appl. Opt. 1995, 34, 4500–4512. [Google Scholar] [CrossRef]
- Liu, C.; Yang, L.; Che, H.; Xia, X.; Zhao, H.; Wang, H.; Gui, K.; Zheng, Y.; Sun, T.; Li, X.; et al. Aerosol optical properties over an urban site in central China determined using ground-based sun photometer measurements. Aerosol Air Qual. Res. 2019, 19, 620–638. [Google Scholar] [CrossRef]
- Che, H.; Zhang, X.; Chen, H.; Damiri, B.; Goloub, P.; Li, Z.; Zhang, X.; Wei, Y.; Zhou, H.; Dong, F.; et al. Instrument calibration and aerosol optical depth validation of the China aerosol remote sensing network. J. Geophys. Res. Atmos. 2009, 114, D03206. [Google Scholar] [CrossRef]
- Zhao, H.; Che, H.; Xia, X.; Wang, Y.; Wang, H.; Wang, P.; Ma, Y.; Yang, H.; Liu, Y.; Wang, Y.; et al. Multiyear ground-based measurements of aerosol optical properties and direct radiative effect over different surface types in northeastern China. J. Geophys. Res. Atmos. 2018, 123, 13887–13916. [Google Scholar] [CrossRef]
- Che, H.; Qi, B.; Zhao, H.; Xia, X.; Eck, T.F.; Goloub, P.; Dubovik, O.; Estelles, V.; Cuevas-Agulló, E.; Blarel, L.; et al. Aerosol optical properties and direct radiative forcing based on measurements from the China aerosol remote sensing network (CARSNET) in eastern China. Atmos. Chem. Phys. 2018, 18, 405–425. [Google Scholar] [CrossRef]
- Zheng, Y.; Che, H.; Wang, Y.; Xia, X.; Hu, X.; Zhang, X.; Zhu, J.; Zhu, J.; Zhao, H.; Li, L.; et al. Evaluation of aerosol microphysical, optical and radiative properties measured with a multiwavelength photometer. Atmos. Meas. Tech. 2022, 15, 2139–2158. [Google Scholar] [CrossRef]
- Sheng, Z.; Che, H.; Chen, Q.; Xia, X.; Liu, D.; Wang, Z.; Zhao, H.; Gui, K.; Zheng, Y.; Sun, T.; et al. Aerosol vertical distribution and optical properties of different pollution events in Beijing in autumn 2017. Atmos. Res. 2019, 215, 193–207. [Google Scholar] [CrossRef]
- Zheng, Y.; Che, H.; Yang, L.; Chen, J.; Wang, Y.; Xia, X.; Zhao, H.; Wang, H.; Wang, D.; Gui, K.; et al. Optical and radiative properties of aerosols during a severe haze episode over the North China Plain in December 2016. J. Meteorol. Res. 2018, 31, 1045–1061. [Google Scholar] [CrossRef]
- Barreto, Á.; Cuevas, E.; Granados-Muñoz, M.J.; Alados-Arboledas, L.; Romero, P.M.; Gröbner, J.; Kouremeti, N.; Almansa, A.F.; Stone, T.; Toledano, C.; et al. The new sun-sky-lunar Cimel CE318-T multiband photometer—A comprehensive performance evaluation. Atmos. Meas. Tech. 2016, 9, 631–654. [Google Scholar] [CrossRef]
- Estellés, V.; Campanelli, M.; Utrillas, M.P.; Expósito, F.; Martínez-Lozano, J.A. Comparison of AERONET and SKYRAD4.2 inversion products retrieved from a Cimel CE318 sunphotometer. Atmos. Meas. Tech. 2012, 5, 569–579. [Google Scholar] [CrossRef]
- Nevada, S.; Alcántara-Ruiz, E.A.; Olmo, F.J.; Alados-Arboledas, L. Langley calibrations of sunphotometer at Sierra Nevada, Granada, Spain. Opt. Pura Apl. 2004, 37, 3263–3269. [Google Scholar]
- Dutton, E.G.; Reddy, P.; Ryan, S.; Deluisi, J.J. Features and effects of aerosol optical depth observed at Mauna Loa, Hawaii: 1982–1992. J. Geophys. Res. Atmos. 1994, 99, 8295–8306. [Google Scholar] [CrossRef]
- Barreto, A.; Cuevas, E.; Pallé, P.; Romero, P.M.; Guirado, C.; Wehrli, C.J.; Almansa, F. Recovering long-term aerosol optical depth series (1976–2012) from an astronomical potassium-based resonance scattering spectrometer. Atmos. Meas. Tech. 2014, 7, 4103–4116. [Google Scholar] [CrossRef][Green Version]
- Levy, R.C.; Remer, L.A.; Kleidman, R.G.; Mattoo, S.; Ichoku, C.; Kahn, R.; Eck, T.F. Global evaluation of the collection 5 MODIS dark-target aerosol products over land. Atmos. Chem. Phys. 2010, 10, 10399–10420. [Google Scholar] [CrossRef]
- Yang, L.; Tian, X.; Liu, C.; Ji, W.; Zheng, Y.; Liu, H.; Lu, X.; Che, H. Evaluation and comparison of MODIS C6 and C6.1 deep blue aerosol products in arid and semi-arid areas of northwestern China. Remote Sens. 2022, 14, 1935. [Google Scholar] [CrossRef]

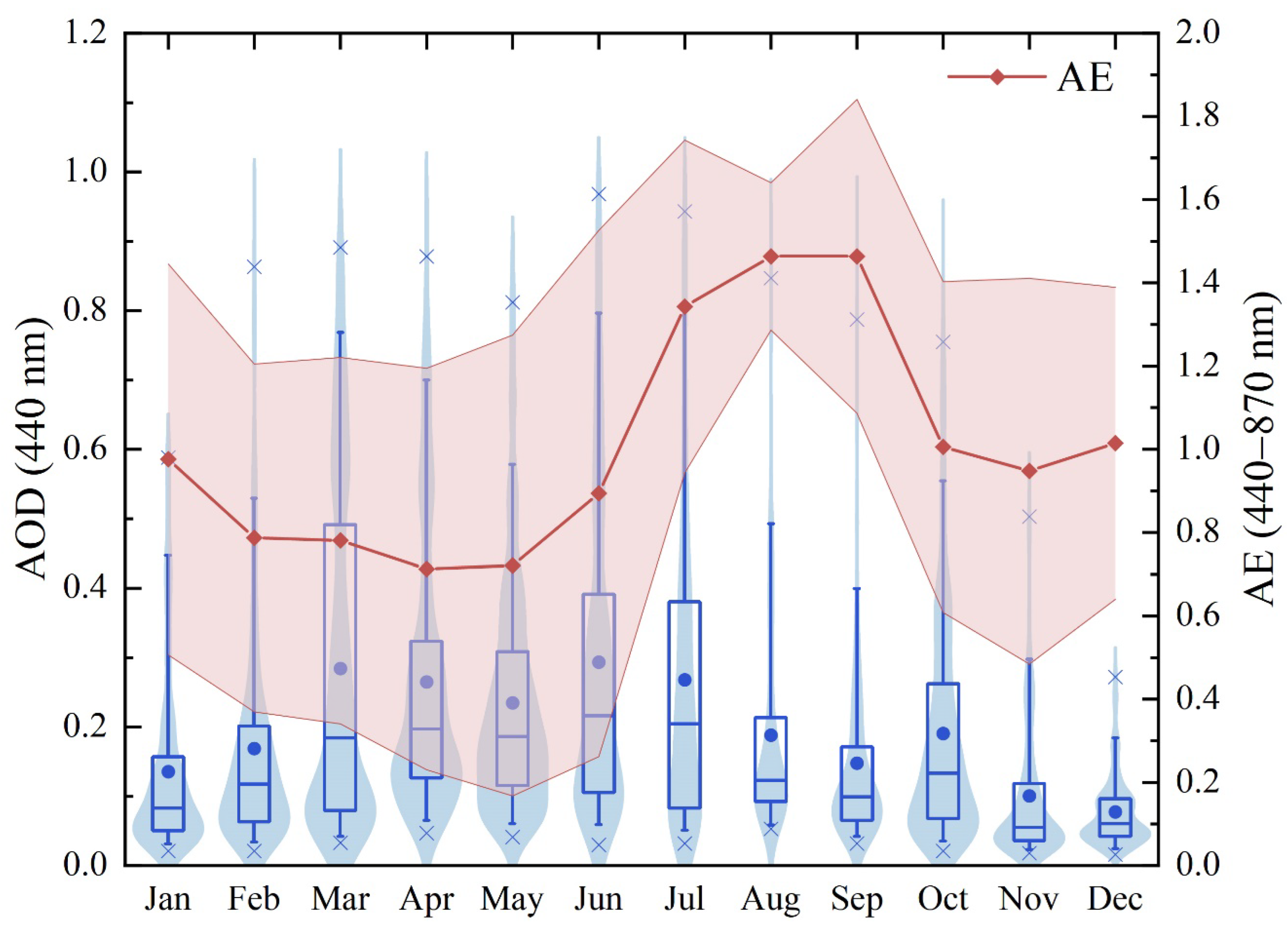


| Daytime | Morning | Afternoon | ||||
|---|---|---|---|---|---|---|
| Month | AOD | Ratio (%) | AOD | Ratio (%) | AOD | Ratio (%) |
| January | 0.14 | 99.00 | 0.12 | 36.97 | 0.15 | 84.15 |
| February | 0.17 | 81.43 | 0.14 | 43.49 | 0.19 | 57.42 |
| March | 0.29 | 100.41 | 0.23 | 59.71 | 0.35 | 62.27 |
| April | 0.30 | 152.34 | 0.23 | 50.70 | 0.36 | 115.39 |
| May | 0.27 | 74.79 | 0.23 | 52.00 | 0.30 | 53.67 |
| June | 0.37 | 106.28 | 0.29 | 93.04 | 0.45 | 56.94 |
| July | 0.38 | 141.51 | 0.19 | 85.69 | 0.51 | 76.94 |
| August | 0.19 | 129.08 | 0.17 | 88.86 | 0.20 | 121.38 |
| September | 0.15 | 151.55 | 0.13 | 106.51 | 0.17 | 117.96 |
| October | 0.20 | 107.87 | 0.17 | 55.93 | 0.22 | 83.07 |
| November | 0.13 | 111.35 | 0.10 | 68.59 | 0.15 | 73.97 |
| December | 0.10 | 93.56 | 0.09 | 63.38 | 0.10 | 79.96 |
| P | T | RH | WD | WS | |
|---|---|---|---|---|---|
| 11 − 18 | 873 ± 2 | −1 ± 1 | 98 ± 1 | 99 ± 32 | 2 ± 1 |
| 11 − 30 | 879 ± 1 | −5 ± 2 | 75 ± 19 | 298 ± 26 | 4 ± 3 |
| 12 − 09 | 881 ± 1 | −8 ± 2 | 50 ± 12 | 243 ± 105 | 4 ± 3 |
| 12 − 19 | 881 ± 1 | −1 ± 2 | 42 ± 6 | 302 ± 17 | 4 ± 1 |
| 12 − 20 | 884 ± 1 | 1 ± 1 | 37 ±46 | 230 ± 76 | 2 ± 1 |
| 12 − 26 | 884 ± 1 | −8 ± 2 | 45 ± 13 | 323 ± 13 | 5 ± 1 |
| 340 nm | 380 nm | 440 nm | 500 nm | 675 nm | 870 nm | 1020 nm | 1640 nm | ||
|---|---|---|---|---|---|---|---|---|---|
| 11 − 18 | R2 | 0.9999 | 0.9999 | 0.9997 | 0.9990 | 0.9978 | 0.9804 | 0.9589 | 0.9770 |
| RSS | 1.7529 × 10−4 | 1.4741 × 10−4 | 1.2844 × 10−4 | 1.8140 × 10−4 | 1.6100 × 10−4 | 9.9779 × 10−4 | 1.3662 × 10−4 | 1.1594 × 10−4 | |
| RSD | 0.1872% | 0.1717% | 0.1603% | 0.1905% | 0.1794% | 0.1413% | 0.1653% | 0.1523% | |
| 11 − 30 | R2 | 0.9993 | 0.9990 | 0.9983 | 0.9975 | 0.9952 | 0.9798 | 0.9723 | 0.9802 |
| RSS | 1.0191 × 10−4 | 1.6877 × 10−4 | 1.4532 × 10−4 | 1.2159 × 10−4 | 1.4447 × 10−4 | 1.2952 × 10−4 | 1.1619 × 10−4 | 1.6613 × 10−4 | |
| RSD | 0.1428% | 0.1837% | 0.1705% | 0.1559% | 0.1700% | 0.1609% | 0.1524% | 0.1823% | |
| 12 − 09 | R2 | 0.9997 | 0.9995 | 0.9990 | 0.9983 | 0.9943 | 0.9746 | 0.9766 | 0.9636 |
| RSS | 1.5700 × 10−4 | 1.3332 × 10−4 | 1.0536 × 10−4 | 1.1614 × 10−4 | 1.0732 × 10−4 | 1.2995 × 10−4 | 1.8142 × 10−4 | 1.0628 × 10−4 | |
| RSD | 0.1772% | 0.1633% | 0.1452% | 0.1524% | 0.1465% | 0.1612% | 0.1905% | 0.1458% | |
| 12 − 19 | R2 | 0.9999 | 0.9998 | 0.9996 | 0.9993 | 0.9986 | 0.9923 | 0.9725 | 0.9918 |
| RSS | 1.2213 × 10−4 | 1.1553 × 10−4 | 1.2823 × 10−4 | 1.8545 × 10−4 | 1.0179 × 10−4 | 1.4898 × 10−4 | 1.0439 × 10−4 | 1.6001 × 10−4 | |
| RSD | 0.1563% | 0.1520% | 0.1601% | 0.1926% | 0.1427% | 0.1726% | 0.1445% | 0.1789% | |
| 12 − 20 | R2 | 0.9999 | 0.9997 | 0.9994 | 0.9993 | 0.9976 | 0.9877 | 0.9806 | 0.9909 |
| RSS | 1.4297 × 10−4 | 1.6543 × 10−4 | 1.4838 × 10−4 | 1.4486 × 10−4 | 1.1633 × 10−4 | 1.7894 × 10−4 | 1.3181 × 10−4 | 1.7672 × 10−4 | |
| RSD | 0.1691% | 0.1819% | 0.1723% | 0.1702% | 0.1525% | 0.1892% | 0.1624% | 0.1880% | |
| 12 − 26 | R2 | 0.9996 | 0.9993 | 0.9987 | 0.9978 | 0.9924 | 0.9508 | 0.9810 | 0.9622 |
| RSS | 1.0444 × 10−4 | 1.2334 × 10−4 | 1.5139 × 10−4 | 1.8241 × 10−4 | 1.3982 × 10−4 | 1.7817 × 10−4 | 1.2893 × 10−4 | 1.7339 × 10−4 | |
| RSD | 0.1445% | 0.1571% | 0.1740% | 0.1910% | 0.1672% | 0.1888% | 0.1606% | 0.1862% | |
| 340 nm | 380 nm | 440 nm | 500 nm | 675 nm | 870 nm | 1020 nm | 1640 nm | |
|---|---|---|---|---|---|---|---|---|
| 11 − 18 | 9.6911 | 9.8333 | 9.2228 | 9.9744 | 10.0075 | 9.5729 | 9.1156 | 9.3191 |
| 11 − 27 | 9.6946 | 9.8313 | 9.2241 | 9.9676 | 10.0106 | 9.5737 | 9.0989 | 9.3209 |
| 11 − 28 | 9.7263 | 9.8543 | 9.2247 | 9.9877 | 10.0143 | 9.5729 | 9.1305 | 9.3147 |
| 11 − 30 | 9.7184 | 9.8565 | 9.2477 | 9.9846 | 10.0316 | 9.5937 | 9.1058 | 9.3416 |
| 12 − 05 | 9.7015 | 9.8356 | 9.2250 | 9.9772 | 10.0156 | 9.5761 | 9.1107 | 9.3258 |
| 12 − 06 | 9.7077 | 9.8417 | 9.2243 | 9.9775 | 10.0242 | 9.5849 | 9.1104 | 9.3417 |
| 12 − 07 | 9.7048 | 9.8522 | 9.2312 | 9.9821 | 10.0250 | 9.5876 | 9.1274 | 9.3355 |
| 12 − 09 | 9.7118 | 9.8589 | 9.2427 | 9.9863 | 10.0117 | 9.5878 | 9.1237 | 9.3367 |
| 12 − 12 | 9.7016 | 9.8421 | 9.2306 | 9.9679 | 10.0116 | 9.5694 | 9.1034 | 9.3145 |
| 12 − 13 | 9.7098 | 9.8489 | 9.2376 | 9.9785 | 10.0196 | 9.5827 | 9.1149 | 9.3274 |
| 12 − 18 | 9.6997 | 9.8367 | 9.2257 | 9.9656 | 10.0128 | 9.5780 | 9.1064 | 9.3264 |
| 12 − 19 | 9.7133 | 9.8574 | 9.2466 | 9.9837 | 10.0248 | 9.5853 | 9.1074 | 9.3293 |
| 12 − 20 | 9.7092 | 9.8479 | 9.2276 | 9.9801 | 10.0232 | 9.5847 | 9.1135 | 9.3308 |
| 12 − 21 | 9.6941 | 9.8323 | 9.2323 | 9.9815 | 10.0193 | 9.5862 | 9.1136 | 9.3301 |
| 12 − 23 | 9.7011 | 9.8462 | 9.2365 | 9.9871 | 10.0213 | 9.5930 | 9.1252 | 9.3325 |
| 12 − 24 | 9.7109 | 9.8461 | 9.2366 | 9.9795 | 10.0090 | 9.5690 | 9.0959 | 9.3200 |
| 12 − 26 | 9.7102 | 9.8568 | 9.2327 | 9.9850 | 10.0204 | 9.5837 | 9.1030 | 9.3217 |
| 12 − 28 | 9.7065 | 9.8377 | 9.2277 | 9.9770 | 10.0214 | 9.5760 | 9.1166 | 9.3322 |
| 12 − 29 | 9.7070 | 9.8305 | 9.2226 | 9.9693 | 10.0094 | 9.5810 | 9.1262 | 9.3248 |
| 12 − 30 | 9.7056 | 9.8410 | 9.2266 | 9.9613 | 10.0031 | 9.5642 | 9.1017 | 9.3171 |
| 1 − 03 | 9.7024 | 9.8371 | 9.2314 | 9.9747 | 10.0271 | 9.5937 | 9.1263 | 9.3450 |
| 1 − 05 | 9.7049 | 9.8556 | 9.2299 | 9.9792 | 10.0182 | 9.5861 | 9.1108 | 9.3425 |
| 1 − 10 | 9.6914 | 9.8414 | 9.2348 | 9.9739 | 10.0228 | 9.5884 | 9.1031 | 9.3355 |
| 1 − 12 | 9.7045 | 9.8377 | 9.2270 | 9.9712 | 10.0151 | 9.5786 | 9.1188 | 9.3253 |
| 1 − 13 | 9.7086 | 9.8490 | 9.2380 | 9.9826 | 10.0256 | 9.5972 | 9.1217 | 9.3406 |
| 1 − 15 | 9.7051 | 9.8465 | 9.2349 | 9.9709 | 10.0191 | 9.5851 | 9.1225 | 9.3324 |
| 1 − 17 | 9.7004 | 9.8390 | 9.2250 | 9.9685 | 10.0157 | 9.5685 | 9.1164 | 9.3157 |
| 1 − 18 | 9.7032 | 9.8482 | 9.2362 | 9.9713 | 10.0198 | 9.5857 | 9.1080 | 9.3293 |
| 1 − 20 | 9.6963 | 9.8384 | 9.2310 | 9.9600 | 10.0186 | 9.5709 | 9.0975 | 9.3182 |
| 1 − 21 | 9.7057 | 9.8460 | 9.2302 | 9.9679 | 10.0055 | 9.5716 | 9.1056 | 9.3115 |
| 1 − 30 | 9.7137 | 9.8462 | 9.2371 | 9.9738 | 10.0103 | 9.5918 | 9.1191 | 9.3351 |
| Mean | 9.7052 | 9.8443 | 9.2317 | 9.9757 | 10.0172 | 9.5813 | 9.1129 | 9.3282 |
| STDEV | 0.0075 | 0.0081 | 0.0065 | 0.0074 | 0.0068 | 0.0086 | 0.0095 | 0.0092 |
| RSS | 0.0017 | 0.0021 | 0.0013 | 0.0017 | 0.0014 | 0.0023 | 0.0028 | 0.0026 |
| RSD | 0.7611% | 0.8279% | 0.6651% | 0.7536% | 0.6893% | 0.8745% | 0.9608% | 0.9305% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Che, H.; Gui, K.; Xia, X.; Zhao, H.; Li, L.; Zhang, L.; Zhang, X.; Zhao, H.; Liang, Y.; et al. Preliminary Assessment and Verification of the Langley Plots Calibration of the Sun Photometer at Mt Foyeding Observatory, Beijing. Remote Sens. 2022, 14, 4321. https://doi.org/10.3390/rs14174321
Zheng Y, Che H, Gui K, Xia X, Zhao H, Li L, Zhang L, Zhang X, Zhao H, Liang Y, et al. Preliminary Assessment and Verification of the Langley Plots Calibration of the Sun Photometer at Mt Foyeding Observatory, Beijing. Remote Sensing. 2022; 14(17):4321. https://doi.org/10.3390/rs14174321
Chicago/Turabian StyleZheng, Yu, Huizheng Che, Ke Gui, Xiangao Xia, Hujia Zhao, Lei Li, Lei Zhang, Xinglu Zhang, Hengheng Zhao, Yuanxin Liang, and et al. 2022. "Preliminary Assessment and Verification of the Langley Plots Calibration of the Sun Photometer at Mt Foyeding Observatory, Beijing" Remote Sensing 14, no. 17: 4321. https://doi.org/10.3390/rs14174321
APA StyleZheng, Y., Che, H., Gui, K., Xia, X., Zhao, H., Li, L., Zhang, L., Zhang, X., Zhao, H., Liang, Y., Wang, H., Wang, Y., & Zhang, X. (2022). Preliminary Assessment and Verification of the Langley Plots Calibration of the Sun Photometer at Mt Foyeding Observatory, Beijing. Remote Sensing, 14(17), 4321. https://doi.org/10.3390/rs14174321










