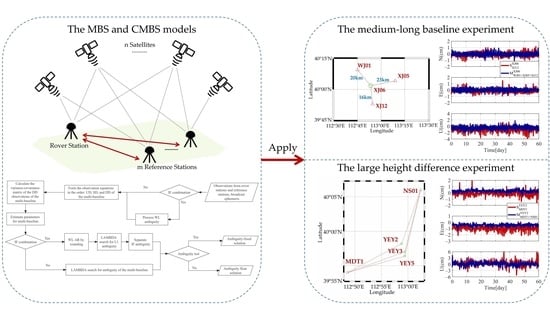
BDS/GPS Multi-Baseline Relative Positioning for Deformation Monitoring
Abstract
:1. Introduction
2. Methods
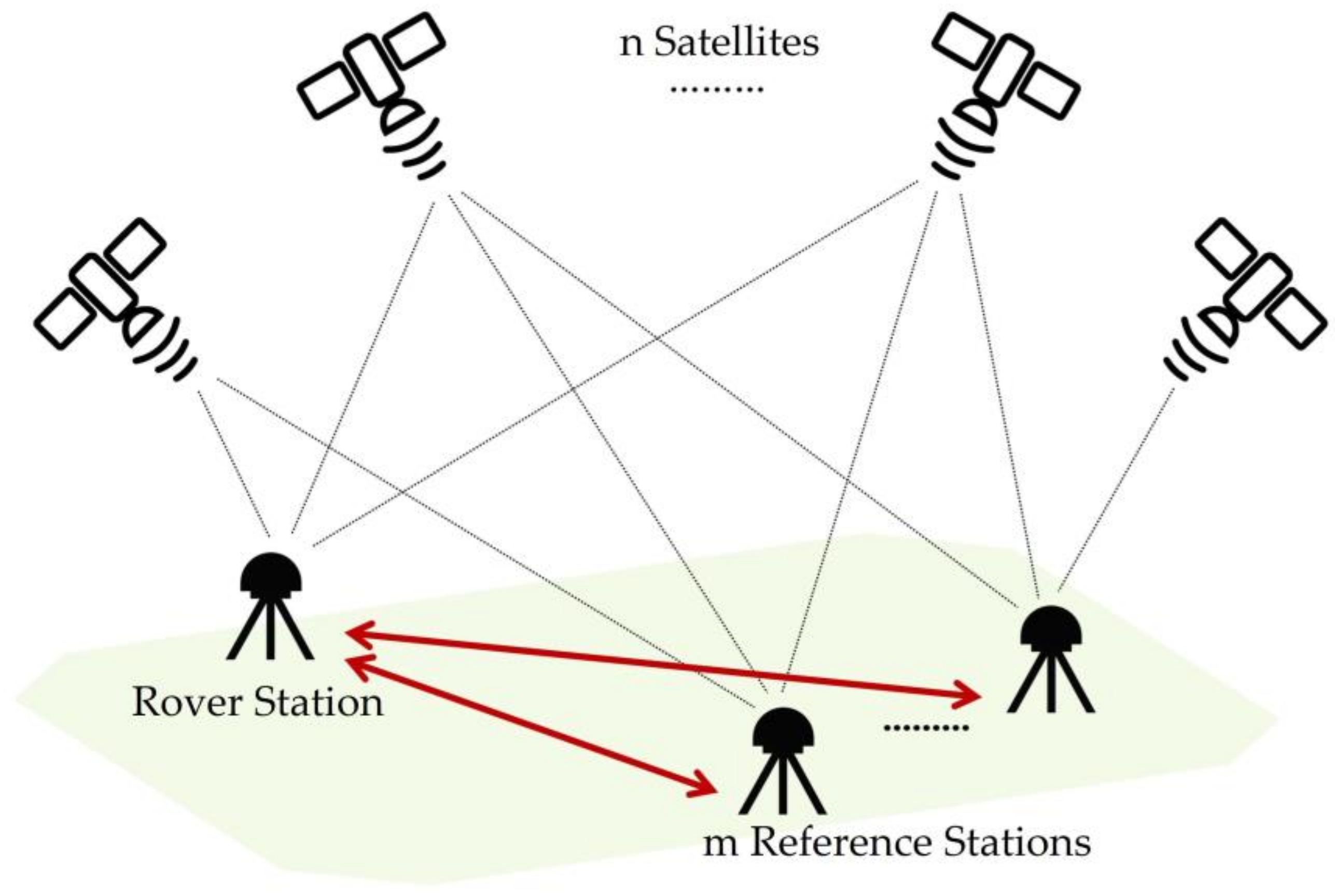
2.1. MBS Mathematical Model
2.1.1. Function Model
2.1.2. Stochastic Model
2.2. MBS Parameter Estimation
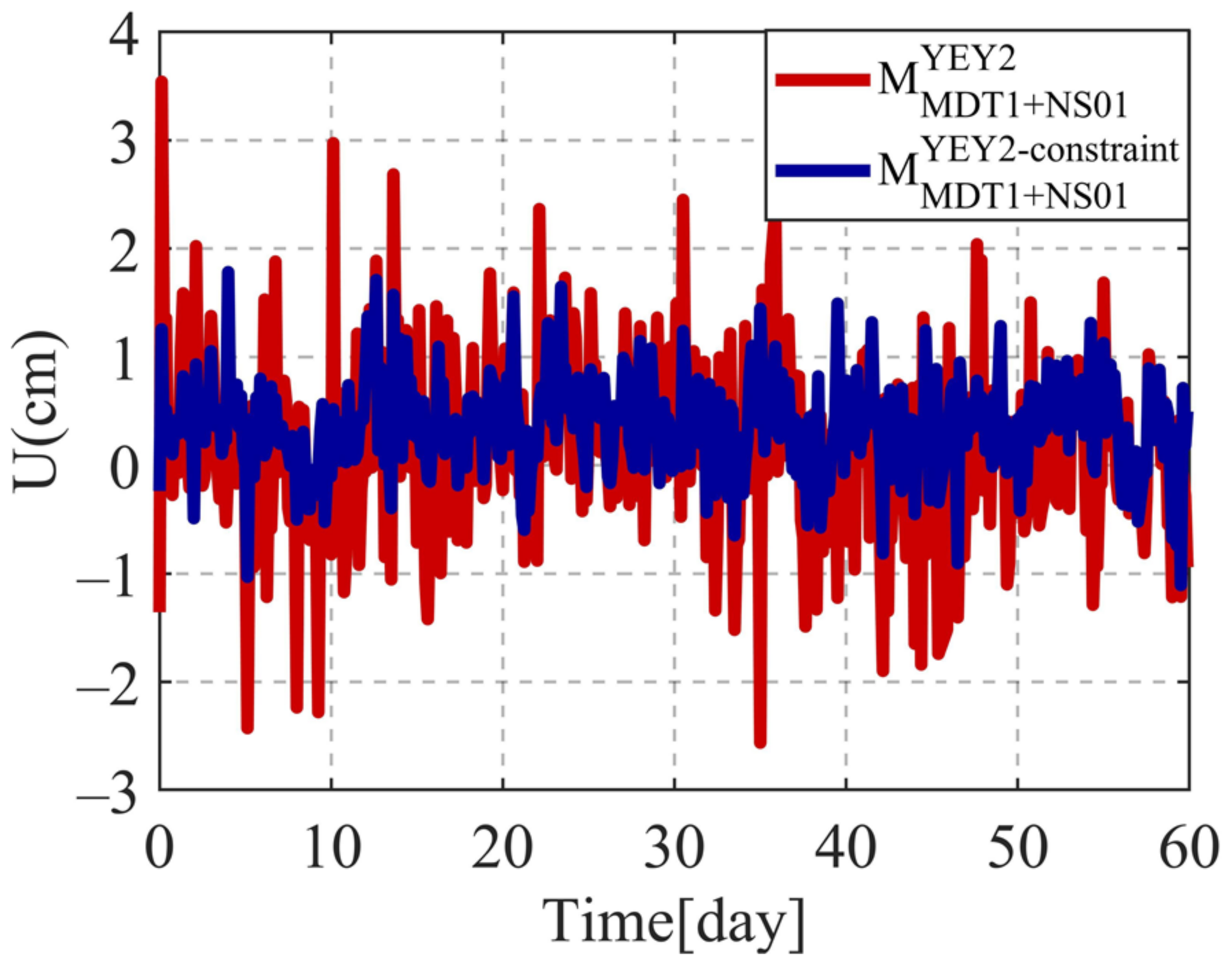
2.3. A Priori Constraint on Tropospheric Delay
2.4. Data Processing Strategy
3. Experiments and Analysis
3.1. Medium-Long Baseline Experiment
3.1.1. Experimental Design
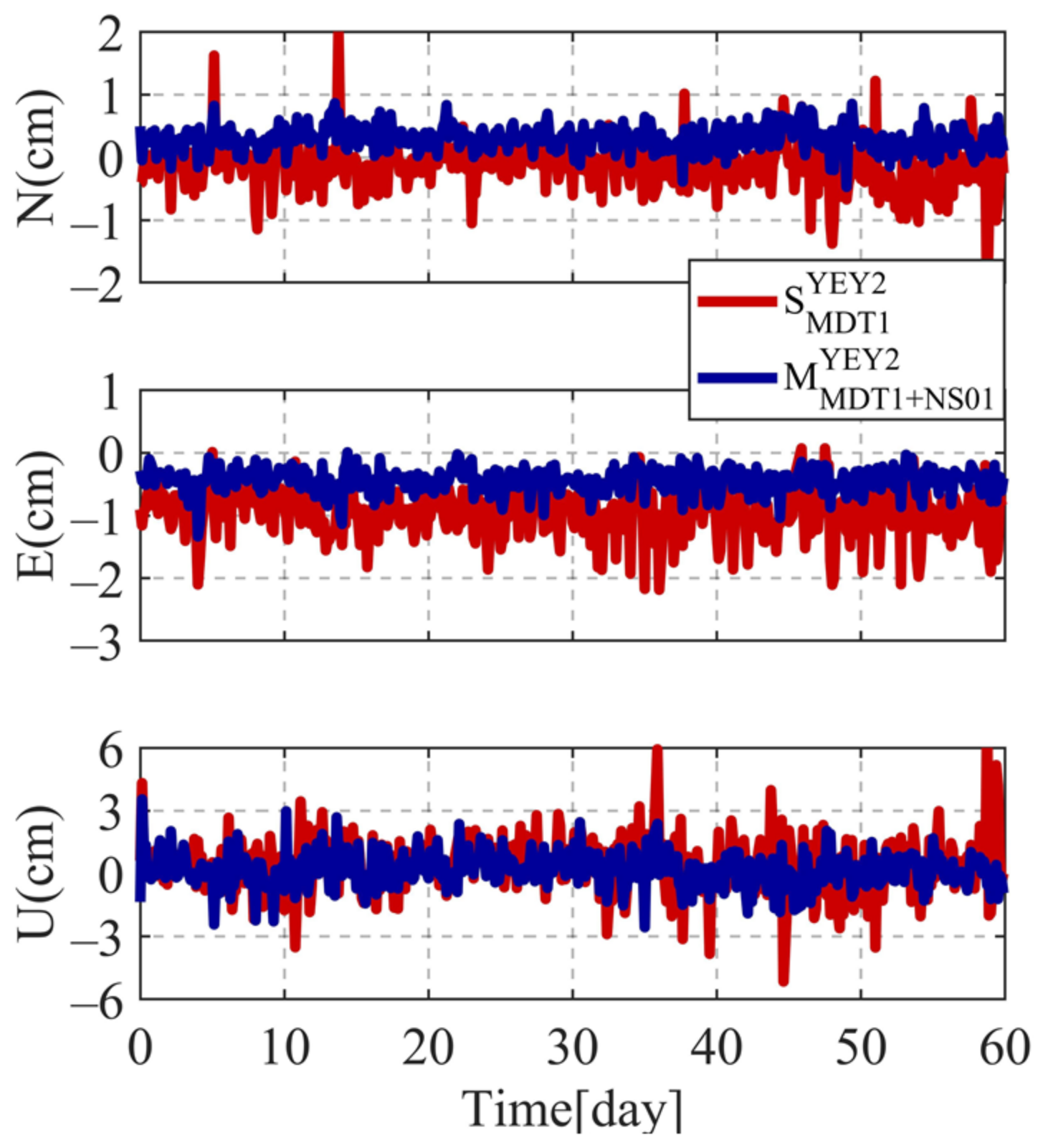
3.1.2. Analysis of Monitoring Accuracy for Different Reference Stations
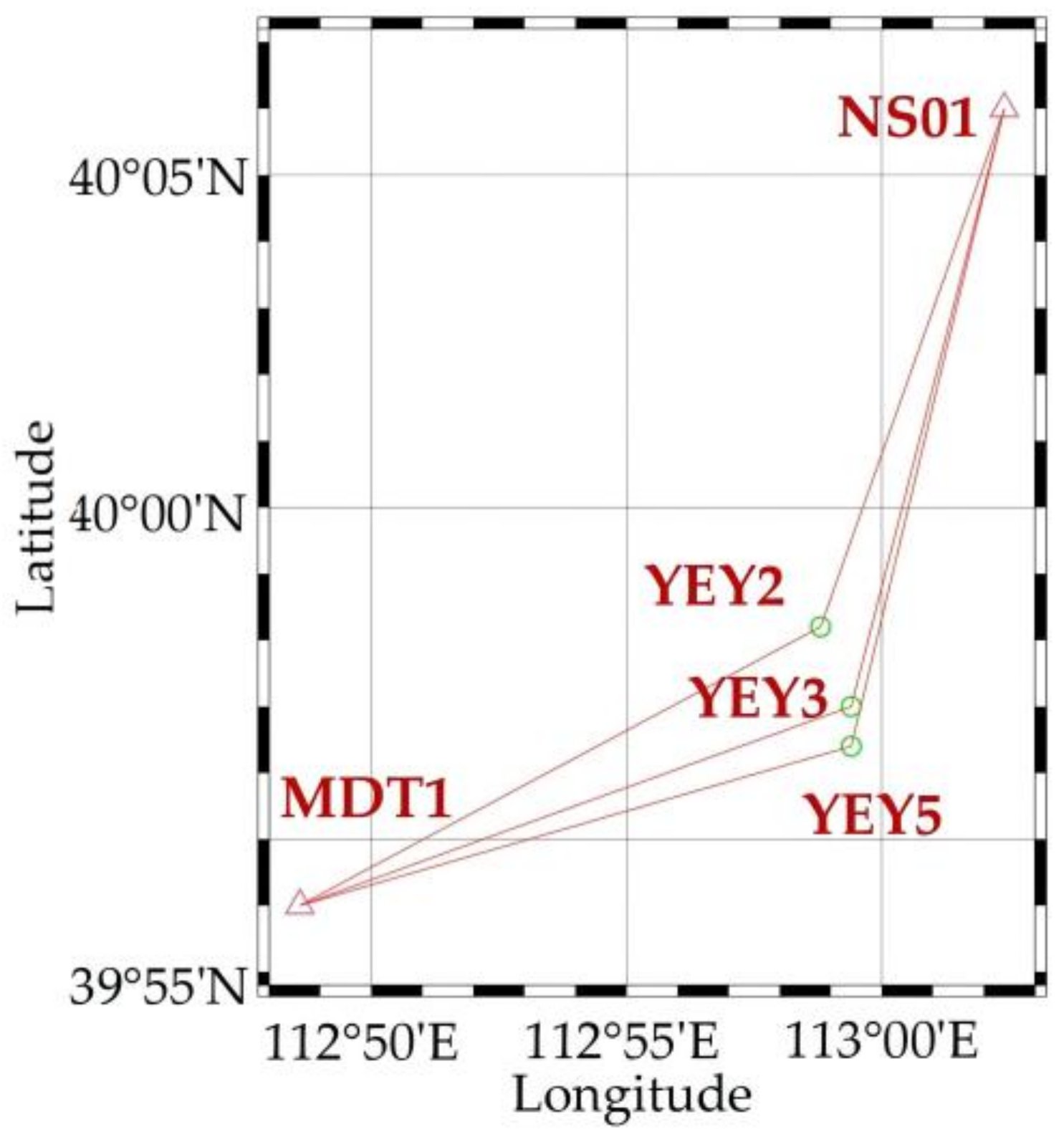
3.2. Large Height Difference Experiment
3.2.1. Experimental Design
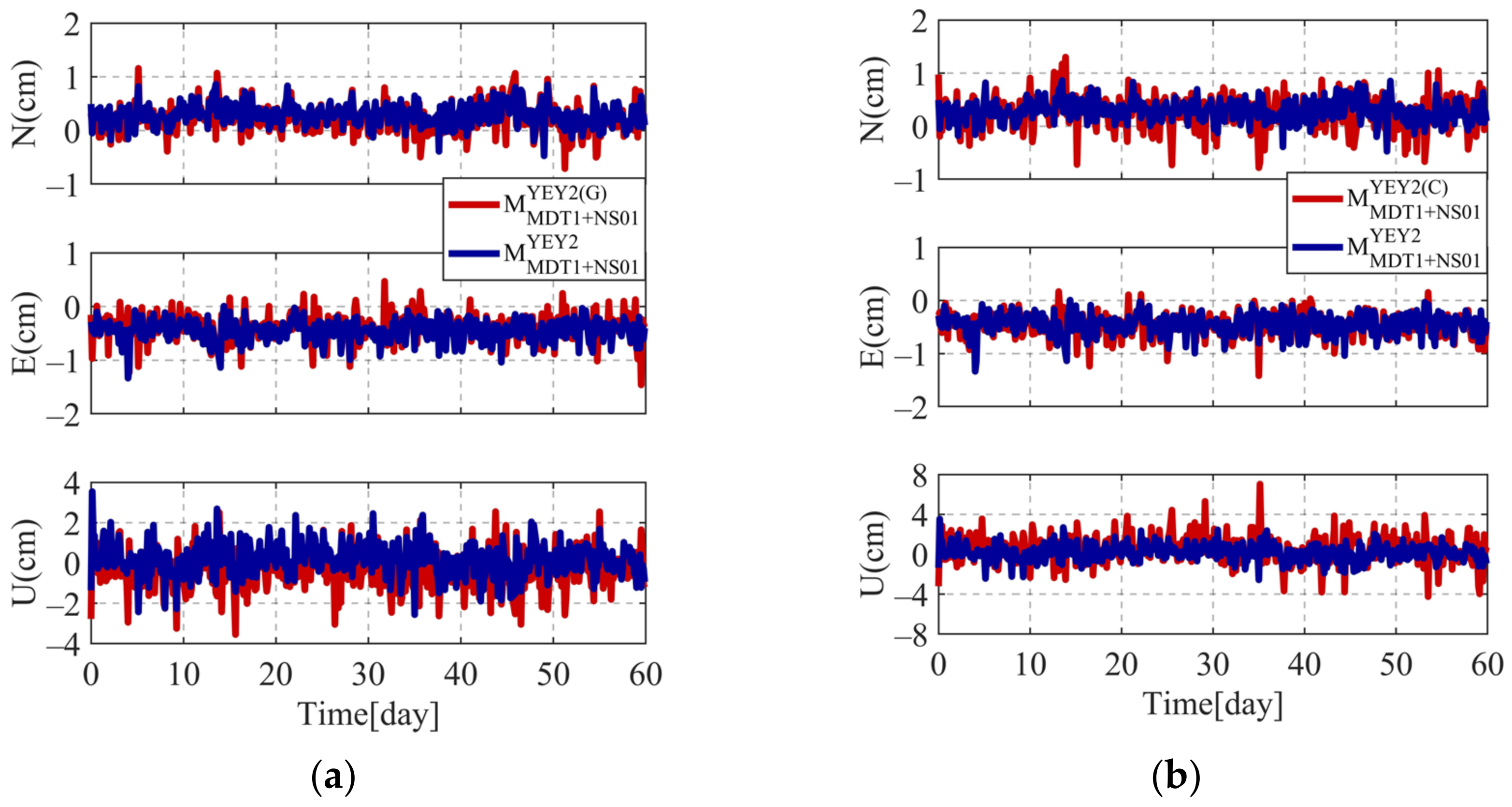
3.2.2. Analysis of Monitoring Accuracy for Different Satellite Systems
3.2.3. Analysis of Monitoring Accuracy for Large Height Difference
4. Conclusions
- For baselines with medium-long lengths and large height differences, the proposed MBS model can provide better monitoring performance than the SBS model. Compared with the SBS model, the MBS model can improve the positioning accuracy of medium-long baselines with an average improvement of about (25.7/19.0/21.5%) and (22.8/24.2/40.0%) in the N/E/U components, with the highest improvement of about (29.4/31.0/29.2%) and (29.4/35.5/44.8%) in the N/E/U components, respectively. For baselines with large height differences, compared with the SBS model, the MBS model can improve the positioning accuracy with an average improvement of about (40.6/48.3/44.7%) and (36.8/53.7/33.7%) in the N/E/U components, with the highest improvement of about (47.4/51.3/66.2%) and (56.9/60.4/58.4%) in the N/E/U components, respectively. The MBS model uses multiple reference stations thus can improve the positioning model strength and observation redundancy. This is especially beneficial for applying GNSS in complex monitoring environments such as canyons, open pits, slopes, large-area ground settlement, and long-spanned bridges and railroads.
- The accuracy of the MBS model is related to the number of reference stations and the quality of the baselines. With comparable baseline quality, the accuracy of the MBS model improves as the number of reference stations increases. Medium-long baseline experimental results show that compared with the SBS model, the MBS model using double reference stations can achieve an average improvement rate of about 24.0%, while the MBS model using triple reference stations can achieve an average improvement rate of about 30.2%.
- Compared with GPS-only and BDS-only positioning, the combined GPS/BDS positioning has an accuracy improvement of an average of 13.8 and 25.8% in the baseline components. Meanwhile, the proposed CMBS model can improve accuracy in the U direction and reach up to 45.0%.
Author Contributions
Funding
Conflicts of Interest
References
- Yu, W.; Peng, H.; Pan, L.; Dai, W.; Qu, X.; Ren, Z. Performance Assessment of High-Rate GPS/BDS Precise Point Positioning for Vibration Monitoring Based on Shaking Table Tests. Adv. Space Res. 2022, 69, 2362–2375. [Google Scholar] [CrossRef]
- Yan, H.; Dai, W.; Xie, L.; Xu, W. Fusion of GNSS and InSAR Time Series Using the Improved STRE Model: Applications to the San Francisco Bay Area and Southern California. J. Geod. 2022, 96, 47. [Google Scholar] [CrossRef]
- Shen, N.; Chen, L.; Liu, J.; Wang, L.; Tao, T.; Wu, D.; Chen, R. A Review of Global Navigation Satellite System (GNSS)-Based Dynamic Monitoring Technologies for Structural Health Monitoring. Remote Sens. 2019, 11, 1001. [Google Scholar] [CrossRef] [Green Version]
- Zhong, P.; Ding, X.; Yuan, L.; Xu, Y.; Kwok, K.; Chen, Y. Sidereal Filtering Based on Single Differences for Mitigating GPS Multipath Effects on Short Baselines. J. Geod. 2010, 84, 145–158. [Google Scholar] [CrossRef]
- Dai, W.; Huang, D.; Cai, C. Multipath Mitigation via Component Analysis Methods for GPS Dynamic Deformation Monitoring. GPS Solut. 2014, 18, 417–428. [Google Scholar] [CrossRef]
- Chen, J.; Yue, D.; Liu, Z.; Xu, C.; Zhu, S.; Chen, H. Experimental Research on Daily Deformation Monitoring of Bridge Using BDS/GPS. Surv. Rev. 2019, 51, 472–482. [Google Scholar] [CrossRef]
- Msaewe, H.A.; Hancock, C.M.; Psimoulis, P.A.; Roberts, G.W.; Bonenberg, L.; de Ligt, H. Investigating Multi-GNSS Performance in the UK and China Based on a Zero-Baseline Measurement Approach. Measurement 2017, 102, 186–199. [Google Scholar] [CrossRef]
- Quan, Y.; Lau, L.; Roberts, G.W.; Meng, X. Measurement Signal Quality Assessment on All Available and New Signals of Multi-GNSS (GPS, GLONASS, Galileo, BDS, and QZSS) with Real Data. J. Navig. 2016, 69, 313–334. [Google Scholar] [CrossRef] [Green Version]
- Roberts, G.W.; Tang, X. The Use of PSD Analysis on BeiDou and GPS 10 Hz Dynamic Data for Change Detection. Adv. Space Res. 2017, 59, 2794–2808. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Du, Y.; Meng, L.; Huang, G.; Wang, J.; Han, J. Application Performance Analysis of Three GNSS Precise Positioning Technology in Landslide Monitoring. In China Satellite Navigation Conference (CSNC) 2017 Proceedings: Volume I; Sun, J., Liu, J., Yang, Y., Fan, S., Yu, W., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2017; Volume 437, pp. 139–150. ISBN 978-981-10-4587-5. [Google Scholar]
- Xi, R.; Chen, H.; Meng, X.; Jiang, W.; Chen, Q. Reliable Dynamic Monitoring of Bridges with Integrated GPS and BeiDou. J. Surv. Eng. 2018, 144, 04018008. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Feng, Y.; Gao, W.; Yang, L. GNSS Ambiguity Resolution with Controllable Failure Rate for Long Baseline Network RTK. J. Geod. 2014, 88, 99–112. [Google Scholar] [CrossRef]
- Wilgan, K.; Hurter, F.; Geiger, A.; Rohm, W.; Bosy, J. Tropospheric Refractivity and Zenith Path Delays from Least-Squares Collocation of Meteorological and GNSS Data. J. Geod. 2017, 91, 117–134. [Google Scholar] [CrossRef] [Green Version]
- Wielgosz, P.; Paziewski, J.; Krankowski, A.; Kroszczyński, K.; Figurski, M. Results of the Application of Tropospheric Corrections from Different Troposphere Models for Precise GPS Rapid Static Positioning. Acta Geophys. 2012, 60, 1236–1257. [Google Scholar] [CrossRef]
- Schüler, T. Impact of Systematic Errors on Precise Long-Baseline Kinematic GPS Positioning. GPS Solut. 2006, 10, 108–125. [Google Scholar] [CrossRef]
- Luo, X.; Ou, J.; Yuan, Y.; Gao, J.; Jin, X.; Zhang, K.; Xu, H. An Improved Regularization Method for Estimating near Real-Time Systematic Errors Suitable for Medium-Long GPS Baseline Solutions. Earth Planets Space 2008, 60, 793–800. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Shen, M.; Deng, C.; Cui, J.; Yang, J. Network-Based Triple-Frequency Carrier Phase Ambiguity Resolution between Reference Stations Using BDS Data for Long Baselines. GPS Solut. 2018, 22, 73. [Google Scholar] [CrossRef]
- Assiadi, M.; Edwards, S.J.; Clarke, P.J. Enhancement of the Accuracy of Single-Epoch GPS Positioning for Long Baselines by Local Ionospheric Modelling. GPS Solut. 2014, 18, 453–460. [Google Scholar] [CrossRef] [Green Version]
- Chu, F.-Y.; Yang, M. GPS/Galileo Long Baseline Computation: Method and Performance Analyses. GPS Solut. 2014, 18, 263–272. [Google Scholar] [CrossRef]
- Zhang, Y.; Kubo, N.; Chen, J.; Chu, F.-Y.; Wang, H.; Wang, J. Contribution of QZSS with Four Satellites to Multi-GNSS Long Baseline RTK. J. Spat. Sci. 2020, 65, 41–60. [Google Scholar] [CrossRef]
- Li, X.; Huang, G.; Zhang, Q.; Zhao, Q. A New GPS/BDS Tropospheric Delay Resolution Approach for Monitoring Deformation in Super High-Rise Buildings. GPS Solut. 2018, 22, 90. [Google Scholar] [CrossRef]
- Paziewski, J. Precise GNSS Single Epoch Positioning with Multiple Receiver Configuration for Medium-Length Baselines: Methodology and Performance Analysis. Meas. Sci. Technol. 2015, 26, 035002. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, W.; Ge, M.; Wickert, J.; Schuh, H. An Enhanced Strategy for GNSS Data Processing of Massive Networks. J. Geod. 2014, 88, 857–867. [Google Scholar] [CrossRef]
- Borko, A.; Even-Tzur, G. Stochastic Model Reliability in GNSS Baseline Solution. J. Geod. 2021, 95, 20. [Google Scholar] [CrossRef]
- Alizadeh-Khameneh, M.A.; Sjöberg, L.E.; Jensen, A.B.O. Optimisation of GNSS Networks—Considering Baseline Correlations. Surv. Rev. 2019, 51, 35–42. [Google Scholar] [CrossRef]
- Wang, J.; Xu, T.; Nie, W.; Xu, G. GPS/BDS RTK Positioning Based on Equivalence Principle Using Multiple Reference Stations. Remote Sens. 2020, 12, 3178. [Google Scholar] [CrossRef]
- Fan, L.; Cui, X.; Lu, M. Precise and Robust RTK-GNSS Positioning in Urban Environments with Dual-Antenna Configuration. Sensors 2019, 19, 3586. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Xu, T.; Nie, W.; Xu, G. A Simplified Processing Algorithm for Multi-Baseline RTK Positioning in Urban Environments. Measurement 2021, 179, 109446. [Google Scholar] [CrossRef]
- Dardanelli, G.; Maltese, A.; Pipitone, C.; Pisciotta, A.; Lo Brutto, M. NRTK, PPP or Static, That Is the Question. Testing Different Positioning Solutions for GNSS Survey. Remote Sens. 2021, 13, 1406. [Google Scholar] [CrossRef]
- Mageed, K.M.A. Comparison of GPS Commercial Software Packages to Processing Static Baselines up to 30 KM. ARPN J. Eng. Appl. Sci. 2015, 10, 11. [Google Scholar]
- Andritsanos, V.D.; Arabatzi, O.; Gianniou, M.; Pagounis, V.; Tziavos, I.N.; Vergos, G.S.; Zacharis, E. Comparison of Various GPS Processing Solutions toward an Efficient Validation of the Hellenic Vertical Network: The ELEVATION Project. J. Surv. Eng. 2016, 142, 04015007. [Google Scholar] [CrossRef]
- Xu, G. GPS Data Processing with Equivalent Observation Equations. GPS Solut. 2002, 6, 28–33. [Google Scholar] [CrossRef]
- Shen, Y.; Xu, G. Simplified Equivalent Representation of GPS Observation Equations. GPS Solut. 2008, 12, 99–108. [Google Scholar] [CrossRef]
- Shen, Y.; Li, B.; Xu, G. Simplified Equivalent Multiple Baseline Solutions with Elevation-Dependent Weights. GPS Solut. 2009, 13, 165–171. [Google Scholar] [CrossRef]
- King, R.W.; Herring, T.A.; McCluscy, S.C. (Eds.) Documentation for the GAMIT GPS Analysis Software 10.6; Technology Report; Massachusetts Institute of Technology: Cambridge, MA, USA, 2015. [Google Scholar]
- Tralli, D.M.; Lichten, S.M. Stochastic Estimation of Tropospheric Path Delays in Global Positioning System Geodetic Measurements. Bull. Géod. 1990, 64, 127–159. [Google Scholar] [CrossRef]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere Mapping Functions for GPS and Very Long Baseline Interferometry from European Centre for Medium-Range Weather Forecasts Operational Analysis Data: TROPOSPHERE MAPPING FUNCTIONS FROM ECMWF. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Song, J.; Park, B.; Kee, C. Comparative Analysis of Height-Related Multiple Correction Interpolation Methods with Constraints for Network RTK in Mountainous Areas. J. Navig. 2016, 69, 991–1010. [Google Scholar] [CrossRef] [Green Version]
- Lou, Y.; Huang, J.; Zhang, W.; Liang, H.; Zheng, F.; Liu, J. A New Zenith Tropospheric Delay Grid Product for Real-Time PPP Applications over China. Sensors 2017, 18, 65. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Kee, C.; Park, B.; Park, H.; Seo, S. Correction Combination of Compact Network RTK Considering Tropospheric Delay Variation over Height. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014; IEEE: Monterey, CA, USA, May, 2014; pp. 95–101. [Google Scholar]
- Tang, W.; Liu, J.; Shi, C.; Lou, Y. Three Steps Method to Determine Double Difference Ambiguities Resolution of Network RTK Reference Station. Geomat. Inf. Sci. Wuhan Univ. 2007, 32, 305–308. [Google Scholar]
- Hatch, R. The Synergism of GPS Code and Carrier Measurements. In Proceedings of the Third International Geodetic Symposium on Satellite Doppler Positioning, Las Cruces, NM, USA, 8–12 February 1982; Volume 2, pp. 1213–1231. [Google Scholar]
- Lu, L.; Liu, W.; Zhang, X. An Effective QR-Based Reduction Algorithm for the Fast Estimation of GNSS High-Dimensional Ambiguity Resolution. Surv. Rev. 2018, 50, 57–68. [Google Scholar] [CrossRef]

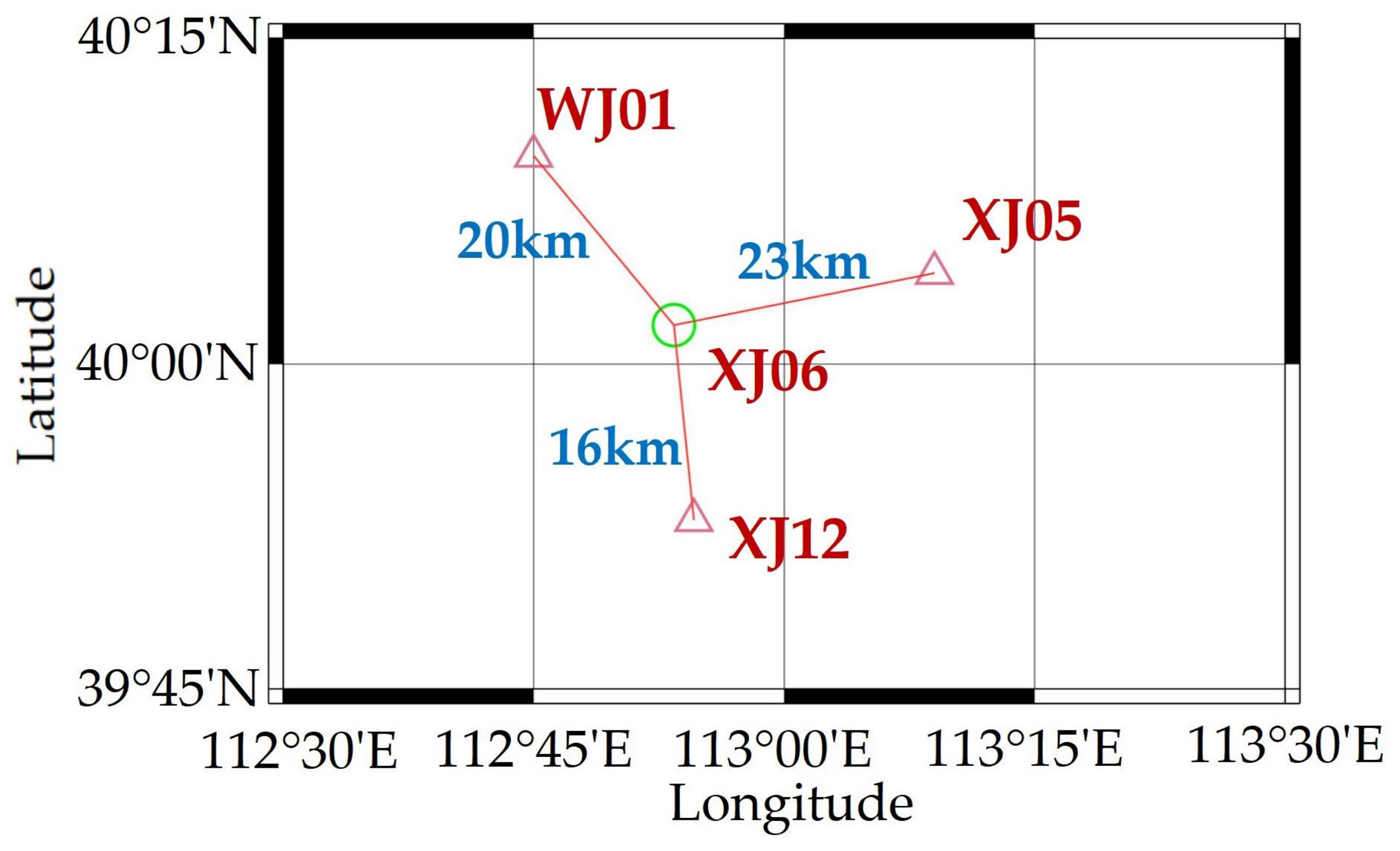



| Strategy | Reference Stations | Rover Station | Model | Baseline Length/km |
|---|---|---|---|---|
| XJ12 | XJ06 | SBS | 16 | |
| WJ01 | XJ06 | SBS | 20 | |
| XJ05 | XJ06 | SBS | 23 | |
| WJ01 + XJ12 | XJ06 | MBS | - | |
| WJ01 + XJ05 | XJ06 | MBS | - | |
| XJ05 + XJ12 | XJ06 | MBS | - | |
| WJ01 + XJ05 + XJ12 | XJ06 | MBS | - |
| Strategy | STD/mm | Improvement/% | RMS/mm | Improvement/% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | N | E | U | N | E | U | |
| 3.4 | 2.9 | 7.2 | - | - | - | 3.4 | 3.1 | 12.5 | - | - | - | |
| 4.9 | 4.3 | 9.9 | - | - | - | 4.9 | 4.4 | 13.2 | - | - | - | |
| 3.3 | 2.4 | 7.9 | - | - | - | 3.5 | 2.5 | 10.5 | - | - | - | |
| 2.7 | 2.8 | 6.5 | 20.6 | 3.5 | 9.7 | 2.9 | 2.8 | 8.7 | 14.7 | 9.7 | 30.4 | |
| 2.6 | 2.4 | 5.7 | 23.5 | 17.2 | 20.8 | 2.7 | 2.4 | 6.9 | 20.6 | 22.6 | 44.8 | |
| 2.4 | 2.0 | 5.3 | 29.4 | 31.0 | 26.4 | 2.4 | 2.0 | 7.3 | 29.4 | 35.5 | 41.6 | |
| 2.4 | 2.2 | 5.1 | 29.4 | 24.1 | 29.2 | 2.5 | 2.2 | 7.1 | 26.5 | 29.0 | 43.2 | |
| Average improvement rate | - | - | - | 25.7 | 19.0 | 21.5 | - | - | 22.8 | 24.2 | 40.0 | |
| Strategy | Reference Stations | Rover Station | Height Differences w.r.t. Reference Stations/m | Model | Tropospheric Constraint |
|---|---|---|---|---|---|
| MDT1 | YEY2 | 263 | SBS | No | |
| MDT1 | YEY3 | 200 | SBS | No | |
| MDT1 | YEY5 | 112 | SBS | No | |
| MDT1 + NS01 | YEY2 | (263, 152) | MBS | No | |
| MDT1 + NS01 | YEY2 | (263, 152) | MBS | No | |
| MDT1 + NS01 | YEY2 | (263, 152) | MBS | No | |
| MDT1 + NS01 | YEY2 | (263, 152) | CMBS | Yes | |
| MDT1 + NS01 | YEY3 | (200, 215) | MBS | No | |
| MDT1 + NS01 | YEY3 | (200, 215) | CMBS | Yes | |
| MDT1 + NS01 | YEY5 | (112, 303) | MBS | No | |
| MDT1 + NS01 | YEY5 | (112, 303) | CMBS | Yes |
| Strategy | STD/mm | Improvement/% | RMS/mm | Improvement/% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | N | E | U | N | E | U | |
| 2.6 | 2.5 | 9.8 | - | - | - | 3.4 | 4.7 | 10.4 | - | - | - | |
| 3.0 | 2.2 | 13.7 | - | - | - | 4.1 | 5.2 | 14.4 | - | - | - | |
| 2.0 | 1.9 | 8.0 | 23.1 | 24.0 | 18.4 | 3.5 | 4.8 | 8.1 | 2.9 | 2.1 | 22.1 | |
| Strategy | STD/mm | Improvement/% | RMS/mm | Improvement/% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | E | U | N | E | U | N | E | U | N | E | U | |
| 3.8 | 3.9 | 13.0 | - | - | - | 4.1 | 10.4 | 13.7 | - | - | - | |
| 3.4 | 4.4 | 13.8 | - | - | - | 5.1 | 12.0 | 14.4 | - | - | - | |
| 3.6 | 4.6 | 13.2 | - | - | - | 12.2 | 9.1 | 13.3 | - | - | - | |
| 2.0 | 1.9 | 8.0 | 47.4 | 51.3 | 38.5 | 3.5 | 4.8 | 8.1 | 14.6 | 53.9 | 40.9 | |
| 2.0 | 1.9 | 4.4 | 47.4 | 51.3 | 66.2 | 3.4 | 4.8 | 5.7 | 17.1 | 53.9 | 58.4 | |
| 2.1 | 2.2 | 8.6 | 38.2 | 50.0 | 37.7 | 2.2 | 6.4 | 10.9 | 56.9 | 46.7 | 24.3 | |
| 2.1 | 2.2 | 5.6 | 38.2 | 50.0 | 59.4 | 2.2 | 6.4 | 9.8 | 56.9 | 46.7 | 31.9 | |
| 2.3 | 2.6 | 8.8 | 36.1 | 43.5 | 33.3 | 7.6 | 3.6 | 10.2 | 37.7 | 60.4 | 23.3 | |
| 2.3 | 2.6 | 8.8 | 36.1 | 43.5 | 33.3 | 7.6 | 3.6 | 10.2 | 37.7 | 60.4 | 23.3 | |
| Average improvement rate | - | - | - | 40.6 | 48.3 | 44.7 | - | - | - | 36.8 | 53.7 | 33.7 |
| Strategy | STD/mm | Improvement/% | RMS/mm | Improvement/% |
|---|---|---|---|---|
| 8.0 | - | 8.1 | - | |
| 4.4 | 45.0 | 5.7 | 29.6 | |
| 8.6 | - | 10.9 | - | |
| 5.6 | 34.9 | 9.8 | 10.1 | |
| 8.8 | - | 10.2 | - | |
| 8.8 | 0.0 | 10.2 | 0.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Dai, W.; Yu, W. BDS/GPS Multi-Baseline Relative Positioning for Deformation Monitoring. Remote Sens. 2022, 14, 3884. https://doi.org/10.3390/rs14163884
Wang H, Dai W, Yu W. BDS/GPS Multi-Baseline Relative Positioning for Deformation Monitoring. Remote Sensing. 2022; 14(16):3884. https://doi.org/10.3390/rs14163884
Chicago/Turabian StyleWang, Haonan, Wujiao Dai, and Wenkun Yu. 2022. "BDS/GPS Multi-Baseline Relative Positioning for Deformation Monitoring" Remote Sensing 14, no. 16: 3884. https://doi.org/10.3390/rs14163884
APA StyleWang, H., Dai, W., & Yu, W. (2022). BDS/GPS Multi-Baseline Relative Positioning for Deformation Monitoring. Remote Sensing, 14(16), 3884. https://doi.org/10.3390/rs14163884