Advances in InSAR Imaging and Data Processing
1. Introduction
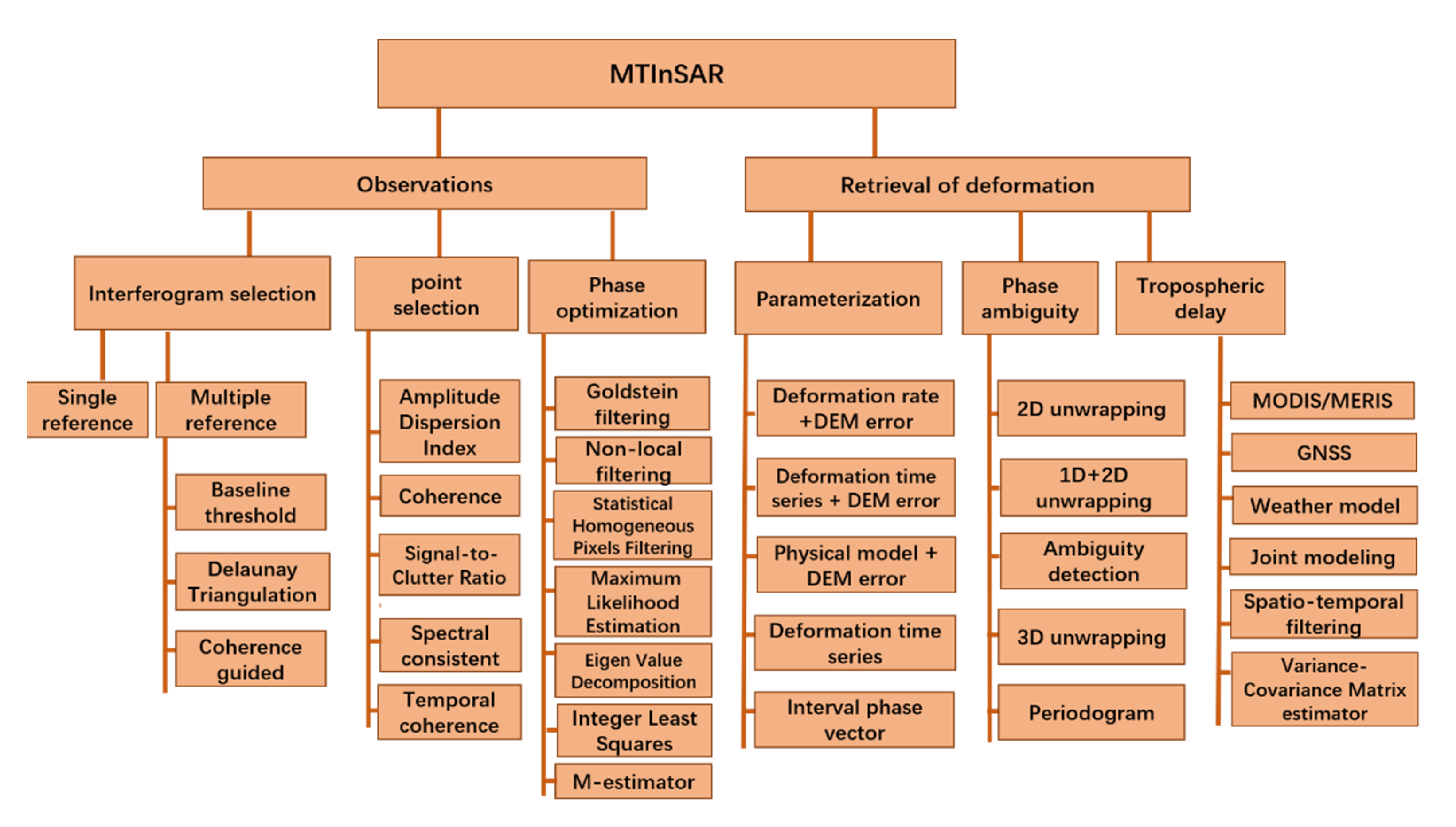
2. MTInSAR Observation Selection and Enhancement
3. Phase Ambiguity Estimation
4. Atmospheric Delay Mitigation
5. Advances in SAR Imaging
6. Applications
6.1. Geohazard Detection
6.2. Deformation Mapping
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hanssen, R. Radar Interferometry: Data Interpretation and Error Analysis, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Rosen, P.A.; Hensley, S.; Joughin, I.; Li, F.K.; Madsen, S.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 83, 333–382. [Google Scholar]
- Lu, Z.; Dzurisin, D. InSAR Imaging of Aleutian Volcanoes: Monitoring a Volcanic Arc from Space; Springer Praxis Books; Geophysical Sciences: Chicago, IL, USA, 2014. [Google Scholar]
- Zhang, L.; Ding, X.L.; Lu, Z. Ground deformation mapping by fusion of multi-temporal interferometric synthetic aperture radar images: A review. Int. J. Image Data Fus. 2015, 6, 289–313. [Google Scholar] [CrossRef]
- Li, F.; Goldstein, R.M. Studies of multi-baseline spaceborne interferometric synthetic aperture radars. IEEE Trans. Geosci. Remote Sens. 1990, 28, 88–97. [Google Scholar] [CrossRef]
- Barber, B.C. The phase statistics of a multichannel radar interferometer. Wave Random Media 1993, 3, 257–266. [Google Scholar] [CrossRef]
- Just, D.; Bamler, R. Phase Statistics of Interferograms with Applications to Synthetic Aperture Radar. Appl. Opt. 1994, 33, 4361–4368. [Google Scholar] [CrossRef]
- Seymour, M.S.; Cumming, I.G. Maximum likelihood estimator for SAR interferometry. In Proceedings of the IGARSS, Pasadena, CA, USA, 8–12 August 1994; pp. 2272–2275. [Google Scholar]
- Joughin, I.R.; Winebrenner, D.P.; Percival, D.B. Probability density functions for multilook polarimetric signatures. IEEE Trans. Geosci. Remote Sens. 1994, 32, 562–574. [Google Scholar] [CrossRef]
- Touzi, R.; Lopes, A. Statistics of the Stokes Parameters and of the Complex Coherence Parameters in One-Look and Multilook Speckle Fields. IEEE Trans. Geosci. Remote Sens. 1996, 34, 519–531. [Google Scholar] [CrossRef]
- Zebker, H.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Lanyi, G.E. The effect of the dynamic wet troposphere on radio interferometric measurements. Radio Sci. 1987, 22, 251–265. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Sica, F.; Cozzolino, D.; Zhu, X.X.; Verdoliva, L.; Poggi, G. InSAR-BM3D: A Nonlocal Filter for SAR Interferometric Phase Restoration. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3456–3467. [Google Scholar] [CrossRef] [Green Version]
- Costantini, M. A Novel Phase Unwrapping Method Based on Network Programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Usai, S. The use of man-made features for long time scale INSAR. In Proceedings of the IGARSS, Singapore, 3–8 August 1997. [Google Scholar]
- Chen, C.W.; Zebker, H.A. Network approaches to two-dimensional phase unwrapping: Intractability and two new algorithms. J. Opt. Soc. Am. A 2000, 17, 401–414. [Google Scholar] [CrossRef]
- Pepe, A.; Lanari, R. On the Extension of the Minimum Cost Flow Algorithm for Phase Unwrapping of Multitemporal Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2374–2383. [Google Scholar] [CrossRef]
- Piyush Shanker, A.; Zebker, H. Edgelist phase unwrapping algorithm for time series InSAR analysis. J. Opt. Soc. Am. A 2010, 27, 605–612. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, X.L.; Lu, Z. Modeling the PSInSAR time-series without phase unwrapping. IEEE Trans. Geosci. Remote Sens. 2011, 49, 547–556. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.L.; Li, Z.W. Hybrid approach for unbiased coherence estimation for multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2459–2473. [Google Scholar] [CrossRef]
- Jiang, M.; Guarnieri, A.M. Distributed scatterer interferometry with the refinement of spatiotemporal coherence. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3977–3983. [Google Scholar] [CrossRef]
- Liang, H.Y.; Zhang, L.; Ding, X.L.; Lu, Z.; Li, X. Toward Mitigating Stratified Tropospheric Delays in Multitemporal InSAR: A Quadtree Aided Joint model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 291–303. [Google Scholar] [CrossRef]
- Zebker, H. Accuracy of a Model-Free Algorithm for Temporal InSAR Tropospheric Correction. Remote Sens. 2021, 13, 409. [Google Scholar]
- Li, Z.; Cao, Y.; Wei, J.; Duan, M.; Wu, L.; Hou, J.; Zhu, J. Time-series InSAR ground deformation monitoring: Atmospheric delay modeling and estimating. Earth-Sci. Rev. 2019, 192, 258–284. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef] [Green Version]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Jung, H.C. A phase-decomposition-based PSInSAR processing method. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1074–1090. [Google Scholar] [CrossRef]
- De Zan, F. Optimizing SAR Interferometry for Decorrelating Scatterers. Ph.D. Thesis, Politecnico di Milano, Milano, Italy, 2008. [Google Scholar]
- Samiei-Esfahany, S. Exploitation of Distributed Scatterers in Synthetic Aperture Radar Interferometry. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 31 May 2017. [Google Scholar]
- Chen, Y.; Sun, Q.; Hu, J. Quantitatively Estimating of InSAR Decorrelation Based on Landsat-Derived NDVI. Remote Sens. 2021, 13, 2440. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Li, T.; Gao, Y.; Zhou, X.; Chen, Q.; Zhang, X.; Yang, C. An Adaptive Weighted Phase Optimization Algorithm Based on the Sigmoid Model for Distributed Scatterers. Remote Sens. 2021, 13, 3253. [Google Scholar] [CrossRef]
- Dong, L.; Wang, C.; Tang, Y.; Zhang, H.; Xu, L. Improving CPT-InSAR Algorithm with Adaptive Coherent Distributed Pixels Selection. Remote Sens. 2021, 13, 4784. [Google Scholar] [CrossRef]
- Pu, L.; Zhang, X.; Zhou, L.; Li, L.; Shi, J.; Wei, S. Nonlocal Feature Selection Encoder–Decoder Network for Accurate InSAR Phase Filtering. Remote Sens. 2022, 14, 1174. [Google Scholar] [CrossRef]
- Yuan, Z.; Chen, T.; Xing, X.; Peng, W.; Chen, L. BM3D Denoising for a Cluster-Analysis-Based Multibaseline InSAR Phase-Unwrapping Method. Remote Sens. 2022, 14, 1836. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S.; Gao, Y.; Li, S.; Jia, Y.; Li, M. Adaptive Square-Root Unscented Kalman Filter Phase Unwrapping with Modified Phase Gradient Estimation. Remote Sens. 2022, 14, 1229. [Google Scholar] [CrossRef]
- Mao, W.; Wang, S.; Xu, B.; Li, Z.; Zhu, Y. An Improved Phase Unwrapping Method Based on Hierarchical Networking and Constrained Adjustment. Remote Sens. 2021, 13, 4193. [Google Scholar] [CrossRef]
- Liu, J.; Yang, H.; Xu, L.; Li, T. Novel Model-Based Approaches for Non-Homogenous Atmospheric Compensation of GB-InSAR in the Azimuth and Horizontal Directions. Remote Sens. 2021, 13, 2153. [Google Scholar] [CrossRef]
- Zhao, Z.; Tian, W.; Deng, Y.; Hu, C.; Zeng, T. Calibration Method of Array Errors for Wideband MIMO Imaging Radar Based on Multiple Prominent Targets. Remote Sens. 2021, 13, 2997. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, Z.; Kim, J.-W. P-Band InSAR for Geohazard Detection over Forested Terrains: Preliminary Results. Remote Sens. 2021, 13, 4575. [Google Scholar] [CrossRef]
- Zhang, L.; Dai, K.; Deng, J.; Ge, D.; Liang, R.; Li, W.; Xu, Q. Identifying Potential Landslides by Stacking-InSAR in Southwestern China and Its Performance Comparison with SBAS-InSAR. Remote Sens. 2021, 13, 3662. [Google Scholar] [CrossRef]
- Qu, F.; Zhang, Q.; Niu, Y.; Lu, Z.; Wang, S.; Zhao, C.; Zhu, W.; Qu, W.; Yang, C. Mapping the Recent Vertical Crustal Deformation of the Weihe Basin (China) Using Sentinel-1 and ALOS-2 ScanSAR Imagery. Remote Sens. 2022, 14, 3182. [Google Scholar] [CrossRef]
- Bao, X.; Zhang, R.; Shama, A.; Li, S.; Xie, L.; Lv, J.; Fu, Y.; Wu, R.; Liu, G. Ground Deformation Pattern Analysis and Evolution Prediction of Shanghai Pudong International Airport Based on PSI Long Time Series Observations. Remote Sens. 2022, 14, 610. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, J.; Yi, H.; Zhu, Y.; Xu, B. Underground Goaf Parameters Estimation by Cross-Iteration with InSAR Measurements. Remote Sens. 2021, 13, 3204. [Google Scholar] [CrossRef]
- Liao, M.; Zhang, R.; Lv, J.; Yu, B.; Pang, J.; Li, R.; Xiang, W.; Tao, W. Subsidence Monitoring of Fill Area in Yan’an New District Based on Sentinel-1A Time Series Imagery. Remote Sens. 2021, 13, 3044. [Google Scholar] [CrossRef]
- Yang, Y.-H.; Chen, Q.; Xu, Q.; Zhao, J.-J.; Hu, J.-C.; Li, H.-L.; Xu, L. Comprehensive Investigation of Capabilities of the Left-Looking InSAR Observations in Coseismic Surface Deformation Mapping and Faulting Model Estimation Using Multi-Pass Measurements: An Example of the 2016 Kumamoto, Japan Earthquake. Remote Sens. 2021, 13, 2034. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, M.; Zhang, H.; Wang, C.; Tang, Y.; Xu, J.; Yan, D.; Wang, C. Detecting Rock Glacier Displacement in the Central Himalayas Using Multi-Temporal InSAR. Remote Sens. 2021, 13, 4738. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Lu, Z. Advances in InSAR Imaging and Data Processing. Remote Sens. 2022, 14, 4307. https://doi.org/10.3390/rs14174307
Zhang L, Lu Z. Advances in InSAR Imaging and Data Processing. Remote Sensing. 2022; 14(17):4307. https://doi.org/10.3390/rs14174307
Chicago/Turabian StyleZhang, Lei, and Zhong Lu. 2022. "Advances in InSAR Imaging and Data Processing" Remote Sensing 14, no. 17: 4307. https://doi.org/10.3390/rs14174307
APA StyleZhang, L., & Lu, Z. (2022). Advances in InSAR Imaging and Data Processing. Remote Sensing, 14(17), 4307. https://doi.org/10.3390/rs14174307





