Machine Learning-Based Rockfalls Detection with 3D Point Clouds, Example in the Montserrat Massif (Spain)
Abstract
:1. Introduction
1.1. Rockfall Source Analysis from Point Cloud Data
1.2. Improvements on Rockfall Detection from Point Cloud Comparison including Machine Learning Algorithms
- We propose an extension of the full end-to-end intelligent framework proposed by Zoumpekas et al. [32] for rockfall detection handling highly imbalanced data by reducing the number of clusters in our data. We further introduce geological properties to the framework itself.
- We implement the proposed intelligent system with real data from two different cliffs of Montserrat massif (NE Spain) to validate its efficacy and effectiveness.
- Our results show great performance and robustness, which is of paramount importance in rockfall detection.
- We provide a baseline methodology and a detection accuracy benchmark for future related experimental analyses.
- We have made fully accessible the applications developed in this work, the 3D point cloud data used, and an example of application in public repositories (see Section 2).
2. Methods
- The adaptation of the M3C2 algorithm to measure differences point-to-point and to obtain the new associated features required for the machine learning processes. The main features are geometric such as difference between point clouds, reference and compared surface orientation, indexes of coplanarity and collinearity.
- The development of a self-calibration method to automatically define the limit of detection (LoD) and differentiate real changes in the rock cliff from the system noise.
- The adaptation of the DBSCAN algorithm for clustering point clouds and create new cluster features of predominance associated with the point differences (retreat or advance) in the cliff surface.
- The analysis of different machine learning models to classify clusters of rockfalls.
2.1. Adaptation of the M3C2 Algorithm
2.2. Automatic Calibration
2.3. DBSCAN Adaptation
2.4. Cluster Classification
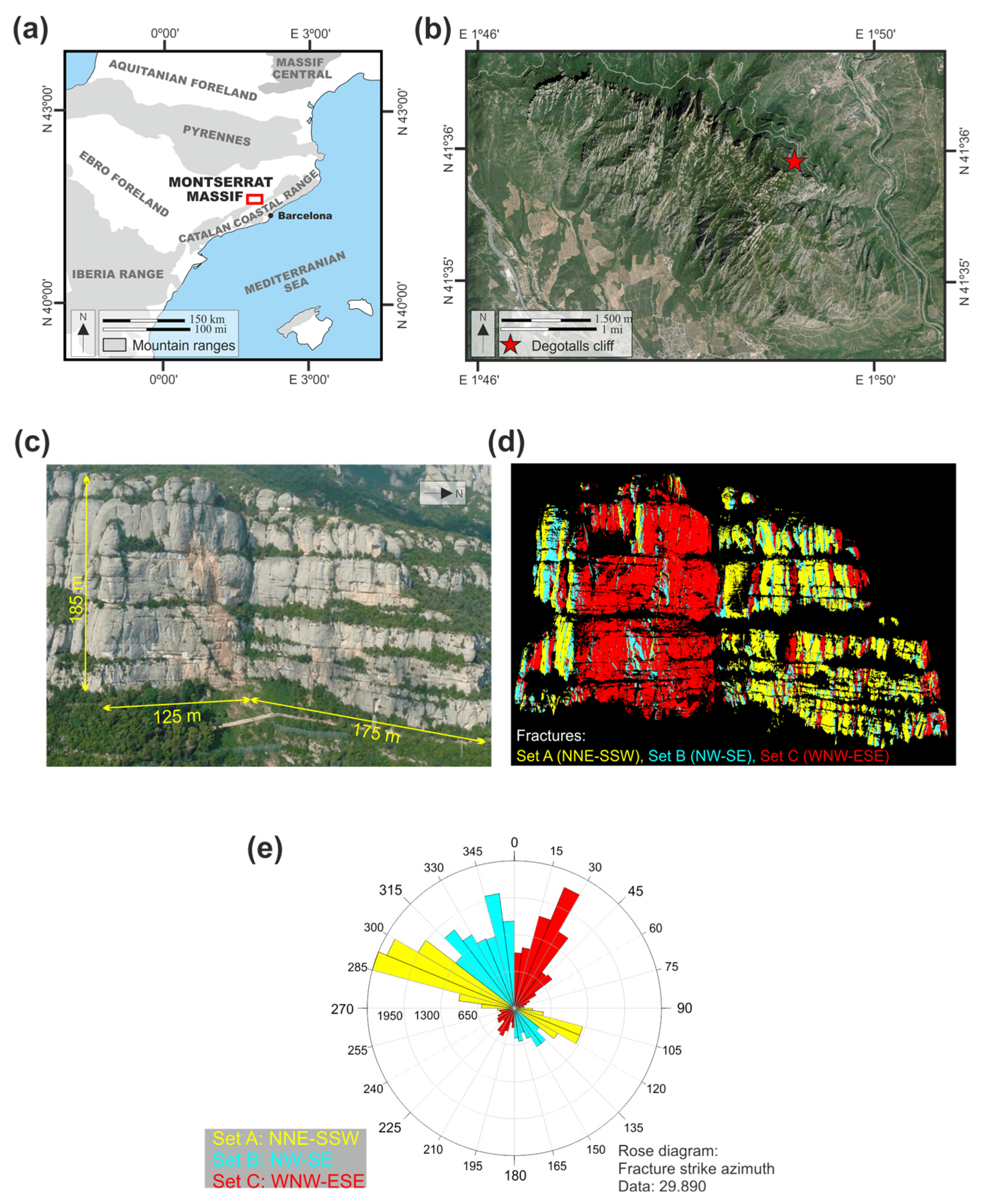
3. Study Sites and Processing
Study Sites
4. Results
5. Discussion
6. Conclusions
- -
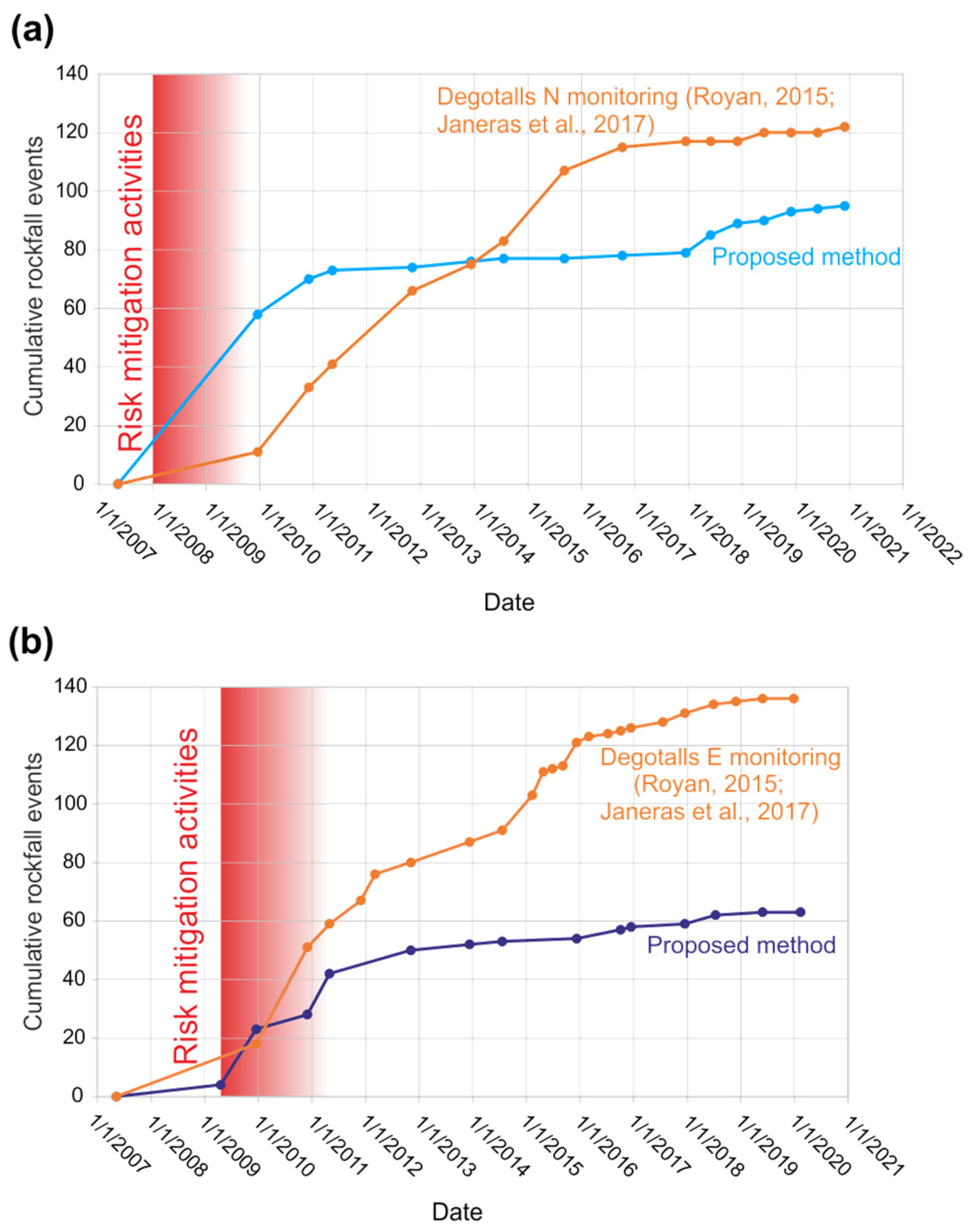
- Monitoring rockfalls in rock cliffs with point cloud is a difficult task that can benefit from machine learning strategies, provided that both techniques are appropriately combined. We validate this assumption with the attempt to identify rockfalls in the rock cliff of the Montserrat massif (Spain).
- -
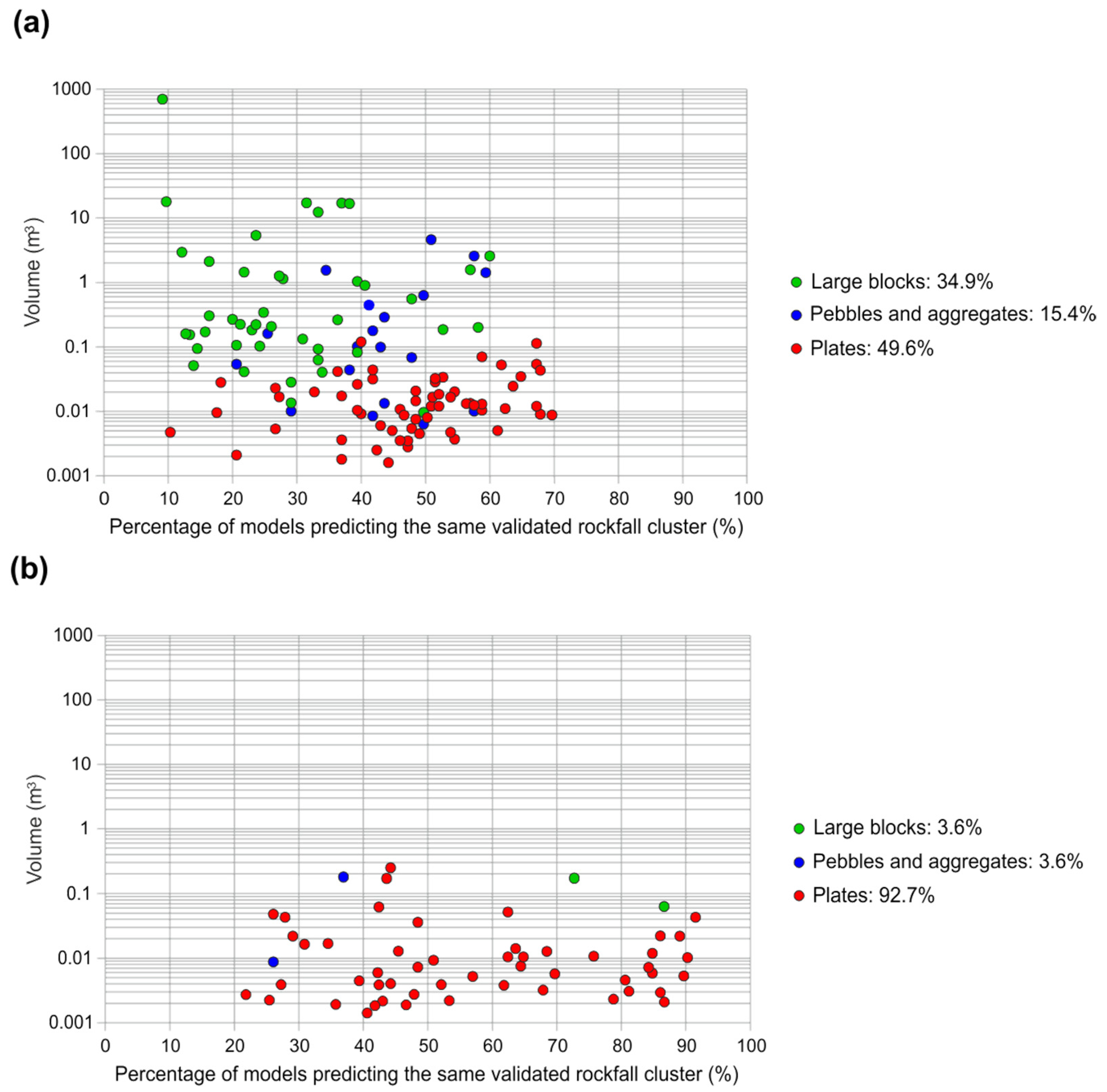
- We have observed the difficulty of correlating classification models, trained with clusters of rockfalls, with the best prediction model. For this reason, we use all the combinations of prediction models to validate the most proposed candidates.
- -
- The success of the rockfall prediction models depends on the homogeneity/heterogeneity of the features that characterize the different categories of the rockfall clusters (large blocks, pebbles and plates) used to train the classification models.
- -
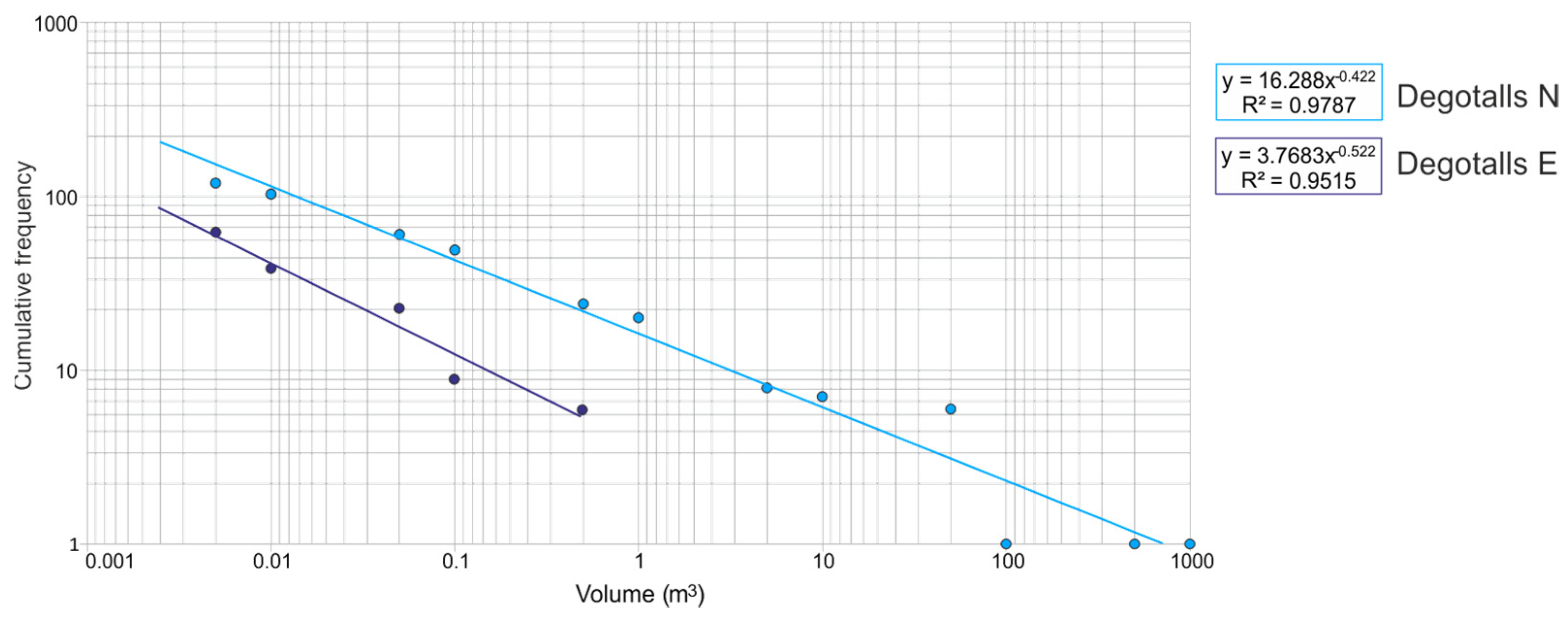
- Rockfalls in the Degotalls (Montserrat, Spain) are currently in a phase of stabilization, and those that occur are of small volume and attributable to plates associated with weathering processes. However, since 2018 a slight increase in cases has been observed.
Author Contributions
Funding

Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Point coordinates |
| 1. Coordinate X |
| 2. Coordinate Y |
| 3. Coordinate Z |
| With intensity |
| 4. Intensity |
| Or RGB texture |
| 5. Red |
| 6. Green |
| 7. Blue |
| Or intensity and texture |
| 8. Intensity |
| 9. Red |
| 10. Green |
| 11. Blue |
Appendix B
| 1. n * | Reference point index |
| 2. m | Compared point index |
| 3. Coordinate X | |
| 4. Coordinate Y | Point reference coordinates |
| 5. Coordinate Z | |
| 6. Code_n * | Reference index texture (0 n/a, 1 Intensity, 2 RGB, 3 RGB + Int) |
| 7. R 1 | |
| 8. G 1 | Texture reference points RGB format |
| 9. B 1 | |
| 10. Intensity 2 | Reference intensity texture |
| 11. Vector_i | |
| 12. Vector_j | Reference vector normal vector components |
| 13. Vector_k | |
| 14. Orientation | Reference strike azimuth (degree) |
| 15. Dip | Reference strike slope (degree) |
| 16. Collinearity | Reference point index of collinearity |
| 17. Coplanarity | Reference point index of coplanarity |
| 18. Selected | Number of points to calculate the normal vector |
| 19. Distance | Distance selected between closest and average |
| 20. Vertical Distance | Vertical distance along vector with direction (+ or −) |
| 21. Horizontal Distance | Horizontal distance component between points |
| 22. Distance closest | Shorter distance between Refer. and Comp. point |
| 23. Coordinate X | |
| 24. Coordinate Y | Point compared coordinates |
| 25. Coordinate Z | |
| 26. Code_m * | Compared index texture (0 n/a, 1 Intensity, 2 RGB, 3 RGB + Int) |
| 27. R 1 | |
| 28. G 1 | Texture compared points RGB format |
| 29. B 1 | |
| 30. Intensity 2 | Compared intensity texture |
| 31. vector_i | |
| 32. vector_j | Compared vector normal vector components |
| 33. vector_k | |
| 34. Orientation | Compared strike azimuth (degree) |
| 35. Dip | Compared strike slope (degree) |
| 36. Collinearity | Compared point index of collinearity |
| 37. Coplanarity | Compared point index of coplanarity |
| 38. Selected | Number of points to calculate the normal vector |
| 39. Angle | Angle between Ref. and Comp. normal vectors |
| 40. Angle_Direction | Angle with direction |
| 41. Minimal_distance | Shortest distance between those inscribed in the geometric figure |
| 42. Average_distance | Average distance between those inscribed in the geometric figure |
| 43. Maxima_distance | Longest distance between those inscribed in the geometric figure |
| 44. Dev. Stand_distance | Dev.Stand distance between those inscribed in the geometric figure |
| 45. Selected points | Number of points inscribed in the geometric figure |
Appendix C
| 1. Cluster identification * | |
| 2. Coordinate X * | |
| 3. Coordinate Y * | Coordinates of cluster centroid |
| 4. Coordinate Z * | |
| 5. Item_number * | Cluster differences number |
| 6. Points_number | Number of points |
| 7. TotalVolume | Cluster total volume |
| 8. PositiveVolume | Volume behind the reference surface and TLS |
| 9. NegativeVolume | Volume in front the reference surface and TLS |
| 10. Area | Planimetric cluster area 2D, perpendicular to TLS |
| 11. Code * | Cluster classification (Unknown, Candidate) |
| 12. Confidence * | Confidence index |
| 13. Predominance_Mean | Mean predominance (noise 0, advance 1, retreat 2) |
| 14. Predominance _Sigma | STD predominance classification (0, 1, 2) |
| 15. Percentage_1_Mean | Mean advance predominance (1) |
| 16. Percentage_1_Sigma | STD advance predominance (1) classification |
| 17. Percentage_0_Mean | Mean noise predominance (0) |
| 18. Percentage_0_Sigma | STD noise predominance (0) classification |
| 19. Percentage_2_Mean | Mean retreat predominance (2) |
| 20. Percentage_2_Sigma | STD retreat predominance (2) classification |
| 21. OrientationSetsRef | Reference cluster strike azimuth |
| 22. OrientationSetsCom | Compared cluster strike azimuth |
| 23. IndexTextureRef * | Reference texture index (0, 1 Int, 2 RGB, 3 RGB + Int) |
| 24. R_Mean_Ref 1 | |
| 25. R_Sigma_Ref 1 | |
| 26. G_mean_Ref 1 | |
| 27. G_Sigma_Ref 1 | |
| 28. B_mean_Ref 1 | Texture. Mean & Std of reference clusters. |
| 29. B_Sigma_Ref 1 | |
| 30. I_Mean_Ref 2 | |
| 31. I_Sigma_Ref 2 | |
| 32. IndexTextureCom * | Compared texture index (0, 1 Int, 2 RGB, 3 RGB + Int) |
| 33. R_mean_Com 1 | |
| 34. R_Sigma_Com 1 | |
| 35. G_mean_Com 1 | |
| 36. G_Sigma_Com 1 | |
| 37. B_mean_Com 1 | Texture. Mean & Std dev. of compared clusters |
| 38. B_Sigma_Com 1 | |
| 39. I_Mean_Com 2 | |
| 40. I_Sigma_Com 2 | |
| 41. AziRef_Mean | Mean strike azimuth of Reference points |
| 42. SloRef_Mean | Mean strike slope of Reference points |
| 43. AziCom_Mean | Mean strike azimuth of Compared points |
| 44. SloCom_Mean | Mean strike slope of Compared points |
| 45. CopRef_Mean | Mean coplanarity of Reference points |
| 46. CopRef_Sigma | STD coplanarity of Reference points |
| 47. ColRef_Mean | Mean collinearity of Reference points |
| 48. ColRef_Sigma | STD collinearity of Reference points |
| 49. CopCom_Mean | Mean coplanarity of Compared points |
| 50. CopCom_Sigma | STD coplanarity of Compared points |
| 51. ColCom_Mean | Mean collinearity of Compared points |
| 52. ColCom_Sigma | STD collinearity of Compared points |
| 53. ang_Mean | Mean angularity between normal vectors |
| 54. ang_Sigma | STD angularity between normal vectors |
| 55. Reference File * | String |
| 56. Compared File * | String |
References
- Erismann, T.H.; Abele, G. Dynamics of Rockslides and Rockfalls; Springer: Berlin/Heidelberg, Germany, 2001; ISBN 978-3-642-08653-3. [Google Scholar]
- Whalley, W.B. Rockfalls. In Slope Instability; Brunsden, D., Prior, D.B., Eds.; Wiley: Chichester, UK, 1984; pp. 217–256. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes Classification of Landslide Types, an Update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- DiFrancesco, P.-M.; Bonneau, D.; Hutchinson, D.J. The Implications of M3C2 Projection Diameter on 3D Semi-Automated Rockfall Extraction from Sequential Terrestrial Laser Scanning Point Clouds. Remote Sens. 2020, 12, 1885. [Google Scholar] [CrossRef]
- Volkwein, A.; Schellenberg, K.; Labiouse, V.; Agliardi, F.; Berger, F.; Bourrier, F.; Dorren, L.K.A.; Gerber, W.; Jaboyedoff, M. Rockfall Characterisation and Structural Protection—A Review. Nat. Hazards Earth Syst. Sci. 2011, 11, 2617–2651. [Google Scholar] [CrossRef]
- Corominas, J.; Copons, R.; Moya, J.; Vilaplana, J.M.; Altimir, J.; Amigó, J. Quantitative Assessment of the Residual Risk in a Rockfall Protected Area. Landslides 2005, 2, 343–357. [Google Scholar] [CrossRef]
- van Veen, M.; Hutchinson, D.J.; Kromer, R.; Lato, M.; Edwards, T. Effects of Sampling Interval on the Frequency—Magnitude Relationship of Rockfalls Detected from Terrestrial Laser Scanning Using Semi-Automated Methods. Landslides 2017, 14, 1579–1592. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J. The Importance of Monitoring Interval for Rockfall Magnitude-Frequency Estimation. J. Geophys. Res. Earth Surf. 2019, 124, 2841–2853. [Google Scholar] [CrossRef]
- Ritchie, A.M. Evaluation of Rockfall and Its Control. Highw. Res. Rec. 1963, 17, 13–28. [Google Scholar]
- Sturzenegger, M.; Stead, D. Quantifying Discontinuity Orientation and Persistence on High Mountain Rock Slopes and Large Landslides Using Terrestrial Remote Sensing Techniques. Nat. Hazards Earth Syst. Sci. 2009, 9, 267–287. [Google Scholar] [CrossRef]
- Abellán, A.; Oppikofer, T.; Jaboyedoff, M.; Rosser, N.J.; Lim, M.; Lato, M.J. Terrestrial Laser Scanning of Rock Slope Instabilities. Earth Surf. Process. Landf. 2014, 39, 80–97. [Google Scholar] [CrossRef]
- Abellan, A.; Derron, M.-H.; Jaboyedoff, M. “Use of 3D Point Clouds in Geohazards” Special Issue: Current Challenges and Future Trends. Remote Sens. 2016, 8, 130. [Google Scholar] [CrossRef]
- Telling, J.; Lyda, A.; Hartzell, P.; Glennie, C. Review of Earth Science Research Using Terrestrial Laser Scanning. Earth Sci. Rev. 2017, 169, 35–68. [Google Scholar] [CrossRef] [Green Version]
- Santana, D.; Corominas, J.; Mavrouli, O.; Garcia-Sellés, D. Magnitude–Frequency Relation for Rockfall Scars Using a Terrestrial Laser Scanner. Eng. Geol. 2012, 145–146, 50–64. [Google Scholar] [CrossRef]
- Corominas, J.; Mavrouli, O.; Ruiz-Carulla, R. Rockfall Occurrence and Fragmentation. In Advancing Culture of Living with Landslides; Springer International Publishing: Cham, Switzerland, 2017; pp. 75–97. [Google Scholar] [CrossRef]
- Fanti, R.; Gigli, G.; Lombardi, L.; Tapete, D.; Canuti, P. Terrestrial Laser Scanning for Rockfall Stability Analysis in the Cultural Heritage Site of Pitigliano (Italy). Landslides 2013, 10, 409–420. [Google Scholar] [CrossRef]
- Mazzanti, P.; Schilirò, L.; Martino, S.; Antonielli, B.; Brizi, E.; Brunetti, A.; Margottini, C.; Scarascia Mugnozza, G. The Contribution of Terrestrial Laser Scanning to the Analysis of Cliff Slope Stability in Sugano (Central Italy). Remote Sens. 2018, 10, 1475. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D Comparison of Complex Topography with Terrestrial Laser Scanner: Application to the Rangitikei Canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Tonini, M.; Abellán, A. Rockfall Detection from Terrestrial Lidar Point Clouds: A clustering approach using R. J. Spat. Inf. Sci. 2013, 8, 95–110. [Google Scholar] [CrossRef]
- Janeras, M.; Jara, J.-A.; Royán, M.J.; Vilaplana, J.-M.; Aguasca, A.; Fàbregas, X.; Gili, J.A.; Buxó, P. Multi-technique Approach to Rockfall Monitoring in the Montserrat Massif (Catalonia, NE Spain). Eng. Geol. 2017, 219, 4–20. [Google Scholar] [CrossRef]
- Bonneau, D.; DiFrancesco, P.M.; Jean Hutchinson, D. Surface Reconstruction for Three-Dimensional Rockfall Volumetric Analysis. ISPRS Int. J. Geo-Inf. 2019, 8, 548. [Google Scholar] [CrossRef]
- Bonneau, D.A.; Hutchinson, D.J. The Use of Terrestrial Laser Scanning for the Characterization of a Cliff-Talus System in the Thompson River Valley, British Columbia, Canada. Geomorphology 2019, 327, 598–609. [Google Scholar] [CrossRef]
- Hendrickx, H.; Le Roy, G.; Helmstetter, A.; Pointner, E.; Larose, E.; Braillard, L.; Nyssen, J.; Delaloye, R.; Amaury, F. Timing, Volume and Precursory Indicators of Rock and Cliff Fall on a Permafrost Mountain Ridge (Mattertal, Switzerland). Earth Surf. Process Landf. 2022, 47, 1532–1549. [Google Scholar] [CrossRef]
- Rosser, N.; Lim, M.; Petley, D.; Dunning, S.; Allison, R. Patterns of Precursory Rockfall Prior to Slope Failure. J. Geophys. Res. 2007, 112, 148–227. [Google Scholar] [CrossRef]
- Kromer, R.; Hutchinson, D.; Lato, M.; Gauthier, D.; Edwards, T. Identifying Rock Slope Failure Precursors Using LiDAR for Transportation Corridor Hazard Management. Eng. Geol. 2015, 195, 93–103. [Google Scholar] [CrossRef]
- Carrea, D.; Abellan, A.; Derron, M.H.; Jaboyedoff, M. Automatic Rockfalls Volume Estimation Based on Terrestrial Laser Scanning Data. In Engineering Geology for Society and Territory—Volume 2: Landslide Processes; Springer International Publishing: Cham, Switzerland, 2015; pp. 425–428. ISBN 9783319090573. [Google Scholar]
- Blanch, X.; Eltner, A.; Guinau, M.; Abellan, A. Multi-Epoch and Multi-Imagery (MEMI) Photogrammetric Workflow for Enhanced Change Detection Using Time-Lapse Cameras. Remote Sens. 2021, 13, 1460. [Google Scholar] [CrossRef]
- Kromer, R.; Walton, G.; Gray, B.; Lato, M.; Group, R. Development and Optimization of an Automated Fixed-Location Time Lapse Photogrammetric Rock Slope Monitoring System. Remote Sens. 2019, 11, 1890. [Google Scholar] [CrossRef]
- Williams, J.; Rosser, N.J.; Hardy, R.; Brain, M.; Afana, A. Optimising 4-D Surface Change Detection: An Approach for Capturing Rockfall Magnitude–Frequency. Earth Surf. Dyn. 2018, 6, 101–119. [Google Scholar] [CrossRef]
- Schovanec, H.; Walton, G.; Kromer, R.; Malsam, A. Development of Improved Semi-Automated Processing Algorithms for the Creation of Rockfall Databases. Remote Sens. 2021, 13, 1479. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Coggan, J.S. Numerical Analysis of Initiation and Progressive Failure in Natural Rock Slopes—the 1991 Randa Rockslide. Int. J. Rock Mech. Min. Sci. 2004, 41, 69–87. [Google Scholar] [CrossRef]
- Zoumpekas, T.; Puig, A.; Salamó, M.; García-Sellés, D.; Blanco-Nuñez, L.; Guinau, M. An Intelligent framework for End-to-End Rockfall Detection. Int. J. Intell. Syst. 2021, 36, 6471–6502. [Google Scholar] [CrossRef]
- Weidner, L.; Walton, G.; Kromer, R. Classification Methods for Point Clouds in Rock Slope Monitoring: A Novel Machine Learning Approach and Comparative Analysis. Eng. Geol. 2019, 263, 105326. [Google Scholar] [CrossRef]
- Brodu, N.; Lague, D. 3D Terrestrial Lidar Data Classification of Complex Natural Scenes Using a Multi-Scale Dimensionality Criterion: Applications in Geomorphology. ISPRS J. Photogramm. Remote Sens. 2012, 68, 121–134. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Evans, J.S.; Hudak, A.T. A Multiscale Curvature Algorithm For Classifying Discrete Return LiDAR in Forested Environments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1029–1038. [Google Scholar] [CrossRef]
- Kromer, R.; Lato, M.; Hutchinson, D.J.; Gauthier, D.; Edwards, T. Managing Rockfall Risk through Baseline Monitoring of Precursors Using a Terrestrial Laser Scanner. Can. Geotech. J. 2017, 54, 953–967. [Google Scholar] [CrossRef]
- Mazzanti, P.; Caporossi, P.; Brunetti, A.; Mohammadi, F.I.; Bozzano, F. Short-Term Geomorphological Evolution of the Poggio Baldi Landslide Upper Scarp via 3D Change Detection. Landslides 2021, 18, 2367–2381. [Google Scholar] [CrossRef]
- Royán, M.J.; Abellán, A.; Jaboyedoff, M.; Vilaplana, J.M.; Calvet, J. Spatio-Temporal Analysis of Rockfall Pre-Failure Deformation Using Terrestrial LiDAR. Landslides 2014, 11, 697–709. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Simoudis, E., Fayyad, U., Han, J., Eds.; AAAI Press: Menlo Park, CA, USA, 1996; pp. 226–231. [Google Scholar]
- Girardeau-Montaut, D.; Roux, M.; Marc, R.; Thibault, G. Change Detection on Points Cloud Data Acquired with a Ground Laser scanner. In Proceedings of the ISPRS WG III/3, III/4, V/3Workshop “Laser Scanning 2005”, Enschede, The Netherlands, 12–14 September 2005; Vosselman, G., Brenner, C., Eds.; 2005; pp. 30–35. Available online: https://www.isprs.org/proceedings/xxxvi/3-w19/ (accessed on 21 June 2022).
- Innovmetric. Polyworks. Quebec City. 2022. Available online: https://www.innovmetric.com (accessed on 18 May 2022).
- Visual Studio 2019. Microsoft. Available online: https://Visualstudio.microsoft.com (accessed on 18 May 2022).
- Barnhart, T.B.; Crosby, B.T. Comparing TwoMethods of Surface Change Detection on an Evolving Thermokarst Using High-Temporal-Frequency Terrestrial Laser Scanning, Selawik River, Alaska. Remote Sens. 2013, 5, 2813–2837. [Google Scholar] [CrossRef]
- Cignoni, P.; Rocchini, C.; Scopigno, R. Metro: Measuring Error on Simplified Surfaces. Comput. Graph. Forum 1998, 17, 167–174. [Google Scholar] [CrossRef]
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson Surface Reconstruction. In Eurographics Symposium on Geometry Processing; Sheffer, A., Poithier, K., Eds.; The Eurographics Association, 2006; Available online: http://diglib.eg.org/handle/10.2312/SGP.SGP06.061-070 (accessed on 18 May 2022).
- Girardeu-Montaut, D. CloudCompare, Version 2.12.1 Alpha. Available online: http://www.cloudcompare.org/ (accessed on 18 May 2022).
- Abellán, A.; Jaboyedoff, M.; Oppikofer, T.; Vilaplana, J.M. Detection of Millimetric Deformation Using a Terrestrial Laser Scanner: Experiment and Application to a Rockfall Event. Nat. Hazards Earth Syst. Sci. 2009, 9, 365–372. [Google Scholar] [CrossRef]
- Jolliffe, I. Principal Component Analysis. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Woodcock, N. Specification of fabric shapes using an Eigenvalue method. Geol. Soc. Am. Bull. 1977, 88, 1231–1236. [Google Scholar] [CrossRef]
- García-Sellés, D.; Falivene, O.; Arbués, P.; Gratacós, O.; Tavani, S.; Muñoz, J.A. Supervised Identification and Reconstruction of Near-Planar Geological Surfaces from Terrestrial Laser Scanning. Comput. Geosci. 2011, 37, 1584–1594. [Google Scholar] [CrossRef]
- Benjamin, J.; Rosser, N.J.; Brain, M.J. Emergent Characteristics of Rockfall Inventories Captured at a Regional Scale. Earth Surf. Process Landf. 2020, 45, 2773–2787. [Google Scholar] [CrossRef]
- Carrea, D.; Abellan, A.; Derron, M.-H.; Gauvin, N.; Jaboyedoff, M. MATLAB Virtual Toolbox for Retrospective Rockfall Source Detection and Volume Estimation Using 3D Point Clouds: A Case Study of a Subalpine Molasse Cliff. Geosciences 2021, 11, 75. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, J.; Liu, L.; Wang, Y. Efficient Rock Mass Point Cloud Registration Based on Local Invariants. Remote Sens. 2021, 13, 1540. [Google Scholar] [CrossRef]
- Zhou, Q.-Y.; Park, J.; Koltun, V. Open3D: A Modern Library for 3D Data Processing. arXiv 2018, arXiv:1801.09847. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Royan, M. Rockfall Characterization and Prediction by Means of Terrestrial LiDAR. Ph.D. Thesis, Universitat de Barcelona, Barcelona, Spain, September 2015. Available online: http://hdl.handle.net/10803/334400 (accessed on 12 June 2022).
- Yen, S.J.; Lee, Y.S. Cluster-Based Under-Sampling Approaches for Imbalanced Data Distributions. Expert Syst. Appl. 2008, 36, 5718–5727. [Google Scholar] [CrossRef]
- Chawla, N.; Bowyer, K.; Hall, L.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
- Stefanowski, J.; Wilk, S. Selective Pre-processing of Imbalanced Data for Improving Classification Performance. In Data Warehousing and Knowledge Discovery; Song, I.Y., Eder, J., Nguyen, T.M., Eds.; DaWaK 2008; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5182, pp. 283–292. [Google Scholar] [CrossRef] [Green Version]
- Sharma, S.; Bellinger, C.; Krawczyk, B.; Zaiane, O.; Japkowicz, N. Synthetic Oversampling with the Majority Class: A New Perspective on Handling Extreme Imbalance. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; pp. 447–456. [Google Scholar] [CrossRef]
- Gazzah, S.; Amara, N.E. New Oversampling Approaches Based on Polynomial Fitting for Imbalanced Data Sets. In Proceedings of the Eighth IAPR International Workshop on Document Analysis Systems, Nara, Japan, 16–19 September 2008; pp. 677–684. [Google Scholar] [CrossRef]
- Barua, S.; Islam, M.; Murase, K. ProWSyn: Proximity Weighted Synthetic Oversampling Technique for Imbalanced Data Set Learning. In Advances in Knowledge Discovery and Data Mining; Pei, J., Tseng, V.S., Cao, L., Motoda, H., Xu, G., Eds.; Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); PAKDD Springer: Berlin/Heidelberg, Germany, 2013; Volume 7819, pp. 317–328. [Google Scholar] [CrossRef]
- Sáez, J.A.; Luengo, J.; Stefanowski, J.; Herrera, F. SMOTE-IPF: Addressing the Noisy and Borderline Examples Problem in Imbalanced Classification by a re-Sampling Method with Filtering. Inf. Sci. 2015, 291, 184–203. [Google Scholar] [CrossRef]
- Lee, J.; Kim, N.; Lee, J.-H. An Over-Sampling Technique with Rejection for Imbalanced Class Learning. In Proceedings of the 9th International Conference on Ubiquitous Information Management and Communication, Bali, Indonesia, 8–10 January 2015; ACM: New York, NY, USA; pp. 1–6. [Google Scholar] [CrossRef]
- Cao, Q.; Wang, S. Applying Over-Sampling Technique Based on Data Density and Cost-Sensitive SVM to Imbalanced Learning. In Proceedings of the 4th International Conference on Information Management, Innovation Management and Industrial Engineering, Shenzhen, China, 26–27 November 2011; Volume 2, pp. 543–548. [Google Scholar] [CrossRef]
- Douzas, G.; Bação, F. Geometric SMOTE: Effective Oversampling for Imbalanced Learning Through a Geometric Extension of SMOTE. arXiv 2017, arXiv:1709.07377. [Google Scholar] [CrossRef]
- Nakamura, M.; Kajiwara, Y.; Otsuka, A.; Kimura, H. LVQ-SMOTE—Learning Vector Quantization based Synthetic Minority Over–sampling Technique for biomedical data. BioData Min. 2013, 6, 16. [Google Scholar] [CrossRef]
- Zhou, B.; Yang, C.; Guo, H.; Hu, J. A Quasi-Linear SVM Combined with Assembled SMOTE for Imbalanced Data Classification. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Batista, G.E.A.P.A.; Prati, R.C.; Monard, M.C. A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Ma, Z.; Mei, G.; Piccialli, F. Machine Learning for Landslides Prevention: A Survey. Neural Comput. Appl. 2021, 33, 10881–10907. [Google Scholar] [CrossRef]
- Hastie, T.; Friedman, J.; Tibshirani, R. The Elements of Statistical Learning; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support Vector Machines for Classification. In Efficient Learning Machines; Apress: Berkeley, CA, USA, 2015; pp. 39–66. [Google Scholar] [CrossRef]
- Murtagh, F. Multilayer Perceptrons for Classification and Regression. Neurocomputing 1991, 2, 183–197. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, H.; Rosset, S.; Hastie, T. Multi-class AdaBoost. Stat. Interface 2009, 2, 349–360. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA; pp. 785–794. [Google Scholar] [CrossRef]
- Anadón, P.; Marzo, M.; Puigdefàbregas, C. The Eocene fan-delta of Montserrat (Southeastern Ebro Basin, Spain). In 6th European Meeting Excursion Guidebook; Milà, M.D., Rosell, J., Eds.; IAS/Institut d’Estudis Ilerdencs: Lleida, Spain, 1985; pp. 109–146. [Google Scholar]
- López-Blanco, M.; Marzo, M.; Burbank, D.W.; Vergés, J.; Roca, E.; Anadón, P.; Piña, J. Tectonic and Climatic Controls on the Development of Foreland Fan Deltas: Montserrat and Sant Llorenç Del Munt Systems (Middle Eocene, Ebro Basin, NE Spain). Sediment. Geol. 2000, 138, 17–39. [Google Scholar] [CrossRef]
- Gómez-Paccard, M.; López-Blanco, M.; Costa, E.; Garcés, M.; Beamud, E.; Larrasoaña, J.C. Tectonic and Climatic Controls on the Sequential Arrangement of an Alluvial Fan/Fan-Delta Complex (Montserrat, Eocene, Ebro Basin, NE Spain). Basin Res. 2012, 24, 437–455. [Google Scholar] [CrossRef]
- Alsaker, E.; Gabrielsen, R.H.; Roca, E. The Significance of the Fracture Pattern of the Late-Eocene Montserrat Fan-Delta, Catalan Coastal Ranges (NE Spain). Tectonophysics 1996, 266, 465–491. [Google Scholar] [CrossRef]
- García-Sellés, D.; Sarmiento, S.; Gratacós, O.; Granado, P.; Carrera, N.; Lakshmikantha, M.R.; Cordova, J.C.; Muñoz, J.A. Fracture analog of the sub-Andean Devonian of southern Bolivia: Lidar applied to Abra Del Condor. In Petroleum Basins and Hydrocarbon Potential of the Andes of Peru and Bolivia; Zamora, G., McClay, K.M., Ramos, V., Eds.; AAPG Memoir, 2018; Volume 117, pp. 577–612. Available online: https://pubs.geoscienceworld.org/books/book/2153/chapter-abstract/120760614/Fracture-Analog-of-the-Sub-Andean-Devonian-of?redirectedFrom=fulltext (accessed on 18 May 2022).
- Teledyne Optech. ILRIS Summary Specification Sheet; Teledyne Optech Incorporated: Vaughan, ON, Canada, 2014. [Google Scholar]
- Mineo, S.; Pappalardo, G.; Mangiameli, M.; Campolo, S.; Mussumeci, G. Rockfall Analysis for Preliminary Hazard Assessment of the Cliff of Taormina Saracen Castle (Sicily). Sustainability 2018, 10, 417. [Google Scholar] [CrossRef] [Green Version]

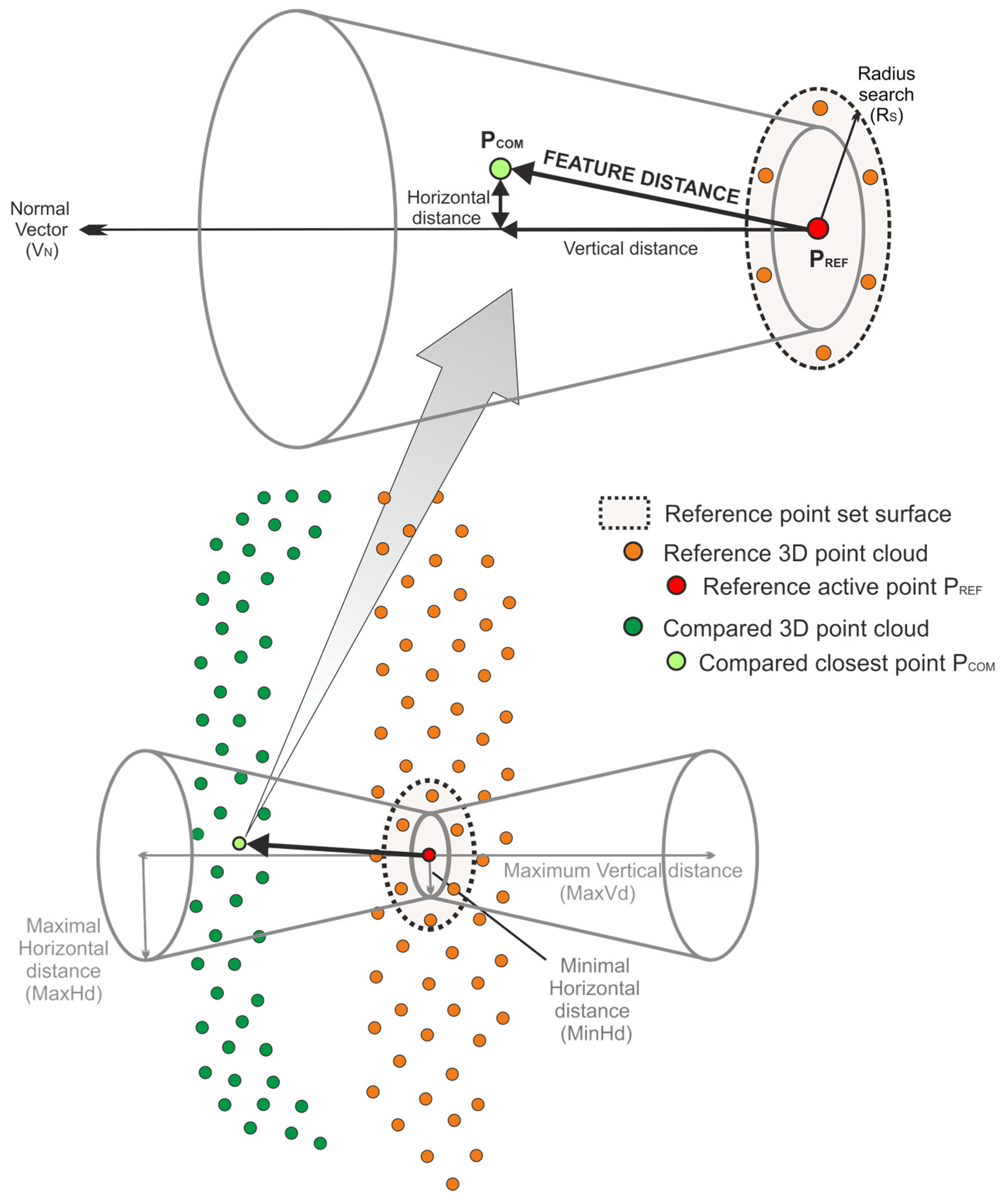
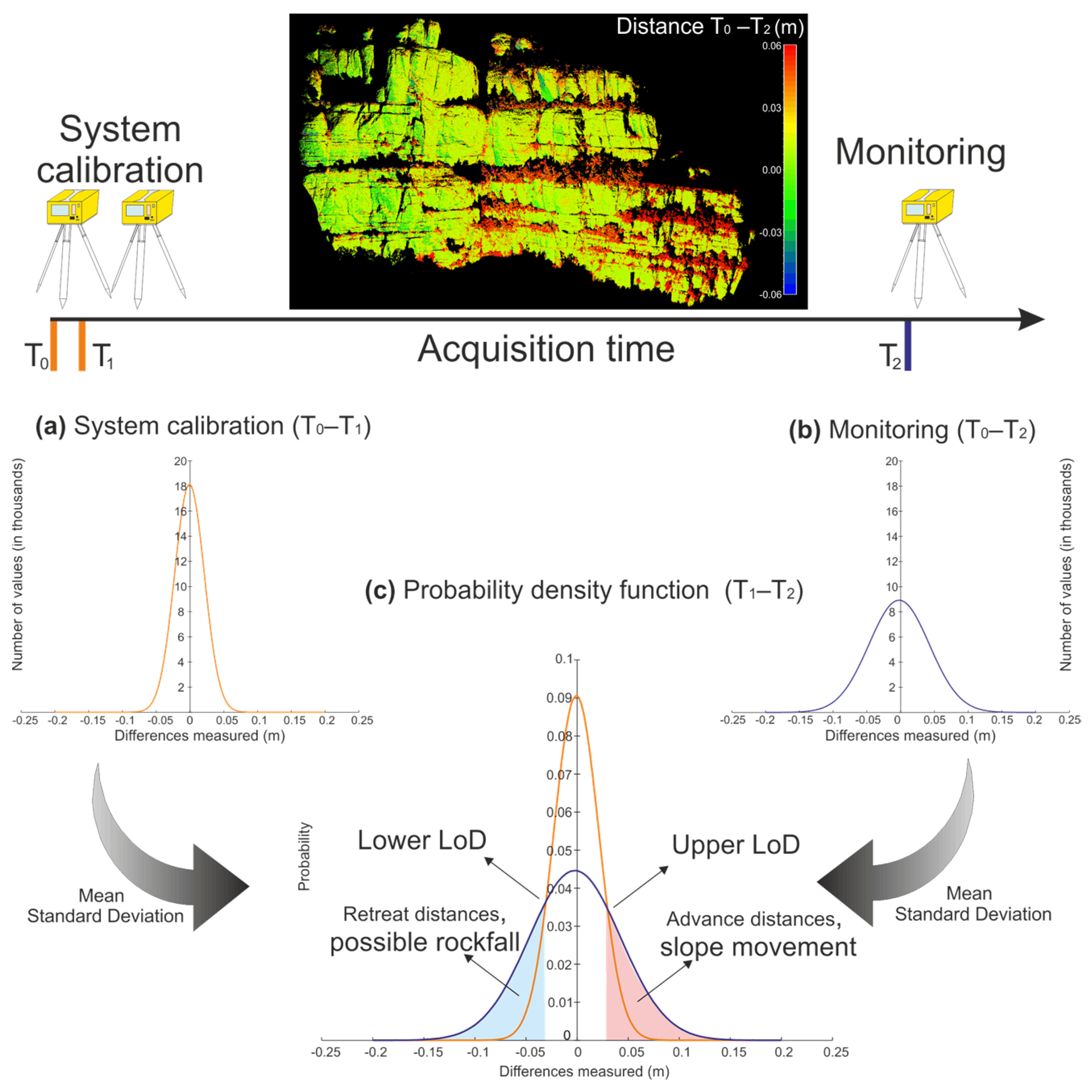
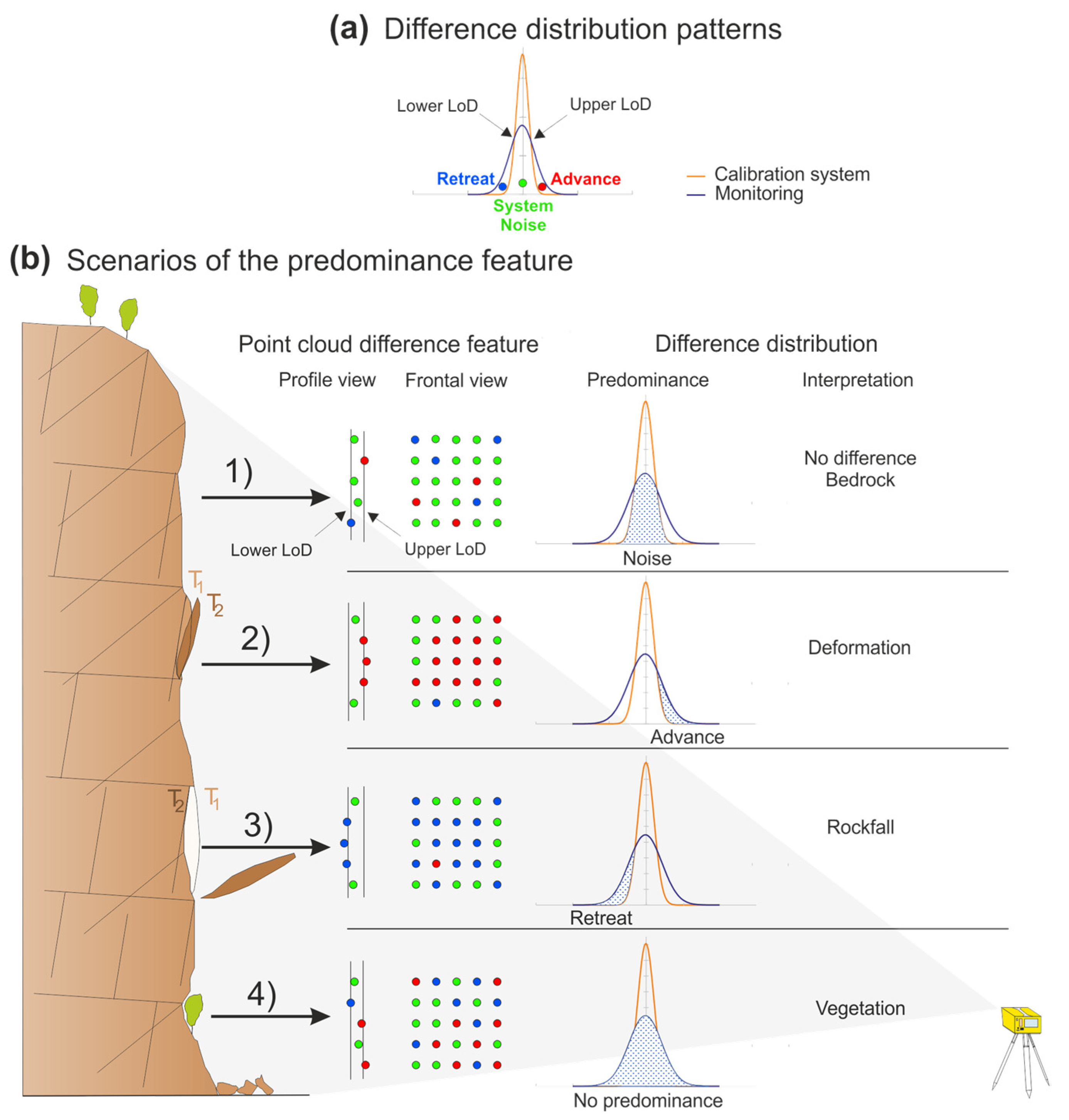
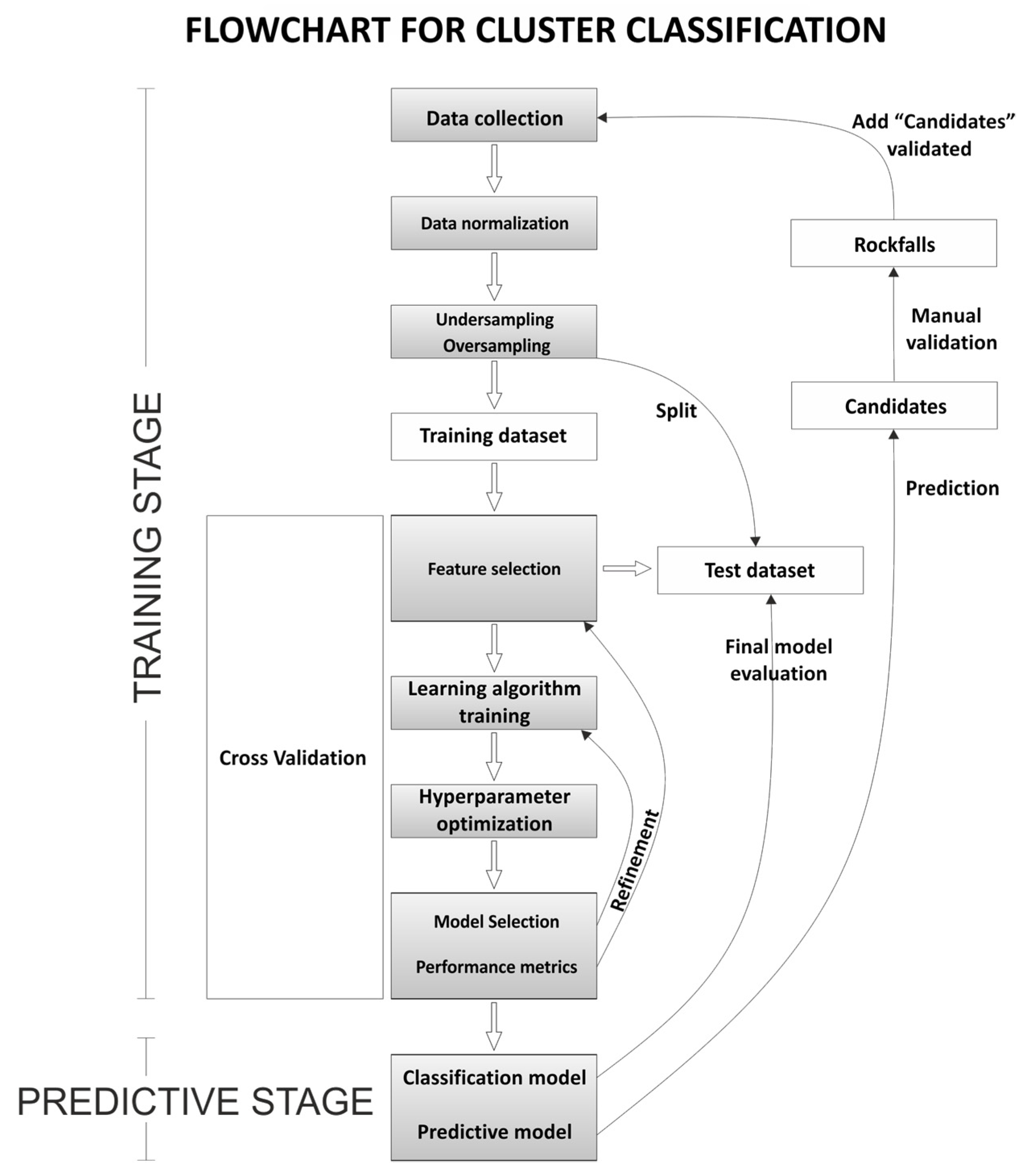



| Features | Significance |
|---|---|
| Distance | Distance between points (reference and compared) |
| Vertical Distance | Distance along the normal vector |
| Horizontal distance | Perpendicular distance to the normal vector |
| Angle between normal | Angularity between normal reference and compared |
| Direction | Direction of the normal vector with respect to the surface |
| Vector | Normal vector (i, j, k) for each point |
| Azimuth | Normal vector decomposed in orientation to North |
| Slope | Normal vector decomposed in orientation to horizontal |
| Collinearity | Distribution degree of neighboring points along a line |
| Coplanarity | Distribution degree of neighboring points along a plane |
| Feature | Significance |
|---|---|
| Predominance | Majority class (advance, retreat, or noise) |
| Noise percentage | Percentage of points classified as noise according the LoD |
| Advance percentage | Percentage of points classified as advance according the LoD |
| Retreat percentage | Percentage of points classified as retreat according the LoD |
| Undersampling | Oversampling |
|---|---|
| Cluster Centroids | SMOTE [58] (Synthetic Minority Oversampling Technique) |
| Cluster Representatives [59] | ADASYN [60] (Adaptive Synthetic Sampling) |
| SPIDER [61] (Selective Pre-processing of Imbalanced Data) SWIM [62] (Sampling with the Majority) Polynom-fit-SMOTE [63] | |
| ProWsyn [64] (Proximity Weighted Synthetic) SMOTE-IPF [65] (SMOTE-Iterative Partitioning Filter) LEE [66] | |
| SMOBD [67] (Synthetic Minority Over-sampling Based on Samples Density) G-SMOTE [68] (Geometric-SMOTE) LVQ-SMOTE [69] (Learning Vector Quantization-SMOTE) Assembled-SMOTE [70] | |
| SMOTE-TomekLinks [71] |
| Single Base | Ensemble |
|---|---|
| Linear Discriminant Analysis [73] | AdaBoost Classifier [74] |
| Quadratic Discriminant Analysis [73] | Random Forest Classifier [73] |
| K-Nearest Neighbors Classifier [73] | Extra Trees Classifier [75] |
| Gaussian Naive Bayes [73] | XGBoost Classifier [76] |
| Decision Tree Classifier [73] | |
| Support Vector Classifier [77] | |
| Multi-Layer Perceptron Classifier [78] |
| Classifier Models | Hyper-Parameters |
|---|---|
| Linear Discriminant Analysis | Solver: svd, lsqr, eigen |
| Quadratic Discriminant Analysis | Reg param: 0.1, 0.3, 0.5 |
| K-Nearest Neighbors Classifier | Number of neighbors: 1, 17 |
| Gaussian Naive Bayes | Var smoothing: logspace (0, −9, num = 100) |
| Decision Tree Classifier | Criterion: gini, entropy; Maximum depth: 3–15 |
| Support Vector Classifier | C: 0.1, 1, 10; Gamma: 1, 0.01; Kernel: rbf |
| Multi-Layer Perceptron Classifier AdaBoost Classifier | Solver: lbfgs, SGD, ADAM; Activation: relu; Hidden layer sizes: 50, 100, 150 Number of estimators: 1–50; Learning rate: 0.2 |
| Random Forest Classifier | Number of estimators: 1–20; |
| Extra Trees Classifier | Criterion: gini, entropy; Maximum depth: 3–15 Number of estimators: 1–20; |
| XGBoost Classifier | Criterion: gini, entropy; Maximum depth: 3–15 Nthread: 4; Booster: gblinear, gbtree; Missing: −999 Learning rate: 0.1, 0.2, 0.3; Number of estimators: 50, 100, 500; Seed: 1337; Disable default metric: True |
| (a) Distance Parameters | Degotalls Cliff (m) |
| Maximum vertical | 0.5 |
| Minimal horizontal | 0.08 |
| Maximal horizontal | 0.10 |
| (b) Clustering Settings | |
| Threshold distance between points (eps) | 0.15 |
| Minimum number of points (minPts) | 10 points |
| (c) Degotalls TLS System Calibration Difference | |
| Mean | −0.000268 |
| Standard deviation | 0.019547 |
| Cliffs | LoD Mean (m) | LoD STD (m) | |
|---|---|---|---|
| Degotalls E: South section | Upper | 0.03242 | 0.00336 |
| Lower | −0.03189 | 0.00453 | |
| North section | Upper | 0.03430 | 0.00590 |
| Lower | −0.03511 | 0.00385 | |
| Degotalls N: | Upper | 0.03928 | 0.01685 |
| Lower | −0.04026 | 0.01626 |
| Outcrop Period | Rockfalls for Training | Best Classifier Model | Best Resampling Method | Real Rockfalls | TP | FP | FN |
|---|---|---|---|---|---|---|---|
| Degotalls E South section | |||||||
| 2007–2009 | 10 * | Quadratic Discr. | Pol. Fit-SMOTE | 8 | 8 | 91 | 0 |
| 2009–2010 | 18 | Linear Discr. A. | Cluster Centr. | 5 | 5 | 7 | 0 |
| 2010–2011 | 23 | KNN C. | Cluster Centr. | 4 | 4 | 139 | 0 |
| 2011–2012 | 27 | XGBoost C. | S. TomekLinks | 4 | 4 | 48 | 0 |
| 2012–2013 | 31 | Extra Trees C. | Cluster Centr. | 2 | 2 | 10 | 0 |
| 2013–2014 | 33 | XGBoost C. | Cluster Centr. | 1 | 1 | 1 | 0 |
| 2014–2015 | 34 | SVC | Cluster Centr. | 1 | 1 | 0 | 0 |
| 2015–2016 | 35 | Linear Discr. A. | Stefanowsky | 3 | 3 | 53 | 0 |
| 2016–2017 | 38 | - | - | 0 | |||
| 2017–2019 | 38 | Linear Discr. A. | Cluster Centr. | 3 | 3 | 9 | 0 |
| 2019–2020 | 41 | - | - | 0 | |||
| 2020–2020 | 41 | Extra Trees C. | Stefanowsky | 2 | 2 | 2 | 0 |
| North section | |||||||
| 2007–2019 | 43 | Quadratic Discr. | LVQ-SMOTE | 22 | 22 | 97 | 0 |
| Degotalls N | |||||||
| 2007–2017 a | 10 * | Linear Discr. A. | Cluster Repres. | 107 | 107 | 1211 | 0 |
| 2007–2017 b | 10 | Decision Tree C. | Cluster Repres. | 107 | 104 | 296 | 3 |
| 2017–2019 a | 117 | Quadratic Discr. | SWIM | 16 | 16 | 455 | 0 |
| 2017–2019 b | 117 | Quadratic Discr. | Pro WSyn | 16 | 15 | 256 | 1 |
| Outcrop Period | Best Classifier Model | Best Resampling Method | Recall | Accuracy |
|---|---|---|---|---|
| Degotalls E South section | ||||
| 2007–2009 | Quadratic Discr. | Pol. Fit-SMOTE | 1 | 0.979 |
| 2009–2010 | Linear Discr. A. | Cluster Centr. | 1 | 0.999 |
| 2010–2011 | KNN C. | Cluster Centr. | 1 | 0.979 |
| 2011–2012 | XGBoost C. | S. TomekLinks | 1 | 0.991 |
| 2012–2013 | Extra Trees C. | Cluster Centr. | 1 | 0.998 |
| 2013–2014 | XGBoost C. | Cluster Centr. | 1 | 0.999 |
| 2014–2015 | SVC | Cluster Centr. | 1 | 1 |
| 2015–2016 | Linear Discr. A. | Stefanowsky | 1 | 0.992 |
| 2016–2017 | - | - | ||
| 2017–2019 | Linear Discr. A. | Cluster Centr. | 1 | 0.998 |
| 2019–2020 | - | - | ||
| 2020–2020 | Extra Trees C. | Stefanowsky | 1 | 0.999 |
| North section | ||||
| 2007–2019 | Quadratic Discr. | LVQ-SMOTE | 1 | 0.968 |
| Degotalls N | ||||
| 2007–2017 a | Linear Discr. A. | Cluster Repres. | 1 | 0.704 |
| 2007–2017 b | Decision Tree C. | Cluster Repres. | 0.972 | 0.906 |
| 2017–2019 a | Quadratic Discr. | SWIM | 1 | 0.891 |
| 2017–2019 b | Quadratic Discr. | Pro WSyn | 0.937 | 0.935 |
| Outcrop Period | Real Rockfalls | TP | FP | FN |
|---|---|---|---|---|
| Degotalls E South section | ||||
| 2007–2009 | 8 | 8 | 91 | 0 |
| 2009–2010 | 5 | 5 | 148 | 0 |
| 2010–2011 | 4 | 4 | 461 | 0 |
| 2011–2012 | 4 | 4 | 258 | 0 |
| 2012–2013 | 2 | 2 | 235 | 0 |
| 2013–2014 | 1 | 1 | 224 | 0 |
| 2014–2015 | 1 | 1 | 188 | 0 |
| 2015–2016 | 3 | 3 | 315 | 0 |
| 2016–2017 | 0 | - | - | - |
| 2017–2019 | 3 | 2 | 517 | 1 |
| 2019–2020 | 0 | - | - | - |
| 2020–2020 | 2 | 2 | 111 | 0 |
| Cluster Feature | Value | Cluster Feature | Value |
|---|---|---|---|
| Cluster Number | 1326 | Points %: Noise | 10.48% |
| Centroid Coord. X | −23.169 m | Advance | 0.21% |
| Coord. Y | 192.847 m | Retreat | 89.31% |
| Coord. Z | −10.063 m | Intensity Ref. | 210.32 |
| Number of points | 428 | Intensity Comp. | 228.43 |
| Positive Volume | 0.27164 m3 | Azimuth Ref. | 165.10° |
| Area | 1.45 m2 | Azimuth Comp. | 166.20° |
| Predominance: Mean | 2 (Retreat) | Slope Ref. | 71.11° |
| Standard deviation | 0.07 | Slope Comp. | 70.91° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blanco, L.; García-Sellés, D.; Guinau, M.; Zoumpekas, T.; Puig, A.; Salamó, M.; Gratacós, O.; Muñoz, J.A.; Janeras, M.; Pedraza, O. Machine Learning-Based Rockfalls Detection with 3D Point Clouds, Example in the Montserrat Massif (Spain). Remote Sens. 2022, 14, 4306. https://doi.org/10.3390/rs14174306
Blanco L, García-Sellés D, Guinau M, Zoumpekas T, Puig A, Salamó M, Gratacós O, Muñoz JA, Janeras M, Pedraza O. Machine Learning-Based Rockfalls Detection with 3D Point Clouds, Example in the Montserrat Massif (Spain). Remote Sensing. 2022; 14(17):4306. https://doi.org/10.3390/rs14174306
Chicago/Turabian StyleBlanco, Laura, David García-Sellés, Marta Guinau, Thanasis Zoumpekas, Anna Puig, Maria Salamó, Oscar Gratacós, Josep Anton Muñoz, Marc Janeras, and Oriol Pedraza. 2022. "Machine Learning-Based Rockfalls Detection with 3D Point Clouds, Example in the Montserrat Massif (Spain)" Remote Sensing 14, no. 17: 4306. https://doi.org/10.3390/rs14174306
APA StyleBlanco, L., García-Sellés, D., Guinau, M., Zoumpekas, T., Puig, A., Salamó, M., Gratacós, O., Muñoz, J. A., Janeras, M., & Pedraza, O. (2022). Machine Learning-Based Rockfalls Detection with 3D Point Clouds, Example in the Montserrat Massif (Spain). Remote Sensing, 14(17), 4306. https://doi.org/10.3390/rs14174306








