Investigation of Displacement and Ionospheric Disturbance during an Earthquake Using Single-Frequency PPP
Abstract
1. Introduction
2. Methodology
2.1. Phase and Code Raw-Observation Functions
2.2. Undifferenced Uncombined Single-Frequency PPP Model
2.3. Parameters Adjustment
2.4. SF-PPP Based Regional VTEC Model
3. Results and Discussion
3.1. Data Processing Method
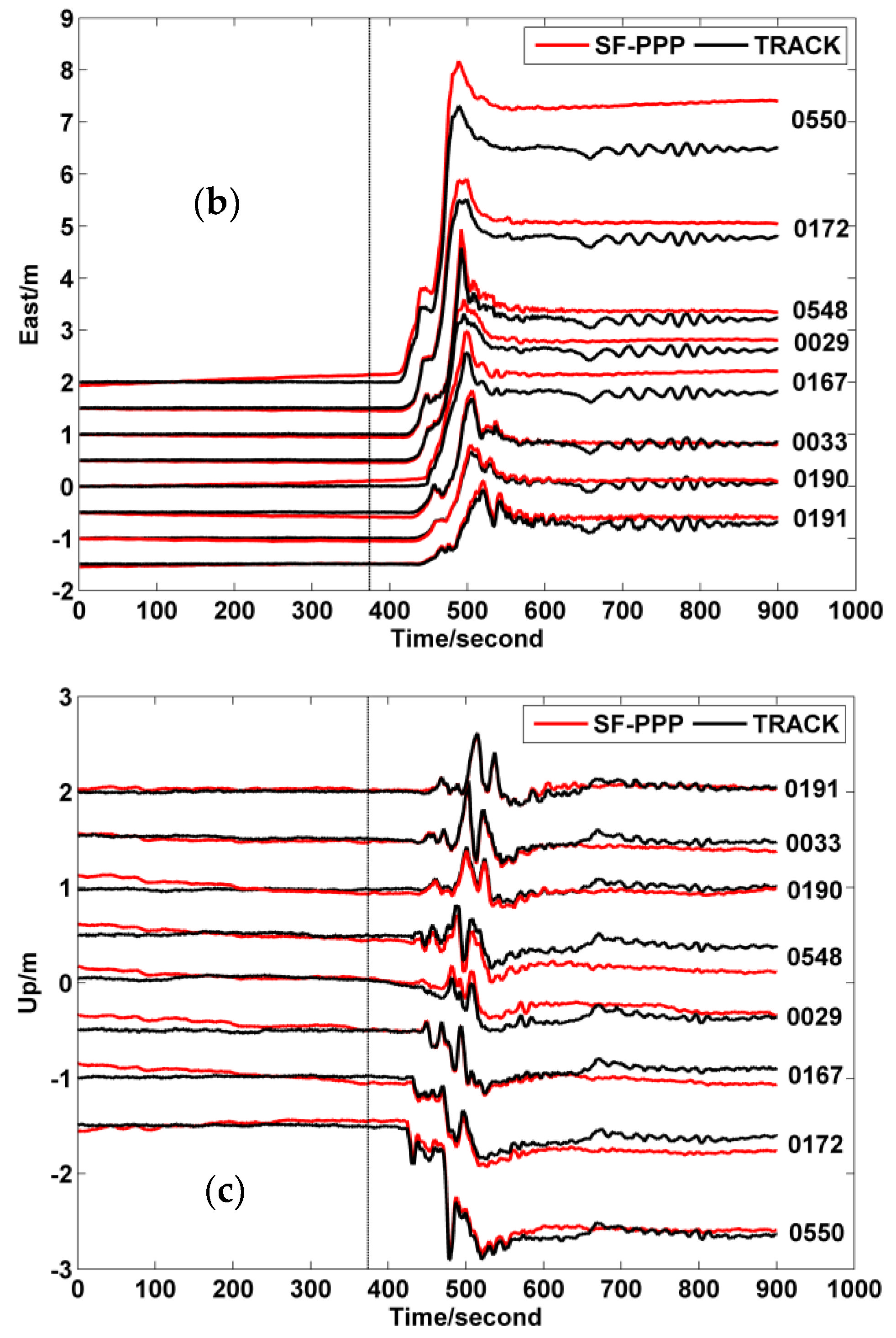
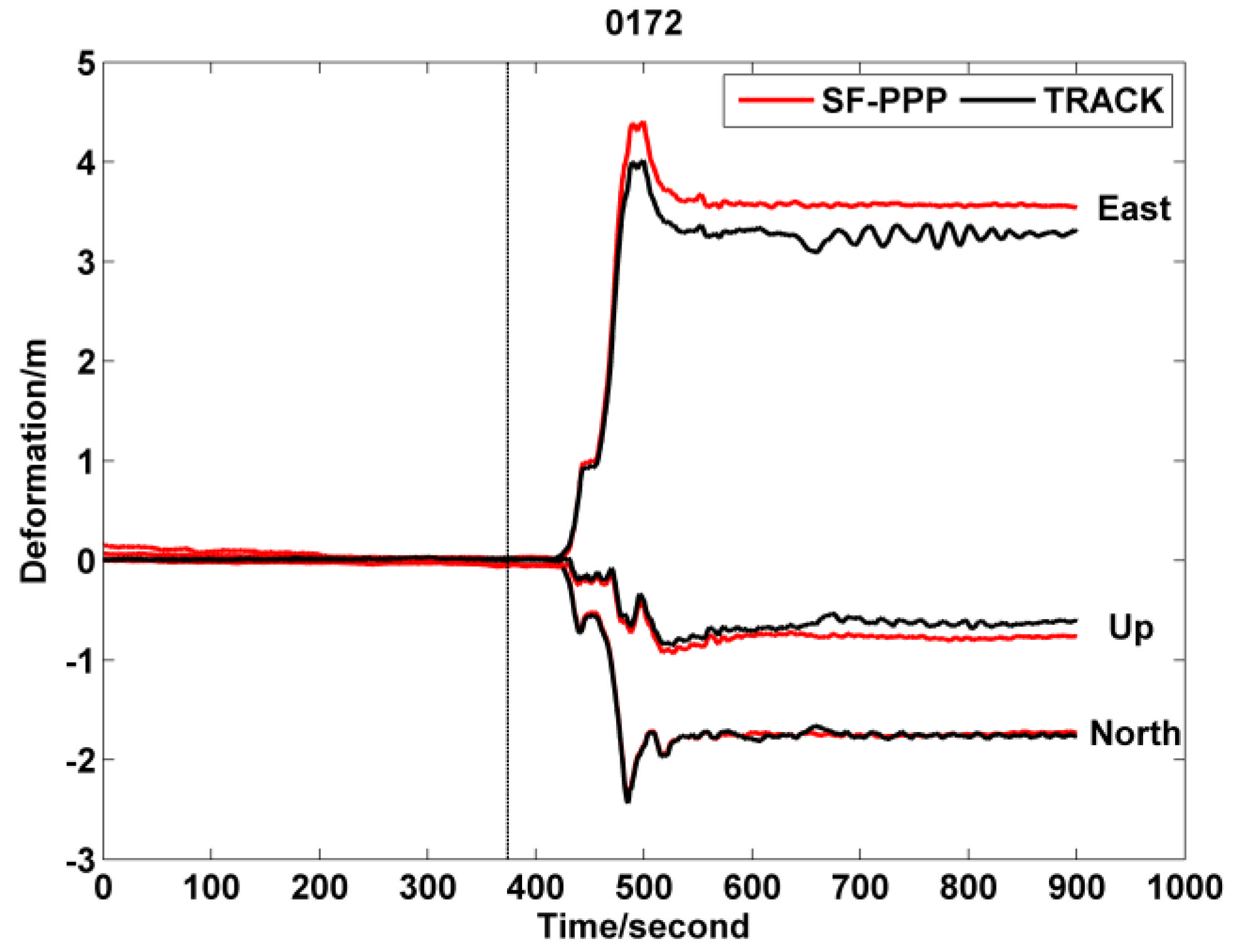
3.2. Earthquake Displacement
3.2.1. Deformation of Tohoku-Oki Earthquake
3.2.2. Dynamic Deformation of Lushan Earthquake
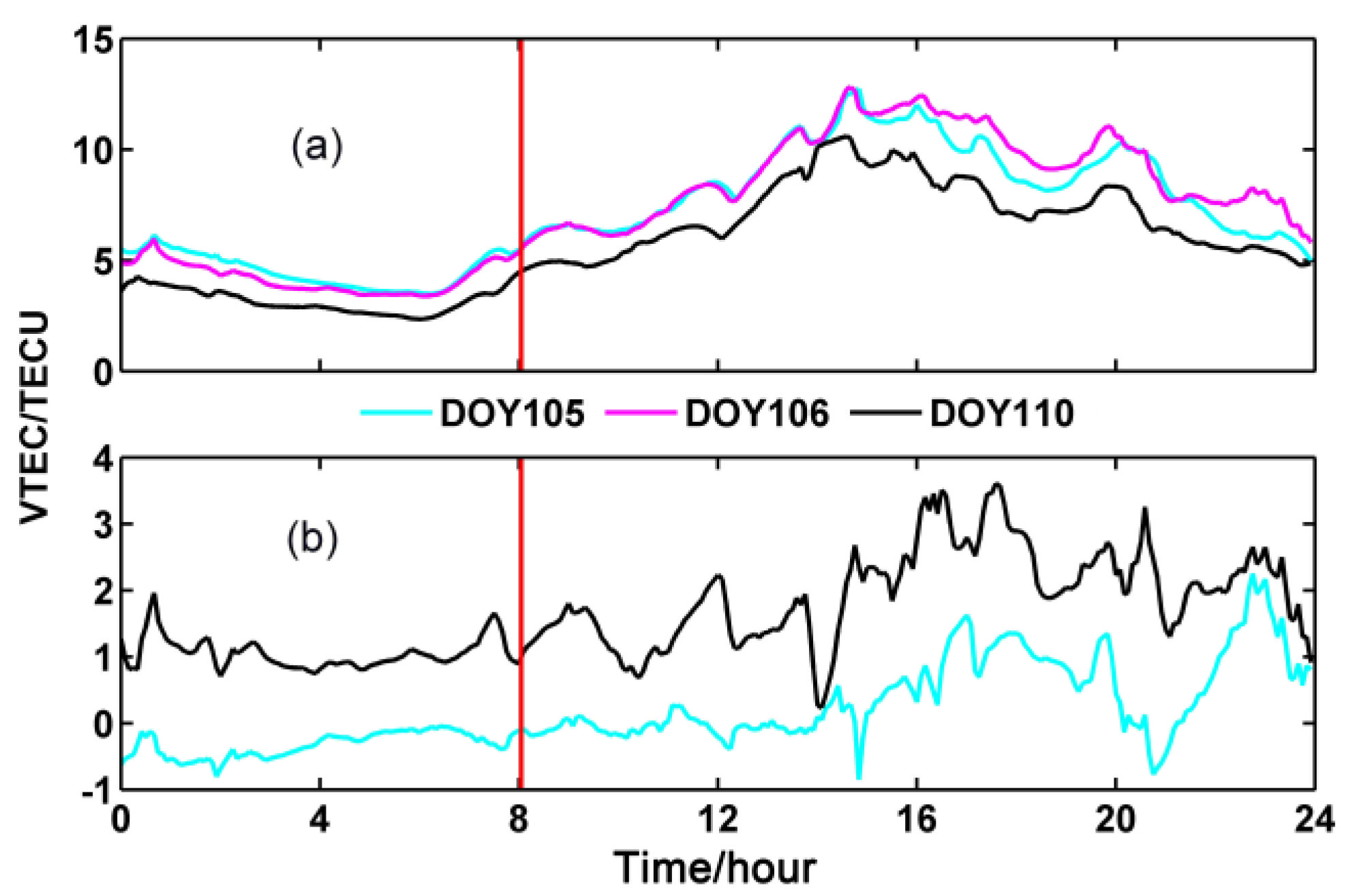
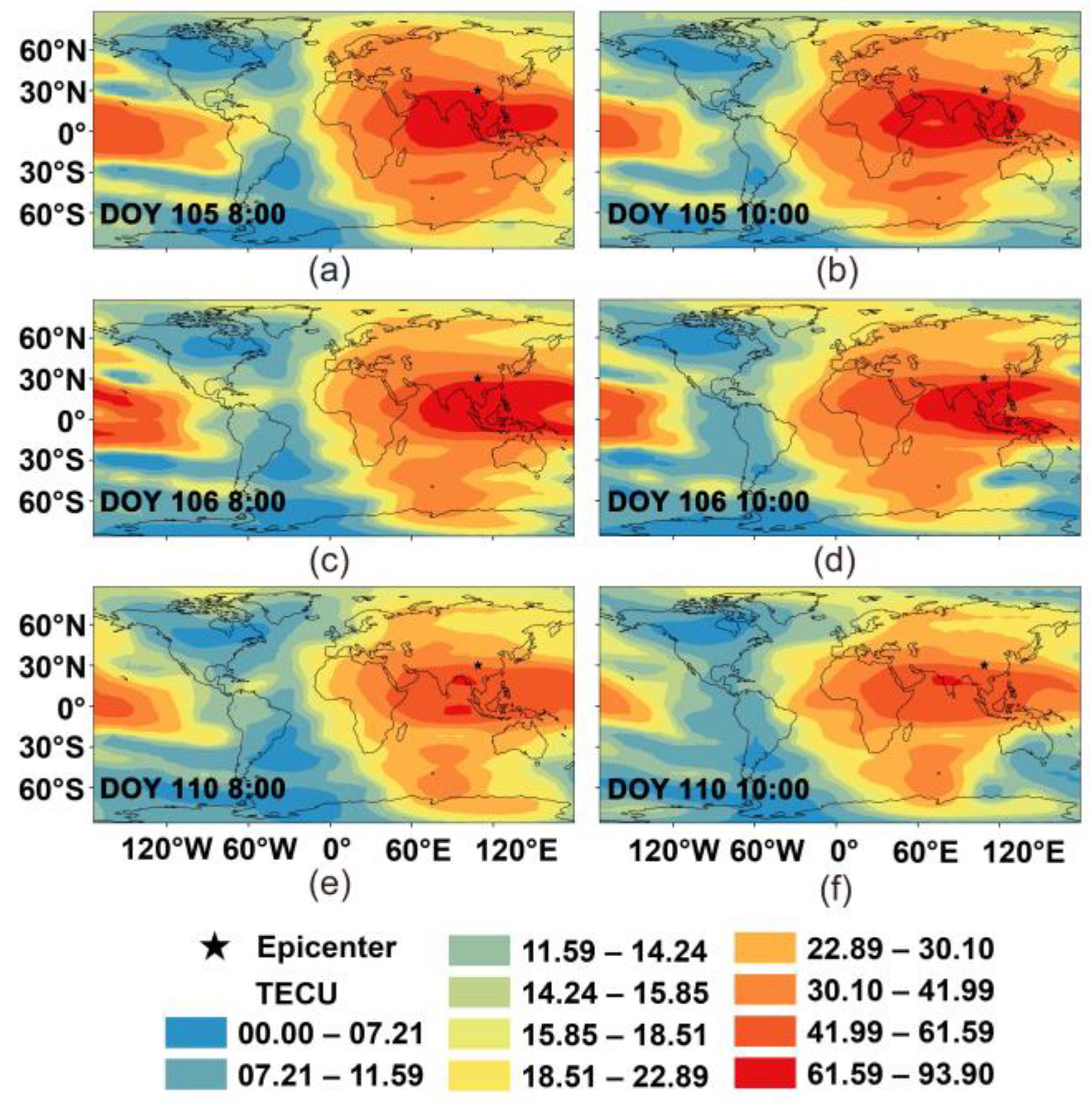
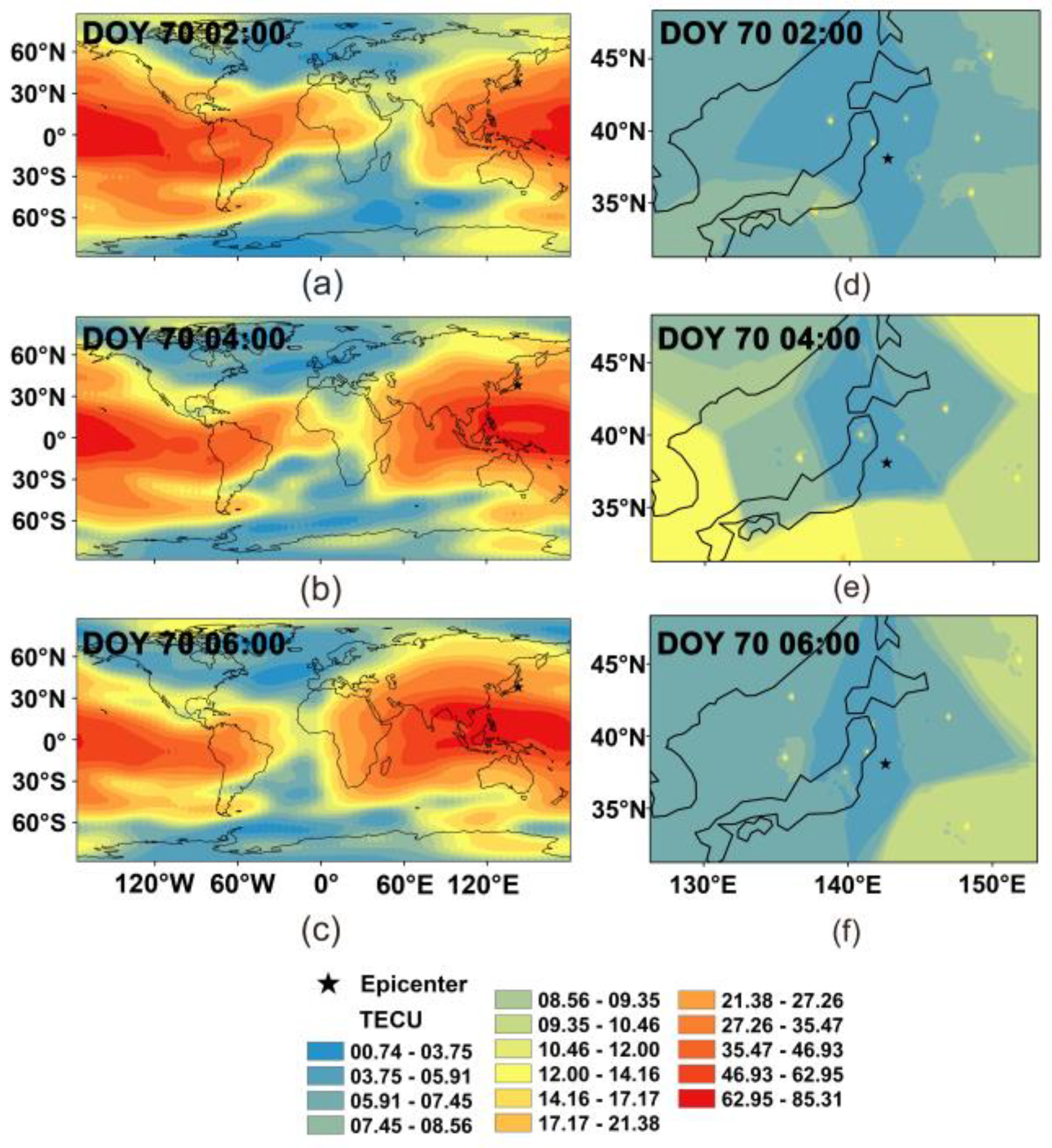
3.3. Ionospheric Disturbance during Earthquake
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ravanelli, M.; Occhipinti, G.; Savastano, G.; Komjathy, A.; Shume, E.B.; Crespi, M. GNSS total variometric approach: First demonstration of a tool for real-time tsunami genesis estimation. Sci. Rep. 2021, 11, 3114. [Google Scholar]
- Song, C.; Xu, C.; Wen, Y.; Yi, L.; Xu, W. Surface deformation and early warning magnitude of 2016 Kaikoura (New Zealand) earthquake from high-rate GPS observations. Chin. J. Geophys. 2017, 60, 602–612. [Google Scholar]
- Tu, R.; Zhang, P.; Zhang, R.; Liu, J. The study of key issues about integration of GNSS and strong-motion records for real-time earthquake monitoring. Adv. Space Res. 2016, 58, 304–309. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Zhang, X.; Zhang, Y.; Guo, B.; Wang, R.; Klotz, J.; Wickert, J. Real-time high-rate co-seismic displacement from ambiguity-fixed precise point positioning: Application to earthquake early warning. Geophys. Res. Lett. 2013, 40, 295–300. [Google Scholar] [CrossRef]
- Tong, X.; Xu, X.; Chen, S. Coseismic Slip Model of the 2021 Maduo Earthquake, China from Sentinel-1 InSAR Observation. Remote Sens. 2022, 14, 436. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Lu, C.; Zhang, Y.; Wang, R.; Wickert, J.; Schuh, H. High-rate GPS seismology using real-time precise point positioning with ambiguity resolution. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6165–6180. [Google Scholar]
- Allen, R.M.; Kanamori, H. The potential for earthquake early warning in southern California. Science 2003, 300, 786–789. [Google Scholar] [CrossRef]
- Li, X.; Guo, B.; Lu, C.; Ge, M.; Wickert, J.; Schuh, H. Real-time GNSS seismology using a single receiver. Geophys. J. Int. 2014, 198, 72–89. [Google Scholar] [CrossRef]
- Zheng, J.; Fang, R.; Li, M.; Lv, H.; Liu, J. Line-Source Model Based Rapid Inversion for Deriving Large Earthquake Rupture Characteristics Using High-Rate GNSS Observations. Geophys. Res. Lett. 2022, 49, e2021GL097460. [Google Scholar] [CrossRef]
- Staňková, H.; Kostelecký, J.; Novosad, M. An Innovative Approach to Accuracy of Co-Seismic Surface Displacement Detection Using Satellite GNSS Technology. Appl. Sci. 2021, 11, 2800. [Google Scholar] [CrossRef]
- Ohno, K.; Ohta, Y.; Hino, R.; Koshimura, S.; Musa, A.; Abe, T.; Kobayashi, H. Rapid and quantitative uncertainty estimation of coseismic slip distribution for large interplate earthquakes using real-time GNSS data and its application to tsunami inundation prediction. Earth Planets Space 2022, 74, 24. [Google Scholar] [CrossRef]
- Niu, A.; Zhao, J.; Yuan, Z.; Ji, P. Pre-Seismic Deformation Related to the Wenchuan Earthquake. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 839–848. [Google Scholar]
- Bouih, M.; Panet, I.; Remy, D.; Longuevergne, L.; Bonvalot, S. Deep mass redistribution prior to the 2010 Mw 8.8 Maule (Chile) Earthquake revealed by GRACE satellite gravity. Earth Planet. Sci. Lett. 2022, 584, 117465. [Google Scholar] [CrossRef]
- Xiang, Y.; Yue, J.; Tang, K.; Li, Z. A comprehensive study of the 2016 Mw 6.0 Italy earthquake based on high-rate (10 Hz) GPS data. Adv. Space Res. 2018, 63, 103–117. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. In Springer Handbook of Global Navigation Satellite Systems, 1st ed.; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 967–982. [Google Scholar] [CrossRef]
- Geng, J.; Jiang, P.; Liu, J. Integrating GPS with GLONASS for high-rate seismogeodesy: High-rate multi-GNSS. Geophys. Res. Lett. 2017, 44, 3139–3146. [Google Scholar] [CrossRef]
- Astafyeva, E. Ionospheric detection of natural hazards. Rev. Geophys. 2019, 57, 1265–1288. [Google Scholar] [CrossRef]
- Occhipinti, G. The seismology of the planet Mongo: The 2015 ionospheric seismology review. In Subduction Dynamics: From Mantle Flow to Mega Disasters, Geophysical Monograph 211; American Geophysical Union: Washington, DC, USA, 2016; pp. 169–182. [Google Scholar]
- Hines, C.O. Internal atmospheric gravity waves at ionospheric heights. Can. J. Phys. 1960, 38, 1441–1481. [Google Scholar] [CrossRef]
- Rishbeth, H. Do earthquake precursors really exist? Eos Trans. Am. Geophys. Union 2007, 88, 296. [Google Scholar] [CrossRef]
- Nagao, T.; Kamogawa, M.; Uyeda, S. Earthquake Precursors and Prediction. In Encyclopedia of Solid Earth Geophysics. Encyclopedia of Earth Sciences Series; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Jordan, T.H.; Chen, Y.T.; Gasparini, P.; Madariaga, R.; Main, I.; Marzocchi, W.; Papadopoulos, G.; Sobolev, G.; Yamaoka, K.; Zschau, J. Operational earthquake forecasting—State of knowledge and guidelines for utilization. Ann. Geophys. 2011, 54, 316–391. [Google Scholar]
- Leonard, R.S.; Barnes, R.A. Observation of ionospheric disturbances following the Alaska earthquake. J. Geophys. Res. 1965, 70, 1250–1253. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Chen, C.; Liu, C.; Chen, C.; Nishihashi, M.; Li, J.; Xia, Y.; Oyama, K.I.; Hattori, K.; et al. Seismoionospheric GPS total electron content anomalies observed before the 12 May 2008 Mw7. 9 Wenchuan earthquake. J. Geophys. Res. Space Phys. 2009, 114, 1–10. [Google Scholar] [CrossRef]
- Tojiev, S.R.; Ahmedov, B.J.; Tillayev, Y.A.; Eshkuvatov, H.E. Ionospheric anomalies of local earthquakes detected by GPS TEC measurements using data from Tashkent and Kitab stations. Adv. Space Res. 2013, 52, 1146–1154. [Google Scholar] [CrossRef]
- Song, Q.; Ding, F.; Yu, T.; Wan, W.; Ning, B.; Liu, L.; Zhao, B. GPS detection of the coseismic ionospheric disturbances following the 12 May 2008 M7. 9 Wenchuan earthquake in China. Sci. China Earth Sci. 2015, 58, 151–158. [Google Scholar] [CrossRef]
- Tariq, M.A.; Shah, M.; Hernández-Pajares, M.; Iqbal, T. Pre-earthquake ionospheric anomalies before three major earthquakes by GPS-TEC and GIM-TEC data during 2015–2017. Adv. Space Res. 2019, 63, 2088–2099. [Google Scholar] [CrossRef]
- McCarthy, D.D.; Boucher, C.; Eanes, R.; Fukushima, T.; Herring, T.; Lieske, J.; Ma, C.; Montag, H.; Pâquet, P.; Reigber, C.; et al. IERS Standards (1989). IERS Tech. Note 1989, 3, 1. [Google Scholar]
- Wu, J.T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. Man Geod. 1993, 18, 91–98. [Google Scholar]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Øvstedal, O. Absolute positioning with single-frequency GPS receivers. GPS Solut. 2002, 5, 33–44. [Google Scholar] [CrossRef]
- Yunck, T.P. Orbit determination. In Global Positioning System-Theory and Applications; Parkinson, B.W., Spilker, J.J., Eds.; AIAA: Washington, DC, USA, 1996. [Google Scholar]
- Beran, T.; Kim, D.; Langley, R.B. High-precision single-frequency GPS point positioning. In Proceedings of the ION ITM 2003, Institute of Navigation, Portland, OR, USA, 9–12 September 2003; pp. 1192–1200. [Google Scholar]
- Shi, C.; Gu, S.; Lou, Y.; Ge, M. An improved approach to model ionospheric delays for single-frequency precise point positioning. Adv. Space Res. 2012, 49, 1698–1708. [Google Scholar] [CrossRef]
- Montenbruck, O. Kinematic GPS positioning of LEO satellites using ionosphere-free single frequency measurements. Aerosp. Sci. Technol. 2003, 7, 396–405. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Y.; Chen, K. Development of a real-time single frequency precise point positioning system and test results. In Proceedings of the ION GNSS 2006, Institute of Navigation, Fort Worth, TX, USA, 26–29 September 2006; pp. 2297–2303. [Google Scholar]
- Beran, T.; Bisnath, S.B.; Langley, R.B. Evaluation of high-precision, single-frequency GPS point positioning models. In Proceedings of the ION GNSS 2004, Institute of Navigation, Long Beach, CA, USA, 21–24 September 2004; pp. 1893–1901. [Google Scholar]
- Le, A.Q.; Tiberius, C.C.J.M.; Van der Marel, H.; Jakowski, N. Use of Global and Regional Ionosphere Maps for Single-Frequency Precise Point Positioning. In Observing our Changing Earth; Springer: Berlin, Germany, 2009; pp. 759–769. [Google Scholar]
- Zhang, B.; Teunissen, P.J.G.; Yuan, Y.; Zhang, H.; Li, M. Joint estimation of vertical total electron content (VTEC) and satellite differential code biases (SDCBs) using low-cost receivers. J. Geod. 2018, 92, 401–413. [Google Scholar] [CrossRef]
- Gao, Z.; Ge, M.; Shen, W.; Zhang, H.; Niu, X. Ionospheric and receiver DCB-constrained multi-GNSS single-frequency PPP integrated with MEMS inertial measurements. J. Geod. 2017, 91, 1351–1366. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, Z.; Ge, M.; Niu, X.; Huang, L.; Tu, R.; Li, X. On the convergence of ionospheric constrained precise point positioning (IC-PPP) based on undifferential uncombined raw GNSS observations. Sensors 2013, 13, 15708–15725. [Google Scholar] [CrossRef] [PubMed]
- Fu, W.; Yang, Y.; Zhang, Q.; Huang, G. Real-time estimation of BDS/GPS high-rate satellite clock offsets using sequential least squares. Adv. Space Res. 2018, 62, 477–487. [Google Scholar] [CrossRef]
- Chen, X.; Ge, M.; Hugentobler, U.; Schuh, H. A new parallel algorithm for improving the computational efficiency of multi-GNSS precise orbit determination. GPS Solut. 2022, 26, 83. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; García-Fer, M. Towards a more realistic ionospheric mapping function. In Proceedings of the XXVIIIth General Assembly, New Delhi, India, 23–29 October 2005. [Google Scholar]
- Chang, G.; Xu, T.; Yao, Y.; Wang, H.; Zeng, H. Ionospheric delay prediction based on online polynomial modeling for real-time cycle slip repair of undifferenced triple-frequency GNSS signals. Measurement 2019, 146, 289–297. [Google Scholar] [CrossRef]
- Shubin, V.N.; Gulyaeva, T.L. Global mapping of total electron content from GNSS observations for updating IRI-Plas model. Adv. Space Res. 2022, 69, 168–175. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, H.; Xu, P.; Geng, J.; Wang, C.; Liu, J. Kriging with unknown variance components for regional ionospheric reconstruction. Sensors 2017, 17, 468. [Google Scholar] [CrossRef]
- De Mesnard, L. Pollution models and inverse distance weighting: Some critical remarks. Comput. Geosci. 2011, 52, 459–469. [Google Scholar] [CrossRef]
- Aldworth, J.; Cressie, N. Prediction of nonlinear spatial functionals. J. Stat. Plan. Inference 2003, 112, 3–41. [Google Scholar] [CrossRef]
- Li, Y.; Xu, C.; Yi, L.; Fang, R. A data-driven approach for denoising GNSS position time series. J. Geod. 2018, 92, 905–922. [Google Scholar] [CrossRef]
- Gruszczynski, M.; Klos, A.; Bogusz, J. Orthogonal transformation in extracting of common mode errors from continuous GPS networks. Acta Geodyn. Geomater. 2016, 13, 291–298. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Mareev, E.A.; Iudin, D.I.; Molchanov, O.A. Mosaic source of internal gravity waves associated with seismic activity. In Seismo-Electromagnetics (Lithosphere–Atmosphere–Ionosphere Coupling); Hayakawa, M., Molchanov, D., Eds.; Terra Scientific Publishing Co.: Tokyo, Japan, 2002; pp. 335–342. [Google Scholar]
- Shalimov, S.; Gokhberg, M. Lithosphere–ionosphere coupling mechanism and its application to the earthquake in Iran on June 20, 1990. A review of ionospheric measurements and basic assumptions. Phys. Earth Planet. Inter. 1998, 105, 211–218. [Google Scholar] [CrossRef]
- Gokhberg, M.B.; Morgounov, V.A.; Yoshino, T.; Tomizawa, I. Experimental measurement of electromagnetic emissions possibly related to earthquakes in Japan. J. Geophys. Res. Solid Earth 1982, 87, 7824–7828. [Google Scholar] [CrossRef]
- Voitov, G.I. Chemical and isotopic-carbon instabilities of the native gas flows in seismically active region. Izv. Earth Sci. 1994, 3, 20–31. [Google Scholar]
- Jiang, W.; Ma, Y.; Liu, H.; Deng, L.; Zhou, X. Investigation of Lushan earthquake ionosphere VTEC anomalies based on GPS data. Earthq. Sci. 2013, 26, 259–265. [Google Scholar] [CrossRef][Green Version]
- Cai, H.; Li, Z.; Wang, M.; Sun, H. Coseismic ionospheric disturbances of Mw7.9 Wenchuan earthquake and Mw9.0 Japan Earthquake. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 716–719. [Google Scholar]

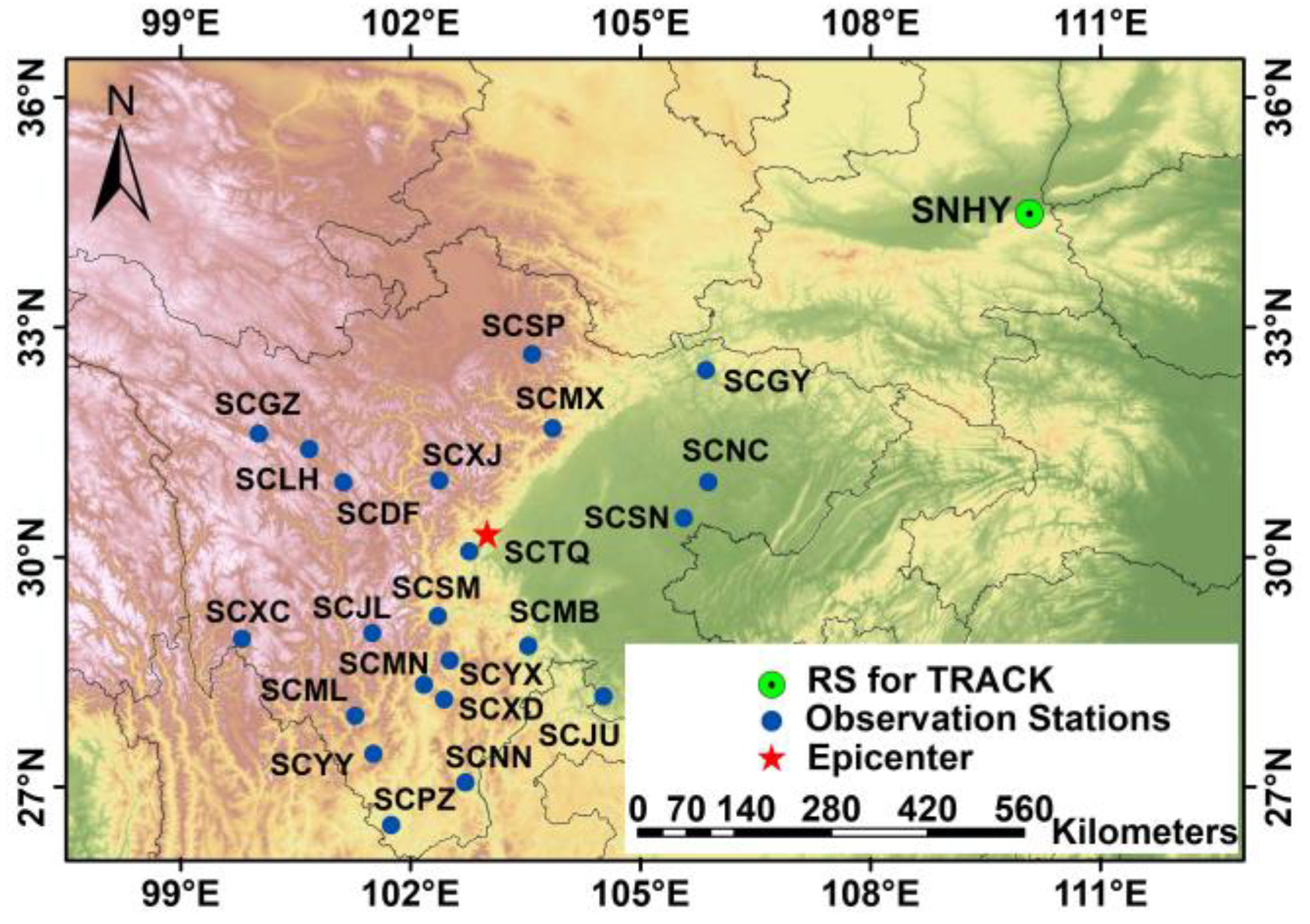
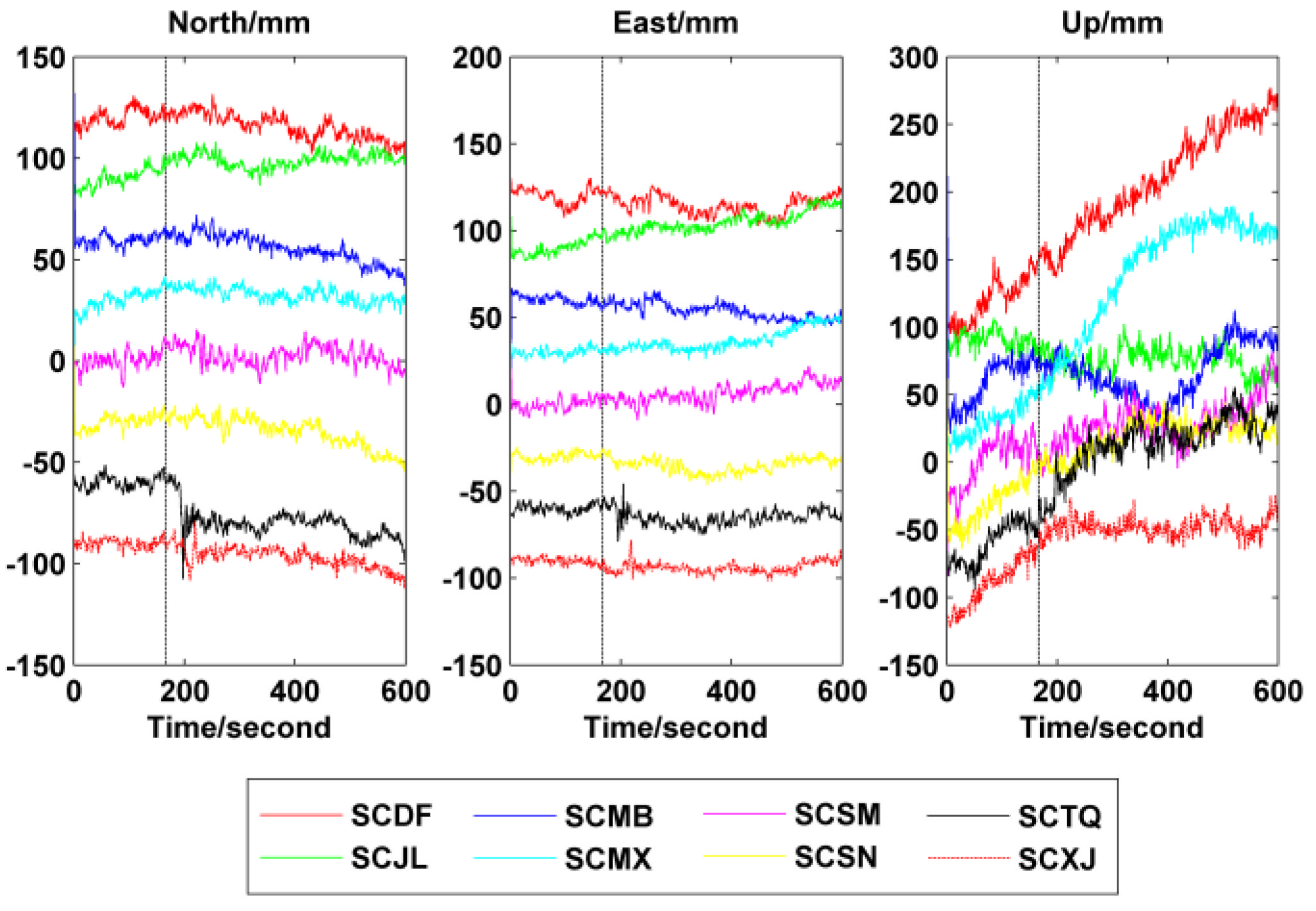
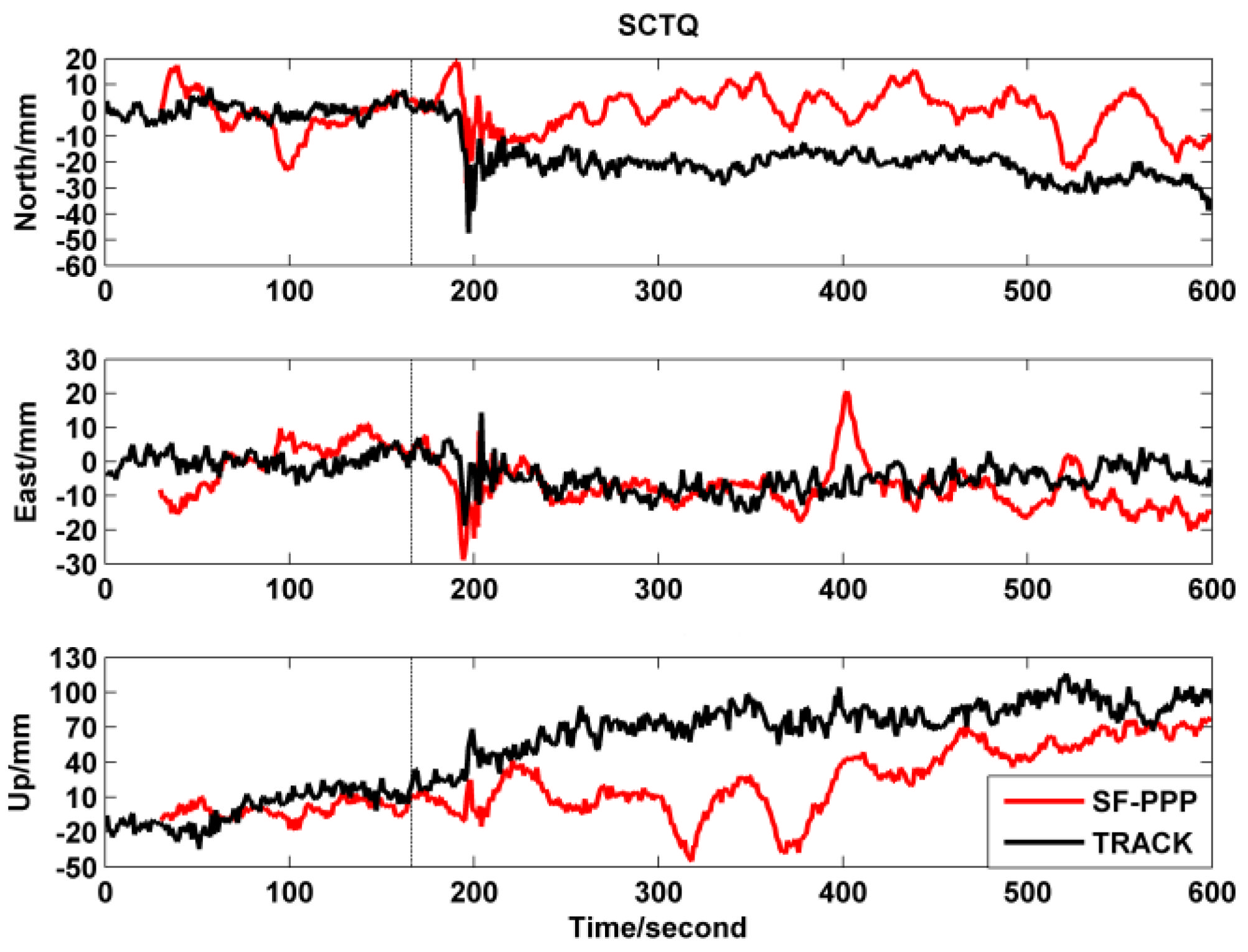
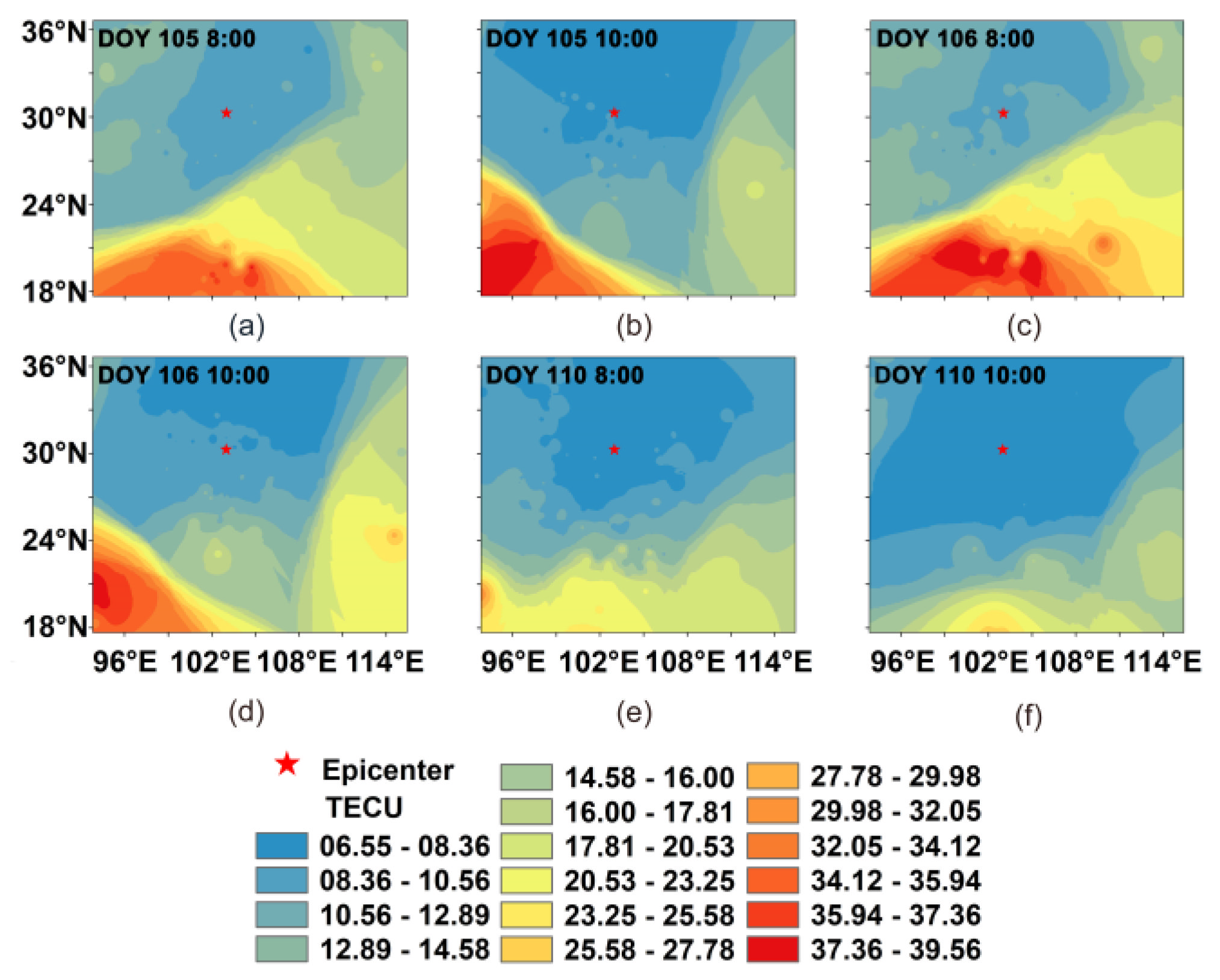

| Site | Distance (km) | Site | Distance (km) | Site | Distance (km) | Site | Distance (km) |
|---|---|---|---|---|---|---|---|
| 0906 | 191.9 | 0201 | 173.0 | 0156 | 284.1 | 0026 | 358.5 |
| 0167 | 160.8 | 0547 | 184.4 | 0543 | 244.8 | 0921 | 333.3 |
| 0172 | 126.3 | 0910 | 168.6 | 0553 | 240.5 | 0030 | 320.5 |
| 0918 | 122.1 | 0029 | 165.4 | 0926 | 233.9 | 0925 | 272.0 |
| 0549 | 126.6 | 0174 | 172.7 | 0190 | 223.6 | 0191 | 264.5 |
| 0550 | 98.8 | 0548 | 161.0 | 0554 | 219.2 | 0932 | 264.1 |
| 0037 | 146.1 | 0934 | 193.5 | 0033 | 212.1 | 0231 | 295.5 |
| 0919 | 145.4 | 0180 | 189.7 | 0199 | 221.3 | 0049 | 271.2 |
| Site | RMS (cm) | |||||
|---|---|---|---|---|---|---|
| North | East | Up | ||||
| TRACK | SF PPP | TRACK | SF PPP | TRACK | SF PPP | |
| 0029 | 2.67 | 48.88 | 1.14 | 23.48 | 3.98 | 58.97 |
| 0033 | 3.12 | 50.88 | 0.87 | 18.01 | 3.90 | 53.69 |
| 0167 | 1.95 | 57.61 | 1.03 | 45.54 | 4.46 | 148.32 |
| 0172 | 2.17 | 48.49 | 1.34 | 14.56 | 3.92 | 36.76 |
| 0190 | 2.66 | 58.33 | 1.02 | 20.60 | 3.93 | 66.42 |
| 0191 | 2.79 | 84.53 | 1.54 | 53.93 | 3.75 | 167.20 |
| 0548 | 2.84 | 47.91 | 1.02 | 18.59 | 4.46 | 51.62 |
| 0550 | 2.45 | 45.93 | 1.23 | 54.15 | 4.06 | 131.09 |
| Site | Distance (km) | Site | Distance (km) |
|---|---|---|---|
| SCDF | 214.4 | SCSM | 134.8 |
| SCJL | 210.0 | SCSN | 231.4 |
| SCMB | 155.6 | SCTQ | 42.7 |
| SCMX | 174.2 | SCXJ | 116.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, J.; Gao, Z.; Yang, C.; Wei, Y.; Peng, J. Investigation of Displacement and Ionospheric Disturbance during an Earthquake Using Single-Frequency PPP. Remote Sens. 2022, 14, 4286. https://doi.org/10.3390/rs14174286
Lv J, Gao Z, Yang C, Wei Y, Peng J. Investigation of Displacement and Ionospheric Disturbance during an Earthquake Using Single-Frequency PPP. Remote Sensing. 2022; 14(17):4286. https://doi.org/10.3390/rs14174286
Chicago/Turabian StyleLv, Jie, Zhouzheng Gao, Cheng Yang, Yingying Wei, and Junhuan Peng. 2022. "Investigation of Displacement and Ionospheric Disturbance during an Earthquake Using Single-Frequency PPP" Remote Sensing 14, no. 17: 4286. https://doi.org/10.3390/rs14174286
APA StyleLv, J., Gao, Z., Yang, C., Wei, Y., & Peng, J. (2022). Investigation of Displacement and Ionospheric Disturbance during an Earthquake Using Single-Frequency PPP. Remote Sensing, 14(17), 4286. https://doi.org/10.3390/rs14174286







