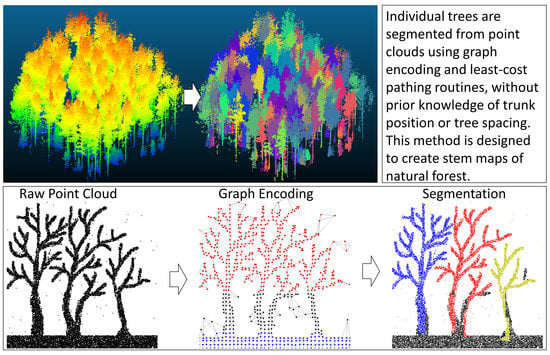
An Unsupervised Canopy-to-Root Pathing (UCRP) Tree Segmentation Algorithm for Automatic Forest Mapping
Abstract
:1. Introduction
1.1. Image-Based Stem Mapping
1.2. Airborne LiDAR-Based Stem Mapping
1.3. High-Resolution Point Cloud Stem Mapping
2. Materials and Methods
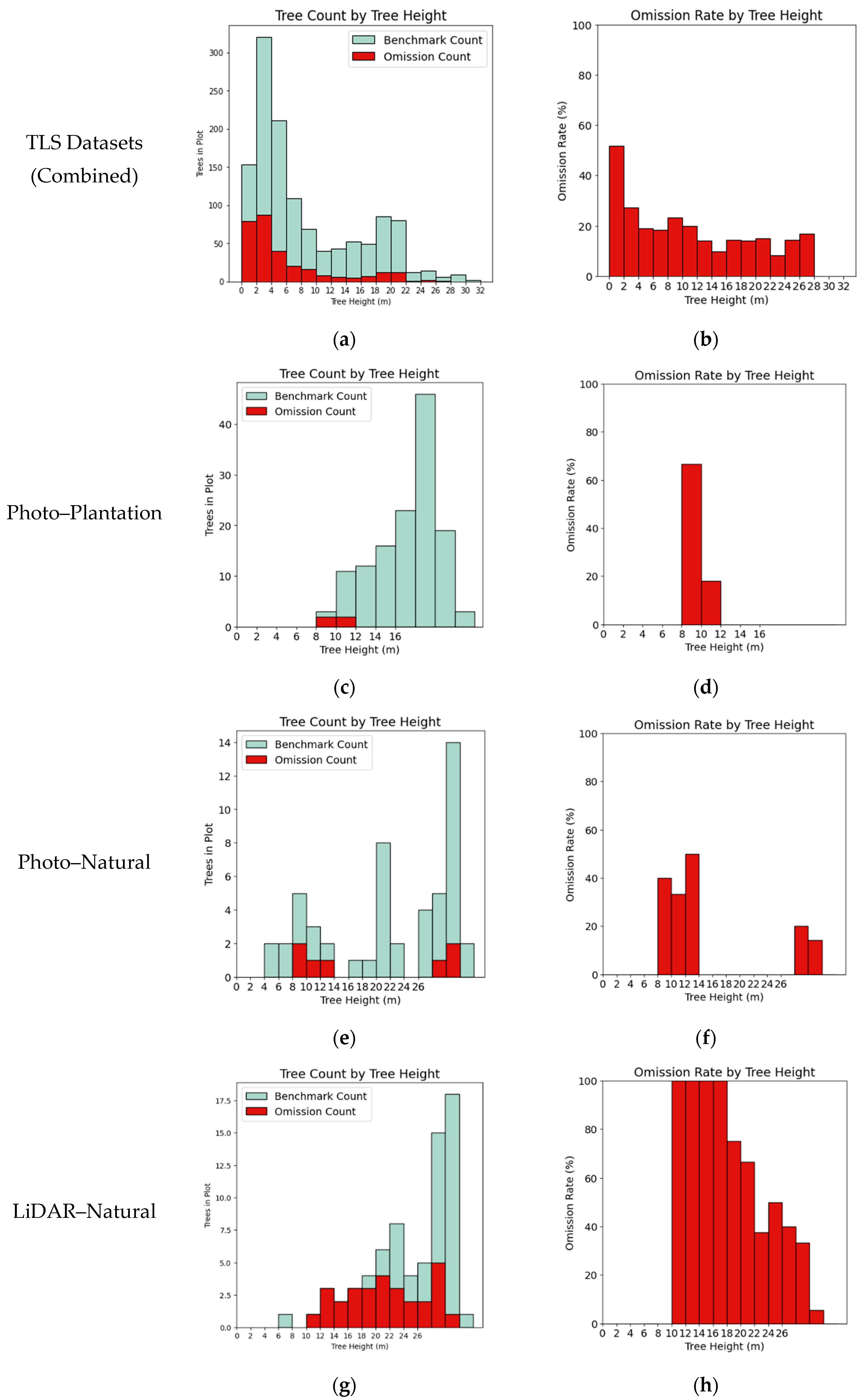
2.1. Datasets
2.1.1. TLS Datasets
2.1.2. Martell Forest
2.1.3. UAV LiDAR Datasets
2.1.4. UAV Photogrammetric Datasets
2.2. Segmentation Method
2.2.1. Point Cloud Normalization
2.2.2. Superpoint Encoding
2.2.3. Rough Classification
2.2.4. Network Construction
2.2.5. Least-Cost Routing
- The route is a list of consecutively adjacent superpoints: , where ;
- The first superpoint in the route is the selected canopy superpoint: ;
- The last superpoint in the route is a ground superpoint: ;
- The last superpoint in the route is the only ground superpoint: for .
2.2.6. Final Segmentation
2.3. Method Comparisons
2.4. Tree Matching
2.5. Evaluation Metrics
3. Results
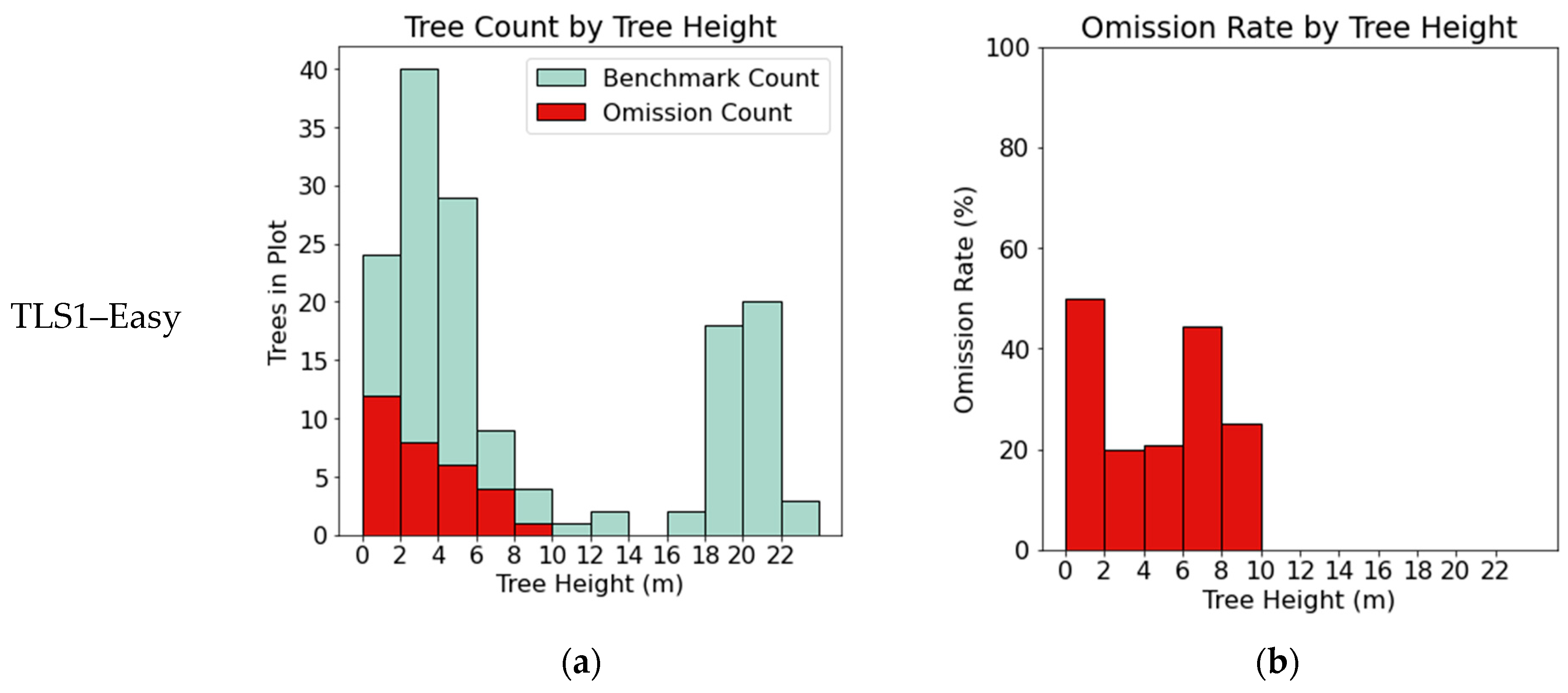
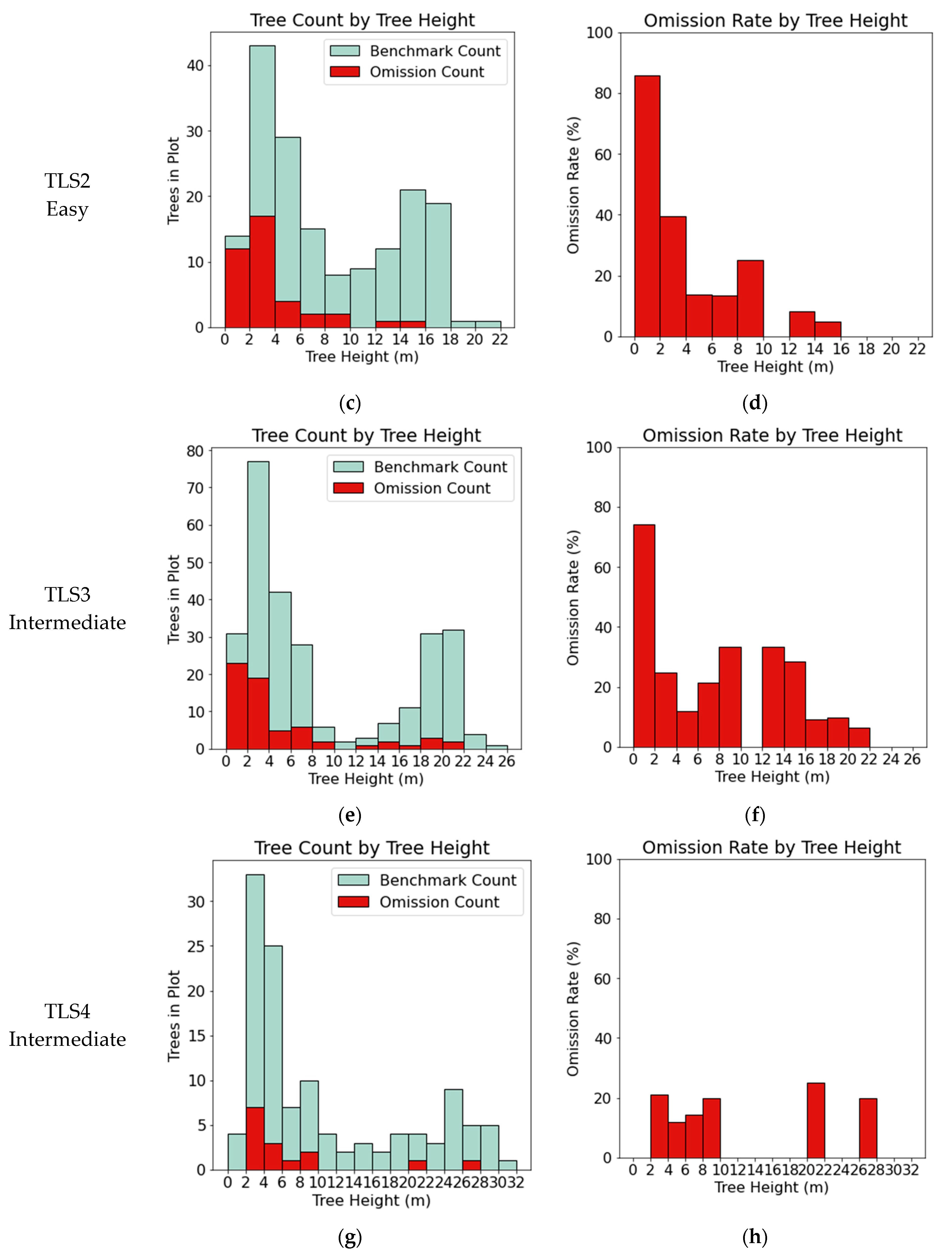
3.1. TLS Benchmark Dataset
3.2. UAV-Based Photogrammetric Dataset
3.3. UAV-Based LiDAR Dataset
4. Discussion
4.1. Segmentation Error
4.2. Canopy-to-Root Routing Direction
4.3. Future Research
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast Automatic Precision Tree Models from Terrestrial Laser Scanner Data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Yun, Z.; Zheng, G. Stratifying Forest Overstory and Understory for 3-D Segmentation Using Terrestrial Laser Scanning Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12114–12131. [Google Scholar] [CrossRef]
- Blackard, J.; Finco, M.; Helmer, E.; Holden, G.; Hoppus, M.; Jacobs, D.; Lister, A.; Moisen, G.; Nelson, M.; Riemann, R. Mapping U.S. Forest Biomass Using Nationwide Forest Inventory Data and Moderate Resolution Information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar] [CrossRef]
- Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Calders, K.; Woodgate, W. Leaf and Wood Classification Framework for Terrestrial LiDAR Point Clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef]
- Peuhkurinen, J.; Maltamo, M.; Malinen, J.; Pitkänen, J.; Packalén, P. Preharvest Measurement of Marked Stands Using Airborne Laser Scanning. For. Sci. 2007, 53, 653–661. [Google Scholar]
- Wulder, M.; Niemann, K.O.; Goodenough, D.G. Local Maximum Filtering for the Extraction of Tree Locations and Basal Area from High Spatial Resolution Imagery. Remote Sens. Environ. 2000, 73, 103–114. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S.; Nelson, R. Lidar Remote Sensing of Forest Biomass: A Scale-Invariant Estimation Approach Using Airborne Lasers. Remote Sens. Environ. 2009, 113, 182–196. [Google Scholar] [CrossRef]
- Pinz, A. A Computer Vision System for the Recognition of Trees in Aerial Photographs. Multisource Data Integr. Remote Sens. 1991, 3099, 111–124. [Google Scholar]
- Gougeon, F.A. A Crown-Following Approach to the Automatic Delineation of Individual Tree Crowns in High Spatial Resolution Aerial Images. Can. J. Remote Sens. 1995, 21, 274–284. [Google Scholar] [CrossRef]
- Culvenor, D.S. TIDA: An Algorithm for the Delineation of Tree Crowns in High Spatial Resolution Remotely Sensed Imagery. Comput. Geosci 2002, 28, 33–44. [Google Scholar] [CrossRef]
- Wang, L.; Gong, P.; Biging, G.S. Individual Tree-Crown Delineation and Treetop Detection in High-Spatial-Resolution Aerial Imagery. Photogramm. Eng. Remote Sens. 2004, 70, 351–357. [Google Scholar] [CrossRef]
- Gougeon, F.A.; Leckie, D.G. The Individual Tree Crown Approach Applied to Ikonos Images of a Coniferous Plantation Area. Photogramm. Eng. Remote Sens. 2006, 72, 1287–1297. [Google Scholar] [CrossRef]
- Ke, Y.; Quackenbush, L.J. A Review of Methods for Automatic Individual Tree-Crown Detection and Delineation from Passive Remote Sensing. Int. J. Remote Sens. 2011, 32, 4725–4747. [Google Scholar] [CrossRef]
- Lamar, W.R.; McGraw, J.B.; Warner, T.A. Multitemporal Censusing of a Population of Eastern Hemlock (Tsuga canadensis L.) from Remotely Sensed Imagery Using an Automated Segmentation and Reconciliation Procedure. Remote Sens. Environ. 2005, 94, 133–143. [Google Scholar] [CrossRef]
- Wang, D. Unsupervised Semantic and Instance Segmentation of Forest Point Clouds. ISPRS J. Photogramm. Remote Sens. 2020, 165, 86–97. [Google Scholar] [CrossRef]
- Westling, F.; Underwood, J.; Bryson, M. Graph-Based Methods for Analyzing Orchard Tree Structure Using Noisy Point Cloud Data. Comput. Electron. Agric. 2021, 187, 106270. [Google Scholar] [CrossRef]
- Hyyppä, E.; Yu, X.; Kaartinen, H.; Hakala, T.; Kukko, A.; Vastaranta, M.; Hyyppä, J. Comparison of Backpack, Handheld, Under-Canopy UAV, and Above-Canopy UAV Laser Scanning for Field Reference Data Collection in Boreal Forests. Remote Sens. 2020, 12, 3327. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Línková, L. A New Method for UAV Lidar Precision Testing Used for the Evaluation of an Affordable DJI ZENMUSE L1 Scanner. Remote Sens. 2021, 13, 4811. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Y.; Jaakkola, A.; Kukko, A.; Kaartinen, H.; Hyyppa, J.; Honkavaara, E.; Liu, J. Forest Data Collection Using Terrestrial Image-Based Point Clouds from a Handheld Camera Compared to Terrestrial and Personal Laser Scanning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5117–5132. [Google Scholar] [CrossRef]
- Roberts, J.; Koeser, A.; Abd-Elrahman, A.; Wilkinson, B.; Hansen, G.; Landry, S.; Perez, A. Mobile Terrestrial Photogrammetry for Street Tree Mapping and Measurements. Forests 2019, 10, 701. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A Photogrammetric Workflow for the Creation of a Forest Canopy Height Model from Small Unmanned Aerial System Imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- Carr, J.C.; Slyder, J.B. Individual Tree Segmentation from a Leaf-off Photogrammetric Point Cloud. Int. J. Remote Sens. 2018, 39, 5195–5210. [Google Scholar] [CrossRef]
- Fritz, A.; Kattenborn, T.; Koch, B. UAV-Based Photogrammetric Point Clouds- Tree Stem Mapping in Open Stands in Comparison to Terrestrial Laser Scanner Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-1/W2, 141–146. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International Benchmarking of Terrestrial Laser Scanning Approaches for Forest Inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Ben-Shabat, Y.; Lindenbaum, M.; Fischer, A. 3DmFV: Three-Dimensional Point Cloud Classification in Real-Time Using Convolutional Neural Networks. IEEE Robot. Autom. Lett. 2018, 3, 3145–3152. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep Learning on Point Sets for 3d Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Mizoguchi, T.; Ishii, A.; Nakamura, H.; Inoue, T.; Takamatsu, H. Lidar-Based Individual Tree Species Classification Using Convolutional Neural Network. In Proceedings of the SPIE, Videometrics, Range Imaging, and Applications XIV, Munich, Germany, 26–27 June 2017; Volume 10332, pp. 193–199. [Google Scholar]
- Guan, H.; Yu, Y.; Ji, Z.; Li, J.; Zhang, Q. Deep Learning-Based Tree Classification Using Mobile LiDAR Data. Remote Sens. Lett. 2015, 6, 864–873. [Google Scholar] [CrossRef]
- Hamraz, H.; Jacobs, N.B.; Contreras, M.A.; Clark, C.H. Deep Learning for Conifer/Deciduous Classification of Airborne LiDAR 3D Point Clouds Representing Individual Trees. ISPRS J. Photogramm. Remote Sens. 2019, 158, 219–230. [Google Scholar] [CrossRef]
- Windrim, L.; Bryson, M. Detection, Segmentation, and Model Fitting of Individual Tree Stems from Airborne Laser Scanning of Forests Using Deep Learning. Remote Sens. 2020, 12, 1469. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Liu, J.; Fei, S.; Habib, A. Leaf-Off and Leaf-On UAV LiDAR Surveys for Single-Tree Inventory in Forest Plantations. Drones 2021, 5, 115. [Google Scholar] [CrossRef]
- Sirmacek, B.; Lindenbergh, R. Automatic Classification of Trees From Laser Scanning Point Clouds. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W5, 137–144. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Habib, A. Quality Control and Crop Characterization Framework for Multi-Temporal UAV LiDAR Data over Mechanized Agricultural Fields. Remote Sens. Environ. 2021, 256, 112299. [Google Scholar] [CrossRef]
- Kuželka, K.; Slavík, M.; Surový, P. Very High Density Point Clouds from UAV Laser Scanning for Automatic Tree Stem Detection and Direct Diameter Measurement. Remote Sens. 2020, 12, 1236. [Google Scholar] [CrossRef] [Green Version]
- Itakura, K.; Hosoi, F. Automatic Individual Tree Detection and Canopy Segmentation from Three-Dimensional Point Cloud Images Obtained from Ground-Based Lidar. J. Agric. Meteorol. 2018, 74, 109–113. [Google Scholar] [CrossRef]
- Ayrey, E.; Fraver, S.; Kershaw, J.A.; Kenefic, L.S.; Hayes, D.; Weiskittel, A.R.; Roth, B.E. Layer Stacking: A Novel Algorithm for Individual Forest Tree Segmentation from LiDAR Point Clouds. Can. J. Remote Sens. 2017, 43, 16–27. [Google Scholar] [CrossRef]
- Zhang, W.; Wan, P.; Wang, T.; Cai, S.; Chen, Y.; Jin, X.; Yan, G. A Novel Approach for the Detection of Standing Tree Stems from Plot-Level Terrestrial Laser Scanning Data. Remote Sens. 2019, 11, 211. [Google Scholar] [CrossRef]
- Livny, Y.; Yan, F.; Olson, M.; Chen, B.; Zhang, H.; El-Sana, J. Automatic Reconstruction of Tree Skeletal Structures from Point Clouds. In Proceedings of the ACM SIGGRAPH Asia 2010 Papers on—SIGGRAPH ASIA ’10, Seoul, Korea, 15–18 December 2010; ACM Press: New York, NY, USA, 2010; p. 1. [Google Scholar]
- Neubert, B.; Franken, T.; Deussen, O. Approximate Image-Based Tree-Modeling Using Particle Flows. In Proceedings of the ACM SIGGRAPH 2007 Papers on—SIGGRAPH ’07, San Diego, CA, USA, 4–5 August 2007; ACM Press: New York, NY, USA, 2007; p. 88. [Google Scholar]
- Lin, Y.-C.; Shao, J.; Shin, S.-Y.; Saka, Z.; Joseph, M.; Manish, R.; Fei, S.; Habib, A. Comparative Analysis of Multi-Platform, Multi-Resolution, Multi-Temporal LiDAR Data for Forest Inventory. Remote Sens. 2022, 14, 649. [Google Scholar] [CrossRef]
- Hart, P.; Nilsson, N.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Wang, D. SSSC; GitHub Repository. 2020. Available online: https://github.com/dwang520/SSSC (accessed on 19 November 2021).
- Gale, D.; Shapley, L.S. College Admissions and the Stability of Marriage. Am. Math. Mon. 1962, 69, 9. [Google Scholar] [CrossRef]







| LiDAR-Natural | |
|---|---|
| Altitude | 100 m |
| Lidar Pulse Rate | 240 kHz |
| Flying Speed | 6 m/s |
| Sidelap | 80% |
| Photo-Plantation | Photo-Natural | |
|---|---|---|
| Altitude | 80 m | 110 m |
| Ground Sampling Distance | 1 cm | 1.4 cm |
| Overlap | 90% | 90% |
| Sidelap | 90% | 80% |
| Symbol | Description | Value in This Paper |
|---|---|---|
| Size of the voxel cube used to compute superpoints | 0.3 m | |
| A voxel must contain more than points to be used to create a super point | 10–TLS and Photo Datasets 2–LiDAR Dataset | |
| A threshold value determining the highest elevation for a ‘ground’-classified superpoint | 1.2 m | |
| A threshold value determining the lowest elevation for a ‘canopy’ superpoint | 2 m | |
| The number of nearest neighbors connected to each superpoint in the initial graph construction | 10 | |
| The merge distance within which two tree sets will be merged to form a single tree | 0.9 m |
| Parameter | Value |
|---|---|
| Threshold | 0.125 |
| Height | Ranged from 2–10 |
| NoP | 100 |
| Verticality | Ranged from 0.6–0.8 |
| Length | 2 |
| Merge Range | 0.3 |
| Dataset | Reference Trees | Segmented Trees | Matched Trees | Omissions | Commissions | Completeness% | Correctness % | IoU % | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ours | Wang | Ours | Wang | Ours | Wang | ||||||
| TLS1–Easy | 152 | 139 | 121 | 31 | 18 | 79 | 38 | 87 | 93 | 71 | 37 |
| TLS2–Easy | 172 | 137 | 133 | 39 | 4 | 77 | 38 | 97 | 94 | 75 | 37 |
| TLS3–Intermediate | 275 | 256 | 211 | 64 | 45 | 76 | 50 | 82 | 93 | 65 | 48 |
| TLS4–Intermediate | 121 | 168 | 106 | 15 | 62 | 87 | 23 | 63 | 76 | 57 | 22 |
| TLS5–Difficult | 242 | 256 | 187 | 55 | 69 | 77 | 55 | 73 | 83 | 60 | 50 |
| TLS6–Difficult | 292 | 256 | 200 | 92 | 56 | 68 | 1 | 78 | 80 | 57 | 1 |
| Totals | 1254 | 1212 | 958 | 296 | 254 | 76 | 37 | 79 | 90 | 64 | 36 |
| Dataset | Reference Trees | Segmented Trees | Matched Trees | Omissions | Commissions | Completeness% | Correctness % | IoU % | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ours | Wang | Ours | Wang | Ours | Wang | ||||||
| Photo–Plant. | 133 | 129 | 129 | 4 | 0 | 96 | 54 | 100 | 96 | 96 | 52 |
| Photo–Natural | 51 | 54 | 44 | 7 | 10 | 86 | 25 | 81 | 84 | 72 | 24 |
| LiDAR–Natural | 71 | 49 | 42 | 29 | 7 | 59 | 15 | 85 | 83 | 53 | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carpenter, J.; Jung, J.; Oh, S.; Hardiman, B.; Fei, S. An Unsupervised Canopy-to-Root Pathing (UCRP) Tree Segmentation Algorithm for Automatic Forest Mapping. Remote Sens. 2022, 14, 4274. https://doi.org/10.3390/rs14174274
Carpenter J, Jung J, Oh S, Hardiman B, Fei S. An Unsupervised Canopy-to-Root Pathing (UCRP) Tree Segmentation Algorithm for Automatic Forest Mapping. Remote Sensing. 2022; 14(17):4274. https://doi.org/10.3390/rs14174274
Chicago/Turabian StyleCarpenter, Joshua, Jinha Jung, Sungchan Oh, Brady Hardiman, and Songlin Fei. 2022. "An Unsupervised Canopy-to-Root Pathing (UCRP) Tree Segmentation Algorithm for Automatic Forest Mapping" Remote Sensing 14, no. 17: 4274. https://doi.org/10.3390/rs14174274
APA StyleCarpenter, J., Jung, J., Oh, S., Hardiman, B., & Fei, S. (2022). An Unsupervised Canopy-to-Root Pathing (UCRP) Tree Segmentation Algorithm for Automatic Forest Mapping. Remote Sensing, 14(17), 4274. https://doi.org/10.3390/rs14174274