Microwave Emissivity of Typical Vegetated Land Types Based on AMSR2
Abstract
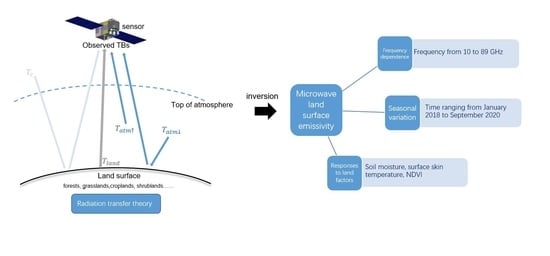
:1. Introduction
2. Data and Instantaneous MLSE Retrieval
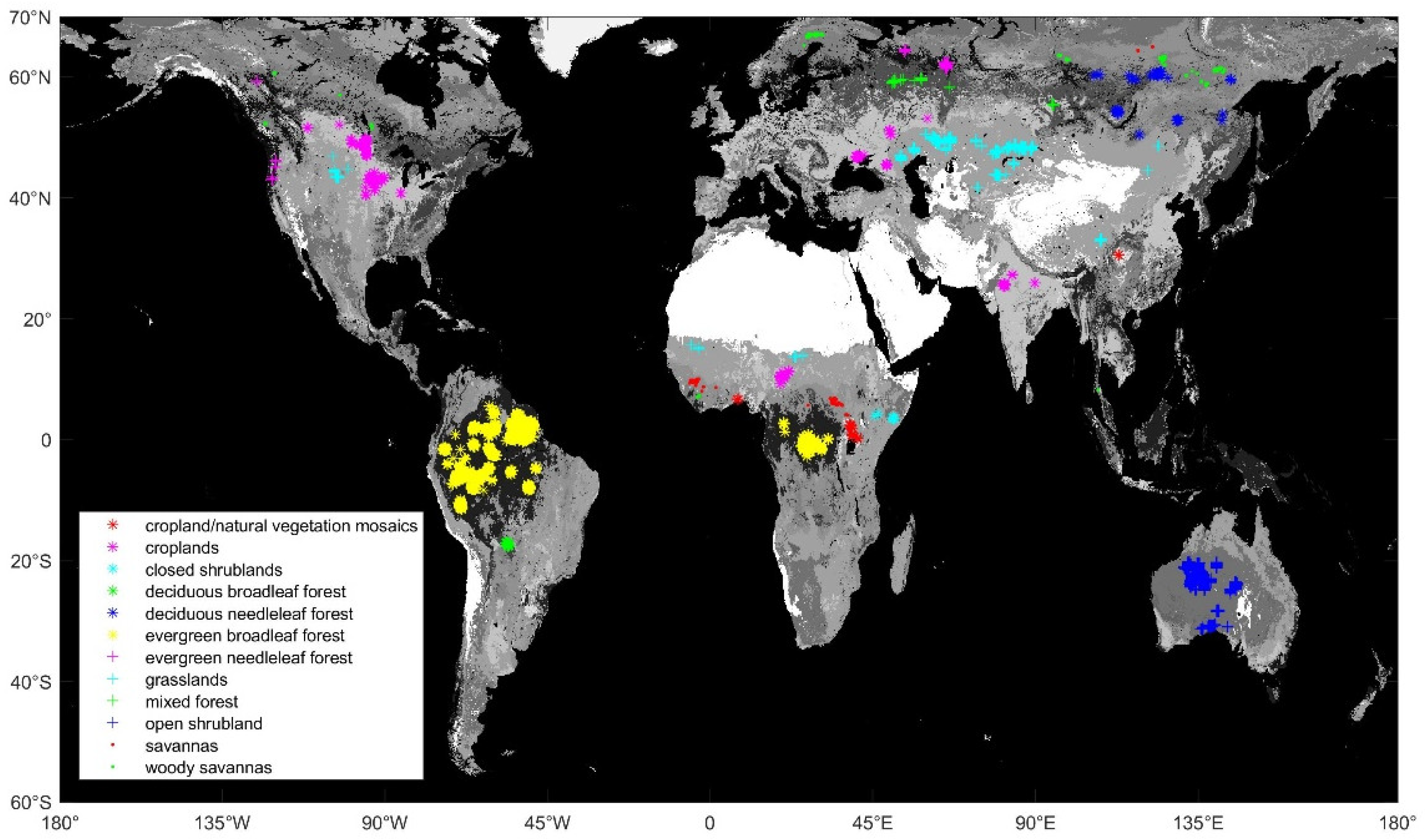
2.1. Passive Microwave Radiometers and Ancillary Data
2.2. Instantaneous MLSE Retrieval
3. Results
3.1. MLSE Spectral Features from 10.65 to 89 GHz
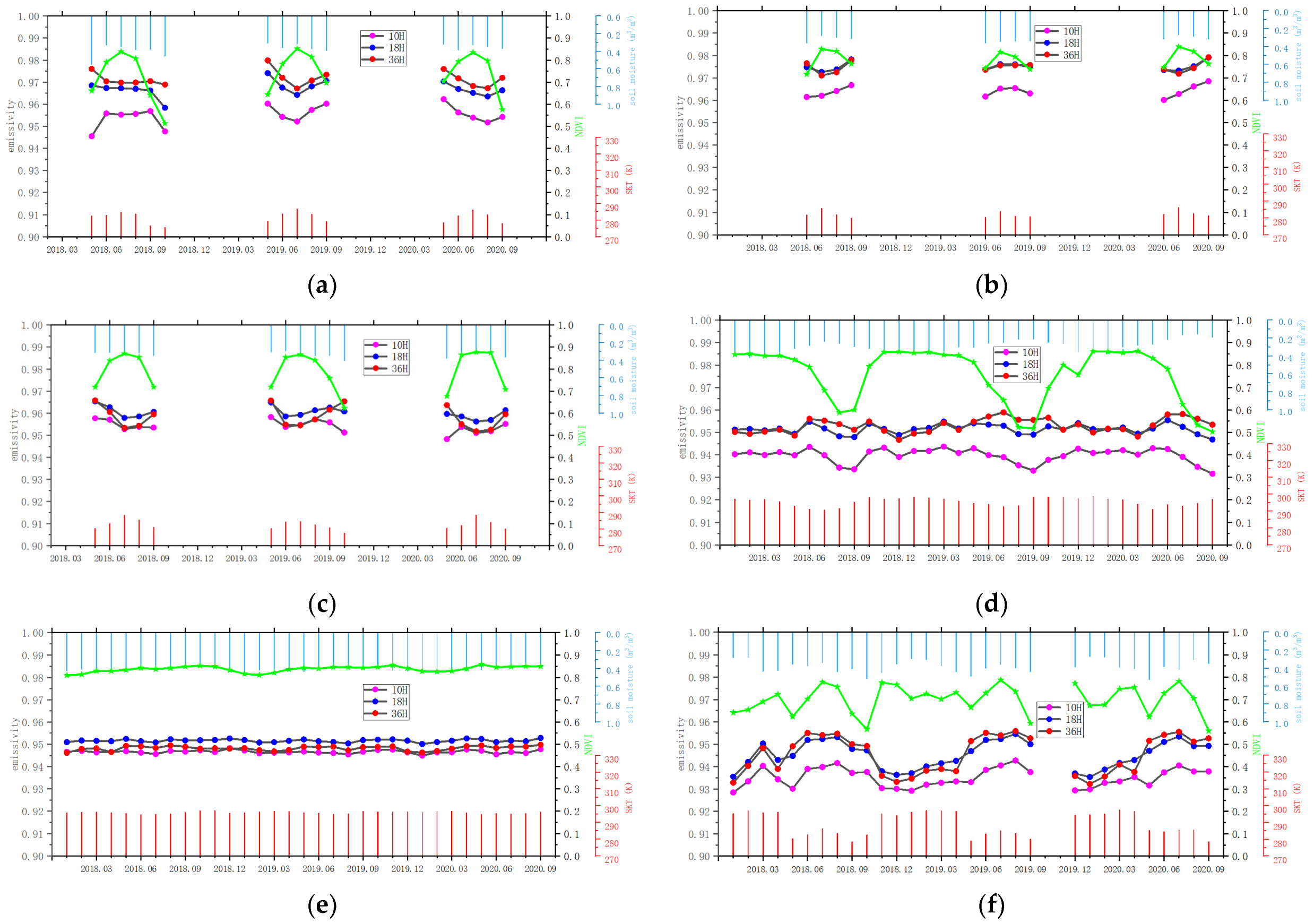
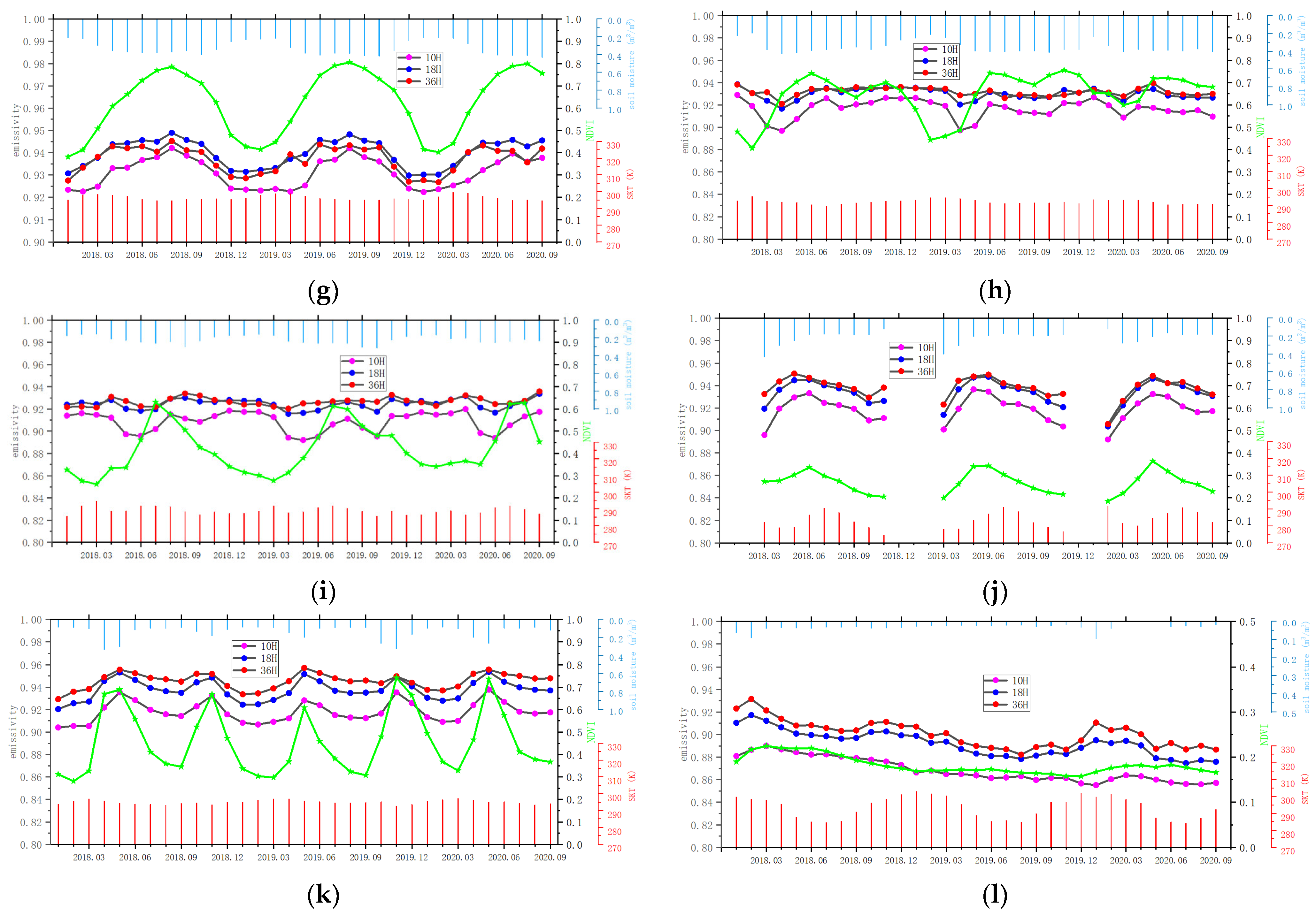
3.2. Temporal Variations of MLSE
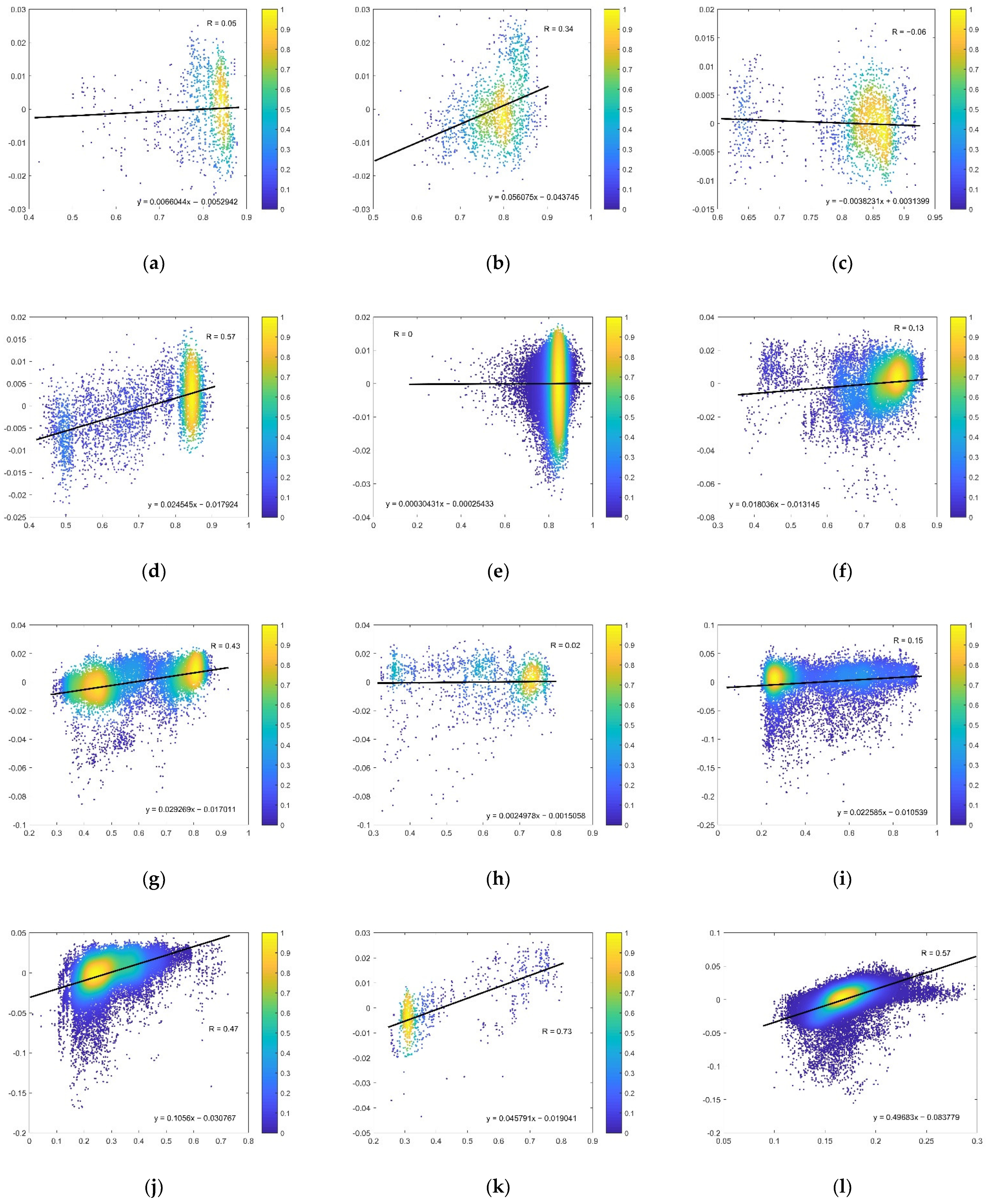
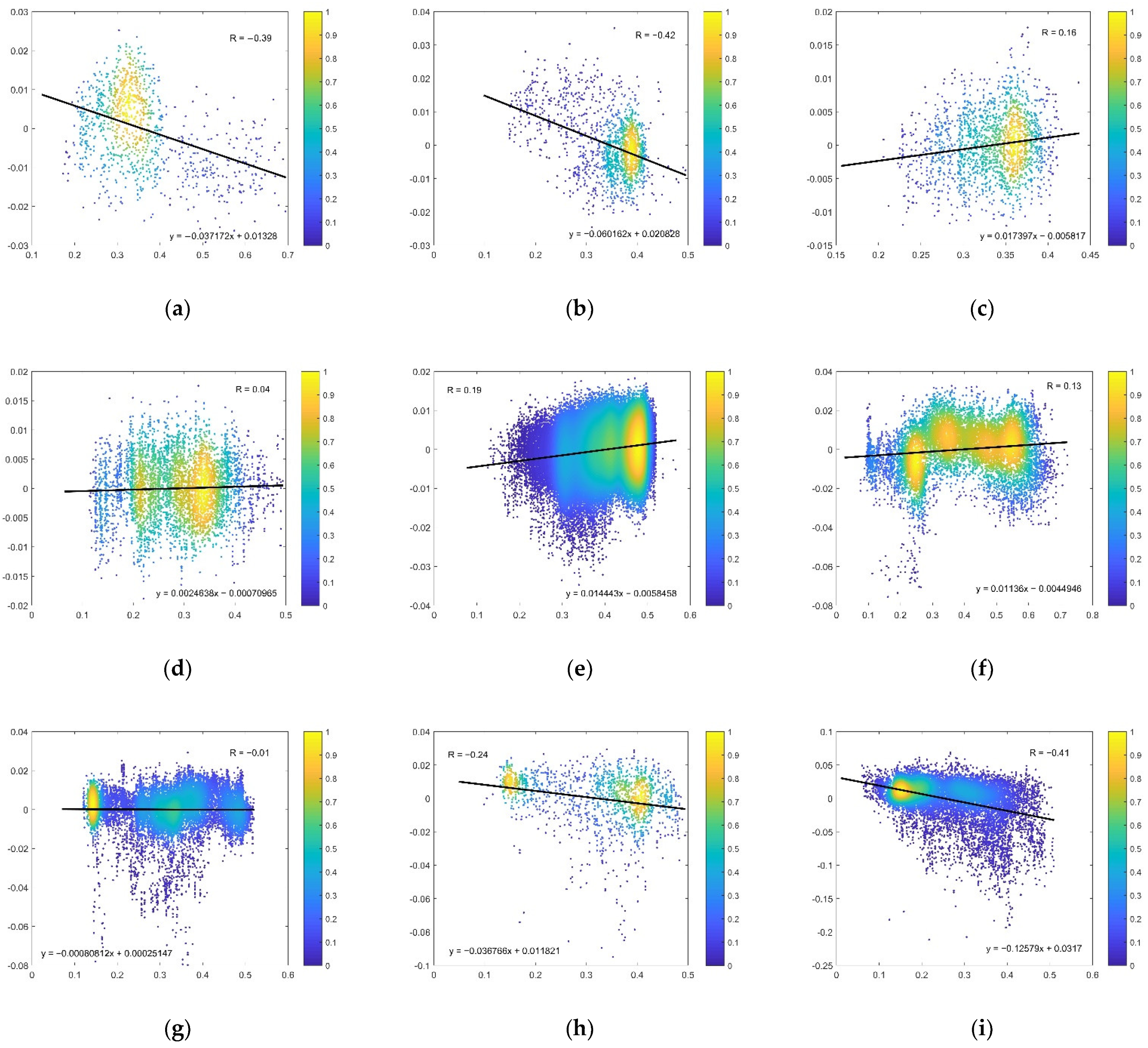
3.3. Responses of 10H Emissivity to SKT, NDVI and SMC
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Vegetation Type | ||||
|---|---|---|---|---|
| ENF | 2.4331 × 10−4 | 0.8955 | 0.0561 | −0.0437 |
| EBF | −5.2223 × 10−4 | 1.1011 | 0.0028 | −0.0024 |
| DNF | −0.0011 | 1.2562 | 0.0066 | −0.0053 |
| DBF | −3.5249 × 10−4 | 1.0440 | 0.0252 | −0.0184 |
| MF | −5.0590 × 10−4 | 1.0987 | −0.0026 | 0.0021 |
| CS | −0.0019 | 1.4812 | 0.0458 | −0.0190 |
| OS | −2.6528 × 10−4 | 0.9407 | 0.5164 | −0.0862 |
| WS | −1.7500 × 10−4 | 0.9892 | 0.0181 | −0.0132 |
| savannas | −0.0019 | 1.4860 | 0.0034 | −0.0010 |
| grasslands | −4.1465 × 10−4 | 1.0411 | 0.1184 | −0.0337 |
| croplands | 4.6557 × 10−4 | 0.7687 | 0.0233 | −0.0109 |
| CNV | −3.9747 × 10−4 | 1.0312 | −0.0022 | 0.0013 |
References
- Li, R.; Hu, J.; Wu, S.; Zhang, P.; Letu, H.; Wang, Y.; Wang, X.; Fu, Y.; Zhou, R.; Sun, L. Spatiotemporal Variations of Microwave Land Surface Emissivity (MLSE) over China Derived from Four-Year Recalibrated Fengyun 3B MWRI Data. Adv. Atmos. Sci. 2022, 39, 1536–1560. [Google Scholar] [CrossRef]
- Qiu, Y.; Guo, H.; Shi, J.; Lemmetyinen, J.; Shi, L. An emissivity-based land surface temperature retrieval algorithm. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar] [CrossRef]
- Yin, C.L.; Meng, F.; Yu, Q.R. Calculation of land surface emissivity and retrieval of land surface temperature based on a spectral mixing model. Infrared Phys. Technol. 2020, 108, 103333. [Google Scholar] [CrossRef]
- Zhao, T.; Shi, J.; Bindlish, R.; Jackson, T.; Cosh, M.; Jiang, L.; Zhang, Z.; Lan, H. Parametric exponentially correlated surface emission model for L-band passive microwave soil moisture retrieval. Phys. Chem. Earth Parts ABC 2015, 83, 65–74. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, N.J.; Aires, F.; Richaume, P.; Kerr, Y.H.; Prigent, C.; Kolassa, J.; Drusch, M. Soil Moisture Retrieval Using Neural Networks: Application to SMOS. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5991–6007. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Jackson, T.J.; O’Neill, P.; De Lannoy, G.; de Rosnay, P.; Walker, J.P.; Ferrazzoli, P.; Mironov, V.; Bircher, S.; Grant, J.P.; et al. Modelling the passive microwave signature from land surfaces: A review of recent results and application to the L-Band SMOS & SMAP soil moisture retrieval algorithms. Remote Sens. Environ. 2017, 192, 238–262. [Google Scholar] [CrossRef]
- Li, Z.L.; Leng, P.; Zhou, C.; Chen, K.S.; Zhou, F.C.; Shang, G.F. Soil moisture retrieval from remote sensing measurements: Current knowledge and directions for the future. Earth-Sci. Rev. 2021, 218, 103673. [Google Scholar] [CrossRef]
- Moradizadeh, M.; Srivastava, P.K. A new model for an improved AMSR2 satellite soil moisture retrieval over agricultural areas. Comput. Electron. Agric. 2021, 186, 106205. [Google Scholar] [CrossRef]
- Zhang, S.; Weng, F.; Yao, W. A Multivariable Approach for Estimating Soil Moisture from Microwave Radiation Imager (MWRI). J. Meteorol. Res. 2020, 34, 732–747. [Google Scholar] [CrossRef]
- Li, R.; Min, Q. Dynamic response of microwave land surface properties to precipitation in Amazon rainforest. Remote Sens. Environ. 2013, 133, 183–192. [Google Scholar] [CrossRef]
- Li, R.; Wang, Y.; Hu, J.; Wang, Y.; Min, Q.; Bergeron, Y.; Valeria, O.; Gao, Z.; Liu, J.; Fu, Y. Spatiotemporal variations of satellite microwave emissivity difference vegetation index in China under clear and cloudy skies. Earth Space Sci. 2020, 7, e2020EA001145. [Google Scholar] [CrossRef]
- Wang, Y.P.; Li, R.; Min, Q.L.; Fu, Y.F.; Wang, Y.; Zhong, L.; Fu, Y.Y. A three-source satellite algorithm for retrieving all-sky evapotranspiration rate using combined optical and microwave vegetation index at twenty AsiaFlux sites. Remote Sens. Environ. 2019, 235, 111463. [Google Scholar] [CrossRef]
- Shahroudi, N.; Rossow, W. Using land surface microwave emissivities to isolate the signature of snow on different surface types. Remote Sens. Environ. 2014, 152, 638–653. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, T.; Zhong, X.; Shao, W.; Li, X. Support vector regression snow-depth retrieval algorithm using passive microwave remote sensing data. Remote Sens. Environ. 2018, 210, 48–64. [Google Scholar] [CrossRef]
- Ringerud, S.; Kummerow, C.; Peters-Lidard, C.; Tian, Y.; Harrison, K.A. Comparison of Microwave Window Channel Retrieved and Forward-Modeled Emissivities Over the U.S. Southern Great Plains. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2395–2412. [Google Scholar] [CrossRef]
- Ringerud, S.; Kummerow, C.D.; Peters-Lidard, C.D. A Semi-Empirical Model for Computing Land Surface Emissivity in the Microwave Region. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1935–1946. [Google Scholar] [CrossRef]
- Prigent, C.; Aires, F.; Rossow, W.B. Land surface microwave emissivities over the globe for a decade. Bull. Amer. Meteorol. Soc. 2006, 87, 1573–1584. [Google Scholar] [CrossRef]
- Prigent, C.; Rossow, W.B.; Matthews, E. Microwave land surface emissivities estimated from SSM/I observations. J. Geophys. Res. Atmos. 1997, 102, 21867–21890. [Google Scholar] [CrossRef]
- Prigent, C.; Rossow, W.B.; Matthews, E. Global maps of microwave land surface emissivities: Potential for land surface characterization. Radio Sci. 1998, 33, 745–751. [Google Scholar] [CrossRef]
- Prakash, S.; Norouzi, H.; Azarderakhsh, M.; Blake, R.; Tesfagiorgis, K. Global land surface emissivity estimation from AMSR2 observations. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1270–1274. [Google Scholar] [CrossRef] [Green Version]
- Moncet, J.; Liang, P.; Galantowicz, J.F.; Lipton, A.E.; Uymin, G.; Prigent, C.; Grassotti, C. Land surface microwave emissivities derived from AMSR-E and MODIS measurements with advanced quality control. J. Geophys. Res. 2011, 116, D16104-1–D16104-20. [Google Scholar] [CrossRef]
- Norouzi, H.; Rossow, W.; Temimi, M.; Prigent, C.; Azarderakhsh, M.; Boukabara, S.; Khanbilvardi, R. Using microwave brightness temperature diurnal cycle to improve emissivity retrievals over land. Remote Sens. Environ. 2012, 123, 470–482. [Google Scholar] [CrossRef]
- Karbou, F.; Prigent, C. Calculation of microwave land surface emissivity from satellite observations: Validity of the specular approximation over snow-free surfaces? IEEE Geosci. Remote Sens. Lett. 2005, 2, 311–314. [Google Scholar] [CrossRef]
- Furuzawa, F.A.; Masunaga, H.; Nakamura, K. Development of a land surface emissivity algorithm for use by microwave rain retrieval algorithms. Remote Sens. Atmos. Clouds Precip. IV 2012, 8523, 269–280. [Google Scholar] [CrossRef]
- Turk, F.J.; Li, L.; Haddad, Z. A physically based soil moisture and microwave emissivity data set for Global Precipitation Measurement (GPM) applications. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7637–7650. [Google Scholar] [CrossRef]
- Prigent, C.; Rossow, W.B.; Matthews, E.; Marticorena, B. Microwave radiometric signatures of different surface types in deserts. J. Geophys. Res. Atmos. 1999, 44, 12147–12158. [Google Scholar] [CrossRef]
- Guan, Y.H.; Wang, W.J.; Lu, Q.F.; Bao, Y.S.; Zheng, T.W. Linear retrieval of microwave land surface emissivity over the desert area in January. Laser Optoelectron. Prog. 2021, 57, 284–296. [Google Scholar]
- Bao, Y.S.; Mao, F.; Min, J.Z.; Min, J.Z.; Wang, D.M.; Yan, J. Retrieval of bare soil moisture from FY—3B/MWRI data. Remote Sens. Land Resour. 2014, 26, 131–137. [Google Scholar]
- Prigent, C.; Matthews, E.; Aires, F.; Rossow, W.B. Remote sensing of global wetland dynamics with multiple satellite data sets. Geophys. Res. Lett. 2001, 28, 4631–4634. [Google Scholar] [CrossRef]
- Prigent, C.; Aires, F.; Rossow, W.; Matthews, E. Joint characterization of vegetation by satellite observations from visible to microwave wavelengths: A sensitivity analysis. J. Geophys. Res. Atmos. 2001, 106, 20665–20685. [Google Scholar] [CrossRef]
- Hu, J.; Fu, Y.; Zhang, P.; Min, Q.; Gao, Z.; Wu, S.; Li, R. Satellite Retrieval of Microwave Land Surface Emissivity under Clear and Cloudy Skies in China Using Observations from AMSR-E and MODIS. Remote Sens. 2021, 13, 3980. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Jiang, L.M.; Qiu, Y.B.; Wu, S.L.; Shi, J.C.; Zhang, L.X. Study of the Microwave Emissivity Characteristics over Different Land Cover Types. Spectrosc. Spectr. Anal. 2010, 30, 1446–1451. [Google Scholar]
- Prigent, C.; Chevallier, F.; Karbou, F.; Peter, B.; Graeme, K. AMSU-A land surface emissivity estimation for numerical weather prediction assimilation schemes. J. Appl. Meteorol. 2005, 44, 416–426. [Google Scholar] [CrossRef] [Green Version]
- Shi, L.J.; Qiu, Y.B.; Shi, J.C. Study of the microwave emissivity characteristics of vegetation over the North Hemisphere. Spectrosc. Spectr. Anal. 2013, 33, 1157–1162. [Google Scholar]
- Wang, Y.Q.; Shi, J.C.; Liu, Z.H. Retrieval algorithm for microwave surface emissivities based on multi-source, remote-sensing data: An assessment on the Qinghai-Tibet Plateau. Sci. China Earth Sci. 2013, 56, 93–101. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, Z.; Liu, Z.; Zeng, Z.; Ciais, P.; Huang, M.; Liu, Y.; Piao, S. Seasonal and interannual changes in vegetation activity of tropical forests in Southeast Asia. Agric. For. Meteorol. 2016, 224, 1–10. [Google Scholar] [CrossRef]
- Shi, J.; Jackson, T.; Tao, J.; Du, J.; Bindlish, R.; Lu, L.; Chen, S. Microwave vegetation indices for short vegetation covers from satellite passive microwave sensor AMSR-E. Remote Sens. Env. 2008, 112, 4285–4300. [Google Scholar] [CrossRef]
- Norouzi, H.; Temimi, M.; Rossow, W.; Pearl, C.; Azarderakhsh, M.; Khanbilvardi, R. The sensitivity of land emissivity estimates from AMSR-E at C and X bands to surface properties. Hydrol. Earth Syst. Sci. 2011, 15, 3577–3589. [Google Scholar] [CrossRef]
- Yang, H.; Weng, F. Error Sources in Remote Sensing of Microwave Land Surface Emissivity. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3437–3442. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Harrison, K.W.; Prigent, C.; Norouzi, H.; Aires, F.; Masunaga, H. Quantifying Uncertainties in Land-Surface Microwave Emissivity Retrievals. IEEE Trans. Geosci. Remote Sens. 2014, 52, 829–840. [Google Scholar] [CrossRef]
- Norouzi, H.; Temimi, M.; Prigent, C.; Turk, J.; Khanbilvardi, R.; Tian, Y.; Furuzawa, F.A.; Masunaga, H. Assessment of the consistency among global microwave land surface emissivity products. Atmos. Meas. Tech. Discuss. 2014, 7, 9993–10013. [Google Scholar] [CrossRef]
- Prakash, S.; Norouzi, H.; Azarderakhsh, M.; Blake, R.; Prigent, C.; Khanbilvardi, R. Estimation of consistent global microwave land surface emissivity from AMSR-E and AMSR2 observations. J. Appl. Meteorol. Climatol. 2018, 57, 907–919. [Google Scholar] [CrossRef]
- Okuyama, A.; Imaoka, K. Intercalibration of Advanced Microwave Scanning Radiometer-2 (AMSR2) brightness temperature. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4568–4577. [Google Scholar] [CrossRef]
- NASA. NASA Global Precipitation Measurement (GPM) Level 1C Algorithms; Version 1.6; National Aeronautics and Space Administration: Greenbelt, MD, USA, 2016.
- Owe, M.; de Jeu, R.; Walker, J. A methodology for surface soil moisture and vegetation optical depth retrieval using the microwave polarization difference index. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1643–1654. [Google Scholar] [CrossRef] [Green Version]
- Min, Q.L.; Lin, B.; Li, R. Remote sensing vegetation hydrological states using passive microwave measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 124–131. [Google Scholar] [CrossRef]
- Shi, J.C.; Chen, K.S.; Li, Q.; Jackson, T.J.; O’Neill, P.E.; Leung, T. A parameterized surface reflectivity model and estimation of bare-surface soil moisture with L-band radiometer. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2674–2686. [Google Scholar] [CrossRef]
- Qiu, Y.B.; Shi, L.J.; Wu, W.B. Study of the microwave emissivity characteristics over Gobi Desert. IOP Conf. Ser. Earth Environ. Sci. 2014, 17, 012065. [Google Scholar] [CrossRef]
- Li, L.; Njoku, E.G.; Im, E.; Chang, P.S.; Germain, K.S. A preliminary survey of radio-frequency interference over the U.S. in Aqua AMSR-E data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 380–390. [Google Scholar] [CrossRef]
- Wegmuller, U.; Matzler, C.; Weise, T. Absorption von Mikrowellen in Nadelbaumen; Auftragsstudie Zuhanden der PTT; Institute of Applied Physics, University of Bern: Bern, Switzerland, 1993. [Google Scholar]
- Matzler, C. Passive Microwave Signatures of Landscapes in Winter. Meteorol. Atmos. Phys. 1994, 54, 241–260. [Google Scholar] [CrossRef]
- Wang, X.F.; Li, X.G.; Xu, D.H. Simulation and analysis of microwave emissivity of vegetation cover based on CRTM. Mod. Agric. Technol. 2017, 24, 220–221. [Google Scholar]
- Morland, J.C.; Grimes, D.I.; Hewison, T. Satellite observations of the microwave emissivity of a semi-arid land surface. Remote Sens. Environ. 2001, 77, 149–164. [Google Scholar] [CrossRef]
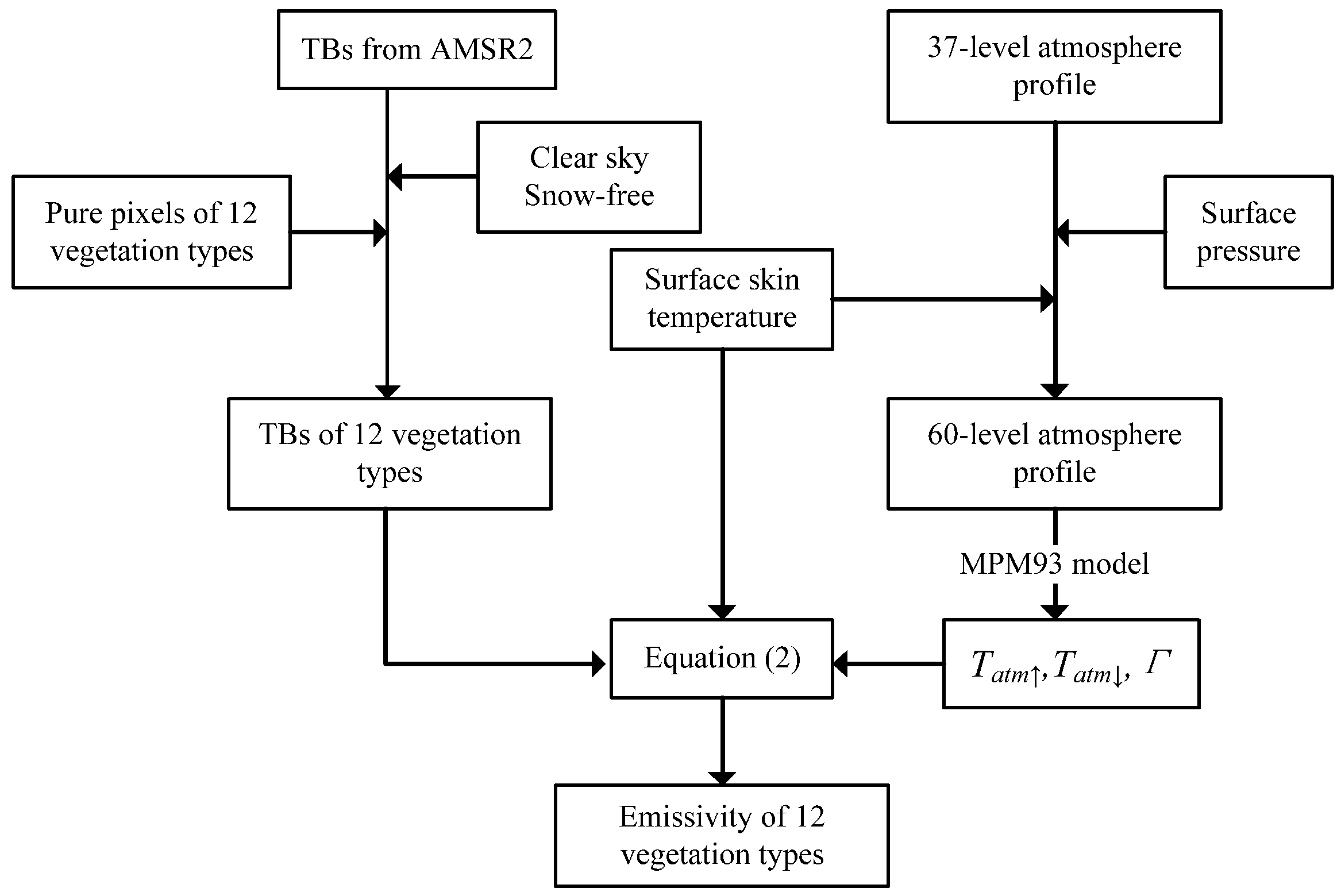




| Datasets | Parameters | Spatial Resolution | Temporal Resolution |
|---|---|---|---|
| L1C AMSR2 | TBs | Varying with frequency | - |
| ERA5 hourly data on pressure levels | liquid water profile,water vapor profile, and atmosphere temperature profile | 0.25 degrees | 1 h |
| ERA5 hourly data on single level | SKT, surface pressure (SP), total column cloud liquid water content, snow depth and volume of water in soil layer of 0–7 cm | 0.25 degrees | 1 h |
| MCD12C1 | global land cover types | 0.05 degrees | - |
| MOD13C1 | NDVI | 0.05 degrees | 16 days |
| Abbreviations | Land Cover Type | Screening Criteria | Count of Pure Pixels |
|---|---|---|---|
| ENF | evergreen needleleaf forests | < 5 | 183/N |
| EBF | evergreen broadleaf forests | = 0 | 8901/N & S |
| DNF | deciduous needleleaf forests | < 5 | 71/N |
| DBF | deciduous broadleaf forests | < 5 | 125/S |
| MF | mixed forests | < 5 | 128/N |
| CS | closed shrublands | < 5 | 23/N |
| OS | open shrublands | = 0 | 3323/S |
| WS | woody savannas | < 5 | 746/N |
| - | savannas | < 1 | 606/N |
| - | grasslands | = 0 | 1862/N |
| - | croplands | < 1 | 522/N |
| CNV | cropland/natural vegetation mosaics | < 5 | 48/N |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, Z. Microwave Emissivity of Typical Vegetated Land Types Based on AMSR2. Remote Sens. 2022, 14, 4276. https://doi.org/10.3390/rs14174276
Wang X, Wang Z. Microwave Emissivity of Typical Vegetated Land Types Based on AMSR2. Remote Sensing. 2022; 14(17):4276. https://doi.org/10.3390/rs14174276
Chicago/Turabian StyleWang, Xueying, and Zhenzhan Wang. 2022. "Microwave Emissivity of Typical Vegetated Land Types Based on AMSR2" Remote Sensing 14, no. 17: 4276. https://doi.org/10.3390/rs14174276
APA StyleWang, X., & Wang, Z. (2022). Microwave Emissivity of Typical Vegetated Land Types Based on AMSR2. Remote Sensing, 14(17), 4276. https://doi.org/10.3390/rs14174276