Ground-Based SAR Moving Target Refocusing Based on Relative Speed for Monitoring Mine Slopes
Abstract
1. Introduction
2. Moving Target Signal Model
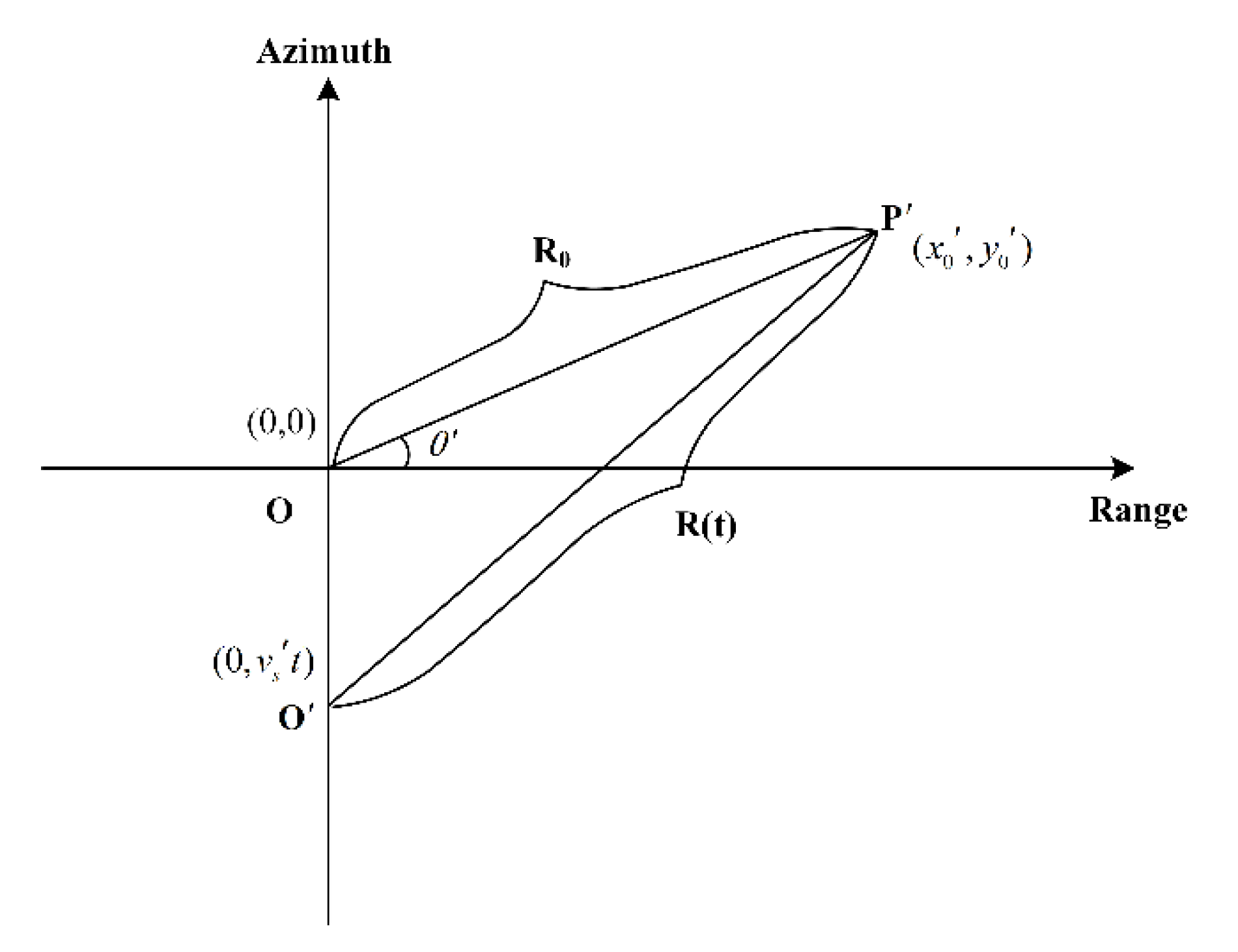
3. Relative Speed-Based Moving Target Signal Model
3.1. Relative Speed Transformation
3.2. Analysis on Relative Speed Model
3.3. Analysis of Searching Refocusing Parameters
4. Refocus Imaging Algorithm
5. Experiments
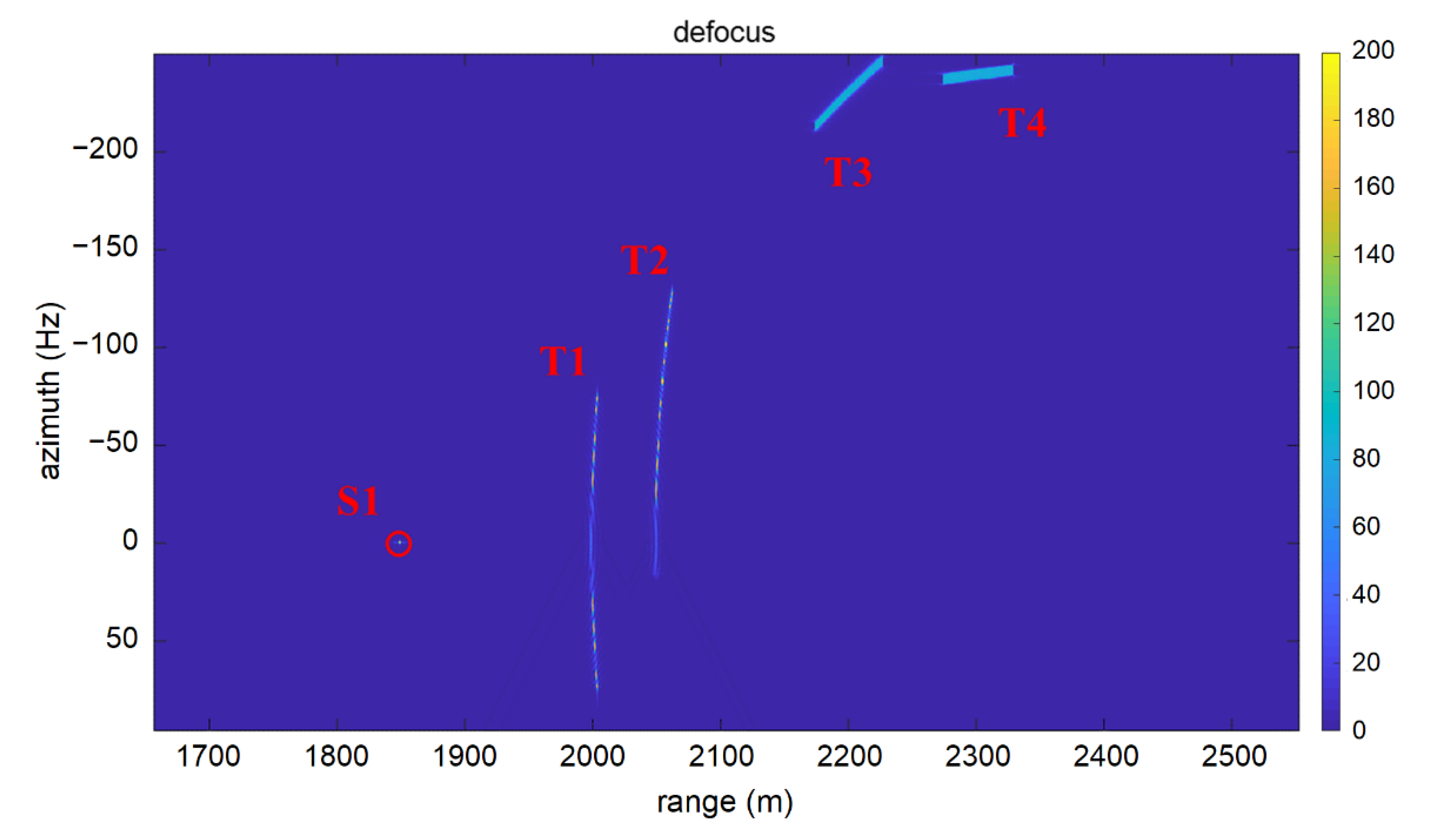
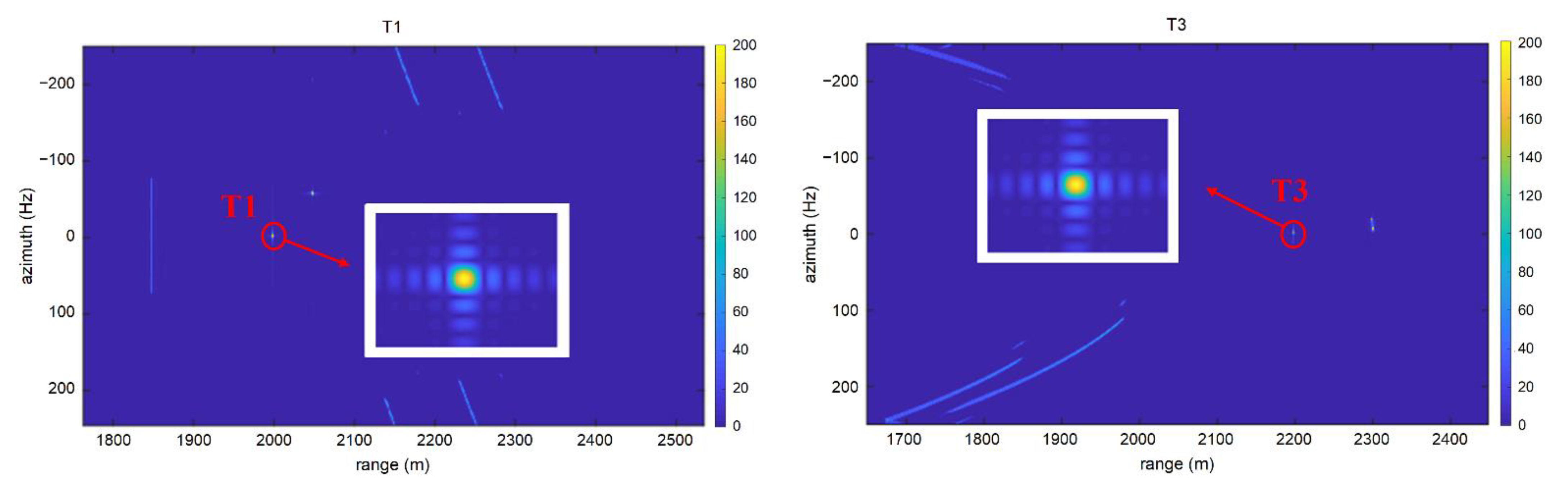
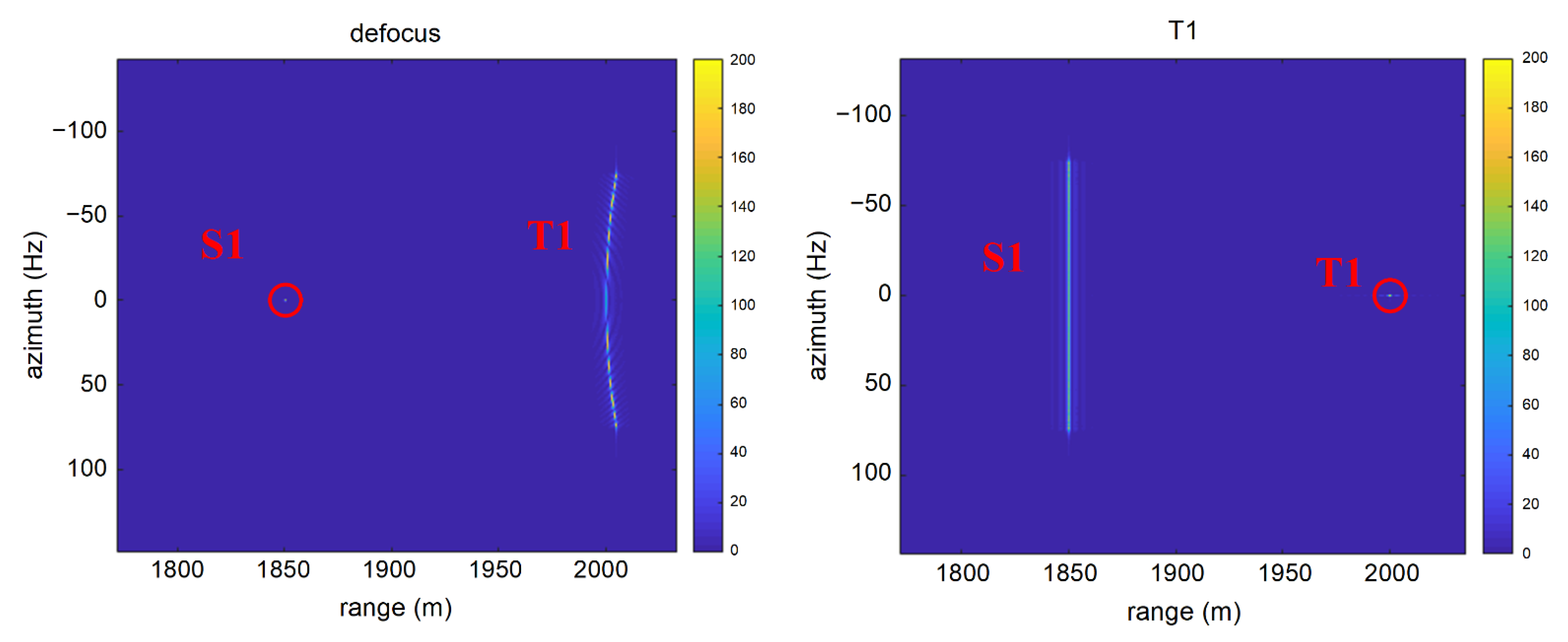
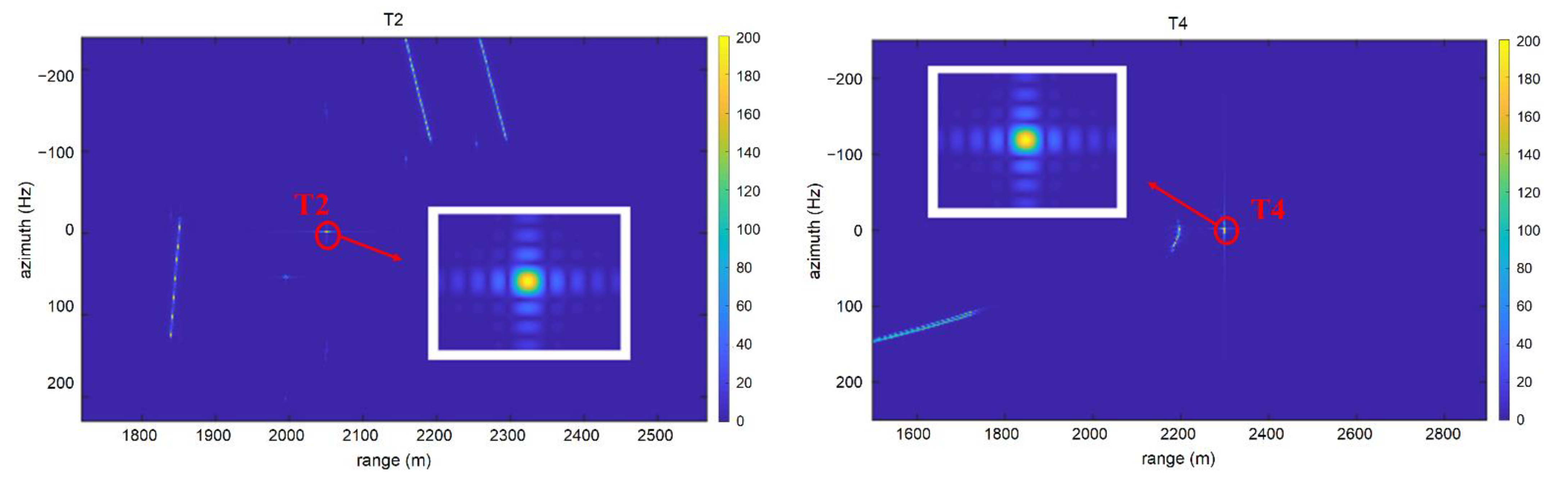
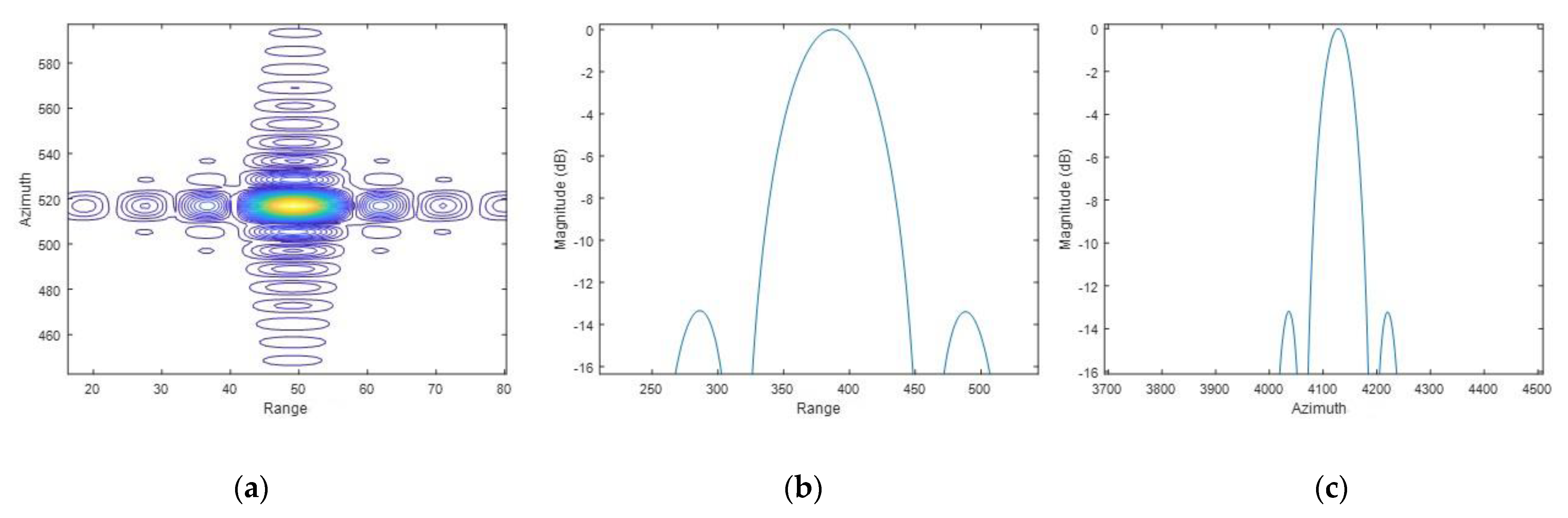
5.1. Point Target Simulation
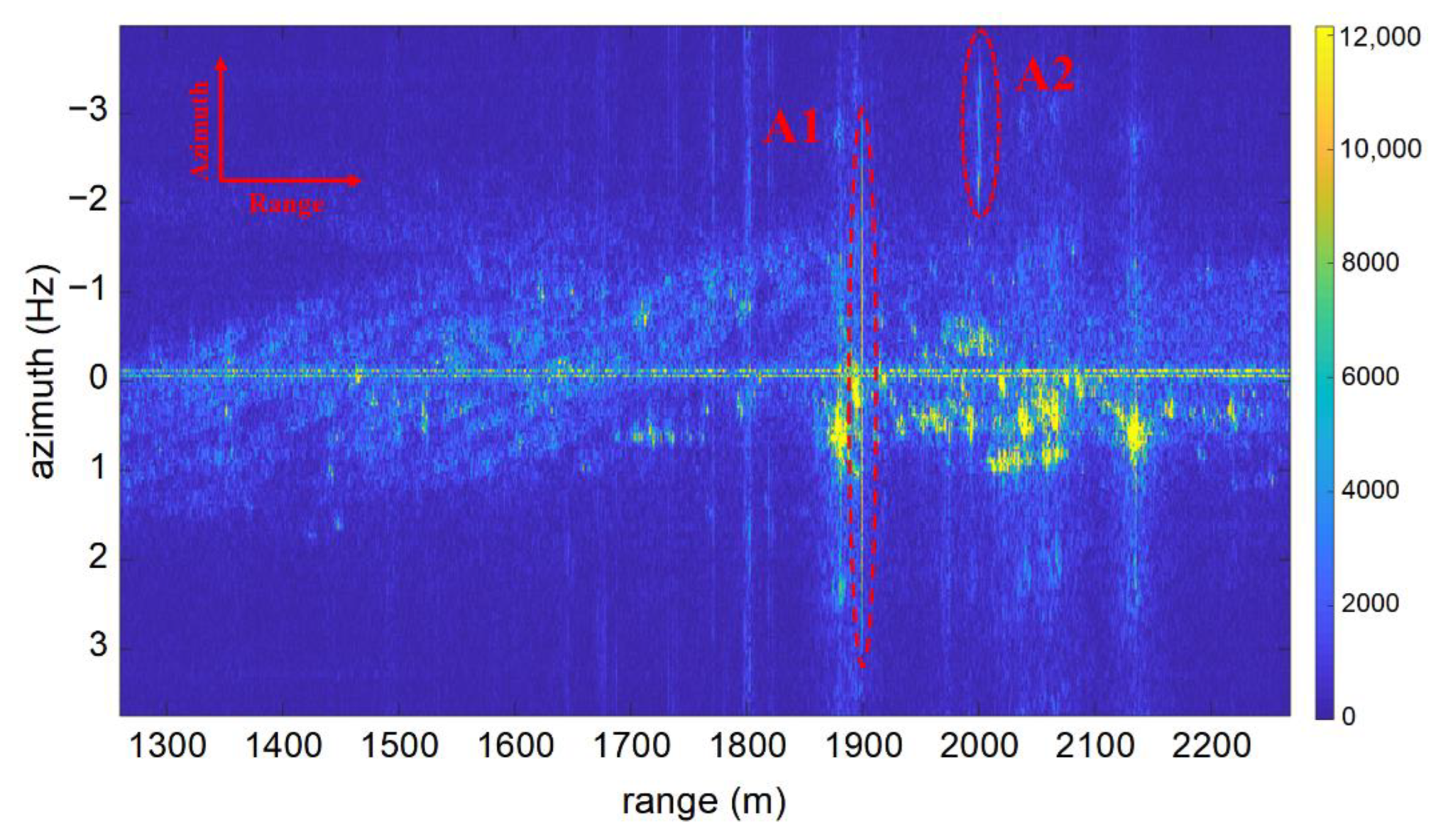
5.2. Synthetic Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Liu, B.; Ge, D.; Li, M.; Zhang, L.; Wang, Y.; Zhang, X. Using GB-SAR technique to monitor displacement of open pit slope. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5986–5989. [Google Scholar]
- Tarchi, D.; Casagli, N.; Fanti, R.; Leva, D.D.; Luzi, G.; Pasuto, A.; Pieraccini, M.; Silvano, S. Landslide monitoring by using ground-based SAR interferometry: An example of application to the Tessina landslide in Italy. Eng. Geol. 2003, 68, 15–30. [Google Scholar] [CrossRef]
- Perry, R.P.; Dipietro, R.C.; Fante, R.L. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Zhou, F.; Wu, R.; Xing, M.; Bao, Z. Approach for single channel SAR ground moving target imaging and motion parameter estimation. IET Radar Sonar Navig. 2007, 1, 59–66. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Y.; Zhu, Z. A keystone transform without interpolation for SAR ground moving-target imaging. IEEE Geosci. Remote Sens. Lett. 2007, 4, 18–22. [Google Scholar] [CrossRef]
- Li, G.; Xia, X.-G.; Peng, Y.-N. Doppler keystone transform: An approach suitable for parallel implementation of SAR moving target imaging. IEEE Geosci. Remote Sens. Lett. 2008, 5, 573–577. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Xia, X.-G.; Wu, Y.; Bao, Z. Robust ground moving-target imaging using deramp–keystone processing. IEEE Geosci. Remote Sens. 2012, 51, 966–982. [Google Scholar] [CrossRef]
- Zhu, S.; Liao, G.; Qu, Y.; Zhou, Z.; Liu, X. Ground moving targets imaging algorithm for synthetic aperture radar. IEEE Geosci. Remote Sens. 2010, 49, 462–477. [Google Scholar] [CrossRef]
- Jao, J.K. Theory of synthetic aperture radar imaging of a moving target. IEEE Geosci. Remote Sens. 2001, 39, 1984–1992. [Google Scholar] [CrossRef]
- Dong, Q.; Xing, M.-D.; Xia, X.-G.; Zhang, S.; Sun, G.-C. Moving target refocusing algorithm in 2-D wavenumber domain after BP integral. IEEE Geosci. Remote Sens. Lett. 2017, 15, 127–131. [Google Scholar] [CrossRef]
- Sjogren, T.K.; Vu, V.T.; Pettersson, M.I.; Gustavsson, A.; Ulander, L.M.H. Moving target relative speed estimation and refocusing in synthetic aperture radar images. IEEE Trans. Aero. Elec. Syst. 2012, 48, 2426–2436. [Google Scholar] [CrossRef][Green Version]
- Vu, V.T.; Pettersson, M.I.; Sjögren, T.K. Moving target focusing in SAR image with known normalized relative speed. IEEE Trans. Aero. Elec. Sys. 2017, 53, 854–861. [Google Scholar] [CrossRef]
- Wan, J.; Zhou, Y.; Zhang, L.; Chen, Z.; Yu, H. Efficient Algorithm for SAR Refocusing of Ground Fast-Maneuvering Targets. Remote Sens. 2019, 11, 2214. [Google Scholar] [CrossRef]
- Shu, Y.; Wan, J.; Li, D.; Chen, Z.; Liu, H. Fast Approach for SAR Imaging of Ground-Based Moving Targets Based on Range Azimuth Joint Processing. Remote Sens. 2022, 14, 2965. [Google Scholar] [CrossRef]
- Meta, A.; Hoogeboom, P.; Ligthart, L.P. Signal Processing for FMCW SAR. IEEE Geosci. Remote Sens. 2007, 45, 3519–3532. [Google Scholar] [CrossRef]
- de Wit, J.J.M.; Meta, A.; Hoogeboom, P. Modified range-Doppler processing for FM-CW synthetic aperture radar. IEEE Geosci. Remote Sens. Lett. 2006, 3, 83–87. [Google Scholar] [CrossRef]
- Meta, A.; Hoogeboom, P.; Ligthart, L.P. Non-linear Frequency Scaling Algorithm for FMCW SAR Data. In Proceedings of the 2006 European Radar Conference, Manchester, UK, 13–15 September 2006; pp. 9–12. [Google Scholar]
- Guarnieri, A.M.; Scirpoli, S. Efficient wavenumber domain focusing for ground-based SAR. IEEE Geosci. Remote Sens. Lett. 2009, 7, 161–165. [Google Scholar] [CrossRef]
- Guo, S.; Dong, X. Modified Omega-K algorithm for ground-based FMCW SAR imaging. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 1647–1650. [Google Scholar]
- Yuan, Z.; Qiming, Z.; Yanping, W.; Yun, L.I.N.; Yang, L.I.; Zechao, B.A.I.; Fang, L.I. An approach to wide-field imaging of linear rail ground-based SAR in high squint multi-angle mode. J. Syst. Eng. Electron. 2020, 31, 722–733. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, J.; Lei, P.; Li, G.; Hong, W. High-resolution SAR-based ground moving target imaging with defocused ROI data. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1062–1073. [Google Scholar] [CrossRef]
- Jiang, Z.-H.; Huang-Fu, K.; Wan, J.-W. A chirp transform algorithm for processing squint mode FMCW SAR data. IEEE Geosci. Remote Sens. Lett. 2007, 4, 377–381. [Google Scholar] [CrossRef]
- Wang, R.; Loffeld, O.; Nies, H.; Knedlik, S.; Hagelen, M.; Essen, H. Focus FMCW SAR data using the wavenumber domain algorithm. IEEE Trans. Geosci. Remote Sens. 2009, 48, 2109–2118. [Google Scholar] [CrossRef]
- Ribalta, A. Time-domain reconstruction algorithms for FMCW-SAR. IEEE Trans. Geosci. Remote Sens. Lett. 2010, 8, 396–400. [Google Scholar] [CrossRef]
- Cheng, P.; Xin, Q.; Wan, J.; Wang, Z. Refocusing of ground moving targets for range migration algorithm in FMCW SAR. In Proceedings of the SAR Image Analysis, Modeling, and Techniques XV, Toulouse, France, 15 October 2015; p. 96420R. [Google Scholar]
- Zhang, H.; Ni, J.; Xiong, S.; Luo, Y.; Zhang, Q. Omega-KA-Net: A SAR Ground Moving Target Imaging Network Based on Trainable Omega-K Algorithm and Sparse Optimization. Remote Sens. 2022, 14, 1664. [Google Scholar] [CrossRef]
- Casalini, E.; Frioud, M.; Small, D.; Henke, D. Refocusing FMCW SAR moving target data in the wavenumber domain. IEEE Geosci. Remote Sens. 2019, 57, 3436–3449. [Google Scholar] [CrossRef]
- Meta, A.; Hoogeboom, P.; Ligthart, L.P. Correction of the effects induced by the continuous motion in airborne FMCW SAR. In Proceedings of the 2006 IEEE Conference on Radar, Verona, NY, USA, 24–27 April 2006; p. 8. [Google Scholar]
- Liang, Y.; Wang, H.; Xing, M.; Bao, Z. Imaging Study of High Squint SAR Based on FMCW. In Proceedings of the 2007 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 5–9 November 2007; pp. 6–9. [Google Scholar]
- Liang, X.; Wei, Q. Wavenumber domain algorithm for squint FMCW SAR. In Proceedings of the 2011 6th International Forum on Strategic Technology, Harbin, China, 22–24 August 2011; pp. 1256–1260. [Google Scholar]
- Liang, Y.; Wang, H.X.; Xing, M.D.; Bao, Z. Slow ground moving target parameter estimation and imaging in FMCW SAR. Syst. Eng. Electr. 2011, 33, 1001–1006. [Google Scholar] [CrossRef]
- Bao, Z.; Xing, M.D.; Wang, T. Radar Imaging Techniques; Publishing House of Electronics Industry: Beijing, China, 2006. [Google Scholar]
- Meta, A.; Hoogeboom, P. Signal processing algorithms for FMCW moving target indicator synthetic aperture radar. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, 2005. IGARSS ‘05., Seoul, Korea, 29 July 2005; p. 4. [Google Scholar]
- Liang, Y.; Wang, H.-X.; Xing, M.-D.; Bao, Z. The analysis of FMCW SAR signal and image study. J. Electr. Inform. Technol. 2008, 30, 1017–1021. [Google Scholar] [CrossRef]
- State Administration of Work Safety. National Mine Safety Administration. Coal Mine Safety Code; China Coal Industry Publishing House: Beijing, China, 2016.
- Tang, S.; Zhang, L.; Guo, P.; Liu, G.; Sun, G.C. Acceleration Model Analyses and Imaging Algorithm for Highly Squinted Airborne Spotlight-Mode SAR with Maneuvers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1120–1131. [Google Scholar] [CrossRef]


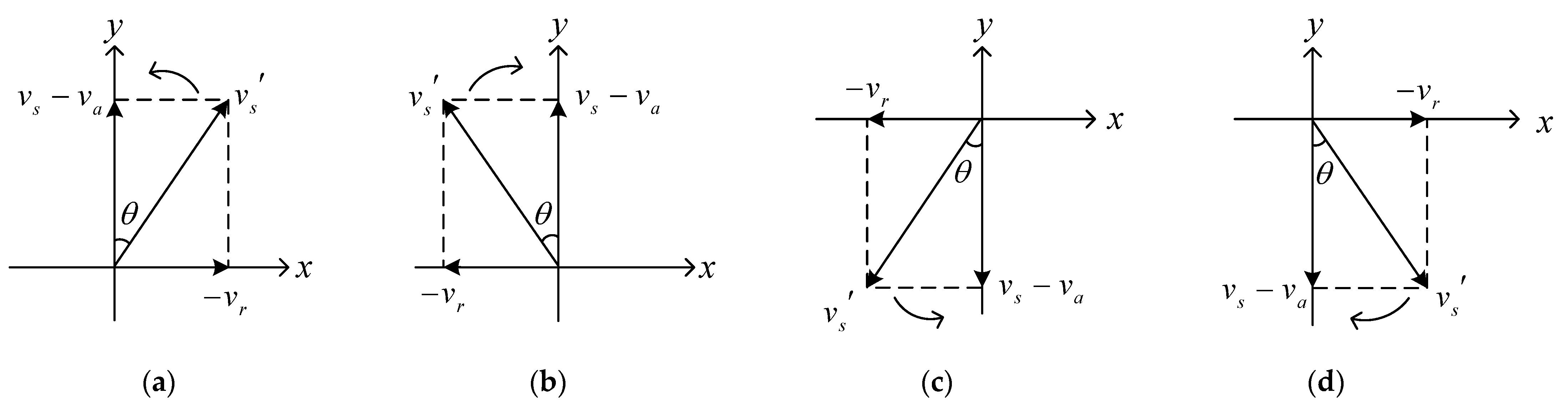




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Center frequency | 17 GHz | PRF | 500 Hz |
| Signal bandwidth | 400 MHz | Near range | 500 m |
| Radar speed | 0.03 m/s | Far range | 2500 m |
| Pulse duration | 0.002 s | Rail length | 0.8 m |
| Target | Coordinate [m] | Vr [m/s] | Va [m/s] |
|---|---|---|---|
| S1 | (1850, 0) | 0 | 0 |
| T1 | (2000, 0) | 0 | 10 |
| T2 | (2050, 100) | 0 | 10 |
| T3 | (2200, 0) | 2 | 5 |
| T4 | (2300, 100) | 2 | 2 |
| Target | Coordinate [m] | Vr [m/s] | Va [m/s] |
|---|---|---|---|
| A1 | (1900, 0) | 0 | 3 |
| A1 | (2000, 50) | 0 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, W.; Wang, S.; Lin, Y.; Li, Y.; Ding, F.; Wang, Y. Ground-Based SAR Moving Target Refocusing Based on Relative Speed for Monitoring Mine Slopes. Remote Sens. 2022, 14, 4243. https://doi.org/10.3390/rs14174243
Shen W, Wang S, Lin Y, Li Y, Ding F, Wang Y. Ground-Based SAR Moving Target Refocusing Based on Relative Speed for Monitoring Mine Slopes. Remote Sensing. 2022; 14(17):4243. https://doi.org/10.3390/rs14174243
Chicago/Turabian StyleShen, Wenjie, Shuo Wang, Yun Lin, Yang Li, Fan Ding, and Yanping Wang. 2022. "Ground-Based SAR Moving Target Refocusing Based on Relative Speed for Monitoring Mine Slopes" Remote Sensing 14, no. 17: 4243. https://doi.org/10.3390/rs14174243
APA StyleShen, W., Wang, S., Lin, Y., Li, Y., Ding, F., & Wang, Y. (2022). Ground-Based SAR Moving Target Refocusing Based on Relative Speed for Monitoring Mine Slopes. Remote Sensing, 14(17), 4243. https://doi.org/10.3390/rs14174243








