Abstract
Low Earth orbit (LEO) satellite constellations are currently being explored to provide global and seamless coverage for IoT-over-Satellite applications. Random access techniques require low transmission overhead providing a compatible route for IoT-over-Satellite applications, however, coming at the expense of the offered quality-of-service. In this paper, we develop a realistic uplink performance framework that incorporates many practical parameters such as the satellite availability, packet collision and interference, Doppler shift, and impairments experienced in a typical Satellite-to-Ground channel. The framework is capable of assessing multiple key performance indicators of the overall IoT-over-Satellite random access system. The performance is presented in terms of the bit error rate, packet error rate, and the energy wasted per IoT device. To emulate a realistic IoT-over-Satellite network, LoRa modulated traffic is first generated and injected into the Satellite-to-Ground channel. The results indicate high resistance to Doppler shifts even without any Doppler correction and provide some resistance to highly congested environments.
1. Introduction
The deployment of Internet of Things (IoT) networks is growing rapidly, providing the backbone for a wide range of applications, such as smart cities monitoring, asset tracking, resource management, and emergency services [1,2,3,4]. Some of these applications are located in remote areas, where they are unable to access the terrestrial network, and lack business value to deploy a dedicated network. Therefore, solutions such as IoT-over-Satellite emerge to support such applications due to its extended coverage and seamless continuum [5,6,7,8]. Many different IoT-over-Satellite systems are therefore suggested by different international standard organizations, such as Third Generation Partnership Projects (3GPP) and International Telecommunication Union (ITU) [9,10]. Recently, numerous satellite constellations, such as Starlink, OneWeb, and Kuiper, are being deployed or are in planning to be deployed, relying on large numbers of low Earth orbit (LEO) satellites [11,12,13] mainly for broadband Internet access. Moreover, Orbcomm, Myriota, and Fleet Space have adopted a business model that supports narrow-band IoT-over-Satellite services [14,15,16]. In order to provide seamless satellite coverage, Walker constellations are widely deployed and LEO networks have become an appealing alternative to remote terrestrial deployments due to their inherent low altitude and lower launch costs to allow a modest constellation deployment of LEO satellites. Additionally, LEO constellations enable lower path-loss and reduced round-trip delay, making them an attractive option for low-power IoT-over-Satellite applications for massive machine-type communication (mMTC) and ultra reliable low latency communication (uRLLC) [17]. This is noticeable when comparing LEO satellites to traditional Geostationary Earth orbits (GEO) typically requiring larger antennas and transmit powers to counter the high path-loss [18].
Despite the benefits of relying on LEO constellations for IoT applications, many challenges persist. The path-loss is still significantly higher than terrestrial and aerial communication systems, therefore IoT-over-Satellite is not as effective for regions that have high densities of terrestrial base stations or aerial receivers, making IoT-over-Satellite only convenient in regions that lack this infrastructure. Moreover, the coverage spot provided by a single LEO satellite is smaller relative to its GEO counterparts making it difficult to achieve connectivity for extended periods of time due to the dynamic nature of the orbit. For smaller constellations the LEO backhaul connectivity of satellites might be limited, hence on-board demodulation and storage of radio packets is needed. Nevertheless, IoT communications are dominated by uplink traffic and while a large satellite footprint provides extended coverage, it also results in high aggregate interference [19]. Although interference mitigation methods such as frequency reuse and beam multiplexing can be used, the interference levels seen by a satellite are still relatively large. Therefore, the utilization mechanisms of the radio spectrum are critical to ensure that the network is providing the prescribed quality-of-service.
Unlike other technologies that use the licensed spectrum, LoRa is designed to operate in the congested shared spectrum. This strategy facilitates the rapid deployment of IoT networks due to reduced administrative and licensing hurdles of securing the license spectrum. LoRa is a physical layer wireless communication technology designed for long-range communication at a low bit rate and low power to enable wireless communication of battery-powered devices. LoRa communication scheme mainly utilizes Chirp Spread Spectrum (CSS) to spread the symbols across a wider spectrum in order to mitigate the effect of narrowband interference [20]. Using CSS in LoRa also aims at reducing co-channel interference from other LoRa devices and from other narrowband transmissions. Despite all the promises of LoRa, uplink interference is still a critical issue in IoT-over-Satellite systems as LoRa typically uses a long time to transmit its frame, exposing it to other transmission overlaps. Therefore, investigating the performance of IoT-over-Satellite systems using LoRa can provide an insight of the feasibility of deploying LPWAN on IoT-over-Satellite network.
In this paper, we present a LEO mega satellite constellation framework that depicts the performance of different constellation patterns for IoT-over-Satellite communications, and different random access techniques. This framework is based on a comprehensive physical-layer emulator to provide insights into key network performance indicators such as the probability of success, and energy consumption. Additionally, to mitigate the co-channel interference and Doppler shift effect with reduced power consumption, the IoT-over-Satellite network utilized LoRa CSS, as an example, in four different random access mechanisms, namely; (i) pure ALOHA, (ii) scheduled access, (iii) scheduled access with repetition, and (iv) scheduled round robin. The contributions of this work are summaries as follows:
- It presents an emulation framework that predicts the uplink LoRa performance for IoT-over-Satellite networks.
- It evaluates the uplink packet error rate (PER) and bit error rate (BER) of the practical Walker-Delta constellations and the Walker-Star constellations.
- It evaluates the uplink PER and BER of the IoT-over-Satellite system in four different access methods in a shared radio spectrum.
- It shows the impact of fading, Doppler shift, and practical interference to the IoT-over-Satellite system performance.
- It provides a methodology for capturing the amount of wasted energy of the IoT end-devices in different access methods.
- It evaluates the impact of intra-SF interference in LoRa communication.
2. Background and Related Work
Depending on various trade-offs related to spectral efficiency, system complexity, and energy usage, different IoT-over-Satellite architectures are investigated. For example, the 3GPP defines two IoT-over-Satellite methods for mMTC applications using shared frequency bands [9]; these two methods rely on (i) direct satellite access and (ii) hybrid access. In direct-access networks, IoT devices send their payloads directly to a satellite, where satellites act as an intermediate node that relays the data to the destination via feeder link, where Figure 1 depicts this concept. Since IoT devices can connect to the satellite directly without any terrestrial gateways, this makes such topology ideal for rural areas where the terrestrial infrastructure is lacking. Suggestions for IoT-over-Satellite networks that rely on direct access can be found in research papers [18,21], where [21] illustrated the performance of direct to satellite IoT networks using LoRa based on the simulation, and [18] explores the potential possibilities of spectrum-sharing between LEO satellite constellation and terrestrial networks.

Figure 1.
Illustration of the direct satellite access IoT network architecture.
On the other hand, hybrid satellite networks allow IoT devices to communicate via either the terrestrial or satellite infrastructure. Both the terrestrial and satellite networks are coordinated to facilitate hand-over between them to ultimately providing seamless global coverage. Thereby, the hybrid satellite system can combine the advantages of both terrestrial and satellite networks, providing global coverage while maintaining more efficient communications in suburban and urban environments. Figure 2 shows the architecture of the hybrid satellite network. In order to allow inter-operation between satellite and terrestrial networks, adapting terrestrial LPWAN directly to the IoT-over-Satellite system is currently being investigated with some promising implementations [8,18,22,23].
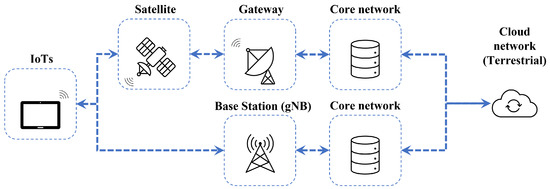
Figure 2.
Illustration of the hybrid IoT-over-Satellite network architecture.
To estimate the quality of service (QoS) provided by the communication link, analysis of IoT-over-Satellite systems under different LPWAN communication protocols provides insight into the performance of the system. Analysis of IoT-over-Satellite using licensed band LPWAN technology can be found in [24], where the uplink performance of Narrowband IoT (NB-IoT) over satellite system is presented, showing the feasibility of using terrestrial NB-IoT technology for the satellite applications. Moreover, the performance analysis of the satellite uplink using LTE technology is also presented in [25]. Alternatively, the performance of the unlicensed band LPWAN protocol is investigated in [26], in which the LoRa derivative over a geostationary satellite link is measured using both extensive simulations and test-bed measurements, while in [27], the author used auto-correlation and cross-correlation in the time and frequency domains to investigate the acquisition performance of different types of chirp signals, showing the potential of chirp-based systems on LEO communication links.
As next generation wireless systems emerge, more services are occupying the shared spectrum frequently. This is exacerbated from the satellite’s perspective where all devices within its footprint can contribute towards interference. In terrestrial networks, spectrum regulators continuously set strict regulations to the shared spectrum to reduce transmission congestion. The same is extended to geostationary satellites where spectrum regulators from the different countries covering a fixed footprint. However, LEO satellites are rapidly orbiting and continuously changing their footprint, therefore, more efforts are required to properly regulate the shared spectrum for LEO constellations [19]. IoT-over-Satellite networks are expected to employ random access methods, in a way or another, similar to IoT terrestrial networks [8]. However, random access methods could lead to significant uplink interference and degraded capacity levels if not carefully designed. As a result, IoT technologies for satellite applications need to implement intelligent interference mitigation techniques to enhance the performance.
To enhance the interference mitigation, some complex access methods are introduced in the literature for IoT-over-Satellite. In [28], the performance of a satellite link using other access schemes, including time division multiple access (TDMA), FDMA, power division multiple access (PDMA), and turbo code division multiple access (TCDMA), have been assessed. On the other hand, in [29], the authors present a data exchange rate comparison for IoT-over-Satellite using Constrained Application Protocol/UDP (CoAP/UDP) and MQ Telemetry Transport/TCP (MQTT/TCP) via a contention resolution diversity slotted ALOHA (CRDSA) medium access control (MAC) layer. Recently, many LPWAN technologies incorporate the use packet repetition to enhance remote connectivity [30,31]. Moreover, random access with packet repetition, such as contention resolution ALOHA (CRA), CRDSA, and irregular repetition slotted ALOHA (IRSA) have been proposed for IoT-over-Satellite in the literature [32,33,34,35]. In IRSA and CRDSA, IoT devices are required to transmit two or multiple copies of the same packet in different time slots to increase the transmission performance. An advanced access method called the Enhanced Spread Spectrum ALOHA (ESS ALOHA) can also be found in [36]. The ESS ALOHA can achieve higher throughput compared to ALOHA without the need for scheduling. Although the advanced random access and multiple access techniques can provide better interference mitigation, these techniques require the implementation of the successive interference cancellation (SIC), which in turn increases the system complexity of the ground devices. On the other hand, a packet demodulator can be incorporated on the satellite end of the network. In addition, the need for network synchronization and the increased power consumption requirements dims the CRDSA viability for IoT-over-Satellite communications.
In order to understand the performance of an access method for IoT-over-Satellite for a given scenario, the convention is to perform extensive network simulations. In [37], the authors detail a simulation framework for an IoT-over-Satellite link performance. Although the simulator can provide practical performance modeling by relying on the user population and be extended by the anticipated distribution of IoT devices, it only takes into account a single LEO satellite link. On the other hand, in order to have tractable performance analysis of IoT-over-Satellite for a dense LEO constellation, analytic modeling using tools from stochastic geometry has recently emerged in [38,39,40].
To facilitate the investigation of random uplink access performance in IoT-over-Satellite network, this paper presents a systematic end-to-end emulation framework aiming to provide realistic performance analysis for practical dense LEO constellations such as Walker-Delta and Walker-Star. The framework can incorporate different access methods as well as different LPWAN technologies to assess their performance over a realistic Satellite-to-Ground channel and the source code for the emulation can be accessed on Github [41]. In this paper, we evaluated the performance based on LoRa IoT-over-Satellite network for different random access methods via the shared radio spectrum. The devices are assumed to operate on an identical spreading factor while jointly utilizing radio resources. The performance of the network is measured via two key indicators; (i) the BER and (ii) the energy consumption/wasted.
3. Method
3.1. System Model
The emulation model developed in this work capture the elements of practical IoT-over-Satellite links consisting of:
- Terrestrial IoT devices/sensors.
- Other IoT devices contributing to co-channel interference.
- Satellite constellation, where the satellites act as the gateway (base station).
The emulator generates transmissions that jointly share a random access channel capitalizing on different access methods that are detailed in Section 3.3. Moreover, the developed framework capitalizes on a Matlab-scripted emulator [42] to generate LoRa transmissions for the IoT devices. The block diagram of the utilized model is illustrated in Figure 3. Note that, in this paper, we evaluate the performance based on the LoRa physical layer, however, this framework can also accommodate other LPWAN technologies by incorporating different physical layer protocols instead of the LoRa protocol used in this paper. The aggregated terrestrial interference is assumed to be incorporated within the background noise. This is due to different modulation and coding schemes that originate from the different signals in the shared spectrum [43]. On the other hand, terrestrial LoRa interference is already considered within the ground IoT devices. The details of the framework including the geometric model, availability, and channel models are detailed in the following subsections.
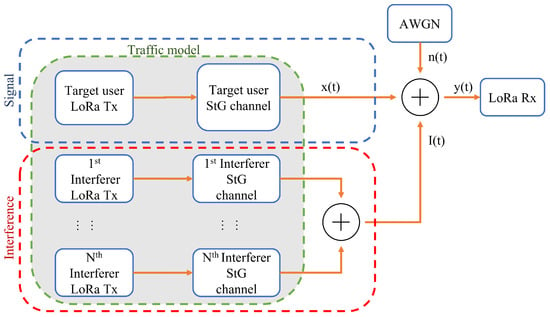
Figure 3.
Block diagram of the presented LoRa IoT-over-Satellite emulation framework. The uplink performance is estimated based on practical environment parameters.
3.1.1. Geometric Model-IoT Devices
We assume that the ground user IoT devices are randomly distributed over Earth’s surface, represented by the homogeneous Binomial point process (BPP), with an average density , where is the spatial duty cycle of the active IoT devices and is the density of all users including active and inactive IoT devices. We also assume that all active IoT devices are sharing the same channel frequency. Using BPP for the spatial distribution aims at providing a theoretical lower bound of the performance and not to replicate case-specific implementation scenarios. However, the emulator can also incorporate practical distributions to increase the authenticity of the results.
3.1.2. Geometric Model—Satellite Availability
In this model, we assume that each user is associated with its nearest satellite, i.e., the satellite that is closest to the user’s zenith angle [38]. This scheme provides best channel conditions for the ground user. As such we define the contact angle, , as the Earth-centered zenith angle of the nearest satellite to the observer IoT device calculated as follows,
where ; R⊕ is the Earth’s average radius, h is the satellite altitude, and d represents the slant distance between the IoT device and the satellite. For the observer IoT device to be within the satellite footprint, the condition φo < φmax must be met where φmax is the maximum zenith angle of the footprint. The maximum zenith angle occurs when the IoT device is at the edge of the satellite’s beam, which can be represented as follows [44],
where = R⊕/(h + R⊕), ψo is the maximum effective beamwidth, and ψ the satellite’s antenna beamwidth. Figure 4 illustrates the maximum satellite footprint limited by horizon depicted as the green patches and the blue patches representing the satellite footprint when limited by the satellite antenna beamwidth. It shows that the satellite footprint is further limited by the satellite antenna beamwidth. To simplify the calculation, we assume the narrower-beam antenna from satellites to bypass this issue. After calculating the maximum zenith angle and the zenith angle, the satellite availability at that instance can be obtained by the Boolean condition of φ < φmax, the average satellite availability which is the ratio of satellite available time per day can be calculated by the following equation,
where 𝟙(∃x:φx < φmax)is the indicator function when at least a satellite x is within maximum zenith angle, and Td is the seconds per day, which is equal to 86,400 s. Figure 5 illustrates the comparison of the average satellite availability using practical satellite constellations. It shows that the satellite availability of the Walker-Star constellation is lower than the availability of the Walker-Delta constellation near the equator (for the same satellite number and for a narrow beamwidth), while the random satellite constellation has the lowest, and nearly constant, availability at different locations.
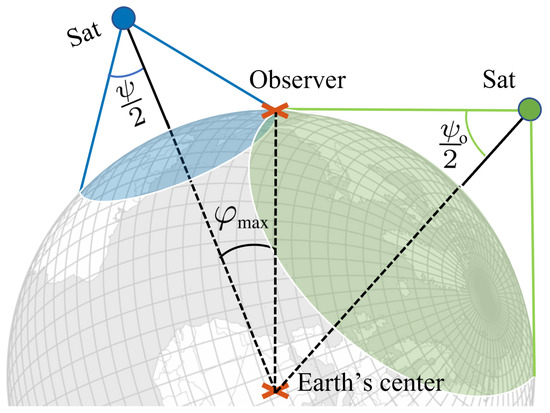
Figure 4.
Illustration of the satellite footprint, whereby the blue patch represents the footprint when limited by the satellite antenna beamwidth, , and the green patch represents the maximum satellite footprint limited by the Earth’s occlusion, i.e., horizon-limited, .
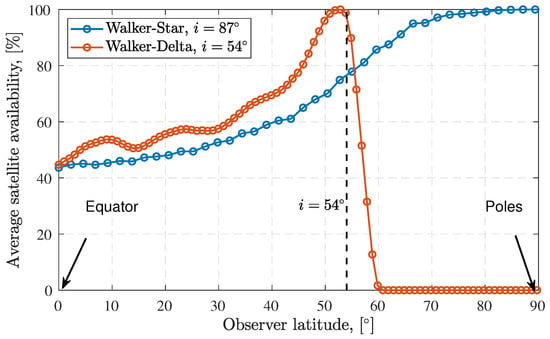
Figure 5.
An example of the average satellite availability for variable ground device latitudes with and km. The satellite antenna beamwidth is set to 80 whereas the remaining constellation parameters considered are summarized in Table 1.
3.1.3. Satellite Constellation Model
In this framework we consider practical constellations in order to obtain insights into realistic network performance. The constellation models adopted in this work are in the form of Walker-Delta and Walker-Star constellations which are illustrated in Figure 6. These two constellations are widely used in the satellite communication industry, for example in recent deployments by SpaceX’s StartLink and by OneWeb. Walker constellations can be described with the parameter vector [44], where h is the constellation altitude, i is the orbital planes’ inclination, is the total number of satellites in the constellation, P is the number of orbital planes, and F is the phasing parameter representing the shift between satellite relative locations in subsequent orbital planes. The orbital planes are equally spaced around Earth’s rotational axis and each plane consists of satellites that are equally spaced along the circular orbit. Below we explain the difference between Walker-Delta and Walker-Star:
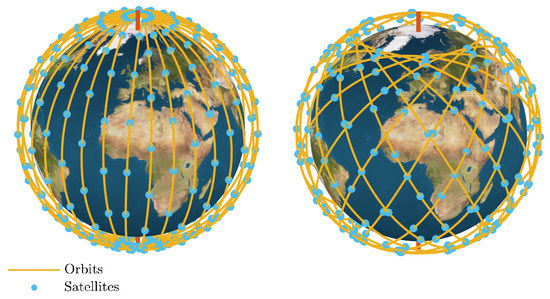
Figure 6.
Illustration of the Walker-Star (left) constellation for and Walker-Delta (right) constellation for .
- Walker-Delta Constellation: The Walker-Delta constellation is widely adopted by many satellite projects, such as Starlink and Kupier [11,13]. Walker-Delta constellations reduce the variation in the inter-distances between satellites providing a denser distribution of satellites around the equator and mid-latitude locations [45], illustrated in Figure 5. In addition, Walker-Delta configuration enables the utilization of inter-satellite links (ISLs) facilitating communication between the different satellites in the constellation. In Walker-Delta the orbital planes are equally spaced and rotated around the earth rotational axis, with a right ascension of the ascending node angle (RAAN) .
- Walker-Star Constellation: The Walker-Star constellation is also widely adopted by current commercial satellite providers, such as Iridium and OneWeb [12,46]. Walker-Star constellations typically have their inclination angle, i, close to 90. This configuration enables true global availability where even the poles are provided coverage unlike Walker-Delta constellations. However, this comes at the cost of an unnecessarily high density of satellites at the poles along with slightly reduced density at the equator. Figure 5 shows a comparison between the availability of Walker-Delta and Walker-Star constellations, the altitude and number of satellites are intentionally reduced to show the variation in availability time. Such low availability is acceptable in delay-tolerant IoT applications, however broadband networks are designed with either larger higher altitudes and/or larger number of satellites in order to provide 100% coverage time. Another difference to the Walker-delta is that the orbital planes RAAN in Walker-Star are spread across the range 0 to instead of 0 to , i.e.,
Mercator projection of both Walker-Star and Walker-Delta constellations are shown in Figure 7, where the blue patches represent the footprint of the satellites in the constellation. The constellation parameters are summarized in Table 1.
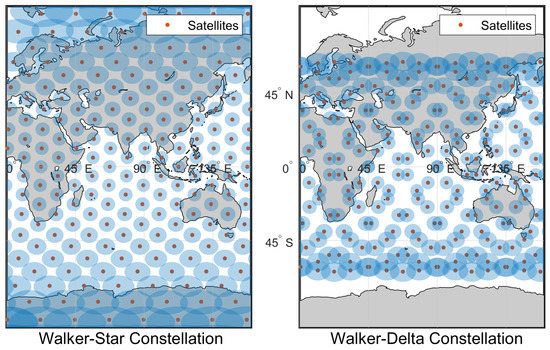
Figure 7.
The Mercator projection of Walker-Star (left) for and Walker-Delta (right) constellations with same paramters except , the blue patches represent the satellite footprints. Note that the satellite antenna beamwidth is set to 80, in both constellations.

Table 1.
Simulation Parameters.
Table 1.
Simulation Parameters.
| Parameters | Symbol | Simulation Value |
|---|---|---|
| Satellite constellation altitude | h | 550 [km] |
| Number of satellites | 480 | |
| Orbital planes | P | 16 |
| Phasing parameter | F | 8 |
| Density of IoT devices | 1.5625 [units per km] | |
| Earth’s radius | 6371 [km] | |
| Carrier frequency | fo †1 | 915 [MHz] |
| Transmit power | Pt | 27 [dBm] |
| Satellite antenna beamwidth | ψ | 80° |
| Satellite antenna Gain | G | 9 [dB] |
| Duty cycle †4 | ν | 1.45 × 10−4% |
| Bandwidth | B | 125 [kHz] |
| Noise power †5 | W | −115 [dBm] |
| LoS probability parameter | 0.4 | |
| LoS excess mean | 0 | |
| LoS excess standard deviation | 1 | |
| NLoS mean | 8 | |
| NLoS standard deviation | 10 | |
| LoRa spreading factor | SF | 7 |
| RF-to-electric conversion factor | 4 | |
| Overhead power per packet | 210 [mW] | |
| Overhead power due to sync. | 250 [mW] | |
| LoRa air time | 61.7 [ms] |
†1 §-band center frequency in 3GPP parameters [9]. †2 Satellite-to-ground model based on [47]. †3 Measurement based on [48]. †4 Noise power when T = 290 °K and noise figure NF = 6 dB. †5 Assumed that each IoT device transmits twice per day. i.e., ν = 2Tm/Td.
3.2. Interference and Channel Model
The received signal of a wireless communication link impaired with interference and Gaussian noise can be represented as follows,
where is the complex channel response function, is the uplink signal transmitted by the target IoT device i, while represents the interference signal, and is the complex additive white Gaussian noise (AWGN) with an average noise power W. Note that the summation represents other devices that are jointly transmitting over the channel resources, leading to co-channel interference.
The Satellite-to-Ground signals encounter propagation losses due to large-scale and small-scale fading as well as other additional losses, such as scintillation caused by the small-scale inhomogeneity of the refractive index, attenuation due to atmospheric gases absorption, and fading due to rain [9]. As such, we depict the channel response by utilizing the channel model derived in [47], which represents the path-loss by the free-space path-loss and an additional excess path-loss resenting large-scale fading caused by terrestrial clutter. The channel response is therefore obtained as follows,
where G represents the satellite antenna gain, l is the free-space path-gain, is the excess path-gain, and is the Doppler shift due to the satellite motion relative to the ground user on Earth’s surface.
3.2.1. Free-Space Path-Loss and Excess Path-Loss
The free-space path-gain l is expressed as follows,
where c is the speed of light, and is the carrier frequency. The satellite antenna gain G is assumed to be based on an ideal antenna gain and is obtained as follows,
In the emulation, the ideal antenna model is utilized where all transmit power is uniformly confined to the beam’s solid angle. However, the emulator can also take different practical antenna patterns to assess the scenario-specific uplink performance. The excess path-gain is assumed to follow a Gaussian mixture model (GMM) as follows [47],
where is the probability of line-of-sight (LoS), is the probability of non-line-of-sight (NLoS) and represents the normal distribution with mean and standard deviation . Note that the Satellite-to-Ground path-loss model is originally developed for urban/suburban regions. However, using the parameter set in the 3GPP technical report, we can extend this model to include rural cases [9]. The is calculated based on the function derived in [47],
where is a parameter related to the terrestrial clutter density and height.
3.2.2. Doppler Shift Model
LEO satellites are traveling at a high relative speed with respect to the observer, causing a high level of Doppler frequency shift leading to possible demodulation failure if shifts beyond are not compensated [49]. In order to obtain the Doppler shift between the observer and the satellite, the slant distance between the two points during time t is calculated as . The emulator calculates the velocity by numerical differentiation. As such, the Doppler shift for an IoT device i is given by, . Figure 8 illustrates the impact of Doppler shift on the IoT-over-Satellite system using case II as an example. Compared to the same case without Doppler shift, the BER increases significantly when the transmit power exceeds 20 dBm.
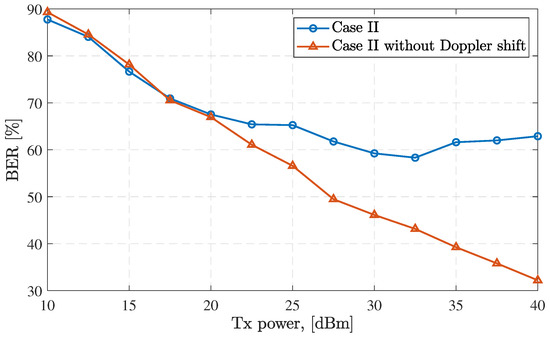
Figure 8.
Comparison of the uplink BER varying with transmit power for case II with and without the Doppler shift.
3.3. Access Models for IoT-over-Satellite
In order to assess the uplink performance of IoT-over-Satellite system for different MAC layer configurations, the framework emulates IoT-over-Satellite uplink transmissions in four access models: (i) pure-ALOHA, (ii) scheduled access, (iii) scheduled access with repetition, and (iv) scheduled round robin transmissions. A conceptual snapshot of the transmissions under the random access scenarios is illustrated in Figure 9. The IoT traffic implemented in this work is randomly generated, i.e., each device randomly transmits its signals in cases I–III. Case IV deals with a hypothetical scenario where we assume that the traffic is scheduled to showcase the upper limit and not a practical scenario. The details are further explained below,
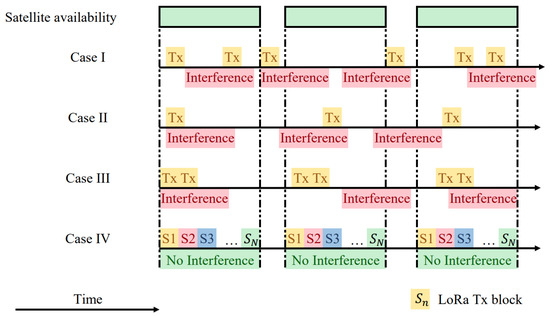
Figure 9.
Illustration of the different IoT-over-Satellite uplink access models that are considered in this framework.
3.3.1. Case I: Pure-ALOHA
The simplest random access method is pure-ALOHA access where we assume that all the IoT devices transmit with no scheduling or channel sensing involved. This means that regardless of the satellite availability, IoT devices will wake up, transmit, and then go back to sleep. As such, we should expect low probability of success results from this completely random access method due to two reasons: (i) Satellites might be unavailable to receive the packet, and (ii) elevated interference due to packets overlapping. Case I in Figure 9 depicts the expected behavior of pure-ALOHA where the IoT devices transmit at any instance.
3.3.2. Case II: Scheduled Access
To improve packet delivery rate, scheduled random access has been widely used for IoT networks [50]. In many applications, IoT devices are required to remain in sleep mode to prolong the battery lifespan and only wake up to transmit based on different scheduling algorithms which may be periodical or event triggered. In this case, we assume that the IoT devices are scheduled to transmit only when at least one satellite is capable of receiving IoT packets. In other words, an IoT device is capable of transmitting its signal when a satellite is available. Case II in Figure 9 illustrates the transmission pattern under scheduled random access, where the IoT payload (yellow blocks) is only transmitted when at least one satellite is available (green blocks). Therefore, we expect packet collisions to be the sole factor behind high PERs.
3.3.3. Case III: Scheduled Access with Packet Repetition
In case IIIIoT devices are assumed to transmit L number copies of data packets randomly within the scheduled satellite availability periods. Transmission repetition increases the chances of transmission success by creating packet redundancy.
3.3.4. Case IV: Scheduled Round Robin Transmission
In this scheme, we assume that the network is capable of allocating time-slots to different IoT devices while at least one satellite is available. Note that this access method is not random in nature since time-slots are being deterministically allocated. Prior to transmitting, an IoT device will be allocated to a transmitting queue that ends when all IoT devices within the satellite footprint transmit their signals. As such, the IoT devices are assumed to be operating in an ideal condition where they are capable of dividing the time slots among each other with the aid of round robin scheduling algorithms. The round robin scheduling method had been widely used in wireless communication to provide fair sharing of the radio resources [51,52], where co-channel interference is mitigated. Nevertheless, this access method significantly increases the complexity of IoT requiring two way communication and protocols.
3.4. LoRa Emulator
In this paper, we utilize LoRa as an example to demonstrate the feasibility of directly adopting the terrestrial LPWAN technologies into IoT-over-Satellite systems. The structure of the LoRa emulator consists of two main components: (i) LoRa transmit signal emulator, which is responsible for creating LoRa waveform based on the payload data, and the (ii) LoRa receiver responsible for the demodulation and the decoding of the LoRa packet pack into the payload data.
3.4.1. LoRa Modulation
LoRa is one of the LPWAN modulation techniques to achieve long-range and low power communication by spreading payload symbols across a wide spectrum to increase the energy per symbols and therefore mitigating the effect of narrowband interference. In LoRa the symbols are encoded into cyclic chirp signals using CSS technique, where the starting frequency and the ending frequency of a chirp signal encodes the value of the symbol. The chirp rate is controlled by a parameter called the spreading factor (SF) where higher SF stretched the symbol for longer time on air. Higher SFs increase the receiver sensitivity due to the increased energy per symbol, but on the other hand, higher SFs also reduce the data rate and increases the energy consumption of the LoRa IoT device. As such, a trade-off between packet success rate and energy consumption need to be carefully calculated to maintain the sustainability of the system [48].
3.4.2. LoRa Demodulation
Before reaching the receiver LoRa waveform is passed through the Ground-to-Satellite channel model mentioned in Section 3.2. The demodulation at the receiver involves a two-step process where the demodulator will first dechirp the received signal and then demodulate the resulting Multiple frequency-shift keying (MFSK) signal. In order to perform the dechirping, the received signal is mixed with a train of inverted chirps with zero frequency offset as follows,
where represents the train of inverted chirps. Focusing on the target signal , the dechirped signal, i.e., the FSK signal will take the following form,
where is the frequency offset of the symbol of the received LoRa packet with content value m, is the frequency offset parameter, and is the symbol duration. Note that symbol synchronization is critical to ensure the accuracy of the demodulation. After the dechirping process, the obtained MFSK signal is then demodulated by a non-coherent demodulator. The demodulator implements the energy detection of the MFSK signal using fast Fourier transform (FFT) to extract the dominant component from the power spectrum density (PSD), where the dominant component represents the original shift containing the encoded LoRa symbols. And thus, the LoRa symbols can be retrieved as follows [42],
where is the fast Fourier transform of the dechirped signal , is the rounding function and is the encoded LoRa symbol value. In this work, we investigate the impact of intra-SF interference, i.e., all devices share the same SF. The interference generated by other SF is not included due to the high orthogonality between different SF and the main focus of this paper is the impact of different random access, and satellite constellation parameters [53]. The interference generated by other SF is not included due to the high orthogonality between different SF. The reason for using the fixed SF7 is because SF7 requires the most reliable link when compared to other SF settings. If all the ground devices use SF7, the neglective impact of using a single fixed SF can also be observed if there are any destructive colliding packets. In order terms, we can use SF7 to emulate the worst-case scenario. Secondly, SF7 is energy-friendly compared to other SFs, and in order to minimize the Doppler shift impact, the frequency shift should not exceed , where . The higher the SF, the smaller the is. Moreover, LEO constellations provide high Doppler, rendering the usage of high SF becomes inefficient. The main focus of this paper is the impact of different random access, and satellite constellation parameters, as thus, the impact of intra-SF interference and the impact of the LoRa parameter is out of the scope of this paper.
3.4.3. Energy Consumption
The required electric power needed to transmit a message is dependent on the required RF transmit power , the electric-to-RF conversion factor and the overhead power [48]. For a given data rate and a message time on air , the energy consumption of an IoT packet can be expressed as follows,
where the time on air is obtained as . Energy wasting occurs when a packet is not successfully delivered to its destination. As such, the average wasted energy per transmission is given as follows,
where is the PER. For practical values of these parameters, we rely on empirical measurements obtained from our previous work in [48]. In case III, the energy consumption is obtained from this following equation,
In order to assess the energy wasted due to synchronization, the overhead power due to synchronization is taken into the calculation. Moreover, the energy wasted per transmission can be obtained by the following equation,
Note that we did not add any extra power overhead since we can simply program the IoT devices to transmit at certain periods of time.
4. Emulation Results and Discussion
For convenience we list all simulation parameters in Table 1. We assume a moderate number of satellites in the constellation and a relatively lower constellation altitude to emphasize the impact of satellite constellation. LoRa data rate 3 (DR3) parameter is utilized to provide a realistic emulation, in which the frequency bandwidth is 125 kHz. The transmit power level and the duty cycle follows the specification of LoRa Alliance. Moreover, we adopt the excess path-loss parameters provided in [47].
4.1. Impact of Satellite Constellation
In order to have a better understanding of geometry of satellite constellation on the link performance, we depict in Figure 10 the average uplink BER for the two satellites constellations assuming case I access method is shown as a function of the latitudes of IoT ground devices. The BER is shown to follow the inverse trend of the satellite availability (as demonstrated previously in Figure 5, where the Walker-Star constellation has a higher BER at the equator and mid latitude locations in comparison to Walker-Delta. However, Walker-Delta provides a degraded performance as the latitude increases. This is because Walker-Delta constellations sacrifice the coverage at the poles to provide higher satellite density at lower latitude locations. Walker-Star constellations can match the performance at the equator by increasing the number of satellites or the satellite constellation altitude [12]. The average packet success rate for case I versus the number of satellites in the constellation is shown in Figure 11. Note that the Walker-Delta constellation example is deployed over ±60° latitude, therefore the packet success rate of Walker-Star will inherently be higher when sampling the entire Earth surface.
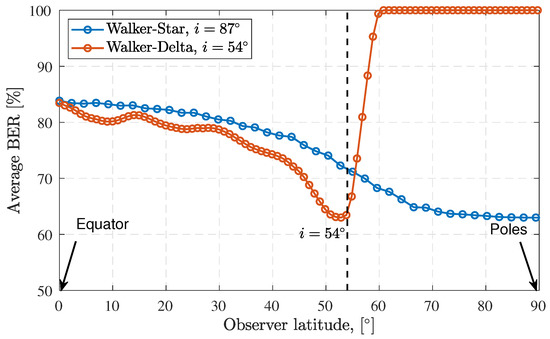
Figure 10.
The average BER for case I while varying the target IoT device latitude, showing the Walker-Star for and Walker-Delta for , the rest of the simulation parameters are listed in Table 1.
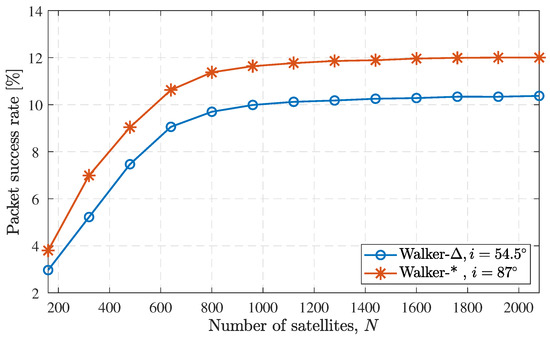
Figure 11.
The packet successful rate for case I as a function of the number of satellites in the constellation. The IoT devices transmit power is .
4.2. Access Methods Comparison
To compare the impact of the different access methods introduced in Section 3.3, we depict in Figure 12 the BER for the different access models against varying transmit power. This figure shows that case III has the best performance, i.e., the BER is lowest in case III, while case I had the worst BER. The finding fulfills our expectation since the BER in case I is impaired with both the lack of satellite availability and packet collision. In contrast, the four repeated transmissions reduce the BER at least by when compared to case I at dBm. To further investigate the performance of case III, we emulate the trend of PER versus different packet repetition number L as shown in Figure 13. The figure shows that PER is improved with the increasing number of repetitions. It also indicates that the rate of improvement slows down with higher repetition.
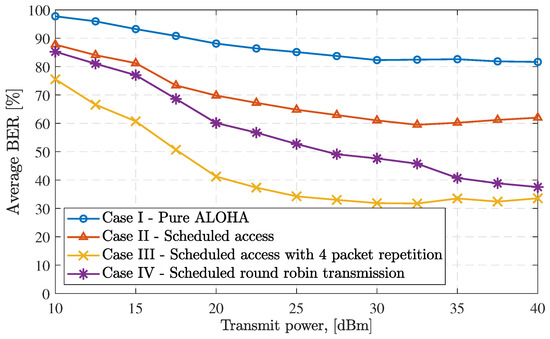
Figure 12.
The average BER as a function of the transmit power for different access cases. The constellation size and altitude are equal to , respectively.
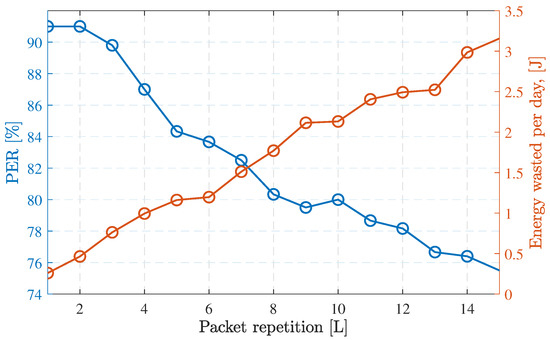
Figure 13.
The PER and energy wasted per day with respect to varying packet repetitions, L, in case III assuming a transmit power .
4.3. Energy Wasted in Different Access Methods
Based on the provided energy model in Section 3.4.3, we simulate and depict the energy wasted for different access scenarios illustrated in Figure 14. Noticeably, case III has the highest energy wastage, which is due to packet re-transmission. Furthermore, the energy wasted for case III is also shown in Figure 13 whereby the energy wasted increases as the number of re-transmissions increases even as the PER is reduced. On the other hand, case IV (without the overhead power due to synchronization) provides lower energy wastage due to the interference-free environment achieved by network synchronization. If we assumed the overhead power due to synchronization is equal to 250 mW, the energy wastage of case IV as shown in Figure 14, is still somewhat lower than the energy wastage in case II, since the power used for synchronization reduces the chance of packet collision. We can see that access methods that heavily rely on scheduling and synchronization, such as case IV, require a large amount of overhead power. However, this is not included in this work because the amount of energy consumed depends on the particular system implementation. The energy wasted can be reduced by increasing the size of the constellation due to the increased availability. However, as the availability approaches its maximum, the energy enhancement saturates. This is illustrated in Figure 15 for both Walker-Delta and Walker-Star where a minimum of 200 mJ energy wastage is achieved as the number of satellites increases and the availability approaches its maximum.
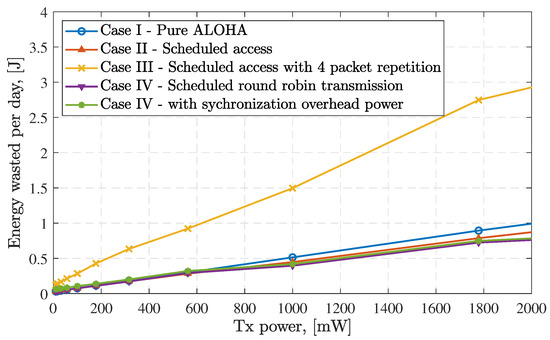
Figure 14.
Illustration of the energy wasted as a function of the transmit power for the different access methods. The maximum number of transmissions is set to two messages per day with a size 12 bytes payload.
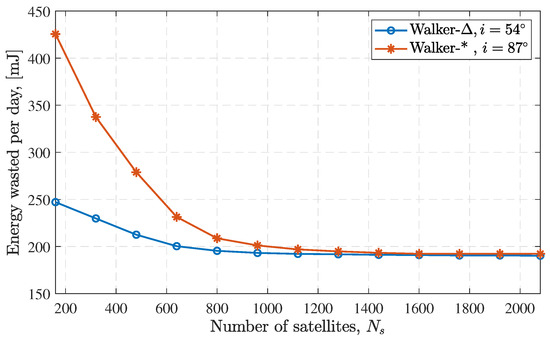
Figure 15.
The energy wasted per day for case I as a function of the number of satellites in the constellation. The IoT devices transmit power is .
4.4. Feasibility of IoT-over-Satellite Using LoRa
The results captured in Figure 10 and Figure 12 are based on the worst-case scenario, in which we assumed that the ground devices are using a highly congested radio band with numerous actively transmitting devices, the lowest spreading factor, and a narrow band is used for the IoT-over-Satellite communication. The result might sound discouraging as the bit error rate can be over when the transmit power is about 27 dBm. However, if the IoT-over-Satellite communication uses the highest spreading factor and a broadened bandwidth in a less congested radio channel, as shown in Figure 16, the PER can be reduced to less than with the same transmit power in cases II to IV. This is due to the increased ratio of energy per bit to the spectral noise density (), reduced interference level, and the higher Doppler shift’s tolerance in the larger bandwidth. Note that the PER in case I is still over due to the PER in case I being dominated by the satellite availability meaning that the PER remains unchanged even if we increase the transmit power. As a result, by using this emulation framework, the IoT-over-Satellite system planner can adjust the parameters of their communication protocol to investigate the performance IoT-over-Satellite system, find the maximum number of allowed users, and optimize their parameter for the communication protocol.
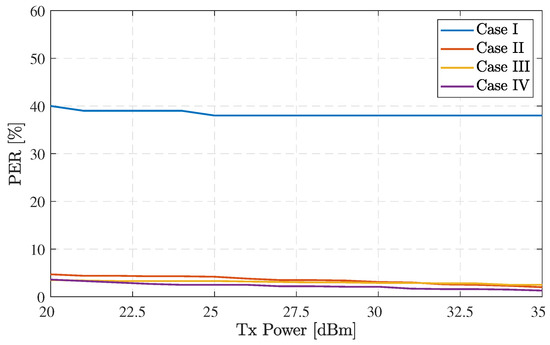
Figure 16.
Illustration of the uplink PER with a different set of LoRa parameters ( B = 500 ) showing the feasibility of using LoRa over Satellite communication.
5. Conclusions
This paper presents a comprehensive framework for the uplink performance of IoT-over-Satellite networks utilizing the LoRa modulation scheme. The framework incorporates realistic access models, practical satellite constellations, and a Satellite-to-Ground propagation channel model. Using practical synthetic LoRa traffic, the performance of a realistic IoT-over-Satellite link is evaluated, where the packet error rate, bit error rate, coverage probability, and energy consumption are obtained. The paper proposes four different access methods for IoT-over-Satellite applications, namely, (i) pure ALOHA, (ii) scheduled access, (iii) scheduled access with repetition, and (iv) scheduled round robin. Results show that the satellite constellation distribution, satellite availability, interference, random access methods, and scheduling techniques significantly contribute to the performance of LEO-based IoT-over-Satellite networks. The feasibility of using LoRa in IoT-over-Satellite communication is also investigated by using a higher spreading factor and broader bandwidth. The source code of the emulation framework is shared on GitHub. Future work will focus on the performance evaluation of different interference mitigation techniques, such as interference cancellation using machine learning, load sharing, and successive interference cancellation.
Author Contributions
Conceptualization, methodology, software, validation: C.C.C., B.A.H. and A.A.-H.; formal analysis, investigation: C.C.C. and B.A.H.; data curation, C.C.C.; writing—original draft preparation, C.C.C.; writing—review and edit, C.C.C., B.A.H. and A.A.-H.; visualization, C.C.C.; supervision, B.A.H. and A.A.-H.; project administration, A.A.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Australian government RTP Stipend Scholarship (RSS).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Byers, C.C. Architectural Imperatives for Fog Computing: Use Cases, Requirements, and Architectural Techniques for Fog-Enabled IoT Networks. IEEE Commun. Mag. 2017, 55, 14–20. [Google Scholar] [CrossRef]
- Ta-Shma, P.; Akbar, A.; Gerson-Golan, G.; Hadash, G.; Carrez, F.; Moessner, K. An Ingestion and Analytics Architecture for IoT Applied to Smart City Use Cases. IEEE Internet Things J. 2018, 5, 765–774. [Google Scholar] [CrossRef]
- Hanes, D.; Salgueiro, G.; Grossetete, P.; Barton, R.; Henry, J. IoT Fundamentals: Networking Technologies, Protocols, and Use Cases for the Internet of Things; Cisco Press: Indianapolis, IN, USA, 2017. [Google Scholar]
- Al Homssi, B.; Al-Hourani, A.; Magowe, K.; Delaney, J.; Tom, N.; Ying, J.; Wolf, H.; Maselli, S.; Kandeepan, S.; Wang, K.; et al. A Framework for the Design and Deployment of Large-Scale LPWAN Networks for Smart Cities Applications. IEEE Internet Things Mag. 2021, 4, 53–59. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, Y.C.; Niyato, D. 6G Visions: Mobile Ultra-Broadband, Super Internet-of-Things, and Artificial Intelligence. China Commun. 2019, 16, 1–14. [Google Scholar] [CrossRef]
- Cioni, S.; De Gaudenzi, R.; Del Rio Herrero, O.; Girault, N. On the Satellite Role in the Era of 5G Massive Machine Type Communications. IEEE Netw. 2018, 32, 54–61. [Google Scholar] [CrossRef]
- Bacco, M.; Boero, L.; Cassara, P.; Colucci, M.; Gotta, A.; Marchese, M.; Patrone, F. IoT Applications and Services in Space Information Networks. IEEE Wirel. Commun. 2019, 26, 31–37. [Google Scholar] [CrossRef]
- De Sanctis, M.; Cianca, E.; Araniti, G.; Bisio, I.; Prasad, R. Satellite Communications Supporting Internet of Remote Things. IEEE Internet Things J. 2016, 3, 113–123. [Google Scholar] [CrossRef]
- 3GPP. Study on New Radio (NR) to Support Non-Terrestrial Networks; Technical Report TR38.811; 3rd Generation Partnership Project (3GPP); 3GPP: Sophia Antipolis, France, 2020. [Google Scholar]
- 3GPP. Solutions for NR to support Non-Terrestrial Networks (NTN); Technical Report TR38.821; 3rd Generation Partnership Project (3GPP); 3GPP: Sophia Antipolis, France, 2021. [Google Scholar]
- Starlink. Starlink. Available online: https://www.starlink.com/ (accessed on 24 July 2022).
- OneWeb. OneWeb. Available online: https://oneweb.net/ (accessed on 24 July 2022).
- Amazon.com, Inc. Project Kuiper. Available online: https://www.aboutamazon.com/news/tag/project-kuiper (accessed on 24 July 2022).
- Deckett, M. ORBCOMM—A Description and Status of the LEO Satellite Mobile Data Communication System. In Proceedings of the 15th International Communicatons Satellite Systems Conference and Exhibit. 2012. Available online: https://arc.aiaa.org/doi/pdf/10.2514/6.1994-1135 (accessed on 24 July 2022). [CrossRef]
- Myriota. Myriota. Available online: https://myriota.com/ (accessed on 24 July 2022).
- Technologies, F.S. Fleet Space Technologies. Available online: https://fleetspace.com/ (accessed on 24 July 2022).
- Gaber, A.; ElBahaay, M.A.; Maher Mohamed, A.; Zaki, M.M.; Samir Abdo, A.; AbdelBaki, N. 5G and Satellite Network Convergence: Survey for Opportunities, Challenges and Enabler Technologies. In Proceedings of the 2020 2nd Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 24–26 October 2020; pp. 366–373. [Google Scholar] [CrossRef]
- Qu, Z.; Zhang, G.; Cao, H.; Xie, J. LEO Satellite Constellation for Internet of Things. IEEE Access 2017, 5, 18391–18401. [Google Scholar] [CrossRef]
- Al Homssi, B.; Al-Hourani, A.; Wang, K.; Conder, P.; Sithamparanathan, K.; Choi, J.; Allen, B.; Moores, B. Next Generation Mega Satellite Networks for Access Equality: Opportunities, Challenges, and Performance. IEEE Commun. Mag. 2022, 60, 18–24. [Google Scholar] [CrossRef]
- Sornin, N.; Luis, M.; Eirich, T.; Kramp, T.; Hersent, O. LoRaWAN Specification; LoRa Alliance: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Fraire, J.A.; Henn, S.; Dovis, F.; Garello, R.; Taricco, G. Sparse Satellite Constellation Design for LoRa-based Direct-to-Satellite Internet of Things. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Chiti, F.; Fantacci, R.; Pierucci, L. Energy Efficient Communications for Reliable IoT Multicast 5G/Satellite Services. Future Internet 2019, 11, 164. [Google Scholar] [CrossRef]
- Marchese, M.; Moheddine, A.; Patrone, F. IoT and UAV Integration in 5G Hybrid Terrestrial-Satellite Networks. Sensors 2019, 19, 3704. [Google Scholar] [CrossRef]
- Cluzel, S.; Franck, L.; Radzik, J.; Cazalens, S.; Dervin, M.; Baudoin, C.; Dragomirescu, D. 3GPP NB-IOT Coverage Extension Using LEO Satellites. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Janhunen, J.; Ketonen, J.; Hulkkonen, A.; Ylitalo, J.; Roivainen, A.; Juntti, M. Satellite Uplink Transmission with Terrestrial Network Interference. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Hofmann, C.A.; Knopp, A. Ultranarrowband Waveform for IoT Direct Random Multiple Access to GEO Satellites. IEEE Internet Things J. 2019, 6, 10134–10149. [Google Scholar] [CrossRef]
- Qian, Y.; Ma, L.; Liang, X. The Performance of Chirp Signal Used in LEO Satellite Internet of Things. IEEE Commun. Lett. 2019, 23, 1319–1322. [Google Scholar] [CrossRef]
- Bhave, P.; Fines, P. System Behavior and Improvements for M2M Devices Using an Experimental Satellite Network. In Proceedings of the 2015 IEEE Region 10 Symposium, Ahmedabad, India, 13–15 May 2015; pp. 13–16. [Google Scholar] [CrossRef]
- Bacco, M.; Colucci, M.; Gotta, A. Application Protocols Enabling Internet of Remote Things via Random Access Satellite Channels. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Manzoor, B.; Homssi, B.A.; Al-Hourani, A.; Kandeepan, S. Optimal Repetition Rate for Maximal Coverage. IEEE Wirel. Commun. Lett. 2021, 10, 800–804. [Google Scholar] [CrossRef]
- Manzoor, B.; Homssi, B.A.; Al-Hourani, A. IoT Coverage Enhancement using Repetition in Energy Constrained Devices: An Analytic Approach. IEEE Trans. Green Commun. Netw. 2021, 6, 1122–1131. [Google Scholar] [CrossRef]
- Bacco, M.; Cassarà, P.; Colucci, M.; Gotta, A. Modeling Reliable M2M/IoT Traffic Over Random Access Satellite Links in Non-Saturated Conditions. IEEE J. Sel. Areas Commun. 2018, 36, 1042–1051. [Google Scholar] [CrossRef]
- Ferrer, T.; Céspedes, S.; Becerra, A. Review and Evaluation of MAC Protocols for Satellite IoT Systems Using Nanosatellites. Sensors 2019, 19, 1947. [Google Scholar] [CrossRef]
- Clazzer, F.; Munari, A. IoT via Satellite: Asynchronous Random Access for the Maritime Channel. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Krondorf, M.; Goblirsch, M.; de Gaudenzi, R.; Cocco, G.; Toptsidis, N.; Acar, G. Towards the Implementation of Advanced Random Access Schemes for Satellite IoT. Int. J. Satell. Commun. Netw. 2020, 38, 177–199. [Google Scholar] [CrossRef]
- De Gaudenzi, R.; Del Rio Herrero, O.; Gallinaro, G.; Cioni, S.; Arapoglou, P.D. Random access schemes for satellite networks, from VSAT to M2M: A survey. Int. J. Satell. Commun. Netw. 2018, 36, 66–107. [Google Scholar] [CrossRef]
- Chan, C.C.; Al-Hourani, A.; Choi, J.; Gomez, K.M.; Kandeepan, S. Performance Modeling Framework for IoT-over-Satellite Using Shared Radio Spectrum. Remote Sens. 2020, 12, 1666. [Google Scholar] [CrossRef]
- Al-Hourani, A. Optimal Satellite Constellation Altitude for Maximal Coverage. IEEE Wirel. Commun. Lett. 2021, 10, 1444–1448. [Google Scholar] [CrossRef]
- Talgat, A.; Kishk, M.A.; Alouini, M.S. Stochastic Geometry-Based Analysis of LEO Satellite Communication Systems. IEEE Commun. Lett. 2021, 25, 2458–2462. [Google Scholar] [CrossRef]
- Homssi, B.A.; Al-Hourani, A. Modeling Uplink Coverage Performance in Hybrid Satellite-Terrestrial Networks; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Chan, C.C.; Al-Hourani, A.; Homssi, B.A. Performance Evaluation of Random Access Methods for IoT-over-Satellite. Available online: https://github.com/s3556682/Performance-Evaluation-of-Random-Access-Methods-for-IoT-over-Satellite (accessed on 24 July 2022).
- Al Homssi, B.; Dakic, K.; Maselli, S.; Wolf, H.; Kandeepan, S.; Al-Hourani, A. IoT Network Design Using Open-Source LoRa Coverage Emulator. IEEE Access 2021, 9, 53636–53646. [Google Scholar] [CrossRef]
- Manzoor, B.; Al-Hourani, A.; Homssi, B.A.; Magowe, K.; Kandeepan, S.; Chavez, K.G. Evaluating Coverage Performance of NB-IoT in the ISM-band. In Proceedings of the 2020 27th International Conference on Telecommunications (ICT), Bali, Indonesia, 5–7 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Al-Hourani, A. A Tractable Approach for Predicting Pass Duration in Dense Satellite Networks. IEEE Commun. Lett. 2021, 25, 2698–2702. [Google Scholar] [CrossRef]
- Savitri, T.; Kim, Y.; Jo, S.; Bang, H. Satellite Constellation Orbit Design Optimization with Combined Genetic Algorithm and Semianalytical Approach. Int. J. Aerosp. Eng. 2017, 2017, 1235692. [Google Scholar] [CrossRef]
- Maine, K.; Devieux, C.; Swan, P. Overview of IRIDIUM Satellite Network. In Proceedings of the WESCON’95, San Francisco, CA, USA, 7–9 November 1995; p. 483. [Google Scholar] [CrossRef]
- Al-Hourani, A.; Guvenc, I. On Modeling Satellite-to-Ground Path-Loss in Urban Environments. IEEE Commun. Lett. 2020, 25, 696–700. [Google Scholar] [CrossRef]
- Al Homssi, B.; Al-Hourani, A.; Chandrasekharan, S.; Gomez, K.M.; Kandeepan, S. On the Bound of Energy Consumption in Cellular IoT Networks. IEEE Trans. Green Commun. Netw. 2020, 4, 355–364. [Google Scholar] [CrossRef]
- Wu, T.; Qu, D.; Zhang, G. Research on LoRa Adaptability in the LEO Satellites Internet of Things. In Proceedings of the 2019 15th International Wireless Communications Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 131–135. [Google Scholar] [CrossRef]
- Laya, A.; Kalalas, C.; Vazquez-Gallego, F.; Alonso, L.; Alonso-Zarate, J. Goodbye, ALOHA! IEEE Access 2016, 4, 2029–2044. [Google Scholar] [CrossRef] [Green Version]
- Bai, K.; Zhang, J. Opportunistic Multichannel ALOHA: Distributed Multiaccess Control Scheme for OFDMA Wireless Networks. IEEE Trans. Veh. Technol. 2006, 55, 848–855. [Google Scholar] [CrossRef]
- Xue, Y.; Kaiser, T.; Gershman, A.B. Channel-Aware ALOHA-Based OFDM Subcarrier Assignment in Single-Cell Wireless Communications. IEEE Trans. Commun. 2007, 55, 953–962. [Google Scholar] [CrossRef]
- Croce, D.; Gucciardo, M.; Mangione, S.; Santaromita, G.; Tinnirello, I. Impact of LoRa Imperfect Orthogonality: Analysis of Link-Level Performance. IEEE Commun. Lett. 2018, 22, 796–799. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).