Shipborne HFSWR Target Detection in Clutter Regions Based on Multi-Frame TFI Correlation
Abstract
:1. Introduction
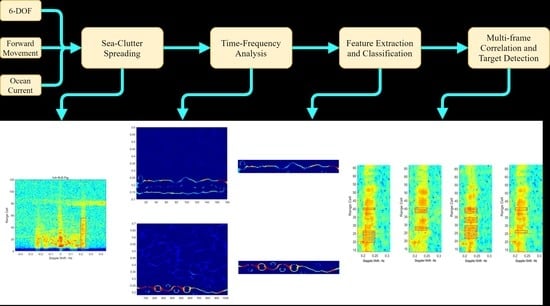
2. Detection Framework
2.1. RD Spectrum of Shipborne HFSWR
2.2. Detection Framework
3. Problem Formulation
3.1. Spreading of Sea Clutter
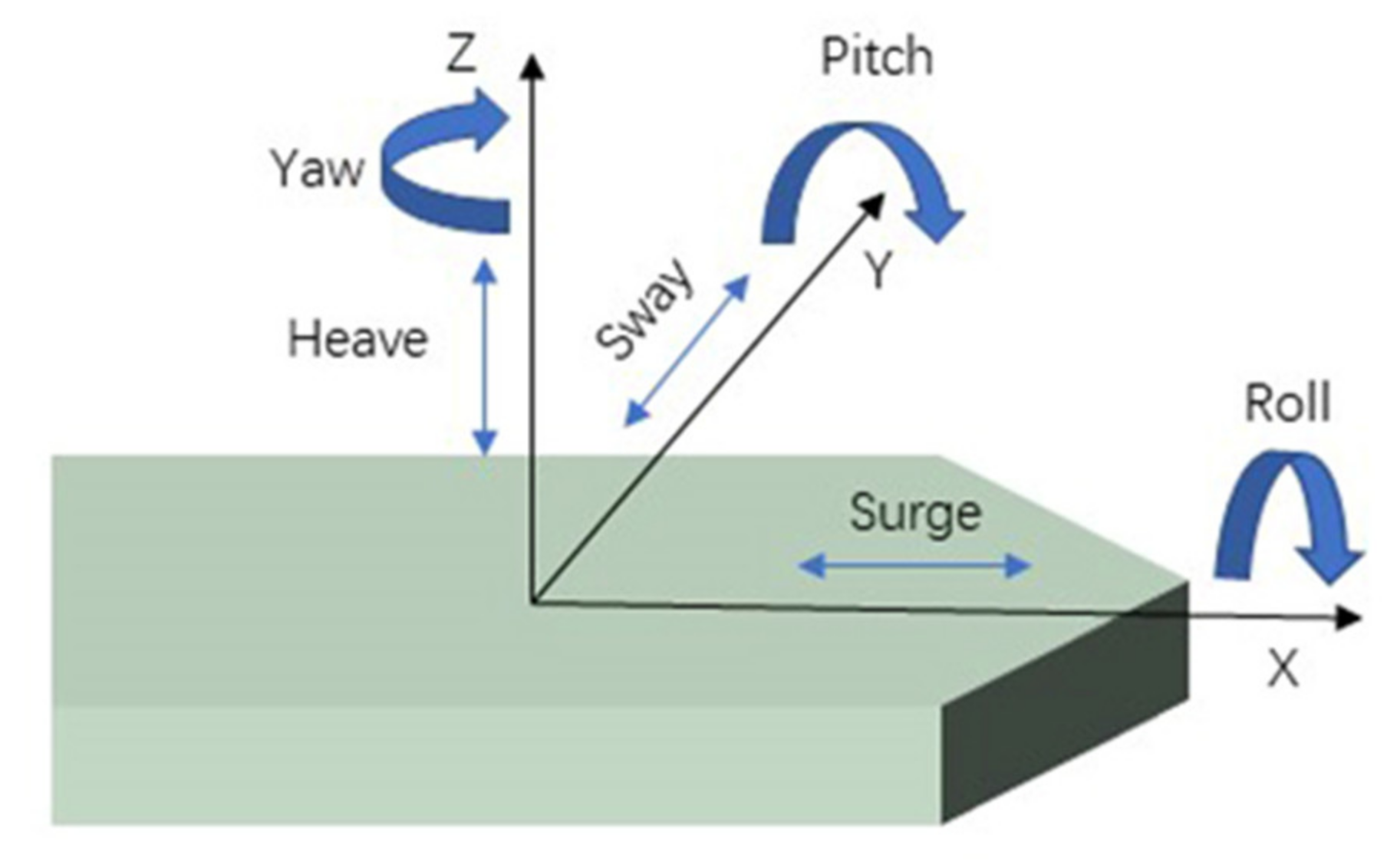
3.2. Modeling of Platform Movement and Motion Due to Ocean Currents
3.2.1. Forward Movement and the Motion from Ocean Currents
3.2.2. Heave Movement
3.2.3. Sway and Surge Movements
3.2.4. Roll Movement
3.2.5. Pitch Movement
3.2.6. Yaw Movement
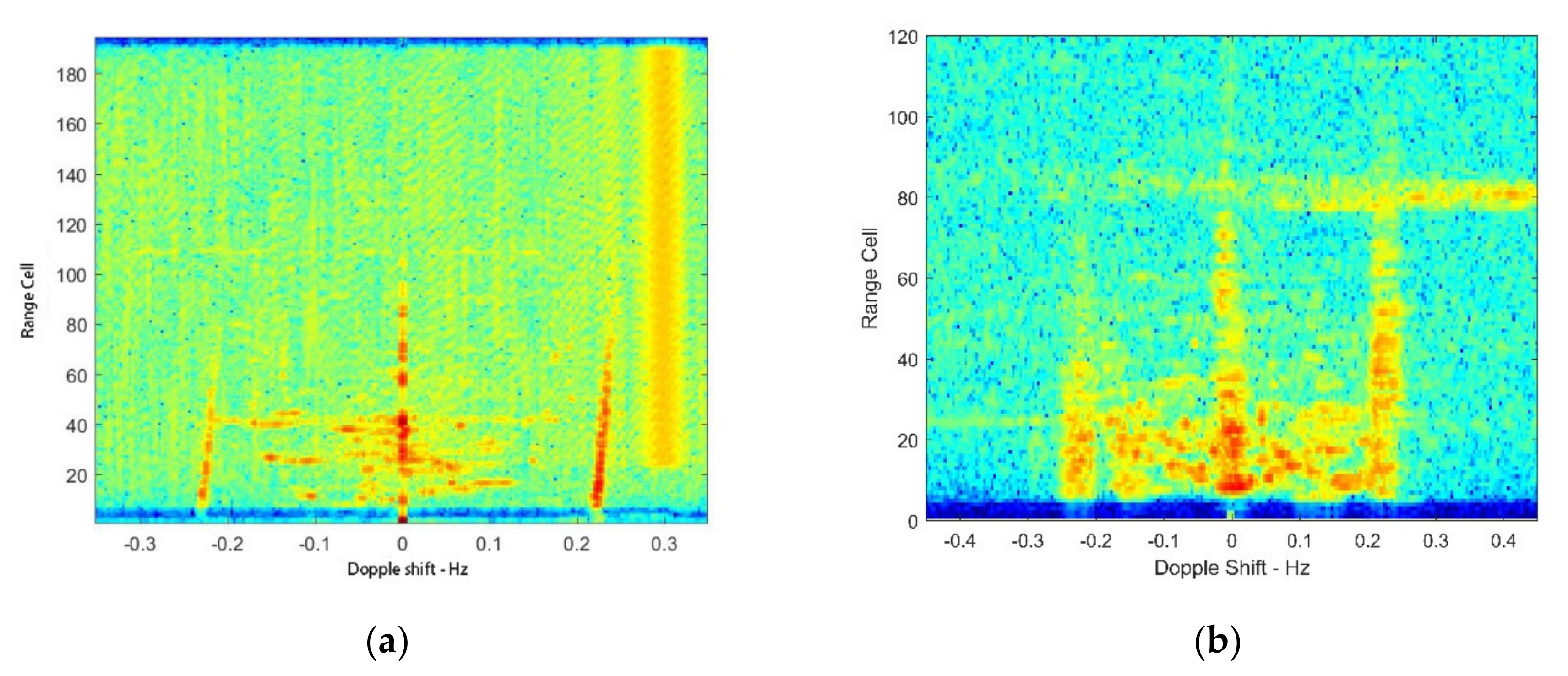
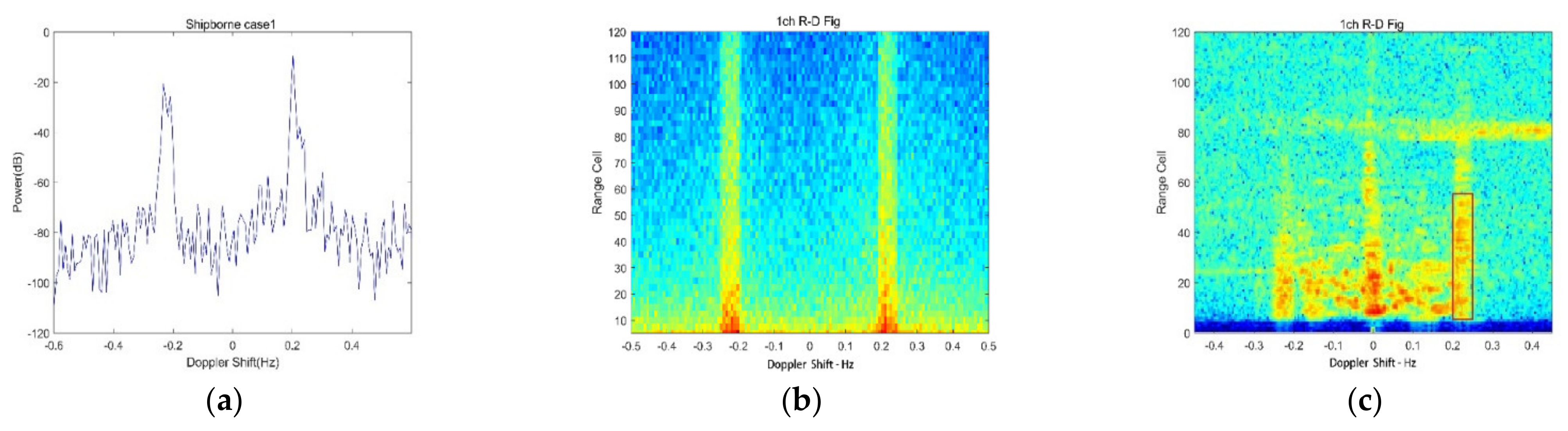
3.3. Simulation and Verification of Sea Clutter Spreading
4. Time-Frequency Analysis
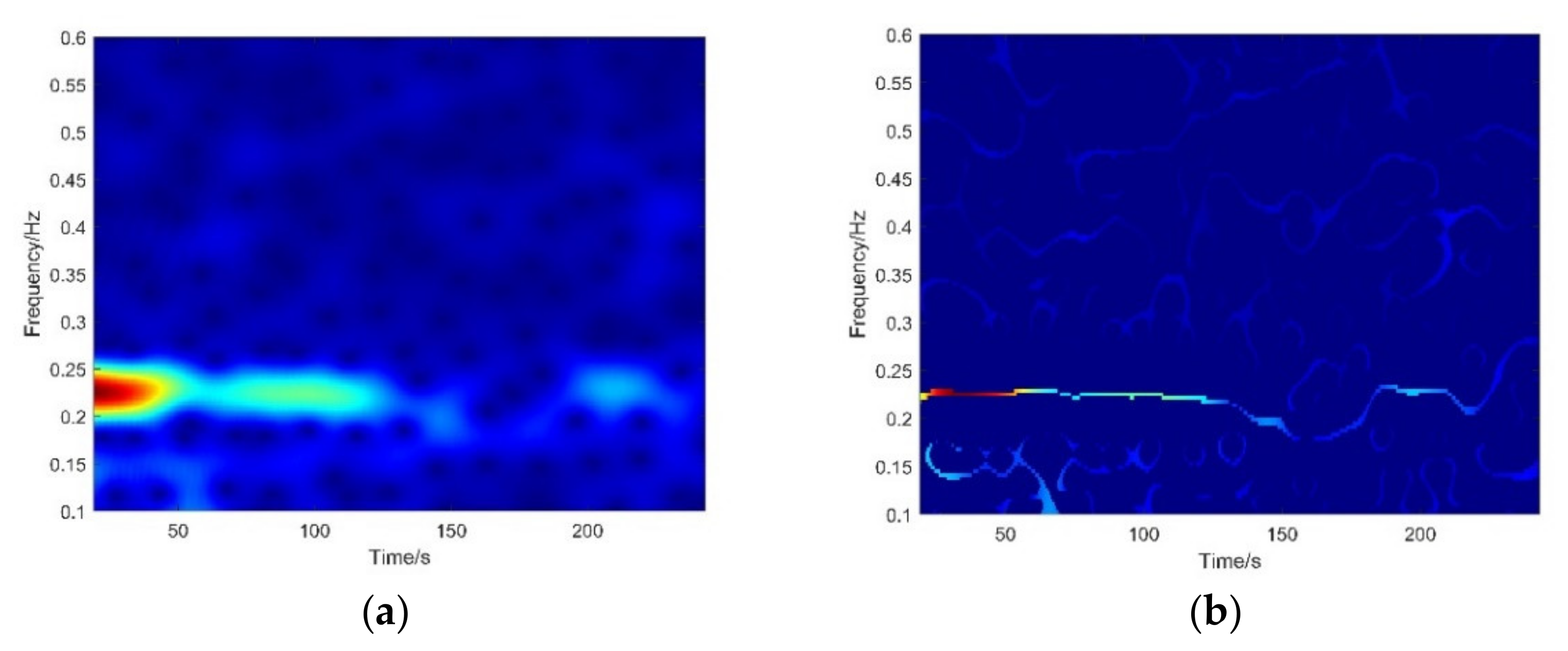
4.1. Time-Frequency Method
4.2. Feature Extraction and Classification
5. Target Detection
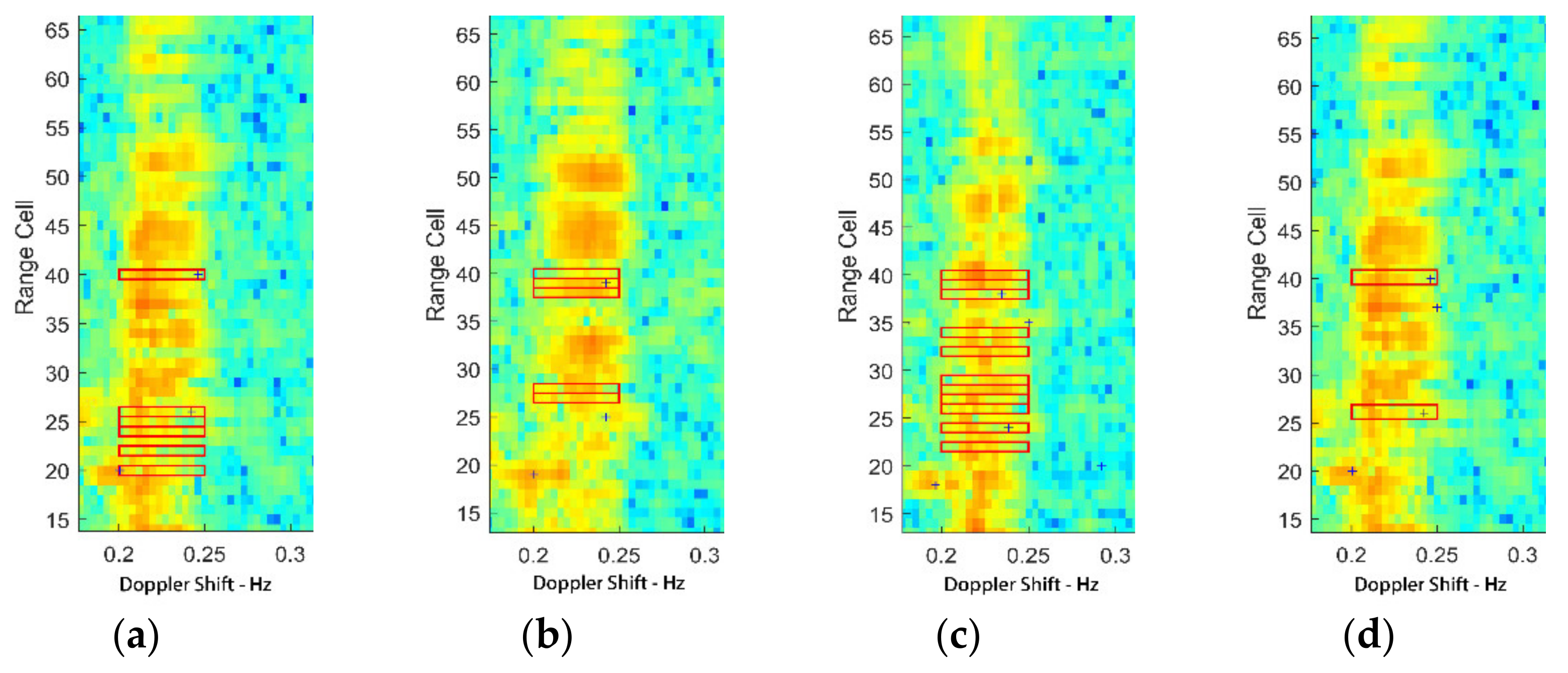
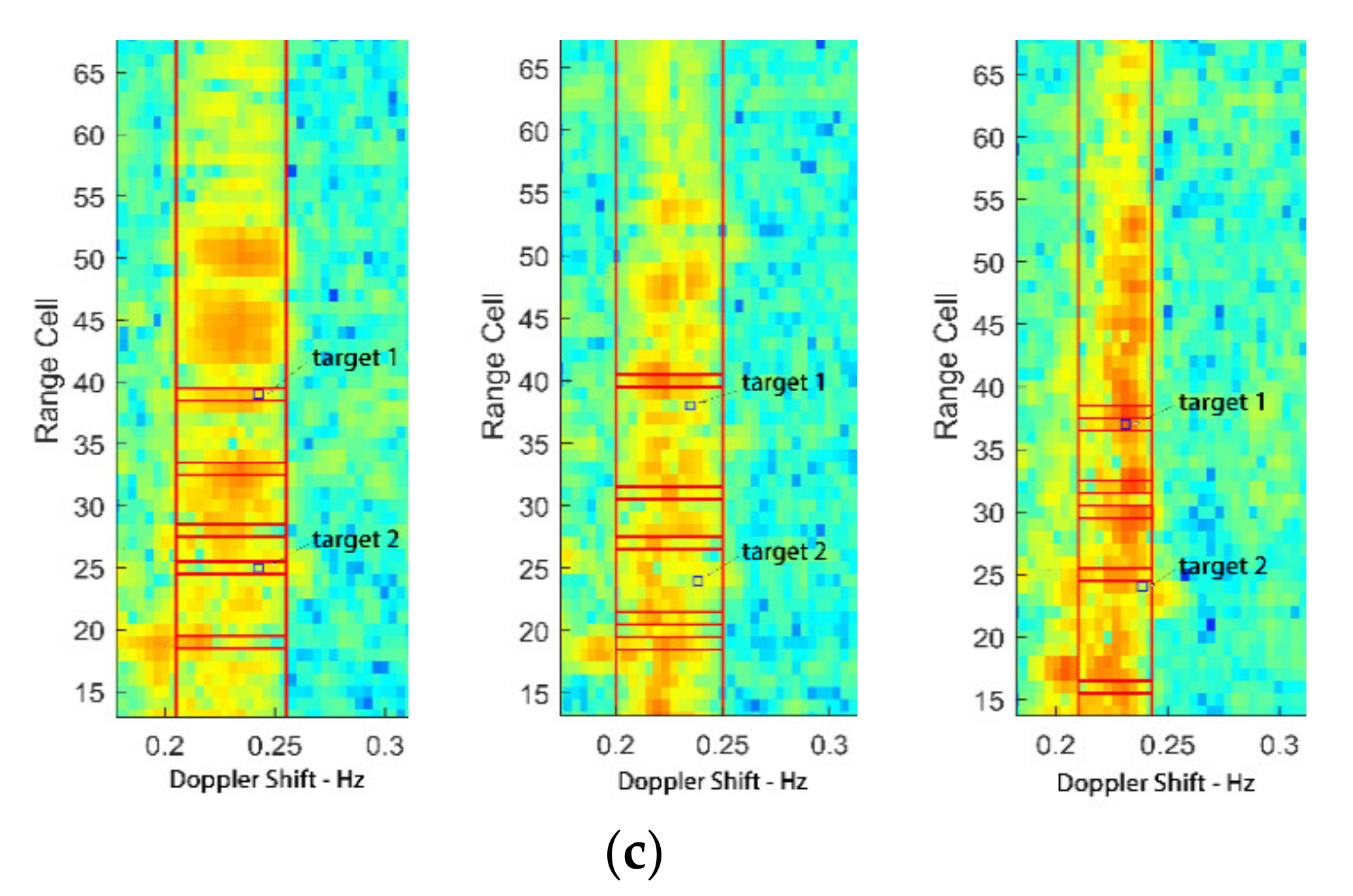
5.1. Multi-Frame Correlation and Target Detection
5.2. Field Experiment
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, L.; Mao, D.; Niu, J.; Wu, Q.M.J.; Ji, Y. Continuous Tracking of Targets for Stereoscopic HFSWR Based on IMM Filtering Combined with ELM. Remote Sens. 2020, 12, 272. [Google Scholar] [CrossRef]
- Xie, J.; Yuan, Y.; Liu, Y. Experimental analysis of sea clutter in shipborne HFSWR. IEE Proc. Radar Sonar Navig. 2001, 148, 67–71. [Google Scholar] [CrossRef]
- Walsh, J.; Huang, W.; Gill, E. The First-Order High Frequency Radar Ocean Surface Cross Section for an Antenna on a Floating Platform. IEEE Trans. Antennas Propag. 2010, 58, 2994–3003. [Google Scholar] [CrossRef]
- Walsh, J.; Huang, W.; Gill, E. The second-order high frequency radar ocean surface cross section for an antenna on a floating platform. IEEE Trans. Antennas Propag. 2012, 60, 4804–4813. [Google Scholar] [CrossRef]
- Ma, Y.; Gill, E.W.; Huang, W. High Frequency Radar Cross Sections of the Ocean Surface Incorporating Pitch and Roll Motions of a Floating Platform. In Proceedings of the 2018 OCEANS-MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–4. [Google Scholar]
- Yao, G.; Xie, J.; Huang, W. First-order ocean surface cross-section for shipborne HFSWR incorporating a horizontal oscillation motion model. IET Radar Sonar Navig. 2018, 12, 973–978. [Google Scholar] [CrossRef]
- Gill, E.W.; Ma, Y.; Huang, W. Motion compensation for high-frequency surface wave radar on a floating platform. IET Radar Sonar Navig. 2018, 12, 37–45. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Q.; Sun, J.; Deng, W. A Space-Time Model of Sea Echo with Shipborne HFSWR Platform Under Varying Velocity Motion. In Proceedings of the 2018 International Symposium on Antennas and Propagation (ISAP), Busan, Korea, 23–26 October 2018; pp. 1–2. [Google Scholar]
- Yang, K.; Zhang, L.; Niu, J.; Ji, Y.; Wu, Q.M.J. Analysis and Estimation of Shipborne HFSWR Target Parameters Under the Influence of Platform Motion. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4703–4716. [Google Scholar] [CrossRef]
- Xiao, Z.; Yan, Z. Radar Emitter Identification Based on Novel Time-Frequency Spectrum and Convolutional Neural Network. IEEE Commun. Lett. 2021, 25, 2634–2638. [Google Scholar] [CrossRef]
- Huang, Z.-L.; Zhang, J.; Zhao, T.-H.; Sun, Y. Synchrosqueezing S-Transform and Its Application in Seismic Spectral Decomposition. IEEE Trans. Geosci. Remote Sens. 2016, 54, 817–825. [Google Scholar] [CrossRef]
- Yu, G.; Wang, Z.; Zhao, P. Multisynchrosqueezing Transform. IEEE Trans. Ind. Electron. 2019, 66, 5441–5455. [Google Scholar] [CrossRef]
- Yu, G.; Yu, M.; Xu, C. Synchroextracting Transform. IEEE Trans. Ind. Electron. 2017, 64, 8042–8054. [Google Scholar] [CrossRef]
- Cai, J.; Zhou, H.; Huang, W.; Wen, B. Ship Detection and Direction Finding Based on Time-Frequency Analysis for Compact HF Radar. IEEE Geosci. Remote Sens. Lett. 2021, 18, 72–76. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, W.; Li, M.; Niu, J.; Jonathan Wu, Q.M. Automatic Detection of Ship Targets Based on Wavelet Transform for HF Surface Wavelet Radar. IEEE Geosci. Remote Sens. Lett. 2017, 14, 714–718. [Google Scholar] [CrossRef]
- Chen, Z.; He, C.; Zhao, H.; Xie, F. Enhanced multi-target detection for HFSWR by sparse-recovery-based 2-D MUSIC. In Proceedings of the OCEANS 2017-Anchorage, Anchorage, AK, USA, 18–21 September 2017; pp. 1–5. [Google Scholar]
- Wang, Y.; Mao, X.; Zhang, J.; Ji, Y. Detection of Vessel Targets in Sea Clutter Using In Situ Sea State Measurements With HFSWR. IEEE Geosci. Remote Sens. Lett. 2018, 15, 302–306. [Google Scholar] [CrossRef]
- Wu, M.; Zhang, L.; Niu, J.; Wu, Q.M.J. Target Detection in Clutter/Interference Regions Based on Deep Feature Fusion for HFSWR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5581–5595. [Google Scholar] [CrossRef]
- Chang, G.; Li, M.; Xie, J.; Zhang, L.; Yu, C.; Ji, Y. Ocean Surface Current Measurement Using Shipborne HF Radar: Model and Analysis. IEEE J. Ocean. Eng. 2016, 41, 970–981. [Google Scholar] [CrossRef]
- Chang, G.; Li, M.; Zhang, L.; Ji, Y.; Xie, J. Measurements of ocean surface currents using shipborne High-Frequency radar. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. Comput. Sci. 2014, preprint. [Google Scholar] [CrossRef]






| Parameter Name | Numerical Values | Unit |
|---|---|---|
| Roll angle | 0.2410 | rad |
| Pitch angle | 1.1807 | rad |
| Declination angle | 49.2000 | rad |
| Sway speed | 0.2000 | m/s |
| Surge speed | 0.2000 | m/s |
| Roll speed | 0.1000 | m/s |
| Pitch speed | 0.0900 | m/s |
| Yaw Speed | 0.1700 | m/s |
| Forward movement speed | 0.2000 | m/s |
| Current speed | 0.3448 | m/s |
| Pattern | Width (Hz) |
|---|---|
| Theoretical Calculations | 0.050 |
| Simulation Result | 0.050 |
| Measured Result | 0.048 |
| Parameters | Values |
|---|---|
| Transmit signal | FMICW |
| Operating frequency (MHz) | 4.7 |
| Coherent integration time (s) | 300 |
| Number of antennas | 5 |
| Antenna spacing | Non-uniform array |
| Type | Patch Size/Stride | Output Size | Depth | #1 × 1 | #3 × 3 Reduce | #3 × 3 | #5 × 5 Reduce | #5 × 5 | Pool Proj | Params | Ops |
|---|---|---|---|---|---|---|---|---|---|---|---|
| convolution | 7 × 7/2 | 112 × 112 × 64 | 1 | 2.7 K | 34 M | ||||||
| max pool | 3 × 3/2 | 56 × 56 × 64 | 0 | ||||||||
| convolution | 3 × 3/1 | 56 × 56 × 192 | 2 | 64 | 192 | 112 K | 360 M | ||||
| max pool | 3 × 3/2 | 28 × 28 × 192 | 0 | ||||||||
| Inception(3a) | 28 × 28 × 256 | 2 | 64 | 96 | 128 | 16 | 32 | 32 | 159 K | 128 M | |
| Inception(3b) | 28 × 28 × 480 | 2 | 128 | 128 | 192 | 32 | 96 | 64 | 380 K | 304 M | |
| Max pool | 3 × 3/2 | 14 × 14 × 480 | 0 | ||||||||
| Inception(4a) | 14 × 14 × 512 | 2 | 192 | 96 | 208 | 16 | 48 | 64 | 364 K | 73 M | |
| Inception(4b) | 14 × 14 × 512 | 2 | 160 | 112 | 224 | 24 | 64 | 64 | 437 K | 88 M | |
| Inception(4c) | 14 × 14 × 512 | 2 | 128 | 128 | 256 | 24 | 64 | 64 | 463 K | 100 M | |
| Inception(4d) | 14 × 14 × 528 | 2 | 112 | 144 | 288 | 32 | 64 | 64 | 580 K | 119 M | |
| Inception(4e) | 14 × 14 × 832 | 2 | 256 | 160 | 320 | 32 | 128 | 128 | 840 K | 170 M | |
| Max pool | 3 × 3/2 | 7 × 7 × 832 | 0 | ||||||||
| Inception(5a) | 7 × 7 × 832 | 2 | 256 | 160 | 320 | 32 | 128 | 128 | 1072 K | 54 M | |
| Inception(5b) | 7 × 7 × 1024 | 2 | 384 | 192 | 384 | 48 | 128 | 128 | 1388 K | 71 M | |
| Avg pool | 7 × 7/1 | 1 × 1 × 1024 | 0 | ||||||||
| Dropout(30%) | 1 × 1 × 1024 | 0 | |||||||||
| Linear | 1 × 1 × 1000 | 1 | 1000 K | 1 M | |||||||
| Softmax | 1 × 1 × 1000 | 0 |
| Network Structure | GoogLeNet | AlexNet | VGG-16 |
|---|---|---|---|
| Total number of tests | 26 | 26 | 26 |
| Detected correctly | 22 | 20 | 21 |
| Time | 1.269 | 0.6 | 2.8 |
| Accuracy | 84.6% | 76.9% | 80.77% |
| Method | Our Method | CNN | Improved CFAR |
|---|---|---|---|
| Target total number of tests | 20 | 20 | 20 |
| Detected correctly | 18 | 13 | 16 |
| 10% | 53.57% | 54.55% | |
| 10% | 35% | 25% | |
| 90% | 65% | 75% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Zhang, L.; Li, G. Shipborne HFSWR Target Detection in Clutter Regions Based on Multi-Frame TFI Correlation. Remote Sens. 2022, 14, 4192. https://doi.org/10.3390/rs14174192
Wang T, Zhang L, Li G. Shipborne HFSWR Target Detection in Clutter Regions Based on Multi-Frame TFI Correlation. Remote Sensing. 2022; 14(17):4192. https://doi.org/10.3390/rs14174192
Chicago/Turabian StyleWang, Tao, Ling Zhang, and Gangsheng Li. 2022. "Shipborne HFSWR Target Detection in Clutter Regions Based on Multi-Frame TFI Correlation" Remote Sensing 14, no. 17: 4192. https://doi.org/10.3390/rs14174192
APA StyleWang, T., Zhang, L., & Li, G. (2022). Shipborne HFSWR Target Detection in Clutter Regions Based on Multi-Frame TFI Correlation. Remote Sensing, 14(17), 4192. https://doi.org/10.3390/rs14174192