Are Indices of Polarimetric Purity Excellent Metrics for Object Identification in Scattering Media?
Abstract
:1. Introduction
2. Methods
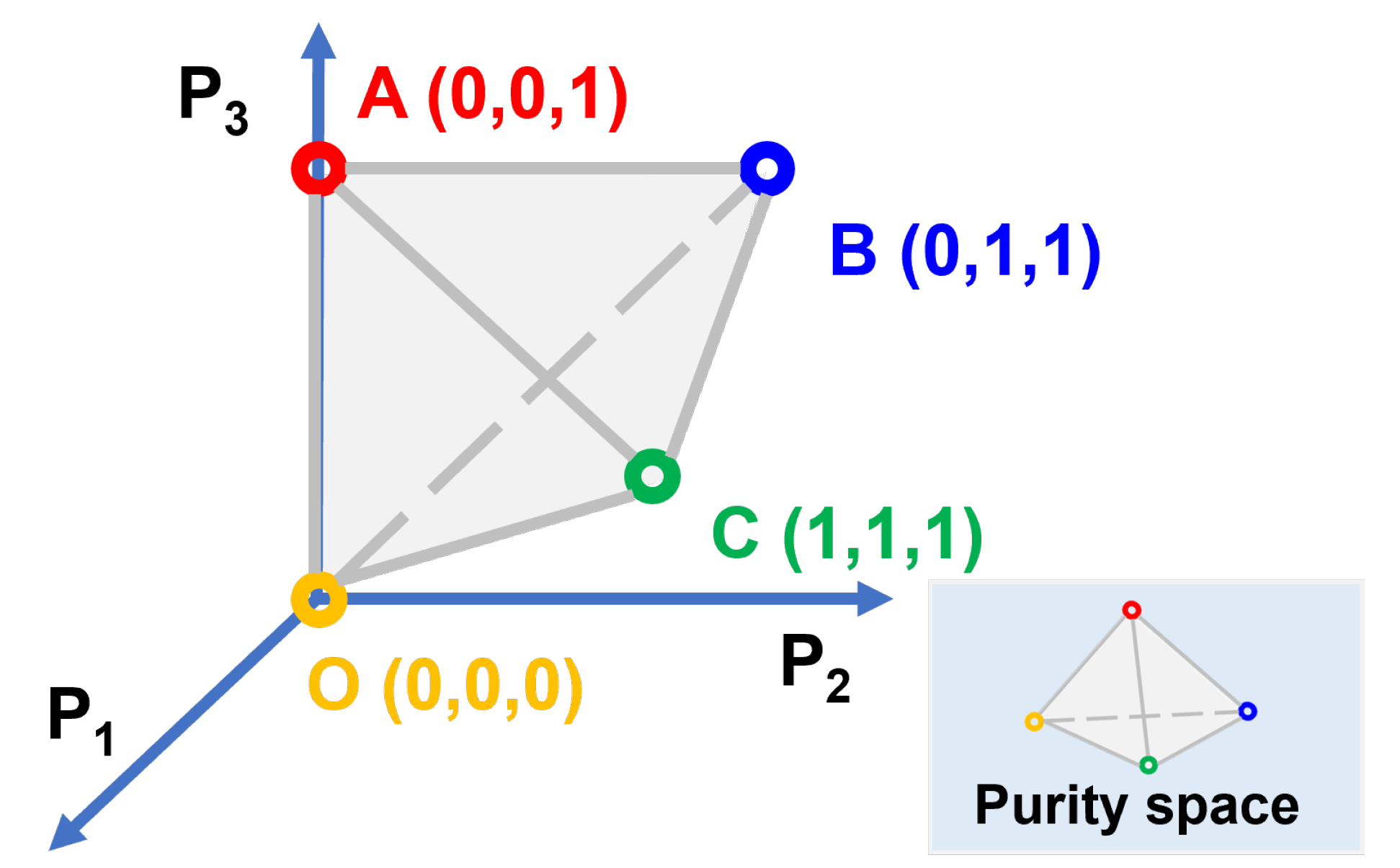
2.1. Mathematical Methods
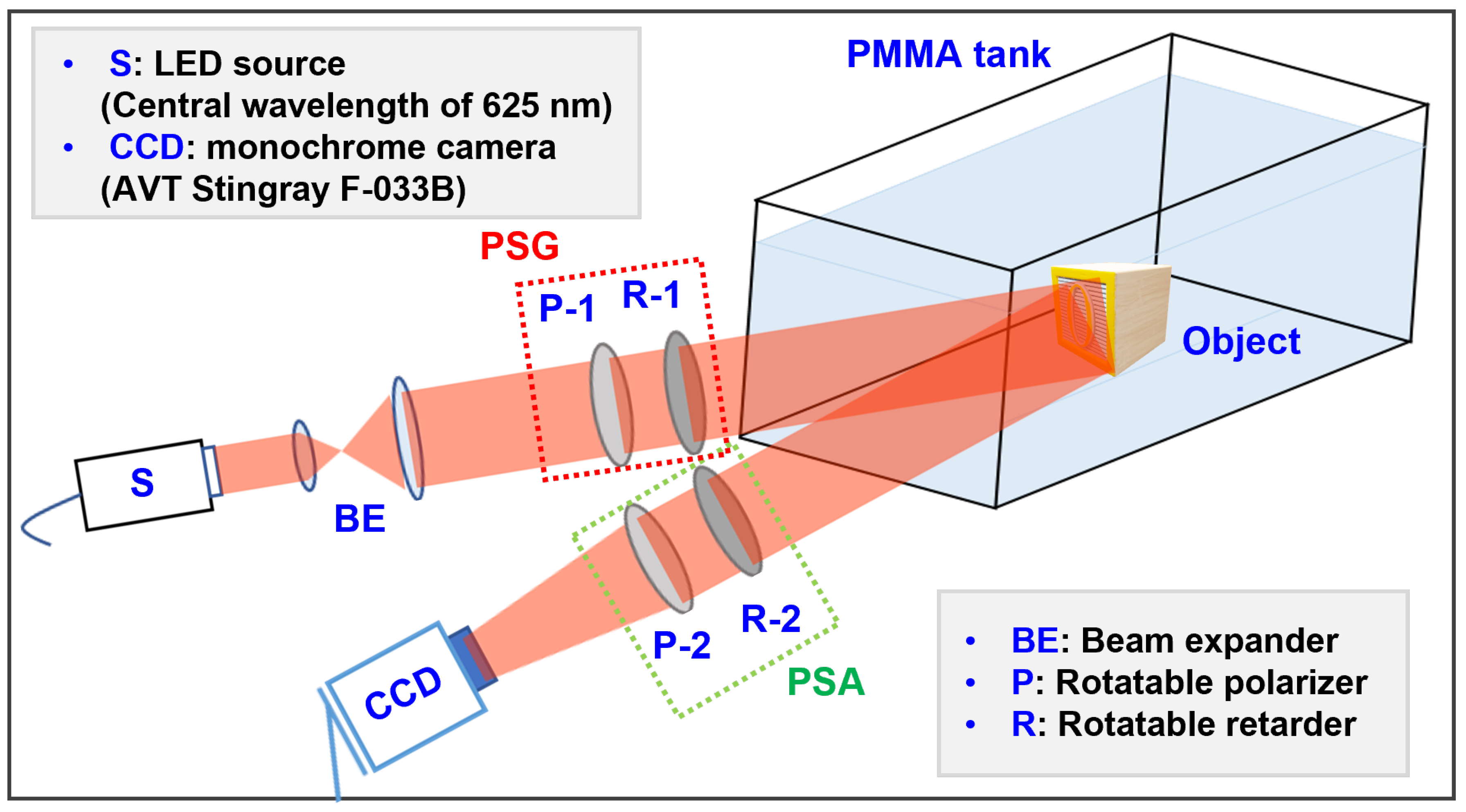
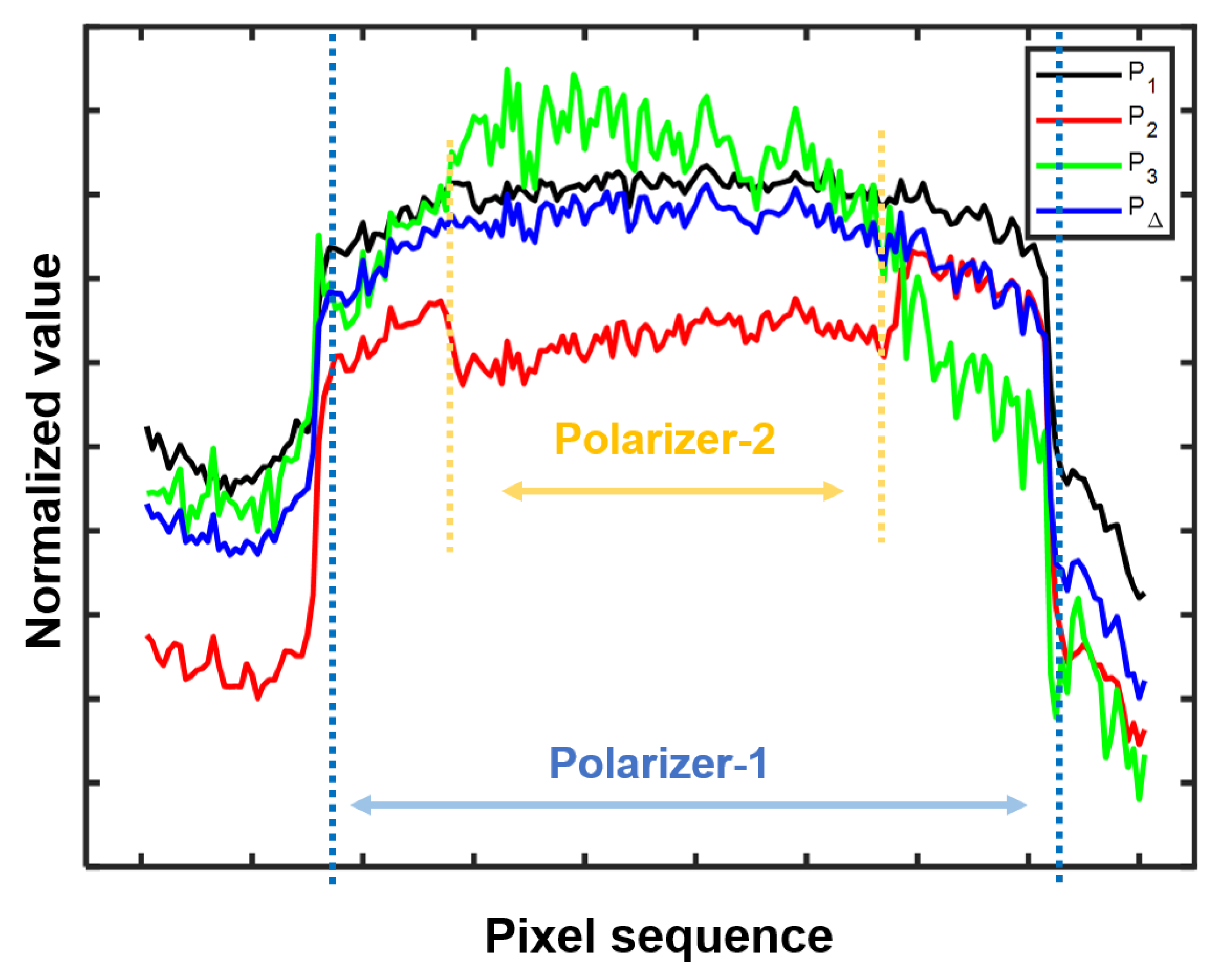
2.2. Mueller Matrix Imaging System
3. Results
3.1. Experiment-1: Imaging Example of MM and IPPs
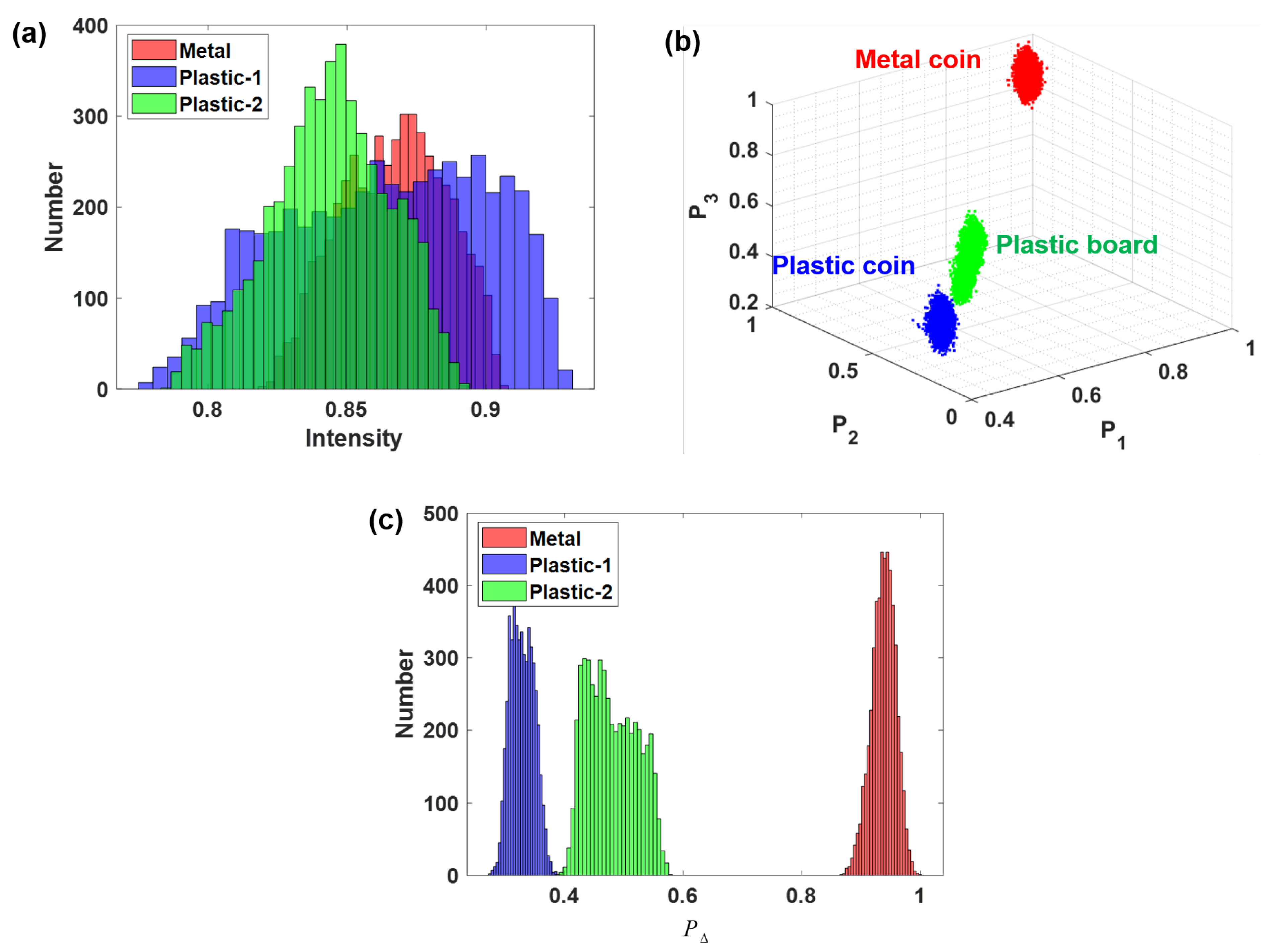
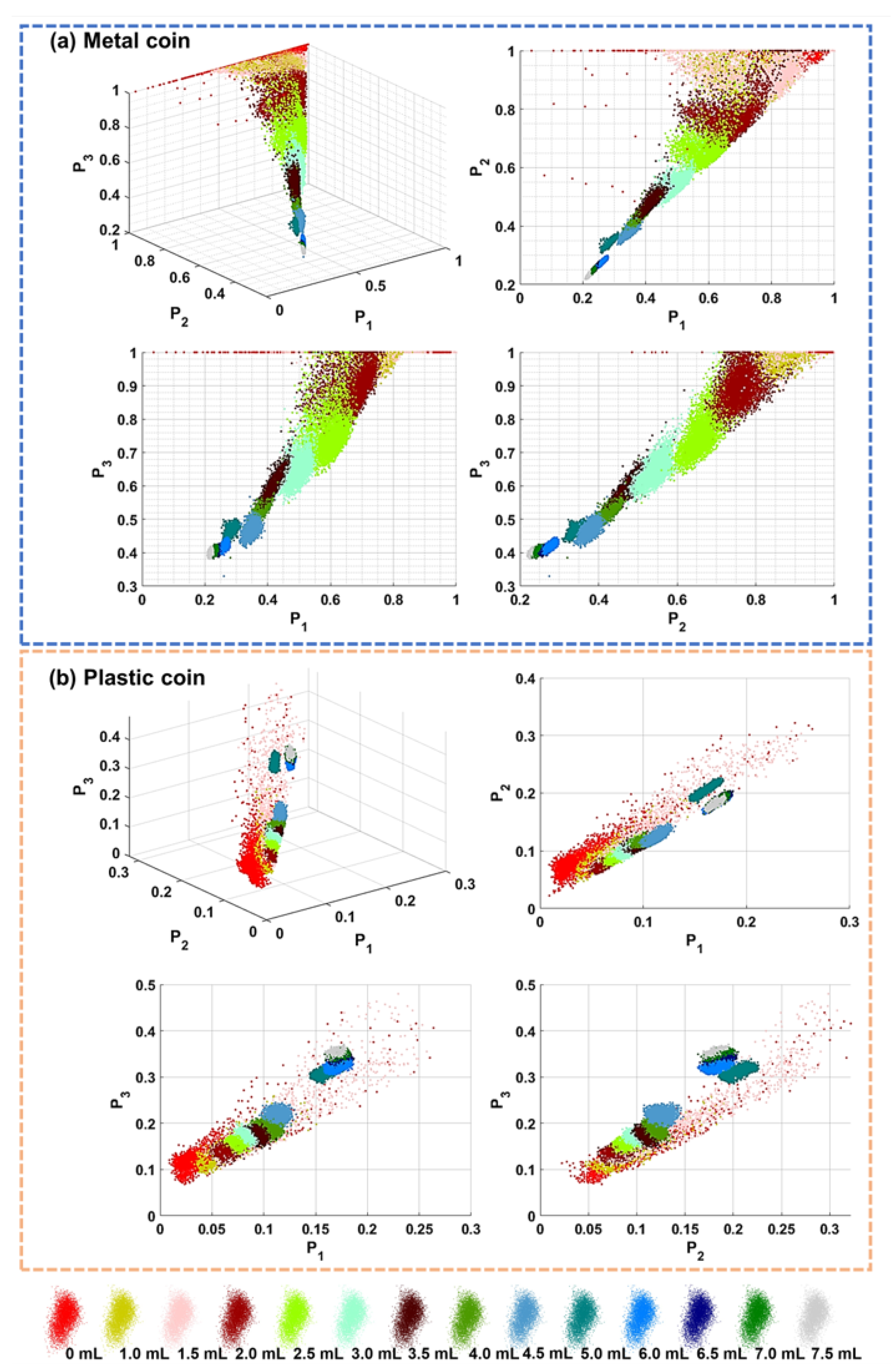
3.2. Experiment-2: Object Identification in a Strong Scattering Medium
3.3. Experiment-3: Comparison between IPPs and in Distinguishing Different Polarizations Information
4. Discussion
4.1. Enhancement for IPPs Images
4.2. A Simple Example of Applying IPPs in Remote Sensing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goldstein, D.H. Polarized Light; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Yan, L.; Li, Y.; Chandrasekar, V.; Mortimer, H.; Peltoniemi, J.; Lin, Y. General review of optical polarization remote sensing. Int. J. Remote Sens. 2020, 41, 4853–4864. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Yan, L.; Yang, B.; Zhang, F.; Xiang, Y.; Chen, W. Polarization Remote Sensing Physics; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Brosseau, C. Fundamentals of Polarized Light: A Statistical Optics Approach; Wiley-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Wang, X.; Hu, T.; Li, D.; Guo, K.; Gao, J.; Guo, Z. Performances of polarization-retrieve imaging in stratified dispersion media. Remote Sens. 2020, 12, 2895. [Google Scholar] [CrossRef]
- Schotland, R.M.; Sassen, K.; Stone, R. Observations by lidar of linear depolarization ratios for hydrometeors. J. Appl. Meteorol. Climatol. 1971, 10, 1011–1017. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Hu, H.; Zhao, L.; Wang, H.; Yu, Y.; Wu, L.; Liu, T. Polarimetric image recovery method combining histogram stretching for underwater imaging. Sci. Rep. 2018, 8, 12430. [Google Scholar] [CrossRef] [PubMed]
- Kong, Z.; Yin, Z.; Cheng, Y.; Li, Y.; Zhang, Z.; Mei, L. Modeling and evaluation of the systematic errors for the polarization-sensitive imaging lidar technique. Remote Sens. 2020, 12, 3309. [Google Scholar] [CrossRef]
- Tan, S.; Narayanan, R.M. Design and performance of a multiwavelength airborne polarimetric lidar for vegetation remote sensing. Appl. Opt. 2004, 43, 2360–2368. [Google Scholar] [CrossRef]
- Millard, K.; Richardson, M. Wetland mapping with LiDAR derivatives, SAR polarimetric decompositions, and LiDAR–SAR fusion using a random forest classifier. Can. J. Remote Sens. 2013, 39, 290–307. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Z.; Turnbull, J.; Song, Q.; Qi, F. Pol-SAR classification based on generalized polar decomposition of Mueller matrix. IEEE Geosci. Remote Sens. Lett. 2016, 13, 565–569. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Yajima, Y.; Yamada, H. A four-component decomposition of POLSAR images based on the coherency matrix. IEEE Geosci. Remote Sens. Lett. 2006, 3, 292–296. [Google Scholar] [CrossRef]
- Parikh, H.; Patel, S.; Patel, V. Classification of SAR and PolSAR images using deep learning: A review. Int. J. Image Data Fusion 2020, 11, 1–32. [Google Scholar] [CrossRef]
- Li, X.; Han, Y.; Wang, H.; Liu, T.; Chen, S.C.; Hu, H. Polarimetric Imaging Through Scattering Media: A Review. Front. Phys. 2022, 10, 815296. [Google Scholar] [CrossRef]
- Li, X.; Le Teurnier, B.; Boffety, M.; Liu, T.; Hu, H.; Goudail, F. Theory of autocalibration feasibility and precision in full Stokes polarization imagers. Opt. Express 2020, 28, 15268–15283. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, W.; Goudail, F.; Chen, S.C. Optimal nonlinear Stokes–Mueller polarimetry for multi-photon processes. Opt. Lett. 2022, 47, 3287–3290. [Google Scholar] [CrossRef]
- Li, X.; Hu, H.; Liu, T.; Huang, B.; Song, Z. Optimal distribution of integration time for intensity measurements in degree of linear polarization polarimetry. Opt. Express 2016, 24, 7191–7200. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Hu, H.; Wang, H.; Wu, L.; Liu, T.G. Influence of noise statistics on optimizing the distribution of integration time for degree of linear polarization polarimetry. Opt. Eng. 2018, 57, 064110. [Google Scholar] [CrossRef]
- Liang, J.; Ren, L.; Ju, H.; Zhang, W.; Qu, E. Polarimetric dehazing method for dense haze removal based on distribution analysis of angle of polarization. Opt. Express 2015, 23, 26146–26157. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Chen, S.C. Enhanced polarization demosaicking network via a precise angle of polarization loss calculation method. Opt. Lett. 2022, 47, 1065–1069. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, B.; He, C.; He, H.; Guo, J.; Wu, J.; Elson, D.S.; Ma, H. Polarization Aberrations in High-Numerical-Aperture Lens Systems and Their Effects on Vectorial-Information Sensing. Remote Sens. 2022, 14, 1932. [Google Scholar] [CrossRef]
- Dong, Q.; Huang, Z.; Li, W.; Li, Z.; Song, X.; Liu, W.; Wang, T.; Bi, J.; Shi, J. Polarization Lidar Measurements of Dust Optical Properties at the Junction of the Taklimakan Desert–Tibetan Plateau. Remote Sens. 2022, 14, 558. [Google Scholar] [CrossRef]
- Yan, L.; Li, Y.; Chen, W.; Lin, Y.; Zhang, F.; Wu, T.; Peltoniemi, J.; Zhao, H.; Liu, S.; Zhang, Z. Temporal and Spatial Characteristics of the Global Skylight Polarization Vector Field. Remote Sens. 2022, 14, 2193. [Google Scholar] [CrossRef]
- Garcia, M.; Edmiston, C.; Marinov, R.; Vail, A.; Gruev, V. Bio-inspired color-polarization imager for real-time in situ imaging. Optica 2017, 4, 1263–1271. [Google Scholar] [CrossRef]
- Wang, X.; Gao, J.; Roberts, N.W. Bio-inspired orientation using the polarization pattern in the sky based on artificial neural networks. Opt. Express 2019, 27, 13681–13693. [Google Scholar] [CrossRef] [PubMed]
- Powell, S.B.; Garnett, R.; Marshall, J.; Rizk, C.; Gruev, V. Bioinspired polarization vision enables underwater geolocalization. Sci. Adv. 2018, 4, eaao6841. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dacke, M.; Nilsson, D.E.; Scholtz, C.H.; Byrne, M.; Warrant, E.J. Insect orientation to polarized moonlight. Nature 2003, 424, 33. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.; Li, Y.; Mortimer, H.; Zhang, R.; Peltoniemi, J.; Liu, X.; Zhang, F. Optical polarized effects for quantitative remote sensing. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B1, 593–598. [Google Scholar] [CrossRef]
- Li, X.; Goudail, F.; Chen, S.C. Self-calibration for Mueller polarimeters based on DoFP polarization imagers. Opt. Lett. 2022, 47, 1415–1418. [Google Scholar] [CrossRef]
- Zhai, P.W.; Kattawar, G.W.; Yang, P. Mueller matrix imaging of targets under an air–sea interface. Appl. Opt. 2009, 48, 250–260. [Google Scholar] [CrossRef]
- Li, X.; Xu, J.; Zhang, L.; Hu, H.; Chen, S.C. Underwater image restoration via Stokes decomposition. Opt. Lett. 2022, 47, 2854–2857. [Google Scholar] [CrossRef]
- Hielscher, A.H.; Eick, A.A.; Mourant, J.R.; Shen, D.; Freyer, J.P.; Bigio, I.J. Diffuse backscattering Mueller matrices of highly scattering media. Opt. Express 1997, 1, 441–453. [Google Scholar] [CrossRef]
- Raković, M.J.; Kattawar, G.W. Theoretical analysis of polarization patterns from incoherent backscattering of light. Appl. Opt. 1998, 37, 3333–3338. [Google Scholar] [CrossRef]
- Gil, J.J. Review on Mueller matrix algebra for the analysis of polarimetric measurements. J. Appl. Remote Sens. 2014, 8, 081599. [Google Scholar] [CrossRef]
- Manhas, S.; Swami, M.K.; Buddhiwant, P.; Ghosh, N.; Gupta, P.; Singh, K. Mueller matrix approach for determination of optical rotation in chiral turbid media in backscattering geometry. Opt. Express 2006, 14, 190–202. [Google Scholar] [CrossRef] [PubMed]
- Berezhnyy, I.; Dogariu, A. Time-resolved Mueller matrix imaging polarimetry. Opt. Express 2004, 12, 4635–4649. [Google Scholar] [CrossRef]
- Cariou, J.; Le Jeune, B.; Lotrian, J.; Guern, Y. Polarization effects of seawater and underwater targets. Appl. Opt. 1990, 29, 1689–1695. [Google Scholar] [CrossRef]
- Borovkova, M.; Peyvasteh, M.; Dubolazov, O.; Ushenko, Y.; Ushenko, V.; Bykov, A.; Deby, S.; Rehbinder, J.; Novikova, T.; Meglinski, I. Complementary analysis of Mueller-matrix images of optically anisotropic highly scattering biological tissues. J. Eur. Opt.-Soc.-Rapid Publ. 2018, 14, 1–8. [Google Scholar] [CrossRef]
- Lu, S.Y.; Chipman, R.A. Interpretation of Mueller matrices based on polar decomposition. J. Opt. Soc. Am. A 1996, 13, 1106–1113. [Google Scholar] [CrossRef]
- Van Eeckhout, A.; Lizana, A.; Garcia-Caurel, E.; Gil, J.J.; Sansa, A.; Rodríguez, C.; Estévez, I.; González, E.; Escalera, J.C.; Moreno, I.; et al. Polarimetric imaging of biological tissues based on the indices of polarimetric purity. J. Biophotonics 2018, 11, e201700189. [Google Scholar] [CrossRef]
- Wang, P.; Li, D.; Wang, X.; Guo, K.; Sun, Y.; Gao, J.; Guo, Z. Analyzing polarization transmission characteristics in foggy environments based on the indices of polarimetric purity. IEEE Access 2020, 8, 227703–227709. [Google Scholar] [CrossRef]
- San José, I.; Gil, J.J. Invariant indices of polarimetric purity: Generalized indices of purity for n × n covariance matrices. Opt. Commun. 2011, 284, 38–47. [Google Scholar] [CrossRef] [Green Version]
- Shen, F.; Zhang, M.; Guo, K.; Zhou, H.; Peng, Z.; Cui, Y.; Wang, F.; Gao, J.; Guo, Z. The depolarization performances of scattering systems based on the Indices of Polarimetric Purity (IPPs). Opt. Express 2019, 27, 28337–28349. [Google Scholar] [CrossRef]
- Tariq, A.; Li, P.; Chen, D.; Lv, D.; Ma, H. Physically realizable space for the purity-depolarization plane for polarized light scattering media. Phys. Rev. Lett. 2017, 119, 033202. [Google Scholar] [CrossRef] [PubMed]
- Gil, J.J. Structure of polarimetric purity of a Mueller matrix and sources of depolarization. Opt. Commun. 2016, 368, 165–173. [Google Scholar] [CrossRef] [Green Version]
- Gil, J.J.; San José, I. Polarimetric subtraction of Mueller matrices. J. Opt. Soc. Am. A 2013, 30, 1078–1088. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Caurel, E.; Ossikovski, R.; Foldyna, M.; Pierangelo, A.; Drévillon, B.; Martino, A.D. Advanced Mueller ellipsometry instrumentation and data analysis. In Ellipsometry at the Nanoscale; Losurdo, M., Hingerl, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 31–143. [Google Scholar]
- Gil, J.J.; San José, I. Reduced form of a Mueller matrix. J. Mod. Opt. 2016, 63, 1579–1583. [Google Scholar] [CrossRef] [Green Version]
- Ossikovski, R. Analysis of depolarizing Mueller matrices through a symmetric decomposition. J. Opt. Soc. Am. A 2009, 26, 1109–1118. [Google Scholar] [CrossRef]
- Ossikovski, R.; Al Bugami, B.; Garcia-Caurel, E.; Cloude, S.R. Polarizer calibration method for Mueller matrix polarimeters. Appl. Opt. 2020, 59, 10389–10395. [Google Scholar] [CrossRef] [PubMed]
- Gil, J.J.; Bernabeu, E. Depolarization and polarization indices of an optical system. Opt. Acta Int. J. Opt. 1986, 33, 185–189. [Google Scholar] [CrossRef]
- Gil, J.J. Polarimetric characterization of light and media: Physical quantities involved in polarimetric phenomena. Eur. Phys.-J.-Appl. Phys. 2007, 40, 1–47. [Google Scholar] [CrossRef]
- Van Eeckhout, A.; Lizana, A.; Garcia-Caurel, E.; Gil, J.J.; Ossikovski, R.; Campos, J. Synthesis and characterization of depolarizing samples based on the indices of polarimetric purity. Opt. Lett. 2017, 42, 4155–4158. [Google Scholar] [CrossRef]
- Gil, J.J. Components of purity of a Mueller matrix. J. Opt. Soc. Am. A 2011, 28, 1578–1585. [Google Scholar] [CrossRef]
- Dubreuil, M.; Delrot, P.; Leonard, I.; Alfalou, A.; Brosseau, C.; Dogariu, A. Exploring underwater target detection by imaging polarimetry and correlation techniques. Appl. Opt. 2013, 52, 997–1005. [Google Scholar] [CrossRef] [PubMed]
- Bicout, D.; Brosseau, C.; Martinez, A.S.; Schmitt, J.M. Depolarization of multiply scattered waves by spherical diffusers: Influence of the size parameter. Phys. Rev. E 1994, 49, 1767. [Google Scholar] [CrossRef] [PubMed]
- Dumont, E.; Cavallo, V. Extended photometric model of fog effects on road vision. Transp. Res. Rec. 2004, 1862, 77–81. [Google Scholar] [CrossRef]
- Li, X.; Hu, H.; Zhao, L.; Wang, H.; Han, Q.; Cheng, Z.; Liu, T. Pseudo-polarimetric method for dense haze removal. IEEE Photonics J. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Reza, A.M. Realization of the contrast limited adaptive histogram equalization (CLAHE) for real-time image enhancement. J. VLSI Signal Process. Syst. Signal Image Video Technol. 2004, 38, 35–44. [Google Scholar] [CrossRef]
- Zuiderveld, K. Contrast limited adaptive histogram equalization. Graph. Gems 1994, 474–485. [Google Scholar]
- Hitam, M.S.; Awalludin, E.A.; Yussof, W.N.J.H.W.; Bachok, Z. Mixture contrast limited adaptive histogram equalization for underwater image enhancement. In Proceedings of the 2013 International Conference on Computer Applications Technology (ICCAT), Sousse, Tunisia, 20–22 January 2013; pp. 1–5. [Google Scholar]
- Liang, J.; Ren, L.; Liang, R. Low-pass filtering based polarimetric dehazing method for dense haze removal. Opt. Express 2021, 29, 28178–28189. [Google Scholar] [CrossRef]
- Qi, P.; Li, X.; Han, Y.; Zhang, L.; Xu, J.; Cheng, Z.; Liu, T.; Zhai, J.; Hu, H. U2R-pGAN: Unpaired underwater-image recovery with polarimetric generative adversarial network. Opt. Lasers Eng. 2022, 157, 107112. [Google Scholar] [CrossRef]
- Hu, H.; Han, Y.; Li, X.; Jiang, L.; Che, L.; Liu, T.; Zhai, J. Physics-informed neural network for polarimetric underwater imaging. Opt. Express 2022, 30, 22512–22522. [Google Scholar] [CrossRef]
- Li, X.; Hu, H.; Goudail, F.; Liu, T. Fundamental precision limits of full Stokes polarimeters based on DoFP polarization cameras for an arbitrary number of acquisitions. Opt. Express 2019, 27, 31261–31272. [Google Scholar] [CrossRef]
- Huang, T.; Meng, R.; Qi, J.; Liu, Y.; Wang, X.; Chen, Y.; Liao, R.; Ma, H. Fast Mueller matrix microscope based on dual DoFP polarimeters. Opt. Lett. 2021, 46, 1676–1679. [Google Scholar] [CrossRef] [PubMed]
- Gottlieb, D.; Arteaga, O. Mueller matrix imaging with a polarization camera: Application to microscopy. Opt. Express 2021, 29, 34723–34734. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Lin, Y.; Li, X.; Qi, P.; Liu, T. IPLNet: A neural network for intensity-polarization imaging in low light. Opt. Lett. 2020, 45, 6162–6165. [Google Scholar] [CrossRef]
- Maitra, S. Analysis of Polarimetric Synthetic Aperture Radar and Passive Visible Light Polarimetric Imaging Data Fusion for Remote Sensing Applications; Rochester Institute of Technology: Rochester, NY, USA, 2013. [Google Scholar]
- Farage, G.; Foucher, S.; Benie, G. Comparison of PolSAR speckle filtering techniques. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 1760–1763. [Google Scholar]
- Ren, Y.; Yang, J.; Zhao, L.; Li, P.; Shi, L. SIRV-based high-resolution PolSAR image speckle suppression via dual-domain filtering. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5923–5938. [Google Scholar] [CrossRef]
- Lee, J.S.; Ainsworth, T.L.; Wang, Y.; Chen, K.S. Polarimetric SAR speckle filtering and the extended sigma filter. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1150–1160. [Google Scholar] [CrossRef]






| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| PSG | ||||
| PSA |
| A–B | 0.002 | 0.481 | 0.355 | 0.549 | 0.426 | 0.317 |
| A–C | 0.014 | 0.323 | 0.242 | 0.383 | 0.277 | 0.396 |
| B–C | 0.011 | 0.187 | 0.124 | 0.211 | 0.169 | 0.091 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, L.; Qi, P.; Zhu, Z.; Xu, J.; Liu, T.; Zhai, J.; Hu, H. Are Indices of Polarimetric Purity Excellent Metrics for Object Identification in Scattering Media? Remote Sens. 2022, 14, 4148. https://doi.org/10.3390/rs14174148
Li X, Zhang L, Qi P, Zhu Z, Xu J, Liu T, Zhai J, Hu H. Are Indices of Polarimetric Purity Excellent Metrics for Object Identification in Scattering Media? Remote Sensing. 2022; 14(17):4148. https://doi.org/10.3390/rs14174148
Chicago/Turabian StyleLi, Xiaobo, Liping Zhang, Pengfei Qi, Zhiwei Zhu, Jianuo Xu, Tiegen Liu, Jingsheng Zhai, and Haofeng Hu. 2022. "Are Indices of Polarimetric Purity Excellent Metrics for Object Identification in Scattering Media?" Remote Sensing 14, no. 17: 4148. https://doi.org/10.3390/rs14174148
APA StyleLi, X., Zhang, L., Qi, P., Zhu, Z., Xu, J., Liu, T., Zhai, J., & Hu, H. (2022). Are Indices of Polarimetric Purity Excellent Metrics for Object Identification in Scattering Media? Remote Sensing, 14(17), 4148. https://doi.org/10.3390/rs14174148









