Polarized Intensity Ratio Constraint Demosaicing for the Division of a Focal-Plane Polarimetric Image

Abstract

Polarization is an independent dimension of light wave information that has broad application prospects in machine vision and remote sensing tasks. Polarization imaging using a division-of-focal-plane (DoFP) polarimetric sensor can meet lightweight and real-time application requirements. Similar to Bayer filter-based color imaging, demosaicing is a basic and important processing step in DoFP polarization imaging. Due to the differences in the physical properties of polarization and the color of light waves, the widely studied color demosaicing method cannot be directly applied to polarization demosaicing. We propose a polarized intensity ratio constraint demosaicing model to efficiently account for the characteristics of polarization detection in this work. First, we discuss the special constraint relationship between the polarization channels. It can be simply described as: for a beam of light, the sum of the intensities detected by any two vertical ideal analyzers should be equal to the total light intensity. Then, based on this constraint relationship and drawing on the concept of guided filtering, a new polarization demosaicing method is developed. A method to directly use raw images captured by the DoFP detector as the ground truth for comparison experiments is then constructed to aid in the convenient collection of experimental data and extensive image scenarios. Results of both qualitative and quantitative experiments illustrate that our method is an effective and practical method to faithfully recover the full polarization information of each pixel from a single mosaic input image.

1. Introduction

1.1. Background

Polarization, together with intensity, frequency, and phase, constitute the basic properties of light from the perspective of waves. Both intensity, which corresponds to brightness, and frequency, which corresponds to color or spectrum, have been widely researched and applied in the fields of vision and remote sensing. The research and application of polarization imaging and processing have developed gradually in recent years. As a new information dimension, polarization information has a significant role in computer vision and remote sensing tasks, providing an essential function in some respects. It has been widely used in tasks such as object detection [1,2], image haze removal [3,4], underwater image enhancement [5], and 3D reconstruction [6,7].

The polarization imaging methods mainly include division of time (DoT), division of amplitude (DoAM), division of aperture (DoAP), and division of focal plane (DoFP) [8]. However, DoT is not capable of real-time imaging, whereas DoAM and DoAP suffer from complex and heavy structures. The DoFP polarization imaging sensor is composed of a micropolarization array (MPA) oriented at 0°, 45°, 90°, and 135° (shown in Figure 1, left). Thus, it can capture linear polarization information in one shot and its structure is simple. However, the DoFP sensor trades polarization information at the expense of spatial resolution, which is similar to color detectors based on the Bayer filter. The raw image obtained by a DoFP or Bayer filter-based sensor is called a mosaic image (seen in Figure 1, right). The goal of demosaicing is to restore a full-size multi-channel image from a raw mosaic image.

Bayer filter-based color image demosaicing has been widely studied and applied in recent decades, and it is an important component of color image processing. However, the research on polarized image demosaicing is still relatively scarce. Although we can learn about polarized image demosaicing from color image demosaicing, it is not exactly the same because color and polarization information have different constraints between adjacent pixels. Comprehensive color science research provides a priori information for color image demosaicing, such as the color difference model [9,10]. Polarized image demosaicing should also fully utilize the inherent physical prior knowledge of polarization detection, which is not fully considered in traditional interpolation methods and explains why they do not perform well on polarized mosaic images.

1.2. Related Work

Demosaicing originated from color image processing. Single-sensor color imaging technology with a color filter array (CFA) is widely used in the digital camera industry. The most popular and widely used CFA is the Bayer CFA, which was released in 1976 [11]. Polarization filter array (PFA) technology was patented in 1995 [12], but most of the practical implementations and technology advances were made between 2009 and now [13]. In recent years, some PFA cameras have appeared on the market, such as 4D Technology’s PolarCam device [14] and Sony’s IMX250MZR polarization-dedicated sensor (Tokyo, Japan) [15]. Although research on color image demosaicing has a long history, research into polarization demosaicing has only recently begun. In this section, we provide an overview of both color image and polarized image demosaicing.

1.2.1. Color Image Demosaicing

Color image demosaicing can be divided into spatial interpolation, frequency-based methods, and data-driven methods. Data-driven methods include sparse representation and neural networks. Spatial interpolation-based demosaicing interpolates along multiple directions to efficiently utilize both interchannel and intrachannel correlations [10,16,17,18]. Frequency selection-based demosaicing takes advantage of the spectral characteristics of raw images [19,20,21]. Sparse representation-based demosaicing considers demosaicing as an inverse problem and exploits sparsity prior by decomposing each image patch into a sparse representation over a dictionary [22,23]. The neural network method uses a large amount of data to train a neural network to estimate the missing pixels [24]. Past experiments and studies have shown that the spatial domain method is more advantageous than the frequency domain method [9]. Although the data-driven method performs well, its recovery effect is extremely dependent on the relevance of training and verification data, meaning it is difficult to widely adapt to complex and changeable actual scenes.

1.2.2. Polarized Image Demosaicing

Polarized image demosaicing is different from color image demosaicing in two main ways. (1) CFA has three channels, so there are two G pixels in every 2 × 2 pixel block. That is, the sampling rate of G is twice that of R and B. In contrast, PFA has four channels, thus the sampling rate of each channel is the same. (2) The signal between CFA channels is constrained by spectral information, and the signal between PFA channels is constrained by polarization information. The first difference means that the common method of first restoring the double-sampled G channel in color image demosaicing is not applicable to polarized images. The second difference means that the color difference model [9,10] of color images does not apply to polarized images.

In recent years, some polarization demosaicing algorithms have been proposed with reference to the superior algorithms in color image demosaicing. Traditional bilinear and bicubic interpolation methods were first used in [25], a gradient-based interpolation method was proposed in [26], an intensity correlation interpolation method was proposed in [27], a polarization channel difference prior method was proposed in [28], and an edge-aware residual interpolation was proposed in [29]. A guided filter [30] works well for color image demosaicing [10], and it is also used in polarization demosaicing [31,32,33,34]. In this paper, a derivative guided filtering method is proposed, which is different from the original guided filter [30] and is more suitable for the constraint relationship between polarization channels. Learning-based image processing methods, neural networks [35,36], and sparse representation-based methods [37,38] have been used to solve this problem. However, such methods usually require datasets to support them. Thus, the quality of the processing result depends on the similarity between the image to be processed and the image training set.

1.3. Contribution

In this paper, we propose a polarized intensity ratio constraint (PIRC) demosaicing method to restore high-quality four-channel polarized images from one-channel mosaic observations captured by a single-chip DoFP polarized sensor. The physical constraint of the PIRC is simple: for a beam of light, the sum of the intensities detected by any two vertical ideal analyzers should be equal to the total light intensity. Based on this constraint, this paper draws on the guided filtering method and proposes a specific cost function for polarization demosaicing. This technique not only considers the texture relationship between pixels but also considers the relationship of polarization information between channels.

The main contributions of this paper are summarized as follows: (1) The actual physical constraints between polarization imaging channels are identified. (2) A PIRC polarization demosaicing method is proposed that considers both the constraints between channels and the relationship between pixels. (3) A method is designed that directly employs raw images as ground truth for comparison experiments, instead of using additional methods to obtain the ground truth. This process facilitates the convenient collection of experimental data with more extensive data scenarios. (4) Extensive experiments are carried out to demonstrate that our proposed method achieves state-of-the-art results.

The remainder of this paper is organized as follows. Section 2 presents the polarized intensity ratio constraint of the polarized image and details the proposed method, Section 3 shows the experiment results, Section 4 discusses the results, and Section 5 concludes the paper.

2. Materials and Methods

2.1. The Constraint of Detected Polarized Intensity

The special constraint relationship between the polarization channels is discussed before introducing our polarization demosaicing method. This relationship is typically overlooked by researchers. Natural light can be regarded as a superposition of a large number of single polarization-state monochromatic lights. A single polarization-state monochromatic plane light wave propagating along the z-axis can be expressed as:

$$\mathit{E}=\mathit{A}\cos (kz-\omega t)$$

(1)

where $\mathit{E}$ is the wave function, $\mathit{A}=A\mathit{a}$ is the amplitude vector of the electric field, $\mathit{a}$ is the unit vector describing the vibration direction, $A$ is the scalar describing the amplitude value, $k=2\pi /\lambda$ is the wavenumber, $\omega =2\pi /T$ is the angular frequency, and $T$ is the vibration period of the light wave. The light intensity $I$ is equal to the square of the electric field amplitude:

$$I={\left|\mathit{A}\right|}^2$$

(2)

E can be decomposed to any two orthogonal components in the O-xy plane. If the decomposition is on the xy-axis, then Equation (1) can be expressed in scalar form:

$$\{\begin{array}{c}{E}_x=A_x\cos (kz-\omega t+{\delta }_x)\\ E_y=A_y\cos (kz-\omega t+{\delta }_y)\end{array}$$

(3)

where $A_x=\left|\mathit{A}\right|\cdot \cos \theta$, $A_y=\left|\mathit{A}\right|\cdot \cos (\frac{\pi }{2}-\theta )$, and $\theta$ represents the angle between $\mathit{A}$ and the x-axis. If the light intensity of each polarization direction is detected under ideal conditions, the following relationships are present:

$$I_x+I_y=A_x{}^2+A_y{}^2={(\left|\mathit{A}\right|\cdot \cos \theta )}^2+{(\left|\mathit{A}\right|\cdot \cos (\frac{\pi }{2}-\theta ))}^2={\left|\mathit{A}\right|}^2\cdot ({\cos }^2\theta +{\sin }^2\theta )=I$$

(4)

According to the above principle, when a beam of linearly polarized light passes through the analyzers with the optical axis directions of 0°, 45°, 90°, and 135° (the 0° direction coincides with the x-axis), the transmitted light intensity should be:

$$\{\begin{array}{l}{I}^{0^{\circ }}=I{\cos }^2(\theta -0^{\circ })=I{\cos }^2\theta =aI\\ I^{{45}^{\circ }}=I{\cos }^2(\theta -{45}^{\circ })=I{\cos }^2(\theta -\frac{\pi }{4})=cI\\ I^{{90}^{\circ }}=I{\cos }^2(\theta -{90}^{\circ })=I{\cos }^2(\theta -\frac{\pi }{2})=(1-a)I\\ I^{{135}^{\circ }}=I{\cos }^2(\theta -{135}^{\circ })=I{\cos }^2(\theta -\frac{\pi }{4}-\frac{\pi }{2})=(1-c)I\end{array}$$

(5)

where $a={\cos }^2\theta$ and $c={\cos }^2(\theta -\frac{\pi }{4})$. From Equation (5), we can obtain:

$$I^{0^{\circ }}+I^{{90}^{\circ }}=I^{{45}^{\circ }}+I^{{135}^{\circ }}=I$$

(6)

If we consider the natural light formed by the noninterference superposition of light of multiple polarization states, Equation (5) can be expressed as:

$$\{\begin{array}{l}{I}^{0^{\circ }}={\displaystyle \sum _k^N{I}_k{\cos }^2{\theta }_k}={\displaystyle \sum _k^N{a}_k{I}_k}\\ I^{{45}^{\circ }}={\displaystyle \sum _k^N{I}_k{\cos }^2({\theta }_k-\frac{\pi }{4})}={\displaystyle \sum _k^N{c}_k{I}_k}\\ I^{{90}^{\circ }}={\displaystyle \sum _k^N{I}_k{\cos }^2({\theta }_k-\frac{\pi }{2})}={\displaystyle \sum _k^N(1-a_k)I_k}\\ I^{{135}^{\circ }}={\displaystyle \sum _k^N{I}_k{\cos }^2({\theta }_k-\frac{\pi }{4}-\frac{\pi }{2})}={\displaystyle \sum _k^N(1-c_k)I_k}\end{array}$$

(7)

According to Equation (7), when natural light is incident, Equation (6) still holds:

$$I^{0^{\circ }}+I^{{90}^{\circ }}=I^{{45}^{\circ }}+I^{{135}^{\circ }}={\displaystyle \sum _k^N{I}_k=}I$$

(8)

that is:

$$\{\begin{array}{l}{I}^{0^{\circ }}=aI\\ I^{{45}^{\circ }}=cI\\ I^{{90}^{\circ }}=(1-a)I\\ I^{{135}^{\circ }}=(1-c)I\end{array}$$

(9)

In the above discussion, the polarimetric extinction ratio and transmittance of the analyzer are assumed to be ideal. In reality, the analyzer is not an ideal one. In order to describe this error, a small offset term should be added to Equation (9):

$$\{\begin{array}{l}{I}^{0^{\circ }}=aI+{\Delta }_1\\ I^{{45}^{\circ }}=cI+{\Delta }_2\\ I^{{90}^{\circ }}=(1-a)I+{\Delta }_3\\ I^{{135}^{\circ }}=(1-c)I+{\Delta }_4\end{array}$$

(10)

Equation (10) describes the constraint relationship between the polarized light intensity observed in the 0°, 45°, 90°, and 135° directions and the total light intensity, which is the starting point of the DoFP polarimetric demosaicing method proposed in this paper.

2.2. Polarized Intensity Ratio Constraint Demosaicing Method

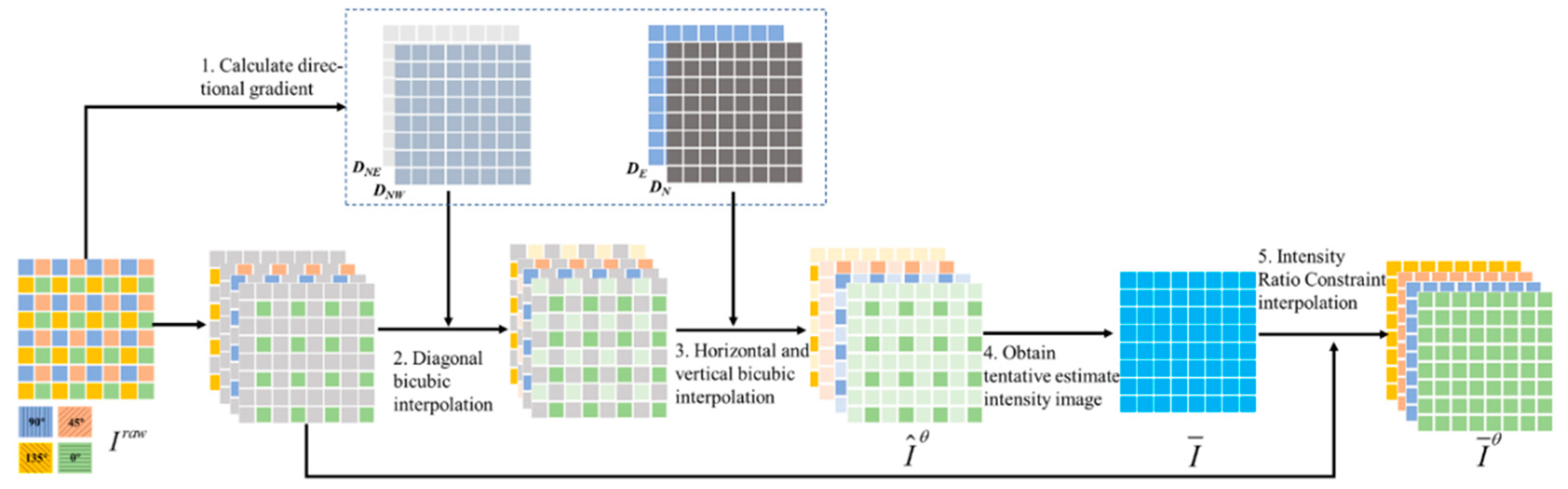
Based on the constraint relationship between polarization channels discussed in Section 3, we propose a new polarized intensity ratio constraint (PIRC) demosaicing method. Our fundamental goal is the following: the image texture and polarization state of each pixel are maintained. Thus, the proposed PIRC demosaicing method is divided into two main steps. First, the intensity image is obtained. The recovered intensity image is expected to retain the truthful image texture; thus, the relationship between neighboring pixels must be fully considered. To achieve this, a directional gradient-based method is applied to interpolate each polarization channel, a tentative estimation value of each polarization channel is obtained, and the full intensity is half of the sum of four channels. Second, based on the full intensity image, each polarization channel is recovered by a mutated guided filter method. The full process is shown in Figure 2. In brief, we apply gradient filtering to the raw images in each channel to obtain tentative values of intensity with each polarization azimuth in any given pixel, and then apply the derived guided filtering to calculate the final estimated value.

In the subsequent description, $I_{i,j}^{\theta }$ without a cap indicates the actual detected polarized light intensity in the $\theta$ direction by the pixel (i, j); ${\widehat{I}}_{i,j}^{\theta }$ with the cap “$\widehat{}$” is the tentative estimate value; and ${\overline{I}}_{i,j}^{\theta }$ with the cap “$\overline{}$” is the final estimate value.

2.2.1. Recover the Intensity Image by Image Gradient

Only one of the polarization directions is detected for each pixel (i, j) of the raw image. Based on the relationship in Equation (10), if its perpendicular direction is estimated, then the full intensity $I_{i,j}$ of location (i, j) can be estimated. For example, when the $I_{i,j}^{45}$ is detected at the location (i, j), the full intensity ${\widehat{I}}_{i,j}$ can be obtained by adding the detected $I_{i,j}^{45}$ to the tentatively estimated ${\widehat{I}}_{i,j}^{135}$. As illustrated in Figure 1, for each pixel (i, j), the four diagonal adjacent pixels are in the perpendicular polarization direction, and the vertical and horizontal adjacent pixels are in two other polarization directions. In order to make full use of the relationship between adjacent pixels, three nondetected polarization directions should be tentatively estimated in each pixel. Thus, the full intensity ${\widehat{I}}_{i,j}$ can be estimated by:

$${\widehat{I}}_{i,j}=(I_{i,j}^{45}+{\widehat{I}}_{i,j}^0+{\widehat{I}}_{i,j}^{90}+{\widehat{I}}_{i,j}^{135})/2$$

(11)

where ${\widehat{I}}_{i,j}^0$, ${\widehat{I}}_{i,j}^{90}$, and ${\widehat{I}}_{i,j}^{135}$ are the tentatively estimated polarization channel values.

Since the recovered intensity image should convey the actual image texture, the image edges and gradients should be fully considered during interpolating. The fundamental idea is that the interpolation should be performed along the edge and not across the edge. We first evaluate the gradient of the raw image in four different directions, east (the horizontal direction), northeast (the diagonal direction with positive tangent), north (the vertical direction), and northwest (the diagonal direction with negative tangent). For each pixel (i, j) of the raw image, four gradient values are calculated on a 7 × 7 window using Equation (12).

$$\{\begin{array}{l}{D}_E(i,j)={\displaystyle \sum _{m=-1,1,3}{\displaystyle \sum _{n=0,2,4}\left|I_{i+m,j+n}^{raw}-I_{i+m,j+n-2}^{raw}\right|}}\hfill \\ D_{NE}(i,j)={\displaystyle \sum _{m=-2,0,2}{\displaystyle \sum _{n=0,2,4}\left|I_{i+m,j+n}^{raw}-I_{i+m+2,j+n-2}^{raw}\right|}}\hfill \\ D_N(i,j)={\displaystyle \sum _{m=0,2,4}{\displaystyle \sum _{n=-1,1,3}\left|I_{i+m,j+n}^{raw}-I_{i+m-2,j+n}^{raw}\right|}}\hfill \\ D_{NW}(i,j)={\displaystyle \sum _{m=-2,0,2}{\displaystyle \sum _{n=-2,0,2}\left|I_{i+m,j+n}^{raw}-I_{i+m+2,j+n+2}^{raw}\right|}}\hfill \end{array}$$

(12)

The process of tentatively estimating the nondetected polarization intensity ${\widehat{I}}_{i,j}^{\theta }$ has two steps, diagonal interpolation and vertical and horizontal interpolation:

Diagonal interpolation. In each pixel, the diagonal interpolation can interpolate the dual value (i.e., the value of the perpendicular direction) of the detected one. If the gradient in the NE direction is larger than the gradient in the NW direction, i.e., $D_{NE}>D_{NW}$, bicubic interpolation is applied to the target pixel along the NW direction. If the gradient in the NW direction is larger than the gradient in the NE direction, i.e., $D_{NW}>D_{NE}$, bicubic interpolation is applied to the target pixel along the NE direction. If there is an equal situation, i.e., $D_{NE}=D_{NW}$, the average of the two bicubic interpolation values is taken. Diagonal interpolation of all four polarization channels should be completed before the next step.

Vertical and horizontal interpolation. As shown in Figure 1, each polarization channel is detected every second row and every second column. Thus, when we do the bicubic interpolation in the N and E directions for the any target pixel (i, j), in only one direction the required adjacent pixel has detected value. Additionally, in another direction, only the estimated value from the above diagonal interpolation process can be used. For example, when $I_{i,j}^{45}$ is detected on pixel (i, j), the adjacent detected $I^{135}$ can be used in both the NE and NW directions (the diagonal directions). Thus, ${\widehat{I}}_{i,j}^{135}$ can be estimated by diagonal interpolation. However, for ${\widehat{I}}_{i,j}^0$ and ${\widehat{I}}_{i,j}^{90}$ there is no detected $I^0$ in the E direction (the horizontal direction) or $I^{90}$ in the N direction (the vertical direction). Thus, in those directions, the ${\widehat{I}}^0$ and ${\widehat{I}}^{90}$ from their own diagonal interpolations are used. If the gradient in the E direction is larger than the gradient in the N direction, i.e., $D_E>D_N$, bicubic interpolation is applied to the target pixel along the N direction. If the gradient in the N direction is not larger than the gradient in the E direction, i.e., $D_N>D_E$, bicubic interpolation is applied to the target pixel along the E direction. If there is an equal situation, i.e., $D_N=D_E$, the average of the two is taken.

2.2.2. Interpolate Each Polarization Channel by Intensity Ratio Constraint

After obtaining the tentative estimate intensity image $\widehat{I}$, each polarization channel ${\overline{I}}^0$, ${\overline{I}}^{45}$, ${\overline{I}}^{90}$, and ${\overline{I}}^{135}$ can be calculated. Considering the constraint of Equation (10), a method derived from the guided filter technique [30] is proposed. This method allows each polarization channel $I^{\theta }$ to adhere to the texture of the intensity image $I$. At the same time, the relationship between the channels is also fully retained, which ensures the correct recovery of polarization information.

In the proposed method, the intensity image $\widehat{I}$ is employed as a guidance image, which is used as a reference to exploit the image structures. The input sparse polarization image is accurately unsampled by the derived guided filter.

For each polarization channel image $I^{\theta }$, $\theta =0^{\circ },{45}^{\circ },{90}^{\circ },{135}^{\circ }$, we define the filter as:

$${\overline{I}}_{i,j}^{\theta }=a_{p,q}^{\theta }{\widehat{I}}_{i,j}+b_{p,q}^{\theta },{\forall }_{i,j}\in {\omega }_{p,q}$$

(13)

where ${\overline{I}}^{\theta }$ is the filtering output and $\widehat{I}$ is the guidance image. Equation (13) assumes that ${\overline{I}}^{\theta }$ is a linear transform of $\widehat{I}$ in a window ${\omega }_{p,q}$ centered at the pixel (p, q), whereas ($a_{p,q}$, $b_{p,q}$) are the linear coefficients assumed to be constant in ${\omega }_{p,q}$. A square window is used for radius $r$, i.e., the side length is $2r+1$. This local linear model ensures that ${\overline{I}}^{\theta }$ has an edge only if $\widehat{I}$ has an edge, because $\nabla {\widehat{I}}^{\theta }=a\nabla \overline{I}$. At the same time, Equation (13) is consistent with Equation (10).

To determine the linear coefficients ($a_{p,q}$, $b_{p,q}$), we minimize the following cost function in the window ${\omega }_{p,q}$:

$$E(a_{p,q}^{\theta },b_{p,q}^{\theta })={\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }\left({(a_{p,q}^{\theta }{\widehat{I}}_{i,j}+b_{p,q}^{\theta }-I_{i,j}^{\theta })}^2+{(\epsilon b_{p,q}^{\theta })}^2\right)}$$

(14)

where $M_{i,j}^{\theta }$ is a binary mask at the pixel ($i$, $j$), which is one for the sampled pixels (i.e., $I_{i,j}^{\theta }$ has the sampling value) and zero for the others. $\epsilon$ is a regularization parameter penalizing large $b_{p,q}^{\theta }$ values to ensure the bias term $b_{p,q}^{\theta }$ is not too large and is only used to fit the nonideal measured value, which is described in Equation (10). Equation (10) is the physical fact we deduce. In Equation (10), the coefficients a and c (analogous to $a_{p,q}^{\theta }$ in Equations (13) and (14)) determine the proportion of I^θ in I, and the bias term Δ (analogous to $b_{p,q}^{\theta }$ in Equations (13) and (14)) only characterizes a small error. Thus, in Equation (13), the output I^θ should be mainly determined by the coefficient $a_{p,q}^{\theta }$. In addition, the bias term $b_{p,q}^{\theta }$ representing the error should be small. That is, regularizing the coefficients of $b_{p,q}^{\theta }$ is appropriate, and it is consistent with physical facts. 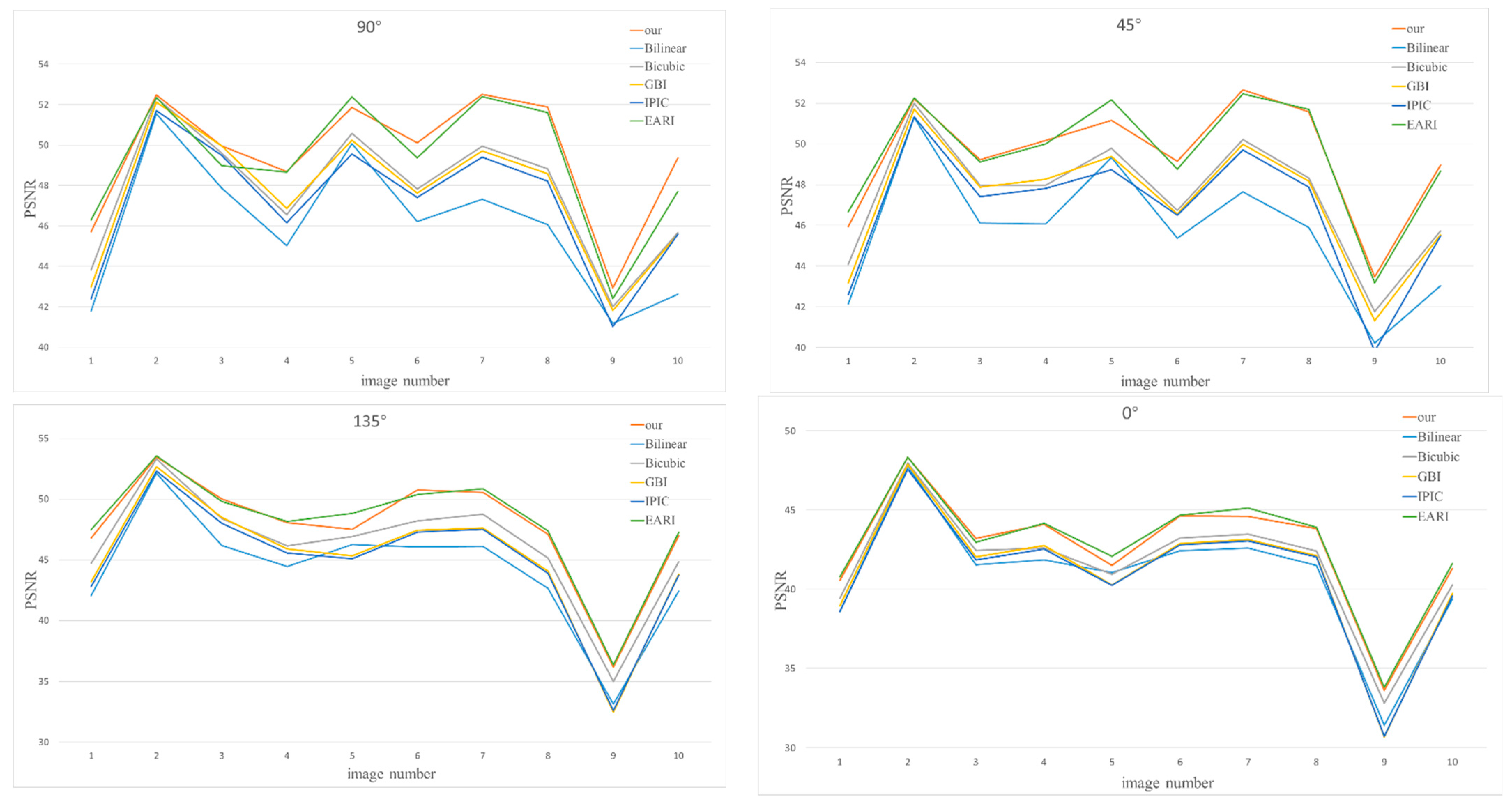Regularizing the coefficients of $b_{p,q}^{\theta }$ instead of $a_{p,q}^{\theta }$ in the cost function is an important difference between our method and the original guided filter [30]. Compared experiment results are shown in Section 3.2.

Equation (14) has a closed-form solution. First, let the partial derivative of the function with respect to $a_{p,q}^{\theta }$ and $b_{p,q}^{\theta }$ be zero:

$$\frac{\partial E}{\partial a_{p,q}^{\theta }}=0=2{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }(a_{p,q}^{\theta }{\widehat{I}}_{i,j}+b_{p,q}^{\theta }-I_{i,j}^{\theta }){\widehat{I}}_{i,j}}$$

(15)

$$\frac{\partial E}{\partial b_{p,q}^{\theta }}=0=2{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }(a_{p,q}^{\theta }{\widehat{I}}_{i,j}+(1+\epsilon )b_{p,q}^{\theta }-I_{i,j}^{\theta })}$$

(16)

Then, from Equation (16), $b_{p,q}^{\theta }$ can be determined:

$$\begin{array}{l}{b}_{p,q}=\frac{1}{(1+\epsilon )}\frac{1}{{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }}}({\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }{I}_{i,j}^{\theta }}-a_{p,q}^{\theta }{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }}{\widehat{I}}_{i,j})\\ \begin{array}{cc}& \end{array}=\frac{1}{(1+\epsilon )}(I_{p,q}^{\theta }-a_{p,q}^{\theta }{u}_{p,q})\end{array}$$

(17)

where $I_{p,q}^{\theta }=\frac{1}{{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }}}{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }{I}_{i,j}^{\theta }}$ and $u_{p,q}=\frac{1}{{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }}}{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }}{\widehat{I}}_{i,j}$ are the mean values of $I_{i,j}^{\theta }$ and ${\widehat{I}}_{i,j}$, respectively, in the window ${\omega }_{p,q}$ under the mask $M_{i,j}^{\theta }$.

Finally, by incorporating Equation (17) into Equation (15), $a_{p,q}^{\theta }$ can be obtained:

$$a_{p,q}^{\theta }=\frac{{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }{I}_{i,j}^{\theta }{\widehat{I}}_{i,j}}-\frac{1}{(1+\epsilon )}{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }{I}_{p,q}^{\theta }{\widehat{I}}_{i,j}}}{{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }{\widehat{I}}_{i,j}^2}-\frac{1}{(1+\epsilon )}{\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }{u}_{p,q}{\widehat{I}}_{i,j}}}$$

(18)

In each pixel (i, j), the linear coefficients (a, b) are different in different overlapping windows ${\omega }_{p,q}$ that cover (i, j). Thus, the average coefficients of all windows overlapping (i, j) are calculated here, i.e., ${\overline{a}}_{i,j}^{\theta }=\frac{1}{\left|\omega \right|}{\displaystyle \sum _{p,q\in {\omega }_{i,j}}{a}_{p,q}^{\theta }}$ and ${\overline{b}}_{i,j}^{\theta }=\frac{1}{\left|\omega \right|}{\displaystyle \sum _{p,q\in {\omega }_{i,j}}{b}_{p,q}^{\theta }}$. Equation (13) can then be rewritten as:

$${\overline{I}}_{i,j}^{\theta }={\overline{a}}_{i,j}^{\theta }{I}_{i,j}+{\overline{b}}_{i,j}^{\theta }$$

(19)

Based on Equation (19), each polarization channel ${\overline{I}}^{\theta }$ with the polarization direction $\theta =0^{\circ },{45}^{\circ },{90}^{\circ },{135}^{\circ }$ can be interpolated. The algorithm’s full steps are shown in Algorithm 1.

Algorithm 1 Polarized Intensity Ratio Constraint Demosaic for Division-of-Focal-Plane Polarimetric Image

Input: RAW mosaic polarization image $I^{raw};$;

1: $I^{raw}\to D_E,D_N,D_{NE},D_{NW}$, by Equation (12);

2: $D_E,D_N,D_{NE},D_{NW}\&I^{raw}\to {\widehat{I}}^{\theta },{\widehat{I}}^{\theta }\to \widehat{I}$, by the method in Section 2.2.2;

3: $\widehat{I}\&I^{raw}\to {\overline{I}}^{\theta }$, by Equation (19).

Output: Four channels polarization images ${\overline{I}}^{\theta },\theta =0^{\circ },{45}^{\circ },{90}^{\circ },{135}^{\circ }$.

2.3. Experiment Settings

2.3.1. Dataset

Ground-truth polarization images were required for a full reference evaluation of the proposed method. One of the methods used to acquire a full-resolution polarization image was to install a polarizer in front of an ordinary camera and obtain four-channel polarization images with polarization angles of 0°, 45°, 90°, and 135° by rotating the polarizer. The literature [39] provided a dataset of polarization images of 10 scenes obtained by this method. Each scene included a set of 0°, 45°, 90°, and 135° polarized images in the near-infrared band. The full-resolution images of each channel were down-sampled to generate an artificial mosaic image, which was then used as the input of the demosaicing algorithm.

In the polarizer rotation method for polarization imaging, it is necessary to ensure that the lighting conditions do not change and the target does not move during the process of shooting four independent images. As a result, this method is only suitable for shooting stationary objects indoors under stable lighting conditions and cannot be adapted to outdoor shooting, significantly limiting polarization image acquisition. Therefore, images collected with the DoFP polarization detector were also used as the dataset in our experiments. However, such mosaic images cannot be directly used as ground truth. To address this, we treated each group of four pixels of the original mosaic image as one pixel, creating a synthesized pixel with four polarization channels. However, the resolution of the original image was reduced by half in this process; that is, the pixel size of the image was changed from $M\times N$ to $\frac{M}{2}\times \frac{N}{2}\times 4$. Therefore, the synthesized four-channel polarization image can be considered to be the same as the above-mentioned full-size polarization image as ground truth and can then be used as the input of the demosaicing algorithm after down-sampling (see Figure 3).

We collected a polarization image dataset using a Lucid Vision Labs Triton TRI050S-P DoFP polarization camera. Three sets of polarization images were collected in different situations, including seven stationary object scenes illuminated by indoor directional light sources (named “still”), five indoor environment scenes illuminated by natural light (named “indoor”), and five outdoor environment scenes (named “outdoor”). The images are provided in Figure 4.

2.3.2. Evaluation Metrics

The well-known evaluation metrics peak signal-to-noise ratio (PSNR) [40] and correlated peak signal-to-noise ratio (CPSNR) were used to measure the accuracy of the polarization information between the reconstructed image and the corresponding ground truth. Between each couple of reference (R) and estimated (E) channels, the PSNR is defined as:

$$PSNR(R,E)=10{\log }_{10}\left(\frac{{(\max R)}^2}{MSE(R,E)}\right)$$

(20)

$$MSE(R,E)=\frac{1}{MN}{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{\Vert R_{i,j}-E_{i,j}\Vert }^2}}$$

(21)

where $MSE(R,E)$ denotes the mean squared error between R and E in one channel. If multiple channels are calculated together when calculating the MSE:

$$MSE(R,E)=\frac{1}{KMN}{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{\Vert R_{i,j}^k-E_{i,j}^k\Vert }^2}}}$$

(22)

Equation (20) then becomes the CPSNR.

The Stokes vector (S₀, S₁, S₂) degree of linear polarization (DoLP) and angle of linear polarization (AoLP) are usually used to characterize linear polarization information. The Stokes vector is calculated by Equation (22):

$$\{\begin{array}{c}{S}_0=(I^0+I^{45}+I^{90}+I^{135})/2\\ S_1=I^0-I^{90}\\ S_2=I^{45}-I^{135}\end{array}$$

(23)

DoLP and AoLP are respectively calculated by Equations (24) and (25):

$$DoLP=\frac{\sqrt{S_1^2+S_2^2}}{S_0}$$

(24)

$$AoLP=\frac{1}{2}{\arctan }_2(S_2,S_1)$$

(25)

where ${\arctan }_2(.)$ is a four-quadrant arctangent function.

3. Results

3.1. Comparative Experiments

The proposed method was compared with the bicubic and bilinear baseline interpolation algorithms [25], and with the gradient-based interpolation method (GBI) [26], interpolation with intensity correlation (IPIC) [27], and edge-aware residual interpolation (EARI) [29]. The experiments were carried out on seven datasets; the four existing databases were PSD [39], JCPD [41], Qiu [42], and EARI [29], and the other three (i.e., still, indoor, and outdoor) were collected by us. Each dataset included several scenes, and the average PSNR and CPSNR values were calculated in each dataset.

Each of the methods compared in the experiments had a different processing scheme for the border pixels around the image. These schemes greatly affected the processing results of boundary pixels. In order to avoid the adverse effect of boundary pixels on the evaluation of the overall performance of the algorithm, we removed the image strips with a width of 4 pixels at the image boundary before calculating the PSNR. In other words, boundary pixels are not included in the PSNR calculation.

The results of these datasets (i.e., the average PSNR and CPSNR of each dataset) are provided in

Table 1. The average PSNR and CPSNR of the comparative results on the PSD [39] dataset.

		Bilinear	Bicubic	GBI	IPIC	EARI	Ours
PSNR	I90°	45.9743	47.7189	47.5476	47.0923	49.2188	49.5521
	I0°	45.7130	47.4576	47.2032	46.7278	49.4986	49.4521
	I45°	40.8210	41.5623	41.0495	40.9053	42.7548	42.5748
	I135°	44.1407	46.1404	45.0915	44.8752	48.0021	47.7359
	I	47.1367	48.9923	48.0670	48.0852	50.7618	50.5035
CPSNR		44.0212	45.3788	44.7658	44.5683	46.8622	46.7302

,

Table 2. The average PSNR and CPSNR of the comparative results on the JCPD [41] “indoor light” dataset.

		Bilinear	Bicubic	GBI	IPIC	EARI	Ours
PSNR	I90°	37.8308	39.0858	39.0689	38.8231	41.9451	42.5955
	I0°	38.0426	39.2896	39.2959	39.0383	42.3034	42.1324
	I45°	38.0524	39.2908	39.3114	39.0639	41.8135	41.6400
	I135°	37.9027	39.1411	39.1632	38.9212	41.8940	41.6849
	I	41.0207	42.6195	42.2517	42.3376	45.6459	45.4912
CPSNR		38.4160	39.6978	39.6642	39.4527	42.4921	42.3369

,

Table 3. The average PSNR and CPSNR of the comparative results on the JCPD [41] “polar light” dataset.

		Bilinear	Bicubic	GBI	IPIC	EARI	Ours
PSNR	I90°	43.3966	44.2719	44.4778	44.2141	45.3170	45.9523
	I0°	41.8220	42.8536	43.0237	42.8074	44.2339	44.4133
	I45°	40.2640	41.2586	41.0635	41.0114	41.7744	42.1586
	I135°	42.2719	43.3034	43.4551	43.1951	44.4374	44.6750
	I	45.4879	46.8313	46.6407	46.6710	47.9939	48.3255
CPSNR		42.2504	43.2872	43.2981	43.1510	44.2396	44.5935

,

Table 4. The average PSNR and CPSNR of the comparative results on the Qiu [42] dataset.

		Bilinear	Bicubic	GBI	IPIC	EARI	Ours
PSNR	I90°	45.4405	45.9100	46.1176	45.8781	47.7405	47.7238
	I0°	45.1386	45.5986	45.8165	45.5700	47.5268	47.4604
	I45°	43.8359	44.2798	44.4799	44.2611	46.3113	46.1561
	I135°	44.1497	44.5925	44.8264	44.5903	46.7437	46.4882
	I	47.5776	48.2071	48.2397	48.2368	50.2006	50.0745
CPSNR		44.7896	45.2569	45.4470	45.2367	47.2583	47.1266

,

Table 5. The average PSNR and CPSNR of the comparative results on the EARI [29] dataset.

		Bilinear	Bicubic	GBI	IPIC	EARI	Ours
PSNR	I90°	42.5052	43.6349	43.5218	43.1572	46.8653	46.5659
	I0°	41.5901	42.4932	42.4689	42.0089	44.5156	44.5318
	I45°	42.3522	43.4642	43.3320	42.9762	46.5403	46.2573
	I135°	41.5906	42.4905	42.4565	42.0234	44.3447	44.3395
	I	44.9012	46.2316	45.7717	45.7528	48.9070	48.7685
CPSNR		42.4162	43.4488	43.3319	42.9681	45.8718	45.7766

,

Table 6. The average PSNR and CPSNR of the comparative results on the “still” dataset.

		Bilinear	Bicubic	GBI	IPIC	EARI	Ours
PSNR	I90°	42.6294	42.7586	43.1299	42.7421	43.3345	43.5794
	I0°	42.6440	42.7406	43.1475	42.7236	43.3126	43.5161
	I45°	42.3462	42.4418	42.8330	42.4047	43.0599	43.2954
	I135°	42.2083	42.3328	42.7339	42.3044	42.9512	43.1924
	I	46.7591	47.2200	47.5390	47.2189	47.6745	48.0496
CPSNR		43.0325	43.1731	43.5595	43.1493	43.7586	44.0018

,

Table 7. The average PSNR and CPSNR of the comparative results on the “indoor” dataset.

		Bilinear	Bicubic	GBI	IPIC	EARI	Ours
PSNR	I90°	42.0446	42.7083	43.1710	42.9867	43.4097	43.9911
	I0°	42.7276	43.3628	43.8270	43.6124	44.3127	44.6737
	I45°	43.3046	43.9254	44.4055	44.1752	44.7508	45.1523
	I135°	42.4136	43.0817	43.5635	43.3420	43.8367	44.3540
	I	46.3890	47.4204	47.9224	47.7924	48.1915	48.8117
CPSNR		43.1252	43.8093	44.2832	44.0801	44.6053	45.0960

and

Table 8. The average PSNR and CPSNR of the comparative results on the “outdoor” dataset.

		Bilinear	Bicubic	GBI	IPIC	EARI	Ours
PSNR	I90°	28.1875	28.4304	28.3835	27.9342	29.6191	29.4768
	I0°	29.1214	29.3598	29.3973	28.9050	30.4234	30.3209
	I45°	28.7657	29.0162	29.0302	28.5602	30.2432	30.0793
	I135°	27.7849	28.0249	27.9010	27.4841	29.1247	28.9946
	I	31.6101	32.0732	31.7485	31.5990	33.2384	33.0928
CPSNR		28.9001	29.1659	29.0954	28.6748	30.3123	30.1762

. The results show that our method and the EARI [29] method alternately achieve state-of-the-art performance (the state-of-the-art results are bold in the tables). More detailed results for each image in all datasets are presented in Appendix A.

We performed our experiments using MATLAB on an Intel Core(TM) i7-8700 @3.20-GHz CPU with 16 GB RAM. The processing time of each method on images of different sizes is shown in

Table 9. Comparison of time cost.

Image Size	Processing Time(s)
	Bilinear	Bicubic	GBI	IPIC	EARI	Ours
1244 × 1024	0.0737	0.0949	0.2542	0.3357	2.0328	1.3846
1024 × 1024	0.0613	0.0800	0.2190	0.2777	1.7020	1.1751
1024 × 768	0.0444	0.0595	0.1856	0.2319	1.2074	0.8586
720 × 540	0.0222	0.0286	0.0794	0.1021	0.5698	0.4334

. All methods were not specifically optimized for acceleration. It can be seen that our method outperforms EARI.

3.2. Controlled Experiments

The regularization parameter $\epsilon$ in Equation (14) can affect the performance of our proposed method. Therefore, we carried out controlled experiments using the dataset from [39] and our “indoor” dataset. As shown in

Table 10. The average PSNR and CPSNR of the controlled experiment results on the PSD [39] dataset.

$\mathit{\epsilon }$	PSNR					CPSNR
	I90°	I0°	I45°	I135°	I
0	49.4534	49.2667	42.4710	47.5507	50.3324	46.6011
0.001	49.5673	49.4367	42.5582	47.7009	50.4826	46.7139
0.005	49.5521	49.4521	42.5748	47.7359	50.5035	46.7302
0.01	49.4934	49.4143	42.5702	47.7339	50.4982	46.7172
0.1	49.4406	49.3700	42.5614	47.7119	50.4832	46.6978
1	49.3792	49.3305	42.5566	47.7177	50.4820	46.6857
10	49.3490	49.3045	42.5505	47.6994	50.4708	46.6724
100	49.3595	49.3158	42.5539	47.7150	50.4789	46.6801

, superior results were obtained when $\epsilon =0.005$.

To compare the difference between our mutated guided filter and original guided filter, the ${(\epsilon b_{p,q}^{\theta })}^2$ term in the cost function Equation (16) was replaced with ${(\epsilon a_{p,q}^{\theta })}^2$:

$$E(a_{p,q}^{\theta },b_{p,q}^{\theta })={\displaystyle \sum _{i,j\in {\omega }_{p,q}}{M}_{i,j}^{\theta }\left({(a_{p,q}^{\theta }{\widehat{I}}_{i,j}+b_{p,q}^{\theta }-I_{i,j}^{\theta })}^2+{(\epsilon a_{p,q}^{\theta })}^2\right)}$$

(26)

Equation (26) is the cost function of the original guided filter. Then, other processing steps of PIRC remained the same, and the results with the different regularization parameter $\epsilon$ were obtained and presented in

Table 11. The results of the original guided filter with different ε on the PSD [33] dataset.

$\mathit{\epsilon }$	PSNR					CPSNR
	I90°	I0°	I45°	I135°	I
0	45.5900	45.7077	42.2698	45.7752	48.2528	45.0309
0.001	45.5987	45.7166	42.2721	45.7821	48.2603	45.0367
0.01	45.6763	45.7954	42.2918	45.8434	48.3269	45.0881
0.05	46.0070	46.1320	42.3697	46.0980	48.6067	45.3019
0.1	46.3239	46.4516	42.4275	46.3039	48.8561	45.4872
1	48.8572	48.9465	42.4346	47.3465	50.2805	46.4396
10	47.5377	47.2827	41.4780	45.6522	48.5795	45.1483
100	46.6212	46.3342	41.0616	44.7765	47.7319	44.4821

. Comparing Table 10 and Table 11, it can be seen that our mutated guided filter has better performance than the original guided filter in this demosaicing task (the superior results are bold in each tables).

3.3. Application Experiments

We conducted visual application experiments to demonstrate the importance and effectiveness of PIRC demosaicing. As the polarization reflection characteristics of the surfaces of different materials are varied, polarization imaging can serve visual tasks such as target detection and scene segmentation. Here, we focused on the potential of distinguishing objects by the difference in polarization characteristics and did not consider target detection or image segmentation algorithms.

Figure 5 show the pseudo-color images synthesized by the polarization images after PIRC demosaicing. The synthesis method directly normalized the calculated DOLP, AOPL, and I, and then filled them into the R, G, and B channels of the color image. This article provides a simple illustration of this process and does not discuss other more advanced fusion methods.

4. Discussion

In Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8, the results show that our method and the EARI [29] method alternately achieved state-of-the-art performance, and both of them outperformed the other methods. Their performances varied on different datasets, which is mainly due to the different texture conditions of the experimental images.

In Table 9, for different algorithms, the results show that the improvement of the accuracy also brought an increase in the calculation time. Bilinear interpolation and bicubic interpolation were the fastest; in contrast, EARI and our PIRC took more time. However, PIRC was still considerably faster than EARI, although their accuracy was similar. In the experiments of this article, we did not do a special acceleration optimization for all of those algorithms. It is expected that our method can meet the needs of real-time applications after the necessary acceleration optimization.

Figure 5 is an outdoor scene. Figure 5a is the light intensity image, and Figure 5b is the pseudo-color image synthesized by polarization information. Figure 5c–g show the targets marked with colored boxes. They are water on the ground, buses, cars, sewer manhole covers, and cars hidden under the canopy, respectively. It can be observed that the targets that are difficult to distinguish in the light intensity image are clearly distinguished in the polarization information fusion image. For example, in Figure 5c, the surface of the stagnant water is smooth, and the specular reflection is obvious, thus the polarization characteristics are significantly different from the surrounding environment. In Figure 5e–g, the car’s glass and the manhole cover on the road are a red tone due to the strong degree of polarization. These polarization characteristics effectively aid in visual tasks, such as detecting, recognizing, and tracking vehicles by UAV, intersection monitoring, and detecting road surface water by unmanned vehicles.

5. Conclusions

This work presented a new polarized intensity ratio constraint demosaicing method for dividing a focal-plane polarimetric image. The method could efficiently utilize both the interchannel and intrachannel correlations and retain the characteristics of polarization detection. Our method first restored the light intensity image following the edge and texture. It then further restored the image of each channel according to the unique constraint relationship between the polarization channels. We directly used the mosaic image obtained by the DoFP sensor as the ground truth for the comparison experiment, which could greatly facilitate data collection and enrich the source of experimental data. The experimental results demonstrated our proposed method was both effective and practical. The findings also showed how polarimetric imaging could benefit computer vision and remote sensing tasks. In the future, we will continue to improve imaging quality. Other future research directions include multi-frame demosaicing, polarized 3D reconstruction, polarized target detection, and polarized target tracking.