High-Frequency Channel Modeling Based on the Multi-Source Ionospheric Assimilation Model
Abstract
:1. Introduction
2. Ionospheric Assimilation Model and High-Frequency Channel Parameter Calculation Method
2.1. Ionospheric Assimilation Model
2.2. HF Channel Modeling
2.3. Parameter Estimation Algorithm
2.3.1. Average Delay at the Center Frequency (Group Delay at the Center Frequency),
2.3.2. Unilateral Delay Broadening,
2.3.3. Average Doppler Shift at the Center Frequency,
2.3.4. The Amplitude Peak of the Received Signal,
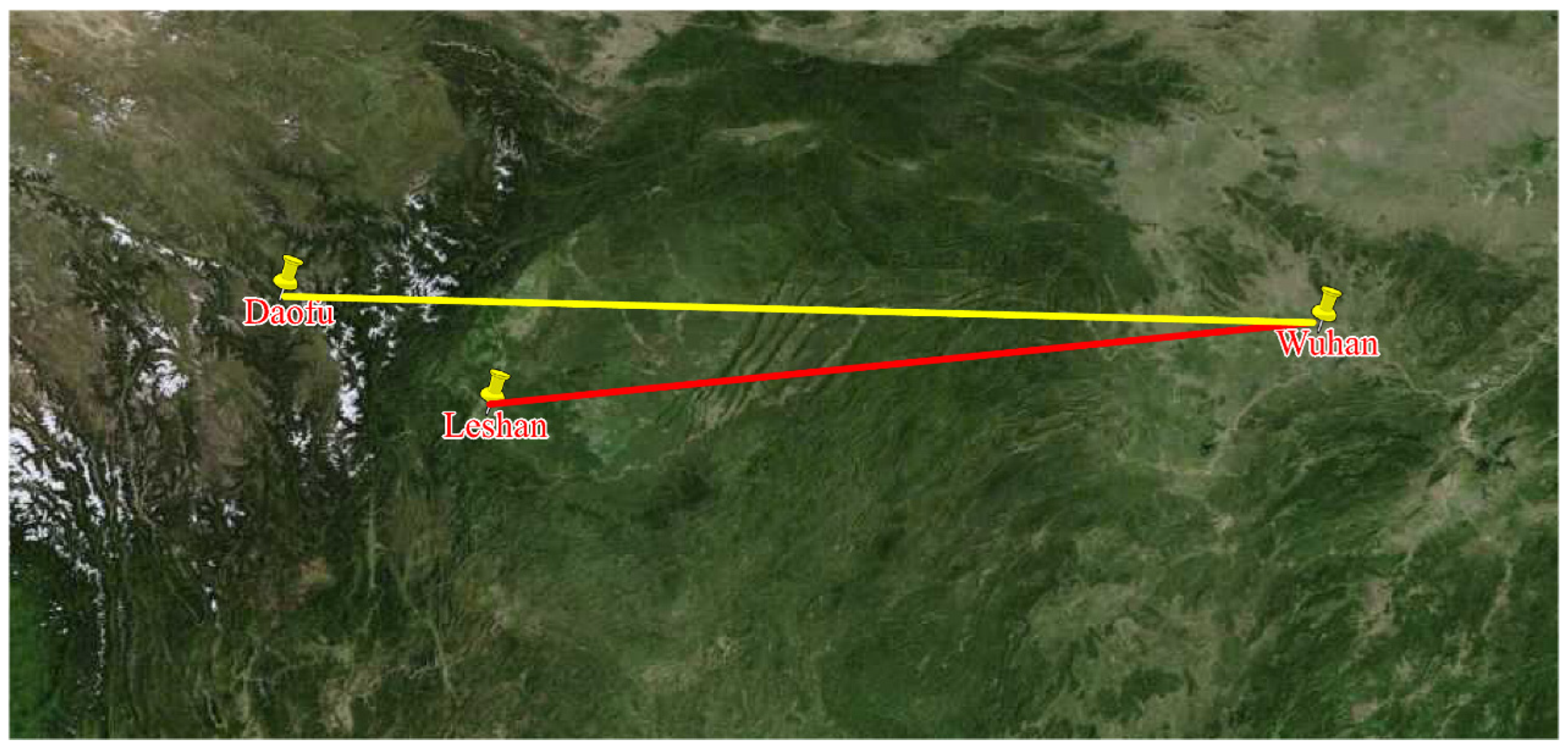
3. HF Oblique Sounding Experiment Content and Experimental Data Processing
- 1.
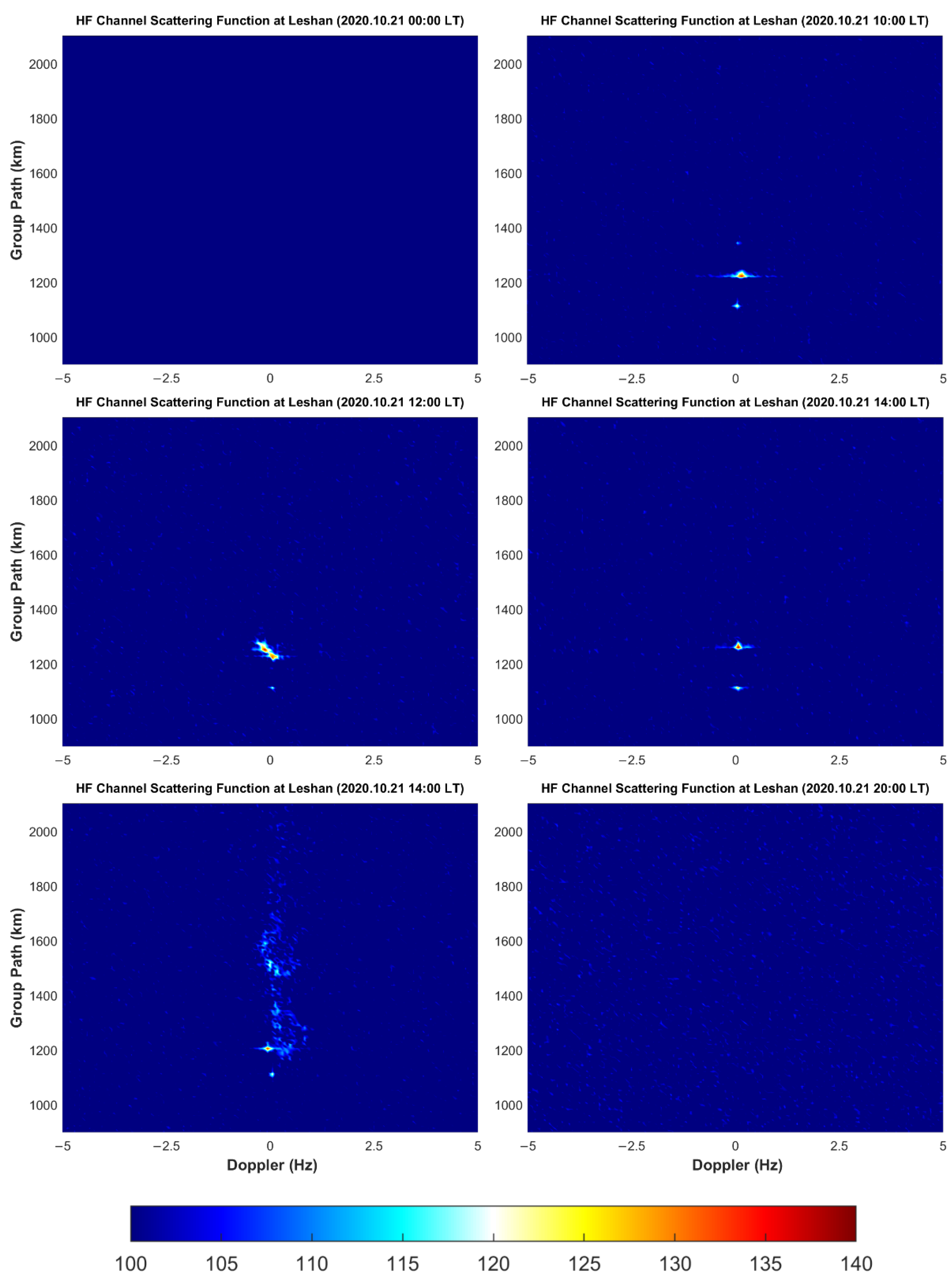
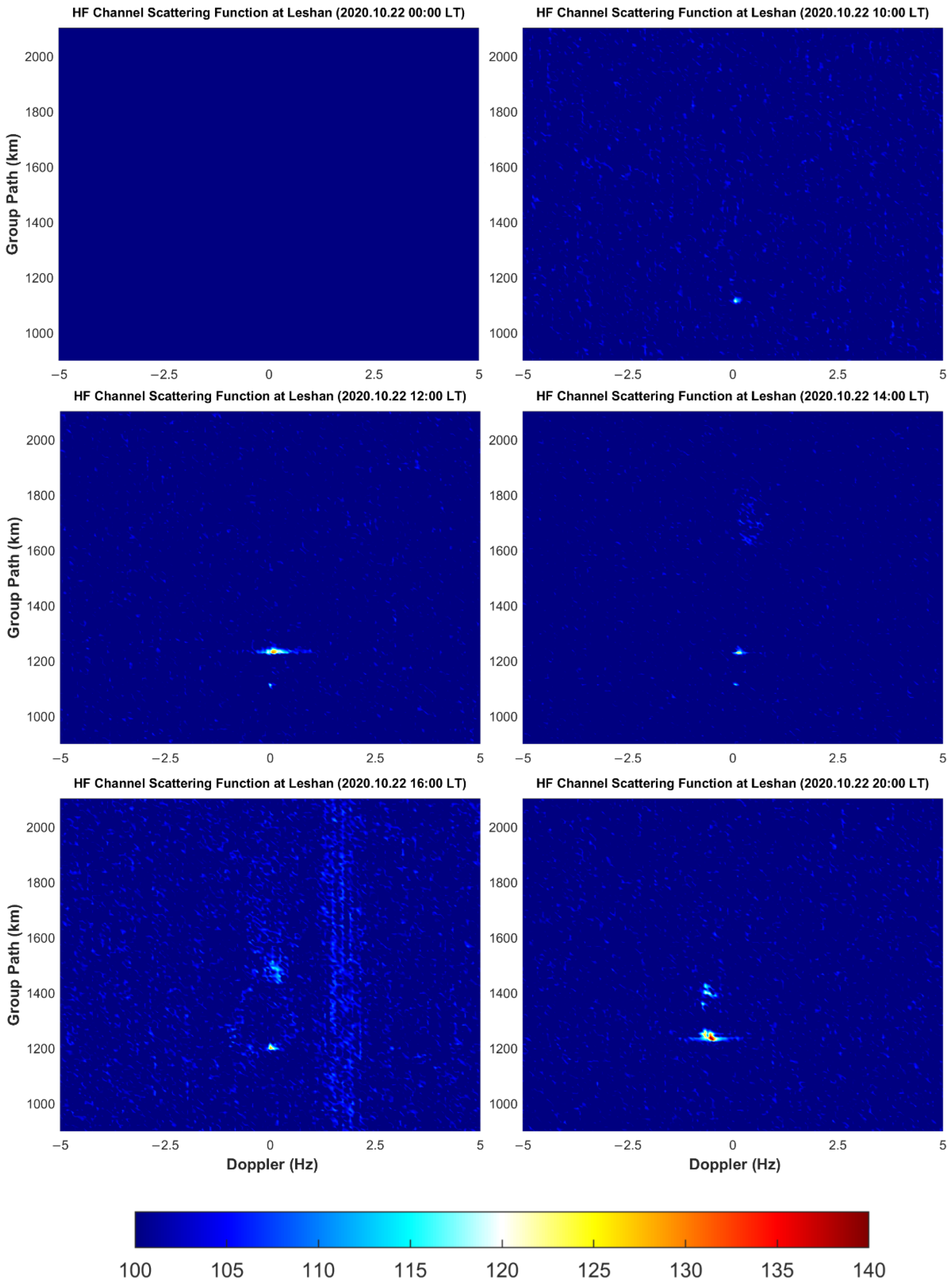
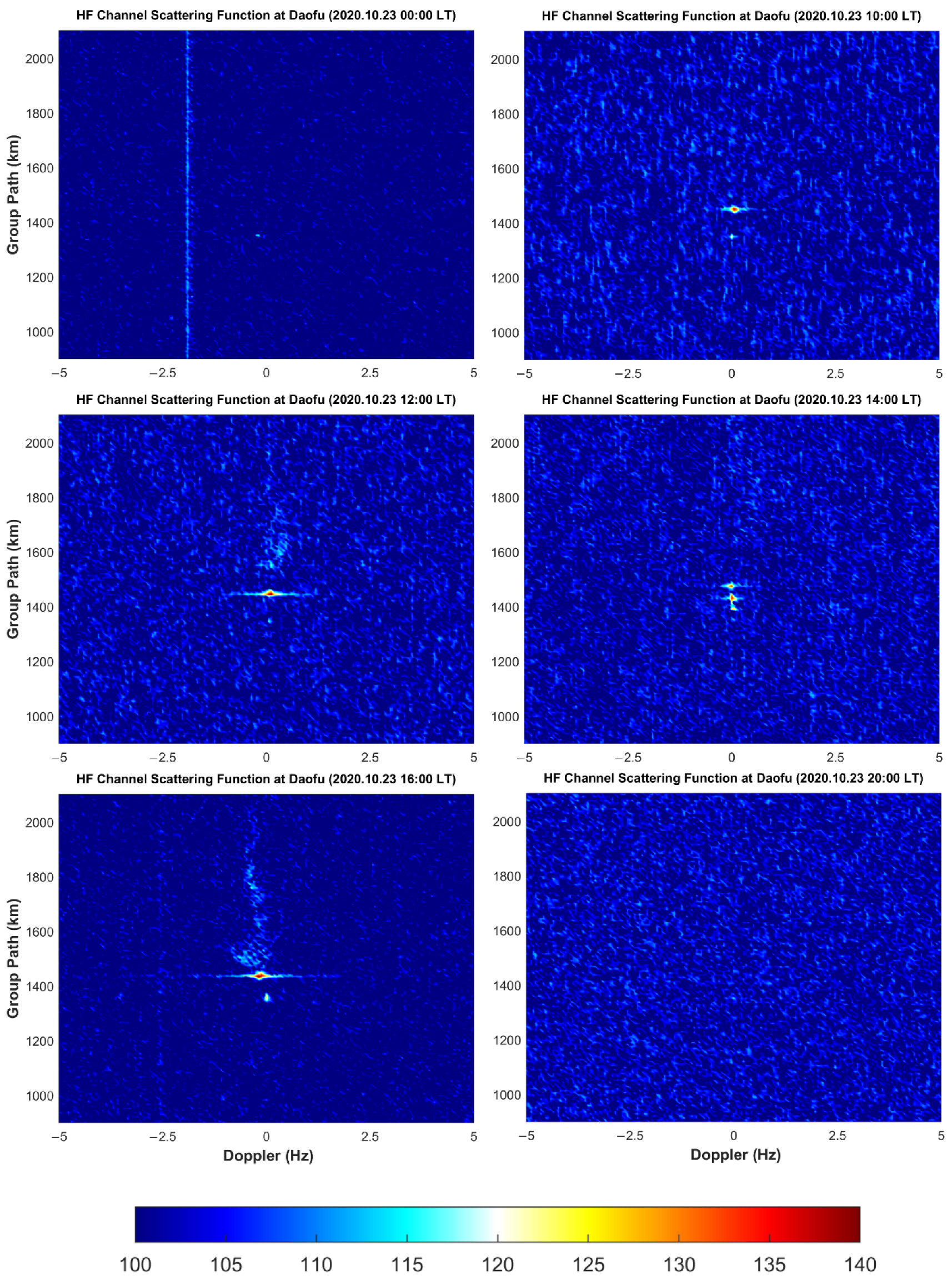
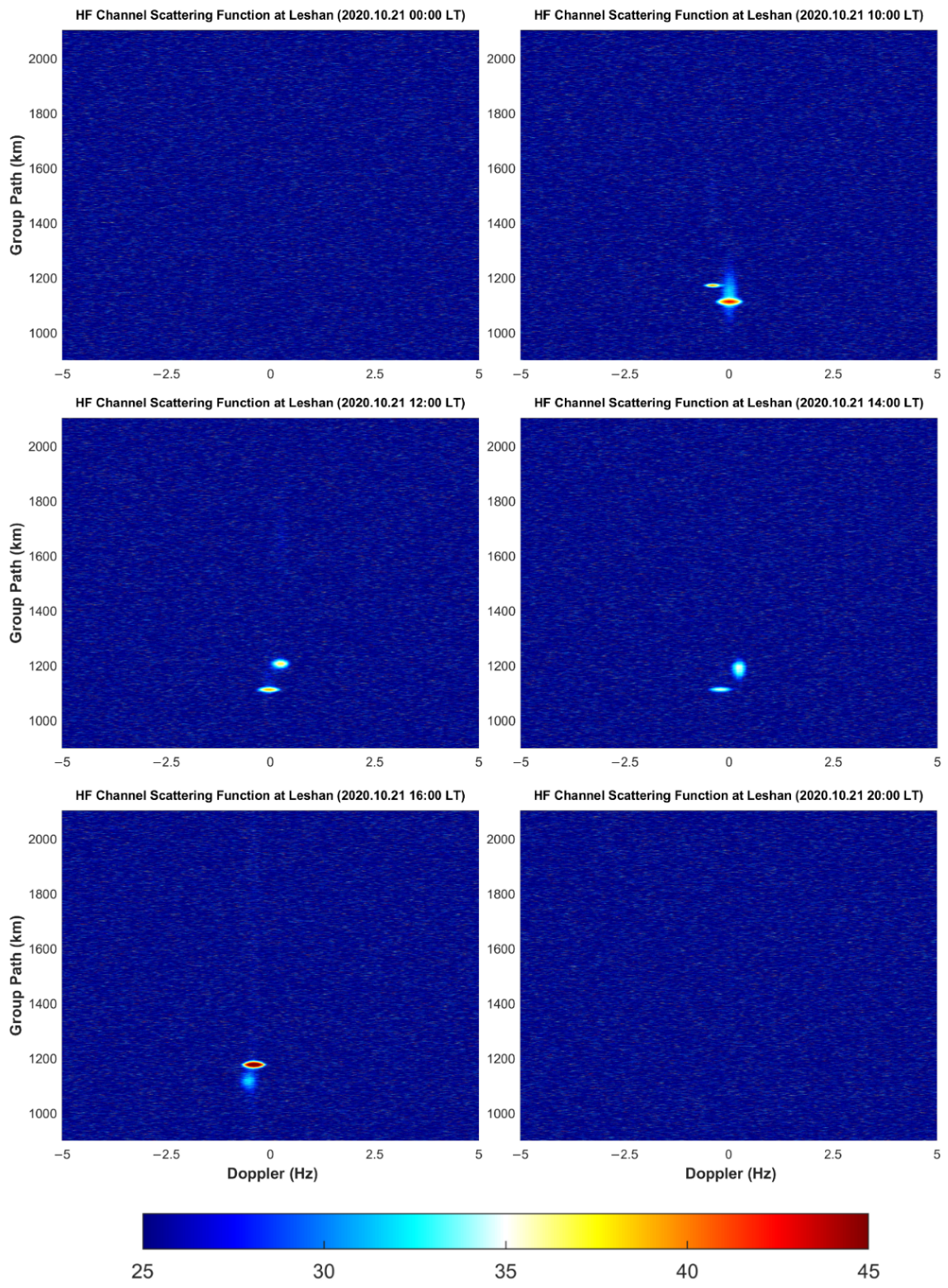
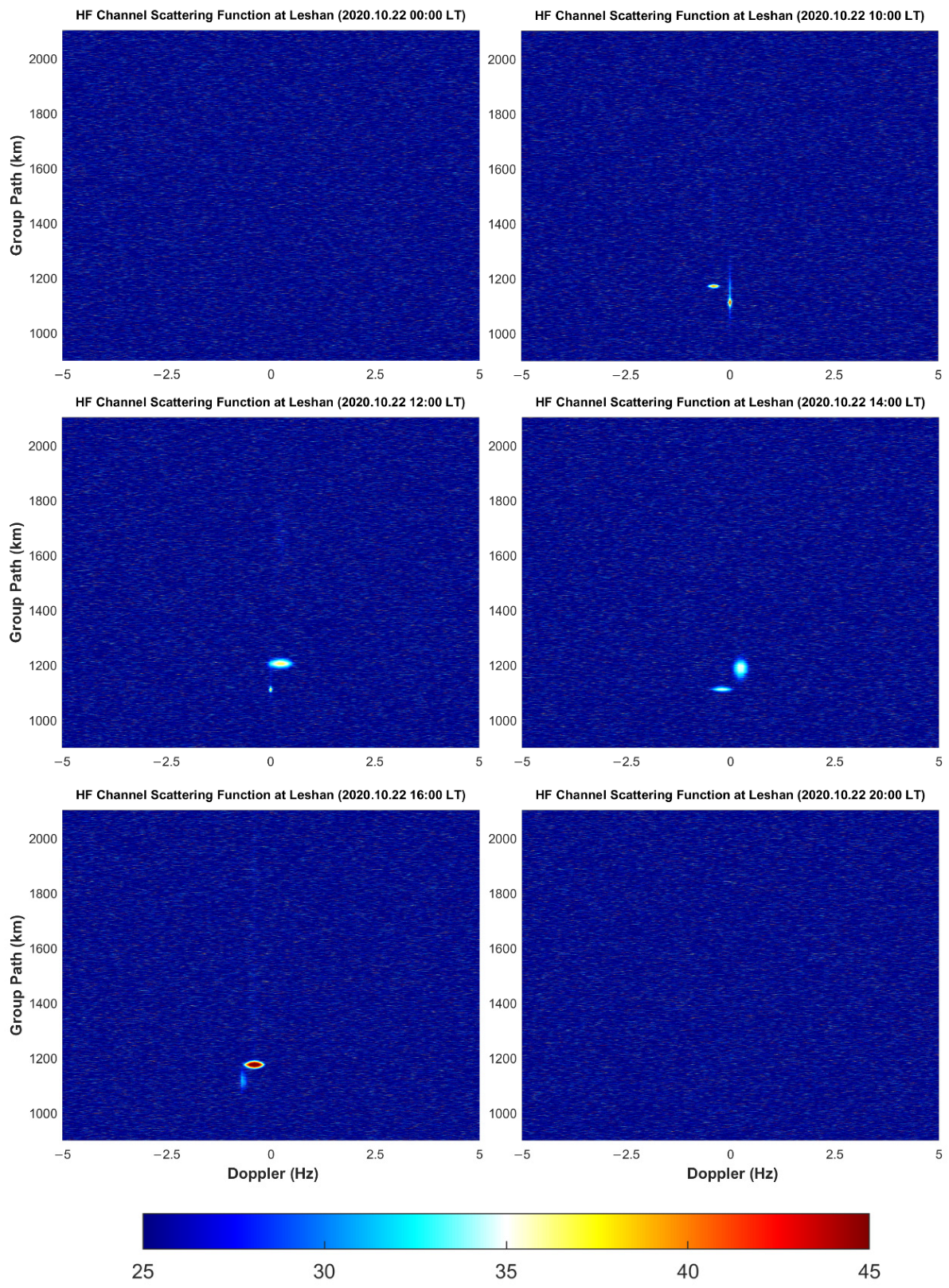
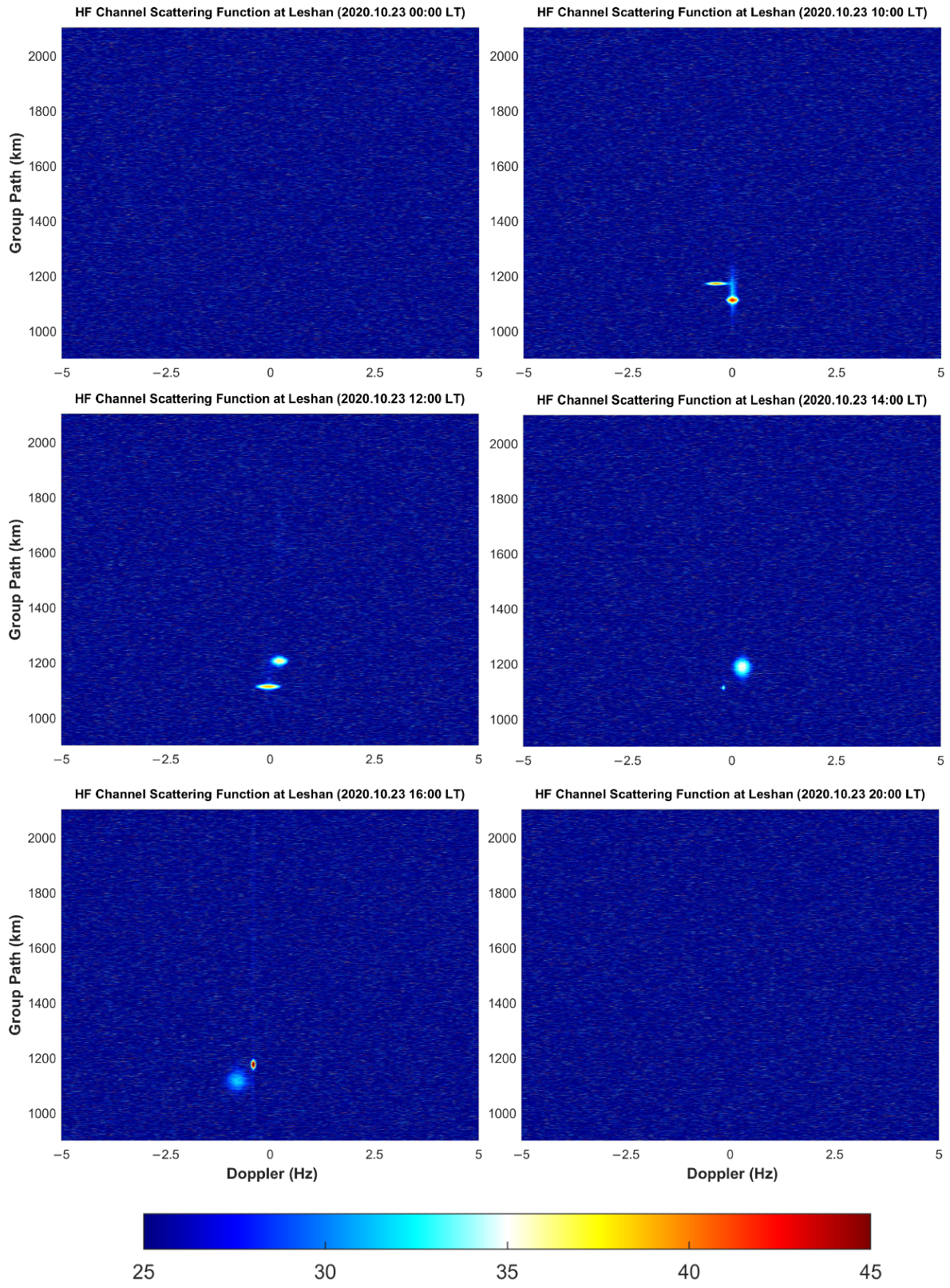
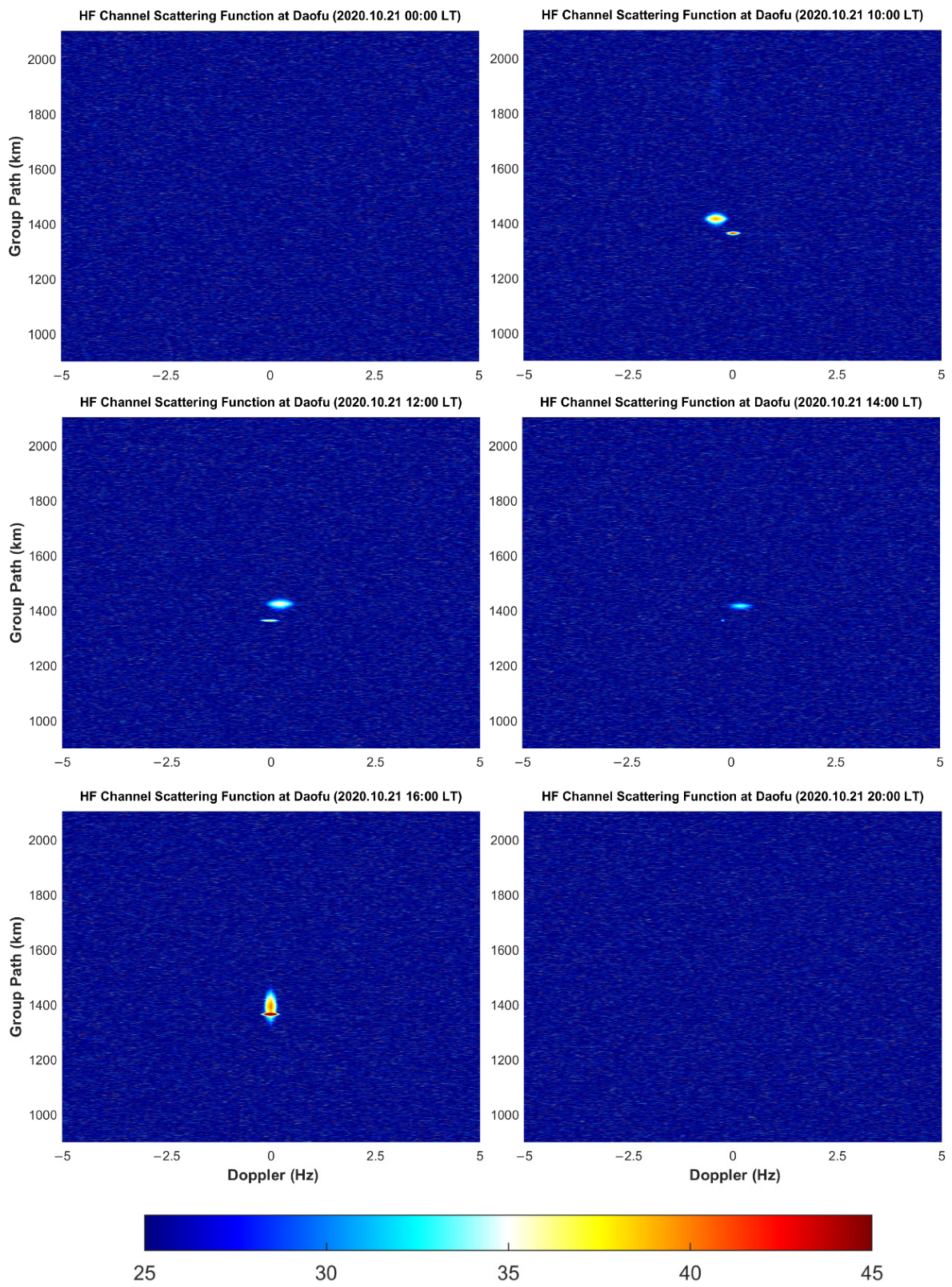
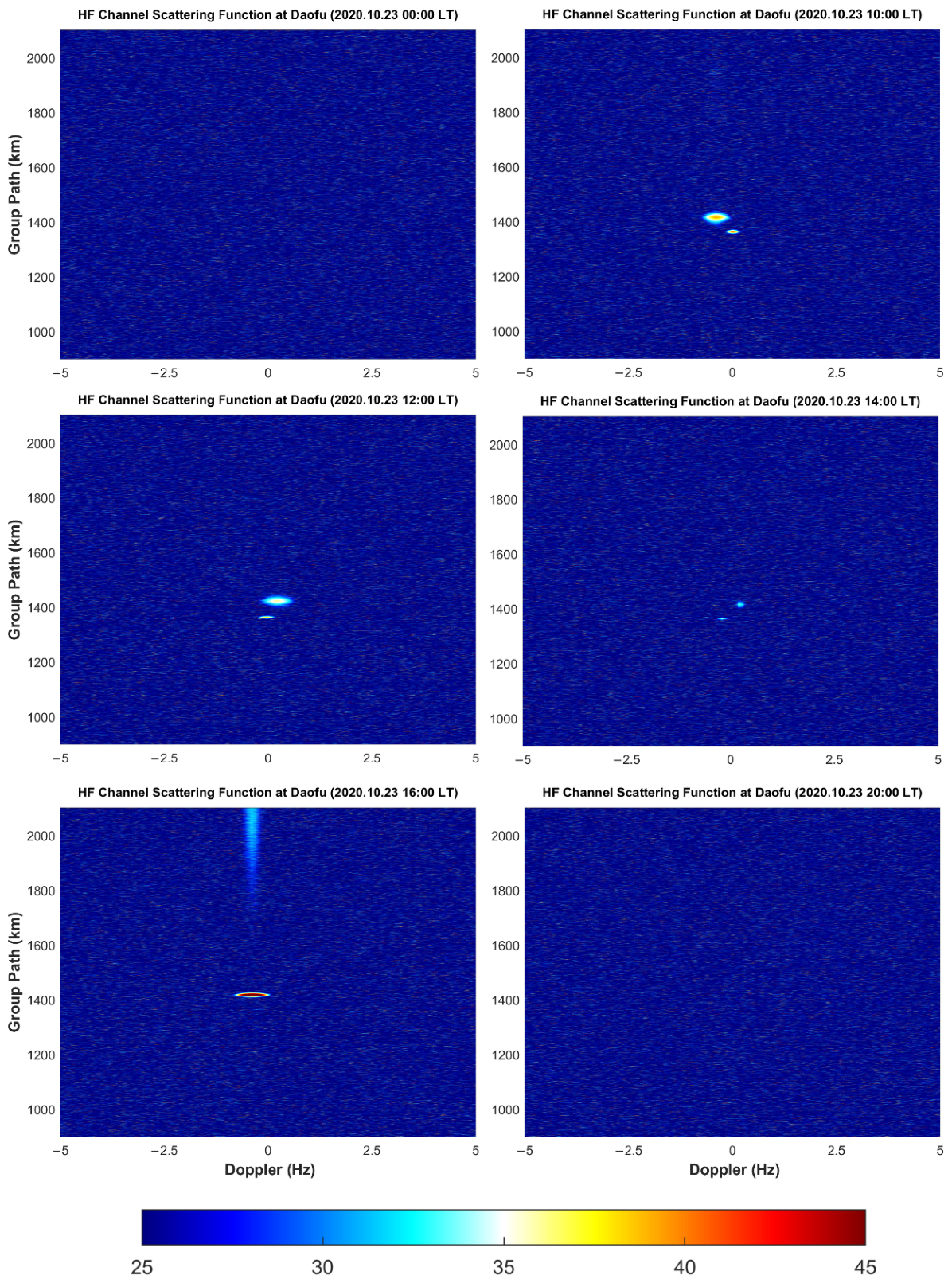
- If elliptic-like bright spots appear in the figure, it means that the receiver can receive signals reflected from the ionosphere. Because there is a stone’s throw between the two receiving sites, the HF channel variation of the Wuhan–Leshan and Wuhan–Daofu links was almost the same. For either Leshan station or Daofu station, the signal transmitted from Wuhan can be received from 10:00 to 16:00 during the day, but no signal can be received at 00:00, during the night. At 20:00, the signal could only be received at Leshan station and Daofu station on 22 October 2020.
- 2.
- Both Leshan station and Daofu station can receive signals of two modes from 12:00 to 16:00 in the daytime, which are shown as two separate elliptic-like bright spots in the figure. The group path of the rays propagating from the E layer was smaller than that of the F layer. The delay, delay broadening, Doppler shift, and Doppler shift broadening of the rays propagating from layer E were all smaller than the corresponding parameters of the rays propagating from layer F, which is also in line with our general cognition.
- 3.
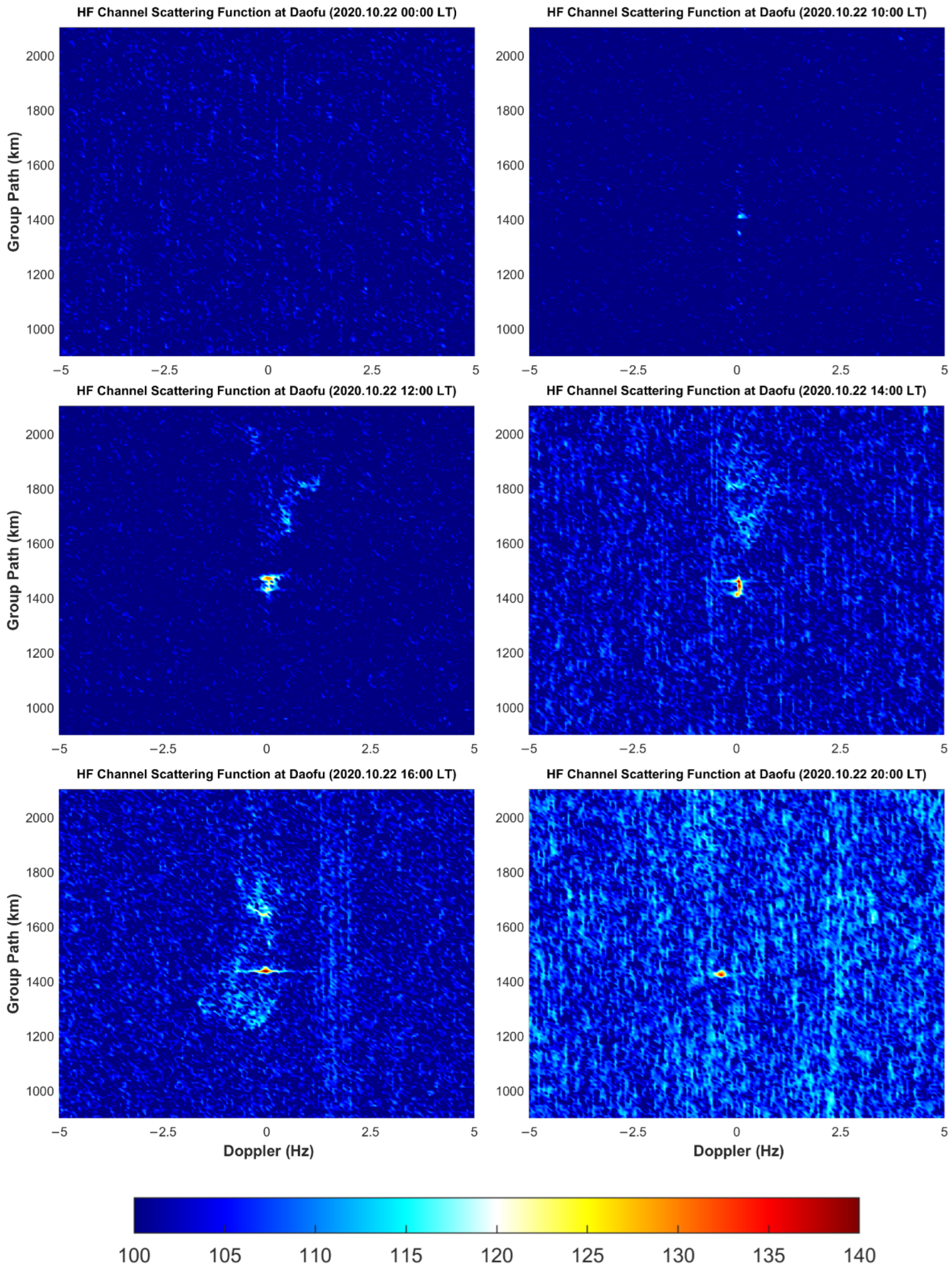
- Because the ground distance of Daofu–Wuhan is larger than that of Leshan–Wuhan, the scattering function diagram of Daofu station was more blurred and noisy. It is worth noting that the ionospheric regions traversed by the rays of the two paths were very close to each other. It can be seen from Figure 3 and Figure 6 that the ionospheric disturbance changes on the two paths were very similar. In Figure 6, the Doppler broadening and time delay broadening of the signal received by the Daofu station during the daytime on 22 October 2020 shows that the ionosphere of the link has a strong disturbance, which can also be seen in Figure 3. Figure 2 and Figure 5 show a similar pattern.
- 4.
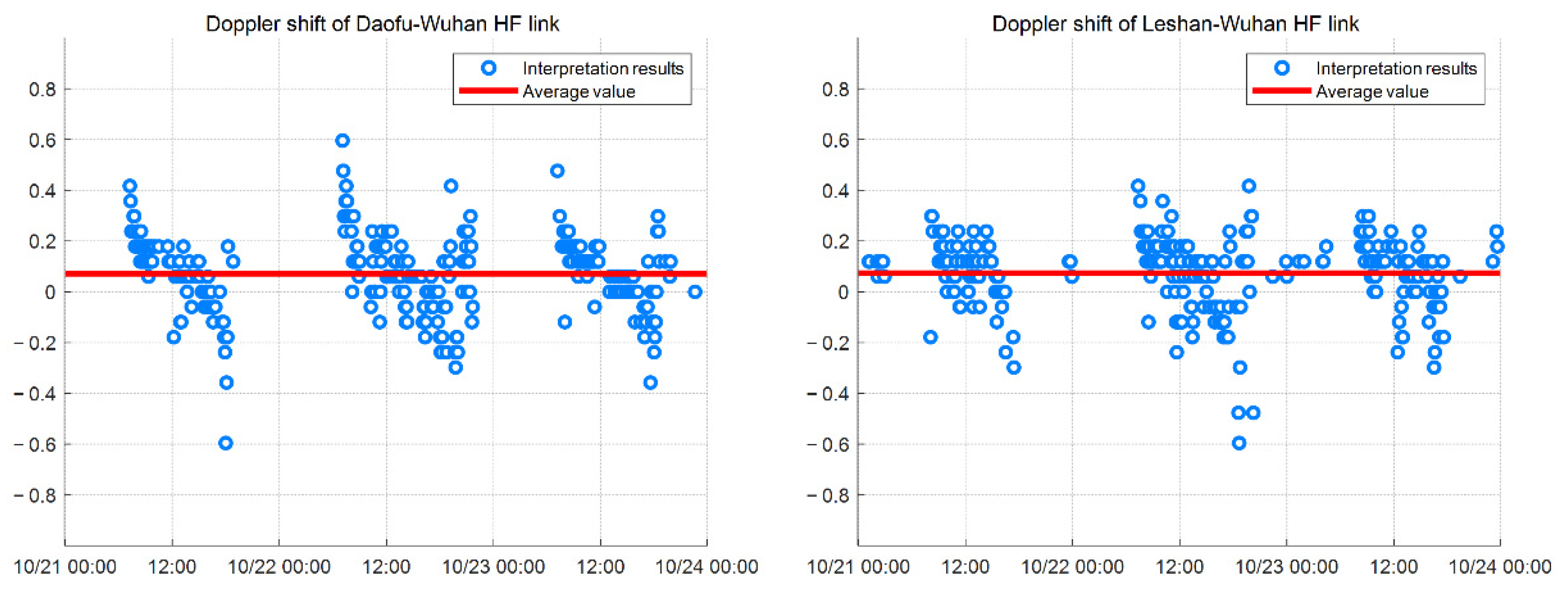
- Because the signals with a frequency of 10.8 MHz were unable to obtain a good oblique measurement reception effect at night, only the state of the ionosphere during the day was analyzed. The average Doppler shifts of the Leshan–Wuhan link and the Daofu–Wuhan link are 0.0733 Hz and 0.0714 Hz, which shows that the channels of the two links are very similar. It is worth noting that the value of the Doppler shift is gradually approaching zero during this time, indicating that the ionosphere was tending to be quiet. By comparison, during the period of 14:00–19:00 LT, the change of the ionosphere is exactly the opposite. This is also very consistent with our theoretical understanding of the diurnal variation of the ionosphere and the Chapman theory. Of course, there are some exceptions. In Figure 8, there are many such cases in the Daofu–Wuhan link on 22 October and the Leshan–Wuhan link on 22 and 23 October. These circumstances may result from the rapid changes in the ionosphere. There are many physical mechanisms that lead to this, such as the irregularities in the E or F layers in the ionosphere, traveling ionosphere disturbances (TID), Magnetic storms, Magnetospheric substorms, and so on.
4. HF Channel Modeling and Simulation
- 1.
- The background electron density was generated based on the multi-source ionospheric assimilation model according to the time, geolocation, and other parameters of the oblique sounding experiment.
- 2.
- According to the radio frequency of the oblique sounding experiment, 3D ray-tracing of the traversing elevation angle was carried out. The group path (group delay), launching elevation, propagation mode, and other parameters in the process of HF radio wave propagation were determined according to the ground distance between the transceiver stations.
- 3.
- Parameters such as propagation loss, received electric field strength, time delay broadening, and Doppler frequency shift were estimated based on the 3D ray-tracing results and the background electron density generated by the multi-source ionospheric assimilation model.
- 4.
- In this paper, the Doppler broadening was set to be random numbers in the range of 0–0.2 Hz (E layer mode) and 0–0.25 Hz (F layer mode), and finally the HF channel was modeled according to Formula (2).
- 1.
- The HF channel modeling was more accurate in the estimation of the group path (group delay) of the HF radio wave, but there were some deviations in the calculation of Doppler and delay broadening. However, it could still be used in practical follow-up projects.
- 2.
- The received signal electric field strength was in the range of 35–45 .
- 3.
- During the ionospheric quiet period, the modeling and simulation accuracy of the HF channel was more accurate, similar to the measured data. During the ionospheric disturbance period (afternoon of 22 October 2020), the HF channel modeling was quite different from the experimental results.
- 4.
- The HF channel modeling and simulation accuracy of the Wuhan–Daofu link were slightly higher than those of the Wuhan–Leshan link, which may be because the GNSS observation station is closer to the Wuhan–Daofu link, so the ionospheric background of assimilation was closer to reality.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heelis, R.A.; Maute, A. Challenges to Understanding the Earth’s Ionosphere and Thermosphere. J. Geophys. Res. Space Phys. 2020, 125. [Google Scholar] [CrossRef]
- Hui, W.; Jie, G.; Kedeng, Z. Influence of the Magnetic Field Strength and Solar Activity on the Thermospheric Zonal Wind. J. Geophys. Res. Space Phys. 2022, 127, e2021JA029741. [Google Scholar] [CrossRef]
- Berdermann, J. Predicting the Effects of Solar Storms on the Ionosphere Based on a Comparison of Real-Time Solar Wind Data with the Best-Fitting Historical Storm Event. Atmosphere 2021, 12, 1684. [Google Scholar]
- Wang, W.; Lei, J.; Burns, A.G.; Solomon, S.; Wiltberger, M.; Xu, J.; Zhang, Y.; Paxton, L.; Coster, A. Ionospheric response to the initial phase of geomagnetic storms: Common features. J. Geophys. Res. Space Phys. 2010, 115, A07321. [Google Scholar] [CrossRef]
- Vasyliūnas, V.M. The physical basis of ionospheric electrodynamics. Ann. Geophys. 2012, 30, 357–369. [Google Scholar] [CrossRef] [Green Version]
- Kelley, M.C.; Kelley, M.; Hellis, R. The Earth’s Ionosphere: Plasma Physics and Electrodynamics, 2nd ed.; Academic Press (Elsevier): San Diego, CA, USA, 2009. [Google Scholar]
- Sen, H.K.; Wyller, A.A. Generalization of the Appleton-Hartree Magneto-Ionic Formula. J. Geophys. Res. 1960, 65, 355–357. [Google Scholar] [CrossRef]
- Arras, C.; Wickert, J.; Beyerle, G.; Heise, S.; Schmidt, T.; Jacobi, C. A global climatology of ionospheric irregularities derived from GPS radio occultation. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Balan, N.; Liu, L.B.; Le, H.J. A brief review of equatorial ionization anomaly and ionospheric irregularities. Earth Planet. Phys. 2018, 2, 3–21. [Google Scholar] [CrossRef]
- Gherm, V.E.; Zernov, N.N.; Strangeways, H.J. HF propagation in a wideband ionospheric fluctuating reflection channel: Physically based software simulator of the channel. Radio Sci. 2005, 40, 1–15. [Google Scholar] [CrossRef]
- Mastrangelo, J.F.; Lemmon, J.J.; Vogler, L.E.; Hoffmeyer, J.; Pratt, L.; Behm, C. A new wideband high frequency channel simulation system. IEEE Trans. Commun. 1997, 45, 26–34. [Google Scholar] [CrossRef]
- Gong, Y.; Li, Y. Greedy Adaptive Modulation Algorithm for Wideband HF Communications. In Proceedings of the 2019 IEEE 19th International Conference on Communication Technology (ICCT), Xi’an, China, 16–19 October 2019; pp. 1026–1031. [Google Scholar]
- Ibrahim, A.A.; Abdelaziz, A.M.; Salah, M.M. OFDM over wideband ionospheric HF channel: Channel modelling & optimal subcarrier power allocation. In Proceedings of the 2018 35th National Radio Science Conference (NRSC), Cairo, Egypt, 20–22 March 2018; pp. 300–308. [Google Scholar]
- Nickisch, L.J.; John, G.S.; Fridman, S.V.; Hausman, M.A.; Coleman, C.J. HiCIRF: A high-fidelity HF channel simulation. Radio Sci. 2012, 47, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Watterson, C.; Juroshek, J.; Bensema, W. Experimental Confirmation of an HF Channel Mode. IEEE Trans. Commun. Technol. 1970, 18, 792–803. [Google Scholar] [CrossRef]
- Milsom, J.D. Wideband Channel Characteristics and Short Spread-Spectrum Link. In Proceedings of the Eighth International Conference on HF Radio Systems and Techniques 2000, Guildford, UK, 10–13 July 2000; Volume 474, pp. 305–309. [Google Scholar]
- Vogler, L.E.; Hoffmeyer, J.A. A model for wideband HF propagation channels. Radio Sci. 2016, 28, 1131–1142. [Google Scholar] [CrossRef]
- Yonghong, W.; Chenglin, W.; Yuanbo, R.; Fuhou, Z. High Frequency Channel Multipath Analysis Based on Ionosphere Dispersion. J. Electron. Inf. Technol. 2020, 42, 2006–2012. [Google Scholar]
- Yuxi, Z.; Tu, X.; Yang, Q.; Pengyin, L. Simulation and Frequency Selection of Improved ITS Aviation Channel Model Based on Nakagami-m Function. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 3374–3379. [Google Scholar]
- Yan, Z.; Zhang, L.; Rahman, T.; Su, D. Prediction of the HF Ionospheric Channel Stability Based on the Modified ITS Model. IEEE Trans. Antennas Propag. 2013, 61, 3321–3333. [Google Scholar] [CrossRef]
- Schunk, R.W.; Scherliess, L.; Sojka, J.J.; Thompson, D.C.; Anderson, D.N.; Codrescu, M.; Minter, C.; Fuller-Rowell, T.J.; Heelis, R.; Hairston, M.; et al. Global Assimilation of Ionospheric Measurements (GAIM). Radio Sci. 2016, 39, 1–11. [Google Scholar]
- Azzarone, A.; Bianchi, C.; Pezzopane, M.; Pietrella, M.; Scotto, C.; Settimi, A. IONORT: A Windows software tool to calculate the HF ray tracing in the ionosphere. Comput. Geosci. 2012, 42, 57–63. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Reinisch, B.W. Real-time HF ray tracing through a tilted ionosphere. Radio Sci. 2006, 41, 1–8. [Google Scholar] [CrossRef]
- Bilitza, D.; McKinnell, L.A.; Reinisch, B.; Fuller-Rowell, T. The international reference ionosphere today and in the future. J. Geod. 2011, 85, 909–920. [Google Scholar] [CrossRef]
- Montenbruck, O.; González Rodríguez, B. NeQuick-G performance assessment for space applications. GPS Solut. 2020, 24, 13. [Google Scholar] [CrossRef] [Green Version]
- Mukhtarov, P.; Pancheva, D.; Andonov, B.; Pashova, L. Global TEC maps based on GNSS data: 1. Empirical background TEC model. J. Geophys. Res. Space Phys. 2013, 118, 4594–4608. [Google Scholar] [CrossRef]
- Zhong, J.; Lei, J.; Dou, X.; Yue, X. Assessment of vertical TEC mapping functions for space-based GNSS observations. GPS Solut. 2016, 20, 353–362. [Google Scholar] [CrossRef]
- Qiao, J.; Liu, Y.; Fan, Z.; Tang, Q.; Li, X.; Zhang, F.; Song, Y.; He, F.; Zhou, C.; Qing, H.; et al. Ionospheric TEC data assimilation based on Gauss–Markov Kalman filter. Adv. Space Res. 2021, 68, 4189–4204. [Google Scholar] [CrossRef]
- Boldovskaya, I.G. Doppler frequency shifts of radio waves reflected by parabolic and quasi-parabolic ionospheric layers. J. Atmos. Sol.-Terr. Phys. 1982, 44, 305–311. [Google Scholar] [CrossRef]
- Titheridge, J.E. The real height analysis of ionograms: A generalized formulation. Radio Sci. 1988, 23, 831–849. [Google Scholar] [CrossRef]



| Indicators Category | Typical Value |
|---|---|
| Detection system | Pulse compression pseudo-random code phase modulation system |
| Detection methods | Fixed-frequency sounding |
| Peak power | 200 W |
| Detection frequency | 4 MHz/10.8 MHz |
| Frequency stability | ≤5 × 10−8/d |
| Doppler range of observation | ±30.5 Hz |
| Doppler resolution | 0.06 Hz |
| Range resolution | 7.68 km |
| Single observation time | 300 s |
| Reception sensitivity | Better than –108 dBm |
| Receiving dynamic range | >70 dB |
| Signal bandwidth | 40 KHz |
| Parameter | The Deviation Value of Leshan–Wuhan Link | The Deviation Value of Daofu–Wuhan Link |
|---|---|---|
| Group path (km) | 33.2043 | 25.2357 |
| Group path broadening (km) | 15.1544 | 19.5368 |
| Doppler frequency shift (Hz) | 0.2498 | 0.1744 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, M.; Zhou, C.; Liu, T.; Qiao, J.; Qiao, W.; Li, C.; Wang, J.; Zhu, J. High-Frequency Channel Modeling Based on the Multi-Source Ionospheric Assimilation Model. Remote Sens. 2022, 14, 4133. https://doi.org/10.3390/rs14174133
Lv M, Zhou C, Liu T, Qiao J, Qiao W, Li C, Wang J, Zhu J. High-Frequency Channel Modeling Based on the Multi-Source Ionospheric Assimilation Model. Remote Sensing. 2022; 14(17):4133. https://doi.org/10.3390/rs14174133
Chicago/Turabian StyleLv, Mingjie, Chen Zhou, Tongxin Liu, Jiandong Qiao, Wei Qiao, Chen Li, Junming Wang, and Jianhua Zhu. 2022. "High-Frequency Channel Modeling Based on the Multi-Source Ionospheric Assimilation Model" Remote Sensing 14, no. 17: 4133. https://doi.org/10.3390/rs14174133
APA StyleLv, M., Zhou, C., Liu, T., Qiao, J., Qiao, W., Li, C., Wang, J., & Zhu, J. (2022). High-Frequency Channel Modeling Based on the Multi-Source Ionospheric Assimilation Model. Remote Sensing, 14(17), 4133. https://doi.org/10.3390/rs14174133







