Abstract
Retrogressive thaw slumps (RTS) are considered one of the most dynamic permafrost disturbance features in the Arctic. Sub-meter resolution multispectral imagery acquired by very high spatial resolution (VHSR) commercial satellite sensors offer unique capacities in capturing the morphological dynamics of RTSs. The central goal of this study is to develop a deep learning convolutional neural net (CNN) model (a UNet-based workflow) to automatically detect and characterize RTSs from VHSR imagery. We aimed to understand: (1) the optimal combination of input image tile size (array size) and the CNN network input size (resizing factor/spatial resolution) and (2) the interoperability of the trained UNet models across heterogeneous study sites based on a limited set of training samples. Hand annotation of RTS samples, CNN model training and testing, and interoperability analyses were based on two study areas from high-Arctic Canada: (1) Banks Island and (2) Axel Heiberg Island and Ellesmere Island. Our experimental results revealed the potential impact of image tile size and the resizing factor on the detection accuracies of the UNet model. The results from the model transferability analysis elucidate the effects on the UNet model due the variability (e.g., shape, color, and texture) associated with the RTS training samples. Overall, study findings highlight several key factors that we should consider when operationalizing CNN-based RTS mapping over large geographical extents.
1. Introduction
Permafrost is defined as the Earth materials that remain at or below 0 °C for at least two consecutive years [1,2]. Over 24% of the land surface of the northern hemisphere is within the permafrost region [2,3]. The susceptibility of Arctic permafrost landscapes to risks of anthropogenic climate change is on the rise [4,5,6]. A plethora of scientific studies have voiced how the repercussions of permafrost thaw in cold permafrost areas are challenging an array of geosystem and ecosystem services. Permafrost thaw escalates the lateral movements of biogeochemical fluxes [7,8,9] and alters coastal marine ecosystems [10]. It impacts tundra geomorphology [11,12,13], vegetation [14], and hydrological functioning [15,16] and increases the release of soil carbon to the atmosphere [17]. In addition to the negative impacts on the natural system, permafrost disturbances pose serious threats on the human-built infrastructure and communities in the Arctic [5,18,19].
Permafrost disturbances have been observed and documented from local- to regional-scales across the Arctic based on field and satellite observation data [13,15,20,21,22]. Terrain alteration attributed to thermal erosion, thermal denudation, and thermokarst is considered the most prominent disturbance occurring in ice-rich landscapes [23,24,25]. Among other permafrost landforms, retrogressive thaw slumps (RTS, also called ground-ice slumps [26]) are recognized as one of the most active, rapid, and dramatic thermokarst landforms in the Arctic [27,28,29]. In a generic context, an RTS resembles and shares the anatomical structure of a landslide that occurs in non-permafrost regions. The RTS process creates large open depressions (a horseshoe- or bowl-shaped depression with a steep headwall) on hillslopes due to soil wasting and vegetation displacement [30]. In most cases, the resulting debris flow is terminated by a stream or a lake or the ocean.
Permafrost literature provides formal definitions for RTSs based on several criteria, such as morphography (overall appearance), morphometry (shape and surface geometry), formation process, underlying geology, and association of forms (Table 1). The Glossary of permafrost and related ground-ice terms [31] defined RTS as a “slope failure mechanism characterized by the melting of ground ice and downslope sliding and flowing of the resulting debris”. Ref. [32] made the distinction between RTS and active layer slides based on their formation process, while [33] identified RTS as “active geomorphological features in permafrost terrain that consist of steep ice-rich headwall and mud flowing along a gentle gradient”. Ref. [34] reported that RTSs typically have a small size (<10 ha, but in some instance reaching up to ~1 km2) with a wide range of morphology and dynamics.
The areal extent, geographical distribution, and the number of RTSs have increased significantly over the past several decades due to the warming climate [13,34,35,36,37]. Increasing subsurface temperatures and higher precipitation have accelerated permafrost degradation, causing decreased hillslope stability in low-Arctic permafrost regions [23,38,39]. In the high Arctic, warmer summers are responsible for the increase in RTS occurrence [12,13].
The RTS activity poses significant implications on geomorphological, hydrological, biogeochemical, and ecological processes from local to regional scales [34,40]. Terrain affected by RTSs shows increased nutrient availability, soil pH, snow pack, ground temperatures, and active layer thickness—all of which affect plant community structure [35]. Thermal erosion and slope disturbance processes associated with RTSs create favorable microsites (i.e., bare, warmer, more nutrient-rich, and less vegetated) for shrub recruitment [30] and habitats for birds and mammals [41]. The RTS activity significantly affects the geochemistry of streams by increasing their solute load well above that of pristine streams [27], as well as decreasing DOC concentrations downstream of slumps [42]. Accordingly, the freshwater food-web responds through an increase in benthic production [43]. Abrupt thaws, which RTSs present an example of, are estimated to release 40% of the mean net carbon emissions posed by gradual thawing in long-term projections [17].
The mapping, monitoring, and documentation of abrupt permafrost thaw is crucial to increase our spatio-temporal understanding of permafrost landscape dynamics in the Arctic [21]. Site-scale observations provide valuable insights on the RTS process. However, such localized observations limit our ability to gain synoptic perspectives on regional to pan-Arctic scales [44,45]. Due to the innate dynamic nature of RTSs, remotely sensed imagery and digital elevation data make ideal data sets for landform change analysis [46]. Early studies on RTS activity utilized aerial photography in conjunction with photogrammetric techniques and manual image interpretation. Coarse-to-moderate-resolution satellite sensors, such as MODIS, Landsat, SPOT, Sentinel, and SAR platforms, enable consistent data acquisitions for mapping abrupt thaw incidents. The emergence of commercial very high spatial resolution (VHSR) satellite sensors, such as the sensors of Maxar Inc. (IKONOS, QuickBird, GeoEye, and WorldView-1,2, and 3) and the recently launched Planet Cubesats have shifted the trajectory of permafrost landform mapping applications.
We conducted a literature review on previous research that utilized various type of remote sensing data in RTS mapping and monitoring applications (Table 2). The table includes the characteristics of Earth observation platforms, sensors, data types, study areas, processing extents, and analysis methods. Most studies have been constrained to smaller geographical extents and were performed using manual and/or semi-automated image analysis techniques. A few, such as the studies by [23,24,37,47], presented large-area mapping efforts using coarse-resolution satellite image data (e.g., 30 m Landsat imagery). There has been a growing tendency of utilizing VHSR satellite imagery in RTS detection based on computer vision/artificial intelligence (AI) algorithms. For example, Ref. [34,48] utilized Planet and Cubesat data to map RTSs in limited geographical extents. An operational implementation of RTS (or any other permafrost landform) mapping using VHSR imagery at regional scales has been largely challenged by image data (big data) volume and methodological gaps in automated image analysis workflows. To address this challenge, we have developed an operational-scale GeoAI pipeline (Mapping application Arctic Permafrost Land Environment—MAPLE, [49]) that harnesses AI and high-performance computing (HPC) resources to deploy automated mapping using tens of thousands of commercial satellite images. The first MAPLE workflow example mapped ice-wedge polygons across the Arctic [50,51].
Deep learning (DL) convolutional neural network (CNN) algorithms are pioneered in and designed for everyday image analysis tasks. In comparison to everyday image analysis, remote sensing image scene understanding deviates in multiple ways, such as the imaging sensors and their characteristics (e.g., multiple spectral channels), coverage and viewpoints, and the geo-objects captured by the imagery and their properties [52]. Therefore, prior to an operational scale adaptation of DLCNN algorithms, it is important to understand the effect of input data characteristics and the key steps involved in image pre- and post-processing on the overall performances of the DLCNN model predictions.
DLCNN-based analysis requires the partitioning of input images into manageable sub-arrays depending on the pre-defined network input size (e.g., 256 pxl × 256 pxl or 512 pxl × 512 pxl) of the DLCNN architecture due to the array dimensions of image scene (e.g., typical satellite image scene has dimensions of 40,000 pxl × 40,000 pxl) and limitation of graphics processing unit (GPU) memory. Resizing image tiles is required when the network input size is smaller than the input image tile. This is particularly true in transfer learning, in which we must stay with the pre-defined network input size of the architecture to gain the advantage of pre-trained weights of the neurons. However, the resizing process could potentially degrade the amount of information (e.g., spectral, spatial, and textural details) needed to accurately describe the target of interest. The image tiling process could affect the extent of the target of interest embedded in a single image tile. For instance, if the target of interest (e.g., an RTS) is significantly larger than the input network size, the DLCNN model will struggle to learn the contextual information that describes the spatial association between the target of interest and its surrounding. Unlike in everyday objects (e.g., car, traffic sign, flower), semantics (higher-level meanings) of geo-objects are not necessarily pivoted to the properties (e.g., color, size, texture) of the object itself but are organized into multiple spatial scales [53,54]. Another important aspect to consider is the interoperability of a trained DLCNN across a large area comprising varying terrain and landcover characteristics [52]. The production of training data via manual annotation is a time- and labor-intense process. Therefore, we always seek a limited set of training samples that sufficiently capture the variability of the target objects.
Our overarching goal is to integrate a new workflow to the MAPLE for the automated detection and characterization of RTSs using VHSR imagery. The specific objectives are to understand: (1) the optimal combination of input image tile size (array size) and the DLCNN network input size (resizing factor/spatial resolution) and (2) the interoperability of the trained DLCNN models across heterogeneous study sites based on limited sets of training samples.

Table 1.
Definitions, morphometric/morphological characteristics, and prevalence of retrogressive thaw slumps.
Table 1.
Definitions, morphometric/morphological characteristics, and prevalence of retrogressive thaw slumps.
| Reference | Description | Morphology/Morphometry | Prevalence |
|---|---|---|---|
| [31] | A slope failure mechanism characterized by the melting of groundice, and downslope sliding and flowing of the resulting debris. Retrogressive thaw slumps consist of a steep headwall that retreats in a retrogressive fashion due to thawing and that slides down the face of the headwall and flows away. | A steep headwall that retreats in a retrogressive fashion. Debris flow formed by the mixture of thawed sediment and meltwater | Slumps are common in ice-rich glaciolacustrine sediments and fine-grained diamictons. |
| [33] | Active geomorphological features in permafrost terrain. They consist of steep ice-rich headwall and a mudflow of a gentle gradient. | Banks of northern rivers | |
| [55] | A type of backwasting thermokarst common along arctic coasts characterized by massive ground ice. | ||
| [56] | Comprise a steep headwall and footslope of lower gradient. Thawing turns ice-rich permafrost into a mud slurry that falls to the base of the exposure to form the scar area. | ||
| [35] | Consists of a headwall of exposed ground ice and a foot slope of viscous, thawed sediments | Several hectares in size | |
| [57] | Dynamic thermokarst features in ice-rich permafrost terrain. | Along the shorelines of lakes and rivers, coastlines and hillslopes | |
| [13] | Horseshoe or cusp-shaped mass wasting features consisting of an ablating headwall of ice-rich permafrost that feeds downslope flows of fluidized sediment. | Headwall | |
| [58] | Thermokarst landforms resulting from the thawing of ice-rich permafrost. Triggering mechanisms including lateral stream erosion and active layer detachments are responsible for RTSs. | ||
| [34] | Typical landforms related to processes of rapidly thawing and degrading hillslope permafrost. Occurred due to mass-wasting processes. | Typically have a small size (<10 ha, with a few exceptions reaching up to ~1 km2), as well as a wide range of appearances and dynamics | Regions with massive amounts of buried ice, as preserved in the moraines of former glaciations or regions with thick syngenetic ice-wedges in yedoma permafrost or icy epigenetic permafrost |
| [47] | RTS are abrupt permafrost disturbances that result from slope failure after thawing of ice-rich permafrost. Fluvial processes, thermo-erosion or mass wasting following heavy precipitation events and the exposure of ice-rich permafrost | RTSs vary in size, ranging from under 0.15 ha to mega slumps of 52 ha and more | Ice-rich yedoma regions or formerly glaciated areas that still contain permafrost-preserved buried glacial ice |

Table 2.
A selected list of literature related to retrogressive thaw slump mapping using remote sensing data.
Table 2.
A selected list of literature related to retrogressive thaw slump mapping using remote sensing data.
| Reference | Study Area | Data | Mode | Resolution | Analysis | Comment |
|---|---|---|---|---|---|---|
| [59] | Dome Wallis wellsite, King Christian Island, Chevron Parker river, wellsite, Banks Island in Canada | Aerial photographs | Optical | - | general discussion about terrain disturbances | |
| [60] | Russian Arctic region | Field observations and aerial imagery | Optical | - | Manual image interpretation | related to ground ice and relief evolution |
| [61] | Fosheim peninsula, Ellesmere Island, NWT in Canada | SPOT Panchromatic | Optical | 10 m | Manual comparison. Image enhancement using histogram stretching, | 16 sites |
| [62] | Eureka, Ellesmere Island, Nunavut in Canada | Topographic maps. Aerial photographs and field measurements | Optical | - | Area of 1887 km2 | |
| [55] | Herschel island, Yukon territory; Mackenzie delta region, NWT, in Canada | RADARSAT-1, SAR, SPOT | Optical | 5–10 m | collection of abstracts | |
| [55] | Herschel Island in Canada | IKONOS satellite imagery | Optical | 1 m | Differential global positioning system surveys and stereo-photogrammetric methods | Data from 1952, 1970, 2004 |
| [63] | Herschel Island in Canada | IKONOS satellite imagery | Optical | 2 m DEM | Photogrammetric processing | Data from 1952, 1970, 2000 |
| [64] | Mackenzie delta region, NWT, in Canada | Aerial imagery | Optical | 1:40,000 1:54,000 1:30,000 | Manual | Area of 3739 km2 |
| [65] | Mayo, central Yukon in Canada | Aerial imagery and ground surveys | Optical | - | - | Three thaw slumps |
| [56] | tundra uplands east of the Mackenzie Delta in Canada | Aerial imagery and ground surveys | Optical | - | Area of 3370 km2 | |
| [66] | Kavik Plateau; Richardson Mountains NWT in Canada | Aerial imagery | Optical | - | Manual | Data from 1950–2004 |
| [67] | Herschel Island in Canada | TerraSAR-X, RADARSAT-2 and ALOS-PALSAR | Microwave | Automated | Area of 108 km2 Years 2007–2011 | |
| [57] | Richardson Mountains, NWT, in Canada | Landsat TM/ETM imagery | Optical | 30 m | Automated; Tasseled Cap brightness, wetness and greenness indices | Area pf 18,000 km2 Data from 1985–2011 |
| [68] | Fosheim Peninsula of northern Ellesmere Island in Canada | SPOT imagery | Optical | 10 m | Manual | |
| [23] | Peel Plateau, northwestern NWT in Canada | SPOT imagery | Optical | 10 m | Manual (least one trained observer and one expert reviewer) | 1,274,625 km2 Data from 2005–2010 |
| [69] | Richardson Mountains and Peel Plateau region, NWT in Canada | Landsat TM/ETM imagery | Optical | 30 m | Automated; Tasseled Cap (TC) trend analysis | Data from 1990–2010 |
| [70] | Yukon Coast in Canada | high-resolution satellite imagery (?); Aerial imagery; LiDAR | Optical, LiDAR | Data from 1952–1972 and 1972–2011 | ||
| [71] | Yukon Coastal Plain in Canada; Bykovsky Peninsula in Russia | TanDEM-X | Microwave | 30 cm vertical | Area of 238 km Data from 2011 | |
| [72] | The Stony Creek and Vittrekwa River watersheds of the Peel Plateau in Canada | Samples collected by on-foot and helicopter | Area of 3000 km2 | |||
| [28] | Noatak valley in Alaska | Aerial imagery | Optical | 4–7 cm | digital photogrammetry | Area of 2900 km2 |
| [13] | Eureka Sound Lowlands, Ellesmere and Axel Heiberg Islands in Canada | Worldview-1, Worldview-2, Worldview-3, Arctic DEM | Optical | 1 m | Manual | 30-year record from 1989 to2018 of field observation; 2011–2018 of field/VHSR mapping |
| [73] | Qinghai-Tibet Plateau. China | Gaofen-1. WorldView-1, SPOT-5 satellite imagery | Optical | 2.0 m, 0.5 m, 2.5 m | manual interpretation | Data from 2008 to 2017 |
| [25] | NWT, Canada | TanDEM-X | Microwave | Data from 2011 | ||
| [58] | Tibetan Plateau, China | PlanetScope imagery | Optical | 3 m | Automated; Siamese neural network | Data from 2017–2018 |
| [74] | Tibetan Plateau, China | PlanetScope imagery | Optical | 3 m | Automated; Deep learning CNNs (DeepLabV3+) | Area of 5200 km2 Data from year 2018 |
| [75] | Ymala, Gydan, Taymyr, Chukotka in Russia; Noalak in Alaska; Peel, Tuktoyaktuk, Banks, Elsmere in Canada | TanDEM-X | Microwave | Area of 220,000 km2 Data from 2010–2017 | ||
| [25] | NWT, Canada | TanDEM-X | Microwave | Data from 2011–2017 | ||
| [29] | Mackenzie River Delta and on Banks Island in Canada | TanDEM-X | Microwave | |||
| [48] | Tibetan Plateau, China | PlanetScope imagery | Optical | 3 m | Deep learning CNNs (DeepLabV3+) | |
| [34] | Lena River, Horton Delta, Herschel Island, Kolguev Island, Tuktoyaktuk Peninsula, Banks Island in Canada | PlanetScope imagery, ArcticDEM and multi-temporal Landsat Tasseled Cap Trend data | Optical | 3 m optical and 2 m ArcticDEM | automated; (UNet, UNet++, DeepLabv3) | Area of 100 km2 |
| [48] | Beiluhe region, Tibetan plateau in China | Cubesat imagery | Optical | 3 m | siamese neural network | |
| [47] | High latitudes of Siberia in Russia, | Landsat and Sentinel-2 images: time series; Rapideye, Planetscope imagery | Optical | 30 m, 5 m, 3 m | LandTrendr algorithm | Area of 8.1 × 106 km2 Data from 2001–2019 |
2. Methods
2.1. Study Area and Image Data
We selected two study areas: (1) Banks Island (~3700 km2), Northwest Territories, and (2) Axel Heiberg Island and Ellesmere Island (~4000 km2), Nunavut, Canada (Figure 1), to produce hand-annotated RTS samples, to train/validate/test the deep learning models, and to investigate the interoperability of the trained deep learning model across the two study sites.
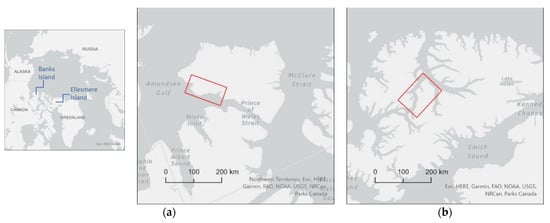
Figure 1.
Inset map shows the geographical setting of the study area. Enlarged views shown in (a,b) depict the areas of interest from Banks Island and the Eureka Sound Lowlands (Axel Heiberg and Ellesmere Islands), respectively. The red hollow box shows the total area mapped using the UNet deep learning model.
Banks Island is the westernmost island, whereas Ellesmere Island and Axel Heiberg Island are the two northernmost islands in the Canadian Arctic Archipelago. The study area (Figure 1b and Figure 2) encompassing southeastern Axel Heiberg Island and west central Ellesmere Island (Fosheim Peninsula) is known as, and will henceforth be termed in the manuscript, as the Eureka Sound Lowlands (ESL). Mean annual air temperature and mean annual precipitation measured at Sachs Harbor, Banks Island, are −12.8 °C and 152 mm, respectively [12], and are −19.7 °C and 68 mm, respectively, measured at the Eureka Weather Station on Ellesmere Island [76].

Figure 2.
Field photos showing RTS activity in Ellesmere Island (left) and Axel Heiberg Island (right) acquired in years 2018 and 2016, respectively.
Both Banks Island and ESL are entirely within the zone of continuous permafrost, where the thickness exceeds 500 m and has medium-to-high ground ice contents in the upper 10 to 20 m [77]. Both regions contain extensive ice-wedge polygon coverage and have long been subject to thermokarst activity. On Banks Island, common thermokarst features include thermokarst lakes and RTS [78]. In the ESL, RTSs are common [13], as well as active layer detachment slides [79]. Both Banks Island and the ESL have experienced a widespread increase in RTS initialization and activity linked to increasing summer air temperatures within the last decade [12,13].
We manually annotated RTSs from Worldview-02 (WV-02) imagery that were acquired during the summer time between the years 2010 and 2015 (Banks Island) and 2011 and 2020 (ESL) (Table 3). We utilized 120 WV02 images from both study areas for the final model predictions. All of the pre-processed (i.e., pansharpened and orthorectified) satellite images were provided by the Polar Geospatial Center at the University of Minnesota.

Table 3.
General characteristics of the satellite imagery utilized in hand-annotation.
2.2. Training Data Production
We tasked three analysts in the manual RTS annotation process. One analyst inspected the accuracy of the hand-annotations produced by the other two. To maintain the consistency in the on-screen digitizing process, we asked analysts to adhere to a fixed visual scale. Based on a series of visual inspections across multiple images and varying sizes of RTSs, we found that scale of 1:2000 provides sufficient visual cues and context to accurately delineate the RTS boundaries. In order to minimize bias coming from color artefacts and to emphasize the RTS from the background, we visualized the imagery as false color composites (green (band 1), red (band 2), near-infrared (band 3)). Generally, false color composites offer a greater level of spectral details to the visual analyst to detect and delineate the targets of interest accurately. Based on the feedback from the permafrost experts and following the formal definition of RTS (Table 1), the boundary delineation was executed as much as possible to reflect a meaningful link between image elements (e.g., color, shape, tone, texture, context) and in situ morphometric/morphological characteristics of RTSs (e.g., headwall, banks, toe, etc.). We produced 475 RTS training samples from each of the study areas (Table 4).

Table 4.
Summary statistics of the hand-annotated RTS training samples from Banks Island and the Eureka Sound Lowlands.
2.3. Retrogressive Thaw Slump Modelling Framework
Our experimental design (Figure 3) aims to answer three research questions: (1) Does image tile size affect RTS prediction accuracies and DLCNN model performances? (2) Does network input size (image resolution) affect RTS prediction accuracies and DLCNN model performances? Finally, (3) What is the degree of interoperability of trained DLCNN models across heterogeneous landscapes? The former two fall under Objective 1, and the latter falls under Objective 2.
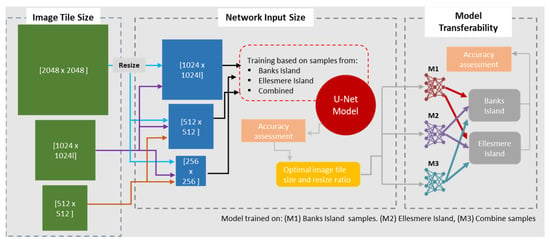
Figure 3.
A simplified schematic of the overall experimental design.
In order to refrain from any terminological ambiguities, here onwards we will use the term image scene to refer to an entire satellite image (generally covers 20 km × 20 km on the ground or 40,000 pxl × 40,000 pxl multidimensional array with four spectral channels), and the term image tile will refer to a subsetted array obtained by tilling the image scene according to predefined tile dimensions (i.e., image tile size). The array size that the DLCNN architecture is designed to admit is referred as the network input size. For simplicity, we will express the array sizes without the notation of ‘pxl’.
To address Objective-1, we partitioned the training image scenes from Banks Island and the ESL into three cohorts of image tile sizes as follows: (1) 2048 × 2048 (~spatial extent: 1 km × 1 km), (2) 1024 × 1024 (~spatial extent: 500 m × 500 m), and (3) 512 × 512 (~spatial extent: 250 m × 250 m). The resulting image tiles from each cohort were grouped into DLCNN model training, validation, and testing with the split rule of 80:10:10, respectively. We tasked this procedure separately on the hand-annotated samples from Banks Island and the ESL and on the combined hand-annotated samples from both Banks Island and the ESL (see middle panel of Figure 3). The network input size was set to three array sizes as 1024 × 1024, 512 × 512, and 256 × 256.
As seen on Figure 3, the arrows (represented as blue, purple, and orange) moving from image tiles to network inputs indicate different model implementation scenarios. For instance, the blue arrow represents the scenario of an image scene that has been partitioned into larger image tiles with the dimension of 2048 × 2048. This tile size was then introduced to the DLCNN model via three network input sizes (1024 × 1024, 512 × 512, and 256 × 256). In order to fit the image tile into the network, each path went through the image-resizing process. In a similar fashion, image tile sizes of 1024 × 1024 and 512 × 512 were introduced to the network. Some of the pathways involved array resizing, whereas others did not. For instance, an image tile of 1024 × 1024 can be directly introduced to the network without the resizing operation (see Figure 3).
To improve the clarity of the multiple scenarios involved in the analysis, we have illustrated the pathways associated with image tile size and network input size by taking image tile size of 2048 × 2048 as an example in Figure 4. It depicts a 2048 × 2048 image tile that is channeled through two pathways:
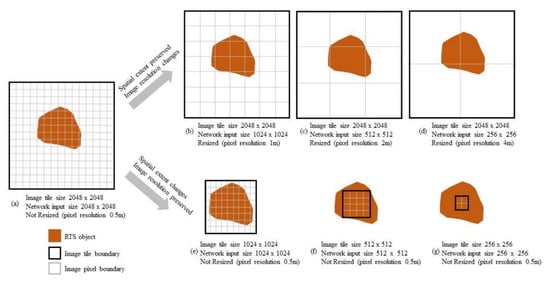
Figure 4.
Image tile size and network input size scenarios considered in the analysis. As an example, here are the scenarios associated with an image input tile size of 2048 × 2048: The original image scene resolution (pixel size) is 0.5 m.
(1) Image tile size (spatial footprint) is unchanged while the network input size (pixel resolution) is changed to maintain the spatial extent (see Figure 4b–d);
(2) Image tile size (spatial footprint) is changed while the network input size (pixel resolution) is unchanged (Figure 4e,f).
In Figure 4, for the sake of visual clarity, we have placed the RTS object in the middle of the image tile. As seen in Figure 4a–c, the RTS object is spatially contained within the image tile; however, the amount of information that is needed to describe the RTS (e.g., edges, texture, shape) degrades due to the increasing pixel size. In contrast, the other pathway (Figure 4a,c–e) maintains a constant spatial resolution, while reducing the spatial footprint size. This causes the RTS object to be included in multiple image tiles (see Figure 4e). Ultimately, we compared the prediction accuracies of all the scenarios to find the optimal combination(s) of the input image size and the network input size.
Findings of Objective-1 provided the basis for Objective-2. Objective-2 explores the interoperability of the DLCNN model across two study sites (Figure 3). We selected the DLCNN models that were trained based on the optimal array sizes. The trained models, M1, M2, and M3 (see right hand panel of Figure 3), represent the best preforming models, which were trained using hand-annotated RTS samples from Banks Island, ESL, and combined RTS samples from both study sites, respectively. Prediction performances of all three models were tested on both Banks Island and the ESL (Figure 3).
2.4. Deep Learning Convolutional Neural Net Architecture
Some of the DLCNN architectures are tailored towards image classification and object detection, while others delve into semantic segmentation (also sematic object instance segmentation) operations. In the sematic object instance segmentation, each of the objects seen in the image are delineated and labelled individually. Among many, popular semantic segmentation architectures include: UNet [80], DeepLab [81], SegNet [82], RefineNet [83], and Mask-RCNN [84]. In our study design, we selected the UNet model as the central DLCNN architecture. The UNet model is computationally efficient model. It has demonstrated a greater success in various image analysis tasks. A detailed explanation about the UNet model architecture is beyond the scope of this study; thus, here we provide a brief and simplified description.
UNet is a U-shaped, fully convolutional neural net model (Figure 5). It comprises two routes: encoding and decoding. The encoding path is also called the analysis path or the contracting path, and the decoding path is known as the synthesis path or expansive path. The former shapes the typical convolution network consisting of many layers such as convolution, Rectified linear unit (ReLU), and max pooling. The function of the encoding path is to reduce the dimensionality of the input layers and increase the number of feature channels. In this route, a 3 × 3 convolution is followed by a ReLU and a 2 × 2 max-pooling that down-samples and doubles the feature channels. On the other hand, the decoding or synthesis path functions opposite to the former one. It reduces the number of channels and increases the spatial dimensions of the layers. The number of channels is halved in an up-sampling process using 2 × 2 convolution at the starting of the decoding route. Afterward, 3 × 3 convolution layers followed by ReLU are used. Skip connections are provided in the architecture that helps in the concatenation of the corresponding feature layer from the encoding path to recover the lost information during down-sampling in the encoding route (Figure 5) [85]. Finally, the dimension of the layers is restored using 1 × 1 convolution to generate a pixel-wise classified predicted map.
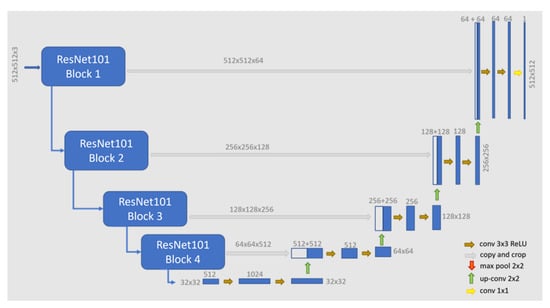
Figure 5.
Generalized architecture of the U-Net deep learning CNN model with the backbone of Resnet101.
To perform the model training with a limited amount of training samples, we used the transfer leaning strategy. This was achieved by replacing the contractive path of the generic UNet model with a backbone (ResNet 101, [86]). Inclusion of the backbone ResNet 101, which has been trained on ImageNet data, enables the initiation of training process based on the existing pre-trained weights. ImageNet is a very large image dataset (14,197,122 annotated images) organized according to the semantic hierarchy of WordNet. Overall, the transfer learning strategy reduces the model overfitting that is common in small-sample training operations.
2.5. Model Training and Accuracy Assessment
As seen in Figure 3 and Figure 4 and explained in Section 2.3, we conducted a series of training scenarios to address the central research questions. Table 5 depicts the parameter setting that was utilized in each of the scenarios. We selected optimal models based on the training and validation loss curves. Different mini-batch sizes were selected to accommodate GPU memory limitations. All the model training and prediction simulations were implemented on a Linux server with the hardware configuration of Intel(R) 8-core i7 CPU @ 3.60 GH and NVIDIA GeForce RTX 2080 with 11 GB memory. The key python libraries used in the image analysis pipeline included PyTorch 1.9, Segmentation-model-pytorch, open CV, GDAL, albumentations, and scikit-learn.

Table 5.
Model training parameter settings.
We employed data augmentation methods to synthetically increase the number of training samples. We used three augmentation methods: vertical flips, horizontal flips, and random rotations of 90 degrees. In each epoch, we applied these augmentations with 0.5 probability to the original training dataset to generate a new augmented dataset. The Adam optimization algorithm was used [87] with Dice loss [88] in model training.
Standard accuracy metrics, such as precision, recall, F1 score, and confusion matrix, were used to assess the model prediction accuracies on the test RTS data set. When calculating accuracy metrics, we purposely used intersection over union (IoU) of 0.8 to impose stringent conditions on the geometrical congruency between the ground-truths (hand-annotation) and the model predictions. We corroborated the quantitative analysis with thorough visual inspections. This is particularly important in evaluating the segmentation quality of RTS with respect to the hand-annotation.
2.6. Model Interoperability Analysis Using Haralick Textures
It is imperative to examine what underlying image properties cause a trained model to fail when it is transferred from one landscape to another to detect the same geo-object. Apart from other low-level motifs (features), image texture is considered as a powerful image descriptor in both manual and automated detections. Texture explains the spatial distribution of intensities within the image [89]. In addition to the high-frequency (i.e., edge) information, texture could serve as a strong contributor in RTS detection. A trained DLCNN model could exhibit weak interoperability if the underlying training data are unable to capture and explain the textural variability in the targets of interest (e.g., RTS).
To further support our model interoperability assessment, we computed thirteen Haralick texture [90] features for the hand-annotated RTS samples from Banks Island and the ESL. The texture measures include: (1) Angular Second Moment, (2) Contrast, (3) Correlation, (4) Variance, (5) Inverse difference momentum, (6) Sum Average, (7) Sum Variance, (8) Sum Entropy, (9) Entropy, (10) Difference Variance, (11) Difference Entropy (12), and (13) Information Measure of Correlation [90].
Haralick texture measures could be correlated and redundant. Therefore, we conducted a principal component analysis (PCA, [89]) to reduce the dimensionality in thirteen texture measures. The PCA is a statistical tool, which is used to extract and express the pattern of the data in different dimensions. It reduces the complexity of a large dataset and summarizes the information by means of a newly formed small set of significantly important variables known as principal components (PC). These PCs represent the summary of the original data and should account for the variances from different variables [91]. The PCA analysis of all the Haralick textures for each Island was conducted on R software using the function called prcomp (www.r-project.org) (accesed on 2 February 2022).
To avoid any ambiguity in texture analysis and its connection to the overall study design, we should note the fact that Haralick textures were not used as additional input layers in the UNet model training, validation, or prediction process. Our model training only relied on the spectral channels of the satellite imagery. We utilized Haralick textures to demonstrate the possible variations in RTSs that we observe in Banks Island and ESL Use of textures in addition to spectral channels of the images for training CNN models is beyond the scope this study.
3. Results
Summary statistics of the hand-annotated RTS samples from Banks Island (n = 475) and the ESL (n = 475) are shown in Figure 6. Histograms of RTSs’ geometrical properties, such as area, length (major axis), width (minor axis), and length to width ratio describe the basic size and shape characteristics of the hand-annotated RTS samples from Banks Island and ESL. In general, the RTS training samples from Banks Island and the ESL reported median sizes of 7.03 ha and 4.67 ha, respectively. The RTS samples from Banks Island showed a higher variability. A similar trend was also observed for other geometrical properties. Statistical comparison of median values of area, length, width, and length to width ratio between two sites showed significant differences (p-value < 0.05) (Table 6).
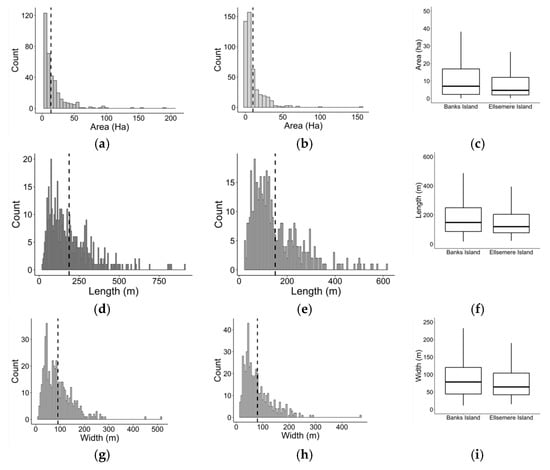
Figure 6.
Distribution and comparison of area, width, and length parameters of the hand-annotated RTS samples from Banks Island and the Eureka Sound Lowlands. Histograms (a,b), (d,e), and (g,h) represent the RTS data distribution of area, length, and width, respectively, for two study sites. Boxplots (c,f,l) depict the area, length, and width of RTS samples from two study sites. (a) Histogram of RTS area based on hand-annotated samples from Banks Island. (b) Histogram of RTS area based on hand-annotated samples from the Eureka Sound Lowlands. (c) RTS area comparison of hand-annotated samples between the Eureka Sound Lowlands and Banks Island. (d) Histogram of RTS length (major axis) based on hand-annotated samples from Banks Island. (e) Histogram of RTS length (major axis) based on hand-annotated samples from the Eureka Sound Lowlands. (f) RTS length comparison of hand-annotated samples between the Eureka Sound Lowlands and Banks Island. (g) Histogram of RTS width (minor axis) based on hand-annotated samples from Banks Island. (h) Histogram of RTS width (minor axis) based on hand-annotated samples from the Eureka Sound Lowlands. (i) RTS width comparison of hand-annotated samples between the Eureka Sound Lowlands and Banks Island.

Table 6.
Statistical comparison of basic geometry (size and shape) of hand-annotated RTS samples from the Eureka Sound Lowlands and Banks Island using independent Wilcoxson rank sum test. (Sample size (n) = 475).
Boxplots shown in Figure 7 report the comparison of thirteen Haralick texture measures (H1–H13). Table 7 depicts the statistical comparison of texture measures of RTSs between Banks Island and the ESL. The test results of the non-parametric independent Wilcoxon rank-sum test showed that the median values of each of the texture measures from two study sites were significantly (p-value < 0.05) different. Based on the results from the PCA, PC1 explained over 80% of the variability in the RTS data from both study sites (Figure 8).
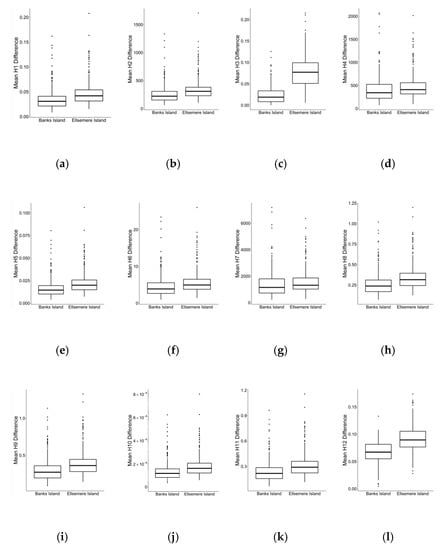
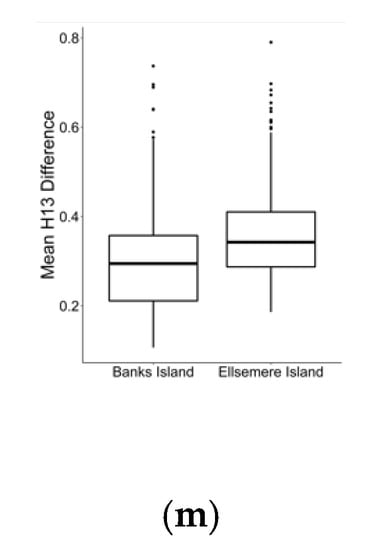
Figure 7.
Boxplots (a–m) showing Haralik texture feature comparisons of hand-annotated RTS from the Eureka Sound Lowlands and Banks Island. (a) H1(Angular second moment). (b) H2 (Contrast). (c) H3 (Correlation). (d) H4 (Variance). (e) H5 (Inverse difference moment). (f) H6 (Sum Average). (g) H7 (Sum Variance). (h) H8 (Sum Entropy). (i) H9 (Entropy). (j) H10 (Difference Variance). (k) H11 (Difference Entropy). (l) H12 (Information Measures of Correlation). (m) H13 (Information Measures of Correlation).

Table 7.
Statistical comparison of Haralik texture features of hand-annotated RTS samples from Eureka Sound Lowlands and Banks Island using independent Wilcoxson test. (n = 475).
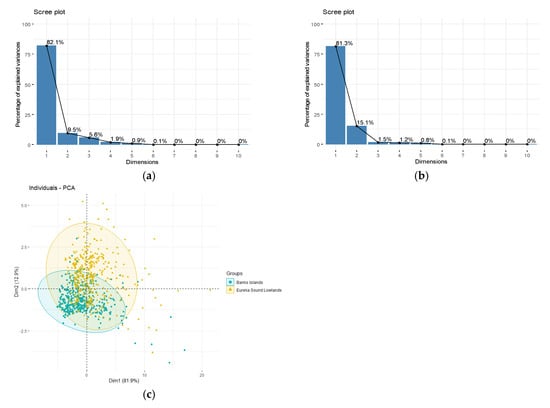
Figure 8.
Principal Component Analysis (PCA) of Haralick texture features of RTS samples from Banks Island and the Eureka Sound Lowlands. Scree plots (a,b) show eigenvalues of thirteen textures. (c) Cluster plot of PC1 and PC2.
We conducted the UNet model training for all the scenarios (i.e., for different image tile sizes and network inputs sizes) across 50 epochs with the expectation of obtaining full loss curves along with accuracy plots (F1 score). Figure 9, Figure 10 and Figure 11 report the Dice loss curves and F1 scores for the training from Banks Island, the ESL, and the combined RTS data from both study sites, respectively. As seen in Dice loss plots, the divergence of the training and validation occurred at different epochs for each of the training scenarios. We selected the optimal UNet weight files based on the Dice loss plot divergences and the F1-score.
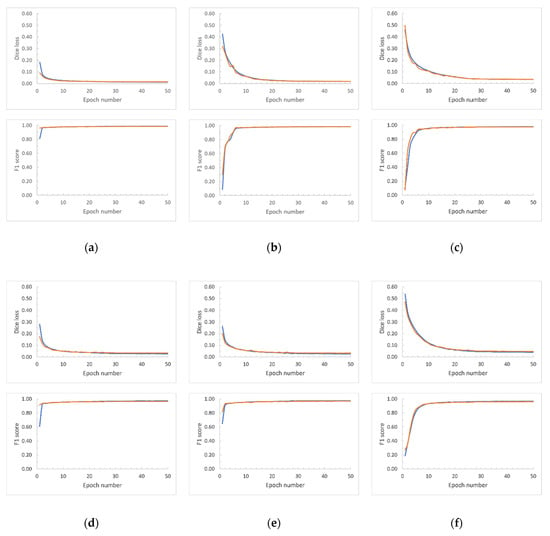
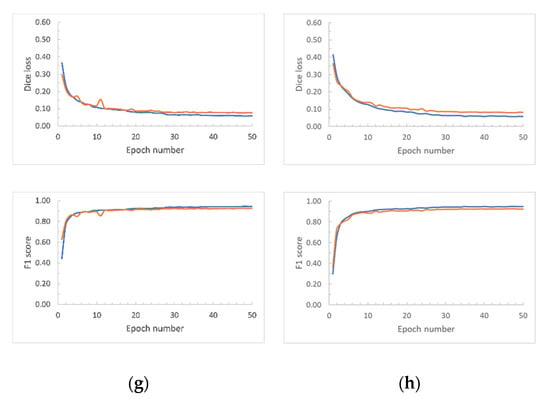
Figure 9.
Training (blue line) and validation (orange line) Dice loss curves based on the hand-annotated data from Banks Island. Array sizes are shown in pixels. (a) Image tile size: 2048 × 2048, Network input size: 1024 × 1024. (b) Image tile size: 2048 × 2048. Network input size: 512 × 512. (c) Image tile size: 2048 × 2048. Network input size: 256 × 256. (d) Image tile size 1024 × 1024. Network input size: 1024 × 1024. (e) Image tile size 1024 × 1024. Network input size: 512 × 512. (f) Image tile size 1024 × 1024. Network input size: 256 × 256. (g) Image tile size 512 × 512. Network input size: 512 × 512. (h) Image tile size: 512 × 512. Network input size: 256 × 256.
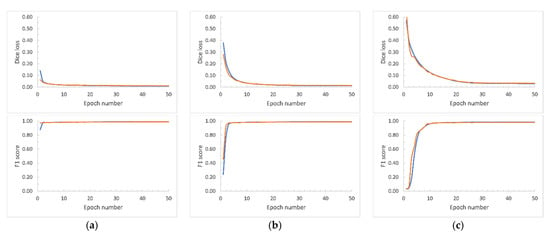
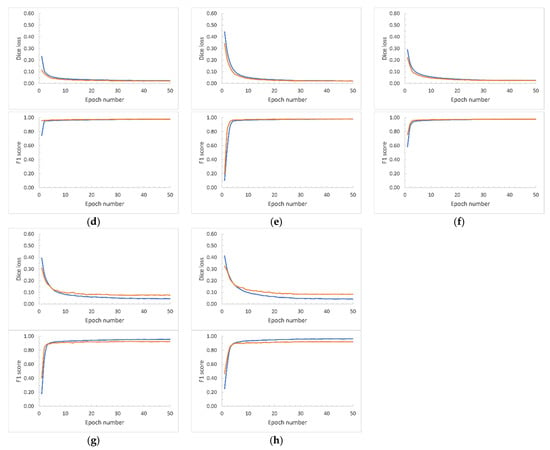
Figure 10.
Training (blue line) and validation (orange line) Dice loss curves based on the hand-annotated data from the Eureka Sound Lowlands. Array sizes are shown in pixels. (a) Image tile size: 2048 × 2048; Network input size: 1024 × 1024. (b) Image tile size: 2048 × 2048; Network input size: 512 × 512. (c) Image tile size: 2048 × 2048; Network input size: 256 × 256. (d) Image tile size: 1024 × 1024; Network input size: 1024 × 1024. (e) Image tile size: 1024 × 1024; Network input size: 512 × 512. (f) Image tile size: 1024 × 1024; Network input size: 256 × 256. (g) Image tile size: 512 × 512; Network input size: 512 × 512. (h) Image tile size: 512 × 512; Network input size: 256 × 256.
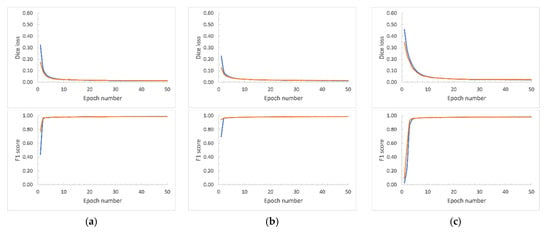
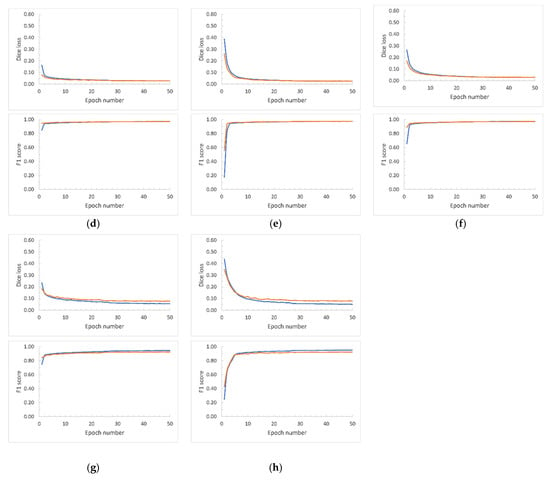
Figure 11.
Training (blue line) and validation (orange line) Dice loss curves based on the hand-annotated data from the Eureka Sound Lowlands and Banks Island (combined RTS training data). Array sizes are shown in pixels. (a) Image tile size: 2048 × 2048. Network input size: 1024 × 1024. (b) Image tile size: 2048 × 2048. Network input size: 512 × 512. (c) Image tile size: 2048 × 2048. Network input size: 256 × 256. (d) Image tile size: 1024 × 1024. Network input size: 1024 × 1024. (e) Image tile size: 1024 × 1024. Network input size: 512 × 512. (f) Image tile size: 1024 × 1024. Network input size: 256 × 256. (g) Image tile size: 512 × 512. Network input size: 512 × 512. (h) Image tile size: 512 × 512. Network input size: 256 × 256.
Figure 12, Figure 13 and Figure 14 show the model accuracy budget associated with each of the optimal model weight files when tested on the test RTS samples from Banks Island, the ESL, and the combined RTS samples, respectively. Each figure represents the test accuracies associated with three image tile sizes (2048 × 2048, 1024 × 1204, and 512 × 512) and corresponding network inputs sizes (1024 × 1024, 5125 × 512, and 256 × 256). When analyzing the test accuracy budget based on the RTSs from each of the study sites and the combined RTSs, it is evident that the trained models showed the highest accuracies when they had the combination of image tiles size of 2048 × 2048 and network input tile size of 1024 × 1204. Confusion matrices from Banks Island (Figure 12a–c) report the highest true RTS (83%) rate and the lowest false RTS (17%) rate when the image tile of 2048 × 2048 is resized to the network input size of 1024 × 1024.
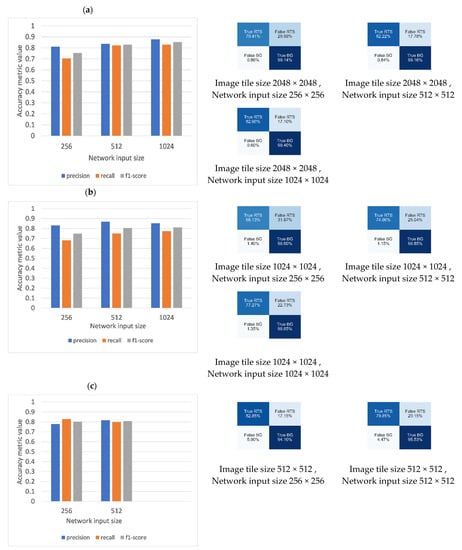
Figure 12.
Model test accuracy based on the hand annotated RTS from Banks Island. (a) Image tile size of 2048 × 2048 resized to network input sizes of 256 × 256, 512 × 512, and 1024 × 1024. (b) Image tile size of 1024 × 1024 resized to network input sizes of 256 × 256, 512 × 512, and without resizing as 1024 × 1024. (c) Image tile size of 512 × 512 resized to network input size of 256 × 256 and without resizing as 512 × 512. Bar charts depict accuracy measures of Precision, recall, and F1 score. Corresponding confusion matrix for each of the scenarios shown on the right.
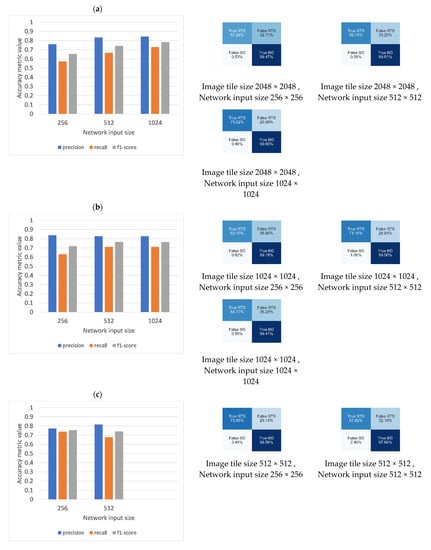
Figure 13.
Model test accuracy based on the hand-annotated RTS from the Eureka Sound Lowlands. (a) Image tile size of 2048 × 2048 resized to network input sizes of 256 × 256, 512 × 512, and 1024 × 1024. (b) Image tile size of 1024 × 1024 resized to network input sizes of 256 × 256, 512 × 512, and without resizing as 1024 × 1024. (c) Image tile size of 512 × 512 resized to network input size of 256 × 256 and without resizing as 512 × 512. Bar charts depict accuracy measures of Precision, recall, and F1 score. Corresponding confusion matrix for each of the scenarios shown on the right.
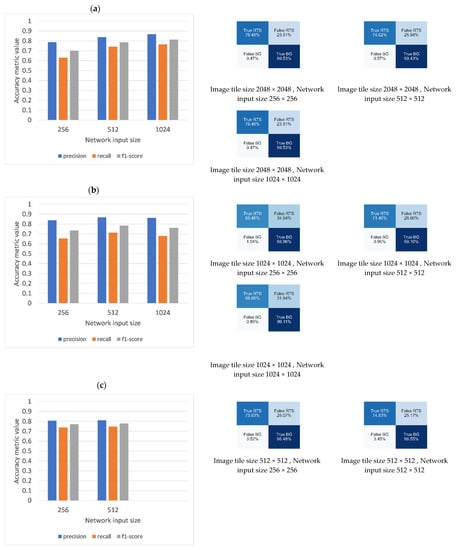
Figure 14.
Model test accuracy based on the hand-annotated RTS from both Banks Island and the Eureka Sound Lowlands (combined RTS samples). (a) Image tile size of 2048 × 2048 resized to network input sizes of 256 × 256, 512 × 512, and 1024 × 1024. (b) Image tile size of 1024 × 1024 resized to network input sizes of 256 × 256, 512 × 512, and without resizing as 1024 × 1024. (c) Image tile size of 512 × 512 resized to network input size of 256 × 256 and without resizing as 512 × 512. Bar charts depict accuracy measures of Precision, recall, and F1 score. Corresponding confusion matrix for each of the scenarios shown on the right.
There is a marked leap in the false positive rate of RTSs due to an increasing resizing factor. When the image tile of 2048 × 2048 is resized to the network input tile size of 256 × 256, the false RTS rate reaches up to 30% (Figure 12a). The highest true RTS rate (73%) was reported by the image tile size to network input size combination of 2048 × 2048. The lowest false RTS rate (27%) was reported by the image tile size to network input size combination of 1024 × 1024 (Figure 13). The models that were trained using the combined RTS data (i.e., RTS samples from both Banks Island and ESL) also highlighted the impact of image tile size and resizing factor on model prediction accuracies. The combination 2048 × 2048 to 1024 × 1024 secured the highest true RTS rate (76%).
The impact of image tile size on the UNet model performances is visible when comparing the accuracy plots and confusion matrices (see Figure 13a,b, Figure 14a,b and Figure 15. A reduction in the image tile size reduces the inclusion of the background (in other words, the target dominates the image tile). This class imbalance between the target and the background leads to higher rates of false background. For instance, as seen in Figure 14b,c, when the image tile (512 × 512) is introduced without resizing to the network (512 × 512), the false background rate was 3%. However, when the image tile (1024 × 1024) is introduced without resizing to the network (1024 × 1024), the false background rate was 1%.
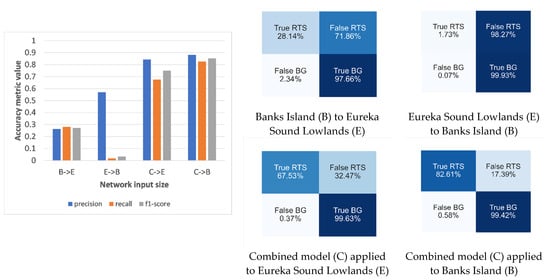
Figure 15.
Effect of model transferability on the RTS prediction accuracy. Transferability scenarios considered include: (1) the DLCNN model trained on the RTS data from Banks Island (B) and applied to test data from Eureka Sound Lowlands (E), (2) the DLCNN model trained on the RTS data from Ellesmere Island (E) and applied to test data from Banks Island (B), (3) the DLCNN model trained on the combined RTS data and applied to Eureka Sound Lowlands (E), and (4) the DLCNN model trained on the combined RTS data and applied to Banks Island (B). Bar charts depict accuracy measures of Precision, recall, and F1 score. Corresponding confusion matrix for each of the scenarios shown on the right.
Accuracy metric values and confusion matrices pertaining to the model transferability analysis are shown in Figure 15. We used the combination of image tile size (2048 × 2048) and network input size (1024 × 1024) in the transferability analysis. We considered four transferability pathways:
(1) Train the UNet model based on Banks Island (B) data and test it on the RTSs from ESL (E) (B- > E);
(2) Train the UNet model based on ESL (E) and test it on the RTSs from Banks Island (E- > B);
(3) Train the UNet model based combined samples (C) and test it on the RTSs from Banks Island (C- > B);
(4) Train the UNet model using combined samples and test it on the RTSs from ESL (C- > E).
The model transferability pathway of E- > B exhibited the lowest values for the F1 score and for the Recall compared to the other three pathways. It reported a very low true RTS detection rate of 2%. Comparatively, the B- > E pathway performed well with a true RTS detection rate of 26%. This explains that the model trained using RTSs from Banks Island show some degree of elasticity compared to the model trained using RTS samples from ESL. When both RTS sample sets are combined, the trained model exhibited a conspicuous improvement in prediction accuracies. In both the C- > E and C- > B pathways, the F1 score was over 0.75. When comparing the true RTS rates, the C- > E and C- > B pathways reported rates of 68% and 83%, respectively. Overall, the combined model performed well in Banks Island, exhibiting a greater degree of generalizability.
A set of enlarged views, along with model predictions, are shown in Figure 16, Figure 17 and Figure 18. These figures show the impact of image tile size and network input size on the DLCNN model performances. In Figure 16, the input image tiles (a,e,i) of 2048 × 2048 (0.5 m spatial resolution) are resized into three network input sizes (1024 × 1024 (b,f,j), 512 × 512 (c,g,k), and 256 × 256 (d,h,f)). In all cases, the spatial footprint of the image tile is kept unchanged, while the spatial resolution is degraded progressively. It is evident that resizing of 2048 × 2048 to 1024 × 1024 provided the highest geometrical congruency of the predicted RTS object (see yellow outline) and the actual RTS seen in the image (see white arrow). Accuracy of RTS boundary detection has decreased with respect to increasing resizing factor (see Figure 16g,h). For smaller RTS objects, as shown in Figure 16j–i, a higher resizing factor (e.g., 2048 × 2048 to 256 × 256) can lead to missed detections (For example, no detections seen in Figure 16i).
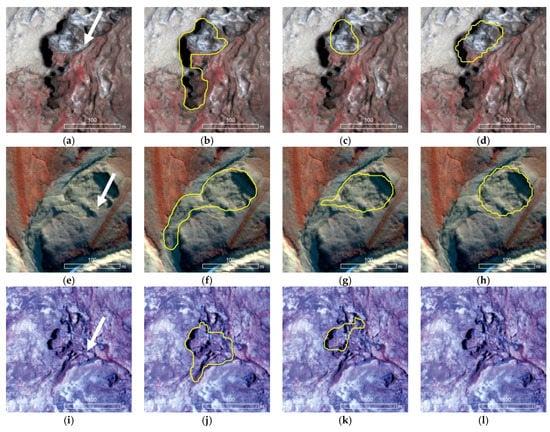
Figure 16.
Example zoomed-in views of DLCNN model predictions on the test data from selected location of Banks Island and the Eureka Sound Lowlands. Examples exhibit training and prediction of input image tiles 2048 × 2048 (a,e,i) with resizing into 3 different network input sizes: 1024 × 1024 (b,f,j); 512 × 512 (c,g,k), and 256 × 256 (d,h,l). Outline of the predicted RTS is shown in yellow. White arrows indicate the location of the RTS. Underlying imagery is at 0.5 m resolution as false color composites.
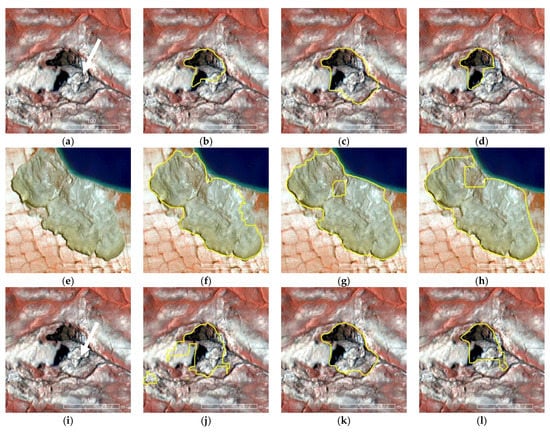
Figure 17.
Example zoomed-in views of DLCNN model predictions on the test data from selected location of Banks Island and the Eureka Sound Lowlands. Examples exhibit training and prediction of input image tiles of 1024 × 1024 (a,e,i) without resizing 1024 × 1024 (b,f,j) and with resizing into two network input sizes: 512 × 512 (c,g,k), and 256 × 256 (d,h,l). Outline of the predicted RTS is shown in yellow outline. White arrows indicate the location of RTS. Underlying imagery is at 0.5 m resolution as false color composites.
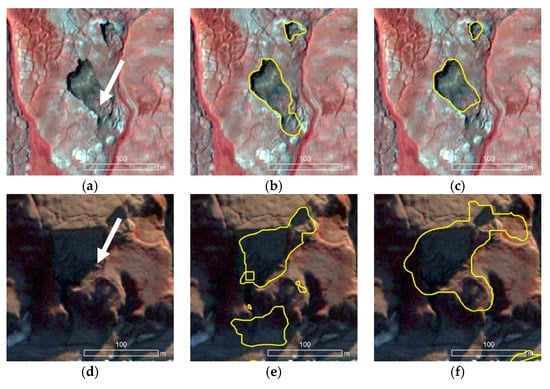

Figure 18.
Example zoomed-in views of DLCNN model predictions on the test data from selected location of Banks Island and the Eureka Sound Lowlands. Examples show training and prediction of input image tiles of 512 × 512 (a,d,g) without resizing 512 × 512 (b,e,h) and with resizing into one network input size: 256 × 256 (c,f,i). Outline of the predicted RTS is shown in yellow outline. White arrows indicate the location of RTS. Underlying imagery is at 0.5 m resolution as false color composites.
A closer inspection on Figure 17 can provide further insights to understand the relationship between the RTS object size and the resizing factor. In this case, the image tiles of 1024 × 1024 resolution have progressively been resized to two network input sizes (512 × 512 and 2565 × 256). For large RTS objects, the shape and geometrical congruency are mostly intact despite the increasing resizing factor (see Figure 16f–h). Figure 18 illustrates the model prediction results pertaining to the image tiles of 512 × 512 and 256 × 256.
Zoomed-in views shown in Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23 aim to further explain how the resizing factor affect the DLCNN model performances. In the cases shown in Figure 21 and Figure 22, the spatial footprint size of the image tile is preserved. However, the spatial resolution (0.5 m) is down-sampled to match different network input sizes. We employed the Canny edge detection algorithm on the original image tile and the resized images to visualize the changes in high frequency information (i.e., edges). For large, homogenous, well-pronounced, and spatially discrete RTS objects (see Figure 21), the impact of resizing factor is trivial. However, in the case of small-size and closely packed RTSs, the model performances could be influenced by the degrading resolution (see Figure 20c,d). Losing high-frequency information due to increasing the resizing factor (512 × 512 and 256 × 256) would degrade the boundary detection and object separability. For instance, see red arrows on the resized images and corresponding Canny edge rasters in Figure 20c,d,g,h).


Figure 19.
Exampled zoomed-in views (a–d) showing the effect of image resizing (spatial resolution degradation) on model predictions. Canny edge images of corresponding original and resized images are shown in (e–h). White arrows indicate the location of RTS. Underlying imagery is at 0.5 m resolution with false color composite. (a) Original image tile (2048 × 2048) at 0.5 m resolution. (b) Resized image at 1 m resolution (1024 × 1024). (c) Resized image at 2 m resolution (512 × 512). (d) Resized image at 4 m resolution (256 × 256). (e) Canny edge raster at 0.5 m resolution. (f) Canny edge raster at 1 m resolution. (g) Canny edge raster at 2 m resolution. (h) Canny edge raster at 4 m resolution.

Figure 20.
Exampled zoomed-in views (a–d) showing the effect of image resizing (spatial resolution degradation) on model predictions. Canny edge images of corresponding original and resized images are shown in (e–h). White arrows indicate the location of RTS. Underlying imagery is at 0.5 m resolution with false color composite. (a) Original image at 0.5 m resolution. (b) Resized image at 1 m resolution (1024 × 1024). (c) Resized image at 2 m resolution (512 × 512). (d) Resized image at 4 m resolution (256 × 256). (e) Canny edge raster at 0.5 m resolution. (f) Canny edge raster at 0.5 m resolution. (g) Canny edge raster at 2 m resolution. (h) Canny edge raster at 4 m resolution.

Figure 21.
Fluctuation of the model-predicted RTS boundary (here zoomed into headwall of the RTS) with respect to image resizing factor (spatial resolution degradation). (a) Model-predicted boundaries when the original image tile (2048 × 2048) is resized to match the network input sizes of 1024 × 1024 (green outline), 512 × 512 (cyan outline), and 256 × 256 (purple outline). Visuals of corresponding resized images are shown in (b–d). Underlying imagery are shown in false color composites. (a) DLCNN model response to resizing scenario of 2048 × 2048 to 1024 × 1024 (green outline), 2048 × 2048 to 512 × 512 (cyan outline) and 2048 × 2048 to 256 × 256 (purple outline). (b) Resized input image tile at 1 m resolution (1024 × 1024). (c) Resized image tile at 2 m resolution (512 × 512). (d) Resized image input tile at 4 m resolution (256 × 256).
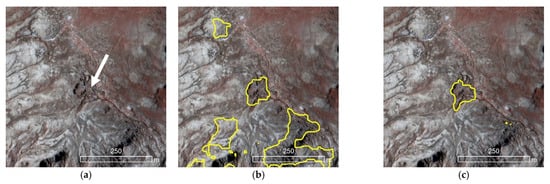
Figure 22.
Example zoomed-in views showing model transferability across study sites. (a) Original image from Ellesmere Island. (b) The DLCNN model trained on Banks Island’s RTS samples and applied to the Eureka Sound Lowlands. (c) The DLCNN model trained on combined RTS samples and applied to Eureka Sound Lowlands. White arrows indicate the location of RTS. Underlying imagery is at 0.5 m resolution as false color composites.

Figure 23.
Example zoomed-in views capturing model transferability across study sites. (a) Original image from Banks Island. (b) The DLCNN model trained on Eureka Sound Lowlands’ RTS samples and applied to Banks Island. (c) The DLCNN model trained on combined RTS samples and applied to Banks Island. White arrows indicate the location of RTS. Underlying imagery is at 0.5 m resolution with false color composite.
Figure 21 shows example RTSs with predicted boundaries under different resizing scenarios. We can observe an abrupt reduction in spatial accuracy when the input image tile of 2048 × 2048 is resized to match the network input size of 256 × 256 (see purple outline in Figure 21a). The position of the predicted headwall has shifted downslope by approximately 20 m (see white arrow in Figure 21a) compared to other predicted boundaries (see green, purple, and cyan outlines in Figure 21a).
Example visual inspections related to model transferability analyses are shown in Figure 22 and Figure 23 (ESL), and Figure 22 (Banks Island). Figure 22b shows the predicted RTSs (see yellow outlines) from the DLCNN model that was trained using RTS samples from Banks Island. This represents the transferability pathway of B- > E. Figure 22c shows the predicted RTSs from the model that was trained using combined RTS samples. This pertains to the transferability pathway of C- > E. When comparing Figure 22a,b, it is obvious that the model transferability is allowed but at the expense of higher false positive rates. The UNet model that was trained using combined RTS samples showed the best prediction results. This observation aligns with our quantitative assessment (see Figure 15).
The reverse direction (E- > B) is considered in Figure 23b. In this case, the predictions were made on Banks Island using the UNet model that was trained using the RTS samples from ESL. Interestingly, despite the crisp appearance and the large size of the RTSs (see white arrows on Figure 23a), the model was unable to make at least a single prediction. This example further reinforces our quantitative results on model transferability analysis (Figure 15). Figure 20c shows an accurate detection of RTSs when the model was trained using combined RTS data (C- > E).
Based on the finding from our analyses; (1) image tile size and network input size and (2) model transferability, we applied the final UNet model over two study areas to map RTSs. In the prediction mode, we used 2048 × 2048 as the image tile size and 1024 × 1024 as the network input size. Figure 24 and Figure 25 depict the summarized RTS area for Banks Island and the ESL, respectively. For the sake of representation purposes, we have overlain a hexagonal grid (cell size of 100 ha) and calculated the detected RTS area in each hexagon.
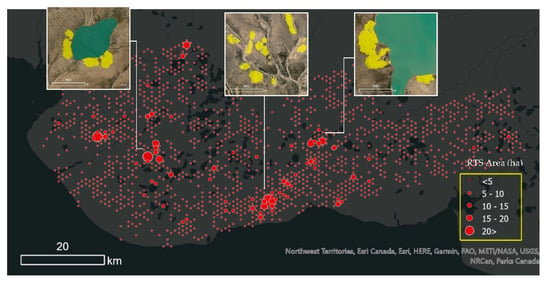
Figure 24.
Retrogressive thaw slump (RTS) map for Banks Island based on the predictions of the optimal DLCNN model that was trained based on combined hand-annotated samples and optimal image tile size and network input size. The size of the map symbol (red circle) is proportional to the area (in ha) of the RTS falling inside a hexagonal grid. Each grid cell covers 100 ha. Yellow shading on zoomed-in views indicates detected RTS.
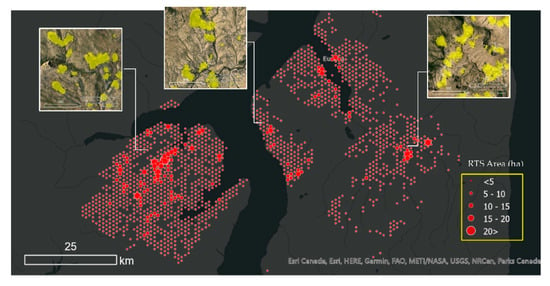
Figure 25.
Retrogressive thaw slump (RTS) map for the Eureka Sound Lowlands based on the predictions of the optimal DLCNN model that was trained based on combined hand-annotated samples and optimal image tile size and network input size. The size of the map symbol (red circle) is proportional to the area (in ha) of the RTS falling inside a hexagonal grid. Each grid cell covers 100 ha. Yellow shading on zoomed-in views indicates detected RTS.
4. Discussion
As seen in our quantitative assessments and visual inspections, when the RTS object is substantially larger than the image tile size, the model learns features from the object itself but overlooks the contextual information. Thus, when deciding the image tile size in an operational image analysis pipeline, one should be conversant to the size distribution of the geo-object of interest rather pursuing an arbitrary array size or solely relying on the pre-defined CNN network input size. It is also important to consider the spatial continuity of the geo-object of interest; for instance, ice-wedge polygons typically represent a repeated pattern on the ground [92,93], while RTSs stand out as discrete landform units from the surrounding landscape.
A moderate level of resizing causes the homogenization of image pixels. It reduces the intra-class variability of VHSR imagery [94,95]. The resizing process also benefits the inclusion of additional contextual information while maintaining the spatial footprint size. The F1 scores from multiple simulation scenarios consistently elected the resizing of the image tile size of 2048 × 2048 into network input size of 1024 × 1024 as the best setting for the model predictions. Our results demonstrate the importance of maintaining the optimal spatial footprint, which captures sufficient contextual information to increase the heterogeneity between the object of interest and its surrounding. Another angle to explain the interdependence of object size, image tile size, and network input size is the class imbalance between the background and the foreground. Both scenarios of background-dominated image tiles and object-dominated image tiles cause class imbalances and negatively influence the model’s performance.
Our findings captured the model response to the spatial resolution variations in the input imagery. Image tile resizing mimics multiple spatial resolutions. The low spatial resolution images help the DLCNN to capture more global feature representations, but the finer features can be lost. Our findings clearly demonstrate the deterioration in model predictions in response to the decreasing spatial resolution. When the spatial resolution is degraded to the 4 m resolution, the detection rate was immediately reduced. This is due to the dilution of small RTSs with the background. The boundaries of large objects showed high spatial errors due the lack of high-frequency (edge) information. High-resolution images allow the model to learn and capture finer details but overlook the global features due to the increasing spectral heterogeneity of pixels.
We should realize the fact that there is always a trade-off between spatial resolution of the imagery and the level of abstraction that we pursued to achieve in a mapping application [96,97]. If the goal is to track the temporal migration of the RTS’s headwall (or monitoring the changes happening to the overall RTS anatomy), one must pay close attention to the spatial resolution of the underlying imagery. Otherwise, proceeding calculations could be error-prone. If the goal is to enumerate the presence or absence of an RTS over a large area, the impact of spatial resolution might be trivial. The selection of the optimal input image resolution is therefore vital in the successful adaptation of DLCNNs in RTS mapping.
Our experimental design contained an array of model training scenarios. The learning rate is one of the most sensitive hyper-parameters. Using decay learning rate will help to reduce the effects of overfitting when training the network [98]. We utilized learning rate decay to avoid overfitting during training. Another important hyper-parameter is the batch size, since it controls the accuracy of the estimate of the error gradient when training CNNs. Ref. [99] suggest that it is beneficial to increase the mini-batch size rather than decaying the learning rate in training. This was evident when we tried to train 2048 images with a 2048 network size. In this case, we had to set the mini-batch size to 1 due to the GPU’s memory constraints. This resulted in the overfitting of the model with extremely high accuracies for the training dataset and low accuracies for the validation data set. In contrast, too-large batch sizes can decrease the generalization of the model [100,101]. Therefore, we selected mini-batch sizes of 4 to 16 in the training schedule to avoid under-/over-fitting of the model.
The performance of DLCNNs largely depend on the quantity, quality, and accuracy of the training data samples. If the hand-annotated samples are unable to capture variability in the target object itself (e.g., RTS) and as well as its surroundings (e.g., microtopography, vegetation, geology, etc.), the transferability of the DLCNN model across different landscapes as well as image data inputs can be difficult. Results from the model transferability experiment elucidate the impact of spectral, spatial, and textural variations of RTS samples on the robustness of the DLCNN model.
In addition to the results from the geometry-based analysis of RTSs (size and basic shape), comparative results from the Haralick texture features of RTSs and the background terrain exhibit useful information to explain the question of why certain transferability pathways favored over the others. It is evident that the mean difference of the textural features between the RTS and the background is significantly higher in the ESL than those of Banks Island. Results from the principal component analysis further suggested the greater dispersion of image texture in the hand-annotated RTS data from the ESL. This explains why the model became brittle when migrating from the ESL to Banks Island.
In general, RTS objects (or the exposed ground) carry similar spectral characteristics regardless of the terrain conditions. In the absence of (or sparse) vegetation in the high Arctic, spectral contrast between the foreground and the background could be subtle. However, landform objects could own distinct spectral characteristics. Thus, in the model training process, inclusion of pre-mined texture features in addition to the spectral channels could improve the accuracy of RTS recognition. This could further help in lowering the effort on additional training data production to capture landscape variability.
The quality of training data can largely influence the accuracy (as well as the meaningfulness) of model predictions. It is particularly crucial in remote sensing image analysis. Annotation is a human-driven process. Delineation of landforms at large and RTS in specific could be a challenging task as it depends on the expertise of the analyst, the scale at which the image is analyzed, and the properties of the image data. Accurate boundary delineation of an RTS by a novice could be substantially different than a domain expert. In the context of RTS mapping, it is true that we pursue an abrupt discontinuity in the terrain based on the visual cues primarily associated with the edge information. In other words, one could delineate the boundary of an RTS in the absence of color information. Headwalls are key feature of RTSs, and it these be the most powerful visual cues used in the annotation process. However, continuity of the RTS downslope is rather ill-defined unless the toe area has a terminal object, such as a lake, a river, or the coast. In the absence of a terminal object, we must make a decision on where to stop the annotation and close the polygon. This cutoff point is subjective and domain-knowledge-dependent. Early stopping of the RTS outlining process (without further moving downslope from the headwall) would prevent the inclusion of crucial anatomical features of RTSs.
When we closely inspected RTS annotations from other studies, it was evident that the annotation process lacks formality and consistency. Among many, some of the important questions arising in the annotation process include: Should annotation include debris flow? deposition area? If those should be included, how far away from the headwall should they be? In some instances, debris flow is more extensive than the RTS itself. The taxonomy of RTSs based on the age/structure/function is another aspect to consider in the annotation process. The study scope was not to formalize the domain knowledge of RTS or construct ontologies. However, our careful literature survey on RTS definitions would spur the interest for a critical discussion on the semantics of RTS and the execution of a knowledge formalization process.
5. Conclusions
Operational scale mapping of landforms, particularly in Arctic permafrost landscapes that extend over millions of square kilometers, require sophisticated image analysis algorithms. Owing to the inherent differences in array size, multiple spectral channels, and scene complexity of very high spatial resolution satellite imagery coupled with landscape variability and unique semantics embedded with geo-objects, it is important to understand the opportunities and the challenges associated with deep learning convolutional neural net (DLCNN) algorithms pertaining to the characteristics of input image data, target object(s), and the automated classification problem in hand. In this study, centering on retrogressive thaw slumps (RTSs) as the model landform object and sub-meter resolution satellite imagery as the input data stream, we systematically investigated a set of candidate factors that decide the DLCNN model performances and the interoperability of the model across heterogenous landscapes. Our results demonstrated the impact of image tile size, network input size, and resizing ratio (spatial resolution) on the DLCNN model prediction accuracies. It was found that maintaining optimal array sizes for the input image tile and the CNN network are critical for the accurate delineation of the RTS boundary. A representative training data set should account the spectral, spatial, textural, and contextual variabilities of RTSs across different permafrost-region landscapes. Our results clearly demonstrated that the robustness of the CNN model is largely pivoted to the underlying training data. Thus, the model transferability (or the generalizability) is a vital aspect to consider when operationalizing CNN-based RTS mapping over large geographical extents. The current study focuses on one DLCNN architecture (UNet). In future research, we aim to compare the performances of different DCLNN architectures and their robustness in RTS mapping tasks.
Author Contributions
Conceptualization, C.W.; Data curation, E.M.; Formal analysis, M.R.U.; Software, M.R.U.; Validation, D.J.; Visualization, A.H., D.J. and E.M.; Writing—original draft, C.W.; Writing—review & editing, M.R.U., A.K.L., M.K.W.J. and B.M.J. All authors have read and agreed to the published version of the manuscript.
Funding
National Science Foundation, Grant Numbers 1927872, 1927723, 1927729, 1927720, 1927920, 1929170. National Aeronautics and Space Administration, Grant Number 80NSSC21K1820.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Black, R.F.; Muller, S.W. Permafrost or Permanently Frozen Ground and Related Engineering Problems. Geogr. Rev. 1948, 38, 686. [Google Scholar] [CrossRef]
- Brown, J.; Ferrians, O.J.J.; Heginbottom, J.A.; Melnikov, E.S. Circum-Arctic map of permafrost and ground-ice conditions. In Circum-Pacific Map Series CP-45, Scale 1:10,000,000, 1 Sheet; USGS in Cooperation with the Circum-Pacific Council for Energy and Mineral Resources: Washington, DC, USA, 1997; Available online: https://www.researchgate.net/publication/303677186_CircumArctic_map_of_permafrost_and_groundce_conditions_Washington_DC_US_Geological_Survey_in_Cooperation_with_the_CircumPacific_Council_for_Energy_and_Mineral_Resources_Circum-Pacific_Map_Series_C (accessed on 4 January 2022).
- Zhang, H.; Zhang, J.; Zhang, Z.; Chen, J.; You, Y. A consolidation model for estimating the settlement of warm permafrost. Comput. Geotech. 2016, 76, 43–50. [Google Scholar] [CrossRef]
- Melvin, A.M.; Larsen, P.; Boehlert, B.; Neumann, J.E.; Chinowsky, P.; Espinet, X.; Martinich, J.; Baumann, M.S.; Rennels, L.; Bothner, A.; et al. Climate change damages to Alaska public infrastructure and the economics of proactive adaptation. Proc. Natl. Acad. Sci. USA 2017, 114, E122–E131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hjort, J.; Streletskiy, D.; Doré, G.; Wu, Q.; Bjella, K.; Luoto, M. Impacts of permafrost degradation on infrastructure. Nat. Rev. Earth Environ. 2022, 3, 24–38. [Google Scholar] [CrossRef]
- Smith, S.L.; O’Neill, H.B.; Isaksen, K.; Noetzli, J.; Romanovsky, V.E. The changing thermal state of permafrost. Nat. Rev. Earth Environ. 2022, 3, 10–23. [Google Scholar] [CrossRef]
- Abbott, B.W.; Jones, J.B.; Godsey, S.E.; Larouche, J.R.; Bowden, W.B. Patterns and persistence of hydrologic carbon and nutrient export from collapsing upland permafrost. Biogeosciences 2015, 12, 3725–3740. [Google Scholar] [CrossRef] [Green Version]
- Coch, C.; Lamoureux, S.F.; Knoblauch, C.; Eischeid, I.; Fritz, M.; Obu, J.; Lantuit, H.; Lamoureux, S.; Eischeid, I.; Fritz, M. Summer rainfall dissolved organic carbon, solute, and sediment fluxes in a small Arctic coastal catchment on Herschel Island (Yukon Territory, Canada). Arctic Sci. 2018, 4, 750–780. [Google Scholar] [CrossRef] [Green Version]
- Levenstein, B.; Lento, J.; Culp, J. Effects of prolonged sedimentation from permafrost degradation on macroinvertebrate drift in Arctic streams. Limnol. Oceanogr. 2021, 66, S157–S168. [Google Scholar] [CrossRef]
- Tanski, G.; Wagner, D.; Knoblauch, C.; Fritz, M.; Sachs, T.; Lantuit, H. Rapid CO2 Release from Eroding Permafrost in Seawater. Geophys. Res. Lett. 2019, 46, 11244–11252. [Google Scholar] [CrossRef] [Green Version]
- Farquharson, L.M.; Romanovsky, V.E.; Cable, W.L.; Walker, D.A.; Kokelj, S.V.; Nicolsky, D. Climate change drives widespread and rapid thermokarst development in very cold permafrost in the Canadian High Arctic. Geophys. Res. Lett. 2019, 46, 6681–6689. [Google Scholar] [CrossRef] [Green Version]
- Lewkowicz, A.G.; Way, R.G. Extremes of summer climate trigger thousands of thermokarst landslides in a High Arctic environment. Nat. Commun. 2019, 10, 1329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jones, M.K.W.; Pollard, W.H.; Jones, B.M. Rapid initialization of retrogressive thaw slumps in the Canadian high Arctic and their response to climate and terrain factors. Environ. Res. Lett. 2019, 14, 55006. [Google Scholar] [CrossRef]
- Schuur, E.A.G.; Mack, M.C. Ecological response to permafrost thaw and consequences for local and global ecosystem services. Annu. Rev. Ecol. Evol. Syst. 2018, 49, 279–301. [Google Scholar] [CrossRef]
- Liljedahl, A.K.; Boike, J.; Daanen, R.P.; Fedorov, A.N.; Frost, G.V.; Grosse, G.; Hinzman, L.D.; Iijma, Y.; Jorgenson, J.C.; Matveyeva, N.; et al. Pan-Arctic ice-wedge degradation in warming permafrost and its influence on tundra hydrology. Nat. Geosci. 2016, 9, 312–318. [Google Scholar] [CrossRef]
- Lafrenière, M.J.; Lamoureux, S.F. Effects of changing permafrost conditions on hydrological processes and fluvial fluxes. Earth-Sci. Rev. 2019, 191, 212–223. [Google Scholar] [CrossRef]
- Turetsky, M.R.; Abbott, B.W.; Jones, M.C.; Anthony, K.W.; Olefeldt, D.; Schuur, E.A.G.; Grosse, G.; Kuhry, P.; Hugelius, G.; Koven, C.; et al. Carbon release through abrupt permafrost thaw. Nat. Geosci. 2020, 13, 138–143. [Google Scholar]
- Ramage, J.; Jungsberg, L.; Wang, S.; Westermann, S.; Lantuit, H.; Heleniak, T. Population living on permafrost in the Arctic. Popul. Environ. 2021, 43, 22–38. [Google Scholar] [CrossRef]
- Bartsch, A.; Pointner, G.; Nitze, I.; Efimova, A.; Jakober, D.; Ley, S.; Högström, E.; Grosse, G.; Schweitzer, P. Expanding infrastructure and growing anthropogenic impacts along Arctic coasts. Environ. Res. Lett. 2021, 16, 115013. [Google Scholar] [CrossRef]
- Jorgenson, M.T.; Shur, Y.L.; Pullman, E.R. Abrupt increase in permafrost degradation in Arctic Alaska. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Nitze, I.; Grosse, G.; Jones, B.M.; Romanovsky, V.E.; Boike, J. Author Correction: Remote sensing quantifies widespread abundance of permafrost region disturbances across the Arctic and Subarctic. Nat. Commun. 2019, 10, 472. [Google Scholar] [CrossRef]
- Nitze, I.; Cooley, S.W.; Duguay, C.R.; Jones, B.M.; Grosse, G. The catastrophic thermokarst lake drainage events of 2018 in northwestern Alaska: Fast-forward into the future. Cryosphere 2020, 14, 4279–4297. [Google Scholar] [CrossRef]
- Kokelj, S.V.; Tunnicliffe, J.; Lacelle, D.; Lantz, T.C.; Chin, K.S.; Fraser, R. Increased precipitation drives mega slump development and destabilization of ice-rich permafrost terrain, northwestern Canada. Glob. Planet. Chang. 2015, 129, 56–68. [Google Scholar] [CrossRef] [Green Version]
- Swanson, D.K. Permafrost thaw-related slope failures in Alaska’s Arctic National Parks, c. 1980–2019. Permafr. Periglac. Process. 2021, 32, 392–406. [Google Scholar] [CrossRef]
- Bernhard, P.; Zwieback, S.; Leinss, S.; Hajnsek, I. Mapping Retrogressive Thaw Slumps Using Single-Pass TanDEM-X Observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3263–3280. [Google Scholar] [CrossRef]
- Mackay, J.R. Segregated epigenetic ice and slumps in permafrost, Mackenzie Delta area, NWT. Geogr. Bull. 1966, 8, 59–80. [Google Scholar]
- Malone, L.; Lacelle, D.; Kokelj, S.; Clark, I.D. Impacts of hillslope thaw slumps on the geochemistry of permafrost catchments (Stony Creek watershed, NWT, Canada). Chem. Geol. 2013, 356, 38–49. [Google Scholar] [CrossRef]
- Swanson, D.K.; Nolan, M. Growth of retrogressive thaw slumps in the Noatak Valley, Alaska, 2010–2016, measured by airborne photogrammetry. Remote Sens. 2018, 10, 983. [Google Scholar] [CrossRef] [Green Version]
- Bernhard, P.; Zwieback, S.; Leinss, S.; Hajnsek, I. Detection of retrogressive thaw slumps using TanDEM-X observations: Possibilities and limitations. In Proceedings of the EUSAR 2021, 13th European Conference on Synthetic Aperture Radar, Online, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Huebner, D.C.; Bret-Harte, M.S. Microsite conditions in retrogressive thaw slumps may facilitate increased seedling recruitment in the Alaskan Low Arctic. Ecol. Evol. 2019, 9, 1880–1897. [Google Scholar] [CrossRef] [Green Version]
- Harris, S.A.; French, H.M.; Heginbottom, J.A.; Johnston, G.H.; Ladanyi, B.; Sego, D.C.; Van Everdingen, R.O. Glossary of Permafrost and Related Ground-ice Terms. Associate Committee on Geotechnical Research: Ottawa, ON, Canada, 1988; Volume 27. [Google Scholar]
- De Valentina, K. A Geomorphic Investigation of Retrogressive Thaw Slumps and Active Layer Slides on Herschel Island, Yukon Territory. Master’s Thesis, McGill University, Montreal, QC, Canada, 1990. Available online: https://escholarship.mcgill.ca/concern/theses/qj72p8351 (accessed on 10 January 2022).
- Burn, C.R.; Friele, P.A. Geomorphology, vegetation succession, soil characteristics and permafrost in retrogressive thaw slumps near Mayo, Yukon Territory. Arctic 1989, 42, 31–40. [Google Scholar] [CrossRef]
- Nitze, I.; Heidler, K.; Barth, S.; Grosse, G. Developing and Testing a Deep Learning Approach for Mapping Retrogressive Thaw Slumps. Remote Sens. 2021, 13, 4294. [Google Scholar] [CrossRef]
- Lantz, T.C.; Kokelj, S.V.; Gergel, S.E.; Henry, G.H.R. Relative impacts of disturbance and temperature: Persistent changes in microenvironment and vegetation in retrogressive thaw slumps. Glob. Chang. Biol. 2009, 15, 1664–1675. [Google Scholar] [CrossRef]
- Ramage, J.L.; Irrgang, A.M.; Morgenstern, A.; Lantuit, H. Increasing coastal slump activity impacts the release of sediment and organic carbon into the Arctic Ocean. Biogeosciences 2018, 15, 1483–1495. [Google Scholar] [CrossRef] [Green Version]
- Kokelj, S.V.; Lantz, T.C.; Tunnicliffe, J.; Segal, R.; Lacelle, D. Climate-driven thaw of permafrost preserved glacial landscapes, northwestern Canada. Geology 2017, 45, 371–374. [Google Scholar] [CrossRef] [Green Version]
- Bowden, W.B.; Larouche, J.R.; Pearce, A.R.; Crosby, B.T.; Krieger, K.; Flinn, M.B.; Kampman, J.; Gooseff, M.N.; Godsey, S.E.; Jones, J.B.; et al. An integrated assessment of the influences of upland thermal-erosional features on landscape structure and function in the foothills of the Brooks Range, Alaska. In Proceedings of the Tenth International Conference on Permafrost, Salekhard, Russia, 25–29 June 2012; pp. 61–66. [Google Scholar]
- Segal, R.A.; Lantz, T.C.; Kokelj, S.V. Acceleration of thaw slump activity in glaciated landscapes of the Western Canadian Arctic. Environ. Res. Lett. 2016, 11, 34025. [Google Scholar] [CrossRef]
- Costard, F.; Dupeyrat, L.; Séjourné, A.; Bouchard, F.; Fedorov, A.; Saint-Bézar, B. Retrogressive Thaw Slumps on Ice-Rich Permafrost under Degradation: Results from a Large-Scale Laboratory Simulation. Geophys. Res. Lett. 2021, 48, e2020GL091070. [Google Scholar] [CrossRef]
- Cray, H.A.; Pollard, W.H. Use of stabilized thaw slumps by Arctic birds and mammals: Evidence from Herschel Island, Yukon. Can. Field-Nat. 2018, 132, 279–284. [Google Scholar] [CrossRef] [Green Version]
- Littlefair, C.A.; Tank, S.E.; Kokelj, S.V. Retrogressive thaw slumps temper dissolved organic carbon delivery to streams of the Peel Plateau, NWT, Canada. Biogeosciences 2017, 14, 5487–5505. [Google Scholar] [CrossRef] [Green Version]
- Mesquita, P.S.; Wrona, F.J.; Prowse, T.D. Effects of retrogressive permafrost thaw slumping on sediment chemistry and submerged macrophytes in Arctic tundra lakes. Freshw. Biol. 2010, 55, 2347–2358. [Google Scholar] [CrossRef]
- Witharana, C.; Bhuiyan, M.A.E.; Liljedahl, A.K.; Kanevskiy, M.; Jorgenson, T.; Jones, B.M.; Ward Jones, M.K. An Object-Based Approach for Mapping Tundra Ice-Wedge Polygon Troughs from Very High Spatial Resolution Optical Satellite Imagery. Remote Sens. 2021, 13, 558. [Google Scholar] [CrossRef]
- Grosse, G.; Jones, B. Remote sensing leads to better understanding of polar regions. Eos 2018, 99. [Google Scholar] [CrossRef]
- Turner, K.W.; Pearce, M.D.; Hughes, D.D. Detailed Characterization and Monitoring of a Retrogressive Thaw Slump from Remotely Piloted Aircraft Systems and Identifying Associated Influence on Carbon and Nitrogen Export. Remote Sens. 2021, 13, 171. [Google Scholar] [CrossRef]
- Runge, A.; Nitze, I.; Grosse, G. Remote sensing annual dynamics of rapid permafrost thaw disturbances with LandTrendr. Remote Sens. Environ. 2022, 268, 112752. [Google Scholar] [CrossRef]
- Huang, L.; Liu, L.; Luo, J.; Lin, Z.; Niu, F. Automatically quantifying evolution of retrogressive thaw slumps in Beiluhe (Tibetan Plateau) from multi-temporal CubeSat images. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102399. [Google Scholar] [CrossRef]
- Witharana, C.; Bhuiyan, M.A.E.; Liljedahl, A.K. Big Imagery and High Performance Computing as Resources to Understand Changing Arctic Polygonal Tundra. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIV-M-2-2020, 2020. [Google Scholar] [CrossRef]
- Udawalpola, M.R.; Hasan, A.; Liljedahl, A.; Soliman, A.; Terstriep, J.; Witharana, C. An Optimal GeoAI Workflow for Pan-Arctic Permafrost Feature Detection from High-Resolution Satellite Imagery. Photogramm. Eng. Remote Sens. 2022, 88, 181–188. [Google Scholar] [CrossRef]
- Udawalpola, M.; Hasan, A.; Liljedahl, A.K.; Soliman, A.; Witharana, C. Operational-Scale Geoai for Pan-Arctic Permafrost Feature Detection from High-Resolution Satellite Imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 44, 175–180. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Witharana, C.; Liljedahl, A.K. Use of Very High Spatial Resolution Commercial Satellite Imagery and Deep Learning to Automatically Map Ice-Wedge Polygons across Tundra Vegetation Types. J. Imaging 2020, 6, 137. [Google Scholar] [CrossRef]
- Hay, G.J.; Castilla, G. Geographic Object-Based Image Analysis (GEOBIA): A new name for a new discipline. In Object-Based Image Analysis; Springer: Berlin/Heidelberg, Germany, 2008; pp. 75–89. [Google Scholar]
- Lang, S.; Kienberger, S.; Tiede, D.; Hagenlocher, M.; Pernkopf, L. Geons—Domain-specific regionalization of space. Cartogr. Geogr. Inf. Sci. 2014, 41, 214–226. [Google Scholar] [CrossRef] [Green Version]
- Lantuit, H.; Pollard, W.H. Temporal stereophotogrammetric analysis of retrogressive thaw slumps on Herschel Island, Yukon Territory. Nat. Hazards Earth Syst. Sci. 2005, 5, 413–423. [Google Scholar] [CrossRef] [Green Version]
- Kokelj, S.V.; Lantz, T.C.; Kanigan, J.; Smith, S.L.; Coutts, R. Origin and polycyclic behaviour of tundra thaw slumps, Mackenzie Delta region, Northwest Territories, Canada. Permafr. Periglac. Process. 2009, 20, 173–184. [Google Scholar] [CrossRef]
- Brooker, A.; Fraser, R.H.; Olthof, I.; Kokelj, S.V.; Lacelle, D. Mapping the activity and evolution of retrogressive thaw slumps by tasselled cap trend analysis of a Landsat satellite image stack. Permafr. Periglac. Process. 2014, 25, 243–256. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, J.; Storozum, M.; Liu, S.; Gill, J.L.; Xiang, L.; Ren, X.; Wang, J.; Qiang, M.; Chen, F. Long-term herbivore population dynamics in the northeastern Qinghai-Tibetan Plateau and its implications for early human impacts. Rev. Palaeobot. Palynol. 2020, 275, 104171. [Google Scholar] [CrossRef]
- Dwyer, L. A Study of Permafrost Terrain Disturbances, Arctic Canada; University of Ottawa: Ottawa, ON, Canada, 1981. [Google Scholar]
- Romanenko, F.A. Ground ice and relief evolution on the Islands and Coasts of the Russian Arctic. In Proceedings of the Permfrost—Seventh International Conference, Yellowknife, NT, Canada, 23–27 June 1998; pp. 955–959. [Google Scholar]
- Lewkowicz, A.G.; Duguay, C.R. Detection of permafrost features using SPOT panchromatic imagery, Fosheim Peninsula, Ellesmere Island, NWT. Can. J. Remote Sens. 1999, 25, 34–44. [Google Scholar] [CrossRef]
- Couture, N.J. Sensitivity of Permafrost Terrain in a High Arctic Polar Desert: An Evaluation of Response to Disturbance Near Eureka, Ellesmere Island, Nunavut. Master’s Thesis, McGill University, Montreal, QC, Canada, 2000. [Google Scholar]
- Lantuit, H.; Pollard, W.H. Fifty years of coastal erosion and retrogressive thaw slump activity on Herschel Island, southern Beaufort Sea, Yukon Territory, Canada. Geomorphology 2008, 95, 84–102. [Google Scholar] [CrossRef]
- Lantz, T.C.; Kokelj, S.V. Increasing rates of retrogressive thaw slump activity in the Mackenzie Delta region, NWT, Canada. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Burn, C.R.; Zhang, Y. Permafrost and climate change at Herschel Island (Qikiqtaruq), Yukon Territory, Canada. J. Geophys. Res. Earth Surf. 2009, 114, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Lacelle, D.; Bjornson, J.; Lauriol, B. Climatic and geomorphic factors affecting contemporary (1950–2004) activity of retrogressive thaw slumps on the Aklavik plateau, Richardson mountains, NWT, Canada. Permafr. Periglac. Process. 2010, 21, 1–15. [Google Scholar] [CrossRef]
- Short, N.; Brisco, B.; Couture, N.; Pollard, W.; Murnaghan, K.; Budkewitsch, P. A comparison of TerraSAR-X, RADARSAT-2 and ALOS-PALSAR interferometry for monitoring permafrost environments, case study from Herschel Island, Canada. Remote Sens. Environ. 2011, 115, 3491–3506. [Google Scholar] [CrossRef]
- Lewkowicz, A.; Miceli, C.; Duguay, M.; Bevington, A. Electrical Resistivity Tomography (ERT) as an essential tool to investigate sites in discontinuous permafrost. Univ. Ottawa. EUCOP 2014, 33, 138–144. [Google Scholar]
- Lacelle, D.; Brooker, A.; Fraser, R.H.; Kokelj, S.V. Distribution and growth of thaw slumps in the Richardson Mountains—Peel Plateau region, northwestern Canada. Geomorphology 2015, 235, 40–51. [Google Scholar] [CrossRef]
- Ramage, J.L.; Irrgang, A.M.; Herzschuh, U.; Morgenstern, A.; Couture, N.; Lantuit, H. Terrain controls on the occurrence of coastal retrogressive thaw slumps along the Yukon Coast, Canada. J. Geophys. Res. Earth Surf. 2017, 122, 1619–1634. [Google Scholar] [CrossRef]
- Zwieback, S.; Kokelj, S.V.; Günther, F.; Boike, J.; Grosse, G.; Hajnsek, I. Sub-seasonal thaw slump mass wasting is not consistently energy limited at the landscape scale. Cryosphere 2018, 12, 549–564. [Google Scholar] [CrossRef] [Green Version]
- St. Pierre, K.A.; Zolkos, S.; Shakil, S.; Tank, S.E.; St. Louis, V.L.; Kokelj, S.V. Unprecedented increases in total and methyl mercury concentrations downstream of retrogressive thaw slumps in the western Canadian Arctic. Environ. Sci. Technol. 2018, 52, 14099–14109. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Niu, F.; Lin, Z.; Liu, M.; Yin, G. Recent acceleration of thaw slumping in permafrost terrain of Qinghai-Tibet Plateau: An example from the Beiluhe Region. Geomorphology 2019, 341, 79–85. [Google Scholar] [CrossRef]
- Huang, L.; Luo, J.; Lin, Z.; Niu, F.; Liu, L. Using deep learning to map retrogressive thaw slumps in the Beiluhe region (Tibetan Plateau) from CubeSat images. Remote Sens. Environ. 2020, 237, 111534. [Google Scholar] [CrossRef]
- Bernhard, P.; Zwieback, S.; Bergner, N.; Hajnsek, I. Assessing volumetric change distributions and scaling relations of retrogressive thaw slumps across the Arctic. Cryosphere 2022, 16, 1–15. [Google Scholar] [CrossRef]
- Pollard, W.; Ward, M.; Becker, M. The Eureka Sound lowlands: An ice-rich permafrost landscape in transition. In Proceedings of the GeoQuebec, Montreal, QC, Canada, 20 September 2015; p. 402. [Google Scholar]
- Heginbottom, J.A. Canada-Permafrost. Ci.nii.ac.jp. Available online: https://ci.nii.ac.jp/naid/10019265252/ (accessed on 2 February 2022).
- Fraser, R.H.; Kokelj, S.V.; Lantz, T.C.; McFarlane-Winchester, M.; Olthof, I.; Lacelle, D. Climate Sensitivity of High Arctic Permafrost Terrain Demonstrated by Widespread Ice-Wedge Thermokarst on Banks Island. Remote Sens. 2018, 10, 954. [Google Scholar] [CrossRef] [Green Version]
- Lewkowicz, A.G. Dynamics of active-layer detachment failures, Fosheim Peninsula, Ellesmere Island, Nunavut, Canada. Permafr. Periglac. Process. 2007, 18, 89–103. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [Green Version]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Lin, G.; Milan, A.; Shen, C.; Reid, I. RefineNet: Multi-path refinement networks for high-resolution semantic segmentation. In Proceedings of the Proceedings-30th IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, Hawaii, 21–26 July 2017; Volume 2017, pp. 5168–5177. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 386–397. [Google Scholar] [CrossRef] [PubMed]
- Drozdzal, M.; Vorontsov, E.; Chartrand, G.; Kadoury, S.; Pal, C. The importance of skip connections in biomedical image segmentation. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2016; Volume 10008, pp. 179–187. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27 June –30 June 2016; Volume 2016, pp. 770–778. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Sudre, C.H.; Li, W.; Vercauteren, T.; Ourselin, S.; Jorge Cardoso, M. Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer: Cham, Switzerland, 2017; pp. 240–248. [Google Scholar] [CrossRef] [Green Version]
- Brynolfsson, P.; Nilsson, D.; Torheim, T.; Asklund, T.; Karlsson, C.T.; Trygg, J.; Nyholm, T.; Garpebring, A. Haralick texture features from apparent diffusion coefficient (ADC) MRI images depend on imaging and pre-processing parameters. Sci. Rep. 2017, 7, 4041. [Google Scholar] [CrossRef] [Green Version]
- Haralick, R.M.; Shanmugam, K.S.; Bosley, R. Land Use Classification Using Texture Information in Erts-a Mss Imagery; EROS Data Center: Sioux Falls, SD, USA, 1973. [Google Scholar]
- Wang, F. Factor Analysis. In International Encyclopedia of Human Geography; Elsevier: Amsterdam, The Netherlands, 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Witharana, C.; Bhuiyan, M.A.E.; Liljedahl, A.K.; Kanevskiy, M.; Epstein, H.E.; Jones, B.M.; Ward Jones, M.K. Understanding the synergies of deep learning and data fusion of multispectral and panchromatic high resolution commercial satellite imagery for automated ice-wedge polygon detection. ISPRS J. Photogramm. Remote Sens. 2020, 170, 174–191. [Google Scholar] [CrossRef]
- Evans, I.S. Geomorphometry and landform mapping: What is a landform? Geomorphology 2012, 137, 94–106. [Google Scholar] [CrossRef]
- Dragut, L.; Blaschke, T. Automated classification of landform elements using object-based image analysis. Geomorphology 2006, 81, 330–344. [Google Scholar] [CrossRef]
- Hay, G.J.; Dubé, P.; Bouchard, A.; Marceau, D.J. A scale-space primer for exploring and quantifying complex landscapes. Ecol. Model. 2002, 153, 27–49. [Google Scholar] [CrossRef]
- Soliman, A.; Terstriep, J. Keras Spatial Extending deep learning frameworks for preprocessing and on-the-fly augmentation of geospatial data. In Proceedings of the 3rd ACM SIGSPATIAL International Workshop on AI for Geographic Knowledge Discovery; Association for Computing Machinery, Inc.: Chicago, IL, USA, 2019; pp. 69–76. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; der Meer, F.; der Werff, H.; Van Coillie, F. Geographic object-based image analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [Green Version]
- Ismail, A.; Ahmad, S.A.; Soh, A.C.; Hassan, K.; Harith, H.H. Improving convolutional neural network (CNN) architecture (miniVGGNet) with batch normalization and learning rate decay factor for image classification. Int. J. Integr. Eng. 2019, 11, 51–59. [Google Scholar] [CrossRef]
- Smith, L.N. A disciplined approach to neural network hyper-parameters: Part 1—Learning rate, batch size, momentum, and weight decay. arXiv 2018, arXiv:1803.09820. [Google Scholar]
- Hoffer, E.; Hubara, I.; Soudry, D. Train longer, generalize better: Closing the generalization gap in large batch training of neural networks. In Advances in Neural Information Processing Systems; NeurIPS: La Jolla, CA, USA, 2017; Volume 2017, pp. 1732–1742. [Google Scholar]
- Bengio, Y. Practical recommendations for gradient-based training of deep architectures. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7700 LECTU, pp. 437–478. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).