Oceanic Kármán Vortex Streets in the Luzon Strait in the Lee of Didicas Island from Multiple Satellite Missions
Abstract
1. Introduction
2. Materials and Methods
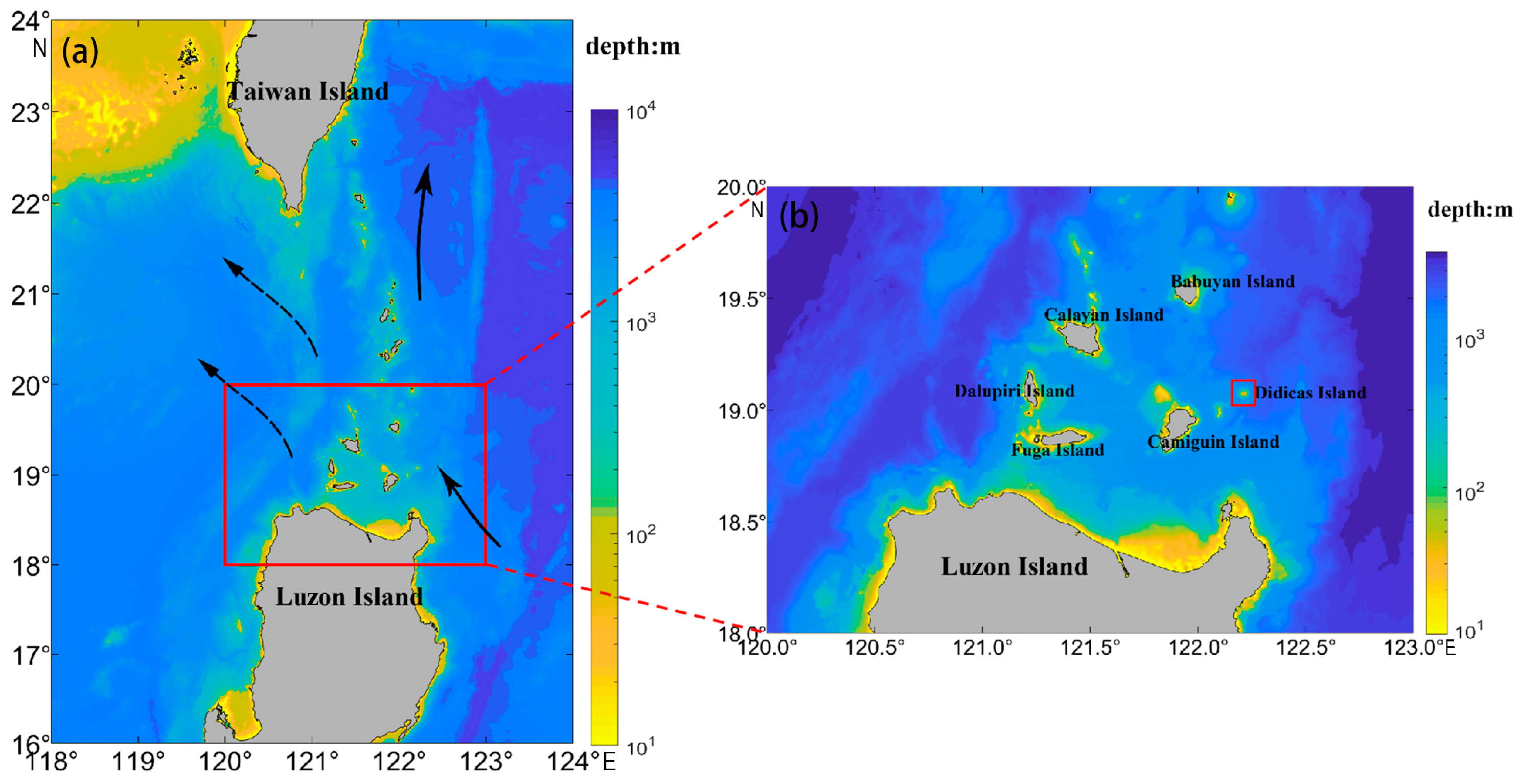
2.1. Study Area
2.2. Satellite Data
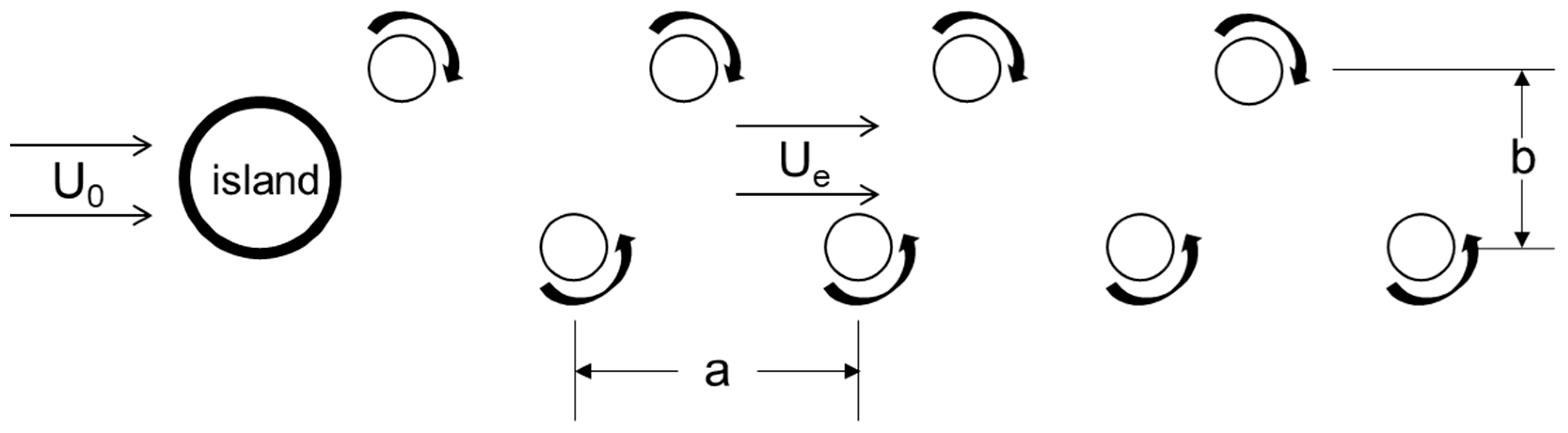
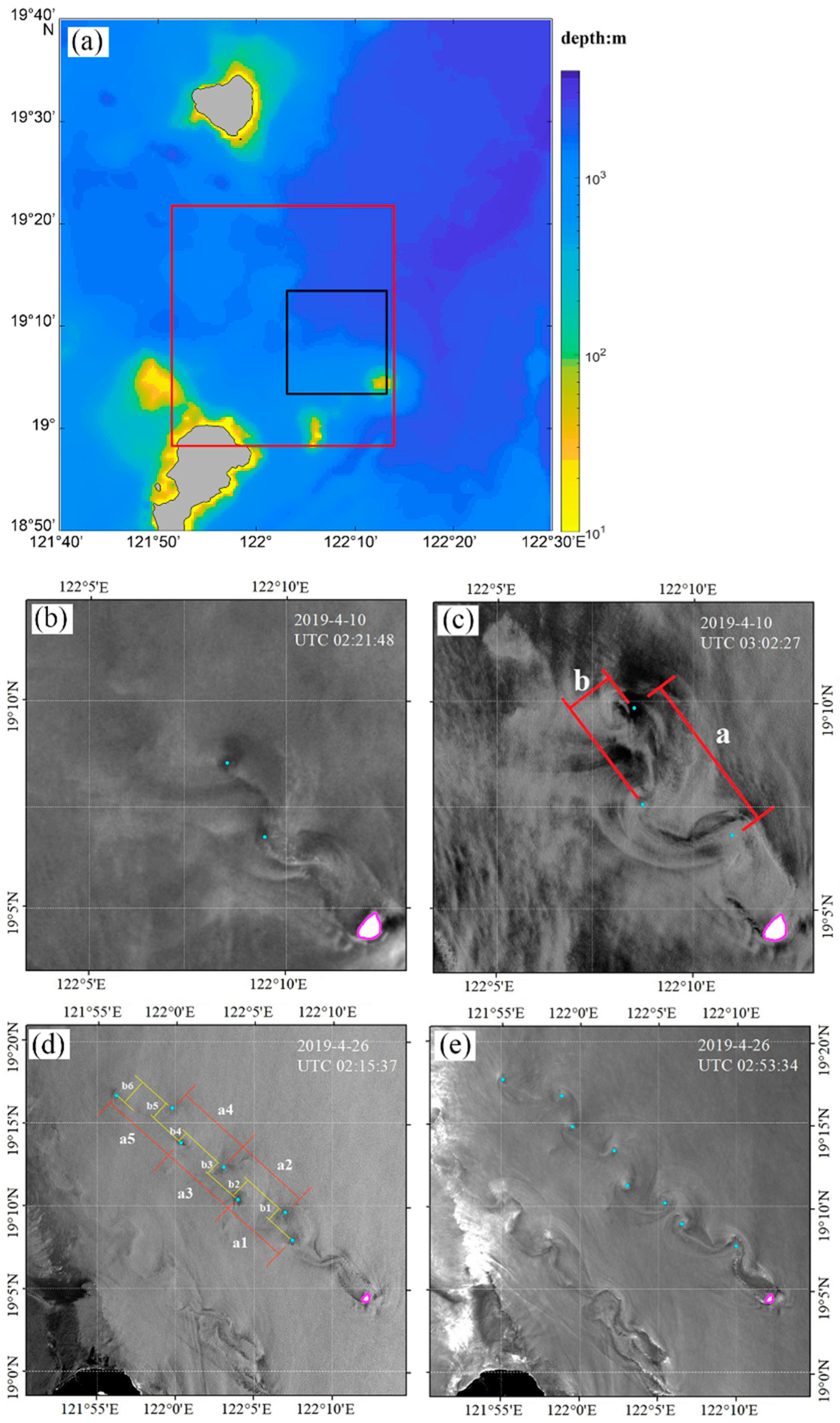
2.3. Property Parameters of Vortex Streets
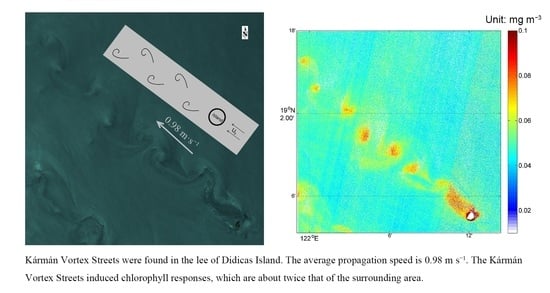
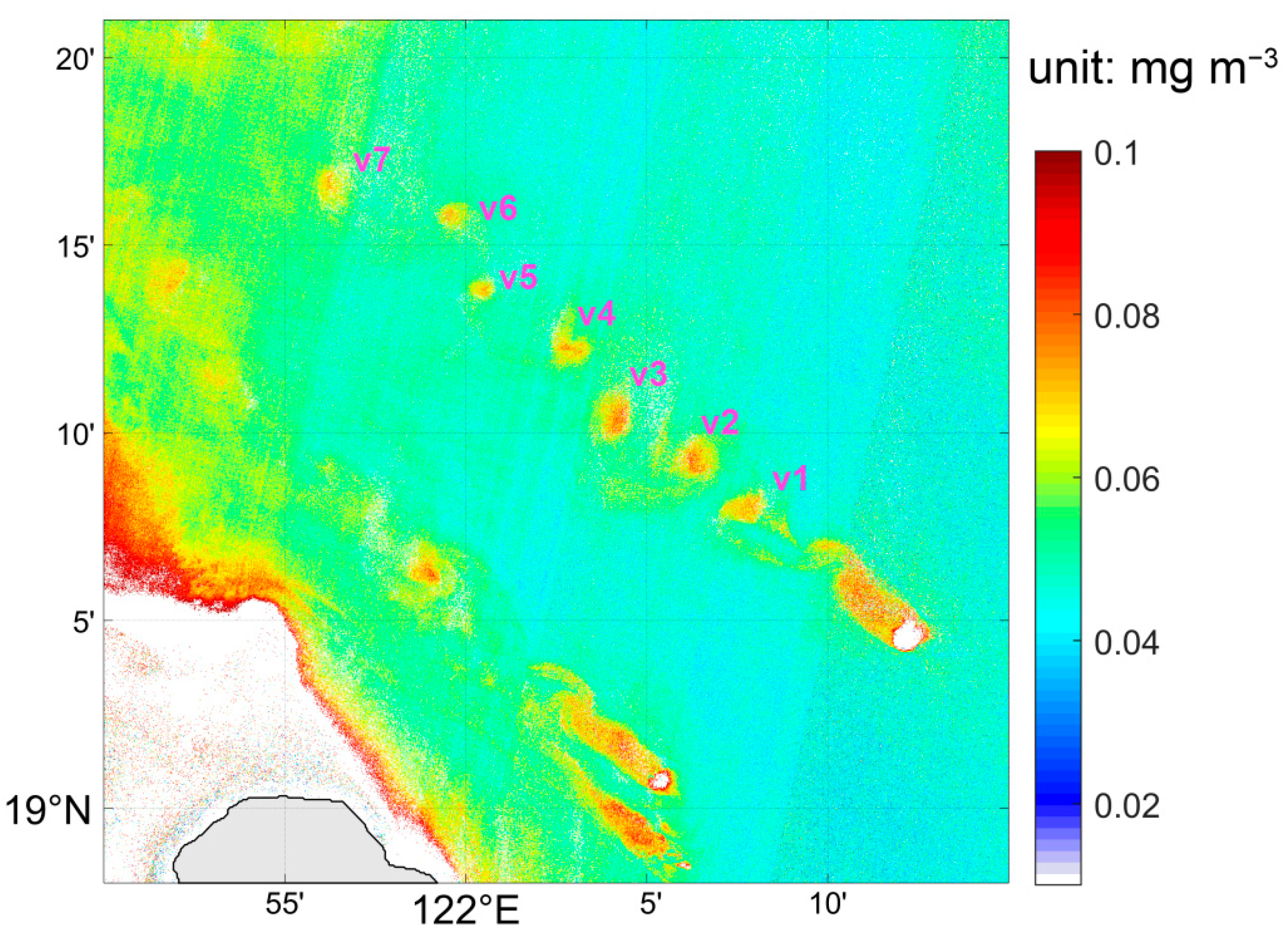
2.4. Chlorophyll-a Retrieval
3. Results
3.1. Probability of Occurrence of the Kármán Vortex Street
3.2. Distribution Pattern of the Kármán Vortex Street
3.3. Propagation Characteristics
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Von Kármán, T. Üeber den Mechanismus des Widerstandes, den ein bewegter Körper in einer Flüssigkeit erfährt. Nachr. Ges. Wiss. Göttinge Math. Phys. Kl 1911, 1911, 509–517. Available online: https://gdz.sub.uni–goettingen.de/id/PPN252457811_1911 (accessed on 20 August 2021).
- Von Kármán, T. Über den Mechanismus des Widerstandes, den ein bewegter Körper in einer Flüssigkeit erfährt. Nachr. Ges. Wiss. Göttinge Math. Phys. Kl 1912, 1912, 547–556. Available online: https://gdz.sub.uni–goettingen.de/id/PPN252457811_1912 (accessed on 20 August 2021).
- Strouhal, V. Ueber eine besondere Art der Tonerregung. Ann. Phys. 1878, 241, 216–251. [Google Scholar] [CrossRef]
- Lord Rayleigh, F.R.S. On the Stability, or Instability, of certain Fluid Motions. Proc. Lond. Math. Soc. 1879, s1-11, 57–72. [Google Scholar] [CrossRef]
- Advisory Board of the Investigation of Suspension Bridges. Aerodynamic Stability of Suspension Bridges: 1952 Report of the Advisory Board on the Investigation of Suspension Bridges. Trans. Am. Soc. Civ. Eng. 1955, 120, 721–781. [Google Scholar] [CrossRef]
- Cohen, E. Wind Load on Towers. Top. Eng. Meteorol. Meteorol. Monogr. Ser. 1960, 4, 25–42. [Google Scholar]
- Roshko, A. On the Wake and Drag of Bluff Bodies. J. Aeronaut. Sci. 1955, 22, 124–132. [Google Scholar] [CrossRef]
- Chopra, K.P.; Hubert, L.F. Kármán Vortex-Streets in Earth’s Atmosphere. Nature 1964, 203, 1341–1343. [Google Scholar] [CrossRef]
- Chopra, K.P.; Hubert, L.F. Mesoscale Eddies in Wake of Islands. J. Atmos. Sci. 1965, 22, 652–657. [Google Scholar] [CrossRef]
- Horváth, Á.; Bresky, W.; Daniels, J.; Vogelzang, J.; Stoffelen, A.; Carr, J.L.; Wu, D.L.; Seethala, C.; Günther, T.; Buehler, S. A Evolution of an Atmospheric Kármán Vortex Street From High-Resolution Satellite Winds: Guadalupe Island Case Study. J. Geophys. Res. Atmos. 2020, 125, e2019JD032121. [Google Scholar] [CrossRef]
- Li, X.; Clemente-Colón, P.; Pichel, W.G.; Vachon, P.W. Atmospheric vortex streets on a RADARSAT SAR image. Geophys. Res. Lett. 2000, 27, 1655–1658. [Google Scholar] [CrossRef]
- Barkley, R.A. Johnston Atoll’s Wake. J. Mar. Res. 1972, 30, 201–216. [Google Scholar]
- Tomczak, M. Island wakes in deep and shallow water. J. Geophys. Res. Ocean. 1988, 93, 5153–5154. [Google Scholar] [CrossRef]
- McWilliams, J.C. Submesoscale currents in the ocean. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160117. [Google Scholar] [CrossRef]
- Zheng, Q.; Lin, H.; Meng, J.; Hu, X.; Song, Y.T.; Zhang, Y.; Li, C. Sub-mesoscale ocean vortex trains in the Luzon Strait. J. Geophys. Res. Ocean. 2008, 113, C04032. [Google Scholar] [CrossRef]
- Hsu, P.-C.; Ho, C.-Y.; Lee, H.-J.; Lu, C.-Y.; Ho, C.-R. Temporal Variation and Spatial Structure of the Kuroshio-Induced Submesoscale Island Vortices Observed from GCOM-C and Himawari-8 Data. Remote Sens. 2020, 12, 883. [Google Scholar] [CrossRef]
- Yu, J.; Zheng, Q.; Jing, Z.; Qi, Y.; Zhang, S.; Xie, L. Satellite observations of sub-mesoscale vortex trains in the western boundary of the South China Sea. J. Mar. Syst. 2018, 183, 56–62. [Google Scholar] [CrossRef]
- Hsu, P.-C.; Chang, M.-H.; Lin, C.-C.; Huang, S.-J.; Ho, C.-R. Investigation of the island-induced ocean vortex train of the Kuroshio Current using satellite imagery. Remote Sens. Environ. 2017, 193, 54–64. [Google Scholar] [CrossRef]
- Caldeira, R.M.A.; Stegner, A.; Couvelard, X.; Araújo, I.B.; Testor, P.; Lorenzo, A. Evolution of an oceanic anticyclone in the lee of Madeira Island: In situ and remote sensing survey. J. Geophys. Res. Ocean. 2014, 119, 1195–1216. [Google Scholar] [CrossRef]
- Liu, F.; Tang, S.; Chen, C. Satellite observations of the small-scale cyclonic eddies in the western South China Sea. Biogeosciences 2015, 12, 299–305. [Google Scholar] [CrossRef][Green Version]
- Dong, C.; McWilliams, J.C.; Shchepetkin, A.F. Island Wakes in Deep Water. J. Phys. Oceanogr. 2007, 37, 962–981. [Google Scholar] [CrossRef]
- Stegner, A. Oceanic Island Wake Flows in the Laboratory. In Modeling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments and Numerical Simulations; Williams, P.D., von Larcher, T., Eds.; Wiley: Hoboken, NJ, USA, 2015; pp. 265–276. [Google Scholar]
- Chang, M.-H.; Tang, T.-Y.; Ho, C.-R.; Chao, S.-Y. Kuroshio-induced wake in the lee of Green Island off Taiwan. J. Geophys. Res. Ocean. 2013, 118, 1508–1519. [Google Scholar] [CrossRef]
- Xiu, P.; Chai, F.; Shi, L.; Xue, H.J.; Chao, Y. A census of eddy activities in the South China Sea during 1993–2007. J. Geophys. Res. 2010, 115, C03012. [Google Scholar] [CrossRef]
- Nan, F.; He, Z.G.; Zhou, H.; Wang, D.X. Three long-lived anticyclonic eddies in the Northern South China Sea. J. Geophys. Res. 2011, 116, C05002. [Google Scholar] [CrossRef]
- Wu, C.-R. Interannual modulation of the Pacific Decadal Oscillation (PDO) on the low-latitude western North Pacific. Prog. Oceanogr. 2013, 110, 49–58. [Google Scholar] [CrossRef]
- Shaw, P.-T. The seasonal variation of the intrusion of the Philippine Sea Water into the South China Sea. J. Geophys. Res. Ocean. 1991, 96, 821–827. [Google Scholar] [CrossRef]
- Centurioni, L.R.; Niiler, P.P.; Lee, D.-K. Observations of Inflow of Philippine Sea Surface Water into the South China Sea through the Luzon Strait. J. Phys. Oceanogr. 2004, 34, 113–121. [Google Scholar] [CrossRef]
- Cooper, J.E. Aeroelastic Response. In Encyclopedia of Vibration; Elsevier: Amsterdam, The Netherlands, 2001; pp. 87–97. [Google Scholar]
- Skrbek, L.; Vinen, W.F. The Use of Vibrating Structures in the Study of Quantum Turbulence. In Progress in Low Temperature Physics; Elsevier: Amsterdam, The Netherlands, 2009; Volume 16, pp. 195–246. [Google Scholar]
- Tsuchiya, K. The clouds with the shape of Kármán vortex street in the wake of Cheju Island, Korea. J. Meteorol. Soc. Japan. Ser. II 1969, 47, 457–465. [Google Scholar] [CrossRef]
- Hu, C.M.; Lee, Z.P.; Franz, B. Chlorophyll algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. Ocean. 2012, 117, C01011. [Google Scholar] [CrossRef]
- Franz, B.A.; Bailey, S.W.; Kuring, N.; Werdell, P.J. Ocean color measurements with the Operational Land Imager on Landsat-8: Implementation and evaluation in SeaDAS. J. Appl. Remote Sens. 2015, 9, 096070. [Google Scholar] [CrossRef]
- Bénard, H. Sur l’inexactitude, pour les liquides réels, des lois théoriques de Kármán relativesa la stabilité des tourbillons alternés. Compt. Rend. Acad. Sci 1926, 182, 1523–1525. [Google Scholar]
- Bénard, H. Sur les lois de la fréquence des tourbillons alternés détachés derriere un obstacle. Compt. Rend. Acad. Sci 1926, 182, 1375–1377. [Google Scholar]
- Matsui, T. Flow visualization studies of vortices. Indian Acad. Sci. Proc. Sect. C Eng. Sci. 1981, 4, 239–257. [Google Scholar] [CrossRef]
- Hamner, W.M.; Hauri, I.R. Effects of island mass: Water flow and plankton pattern around a reef in the Great Barrier Reef lagoon, Australia. Limnol. Oceanogr. 1981, 26, 1084–1102. [Google Scholar] [CrossRef]
- Heinze, A.W.; Truesdale, C.L.; DeVaul, S.B.; Swinden, J.; Sanders, R.W. Role of temperature in growth, feeding, and vertical distribution of the mixotrophic chrysophyte Dinobryon. Aquat. Microb. Ecol. 2013, 71, 155–163. [Google Scholar] [CrossRef]
- Lien, R.C.; Ma, B.; Lee, C.M.; Sanford, T.B.; Mensah, V.; Centurioni, L.R.; Cornuelle, B.D.; Gopalakrishnan, G.; Gordon, A.L.; Chang, M.H.; et al. The Kuroshio and Luzon Undercurrent East of Luzon Island. Oceanography 2015, 28, 54–63. [Google Scholar] [CrossRef]
- Williamson, C.H.K. Vortex Dynamics in the Cylinder Wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]


| Satellite Sensors | Original Spatial Resolution(m) | Product Level | Bands in Visible Spectrum | Swath Width (km) | Scenes Without Clouds | Scenes with Kármán Vortex Street |
|---|---|---|---|---|---|---|
| Landsat-8 | 30 | L1TP | 9 | 185 | 12 | 5 |
| Sentinel-2 | 10/20/60 | L1C | 13 | 290 | 38 | 4 |
| GF-1/6 MSS | 16 | WFV | 4/8 | 800 | 3 | 3 |
| HY-1C CZI | 50 | L1C | 4 | 950 | 4 | 4 |
| Month | Jan. | Feb. | Mar. | Apr. | May. | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Days of Data without Clouds | 2 | 4 | 6 | 8 | 9 | 9 | 5 | 2 | 3 | 4 | 1 | 2 |
| Days of Data with Kármán Vortex Street | 0 | 0 | 0 | 3 | 5 | 1 | 2 | 0 | 0 | 0 | 0 | 0 |
| Date | Satellite | Vortices | (km) | (km) | ||
|---|---|---|---|---|---|---|
| 10 April 2019 | HY-1C | 2 | / | 1.059 | / | 0.963 |
| GF-6 | 3 | 6.918 | 2.687 | 2.577 | 2.442 | |
| 22 April 2019 | HY-1C | 5 | 9.197 | 2.113 | 4.348 | 1.921 |
| GF-6 | 5 | 9.568 | 2.641 | 3.623 | 2.401 | |
| 26 April 2019 | Landsat-8 | 7 | 8.497 | 1.876 | 4.525 | 1.705 |
| GF-6 | 8 | 8.646 | 1.653 | 5.236 | 1.502 | |
| 27 May 2020 | Sentinel-2 | 5 | 8.407 | 1.206 | 6.993 | 1.096 |
| HY-1C | 5 | 8.449 | 1.240 | 6.803 | 1.127 | |
| 30 May 2020 | Landsat-8 | 4 | 9.164 | 2.055 | 4.464 | 1.868 |
| HY-1C | 5 | 8.061 | 2.254 | 3.571 | 2.049 |
| Date | Distance (km) | (m s−1) | (m s−1) | |||||
|---|---|---|---|---|---|---|---|---|
| 10 April 2019 | 2.23 | 0.91 | 1.17 | 0.78 | 2.12 | 129 | 0.123 | 22.30 |
| 22 April 2019 | 2.49 | 1.22 | 1.47 | 0.83 | 2.13 | 162 | 0.098 | 28.10 |
| 26 April 2019 | 2.52 | 1.11 | 1.28 | 0.87 | 2.15 | 140 | 0.111 | 24.37 |
| 27 May 2020 | 1.55 | 0.66 | 0.72 | 0.92 | 3.54 | 79 | 0.120 | 13.78 |
| 30 May 2020 | 2.36 | 0.99 | 1.19 | 0.83 | 2.41 | 131 | 0.106 | 22.79 |
| Date | (m s−1) | (m s−1) | Angle (°) | Angle (°) | Angle Bias (°) | ||
|---|---|---|---|---|---|---|---|
| 10 April 2019 | 0.73 | 1.3 | 0.66 | 1.8 | 131.3 | 119.7 | 11.6 |
| 22 April 2019 | 0.77 | 1.6 | 0.71 | 2.1 | 135.8 | 123.0 | 12.7 |
| 26 April 2019 | 0.82 | 1.4 | 0.71 | 1.8 | 139.7 | 132.3 | 7.5 |
| 27 May 2020 | 0.60 | 1.1 | 0.45 | 1.6 | 136.4 | 139.5 | −3.2 |
| 30 May 2020 | 0.68 | 1.5 | 0.51 | 2.3 | 139.5 | 146.0 | −6.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Liu, Y.; Tang, S.; Li, Q. Oceanic Kármán Vortex Streets in the Luzon Strait in the Lee of Didicas Island from Multiple Satellite Missions. Remote Sens. 2022, 14, 4136. https://doi.org/10.3390/rs14174136
Liu F, Liu Y, Tang S, Li Q. Oceanic Kármán Vortex Streets in the Luzon Strait in the Lee of Didicas Island from Multiple Satellite Missions. Remote Sensing. 2022; 14(17):4136. https://doi.org/10.3390/rs14174136
Chicago/Turabian StyleLiu, Fenfen, Yiting Liu, Shilin Tang, and Qiqing Li. 2022. "Oceanic Kármán Vortex Streets in the Luzon Strait in the Lee of Didicas Island from Multiple Satellite Missions" Remote Sensing 14, no. 17: 4136. https://doi.org/10.3390/rs14174136
APA StyleLiu, F., Liu, Y., Tang, S., & Li, Q. (2022). Oceanic Kármán Vortex Streets in the Luzon Strait in the Lee of Didicas Island from Multiple Satellite Missions. Remote Sensing, 14(17), 4136. https://doi.org/10.3390/rs14174136