Abstract
Global Positioning System (GPS) has been confirmed to be a feasible tool to measure displacement of civil engineering structures. In this paper, we report on an analysis of annual deformations of a pumped-storage power station dam using historical GPS observations. Data spanning more than nine years are resolved using the GAMIT (GPS at MIT) software, and a GPS time-series method is employed to extract linear trends and annual cycle signals. It is evident that the monument located on the main dam has a linear trend, with rates of 1.0 mm/yr and 1.8 mm/yr in east and up directions, respectively. Annual cycles with amplitudes larger than 0.5 mm are shown in coordinate components at all monitoring stations. However, the annual amplitude can be 30–84% lower when a monitoring station whose monument materials and height are similar to other monitoring stations is chosen as the reference station. This suggests that differential thermal expansion of monuments could be 30% to 80% and even higher in baseline time series. A spurious offset style annual signal with 5 mm amplitude that is highly correlated with annual temperature variance is observed in the east–west direction of the monitoring station located at the east side of the reservoir. This suggests that upper ground layer movement correlated with temperature could be responsible for these annual cycles. Meanwhile, no periodic correlations are observed between the water level data and the baseline time series.
1. Introduction
Dams are important hydraulic infrastructures and play a vital role in irrigation, hydroelectricity generation and flood control. The performance of these structures under operational and environmental loads may deteriorate over time due to aging, floods, earthquakes and other factors. Dams may collapse, leading to heavy economic and life losses, if they were not well managed and maintained [1,2]. Therefore, the establishment of a Structural Health Monitoring (SHM) system is extremely important to monitor the performance of dams and to help asset owners make timely maintenance decisions.
Compared with traditional deformation monitoring technologies, Global Navigation Satellite System (GNSS) has the advantages of high sampling rate, real-time and continuous severability, and high-precision monitoring. It has been a feasible tool to monitor the health conditions of dams [3,4,5,6,7,8,9,10,11,12]. Behr et al. and Hudnut and Behr applied Global Positioning System (GPS) technology in dam deformation monitoring and concluded that GPS can achieve precisions of 4–6 mm in horizontal and 12 mm in vertical components, which is sufficient for dam health monitoring [3,4]. Kalkan utilized GPS and conventional measurement to investigate deformations of the Ataturk dam and found that GPS had a comparable accuracy (< ±1 cm) with conventional measurement data [9]. In the following research, Xi et al. employed GPS observations based on water-level fluctuation and analyzed the correlation of water level and deformation by monitoring time series of a dam [13]. Xiao et al. compared the performance of GPS and BeiDou Navigation Satellite System (BDS) deformation monitoring application of a dam [14].
With respect to deformation pattern analysis of dams, self-weight, hydrostatic pressure and temperature variations could be the principal factors that cause deformation of dams. Pytharouli and Stiros applied a power-spectrum method to process the levelling and water-level data to reveal the correlations between long-term deformation results and water-level fluctuation, which is not observable in the time domain [15]. Using a high-order polynomial fitting method, Behr, and Hudnut and Behr found that movement of monitoring stations was highly correlated with the local temperature and probably had a negligible relationship with water-level variation [3,4]. Bayrak investigated the relationship of the reservoir water level and displacement on a dam observed via a total station. They revealed that variation of reservoir water level is an important factor for Yamula Dam deformation [16]. However, no significant relationship was found between the reservoir water level and radial displacements of the Ataturk dam [9]. Time-series analysis methods such as polynomial fitting [17,18,19], autoregressive analysis (AR) [20], principal component analysis (PCA) [21], empirical mode decomposition (EMD) [22], complementary ensemble empirical mode decomposition (CEEMD) [23], etc., have been adopted to model seasonal oscillations in GNSS time series and obtain an internal relationship of deformation time series with temperature and water-level data to build prediction models.
In this study, we aim to isolate the real annual motion of monitoring stations of the Xilongchi Dam and investigate the movement sources, such as temperature and water-level variations, from historical GPS observations using GPS time-series analysis. Since the distance between monitoring stations and the reference station is short, a short-baseline GPS network is the best choice for dam deformation monitoring. Compared with the GPS time series of large-scale deformation-monitoring networks in geophysical research, double-difference (DD) technology can effectively eliminate satellite orbit-related errors and reduce atmospheric delays and geophysical effects such as environmental loading, non-tidal oceanic loading, etc., to achieve a high-precision solution. However, in a short-baseline network, site-specific effects are the vital issue restricting monitoring of real movement of observed objects, and these effects include monument and bedrock thermal expansion, multipath effects and mismodeled antenna phase center variances [24,25]. Thus, in this study, we separate annual deformation signals in GPS coordinate time series and explain annual motion sources on the Xilongchi Dam by comparing them with temperature data and water-level variations.
The rest of the paper is organized as follows. In Section 2, we introduce the test bed, Xilongchi Dam, the detailed station set-ups of the GPS deformation monitoring system and information related to water level and temperature datasets. The GPS data-processing method and GPS time-series method adopted in this paper are also included in Section 2. In Section 3, we present the baseline time series and model the linear trend and periodic signals. In Section 4, temperature and water-level data are compared with the baseline time series to investigate the source of annual signals. In Section 5, the conclusions of this study are presented.
2. Materials and Methods
2.1. Materials
2.1.1. Introduction of Xilongchi Dam
The Xilongchi Pumped-Storage Power Station is located in Xinzhou, Shanxi Province, China, where the geologic condition is relatively stable and is not in a seismic zone. The geographical location of the Xilongchi Reservoir is shown in Figure 1. The head reservoir was formed by excavating up-hill land with a height of 1460 m above mean sea level, and it has a crest length of 401.6 m and dam height of 50 m. The capacity of the reservoir is about 4.94 million m3, and the working depth is 25.5 m. A main dam and an auxiliary dam are constructed on the southern and northern sides of the reservoir, respectively. A rock-fill dam with asphalt–concrete facing is used in the head reservoir dam.
Figure 1.
Geographical location of the Xilongchi Reservoir.
2.1.2. GPS Station Layout
A short-baseline GPS network is set up around the head reservoir with two base stations (TN01 and TN02) and five monitoring stations (L022, L132, S171, S191 and S071). L022 and L132 are located on the main dam and an auxiliary dam, respectively. The layout of the stations is shown in Figure 2. The two base stations are constructed at two stable places with an open viewing environment on the northeast corner (TN02) and southeast corner (TN01) of the reservoir. Each base station has a concrete pillar monument, which consists of reinforced concrete set within a tubular concrete form. A steel sheet was also applied to cover the pillar to maintain the safety of the pillar and to prevent deformation caused by direct solar radiation. The levelling mount and GPS antenna are secured to a stainless-steel pin that is anchored within the top of the pillar. The foundation of the pillar is a cuboid concrete pillar anchored in bedrock. The five monitoring stations are mounted around the reservoir. Each of them has a reinforced cuboid concrete pillar and is 1.3 m high. It should be noted that the main dam monitoring site L022 is connected to the dam body, which is anchored in bedrock. At each station, a TRIMBLE NETRS receiver and a CHOKE RING (TRM29659.00) antenna made by the Trimble in California, America, are installed similarly to the stations used for the International GNSS Service (IGS). Real-time GPS observations at each site are recorded at 5 s intervals and transferred through optical fiber in Radio Technical Commission for Maritime Services (RTCM) format to the server 24 h a day continuously. Before data processing, RTCM format data need to be transferred to the receiver independent exchange format (RINEX).
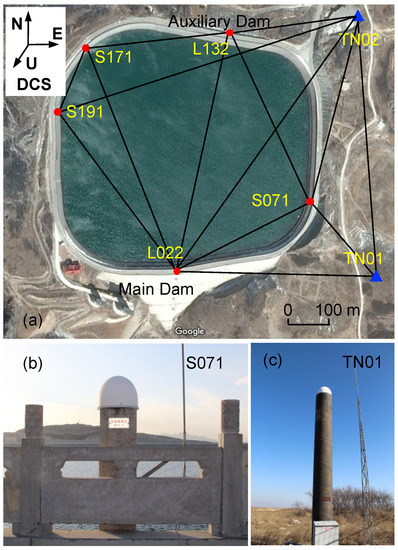
Figure 2.
(a) Station layout at the head reservoir of the Xilongchi pumped-storage power station: (b) monitoring station S071 and (c) reference station TN01.
In this study, the data acquired from 1 July 2009 (in decimal year 2009.52) to 1 August 2018 (in decimal year 2018.58) are processed to generate deformation time series. The coordinates of TN02 are fixed in the data processing as the reference station, and short baselines are formed between monitoring stations (including TN01 and TN02). The detailed information of baselines is shown in Table 1. The long-term stability of reference stations has been analyzed by Liu et al. and Liu [26,27]. No obvious non-tectonic trends were found from a comparison between TN01/TN02 and nearby CORS (Continuously Operating Reference System) stations and IGS stations. Due to hardware failures or extreme weather conditions, data gaps occur occasionally in the time series. Table 1 presents the data integrity rate of the baseline time series. We can see that more than 90% of the data are available for every baseline, which meets the requirements of data integrity for time-series analysis.

Table 1.
Baseline information for the GPS network.
2.1.3. Temperature and Water-Level Datasets
The temperature data come from Wutaishan Weather Station (~70 km from Xilongchi Reservoir) and can be downloaded from the National Climatic Data Center (NCDC) (ftp://ftp.ncdc.noaa.gov/pub/data/gsod, accessed on 3 September 2019). The geographic height of these two spots is similar. The data are available through the end of 2016 and include maximum and minimum values with a 3 h sampling rate. The water-level data are the daily records from the dam safety monitoring department and have centimeter-level accuracy. Unfortunately, the water-level data are only available from 2013 to 2015.
2.2. Methods
2.2.1. GPS Data Processing
We processed the GPS data using the GAMIT (GPS at MIT) software package [28]. With the GAMIT 10.6 software, the daily static baseline solutions were obtained. Since the baseline lengths of our dataset were all shorter than 700 m, tropospheric and ionospheric delays and any common unmodeled components could be eliminated to a negligible level with double-difference observations, which is technology that differences the observations between sites and satellites to remove common errors. In static daily data processing, L1 frequency data were applied to estimate site positions, and L2 frequency data were used to help resolve cycle slips and ambiguities. The first-order difference of Melbourne–Wübbena (MW) and geometry-free (GF) combination time series were employed to detect cycles slips, and short segments (less than 60 epochs) were deleted. Least squares estimation was applied to estimate the parameters, and float ambiguities were fixed using the bootstrapping and decision function method [29]. The satellite orbits were fixed to the IGS final orbits, and the earth rotation and orientation parameters were not estimated. Tidal loading was not considered either. The cutoff elevation angle was 15°, and the sampling interval was 30 s. The detailed data-processing flowchart and strategies are shown in Figure 3 and Table 2.
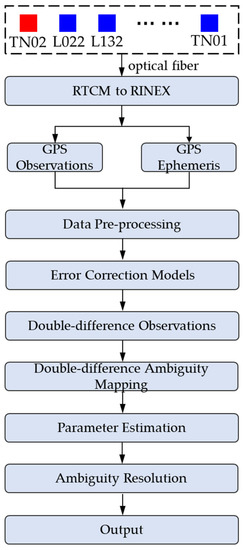
Figure 3.
Data processing flowchart. The red square indicates the reference station, and the blues are monitoring stations.

Table 2.
GPS data processing strategies.
2.2.2. Time-Series Analysis Method
King and Watson and King and Williams demonstrated that an annual signal can be related to global or local geophysical signals such as hydrology and atmospheric loadings [30,31]. Meanwhile, daily or sub-daily signals can also propagate to 24 h solutions to be a factor in creating annual and semiannual signals in long-term time series [31]. However, the baseline length in this study is short. More analyses are needed to identify signal sources.
In order to better understand the characteristics of the long-period signals, the baseline time series were fitted with a model consisting of offset, linear and harmonic terms using the Hector software [32]. In this paper, the annual and semiannual signals were considered in the model. In addition, since the secular trend was reducing, a three-order polynomial was also considered. Thus, the model can be expressed as
where is the annul and semiannual term, and , , are parameters to be estimated. The power-law noise plus white noise (PLWN) stochastic model is also estimated (a detailed noise analysis will be carried out in the future). The fitting results are shown in Figure 4 with green lines in each time series, and the parameter esitmates are shown in Table 3. It should be noted that the north component of baseline L022–TN02 is divided into two time series to be estimated separately: before and after 2012. From the fitting models, the annual signals are apparant in all components of all baselines. Several time series have semiannual signals, espectially in the up component.
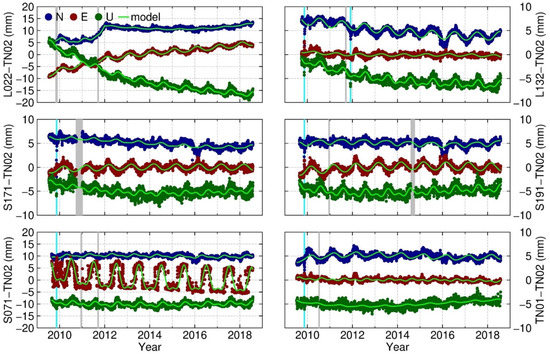
Figure 4.
Baseline coordinate time-series and fitting models (North and Up components are moved upward and downward to distinguish the time series. Note the range of the coordinate axes of L022–TN02 and S071–TN02 is larger than that of other baselines). The vertical cyan lines indicate days when there was heavy snowfall and the snow cover changed the antenna phase center, resulting in aberrant solutions in the time series. The gray slices indicate the data gaps.

Table 3.
Linear trend term (mm/yr) and annual and semiannual signal amplitude estimates (mm).
2.2.3. Lomb–Scargle Periodogram Method
Due to data gaps caused by equipment failure and outliers, the commonly used fast Fourier transform (FFT) cannot be applied in spectral analysis to measure the periodic signal characteristics. Time-series separation or imputation of missing data using interpolation may introduce additional noise or bias or remove long-term periodicities [33,34]. As alternative methods for spectral analysis of unevenly spaced data, least-squares spectral analysis (LSSA) [35,36,37,38] and Lomb–Scargle periodogram [39,40] are often applied to estimate the frequency spectrum of a given time series. In this study, a Lomb–Scargle periodogram was used to show the power spectra of the GPS time series and the temperature and water-level time series.
The Lomb–Scargle periodogram is based on the algorithm developed by Lomb [39] and later by Scargle [40] for spectral analysis of both evenly and unevenly distributed data. It is equivalent to the fitting of a sine curve of the form [34]
where t indicates time; a and b are amplitudes of the curve; T is the period and is time offset. For a given time series, at time , the Lomb–Scargle P(T) for a period T is defined as
where the time offset is defined by
and
The maximum in the periodogram occurs at the same frequency that minimizes the sum of squares of the residuals of the fit of a sine wave to the time series [34].
3. Results
The daily time series (north, east and up) of each baseline generated with the GAMIT software are shown in Figure 4. In the figure, the cyan lines indicate days when there was heavy snowfall and the snow cover changed the antenna phase center, resulting in aberrant solutions in the time series. The gray slices indicate data gaps caused by equipment failures. Outliers that exceed an absolute tolerance of 0.01 m (horizontal) and 0.015 m (vertical) from the median or that have formal errors greater than 0.1 m have been removed from the times series [24].
In Figure 4, periodic signals are exhibited in several components of every baseline, and signal amplitudes may have different patterns. The maximum amplitude is shown in the east component of S071, which has an offset style annual signal. L022 and L132 are located at the main dam and auxiliary dam, respectively. Signals with a linear trend can be observed in some components of these two baselines, especially in the east and up components of L022. The north component of baseline L022 also has an evident linear trend. However, such a linear trend signal is missing from the beginning of 2012.
In Table 3, the linear trend and annual and semiannual parameters have been estimated with (1). Monitoring station L022 has secular components of 1.0 mm/yr and 1.8 mm/yr in east and up components, respectively, and L132 has a trend larger than 0.4 mm/yr in north and east components. All of the baselines have annual amplitudes larger than 0.5 mm in one or more coordinate components. S191 and S071 have annual amplitudes larger than 0.5 mm in all three components. The east component of baseline S071 has the largest annual amplitude of 4.8 mm. As for the semiannual signals, except for TN01, all of the baselines have amplitudes larger than 0.3 mm in the up component, but the largest of 2.0 mm is still shown in the east component of S071.
Figure 5 and Figure 6 show the baseline coordinate time-series power spectra and the power spectra of the residuals after removing the fitting models. We computed the power spectra using the Lomb–Scargle periodogram [39,40]. It reveals that signals in the annual band are obvious, and some components of the baselines are also evident. As for the residuals, the annual and semiannual signals are reduced to the noise level. Table 4 gives the baseline RMS statistics before and after removing the fitting models. It shows the RMSs of all the time series are reduced to the submillimeter level. The small RMSs of TN01–TN02 time series indicate that the noise of the GPS daily solution is at the submillimeter level, and the base stations are stable enough to provide the surveying datum for the deformation monitoring system.
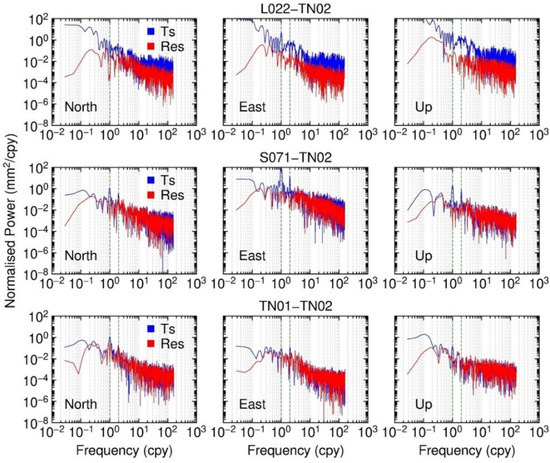
Figure 5.
Baseline coordinate time-series power spectra of L022–TN02, S071–TN02 and TN01–TN02, where the x-axis is frequency with the unit of cycles per year, and the y-axis is the normalized power. The blue lines are the baseline time series, and the red lines are the residuals after removing the fitting models. The vertical green dashed lines indicate annual and semiannual frequency.
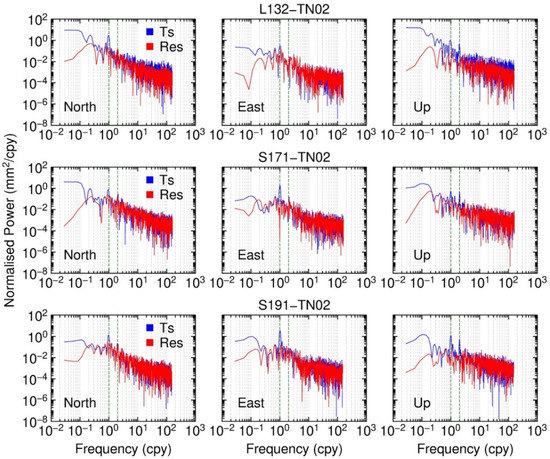
Figure 6.
Baseline coordinate time-series power spectra L132–TN02, S171–TN02 and S191–TN02, where the x-axis is frequency with the unit of cycles per year, and the y-axis is the normalized power. The blue lines are the baseline time series, and the red lines are the residuals after removing the fitting models. The vertical green dashed lines indicate annual and semiannual frequency.

Table 4.
Baseline RMS statistics (station-TN02) before and after removing the fitting models.
4. Discussion
4.1. Annual Signals
As previously mentioned, there are three candidate sources in short GPS baseline annual cycle movements, including differential thermal expansion of monuments, differential time-constant multipath, and errors in phase-center modeling of antennas [24,25]. King and Williams and Jiang et al. found that annual signals are largely invariant to elevation cutoff angles [24,41]. Therefore, the multipath effect has a negligible influence on the annual signals of short baseline GPS time series. Meanwhile, in this study, all the stations were equipped with the same antenna; hence, phase center variation (PCV) modeling errors were out of consideration [42]. However, water-level fluctuation would be one of the important factors to cause movement of stations. Therefore, temperature and water-level variations were the focus of investigating the origin of signals.
Dong et al. and Yan et al. indicated that thermal expansion in monuments or bedrock is responsible for the annual cycle of movement in the vertical component of GPS time series [43,44]. Monument thermal expansion is mainly related to the coefficient of linear thermal expansion of materials, the height of the monument and the variation of temperature. For the two reference stations of the Xilongchi Dam deformation monitoring network, the monument material and height are exactly identical. Therefore, the thermal expansion of the monuments can be differenced by the double-difference method in TN01–TN02. The annual and semiannual cycle movements are relatively small in the east and up components. From Table 1, we see that all the monitoring stations share the same monument materials, and the height differences are fairly small. Considering that the thermal expansion of monuments between monitoring stations can also be differenced, we selected S191 as the reference station to form baselines (station–S191) with other monitoring stations. We processed the GPS data once again with the strategies in Table 2 to get daily baseline solutions (Figure 7).
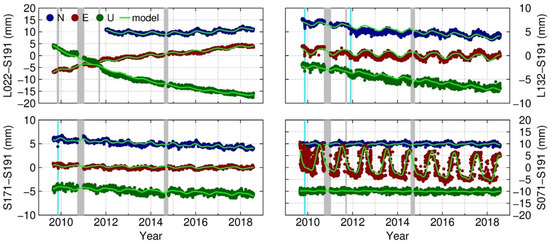
Figure 7.
Baseline coordinate time series and their fitting models. The symbols and ranges of coordinates axes in the figure are same as those in Figure 4. In the north component of L022–S191, the time series were estimated starting from 2012.
Comparing Figure 7 with Figure 4, we can see that the annual amplitudes of baselines are mostly reduced, and some components of baselines are even negligible, such as all three components of S171–S191 and the north and up components of S071–S191. However, some annual amplitudes, such as the east component of L132–S191, become even larger, and spurious signals still exist in the east component of S071–S191.
We estimated the linear trend, annual cycles and semiannual signals of baseline stations–S191, shown in Table 5. The fitting models are also plotted in green lines in Figure 7. Compared with the estimates in Table 3 (station–TN02), the annual amplitudes of station–S191 were mostly 30% to 84% lower than for station–TN02, and the reduction rate of the large amplitudes in station–TN02 (>0.5 mm) mostly reaches up to even more than 50%. However, it increases for the north component of L022–S191 and the east component of L132–S191, and both of them show smaller amplitudes when the reference is TN02. With regard to the semiannual signal, the amplitudes are about 70% to 80% lower than those of station–TN02.

Table 5.
Linear trend and annual and semiannual amplitude estimations (mm). Percent 1 and 2 indicate the annual and semiannual, respectively, amplitude-reducing percentage of station–S191 with respect to station–TN02. The figures in bold are the bold components in Table 3.
The annual amplitude in the east component of L132–S191 is 0.6 mm, which is larger than that of L132–TN02 at 0.3 mm. However, the annual amplitude of S191–TN02 is 0.9 mm. This demonstrates that the increase of the amplitude in L132–S191 is due to the large annual movement of S191. This is also the case for the north component of L022–S191.
According to the previous statements, if S191 is fixed, double-difference can remove the thermal expansion of the monument to a negligible level due to the short baseline, similar materials and the same height. The residual annual signals may likely only be related to the movement of upper ground layers. The spurious signals in the east component of S071 may illustrate the movement of the upper ground layer. Therefore, the annual cycles in station–TN02 seem to be the combination of differential thermal expansion of the monument and upper ground layers related to annual temperature variance.
Table 6 shows the RMS statistics before and after removing the fitting models. It shows that the RMSs are mostly within 0.3–0.5 mm after removing the fitting models, which is lower than that of station–TN02.

Table 6.
Baseline RMS (station-S191)statistics before and after removing the fitting models.
4.2. The Spurious Signals in the East Component of S071–TN02
The east component of S071–TN02 has an offset similar to annual signals, with an amplitude of 4.8 mm, which is extremely larger than other baselines. Analyzing the surroundings of S071, there is a slope to the east side of the station that may shelter the GPS signals when the satellite elevation is lower than 25°, which may cause multipath effects. However, all three components should have a similar multipath effect disturbance [24], not only the east component. Thus, the ~4.8 mm amplitude annual signal may relate to temperature or water fluctuation.
As an example, Figure 8 compares water-level data (a), water data daily difference (b), temperature data (c) and the baseline times series (d) in 2013. Firstly, the water level variance is evident for the day of year (DOY) 1–65, 140–240 and 330–360 in 2013. This is because of power shortages during these periods, meaning the reservoir needed to pump and draw off water frequently to provide electricity, which caused the water level to rise and fall. However, it seems no relationships can be seen by comparing water level (Figure 8a), water level variation (Figure 8b) and baseline time series (Figure 8d). Even though the east component of the baseline time series shows upward offset in the summer, when the water level has large and frequent variance, there are still many cases for which the offset happened in a stationary period of the water’s surface. Thus, the water level may not be the cause of these spurious signals.
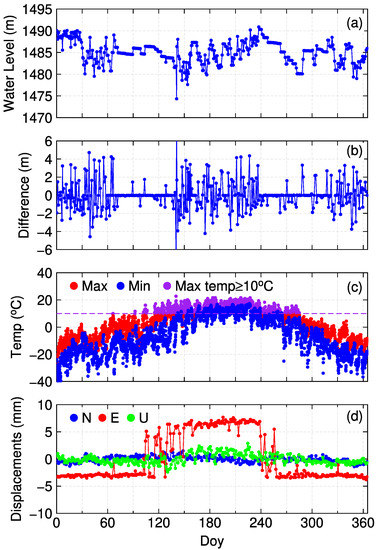
Figure 8.
Water level data (a), water data daily difference (b), temperature data (c) and the baseline times series in 2013 (d). Maximum temperature data larger than 10 °C are shown in purple.
Comparing with the temperature data, we can see that when the baseline offset signal is present, the maximum temperature is mostly larger than 10 °C, which is shown in purple in Figure 8c. Therefore, we give a statistic for the temperature data and baseline time series in the following schemes: the east component of baseline time series (ETS) from 2010–2015 is divided into three sections: ETS > 5.0 mm, 5.0 mm > ETS > −3.0 mm and ETS < −3.0 mm; the maximum values of temperature data are divided into temperature groups as well: T > 10 °C, 10 °C > T > 0 °C and T < 0 °C. Then, we count and calculate the percentage of temperature groups that occurred in the controlled baseline time series groups in Table 7.

Table 7.
Statistics of displacements and maximum temperatures (percentage).
Table 7 shows that over 80 percent of the maximum temperature is higher than 10 °C, and less than 2 percent and even 0 percent are lower than 0 °C, when the ETS is larger than 5.0 mm. On the contrary, nearly 0 percent of the maximum temperatures are higher than 10 °C when the solutions are larger than −3.0 mm. For solutions between 5.0 mm and −3.0 mm, only in 15 percent or fewer of the cases is the maximum temperature higher than 10 °C. Therefore, the spurious signals in the east component of S071–TN02 are highly correlated with the daily temperature data. If the maximum temperature was higher than 10 °C, it seems that something melts to cause an 8 mm displacement in the east side of S071. When the maximum value is lower than 10 and the minimum value mostly lower than 0, the baseline time series will go backwards to the other stable statement. We infer that this could be movement correlated with the temperature of the foundation of the monument that causes this phenomenon. More details, including materials of the foundation, need to be gathered to confirm this in the future.
4.3. Water Level Variation
Although the water level is dependent on the power demand of residents, leading to active phases during the summer and winter and quiet periods in spring and autumn, there are no apparent periodic signals from the water level data (Figure 9). However, instantaneous changes of water level may cause corresponding movement of the stations located at dams. Figure 10 shows an example of water level time series in a quiet period (40 days in total from DOY 146 to 185 in 2015) and an active phase (40 days in total from DOY 326 to 365 in 2015), and the corresponding baseline time series of L022–TN02 and L132–TN02 are also shown. No matter whether in a quiet period or active phase, the baseline time series on dams show no relevant movement with respect to water level variations, even when the water level changes 20 m a day. More research may need to be carried out to identify the relationship between water level and baseline time series.
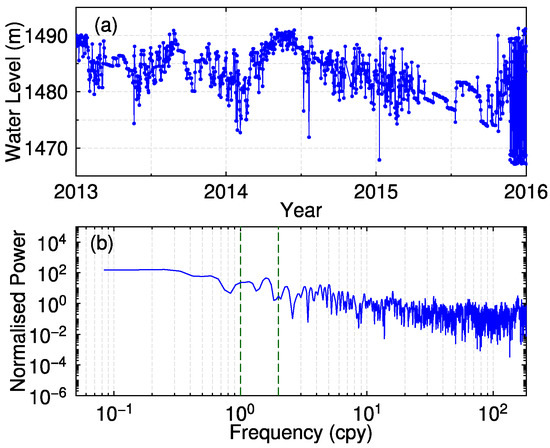
Figure 9.
Water level time series (a) and the corresponding power spectra (b).
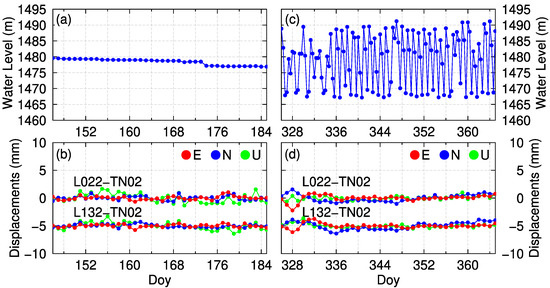
Figure 10.
Water levels (a,c) and baseline time series (b,d) comparison during quiet and active periods. The baseline time series of L132–TN02 are moved downward to −5 mm for clarity.
5. Conclusions
In this paper, we report on an analysis of annual deformations of a pumped-storage power station dam using historical GPS observations. GPS data spanning more than nine years are processed with the GAMIT software to generate static daily solutions. The time series show that the linear trend signals for the dam monitoring stations are obvious, with 1.0 mm/yr and 1.8 mm/yr in the east and up components, respectively, of L022, and 0.5 mm/yr and 0.4 mm/yr in the north and up components, respectively, of L132. However, the movement rate is reducing gradually.
Seasonal cycles occur in all the baseline time series. If the baselines were formed between the monitoring stations and the reference station TN02, amplitudes >0.5 mm can be seen for all baselines in one or more directions. The largest amplitude is shown in the east component of S071 at 4.8 mm. Except for TN01, the amplitudes of semiannual signals in the up component of all the baselines are larger than 0.3 mm, and the largest is in the east component of S071 at 2.0 mm.
Due to the fact that TN01/TN02 share the same monument materials and observation conditions, the annual amplitudes of up components caused by monument and bedrock thermal expansion are eliminated by the double-difference method. Similarly, S191 was selected as the reference station, and baselines station–S191 were formed to obtain the daily time series. Results show that the annual amplitudes of baselines station–S191 could be 30–84% lower than those of station–TN02. Since all the monitoring stations share the same monument materials and height, the thermal expansion of monuments could be differenced. This suggests that the differential thermal expansion of monuments could be over 30% higher in short baseline time series.
The offset style annual cycle in the east component of S071 is highly correlated with annual temperature variations. The offset style movements mostly appear when the maximum air temperature is higher than 10 °C or lower than 0 °C. This suggests that upper ground layer movement correlated with temperature may be responsible for these annual cycles. More details, including materials of the foundations, need to be gathered to confirm this in the future.
From the comparison of water level and baseline time series, no evident periodic relations were found. Further research needs to be done to identify the relationship between them.
Author Contributions
Conceptualization, R.X. and W.J.; methodology, R.X.; software, Q.C.; validation, Q.C. and W.J.; formal analysis, Y.L.; investigation, Y.L.; resources, Y.C.; data curation, S.L.; writing—original draft preparation, R.X.; writing—review and editing, Q.C.; visualization, Y.L.; supervision, W.J.; project administration, W.J.; funding acquisition, R.X. and W.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities under grant number WUT: 2022IVA035. This work was also supported by the Program for Hubei Provincial Science and Technology Innovation Talents (grant no. 2022EJD010), the National Natural Science Foundation of China (grant no. 42004017) and the Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University (grant no. 20-02-06).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, Qusen Chen, upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bukenya, P.; Moyo, P.; Beushausen, H.; Oosthuizen, C. Health monitoring of concrete dams: A literature review. Struct. Health Monit. 2014, 4, 235–244. [Google Scholar] [CrossRef]
- Ardito, R.; Maier, G.; Massalongo, G. Diagnostic analysis of concrete dams based on seasonal hydrostatic loading. Eng. Struct. 2008, 30, 3176–3185. [Google Scholar] [CrossRef]
- Behr, J.; Hudnut, K.; King, N. Monitoring structural deformation at Pacoima dam, California using continuous GPS. In Proceedings of the 11th International Technical Meeting of the Satellite Division of the Institute of Navigation, Nashville, TN, USA, 15–18 September 1998; pp. 59–68. [Google Scholar]
- Hudnut, K.W.; Behr, J.A. Continuous GPS Monitoring of Structural Deformation at Pacoima Dam, California. Seismol. Res. Lett. 1998, 69, 299–308. [Google Scholar] [CrossRef]
- Kulkarni, M.N.; Radhakrishnan, N.; Rai, D. Global positioning system in disaster monitoring of Koyna dam, Western Maharashtra. Surv. Rev. 2006, 38, 629–636. [Google Scholar] [CrossRef]
- Taşçi, L. Dam deformation measurements with GPS. Geod. Cartogr. 2008, 34, 116–121. [Google Scholar] [CrossRef]
- Gökalp, E.; Taşçı, L. Deformation monitoring by GPS at embankment dams and deformation analysis. Surv. Rev. 2009, 41, 86–102. [Google Scholar] [CrossRef]
- Ehiorobo, J.O.; Irughe-Ehigiator, R. Monitoring for horizontal movement in an earth dam using differential GPS. J. Emerg. Trends Eng. Appl. Sci. 2011, 2, 908–913. [Google Scholar]
- Kalkan, Y. Geodetic deformation monitoring of Ataturk Dam in Turkey. Arab. J. Geosci. 2014, 7, 397–405. [Google Scholar] [CrossRef]
- Acosta, L.; de Lacy, M.; Ramos, M.; Cano, J.; Herrera, A.; Avilés, M.; Gil, A. Displacements study of an earth fill dam based on high precision geodetic monitoring and numerical modeling. Sensors 2018, 18, 1369. [Google Scholar] [CrossRef]
- Barzaghi, R.; Cazzaniga, N.E.; De Gaetani, C.I.; Pinto, L.; Tornatore, V. Estimating and Comparing Dam Deformation Using Classical and GNSS Techniques. Sensors 2018, 18, 756. [Google Scholar] [CrossRef]
- Berkant, K.; Leyla, C.; Yilmaz, V. Monitoring the deformation of a concrete dam: A case study on the Deriner Dam, Artvin, Turkey. Geomat. Nat. Haz. Risk 2020, 11, 160–177. [Google Scholar]
- Xi, R.; Zhou, X.; Jiang, W.; Chen, Q. Simultaneous estimation of dam displacements and reservoir level variation from GPS measurements. Measurement 2018, 122, 247–256. [Google Scholar] [CrossRef]
- Xiao, R.; Shi, H.; He, X.; Li, Z.; Jia, D.; Yang, Z. Deformation Monitoring of Reservoir Dams Using GNSS: An Application to South-to-North Water Diversion Project, China. IEEE Access 2019, 7, 54981–54992. [Google Scholar] [CrossRef]
- Pytharouli, S.I.; Stiros, S.C. Ladon dam (Greece) deformation and reservoir level fluctuations: Evidence for a causative relationship from the spectral analysis of a geodetic monitoring record. Eng. Struct. 2005, 27, 361–370. [Google Scholar] [CrossRef]
- Bayrak, T. Modelling the relationship between water level and vertical displacements on the Yamula Dam. Nat. Hazards Earth Syst. Sci. 2007, 7, 289–297. [Google Scholar] [CrossRef]
- Léger, P.; Leclerc, M. Hydrostatic, temperature, time-displacement model for concrete dams. J. Eng. Mech. 2007, 133, 267–277. [Google Scholar] [CrossRef]
- De Sortis, A.; Paoliani, P. Statistical analysis and structural identification in concrete dam monitoring. Eng. Struct. 2007, 29, 110–120. [Google Scholar] [CrossRef]
- Lew, J.S.; Loh, C.H. Structural health monitoring of an arch dam from static deformation. J. Civ. Struct. Health Monit. 2014, 4, 245–253. [Google Scholar] [CrossRef]
- Loh, C.H.; Chen, C.H.; Hsu, T.Y. Application of advanced statistical methods for extracting long-term trends in static monitoring data from an arch dam. Struct. Health Monit. Int. J. 2011, 10, 587–601. [Google Scholar] [CrossRef]
- Hsu, T.Y.; Loh, C.H. Damage detection accommodating nonlinear environmental effects by nonlinear principal component analysis. Struct. Control Health Monit. 2010, 17, 338–354. [Google Scholar] [CrossRef]
- Huang, Y.; Schmitt, F.G.; Lu, Z.; Liu, Y. Analysis of daily river flow fluctuations using empirical mode decomposition and arbitrary order Hilbert spectral analysis. J. Hydrol. 2009, 373, 103–111. [Google Scholar] [CrossRef]
- Agnieszka, W.; Dawid, K. Modeling seasonal oscillations in GNSS time series with Complementary Ensemble Empirical Mode Decomposition. GPS Solut. 2022, 26, 10. [Google Scholar] [CrossRef]
- King, M.A.; Williams, S.D.P. Apparent stability of GPS monumentation from short-baseline time series. J. Geophys. Res. 2009, 114, 1–21. [Google Scholar] [CrossRef]
- Hill, E.M.; Davis, J.L.; Elósegui, P.; Wernicke, B.P.; Malikowski, E.; Niemi, N.A. Characterization of site-specific GPS errors using a short-baseline network of braced monuments at Yucca Mountain, southern Nevada. J. Geophys. Res.-Solid Earth 2009, 114, 1–13. [Google Scholar] [CrossRef]
- Liu, H.; Xiao, Y.; Deng, L.; Bi, G. Analysis of long-term stability of reference stations in GPS deformation monitoring system. J. Geod. Geodyn. 2013, 33, 113–122. (In Chinese) [Google Scholar]
- Liu, X. Xilongchi Upper Reservoir GPS Data Processing and its Time Series Analysis. Master’s Thesis, Wuhan University, Wuhan, China, 2015. (In Chinese). [Google Scholar]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GAMIT-GPS Analysis at MIT, Reference Manual 10.6; Department of Earth, Atmospheric, and Planetary Sciences Massachusetts Institute of Technology: Cambridge, MA, USA, 2015. [Google Scholar]
- Dong, D.; Bock, Y. Global Positioning System network analysis with phase ambiguity resolution applied to crustal deformation studies in California. J. Geophys. Res. Solid Earth 1989, 94, 3949–3966. [Google Scholar] [CrossRef]
- King, M.A.; Watson, C.S. Long GPS coordinate time series: Multipath and geometry effects. J. Geophys. Res. 2010, 115, 1–23. [Google Scholar] [CrossRef]
- King, M.A.; Watson, C.S.; Penna, N.T.; Clarke, P.J. Subdaily signals in GPS observations and their effect at semiannual and annual periods. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Bos, M.; Fernandes, R.; Williams, S.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef]
- Liu, H.; Li, L. Missing Data Imputation in GNSS Monitoring Time Series Using Temporal and Spatial Hankel Matrix Factorization. Remote Sens. 2022, 14, 1500. [Google Scholar] [CrossRef]
- Pytharouli, S.I.; Stiros, S.C. Spectral analysis of unevenly spaced or discontinuous data using the “normperiod” code. Comput. Struct. 2008, 86, 190–196. [Google Scholar] [CrossRef]
- Ghaderpour, E. Least-squares Wavelet and Cross-wavelet Analyses of VLBI Baseline Length and Temperature Time Series: Fortaleza–Hartebeesthoek–Westford–Wettzell. Publ. Astron. Soc. Pac. 2021, 133, 014502. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Pagiatakis, S.D. LSWAVE: A MATLAB software for the least-squares wavelet and cross-wavelet analyses. GPS Solut. 2019, 23, 50. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Ince, E.S.; Pagiatakis, S.D. Least-squares cross-wavelet analysis and its applications in geophysical time series. J. Geod. 2018, 92, 1223–1236. [Google Scholar] [CrossRef]
- Ghaderpour, E. JUST: MATLAB and python software for change detection and time series analysis. GPS Solut. 2021, 25, 85. [Google Scholar] [CrossRef]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II. Statistical aspects of spectral analysis of unevenly spaced data. Astron. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- Jiang, W.; Li, Z.; van Dam, T.; Ding, W. Comparative analysis of different environmental loading methods and their impacts on the GPS height time series. J. Geod. 2013, 87, 687–703. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, H.; Zhou, X.; Li, Z. Analysis of long-term deformation of reservoir using continuous GPS observations. Acta Geod. Cartogr. Sin. 2012, 41, 682–689. (In Chinese) [Google Scholar]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series: Seasonal variations from GPS site time series. J. Geophys. Res.-Solid Earth 2002, 107, ETG 9-1–ETG 9-16. [Google Scholar] [CrossRef]
- Yan, H.; Chen, W.; Zhu, Y.; Zhang, W.; Zhong, M.; Liu, G. Thermal effects on vertical displacement of GPS stations in China. Chin. J. Geophys. 2010, 53, 825–832. (In Chinese) [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).