Exploring Transferable Techniques to Retrieve Crop Biophysical and Biochemical Variables Using Sentinel-2 Data
Abstract
:1. Introduction
2. Materials and Methods
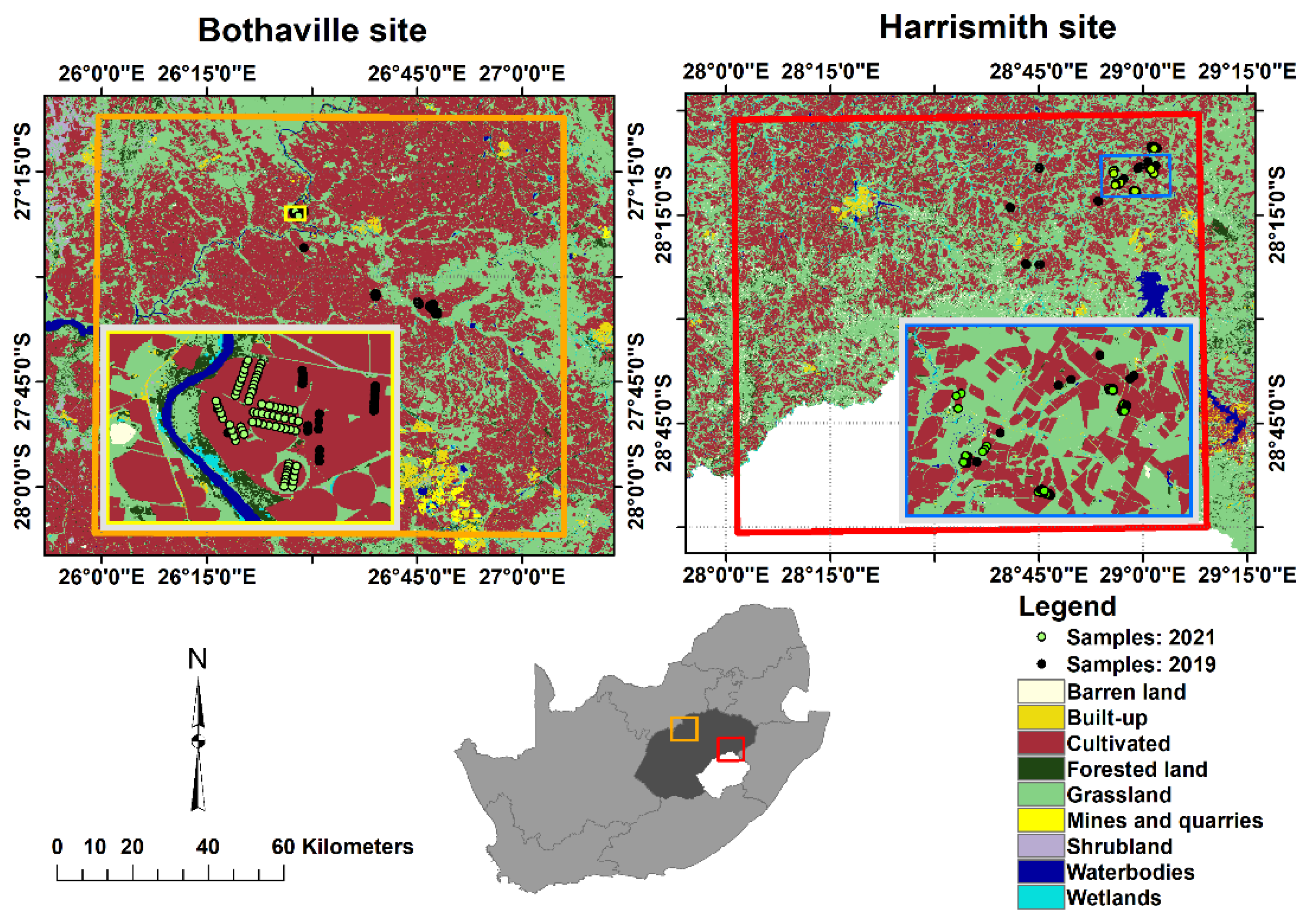
2.1. Characteristics of the Experimental Sites
2.2. Data
2.2.1. In-Situ Data
2.2.2. Remotely Sensing Data
2.3. eXtreme Gradient Boosting
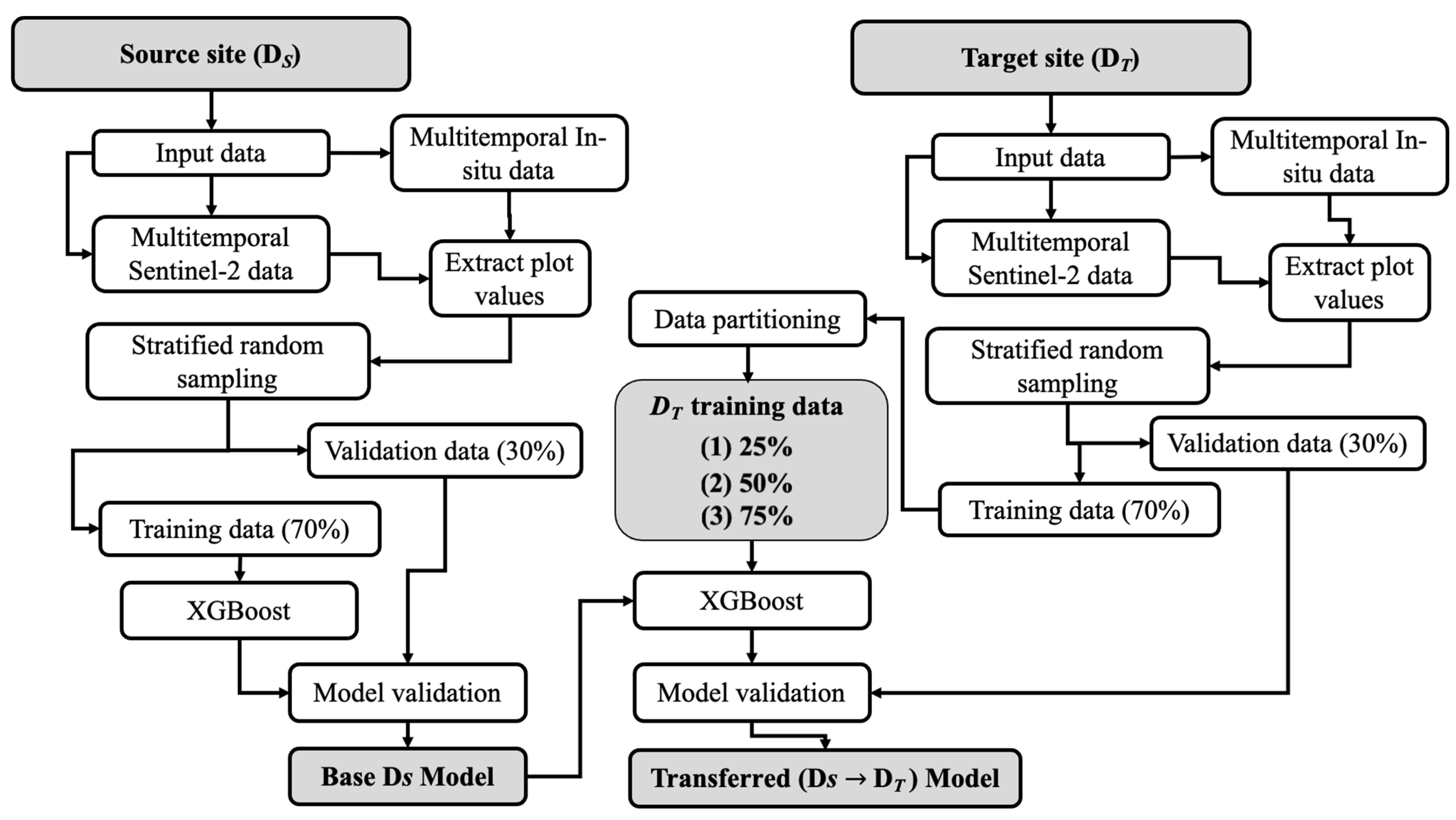
2.4. Spatial Transfer Scenarios
2.5. Model Training and Evaluation
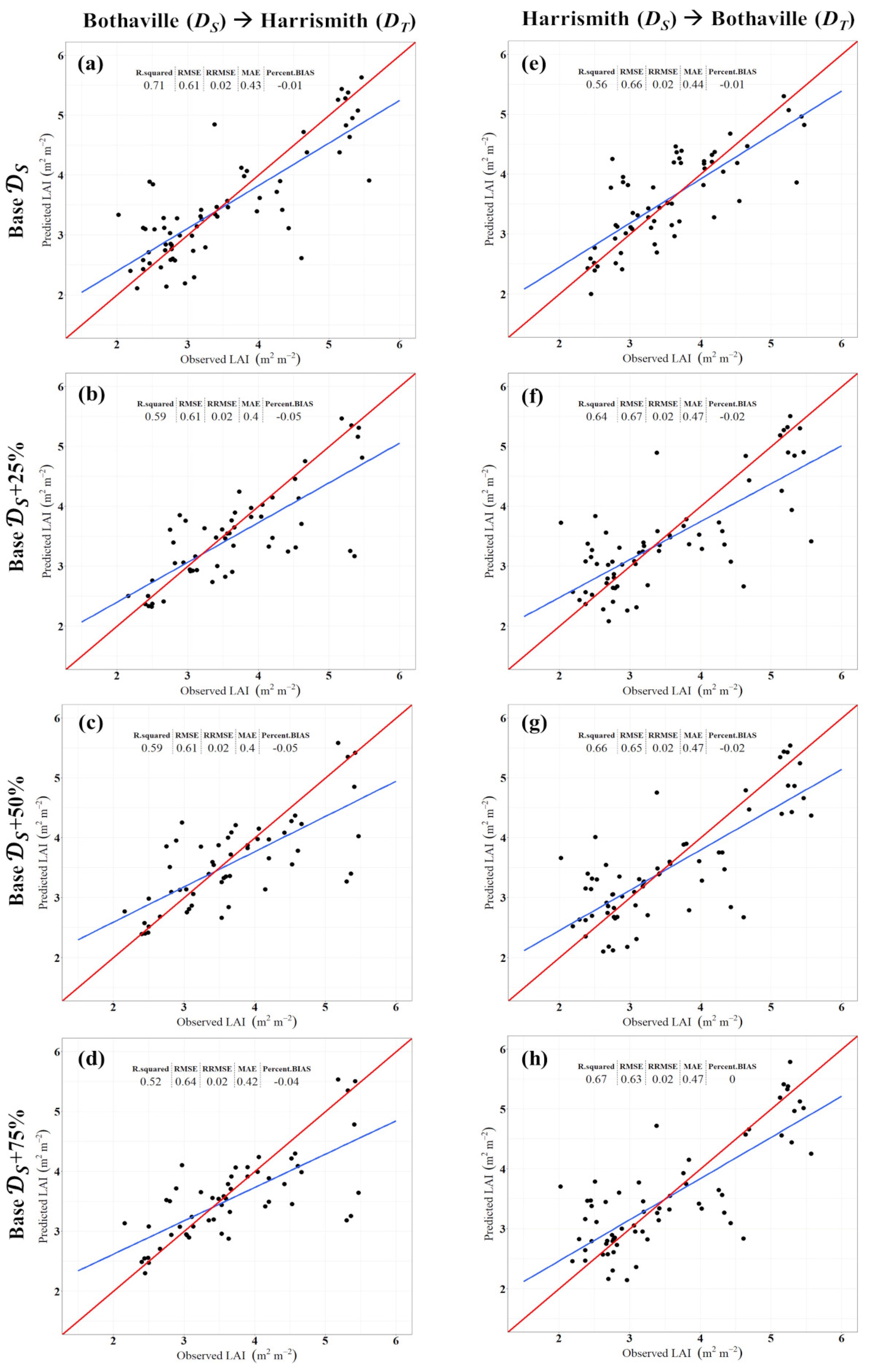
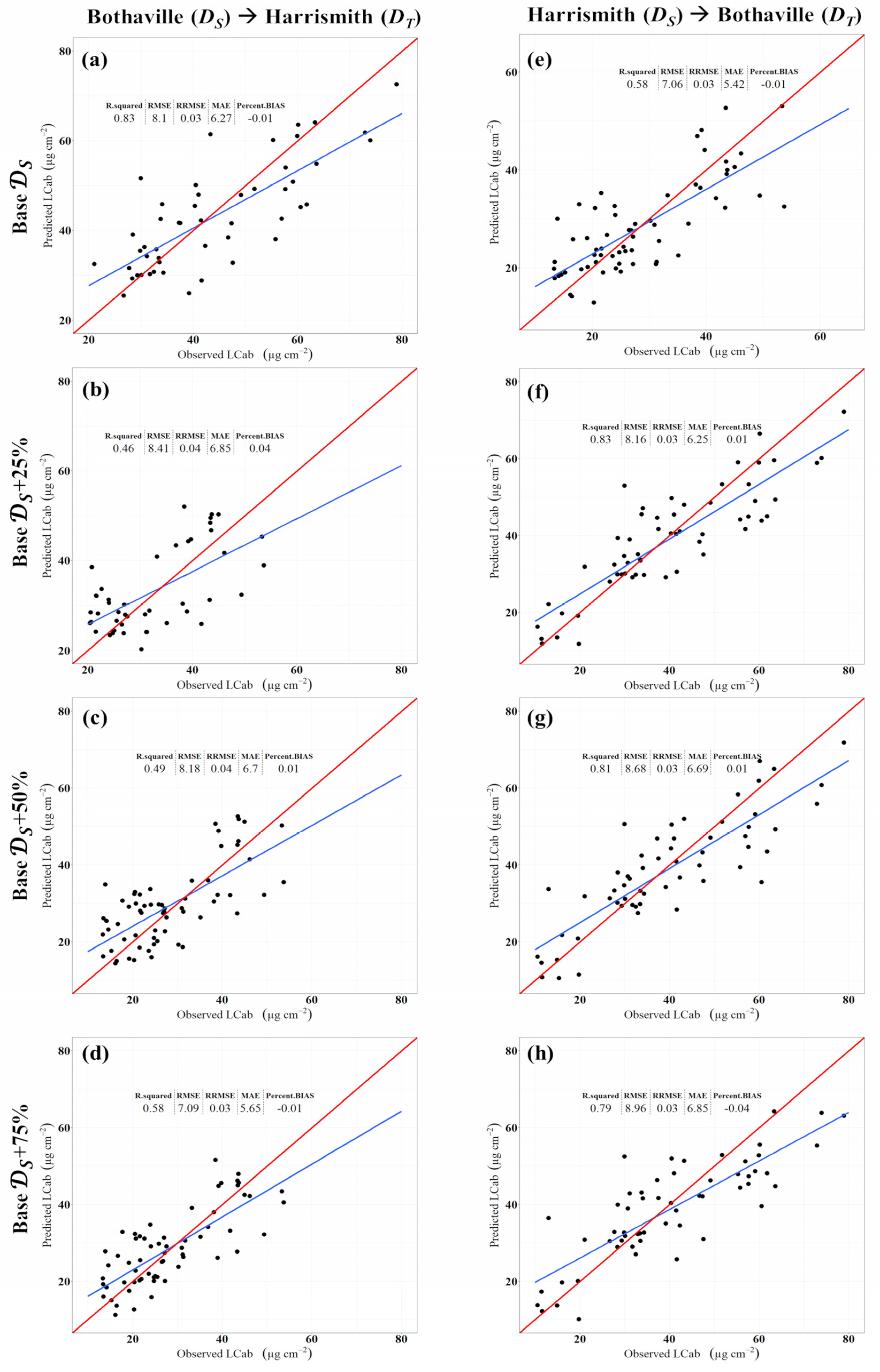
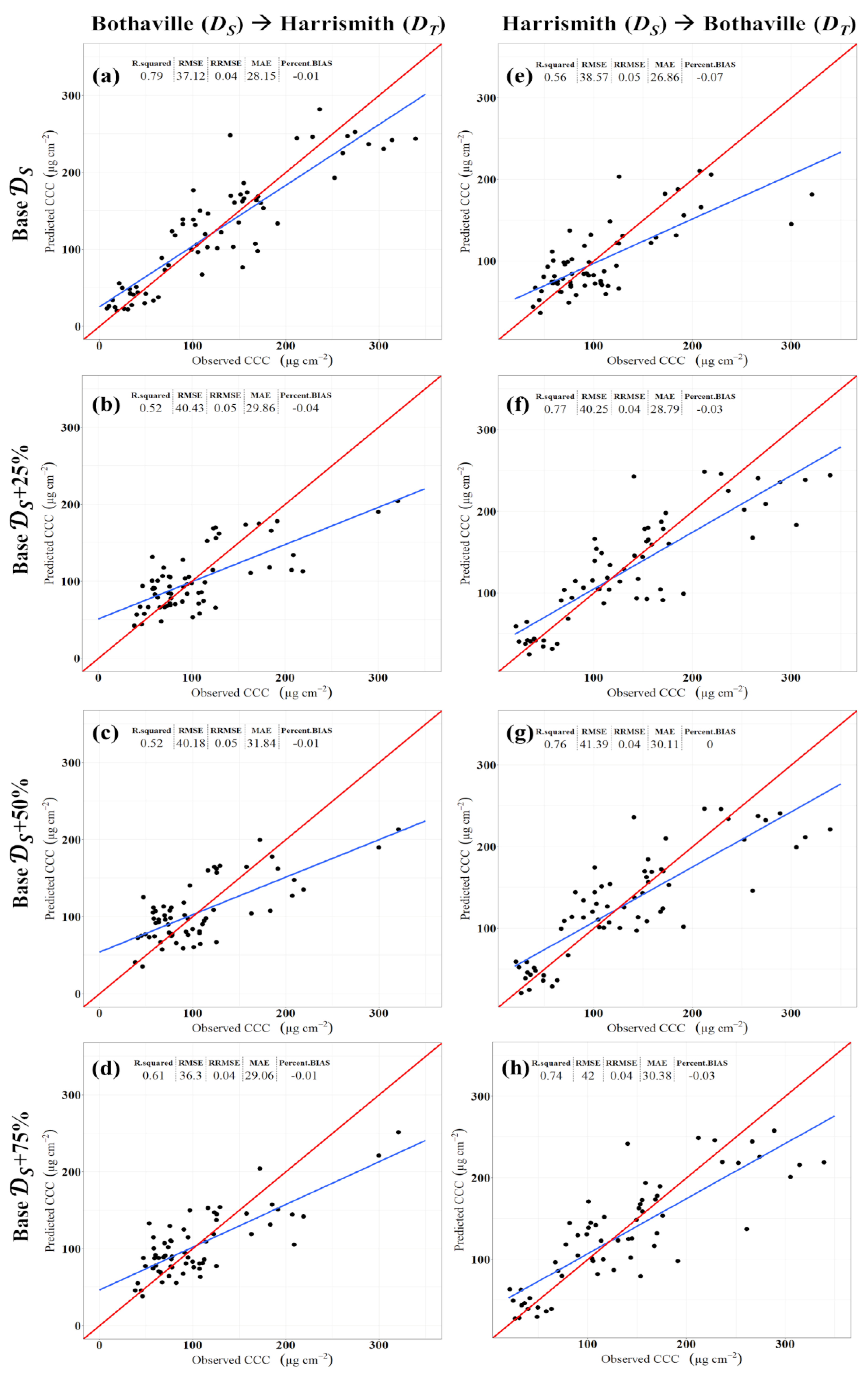
3. Results
4. Discussions
4.1. Effect of Training Samples Available in the Target Site
4.2. Source Model Accuracy and Its Effect on Transferred XGBoost Models
4.3. Sources of Uncertainty
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stamatiadis, S.; Schepers, J.S.; Evangelou, E.; Glampedakis, A.; Glampedakis, M.; Dercas, N.; Tsadilas, C.; Tserlikakis, N.; Tsadila, E. Variable-Rate Application of High Spatial Resolution Can Improve Cotton N-Use Efficiency and Profitability. Precis. Agric. 2020, 21, 695–712. [Google Scholar] [CrossRef]
- Maine, N.; Lowenberg-DeBoer, J.; Nell, W.T.; Alemu, Z.G. Impact of Variable-Rate Application of Nitrogen on Yield and Profit: A Case Study from South Africa. Precis. Agric. 2010, 11, 448–463. [Google Scholar] [CrossRef]
- Boyer, C.N.; Wade Brorsen, B.; Solie, J.B.; Raun, W.R. Profitability of Variable Rate Nitrogen Application in Wheat Production. Precis. Agric. 2011, 12, 473–487. [Google Scholar] [CrossRef]
- Monaghan, J.M.; Daccache, A.; Vickers, L.H.; Hess, T.M.; Weatherhead, E.K.; Grove, I.G.; Knox, J.W. More “Crop per Drop”: Constraints and Opportunities for Precision Irrigation in European Agriculture. J. Sci. Food Agric. 2013, 93, 977–980. [Google Scholar] [CrossRef]
- Chen, S.; Wang, S.; Shukla, M.K.; Wu, D.; Guo, X.; Li, D.; Du, T. Delineation of Management Zones and Optimization of Irrigation Scheduling to Improve Irrigation Water Productivity and Revenue in a Farmland of Northwest China. Precis. Agric. 2020, 21, 655–677. [Google Scholar] [CrossRef]
- Meron, M.; Tsipris, J.; Orlov, V.; Alchanatis, V.; Cohen, Y. Crop Water Stress Mapping for Site-Specific Irrigation by Thermal Imagery and Artificial Reference Surfaces. Precis. Agric. 2010, 11, 148–162. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; Moreno-Martínez, Á.; García-Haro, F.J.; Camps-Valls, G.; Robinson, N.P.; Kattge, J.; Running, S.W. Global Estimation of Biophysical Variables from Google Earth Engine Platform. Remote Sens. 2018, 10, 1167. [Google Scholar] [CrossRef]
- Dimitrov, P.; Kamenova, I.; Roumenina, E.; Filchev, L.; Ilieva, I.; Jelev, G.; Gikov, A.; Banov, M.; Krasteva, V.; Kolchakov, V.; et al. Estimation of Biophysical and Biochemical Variables of Winter Wheat through Sentinel-2 Vegetation Indices. Bulg. J. Agric. Sci. 2019, 25, 819–832. [Google Scholar]
- Gitelson, A.A.; Peng, Y.; Huemmrich, K.F. Relationship between Fraction of Radiation Absorbed by Photosynthesizing Maize and Soybean Canopies and NDVI from Remotely Sensed Data Taken at Close Range and from MODIS 250 m Resolution Data. Remote Sens. Environ. 2014, 147, 108–120. [Google Scholar] [CrossRef]
- Wilhelm, W.W.; Ruwe, K.; Schlemmer, M.R. Comparison of Three Leaf Area Index Meters in a Corn Canopy. Crop Sci. 2000, 40, 1179–1183. [Google Scholar] [CrossRef]
- Bréda, N.J.J. Ground-Based Measurements of Leaf Area Index: A Review of Methods, Instruments and Current Controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global Products of Vegetation Leaf Area and Fraction Absorbed PAR from Year One of MODIS Data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- García-Haro, F.J.; Campos-Taberner, M.; Muñoz-Marí, J.; Laparra, V.; Camacho, F.; Sánchez-Zapero, J.; Camps-Valls, G. Derivation of Global Vegetation Biophysical Parameters from EUMETSAT Polar System. ISPRS J. Photogramm. Remote Sens. 2018, 139, 57–74. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Verger, A.; Smets, B. ATBD for LAI, FAPAR and FCOVER from PROBA-V Products at 300 m Resolution (GEOV3); INRA: Paris, France, 2013; Volume 61. [Google Scholar]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between Leaf Chlorophyll Content and Spectral Reflectance and Algorithms for Non-Destructive Chlorophyll Assessment in Higher Plant Leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow Band Vegetation Indices Overcome the Saturation Problem in Biomass Estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.; Didan, K.; Miura, T. Development of a Two-Band Enhanced Vegetation Index without a Blue Band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Fitzgerald, G.; Rodriguez, D.; O’Leary, G. Measuring and Predicting Canopy Nitrogen Nutrition in Wheat Using a Spectral Index-The Canopy Chlorophyll Content Index (CCCI). Field Crops Res. 2010, 116, 318–324. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Meza, C.M.; Rivera, J.P.; Alonso, L.; Moreno, J. A Red-Edge Spectral Index for Remote Sensing Estimation of Green LAI over Agroecosystems. Eur. J. Agron. 2013, 46, 42–52. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Gitelson, A.A. Remote Estimation of Crop and Grass Chlorophyll and Nitrogen Content Using Red-Edge Bands on Sentinel-2 and-3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Yi, Q.; Wang, F.; Bao, A.; Jiapaer, G. Leaf and Canopy Water Content Estimation in Cotton Using Hyperspectral Indices and Radiative Transfer Models. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 67–75. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Dube, T.; Vundla, T.S.; Mafongoya, P.L. Estimating LAI and Mapping Canopy Storage Capacity for Hydrological Applications in Wattle Infested Ecosystems Using Sentinel-2 MSI Derived Red Edge Bands. GISci. Remote Sens. 2019, 56, 68–86. [Google Scholar] [CrossRef]
- Ramoelo, A.; Skidmore, A.K.; Cho, M.A.; Schlerf, M.; Mathieu, R.; Heitkönig, I.M.A. Regional Estimation of Savanna Grass Nitrogen Using the Red-Edge Band of the Spaceborne Rapideye Sensor. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 151–162. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A.; Nguy-robertson, A.L.; Peng, Y. Remote Sensing of Environment Comparison of Different Vegetation Indices for the Remote Assessment of Green Leaf Area Index of Crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Bsaibes, A.; Courault, D.; Baret, F.; Weiss, M.; Olioso, A.; Jacob, F.; Hagolle, O.; Marloie, O.; Bertrand, N.; Desfond, V.; et al. Albedo and LAI Estimates from FORMOSAT-2 Data for Crop Monitoring. Remote Sens. Environ. 2009, 113, 716–729. [Google Scholar] [CrossRef]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Macé, D.; Pragnère, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of Canopy Biophysical Variables from Bidirectional Reflectance Using Prior Information to Solve the Ill-Posed Inverse Problem. Remote Sens. Environ. 2003, 84, 1–15. [Google Scholar] [CrossRef]
- Atzberger, C. Object-Based Retrieval of Biophysical Canopy Variables Using Artificial Neural Nets and Radiative Transfer Models. Remote Sens. Environ. 2004, 93, 53–67. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Moreno, J.; Camps-Valls, G. Gaussian Processes Uncertainty Estimates in Experimental Sentinel-2 LAI and Leaf Chlorophyll Content Retrieval. ISPRS J. Photogramm. Remote Sens. 2013, 86, 157–167. [Google Scholar] [CrossRef]
- Estévez, J.; Vicent, J.; Rivera-Caicedo, J.P.; Morcillo-Pallarés, P.; Vuolo, F.; Sabater, N.; Camps-Valls, G.; Moreno, J.; Verrelst, J. Gaussian Processes Retrieval of LAI from Sentinel-2 Top-of-Atmosphere Radiance Data. ISPRS J. Photogramm. Remote Sens. 2020, 167, 289–304. [Google Scholar] [CrossRef]
- Amin, E.; Verrelst, J.; Rivera-Caicedo, J.P.; Pipia, L.; Ruiz-Verdú, A.; Moreno, J. Prototyping Sentinel-2 Green LAI and Brown LAI Products for Cropland Monitoring. Remote Sens. Environ. 2021, 255, 112168. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Du, B.; Zhang, L.; Shi, Q. Iterative Reweighting Heterogeneous Transfer Learning Framework for Supervised Remote Sensing Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2022–2035. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Ruder, S. Transfer Learning-Machine Learning’s Next Frontier. Ppt 2017. Available online: https://ruder.io/transfer-learning/ (accessed on 12 November 2021).
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, L.; Hu, H.; Pirasteh, S.; Li, H.; Xie, X. Unsupervised Feature Learning to Improve Transferability of Landslide Susceptibility Representations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3917–3930. [Google Scholar] [CrossRef]
- Tong, X.Y.; Xia, G.S.; Lu, Q.; Shen, H.; Li, S.; You, S.; Zhang, L. Land-Cover Classification with High-Resolution Remote Sensing Images Using Transferable Deep Models. Remote Sens. Environ. 2020, 237, 111322. [Google Scholar] [CrossRef]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S.J. Large-Area Mapping of Canadian Boreal Forest Cover, Height, Biomass and Other Structural Attributes Using Landsat Composites and Lidar Plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
- Persello, C.; Bruzzone, L. Active Learning for Domain Adaptation in the Supervised Classification of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4468–4483. [Google Scholar] [CrossRef]
- Persello, C.; Bruzzone, L. Active and Semisupervised Learning for the Classification of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6937–6956. [Google Scholar] [CrossRef]
- Zhao, B.; Huang, B.; Zhong, Y. Transfer Learning with Fully Pretrained Deep Convolution Networks for Land-Use Classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1436–1440. [Google Scholar] [CrossRef]
- Vuolo, F.; Neugebauer, N.; Bolognesi, S.F.; Atzberger, C.; D’Urso, G. Estimation of Leaf Area Index Using DEIMOS-1 Data: Application and Transferability of a Semi-Empirical Relationship between Two Agricultural Areas. Remote Sens. 2013, 5, 1274–1291. [Google Scholar] [CrossRef]
- Parry, C.; Blonquist, J.M.; Bugbee, B. In Situ Measurement of Leaf Chlorophyll Concentration: Analysis of the Optical/Absolute Relationship. Plant Cell Environ. 2014, 37, 2508–2520. [Google Scholar] [CrossRef] [PubMed]
- Houborg, R.; Boegh, E. Mapping Leaf Chlorophyll and Leaf Area Index Using Inverse and Forward Canopy Reflectance Modeling and SPOT Reflectance Data. Remote Sens. Environ. 2008, 112, 186–202. [Google Scholar] [CrossRef]
- Uddling, J.; Gelang-Alfredsson, J.; Piikki, K.; Pleijel, H. Evaluating the Relationship between Leaf Chlorophyll Concentration and SPAD-502 Chlorophyll Meter Readings. Photosynth. Res. 2007, 91, 37–46. [Google Scholar] [CrossRef]
- Markwell, J.; Osterman, J.C.; Mitchell, J.L. Calibration of the Minolta SPAD-502 Leaf Chlorophyll Meter. Photosynth. Res. 1995, 46, 467–472. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Su, W.; Fu, Y.; Zhu, D.; Xue, J.H.; Huang, J.; Wang, W.; Wu, J.; Yao, C. Super-Resolution Enhancement of Sentinel-2 Image for Retrieving LAI and Chlorophyll Content of Summer Corn. Eur. J. Agron. 2019, 111, 125938. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gitelson, A.A.; Jacquemoud, S.; Schaepman, M.; Asner, G.P.; Gamon, J.A.; Zarco-Tejada, P. Retrieval of Foliar Information about Plant Pigment Systems from High Resolution Spectroscopy. Remote Sens. Environ. 2009, 113, 67–77. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.; Gitelson, A.; Peng, Y.; Viña, A.; Arkebauer, T.; Rundquist, D. Green Leaf Area Index Estimation in Maize and Soybean: Combining Vegetation Indices to Achieve Maximal Sensitivity. Agron. J. 2012, 104, 1336–1347. [Google Scholar] [CrossRef]
- Drusch, M.; del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.; Ma, Q.; Zhang, H.K.; Liu, J. Evaluation of Sentinel-2A Surface Reflectance Derived Using Sen2Cor in North America. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1997–2021. [Google Scholar] [CrossRef]
- Louis, J.; Debaecker, V.; Pflug, B.; Main-Knorn, M.; Bieniarz, J.; Mueller-Wilm, U.; Cadau, E.; Gascon, F. Sentinel-2 SEN2COR: L2A Processor for Users. In Proceedings of the European Space Agency, (Special Publication) ESA SP, Prague, Czech Republic, 9–13 May 2016; Volume SP-740. [Google Scholar]
- Kganyago, M. Using Sentinel-2 Observations to Assess the Consequences of the COVID-19 Lockdown on Winter Cropping in Bothaville and Harrismith, South Africa. Remote Sens. Lett. 2021, 12, 827–837. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Ayumi, V. Pose-Based Human Action Recognition with Extreme Gradient Boosting. In Proceedings of the 14th IEEE Student Conference on Research and Development: Advancing Technology for Humanity, SCOReD 2016, Kuala Lumpur, Malaysia, 13–14 December 2016. [Google Scholar] [CrossRef]
- Gupta, A.; Gusain, K.; Popli, B. Verifying the Value and Veracity of Extreme Gradient Boosted Decision Trees on a Variety of Datasets. In Proceedings of the 11th International Conference on Industrial and Information Systems, ICIIS 2016-Conference Proceedings, Roorkee, India, 3–4 December 2016. [Google Scholar]
- Beltran, J.C.; Valdez, P.; Naval, P. Predicting Protein-Protein Interactions Based on Biological Information Using Extreme Gradient Boosting. In Proceedings of the 2019 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB 2019), Siena, Italy, 9–11 July 2019. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. Package “Xgboost”; GitHub: San Francisco, CA, USA, 2019. [Google Scholar]
- Bischl, B.; Lang, M.; Kotthoff, L.; Schiffner, J.; Richter, J.; Studerus, E.; Casalicchio, G.; Jones, Z.M. Mlr: Machine Learning in R. J. Mach. Learn. Res. 2016, 17, 5938–5942. [Google Scholar]
- Kganyago, M.; Mhangara, P.; Adjorlolo, C. Estimating Crop Biophysical Parameters Using Machine Learning Algorithms and Sentinel-2 Imagery. Remote Sens. 2021, 13, 4314. [Google Scholar] [CrossRef]
- Kganyago, M.; Mhangara, P.; Alexandridis, T.; Laneve, G.; Ovakoglou, G.; Mashiyi, N. Validation of Sentinel-2 Leaf Area Index (LAI) Product Derived from SNAP Toolbox and Its Comparison with Global LAI Products in an African Semi-Arid Agricultural Landscape. Remote Sens. Lett. 2020, 11, 883–892. [Google Scholar] [CrossRef]
- Bochenek, Z.; Dąbrowska-Zielińska, K.; Gurdak, R.; Niro, F.; Bartold, M.; Grzybowski, P. Validation of the LAI Biophysical Product Derived from Sentinel-2 and Proba-V Images for Winter Wheat in Western Poland. Geoinf. Issues 2017, 9, 15–26. [Google Scholar]
- Pasqualotto, N.; Delegido, J.; van Wittenberghe, S.; Rinaldi, M.; Moreno, J. Multi-Crop Green LAI Estimation with a New Simple Sentinel-2 LAI Index (SeLI). Sensors 2019, 19, 904. [Google Scholar] [CrossRef]
- Mason, P.; Reading, B. Systematic Observation Requirements for Satellite-Based Products for Climate. In Proceedings of the 23rd Conference on IIPS, 2007. 11th Symposium on Integrated Observing and Assimilation Systems for the Atmosphere, Oceans, and Land Surface (IOAS-AOLS), San Antonio, TX, USA, 17 January 2007. [Google Scholar]
- Padilla, F.M.; Gallardo, M.; Peña-Fleitas, M.T.; de Souza, R.; Thompson, R.B. Proximal Optical Sensors for Nitrogen Management of Vegetable Crops: A Review. Sensors 2018, 18, 2083. [Google Scholar] [CrossRef]
- Dong, T.; Shang, J.; Chen, J.M.; Liu, J.; Qian, B.; Ma, B.; Morrison, M.J.; Zhang, C.; Liu, Y.; Shi, Y.; et al. Assessment of Portable Chlorophyll Meters for Measuring Crop Leaf Chlorophyll Concentration. Remote Sens. 2019, 11, 2706. [Google Scholar] [CrossRef]
- Martins, V.S.; Barbosa, C.C.F.; de Carvalho, L.A.S.; Jorge, D.S.F.; Lobo, F.D.L.; de Moraes Novo, E.M.L. Assessment of Atmospheric Correction Methods for Sentinel-2 MSI Images Applied to Amazon Floodplain Lakes. Remote Sens. 2017, 9, 332. [Google Scholar] [CrossRef]
- Kganyago, M.; Ovakoglou, G.; Mhangara, P.; Odindi, J.; Adjorlolo, C.; Mashiyi, N. Validation of Atmospheric Correction Approaches for Sentinel-2 under Partly-Cloudy Conditions in an African Agricultural Landscape. SPIE Proc. 2020, 11531, 115310B. [Google Scholar] [CrossRef]
- Doxani, G.; Vermote, E.; Roger, J.C.; Gascon, F.; Adriaensen, S.; Frantz, D.; Hagolle, O.; Hollstein, A.; Kirches, G.; Li, F.; et al. Atmospheric Correction Inter-Comparison Exercise. Remote Sens. 2018, 10, 352. [Google Scholar] [CrossRef] [PubMed]
- Sola, I.; García-Martín, A.; Sandonís-Pozo, L.; Álvarez-Mozos, J.; Pérez-Cabello, F.; González-Audícana, M.; Montorio Llovería, R. Assessment of Atmospheric Correction Methods for Sentinel-2 Images in Mediterranean Landscapes. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 63–76. [Google Scholar] [CrossRef]
- Ollinger, S.V. Sources of Variability in Canopy Reflectance and the Convergent Properties of Plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef]
- Verrelst, J.; Alonso, L.; Camps-Valls, G.; Delegido, J.; Moreno, J. Retrieval of Vegetation Biophysical Parameters Using Gaussian Process Techniques. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1832–1843. [Google Scholar] [CrossRef]
- Orynbaikyzy, A.; Gessner, U.; Conrad, C. Spatial Transferability of Random Forest Models for Crop Type Classification Using Sentinel-1 and Sentinel-2. Remote Sens. 2022, 14, 1493. [Google Scholar] [CrossRef]

| Bothaville | Harrismith | ||||||
|---|---|---|---|---|---|---|---|
| LAI | LCab | CCC | LAI | LCab | CCC | ||
| Base S | n | 166 | 166 | 166 | 147 | 147 | 147 |
| Min | 1.54 | 3.70 | 11.86 | 1.16 | 10.77 | 20.44 | |
| Mean | 3.62 | 34.53 | 126.98 | 3.45 | 26.83 | 92.56 | |
| Max | 5.90 | 74.02 | 288.22 | 6.32 | 56.82 | 333.63 | |
| SD | 1.04 | 15.57 | 66.99 | 0.94 | 10.89 | 51.25 | |
| Base S + 25% | n | 202 | 202 | 202 | 188 | 188 | 188 |
| Min | 1.54 | 3.71 | 11.86 | 1.16 | 3.71 | 11.86 | |
| Mean | 3.57 | 33.07 | 120.18 | 3.53 | 28.35 | 102.25 | |
| Max | 6.35 | 74.02 | 288.22 | 6.32 | 71.35 | 333.63 | |
| SD | 1.01 | 15.06 | 65.33 | 0.98 | 12.33 | 59.63 | |
| Base S + 50% | n | 239 | 239 | 239 | 229 | 229 | 229 |
| Min | 1.54 | 3.71 | 11.86 | 1.16 | 3.71 | 11.86 | |
| Mean | 3.56 | 32.04 | 115.80 | 3.51 | 29.97 | 106.89 | |
| Max | 6.35 | 74.02 | 288.22 | 6.32 | 74.01 | 333.63 | |
| SD | 0.99 | 14.65 | 63.66 | 0.98 | 13.82 | 62.47 | |
| Base S + 75% | n | 276 | 276 | 276 | 270 | 270 | 270 |
| Min | 1.54 | 3.71 | 11.86 | 1.16 | 3.71 | 11.86 | |
| Mean | 3.55 | 31.36 | 113.41 | 3.55 | 30.58 | 110.48 | |
| Max | 6.35 | 74.01 | 333.63 | 6.32 | 74.01 | 333.63 | |
| SD | 1.00 | 14.30 | 63.31 | 1.01 | 14.06 | 63.15 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kganyago, M.; Adjorlolo, C.; Mhangara, P. Exploring Transferable Techniques to Retrieve Crop Biophysical and Biochemical Variables Using Sentinel-2 Data. Remote Sens. 2022, 14, 3968. https://doi.org/10.3390/rs14163968
Kganyago M, Adjorlolo C, Mhangara P. Exploring Transferable Techniques to Retrieve Crop Biophysical and Biochemical Variables Using Sentinel-2 Data. Remote Sensing. 2022; 14(16):3968. https://doi.org/10.3390/rs14163968
Chicago/Turabian StyleKganyago, Mahlatse, Clement Adjorlolo, and Paidamwoyo Mhangara. 2022. "Exploring Transferable Techniques to Retrieve Crop Biophysical and Biochemical Variables Using Sentinel-2 Data" Remote Sensing 14, no. 16: 3968. https://doi.org/10.3390/rs14163968
APA StyleKganyago, M., Adjorlolo, C., & Mhangara, P. (2022). Exploring Transferable Techniques to Retrieve Crop Biophysical and Biochemical Variables Using Sentinel-2 Data. Remote Sensing, 14(16), 3968. https://doi.org/10.3390/rs14163968








