Above-Ground Biomass Prediction for Croplands at a Sub-Meter Resolution Using UAV–LiDAR and Machine Learning Methods
Abstract
:1. Introduction
2. Materials and Methods
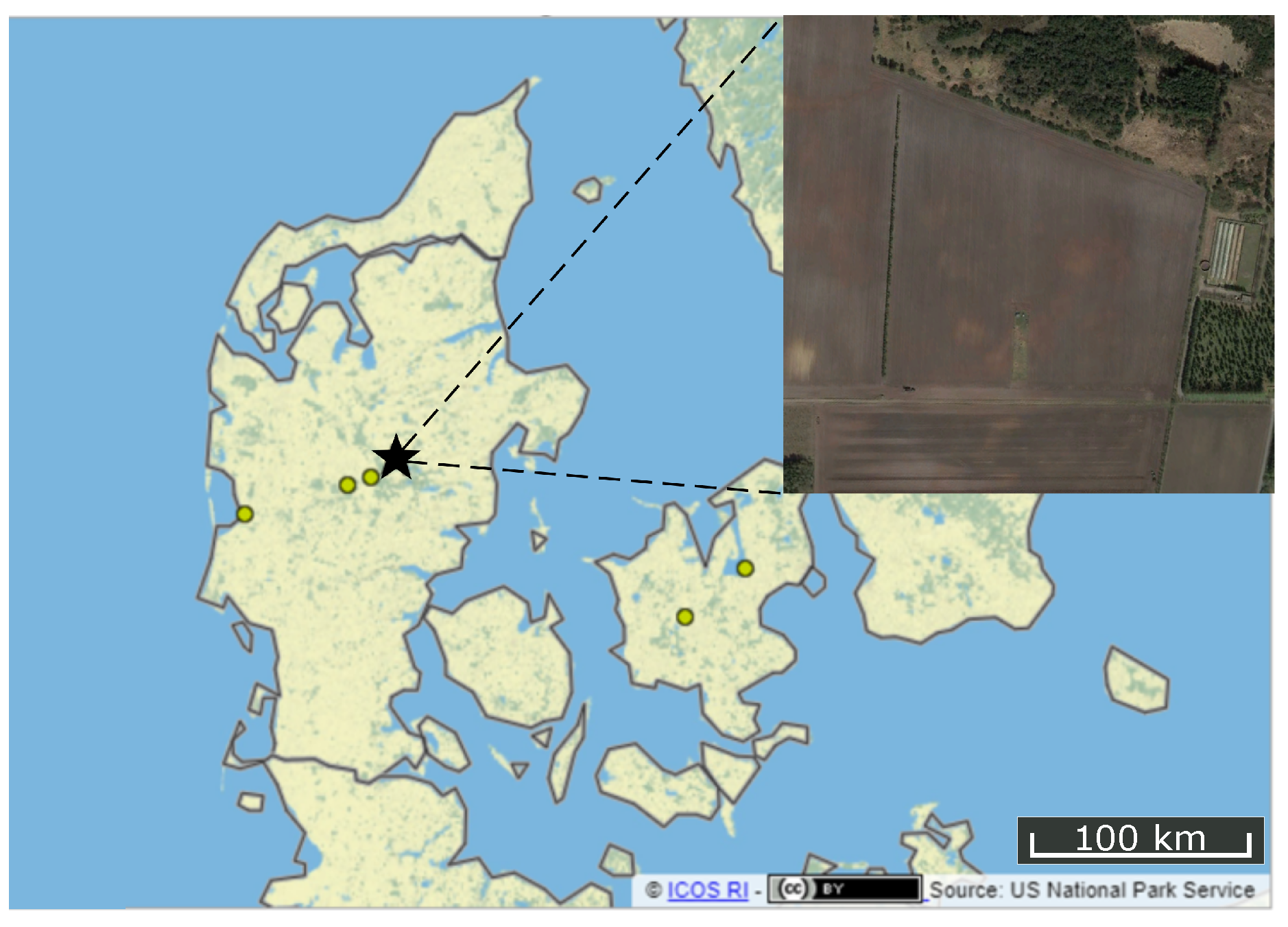
2.1. Study Area
2.2. Instrumentation, Flight Parameters, and Field Measurements
2.3. LiDAR Data Processing
2.3.1. Point Cloud Scene Generation
2.3.2. Point Cloud Scene Processing
- The metrics of height were the mean, median, standard deviation, variance, skewness, and kurtosis;
- The metrics of reflectance were the mean and standard deviation.
2.3.3. Data Post-Processing
2.4. Datasets
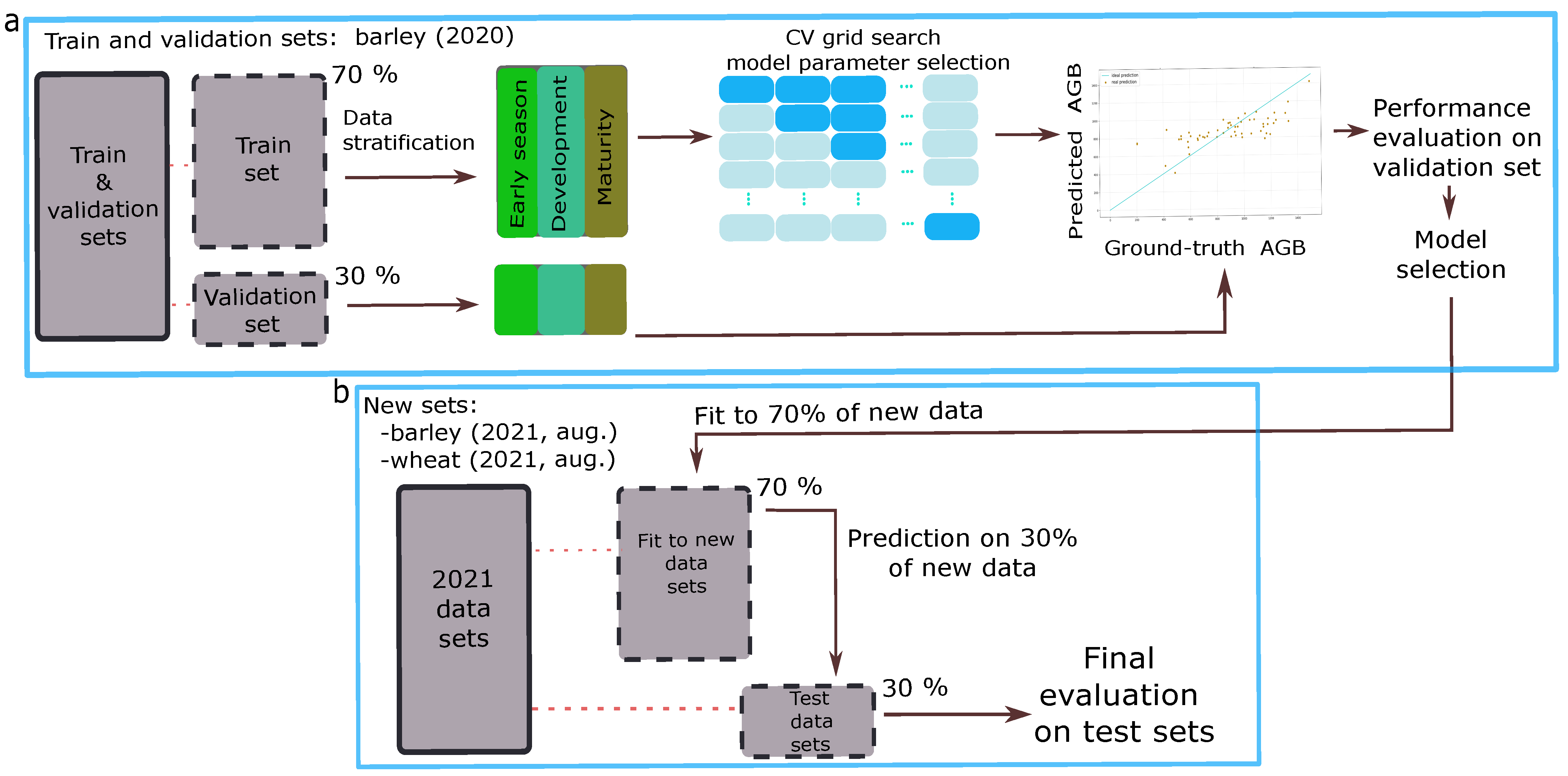
2.5. ML Model Training and Evaluation
2.6. Description of the Selected ML Model
2.7. Generation of AGB Prediction Maps
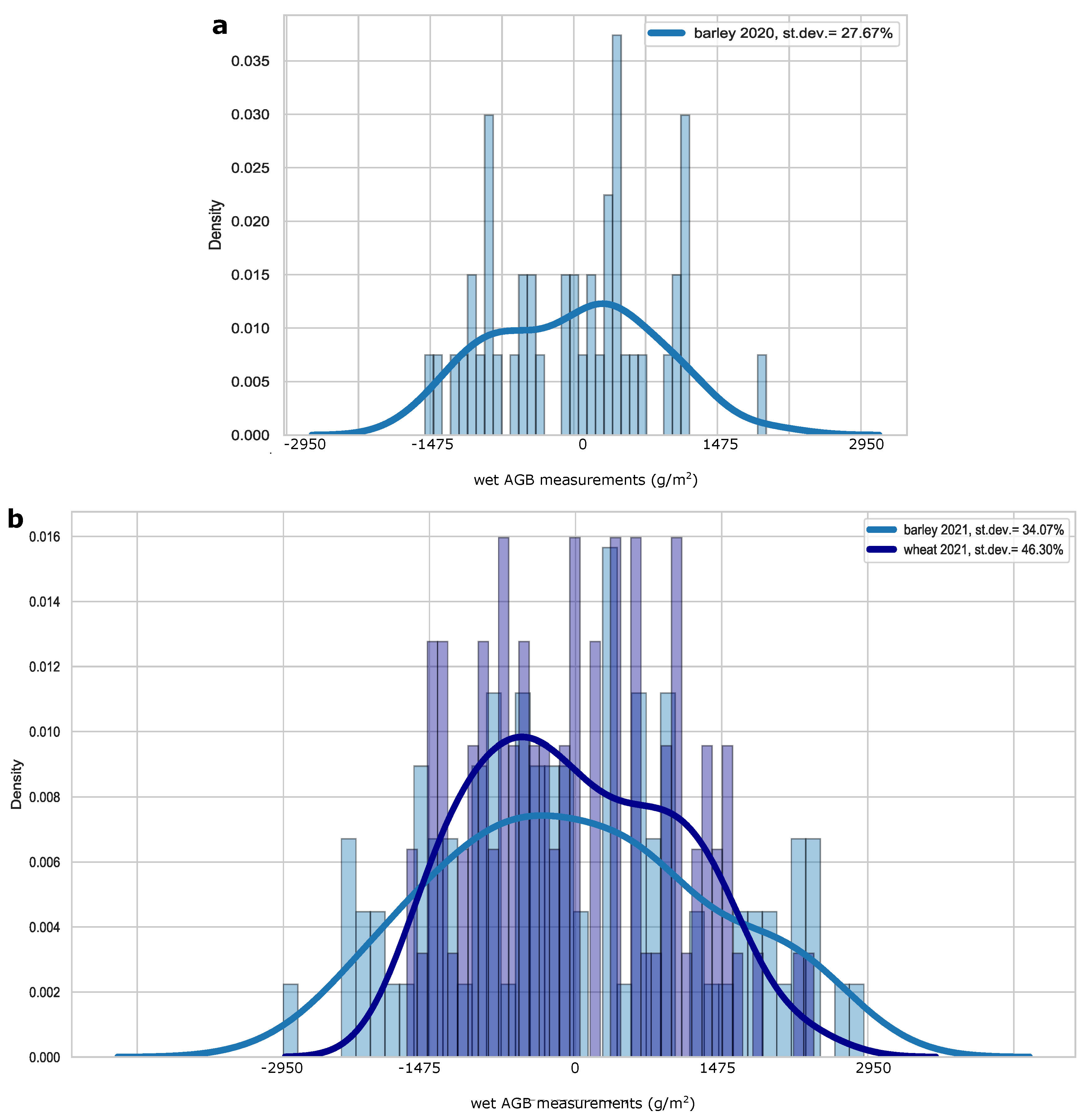
2.8. Uncertainty of AGB Field-Based Measurements
3. Results
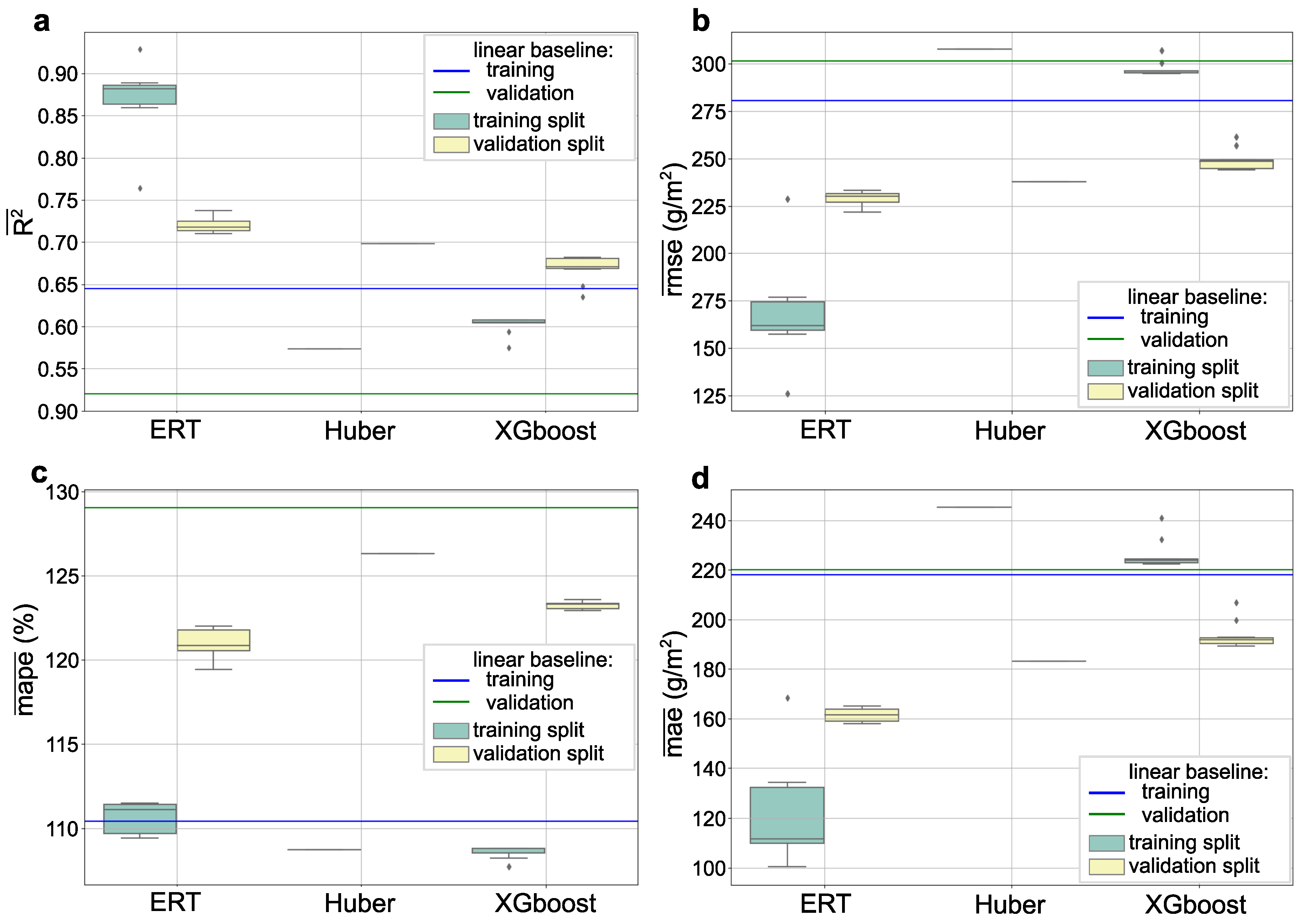
3.1. Model Selection
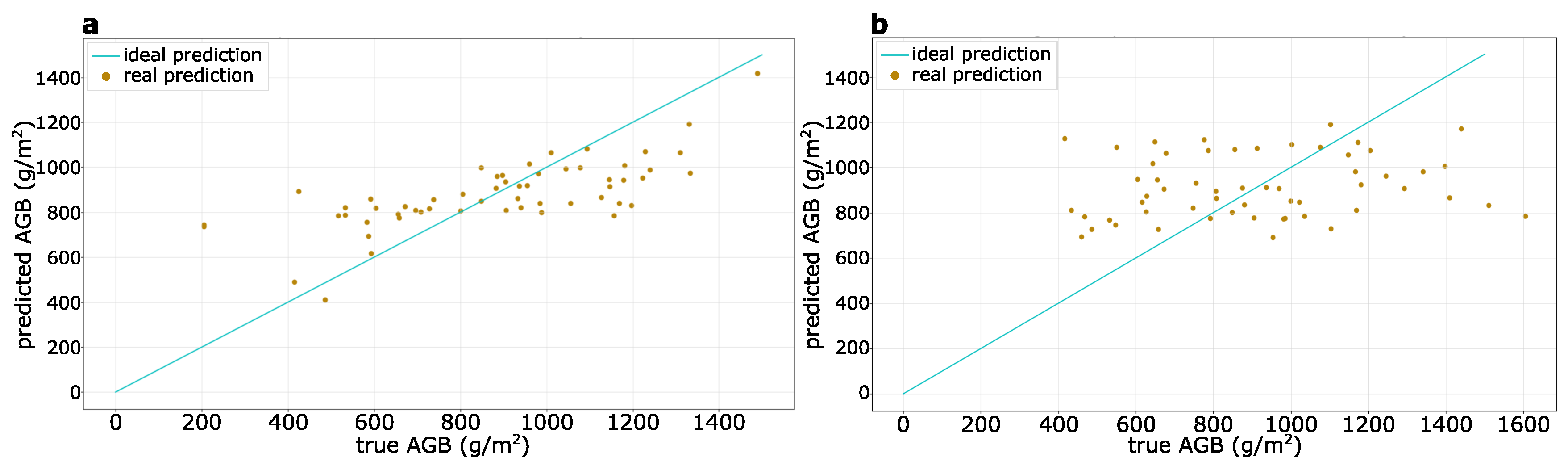
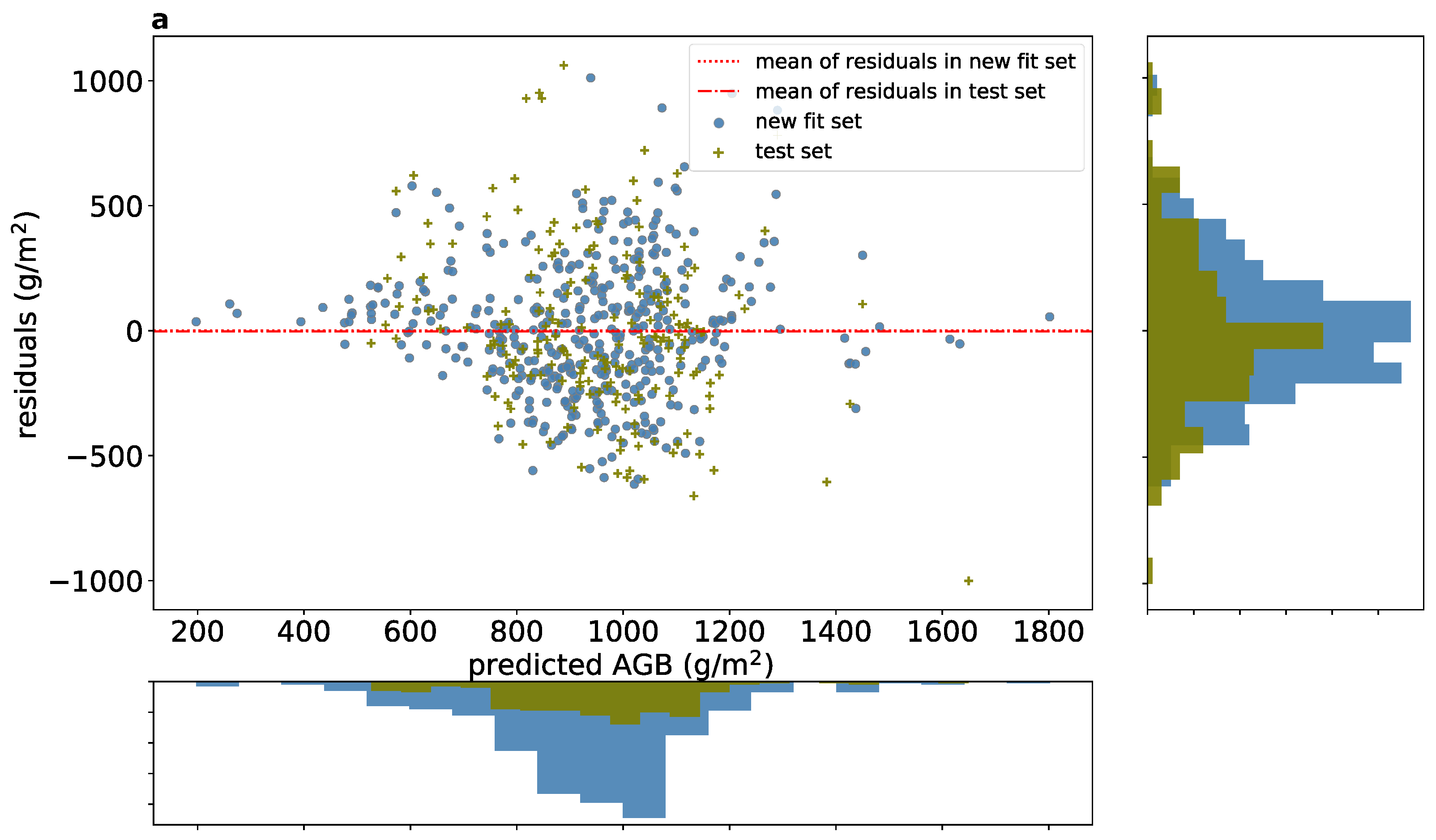
3.2. AGB Prediction at a Sub-Meter Resolution
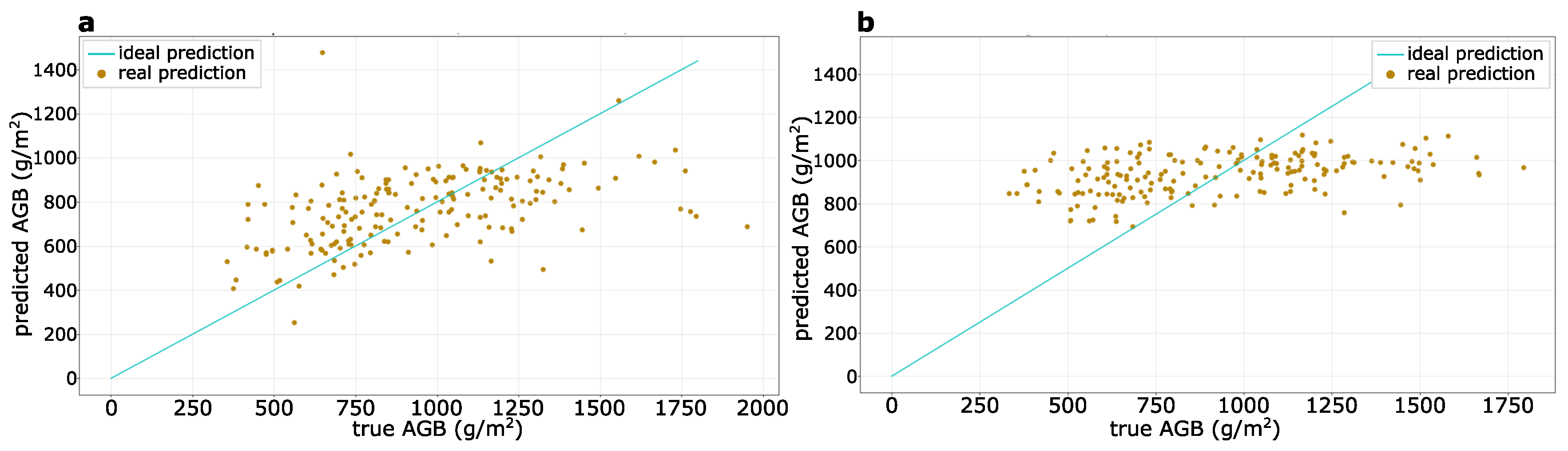
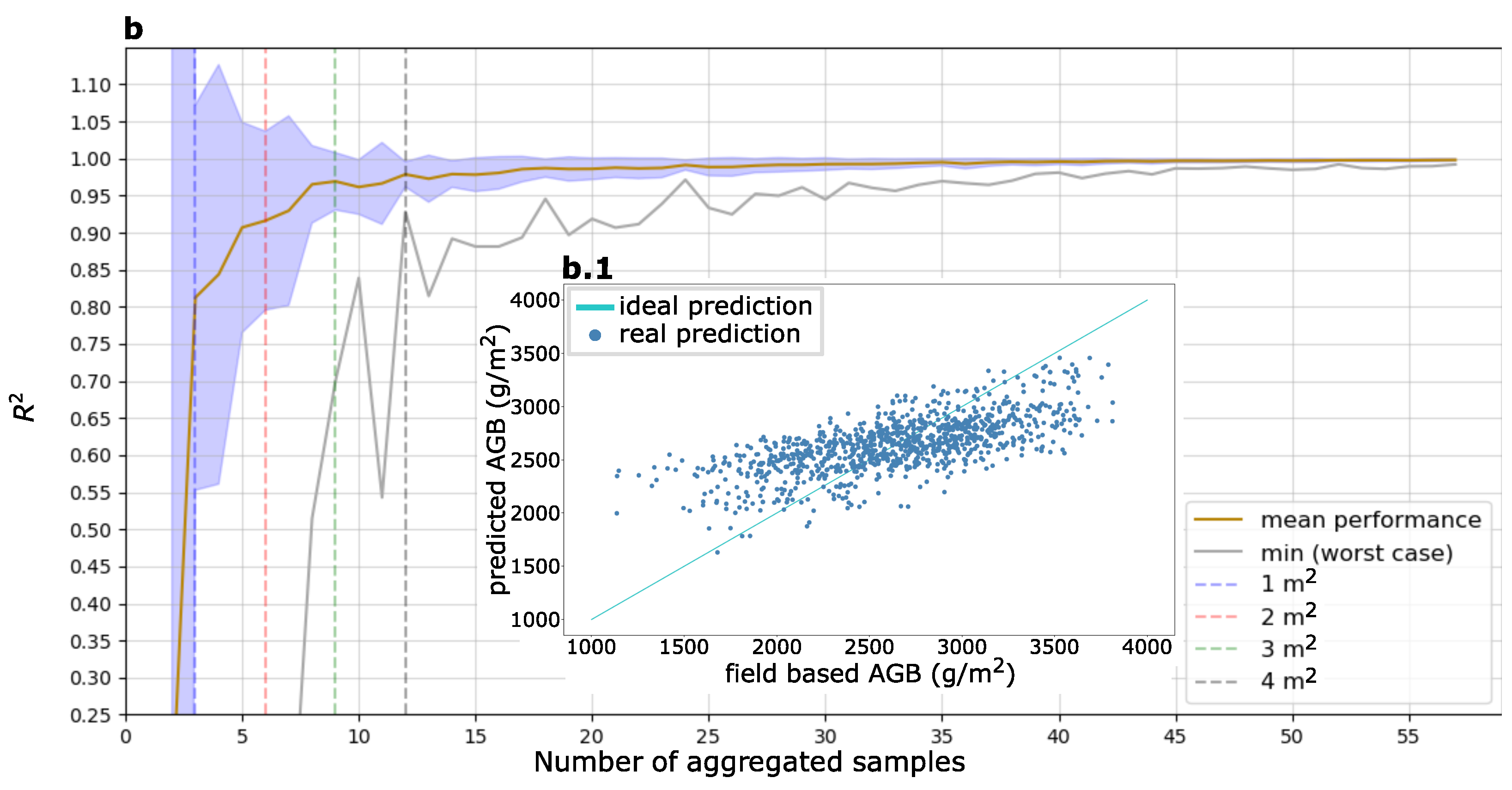
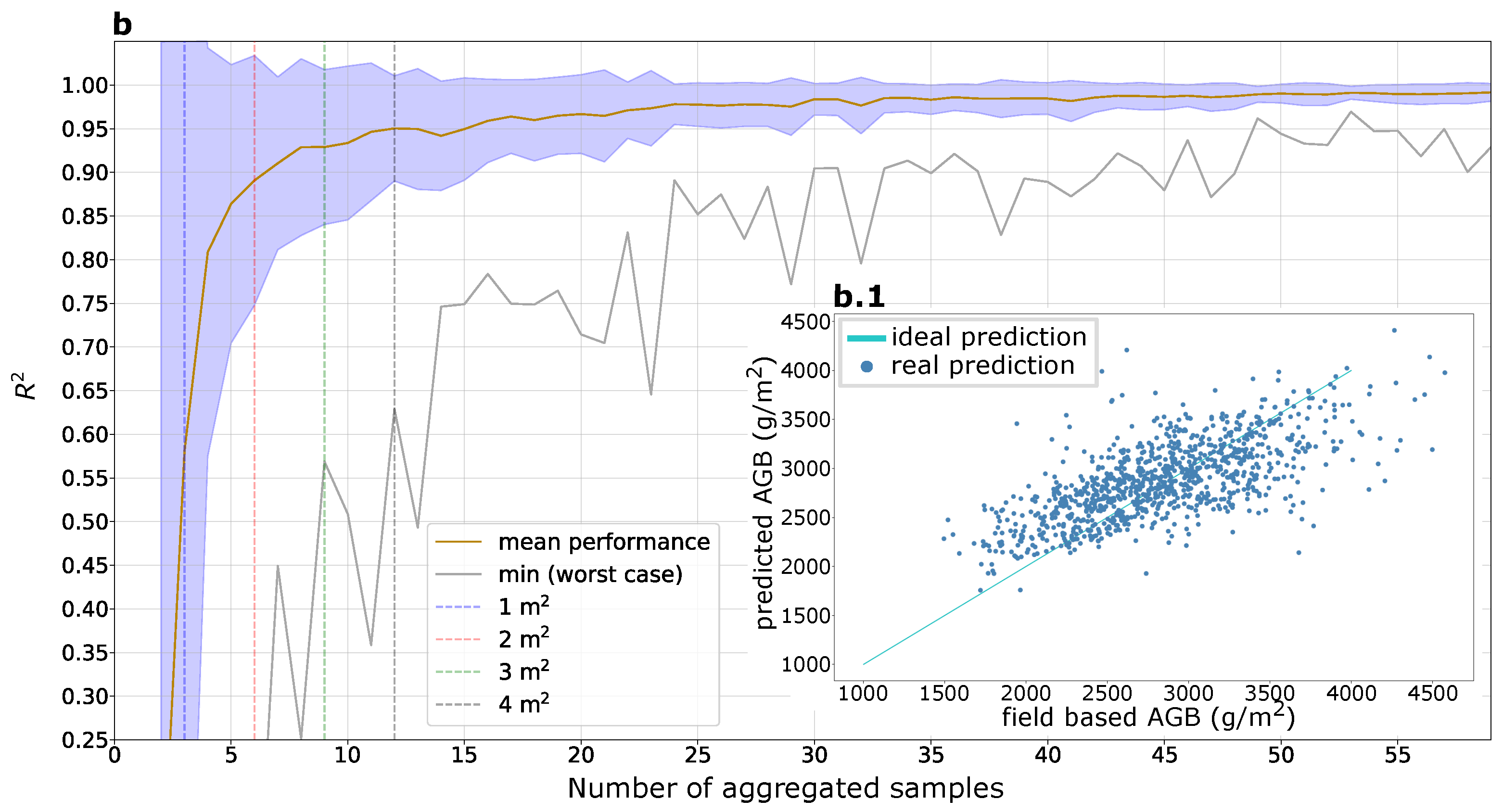
3.3. Aggregated AGB Predictions
4. Discussion
4.1. AGB Prediction
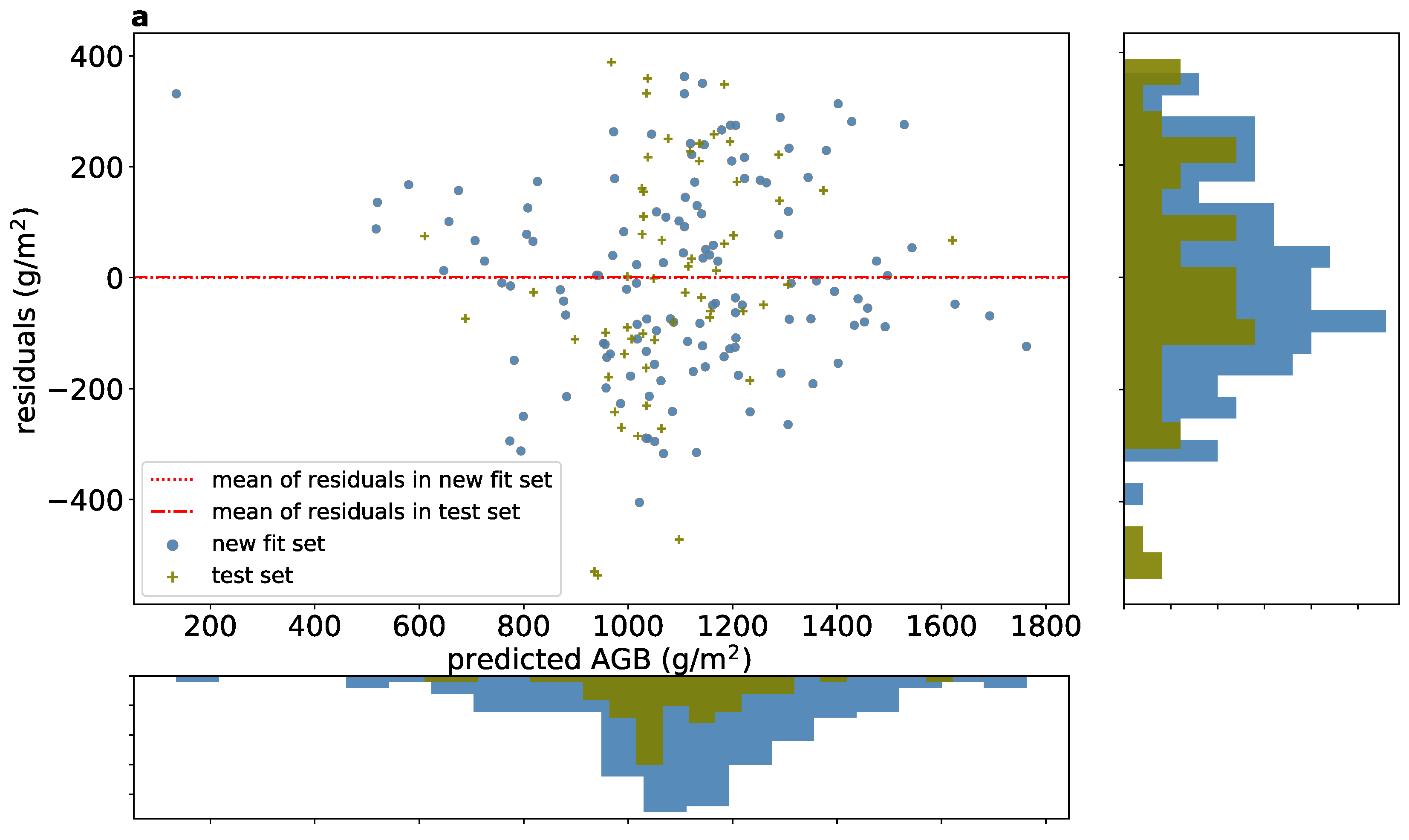
4.2. Aggregation of AGB Predictions
4.3. Applied ML Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AGB | Above-Ground Biomass |
| dGPS | Differential Global Positioning System |
| DTM | Digital Terrain Model |
| ERT | Extremely Randomized Trees |
| FoV | Field of View |
| ICOS | Integrated Carbon Observation System |
| LiDAR | Light Detection and Ranging |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| ML | Machine Learning |
| PCD | Point Cloud Data |
| RMSE | Root Mean Square Error |
| RS | Remote Sensing |
| RTK | Real-Time Kinematic |
| SAR | Synthetic Aperture Radar |
| UAV | Unstaffed Aerial Vehicle |
Appendix A
References
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Daloye, A.M.; Erkbol, H.; Fritschi, F.B. Crop monitoring using satellite/UAV data fusion and machine learning. Remote Sens. 2020, 12, 1357. [Google Scholar] [CrossRef]
- Gebbers, R.; Adamchuk, V.I. Precision agriculture and food security. Science 2010, 327, 828–831. [Google Scholar] [CrossRef]
- Isbell, F.; Adler, P.R.; Eisenhauer, N.; Fornara, D.; Kimmel, K.; Kremen, C.; Letourneau, D.K.; Liebman, M.; Polley, H.W.; Quijas, S.; et al. Benefits of increasing plant diversity in sustainable agroecosystems. J. Ecol. 2017, 105, 871–879. [Google Scholar] [CrossRef]
- Lambin, E.F.; Meyfroidt, P. Global land use change, economic globalization, and the looming land scarcity. Proc. Natl. Acad. Sci. USA 2011, 108, 3465–3472. [Google Scholar] [CrossRef]
- Challinor, A.J.; Ewert, F.; Arnold, S.; Simelton, E.; Fraser, E. Crops and climate change: Progress, trends, and challenges in simulating impacts and informing adaptation. J. Exp. Bot. 2009, 60, 2775–2789. [Google Scholar] [CrossRef]
- Wang, N.; Wang, E.; Wang, J.; Zhang, J.; Zheng, B.; Huang, Y.; Tan, M. Modelling maize phenology, biomass growth and yield under contrasting temperature conditions. Agric. For. Meteorol. 2018, 250, 319–329. [Google Scholar] [CrossRef]
- Raza, A.; Razzaq, A.; Mehmood, S.S.; Zou, X.; Zhang, X.; Lv, Y.; Xu, J. Impact of climate change on crops adaptation and strategies to tackle its outcome: A review. Plants 2019, 8, 34. [Google Scholar] [CrossRef] [PubMed]
- Deryng, D.; Elliott, J.; Folberth, C.; Müller, C.; Pugh, T.A.; Boote, K.J.; Conway, D.; Ruane, A.C.; Gerten, D.; Jones, J.W.; et al. Regional disparities in the beneficial effects of rising CO2 concentrations on crop water productivity. Nat. Clim. Chang. 2016, 6, 786–790. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, C.; Müller, C.; Wang, C.; Ciais, P.; Janssens, I.; Peñuelas, J.; Asseng, S.; Li, T.; Elliott, J.; et al. Emergent constraint on crop yield response to warmer temperature from field experiments. Nat. Sustain. 2020, 3, 908–916. [Google Scholar] [CrossRef]
- Jägermeyr, J.; Müller, C.; Ruane, A.C.; Elliott, J.; Balkovic, J.; Castillo, O.; Faye, B.; Foster, I.; Folberth, C.; Franke, J.A.; et al. Climate impacts on global agriculture emerge earlier in new generation of climate and crop models. Nat. Food 2021, 2, 873–885. [Google Scholar] [CrossRef]
- Tully, K.; Ryals, R. Nutrient cycling in agroecosystems: Balancing food and environmental objectives. Agroecol. Sustain. Food Syst. 2017, 41, 761–798. [Google Scholar] [CrossRef]
- Abalos, D.; van Groenigen, J.W.; Philippot, L.; Lubbers, I.M.; De Deyn, G.B. Plant trait-based approaches to improve nitrogen cycling in agroecosystems. J. Appl. Ecol. 2019, 56, 2454–2466. [Google Scholar] [CrossRef]
- EIT-Food. More Crops Consituents Sensing; EIT-Food: Leuven, Belgium, 2022. [Google Scholar]
- Weih, M.; Hamnér, K.; Pourazari, F. Analyzing plant nutrient uptake and utilization efficiencies: Comparison between crops and approaches. Plant Soil 2018, 430, 7–21. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Remote sensing of above-ground biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef]
- Huete, A.; Liu, H.; Batchily, K.; Van Leeuwen, W. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Luckman, A.; Baker, J.; Honzák, M.; Lucas, R. Tropical forest biomass density estimation using JERS-1 SAR: Seasonal variation, confidence limits, and application to image mosaics. Remote Sens. Environ. 1998, 63, 126–139. [Google Scholar] [CrossRef]
- Hoekman, D.; Quiñones, M. Land cover type and biomass classification using AirSAR data for evaluation of monitoring scenarios in the Colombian Amazon. IEEE Trans. Geosci. Remote Sens. 2000, 38, 685–696. [Google Scholar] [CrossRef]
- Attarchi, S.; Gloaguen, R. Improving the estimation of above ground biomass using dual polarimetric PALSAR and ETM+ data in the Hyrcanian mountain forest (Iran). Remote Sens. 2014, 6, 3693–3715. [Google Scholar] [CrossRef]
- Joshi, N.P.; Mitchard, E.T.; Schumacher, J.; Johannsen, V.K.; Saatchi, S.; Fensholt, R. L-band SAR backscatter related to forest cover, height and aboveground biomass at multiple spatial scales across Denmark. Remote Sens. 2015, 7, 4442–4472. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Pirotti, F.; Callegari, M.; Chen, Q.; Cuozzo, G.; Lingua, E.; Notarnicola, C.; Papale, D. Potential of ALOS2 and NDVI to estimate forest above-ground biomass, and comparison with lidar-derived estimates. Remote Sens. 2016, 9, 18. [Google Scholar] [CrossRef]
- Viergever, K.M. Establishing the Sensitivity of Synthetic Aperture Radar to Above-Ground Biomass in Wooded Savannas. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2008. [Google Scholar]
- Michelakis, D.; Stuart, N.; Lopez, G.; Linares, V.; Woodhouse, I.H. Local-scale mapping of biomass in tropical lowland pine savannas using ALOS PALSAR. Forests 2014, 5, 2377–2399. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.F. High-Resolution NDVI from planet’s constellation of earth observing nano-satellites: A new data source for precision agriculture. Remote Sens. 2016, 8, 768. [Google Scholar] [CrossRef]
- Deng, L.; Mao, Z.; Li, X.; Hu, Z.; Duan, F.; Yan, Y. UAV-based multispectral remote sensing for precision agriculture: A comparison between different cameras. ISPRS J. Photogramm. Remote Sens. 2018, 146, 124–136. [Google Scholar] [CrossRef]
- Bastin, J.F.; Barbier, N.; Couteron, P.; Adams, B.; Shapiro, A.; Bogaert, J.; De Cannière, C. Aboveground biomass mapping of African forest mosaics using canopy texture analysis: Toward a regional approach. Ecol. Appl. 2014, 24, 1984–2001. [Google Scholar] [CrossRef] [PubMed]
- Ploton, P.; Barbier, N.; Couteron, P.; Antin, C.; Ayyappan, N.; Balachandran, N.; Barathan, N.; Bastin, J.F.; Chuyong, G.; Dauby, G.; et al. Toward a general tropical forest biomass prediction model from very high resolution optical satellite images. Remote Sens. Environ. 2017, 200, 140–153. [Google Scholar] [CrossRef]
- Hlatshwayo, S.T.; Mutanga, O.; Lottering, R.T.; Kiala, Z.; Ismail, R. Mapping forest aboveground biomass in the reforested Buffelsdraai landfill site using texture combinations computed from SPOT-6 pan-sharpened imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 65–77. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Tian, Q.; Feng, H.; Xu, K.; Zhou, C. Estimate of winter-wheat above-ground biomass based on UAV ultrahigh-ground-resolution image textures and vegetation indices. ISPRS J. Photogramm. Remote Sens. 2019, 150, 226–244. [Google Scholar] [CrossRef]
- Saatchi, S.; Marlier, M.; Chazdon, R.L.; Clark, D.B.; Russell, A.E. Impact of spatial variability of tropical forest structure on radar estimation of aboveground biomass. Remote Sens. Environ. 2011, 115, 2836–2849. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial laser scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar] [CrossRef]
- Bates, J.S.; Montzka, C.; Schmidt, M.; Jonard, F. Estimating canopy density parameters time-series for winter wheat using UAS Mounted LiDAR. Remote Sens. 2021, 13, 710. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Meyer, V. Lidar detection of individual tree size in tropical forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
- Morsdorf, F.; Eck, C.; Zgraggen, C.; Imbach, B.; Schneider, F.D.; Kükenbrink, D. UAV-based LiDAR acquisition for the derivation of high-resolution forest and ground information. Lead. Edge 2017, 36, 566–570. [Google Scholar] [CrossRef]
- Schneider, F.D.; Morsdorf, F.; Schmid, B.; Petchey, O.L.; Hueni, A.; Schimel, D.S.; Schaepman, M.E. Mapping functional diversity from remotely sensed morphological and physiological forest traits. Nat. Commun. 2017, 8, 1441. [Google Scholar] [CrossRef]
- Schneider, F.D.; Kükenbrink, D.; Schaepman, M.E.; Schimel, D.S.; Morsdorf, F. Quantifying 3D structure and occlusion in dense tropical and temperate forests using close-range LiDAR. Agric. For. Meteorol. 2019, 268, 249–257. [Google Scholar] [CrossRef]
- Kükenbrink, D.; Schneider, F.D.; Schmid, B.; Gastellu-Etchegorry, J.P.; Schaepman, M.E.; Morsdorf, F. Modelling of three-dimensional, diurnal light extinction in two contrasting forests. Agric. For. Meteorol. 2021, 296, 108230. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Xu, X.; Yang, G.; Wang, J. Estimation of winter wheat biomass and yield by combining the aquacrop model and field hyperspectral data. Remote Sens. 2016, 8, 972. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Lauret, N.; Yin, T.; Landier, L.; Kallel, A.; Malenovskỳ, Z.; Al Bitar, A.; Aval, J.; Benhmida, S.; Qi, J.; et al. DART: Recent advances in remote sensing data modeling with atmosphere, polarization, and chlorophyll fluorescence. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2640–2649. [Google Scholar] [CrossRef]
- Demol, M.; Calders, K.; Verbeeck, H.; Gielen, B. Forest above-ground volume assessments with terrestrial laser scanning: A ground-truth validation experiment in temperate, managed forests. Ann. Bot. 2021, 128, 805–819. [Google Scholar] [CrossRef]
- Sofonia, J.; Shendryk, Y.; Phinn, S.; Roelfsema, C.; Kendoul, F.; Skocaj, D. Monitoring sugarcane growth response to varying nitrogen application rates: A comparison of UAV SLAM LiDAR and photogrammetry. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101878. [Google Scholar] [CrossRef]
- Longfei, Z.; Xiaohe, G.; Shu, C.; Guijun, Y.; Meiyan, S.; Quian, S. Analysis of Plant Height Changes of Lodged Maize Using UAV-LiDAR Data. Agriculture 2020, 10, 146. [Google Scholar]
- Trepekli, K.; Friborg, T. Deriving Aerodynamic Roughness Length at Ultra-High Resolution in Agricultural Areas Using UAV-Borne LiDAR. Remote Sens. 2021, 13, 3538. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, X.; et al. Unmanned aerial vehicle remote sensing for field-based crop phenotyping: Current status and perspectives. Front. Plant Sci. 2017, 8, 1111. [Google Scholar] [CrossRef] [PubMed]
- Lu, N.; Zhou, J.; Han, Z.; Li, D.; Cao, Q.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cheng, T. Improved estimation of aboveground biomass in wheat from RGB imagery and point cloud data acquired with a low-cost unmanned aerial vehicle system. Plant Methods 2019, 15, 17. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Liu, L.; Condon, A.G.; Estavillo, G.M.; Coe, R.A.; Bull, G.; Stone, E.A.; Petersson, L.; Rolland, V. Biomass Prediction With 3D Point Clouds From LiDAR. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 1330–1340. [Google Scholar]
- Oehmcke, S.; Li, L.; Revenga, J.; Nord-Larsen, T.; Trepekli, K.; Gieseke, F.; Igel, C. Deep Learning Based 3D Point Cloud Regression for Estimating Forest Biomass. arXiv 2021, arXiv:2112.11335. [Google Scholar]
- Forrester, D.I.; Tachauer, I.H.H.; Annighoefer, P.; Barbeito, I.; Pretzsch, H.; Ruiz-Peinado, R.; Stark, H.; Vacchiano, G.; Zlatanov, T.; Chakraborty, T.; et al. Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate. For. Ecol. Manag. 2017, 396, 160–175. [Google Scholar] [CrossRef]
- Herold, A.; Zell, J.; Rohner, B.; Didion, M.; Thürig, E.; Rösler, E. State and change of forest resources. In Swiss National Forest Inventory–Methods and Models of the Fourth Assessment; Springer: Berlin/Heidelberg, Germany, 2019; pp. 205–230. [Google Scholar]
- Shendryk, Y.; Sofonia, J.; Garrard, R.; Rist, Y.; Skocaj, D.; Thorburn, P. Fine-scale prediction of biomass and leaf nitrogen content in sugarcane using UAV LiDAR and multispectral imaging. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102177. [Google Scholar] [CrossRef]
- Han, L.; Yang, G.; Dai, H.; Xu, B.; Yang, H.; Feng, H.; Li, Z.; Yang, X. Modeling maize above-ground biomass based on machine learning approaches using UAV remote-sensing data. Plant Methods 2019, 15, 10. [Google Scholar] [CrossRef]
- Zha, H.; Miao, Y.; Wang, T.; Li, Y.; Zhang, J.; Sun, W.; Feng, Z.; Kusnierek, K. Improving unmanned aerial vehicle remote sensing-based rice nitrogen nutrition index prediction with machine learning. Remote Sens. 2020, 12, 215. [Google Scholar] [CrossRef]
- Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Beier, C.M.; Klimkowski, D.J.; Volk, T.A. comparison of machine and deep learning methods to estimate shrub willow biomass from UAS imagery. Can. J. Remote Sens. 2021, 47, 209–227. [Google Scholar] [CrossRef]
- Ma, J.; Li, Y.; Chen, Y.; Du, K.; Zheng, F.; Zhang, L.; Sun, Z. Estimating above ground biomass of winter wheat at early growth stages using digital images and deep convolutional neural network. Eur. J. Agron. 2019, 103, 117–129. [Google Scholar] [CrossRef]
- Danish Ministry of Environment, Government of Denmark. Order on the Use of Fertilisers by Agriculture for the 2020/2021 Planning Period. Available online: https://www.retsinformation.dk/eli/lta/2020/1166 (accessed on 25 October 2021).
- Jensen, R.; Herbst, M.; Friborg, T. Direct and indirect controls of the interannual variability in atmospheric CO2 exchange of three contrasting ecosystems in Denmark. Agric. For. Meteorol. 2017, 233, 12–31. [Google Scholar] [CrossRef]
- Davidson, L.; Mills, J.; Haynes, I.; Augarde, C.; Bryan, P.; Douglas, M. Airborne to UAS LiDAR: An analysis of UAS LiDAR ground control targets. In Proceedings of the ISPRS Geospatial Week 2019, Enschede, The Netherlands, 10–14 June 2019. [Google Scholar]
- Jutzi, B.; Eberle, B.; Stilla, U. Estimation and measurement of backscattered signals from pulsed laser radar. In Image and Signal Processing for Remote Sensing VIII; SPIE: New York, NY, USA, 2003; Volume 4885, pp. 256–267. [Google Scholar]
- Gielen, B.; Acosta, M.; Altimir, N.; Buchmann, N.; Cescatti, A.; Ceschia, E.; Fleck, S.; Hortnagal, L.; Klumpp, K.; Kolari, P.; et al. Ancillary vegetation measurements at ICOS ecosystem stations. Int. Agrophys. 2018, 32, 645–664. [Google Scholar] [CrossRef]
- Sechidis, K.; Tsoumakas, G.; Vlahavas, I. On the stratification of multi-label data. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2011; pp. 145–158. [Google Scholar]
- Meier, U. Growth Stages of Mono-and Dicotyledonous Plants; Blackwell Wissenschafts-Verlag: Berlin, Germany, 1997. [Google Scholar]
- Kuester, T.; Spengler, D.; Barczi, J.F.; Segl, K.; Hostert, P.; Kaufmann, H. Simulation of multitemporal and hyperspectral vegetation canopy bidirectional reflectance using detailed virtual 3-D canopy models. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2096–2108. [Google Scholar] [CrossRef]
- Hartigan, J.A. Clustering Algorithms; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1975. [Google Scholar]
- Bock, H.H. Clustering methods: A history of k-means algorithms. In Selected Contributions in Data Analysis and Classification; Springer: Berlin/Heidelberg, Germany, 2007; pp. 161–172. [Google Scholar]
- Owen, A.B. A robust hybrid of lasso and ridge regression. Contemp. Math. 2007, 443, 59–72. [Google Scholar]
- Huber, P.J. Robust statistics. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1248–1251. [Google Scholar]
- Morsdorf, F.; Meier, E.; Kötz, B.; Itten, K.I.; Dobbertin, M.; Allgöwer, B. LIDAR-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ. 2004, 92, 353–362. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K. Xgboost: Extreme gradient boosting. R Package Version 0.4-2 2015, 1, 1–4. [Google Scholar]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Feurer, M.; Hutter, F. Hyperparameter optimization. In Automated Machine Learning; Springer: Cham, Switzerland, 2019; pp. 3–33. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Vosselman, G. Slope based filtering of laser altimetry data. Int. Arch. Photogramm. Remote Sens. 2000, 33, 935–942. [Google Scholar]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved progressive TIN densification filtering algorithm for airborne LiDAR data in forested areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- GreenValley International, Ltd. LiDAR360; GreenValley International, Ltd.: Berkeley, CA, USA, 2021. [Google Scholar]
- Longley, P.A.; Goodchild, M.F.; Maguire, D.J.; Rhind, D.W. Geographic Information Systems and Science; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Burrough, P.A.; McDonnell, R.A.; Lloyd, C.D. Principles of Geographical Information Systems; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Beutel, A.; Mølhave, T.; Agarwal, P.K. Natural neighbor interpolation based grid DEM construction using a GPU. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 172–181. [Google Scholar]
- Walter, J.D.; Edwards, J.; McDonald, G.; Kuchel, H. Estimating biomass and canopy height with LiDAR for field crop breeding. Front. Plant Sci. 2019, 10, 1145. [Google Scholar] [CrossRef]
- Chen, Q.; Laurin, G.V.; Valentini, R. Uncertainty of remotely sensed aboveground biomass over an African tropical forest: Propagating errors from trees to plots to pixels. Remote Sens. Environ. 2015, 160, 134–143. [Google Scholar] [CrossRef]
- Goetz, S.; Dubayah, R. Advances in remote sensing technology and implications for measuring and monitoring forest carbon stocks and change. Carbon Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
- Quiñonero-Candela, J.; Sugiyama, M.; Schwaighofer, A.; Lawrence, N.D. Dataset Shift in Machine Learning; Mit Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Toloşi, L.; Lengauer, T. Classification with correlated features: Unreliability of feature ranking and solutions. Bioinformatics 2011, 27, 1986–1994. [Google Scholar] [CrossRef]
- Gregorutti, B.; Michel, B.; Saint-Pierre, P. Correlation and variable importance in random forests. Stat. Comput. 2017, 27, 659–678. [Google Scholar] [CrossRef]
- Zhang, H.; Nettleton, D.; Zhu, Z. Regression-Enhanced Random Forests. In Statistics Conference Proceedings; Presentations and Posters; 2017; Volume 9, Available online: https://dr.lib.iastate.edu/entities/publication/8c7c1d24-a466-4e37-a5c0-7f7405fa867e (accessed on 13 June 2022).




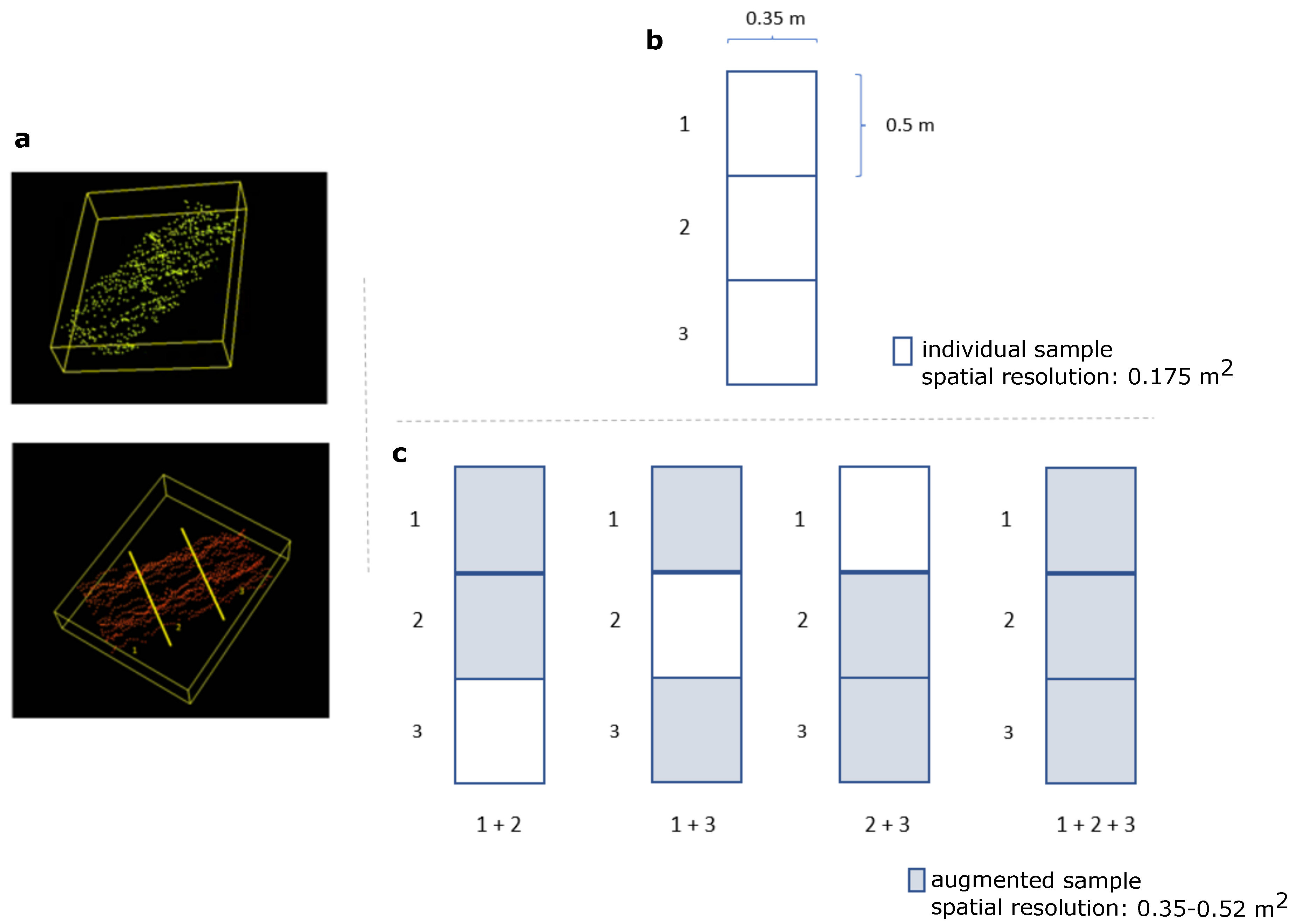

| Growing Season | Dataset | Number of Samples | Sample Size |
|---|---|---|---|
| 2020 | 104 | 1 m × 0.35 m | |
| 2021 | 142 | 0.5 m × 0.35 m | |
| 188 | (1–1.5) m × 0.35 m | ||
| 455 | 0.5 m × 0.35 m | ||
| 609 | (1–1.5) m × 0.35 m |
| Regression Model | Family | Description | Implementation |
|---|---|---|---|
| Extremely Randomized Trees (ERT) | Tree-Based Ensemble | Ensemble of decision trees (parallel setup) [70] in which the output is the average of individual predictions | scikit-learn |
| XGboost | Boosting | Gradient boosting method that is based on stage-wise additive expansions [74,75] | xgboost |
| Huber | Linear | Regularized linear regression that is robust to outliers [67,68] | scikit-learn |
| Linear Regression (Baseline) | Linear | Ordinary least squares linear regression | scikit-learn |
| Regression Model | Hyperparameters | |
|---|---|---|
| Included in Cross-Validation | Total | |
| Extremely Randomized Trees (ERT) | Criterion {mae; mse}, max. depth (None; 1, …, 9), bootstrap {True; False}, max. features {log2; sqrt} | 17 |
| XGboost | Booster {gbtree; gblinear; dart}, step size shrinkage (0.1, …, 0.5), learning rate (0.01, …, 0.1), L1 regularization (0, …, 0.5) | 29 |
| Huber | Epsilon (1.1, …, 1.75), alpha (, …, ), fit intercept {True; False}, tolerance (, …, ) | 6 |
| Linear Regression (Baseline) | Fit intercept {True; False} | 1 |
| Testing Dataset | Spatial Resolution (m2) | RMSE (g/m2) | MAE (g/m2) | MAPE (%) | |
|---|---|---|---|---|---|
| Barley Testing Dataset | 0.35 | 0.48 | 207 | 162 | 42.0 |
| 1.00 | 0.71 | 232 | 214 | 23.0 | |
| 2.00 | 0.93 | 300 | 266 | 13.0 | |
| Wheat Testing Dataset | 0.35 | 0.20 | 288 | 216 | 23.7 |
| 1.00 | 0.58 | 284 | 264 | 19.7 | |
| 2.00 | 0.89 | 400 | 351 | 16.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Revenga, J.C.; Trepekli, K.; Oehmcke, S.; Jensen, R.; Li, L.; Igel, C.; Gieseke, F.C.; Friborg, T. Above-Ground Biomass Prediction for Croplands at a Sub-Meter Resolution Using UAV–LiDAR and Machine Learning Methods. Remote Sens. 2022, 14, 3912. https://doi.org/10.3390/rs14163912
Revenga JC, Trepekli K, Oehmcke S, Jensen R, Li L, Igel C, Gieseke FC, Friborg T. Above-Ground Biomass Prediction for Croplands at a Sub-Meter Resolution Using UAV–LiDAR and Machine Learning Methods. Remote Sensing. 2022; 14(16):3912. https://doi.org/10.3390/rs14163912
Chicago/Turabian StyleRevenga, Jaime C., Katerina Trepekli, Stefan Oehmcke, Rasmus Jensen, Lei Li, Christian Igel, Fabian Cristian Gieseke, and Thomas Friborg. 2022. "Above-Ground Biomass Prediction for Croplands at a Sub-Meter Resolution Using UAV–LiDAR and Machine Learning Methods" Remote Sensing 14, no. 16: 3912. https://doi.org/10.3390/rs14163912
APA StyleRevenga, J. C., Trepekli, K., Oehmcke, S., Jensen, R., Li, L., Igel, C., Gieseke, F. C., & Friborg, T. (2022). Above-Ground Biomass Prediction for Croplands at a Sub-Meter Resolution Using UAV–LiDAR and Machine Learning Methods. Remote Sensing, 14(16), 3912. https://doi.org/10.3390/rs14163912







