Simulating the Changes of Invasive Phragmites australis in a Pristine Wetland Complex with a Grey System Coupled System Dynamic Model: A Remote Sensing Practice
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Using High-Resolution Multispectral Images to Characterize Land Covers
2.3. The Grey System Supported System Dynamic Simulative Model
2.4. A Grey System Modification
3. Results and Discussion
3.1. Digitization Analysis
3.2. Coupling between In Situ Data and Remote Sensing Data: Supervised Classification
3.3. Building a Grey System Coupled System Dynamic Model to Evaluate the Change of Phragmites australis in the Wading River Complex
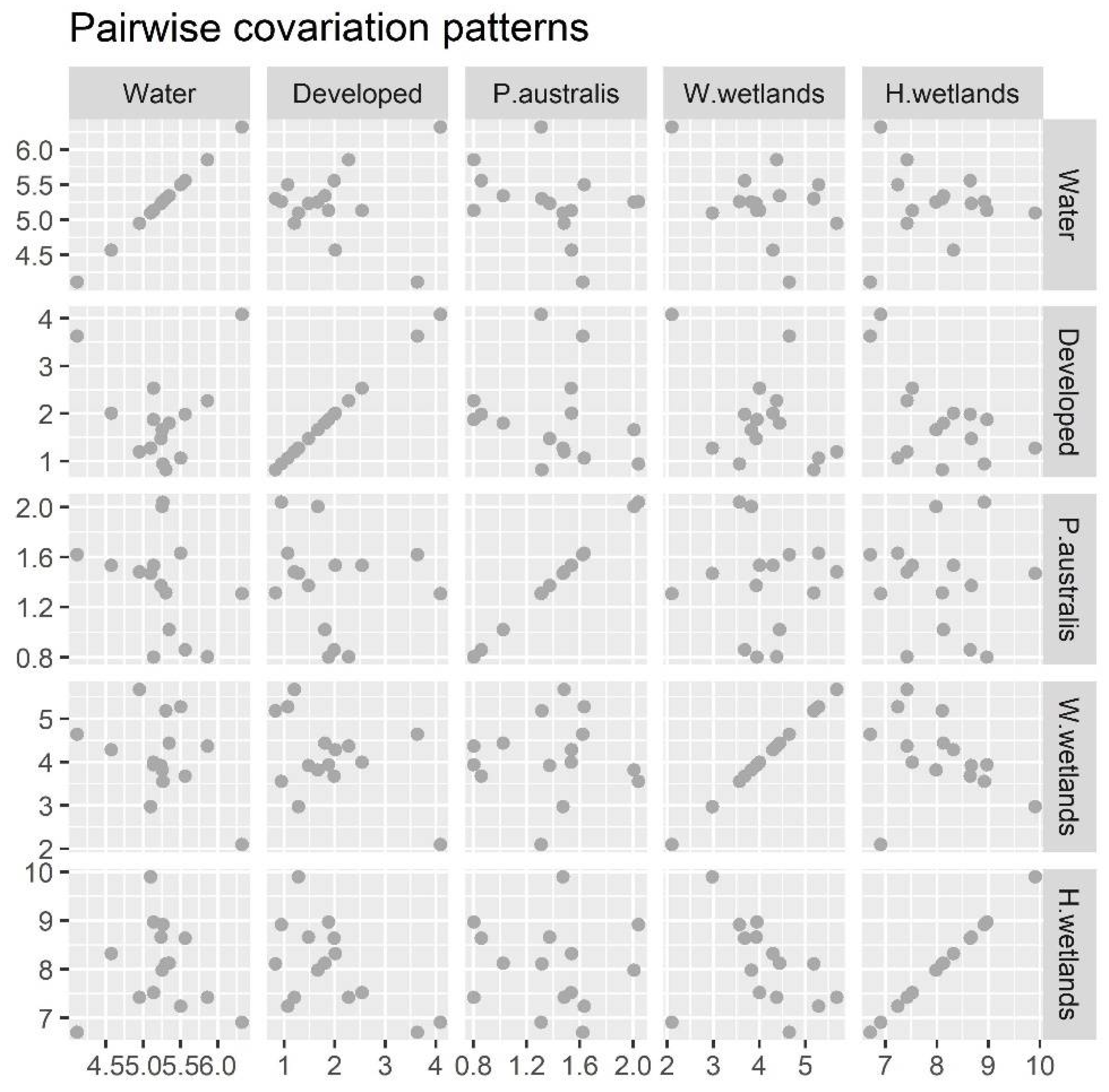
3.4. Tentative Covariations among the Different Land Use Land Cover Types
3.5. Further Refinement of the Tentative Covariation Relationships: Grey System Series Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lodge, D.M.; Williams, S.; MacIsaac, H.J.; Hayes, K.R.; Leung, B.; Reichard, S.; Mack, R.N.; Moyle, P.B.; Smith, M.; Andow, D.A.; et al. Biological invasions: Recommendations for US policy and management. Ecol. Appl. 2006, 16, 2035–2054. [Google Scholar] [CrossRef] [Green Version]
- Hunter, M.E.; Hart, K.M. Rapid Microsatellite Marker Development Using Next Generation Pyrosequencing to Inform Invasive Burmese Python-Python molurus bivittatus-Management. Int. J. Mol. Sci. 2013, 14, 4793–4804. [Google Scholar] [CrossRef] [PubMed]
- Diagne, C.; Leroy, B.; Vaissiere, A.C.; Gozlan, R.E.; Roiz, D.; Jaric, I.; Salles, J.M.; Bradshaw, C.J.A.; Courchamp, F. High and rising economic costs of biological invasions worldwide. Nature 2021, 592, 571. [Google Scholar] [CrossRef]
- Moodley, D.; Angulo, E.; Cuthbert, R.N.; Leung, B.; Turbelin, A.; Novoa, A.; Kourantidou, M.; Heringer, G.; Haubrock, P.J.; Renault, D.; et al. Surprisingly high economic costs of biological invasions in protected areas. Biol. Invasions 2022, 24, 1995–2016. [Google Scholar] [CrossRef]
- Crystal-Ornelas, R.; Hudgins, E.J.; Cuthbert, R.N.; Haubrock, P.J.; Fantle-Lepczyk, J.; Angulo, E.; Kramer, A.M.; Ballesteros-Mejia, L.; Leroy, B.; Leung, B.; et al. Economic costs of biological invasions within North America. Neobiota 2021, 67, 485–510. [Google Scholar] [CrossRef]
- Pimentel, D.; Zuniga, R.; Morrison, D. Update on the environmental and economic costs associated with alien-invasive species in the United States. Ecol. Econ. 2005, 52, 273–288. [Google Scholar] [CrossRef]
- Andersen, M.C.; Adams, H.; Hope, B.; Powell, M. Risk assessment for invasive species. Risk Anal. 2004, 24, 787–793. [Google Scholar] [CrossRef] [PubMed]
- Pengra, B.W.; Johnston, C.A.; Loveland, T.R. Mapping an invasive plant, Phragmites australis, in coastal wetlands using the EO-1 Hyperion hyperspectral sensor. Remote Sens. Environ. 2007, 108, 74–81. [Google Scholar] [CrossRef]
- Long, A.L.; Kettenring, K.M.; Hawkins, C.P.; Neale, C.M.U. Distribution and Drivers of a Widespread, Invasive Wetland Grass, Phragmites australis, in Wetlands of the Great Salt Lake, Utah, USA. Wetlands 2017, 37, 45–57. [Google Scholar] [CrossRef]
- Purmalis, O.; Grinberga, L.; Klavins, L.; Klavins, M. Quality of Lake Ecosystems and its Role in the Spread of Invasive Species. Environ. Clim. Technol. 2021, 25, 676–687. [Google Scholar] [CrossRef]
- Samiappan, S.; Turnage, G.; Hathcock, L.; Casagrande, L.; Stinson, P.; Moorhead, R. Using unmanned aerial vehicles for high-resolution remote sensing to map invasive Phragmites australis in coastal wetlands. Int. J. Remote Sens. 2017, 38, 2199–2217. [Google Scholar] [CrossRef]
- Nielsen, E.M.; Prince, S.D.; Koeln, G.T. Wetland change mapping for the U.S. mid-Atlantic region using an outlier detection technique. Remote Sens. Environ. 2008, 112, 4061–4074. [Google Scholar] [CrossRef]
- Allen, T.R.; Wang, Y.; Gore, B. Coastal wetland mapping combining multi-date SAR and LiDAR. Geocarto Int. 2013, 28, 616–631. [Google Scholar] [CrossRef]
- Windham, L.; Lathrop, R.G. Effects of Phragmites australis (Common Reed) Invasion on Aboveground Biomass and Soil Properties in Brackish Tidal Marsh of the Mullica River, New Jersey. Estuaries 1999, 22, 927–935. [Google Scholar] [CrossRef]
- Able, K.W.; Hagan, S.M.; Brown, S.A. Mechanisms of marsh habitat alteration due to Phragmites: Response of young-of-the-year mummichog (Fundulus heteroclitus) to treatment forPhragmites removal. Estuaries 2003, 26, 484–494. [Google Scholar] [CrossRef]
- Rooth, J.E.; Stevenson, J.C.; Cornwell, J.C. Increased sediment accretion rates following invasion by Phragmites australis: The role of litter. Estuaries 2003, 26, 475–483. [Google Scholar] [CrossRef]
- Karstens, S.; Jurasinski, G.; Glatzel, S.; Buczko, U. Dynamics of surface elevation and microtopography in different zones of a coastal Phragmites wetland. Ecol. Eng. 2016, 94, 152–163. [Google Scholar] [CrossRef]
- Koma, Z.; Seijmonsbergen, A.C.; Kissling, W.D. Classifying wetland-related land cover types and habitats using fine-scale lidar metrics derived from country-wide Airborne Laser Scanning. Remote Sens. Ecol. Conserv. 2021, 7, 80–96. [Google Scholar] [CrossRef]
- Gilmore, M.S.; Wilson, E.H.; Barrett, N.; Civco, D.L.; Prisloe, S.; Hurd, J.D.; Chadwick, C. Integrating multi-temporal spectral and structural information to map wetland vegetation in a lower Connecticut River tidal marsh. Remote Sens. Environ. 2008, 112, 4048–4060. [Google Scholar] [CrossRef]
- Wallis, E.; Raulings, E. Relationship between water regime and hummock-building by Melaleuca ericifolia and Phragmites australis in a brackish wetland. Aquat. Bot. 2011, 95, 182–188. [Google Scholar] [CrossRef]
- McIvor, C.C.; Odum, W.E. Food, Predation Risk, and Microhabitat Selection in a Marsh Fish Assemblage. Ecology 1988, 69, 1341–1351. [Google Scholar] [CrossRef]
- NOAA Fisheries Office of Habitat Conservation. Coastal Wetland Habitat. Available online: https://www.fisheries.noaa.gov/national/habitat-conservation/coastal-wetland-habitat (accessed on 19 May 2022).
- Jabbar, M.T.; Zhou, X.P. Eco-environmental change detection by using remote sensing and GIS techniques: A case study Basrah province, south part of Iraq. Environ. Earth Sci. 2011, 64, 1397–1407. [Google Scholar] [CrossRef]
- Ouyang, X.G.; Guo, F. Paradigms of mangroves in treatment of anthropogenic wastewater pollution. Sci. Total Environ. 2016, 544, 971–979. [Google Scholar] [CrossRef] [PubMed]
- Schmid, T.; Koch, M.; Gumuzzio, J.; Mather, P.M. A spectral library for a semi-arid wetland and its application to studies of wetland degradation using hyperspectral and multispectral data. Int. J. Remote Sens. 2004, 25, 2485–2496. [Google Scholar] [CrossRef]
- Sidhu, N.; Pebesma, E.; Camara, G. Using Google Earth Engine to detect land cover change: Singapore as a use case. Eur. J. Remote Sens. 2018, 51, 486–500. [Google Scholar] [CrossRef]
- Valiela, I.; Cole, M.L. Comparative evidence that salt marshes and mangroves may protect seagrass meadows from land-derived nitrogen loads. Ecosystems 2002, 5, 92–102. [Google Scholar] [CrossRef]
- Wu, D.Q.; Liu, J.; Wang, S.J.; Wang, R.Q. Simulating urban expansion by coupling a stochastic cellular automata model and socioeconomic indicators. Stoch. Environ. Res. Risk Assess. 2010, 24, 235–245. [Google Scholar] [CrossRef]
- Yagoub, M.M.; Kolan, G.R. Monitoring coastal zone land use and land cover changes of Abu Dhabi using remote sensing. Photonirvachak-J. Indian Soc. Remote Sens. 2006, 34, 57–68. [Google Scholar] [CrossRef]
- Dogan, O.K.; Akyurek, Z.; Beklioglu, M. Identification and mapping of submerged plants in a shallow lake using quickbird satellite data. J. Environ. Manag. 2009, 90, 2138–2143. [Google Scholar] [CrossRef] [PubMed]
- Ghioca-Robrecht, D.M.; Johnston, C.A.; Tulbure, M.G. Assessing the use of multiseason quickbird imagery for mapping invasive species in a lake erie coastal marsh. Wetlands 2008, 28, 1028–1039. [Google Scholar] [CrossRef]
- Haghani, A.; Lee, S.Y.; Byun, J.H. A system dynamics approach to land use/transportation system performance modeling—Part I: Methodology. J. Adv. Transp. 2003, 37, 1–41. [Google Scholar] [CrossRef]
- Haghani, A.; Lee, S.Y.; Byun, J.H. A system dynamics approach to land use/transportation system performance modeling—Part II: Application. J. Adv. Transp. 2003, 37, 43–82. [Google Scholar] [CrossRef]
- Rebs, T.; Brandenburg, M.; Seuring, S. System dynamics modeling for sustainable supply chain management: A literature review and systems thinking approach. J. Clean. Prod. 2019, 208, 1265–1280. [Google Scholar] [CrossRef]
- Kollikkathara, N.; Feng, H.A.; Yu, D.L. A system dynamic modeling approach for evaluating municipal solid waste generation, landfill capacity and related cost management issues. Waste Manag. 2010, 30, 2194–2203. [Google Scholar] [CrossRef] [PubMed]
- Guan, D.J.; Gao, W.J.; Su, W.C.; Li, H.F.; Hokao, K. Modeling and dynamic assessment of urban economy-resource-environment system with a coupled system dynamics—geographic information system model. Ecol. Indic. 2011, 11, 1333–1344. [Google Scholar] [CrossRef]
- Navarro, A.; Tapiador, F.J. RUSEM: A numerical model for policymaking and climate applications. Ecol. Econ. 2019, 165, 15. [Google Scholar] [CrossRef]
- Lunadei, L.; Galleguillos, P.; Diezma, B.; Lleo, L.; Ruiz-Garcia, L. A multispectral vision system to evaluate enzymatic browning in fresh-cut apple slices. Postharvest Biol. Technol. 2011, 60, 225–234. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, S.W.P.; Souza, P.W.M. Use of Multi-Sensor Data to Identify and Map Tropical Coastal Wetlands in the Amazon of Northern Brazil. Wetlands 2011, 31, 11–23. [Google Scholar] [CrossRef]
- Malinverni, E.S. Change Detection Applying Landscape Metrics on High Remote Sensing Images. Photogramm. Eng. Remote Sens. 2011, 77, 1045–1056. [Google Scholar] [CrossRef]
- Hof, A.; Wolf, N. Estimating potential outdoor water consumption in private urban landscapes by coupling high-resolution image analysis, irrigation water needs and evaporation estimation in Spain. Landsc. Urban Plan. 2014, 123, 61–72. [Google Scholar] [CrossRef]
- Gil, A.; Yu, Q.; Abadi, M.; Calado, H. Using aster multispectral imagery for mapping woody invasive species in pico da vara natural reserve (azores islands, portugal). Rev. Arvore 2014, 38, 391–401. [Google Scholar] [CrossRef] [Green Version]
- El Alfy, M. Assessing the impact of arid area urbanization on flash floods using GIS, remote sensing, and HEC-HMS rainfall-runoff modeling. Hydrol. Res. 2016, 47, 1142–1160. [Google Scholar] [CrossRef] [Green Version]
- Ma, Q.W.; Gong, Z.Y.; Kang, J.; Tao, R.; Dang, A.R. Measuring Functional Urban Shrinkage with Multi-Source Geospatial Big Data: A Case Study of the Beijing-Tianjin-Hebei Megaregion. Remote Sens. 2020, 12, 2513. [Google Scholar] [CrossRef]
- Guo, D.G.; Xia, Y.; Luo, X.B. GAN-Based Semisupervised Scene Classification of Remote Sensing Image. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2067–2071. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, Y.; Zhou, Q.M.; Zhang, X.C. Effectiveness of Semi-Supervised Learning and Multi-Source Data in Detailed Urban Landuse Mapping with a Few Labeled Samples. Remote Sens. 2022, 14, 648. [Google Scholar] [CrossRef]
- Ganguly, P.; Mukherjee, S. A multifaceted risk assessment approach using statistical learning to evaluate socio-environmental factors associated with regional felony and misdemeanor rates. Phys. A-Stat. Mech. Its Appl. 2021, 574, 125984. [Google Scholar] [CrossRef]
- Sun, Z.C.; Zhao, X.W.; Wu, M.F.; Wang, C.Z. Extracting Urban Impervious Surface from WorldView-2 and Airborne LiDAR Data Using 3D Convolutional Neural Networks. J. Indian Soc. Remote Sens. 2019, 47, 401–412. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.B.; Chen, Z.S. Regional classification of urban land use based on fuzzy rough set in remote sensing images. J. Intell. Fuzzy Syst. 2020, 38, 3803–3812. [Google Scholar] [CrossRef]
- Jensen, T.; Hass, F.S.; Akbar, M.S.; Petersen, P.H.; Arsanjani, J.J. Employing Machine Learning for Detection of Invasive Species using Sentinel-2 and AVIRIS Data: The Case of Kudzu in the United States. Sustainability 2020, 12, 3544. [Google Scholar] [CrossRef]
- He, J.; Li, X.; Liu, P.; Wu, X.; Zhang, J.; Zhang, D.; Liu, X.; Yao, Y. Accurate Estimation of the Proportion of Mixed Land Use at the Street-Block Level by Integrating High Spatial Resolution Images and Geospatial Big Data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6357–6370. [Google Scholar] [CrossRef]
- Chen, T.H.K.; Qiu, C.P.; Schmitt, M.; Zhu, X.X.; Sabel, C.E.; Prishchepov, A.V. Mapping horizontal and vertical urban densification in Denmark with Landsat time-series from 1985 to 2018: A semantic segmentation solution. Remote Sens. Environ. 2020, 251, 112096. [Google Scholar] [CrossRef]
- Larson, K.B.; Tuor, A.R. Deep Learning Classification of Cheatgrass Invasion in the Western United States Using Biophysical and Remote Sensing Data. Remote Sens. 2021, 13, 1246. [Google Scholar] [CrossRef]
- Wang, J.; Shi, T.; Yu, D.; Teng, D.; Ge, X.; Zhang, Z.; Yang, X.; Wang, H.; Wu, G. Ensemble machine-learning-based framework for estimating total nitrogen concentration in water using drone-borne hyperspectral imagery of emergent plants: A case study in an arid oasis, NW China. Environ. Pollut. 2020, 266, 115412. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.L.; Yang, A.X.; Wang, J.Z.; Sagan, V.; Yu, D.L. Machine-learning-based quantitative estimation of soil organic carbon content by VIS/NIR spectroscopy. PeerJ 2018, 6, 24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, S.; Homer, C.; Yang, L.; Danielson, P.; Dewitz, J.; Li, C.; Zhu, Z.; Xian, G.; Howard, D. Overall Methodology Design for the United States National Land Cover Database 2016 Products. Remote Sens. 2019, 11, 2971. [Google Scholar] [CrossRef] [Green Version]
- Mao, H.; Yu, D. A study on the quantitative research of regional carrying capacity. Adv. Earth Sci. 2001, 16, 549–555. [Google Scholar]
- Mao, H.; Yu, D. Regional carrying capacity in Bohai Rim. Acta Geogr. Sin. 2001, 56, 363–371. [Google Scholar]
- Mao, H.; Yu, D. Studies on methodological issues of regional carrying capacity. Prog. Earth Sci. 2001, 16, 549–556. [Google Scholar]
- Yu, D.; Mao, H.; Gao, Q. Study on regional carrying capacity: Theory, method and example—Take the Bohai-Rim area as example. Geogr. Res. 2003, 22, 201–210. [Google Scholar]
- Yu, D.L.; Mao, H.Y. Regional carrying capacity: Case studies of Bohai Rim area. J. Geogr. Sci. 2002, 12, 177–185. [Google Scholar]
- Feng, H.; Yu, D.; Deng, Y.; Weinstein, M.; Martin, G. System dynamic model approach for urban watershed sustainability study. OIDA Int. J. Sustain. Dev. 2012, 5, 70–80. [Google Scholar]
- Forrester, J. Industrial Dynamics and principles of Systems; MIT Press: Cambridge, UK, 1961. [Google Scholar]
- Forrester, J.W. Industrial Dynamics. A major breakthrough for decision makers. Harv. Bus. Rev. 1958, 36, 37–66. [Google Scholar]
- Gu, B.J.; Dong, X.L.; Peng, C.H.; Luo, W.D.; Chang, J.; Ge, Y. The long-term impact of urbanization on nitrogen patterns and dynamics in Shanghai, China. Environ. Pollut. 2012, 171, 30–37. [Google Scholar] [CrossRef] [Green Version]
- Ramachandra, T.V.; Aithal, B.H.; Sanna, D.D. Insights to urban dynamics through landscape spatial pattern analysis. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 329–343. [Google Scholar] [CrossRef]
- Sun, X.; He, J.; Shi, Y.Q.; Zhu, X.D.; Li, Y.F. Spatiotemporal change in land use patterns of coupled human-environment system with an integrated monitoring approach: A case study of Lianyungang, China. Ecol. Complex. 2012, 12, 23–33. [Google Scholar] [CrossRef]
- Qin, H.P.; Su, Q.; Khu, S.T. Assessment of environmental improvement measures using a novel integrated model: A case study of the Shenzhen River catchment, China. J. Environ. Manag. 2013, 114, 486–495. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.L.; Fang, C.L.; Xue, D.; Yin, J.Y. Assessing Urban Public Safety via Indicator-Based Evaluating Method: A Systemic View of Shanghai. Soc. Indic. Res. 2014, 117, 89–104. [Google Scholar] [CrossRef]
- Maass, M.; Balvanera, P.; Bourgeron, P.; Equihua, M.; Baudry, J.; Dick, J.; Forsius, M.; Halada, L.; Krauze, K.; Nakaoka, M.; et al. Changes in biodiversity and trade-offs among ecosystem services, stakeholders, and components of well-being: The contribution of the International Long-Term Ecological Research network (ILTER) to Programme on Ecosystem Change and Society (PECS). Ecol. Soc. 2016, 21, 14. [Google Scholar] [CrossRef] [Green Version]
- Hristoski, I.S.; Kostoska, O.B. System dynamics approach for the economic impacts of ICTs: Evidence from Macedonia. Inf. Dev. 2018, 34, 364–381. [Google Scholar] [CrossRef]
- Jokar, Z.; Mokhtar, A. Policy making in the cement industry for CO2 mitigation on the pathway of sustainable development- A system dynamics approach. J. Clean. Prod. 2018, 201, 142–155. [Google Scholar] [CrossRef]
- Sandor, D.; Fulton, S.; Engel-Cox, J.; Peck, C.; Peterson, S. System Dynamics of Polysilicon for Solar Photovoltaics: A Framework for Investigating the Energy Security of Renewable Energy Supply Chains. Sustainability 2018, 10, 160. [Google Scholar] [CrossRef] [Green Version]
- Barati, A.A.; Azadi, H.; Scheffran, J. A system dynamics model of smart groundwater governance. Agric. Water Manag. 2019, 221, 502–518. [Google Scholar] [CrossRef]
- Pan, H.Z.; Zhang, L.; Cong, C.; Deal, B.; Wang, Y.T. A dynamic and spatially explicit modeling approach to identify the ecosystem service implications of complex urban systems interactions. Ecol. Indic. 2019, 102, 426–436. [Google Scholar] [CrossRef]
- Papachristos, G. System dynamics modelling and simulation for sociotechnical transitions research. Environ. Innov. Soc. Trans. 2019, 31, 248–261. [Google Scholar] [CrossRef]
- Shi, J.; Guo, X.S.; Hu, X.N. Engaging Stakeholders in Urban Traffic Restriction Policy Assessment Using System Dynamics: The Case Study of Xi’an City, China. Sustainability 2019, 11, 3930. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.J.; Li, Y.; Zhou, S.M. System Dynamics Modeling of Dockless Bike-Sharing Program Operations: A Case Study of Mobike in Beijing, China. Sustainability 2019, 11, 1601. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhao, J.B.; Tam, V.W.Y. System dynamics-based stakeholders’ impact analysis of highway maintenance systems. Proc. Inst. Civ. Eng.-Transp. 2019, 172, 187–198. [Google Scholar] [CrossRef]
- Meadows, D.H.; Meadows, D.L.; Randers, J.; Behrens, W.W. The Limits to Growth; Universe Books: New York, NY, USA, 1972; Volume 102, p. 27. [Google Scholar]
- Agostinho, F.; Sevegnani, F.; Almeida, C.; Giannetti, B.F. Exploring the potentialities of emergy accounting in studying the limits to growth of urban systems. Ecol. Indic. 2018, 94, 4–12. [Google Scholar] [CrossRef]
- Fan, J.; Wang, Y.F.; Ouyang, Z.Y.; Li, L.J.; Xu, Y.; Zhang, W.Z.; Wang, C.S.; Xu, W.H.; Li, J.Y.; Yu, J.H.; et al. Risk forewarning of regional development sustainability based on a natural resources and environmental carrying index in China. Earth Future 2017, 5, 196–213. [Google Scholar] [CrossRef]
- Shifflett, S.D.; Culbreth, A.; Hazel, D.; Daniels, H.; Nichols, E.G. Coupling aquaculture with forest plantations for food, energy, and water resiliency. Sci. Total Environ. 2016, 571, 1262–1270. [Google Scholar] [CrossRef]
- Shen, Q.P.; Chen, Q.; Tang, B.S.; Yeung, S.; Hu, Y.C.; Cheung, G. A system dynamics model for the sustainable land use planning and development. Habitat Int. 2009, 33, 15–25. [Google Scholar] [CrossRef]
- Deaton, M.; Winebrake, J.J. Dynamic Modeling of Environmental Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Yu, D.L.; Fang, C.L. The dynamics of public safety in cities: A case study of Shanghai from 2010 to 2025. Habitat Int. 2017, 69, 104–113. [Google Scholar] [CrossRef]
- Deng, J.-L. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Liu, S.F.; Forrest, J. The current developing status on grey system theory. J. Grey Syst. 2007, 19, 111–123. [Google Scholar]
- Liu, S.; Forrest, J.Y.L. Grey Systems: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Deng, J. The Fundamentals of Grey Theory; Huazhong University of Science and Technology Press: Wuhan, China, 2002. (In Chinese) [Google Scholar]
- Liu, S.F.; Dang, Y.G.; Fang, Z.G.; Xie, N.M. The Theory and Applications of Grey System; Science Press: Beijing, China, 2010; p. 415. [Google Scholar]
- Hijmans, R. Raster: Geographic Data Analysis and Modeling. Available online: https://CRAN.R-project.org/package=raster (accessed on 10 June 2022).
- Leutner, B.; Horning, N.; Schwalb-Willmann, J. RStoolbox: Tools for Remote Sensing Data Analysis. Available online: https://CRAN.R-project.org/package=RStoolbox (accessed on 10 June 2022).
- Kuhn, M. Caret: Classification and Regression Training. Available online: https://CRAN.R-project.org/package=caret (accessed on 10 June 2022).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- McDermott, S.M.; Irwin, R.E.; Taylor, B.W. Using economic instruments to develop effective management of invasive species: Insights from a bioeconomic model. Ecol. Appl. 2013, 23, 1086–1100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cordell, S.; Ostertag, R.; Michaud, J.; Warman, L. Quandaries of a decade-long restoration experiment trying to reduce invasive species: Beat them, join them, give up, or start over? Restor. Ecol. 2016, 24, 139–144. [Google Scholar] [CrossRef]
- Kocovsky, P.M.; Sturtevant, R.; Schardt, J. What it is to be established: Policy and management implications for non-native and invasive species. Manag. Biol. Invasions 2018, 9, 177–185. [Google Scholar] [CrossRef] [Green Version]
- Johnston, E.L.; Dafforn, K.A.; Clark, G.F.; Rius, M.; Floerl, O. How anthropogenic activities affect the establishment and spread of non-indigenous species post-arrival. In Oceanography and Marine Biology: An Annual Review; Hawkins, S.J., Evans, A.J., Dale, A.C., Firth, L.B., Hughes, D.J., Smith, I.P., Eds.; CRC Press: Boca Raton, FL, USA, 2017; Volume 55, pp. 389–419. [Google Scholar]
- Padayachee, A.L.; Irlich, U.M.; Faulkner, K.T.; Gaertner, M.; Proches, S.; Wilson, J.R.U.; Rouget, M. How do invasive species travel to and through urban environments? Biol. Invasions 2017, 19, 3557–3570. [Google Scholar] [CrossRef]
- Rodriguez-Rey, M.; Consuegra, S.; Borger, L.; de Leaniz, C.G. Improving Species Distribution Modelling of freshwater invasive species for management applications. PLoS ONE 2019, 14, e0217896. [Google Scholar] [CrossRef]
- Paganelli, D.; Reino, L.; Capinha, C.; Ribeiro, J. Exploring expert perception of protected areas’ vulnerability to biological invasions. J. Nat. Conserv. 2021, 62, 126008. [Google Scholar] [CrossRef]
- Kimball, M.E.; Able, K.W.; Grothues, T.M. Evaluation of Long-Term Response of Intertidal Creek Nekton to Phragmites australis (Common Reed) Removal in Oligohaline Delaware Bay Salt Marshes. Restor. Ecol. 2010, 18, 772–779. [Google Scholar] [CrossRef]
- Huang, X.F.; Zhao, F.; Song, C.; Gao, Y.; Geng, Z.; Zhuang, P. Effects of stereoscopic artificial floating wetlands on nekton abundance and biomass in the Yangtze Estuary. Chemosphere 2017, 183, 510–518. [Google Scholar] [CrossRef]
- Kiviat, E. Ecosystem services of Phragmites in North America with emphasis on habitat functions. Aob Plants 2013, 5, plt008. [Google Scholar] [CrossRef]
- NJDEP. New Jersey Wetland Program Plan 2019–2022. Trenton, NJ. Available online: https://www.epa.gov/sites/default/files/2019-05/documents/njdep_wpp_2019-2022_20mar2019.pdf (accessed on 10 June 2022).
- Wang, J.; Ding, J.; Yu, D.; Teng, D.; He, B.; Chen, X.; Ge, X.; Zhang, Z.; Wang, Y.; Yang, X.; et al. Machine learning-based detection of soil salinity in an arid desert region, Northwest China: A comparison between Landsat-8 OLI and Sentinel-2 MSI. Sci. Total Environ. 2019, 707, 136092. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.L.; Yu, D.L. Monitoring and evaluating spatial variability of soil salinity in dry and wet seasons in the Werigan-Kuqa Oasis, China, using remote sensing and electromagnetic induction instruments. Geoderma 2014, 235, 316–322. [Google Scholar] [CrossRef]


| Year | RF Average Accuracy | RF Kappa | SVM Average Accuracy | SVM Kappa | NN Average Accuracy | NN Kappa |
|---|---|---|---|---|---|---|
| 2011 summer | 0.954 | 0.943 | 0.883 | 0.831 | 0.846 | 0.765 |
| 2011 winter | 0.933 | 0.916 | 0.902 | 0.858 | 0.865 | 0.804 |
| 2012 summer | NA | NA | NA | NA | NA | NA |
| 2012 winter | 0.94 | 0.925 | 0.902 | 0.860 | 0.873 | 0.819 |
| 2013 summer | 0.974 | 0.962 | 0.964 | 0.948 | 0.811 | 0.721 |
| 2013 winter | 0.838 | 0.798 | 0.673 | 0.506 | 0.703 | 0.586 |
| 2014 summer | 0.972 | 0.961 | 0.955 | 0.936 | 0.804 | 0.709 |
| 2014 winter | 0.943 | 0.918 | 0.929 | 0.899 | 0.843 | 0.773 |
| 2015 summer | 0.957 | 0.938 | 0.881 | 0.828 | 0.820 | 0.741 |
| 2015 winter | 0.941 | 0.926 | 0.878 | 0.824 | 0.731 | 0.612 |
| 2016 summer | 0.929 | 0.911 | 0.903 | 0.861 | 0.862 | 0.802 |
| 2016 winter | 0.946 | 0.932 | 0.934 | 0.906 | 0.875 | 0.821 |
| 2017 summer | 0.943 | 0.929 | 0.939 | 0.913 | 0.818 | 0.739 |
| 2017 winter | 0.967 | 0.959 | 0.939 | 0.913 | 0.833 | 0.757 |
| 2018 summer | 0.969 | 0.956 | 0.962 | 0.945 | 0.849 | 0.785 |
| 2018 winter | 0.901 | 0.876 | 0.859 | 0.798 | 0.737 | 0.617 |
| Land Use | 2011 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|
| Water | 5.10 | 5.50 | 5.13 | 5.14 | 5.34 | 5.56 | 5.86 |
| Developed | 1.28 | 1.07 | 1.88 | 2.54 | 1.80 | 1.99 | 2.27 |
| Phragmites australis | 1.47 | 1.63 | 0.80 | 1.53 | 1.02 | 0.86 | 0.80 |
| Woody Wetlands | 2.97 | 5.28 | 3.94 | 4.00 | 4.43 | 3.68 | 4.37 |
| Herbaceous Wetlands | 9.90 | 7.24 | 8.97 | 7.52 | 8.12 | 8.64 | 7.42 |
| Land Use | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
|---|---|---|---|---|---|---|---|---|
| Water | 5.25 | 4.95 | 4.11 | 5.23 | 4.57 | 5.26 | 5.30 | 6.32 |
| Developed | 1.66 | 1.20 | 3.63 | 1.48 | 2.01 | 0.94 | 0.82 | 4.09 |
| Phragmites australis | 2.01 | 1.48 | 1.62 | 1.37 | 1.54 | 2.04 | 1.31 | 1.31 |
| Woody Wetlands | 3.82 | 5.67 | 4.64 | 3.92 | 4.29 | 3.56 | 5.18 | 2.10 |
| Herbaceous Wetlands | 7.98 | 7.42 | 6.71 | 8.66 | 8.32 | 8.92 | 8.11 | 6.91 |
| Year | Water | Phragmites | Developed | Herbaceous Wetland | Woody Wetland |
|---|---|---|---|---|---|
| 2019 | 4.76 | 1.47 | 1.25 | 7.71 | 4.64 |
| 2020 | 4.69 | 1.55 | 1.16 | 7.45 | 4.87 |
| 2021 | 4.68 | 1.56 | 1.14 | 7.40 | 4.92 |
| 2022 | 4.66 | 1.58 | 1.12 | 7.34 | 4.97 |
| 2023 | 4.62 | 1.63 | 1.06 | 7.13 | 5.16 |
| 2024 | 4.51 | 1.75 | 0.92 | 6.59 | 5.69 |
| 2025 | 4.38 | 1.88 | 0.76 | 5.83 | 6.53 |
| 2026 | 4.23 | 2.04 | 0.56 | 4.79 | 7.89 |
| 2027 | 4.22 | 2.06 | 0.54 | 4.69 | 8.03 |
| 2028 | 4.21 | 2.07 | 0.53 | 4.59 | 8.17 |
| 2029 | 4.20 | 2.08 | 0.51 | 4.50 | 8.32 |
| 2030 | 4.18 | 2.10 | 0.50 | 4.40 | 8.47 |
| 2031 | 4.17 | 2.11 | 0.48 | 4.29 | 8.63 |
| 2032 | 4.16 | 2.12 | 0.46 | 4.19 | 8.79 |
| 2033 | 4.14 | 2.14 | 0.44 | 4.08 | 8.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, D.; Procopio, N.A.; Fang, C. Simulating the Changes of Invasive Phragmites australis in a Pristine Wetland Complex with a Grey System Coupled System Dynamic Model: A Remote Sensing Practice. Remote Sens. 2022, 14, 3886. https://doi.org/10.3390/rs14163886
Yu D, Procopio NA, Fang C. Simulating the Changes of Invasive Phragmites australis in a Pristine Wetland Complex with a Grey System Coupled System Dynamic Model: A Remote Sensing Practice. Remote Sensing. 2022; 14(16):3886. https://doi.org/10.3390/rs14163886
Chicago/Turabian StyleYu, Danlin, Nicholas A. Procopio, and Chuanglin Fang. 2022. "Simulating the Changes of Invasive Phragmites australis in a Pristine Wetland Complex with a Grey System Coupled System Dynamic Model: A Remote Sensing Practice" Remote Sensing 14, no. 16: 3886. https://doi.org/10.3390/rs14163886
APA StyleYu, D., Procopio, N. A., & Fang, C. (2022). Simulating the Changes of Invasive Phragmites australis in a Pristine Wetland Complex with a Grey System Coupled System Dynamic Model: A Remote Sensing Practice. Remote Sensing, 14(16), 3886. https://doi.org/10.3390/rs14163886








