Analysis of the Influence of Attitude Error on Underwater Positioning and Its High-Precision Realization Algorithm
Abstract
:1. Introduction
2. Materials and Methods
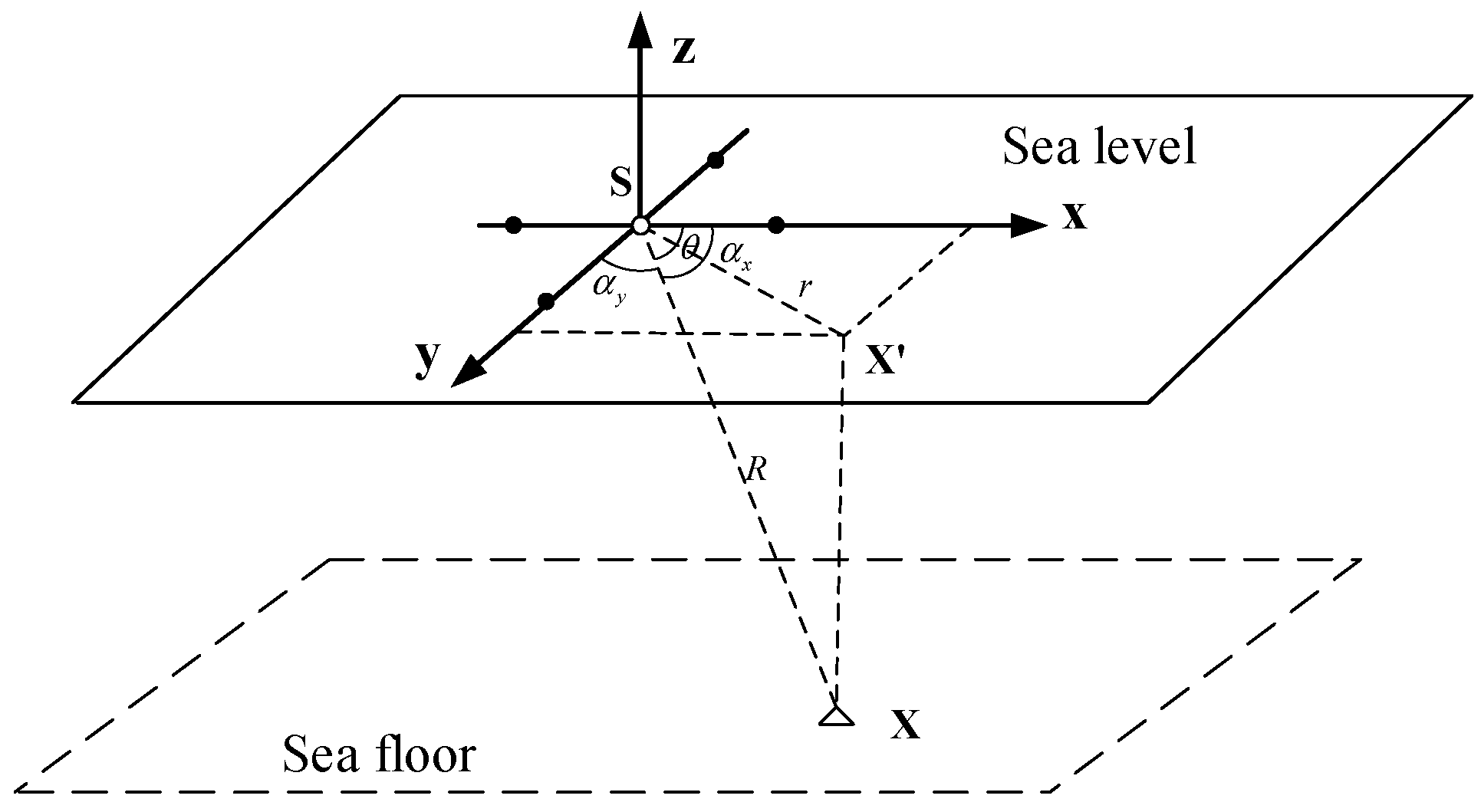
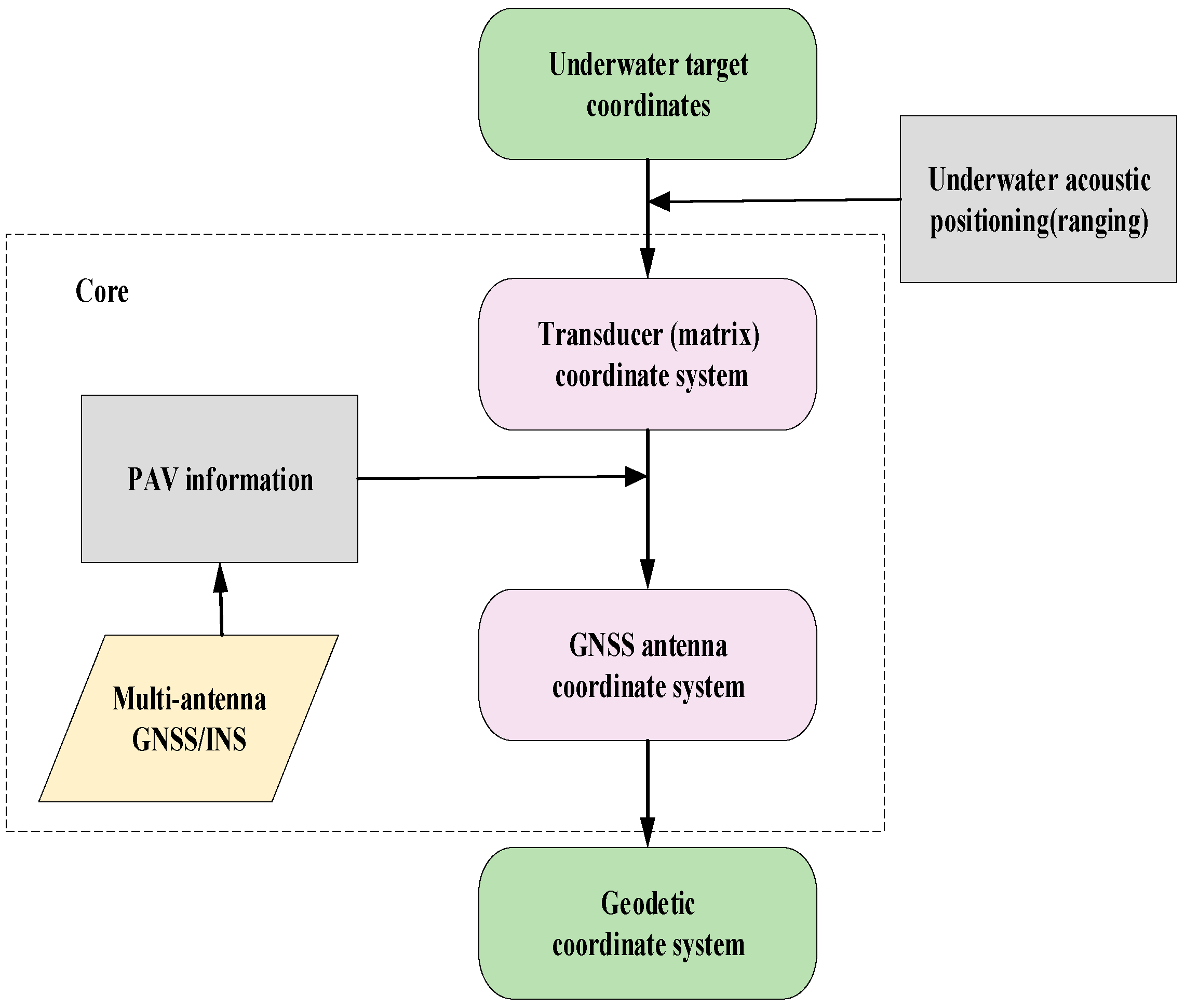
2.1. The Principle of GNSS-A Positioning
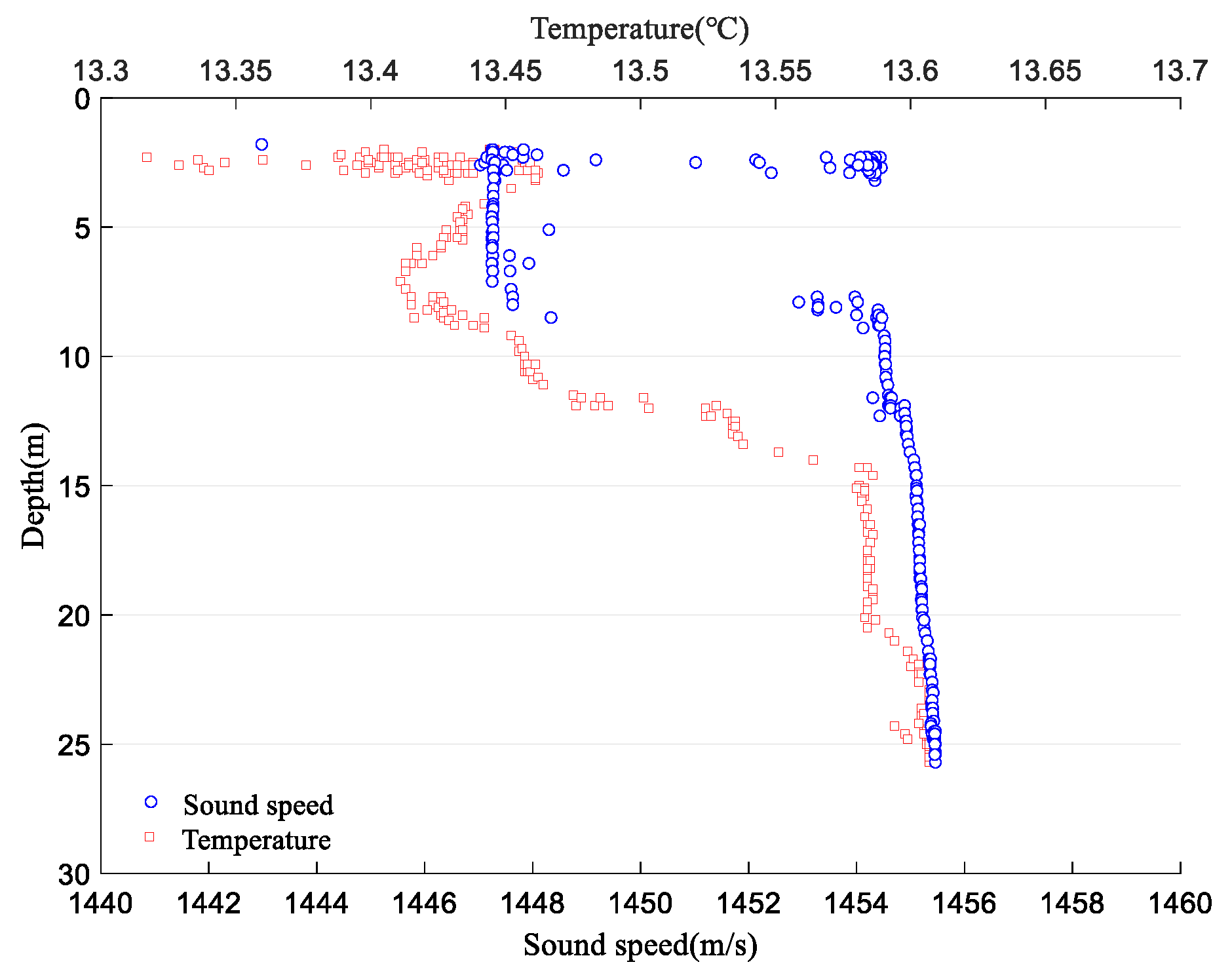
2.2. Influence of Sea Surface Control Point Error on Underwater Positioning
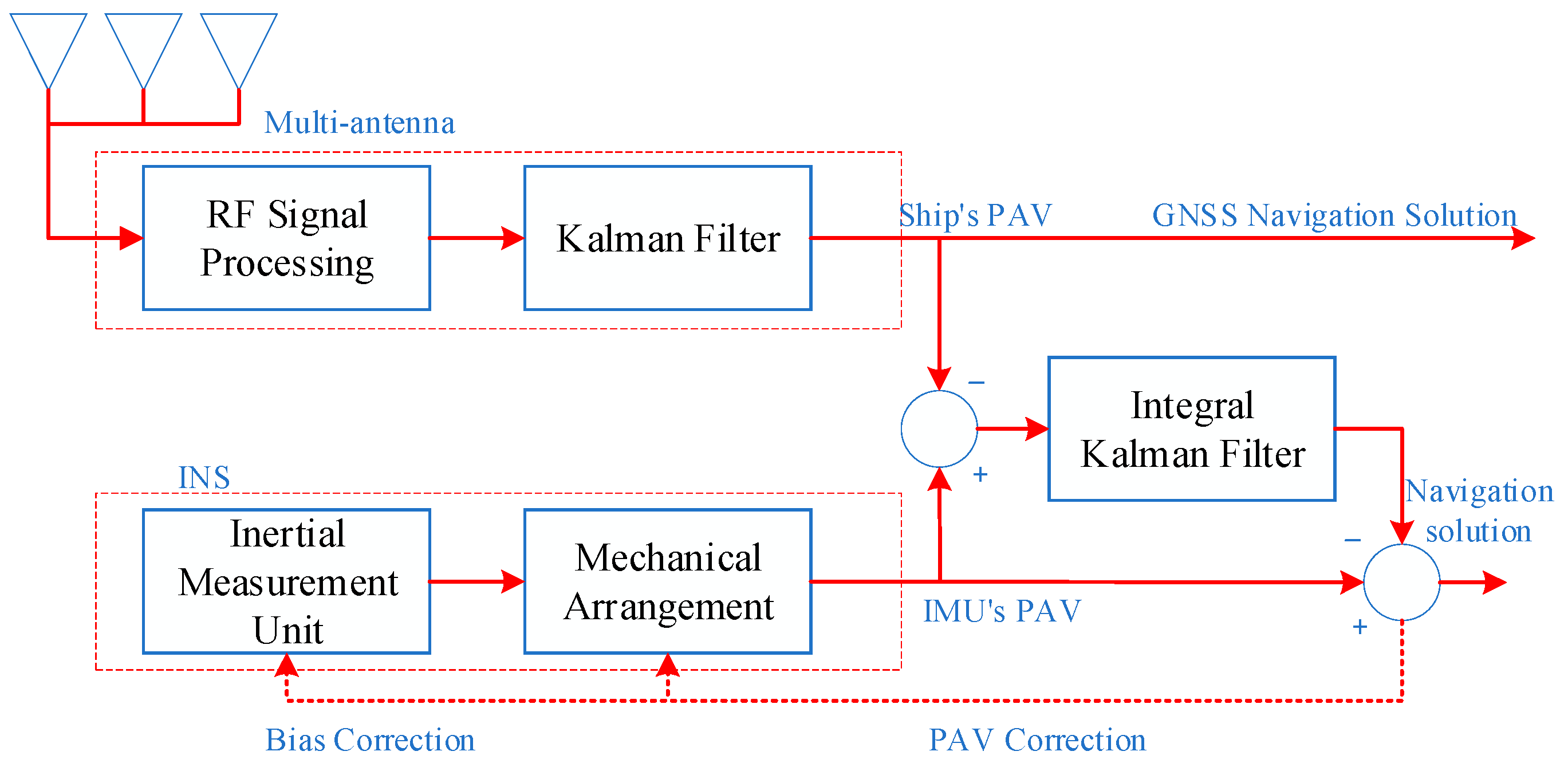
2.3. Multi-Antenna GNSS/INS Positioning Method
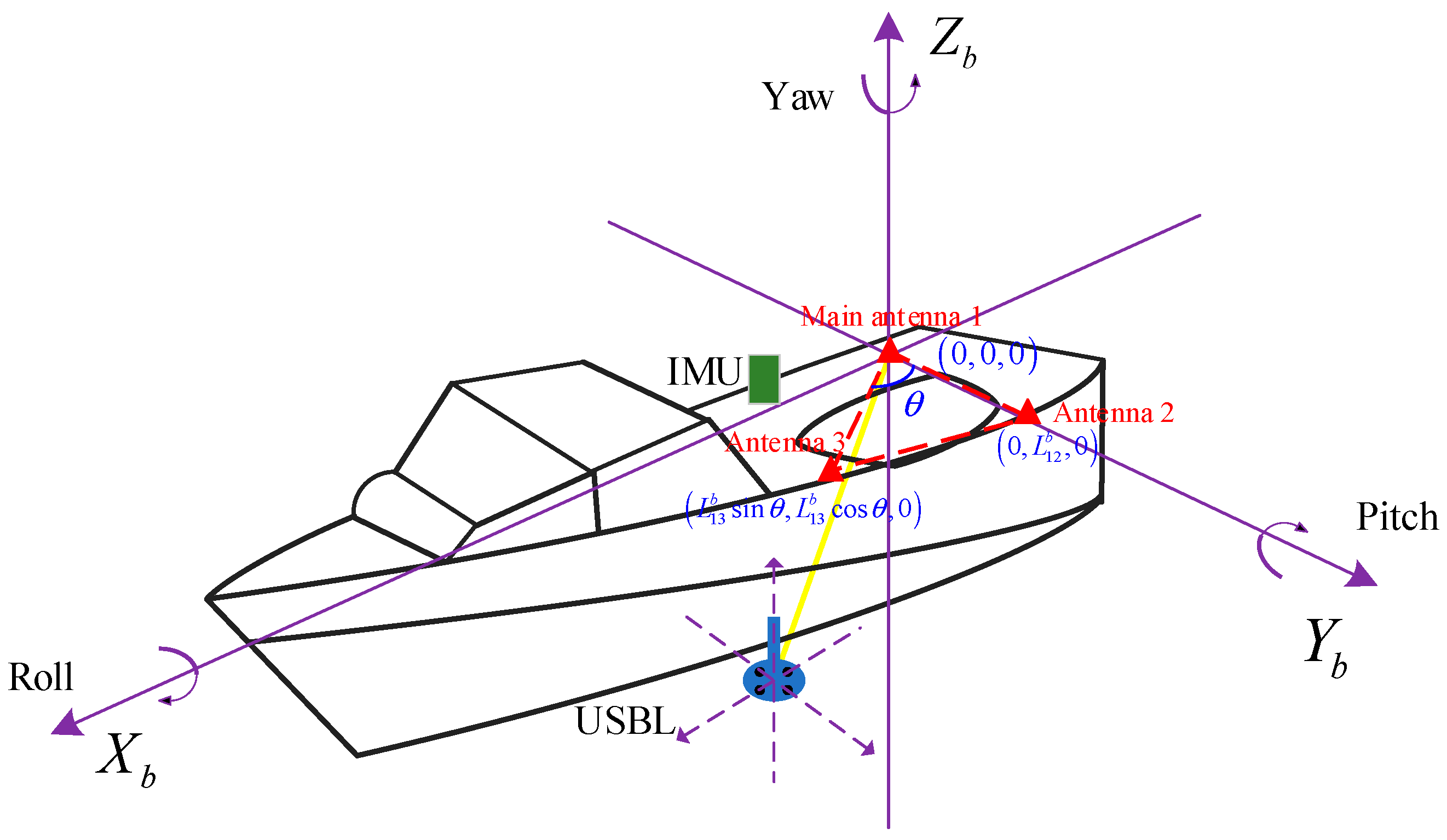
2.3.1. Multi-Antenna Attitude Measurement Method
2.3.2. Multi-Antenna GNSS/INS Loose Combination Algorithm
3. Results
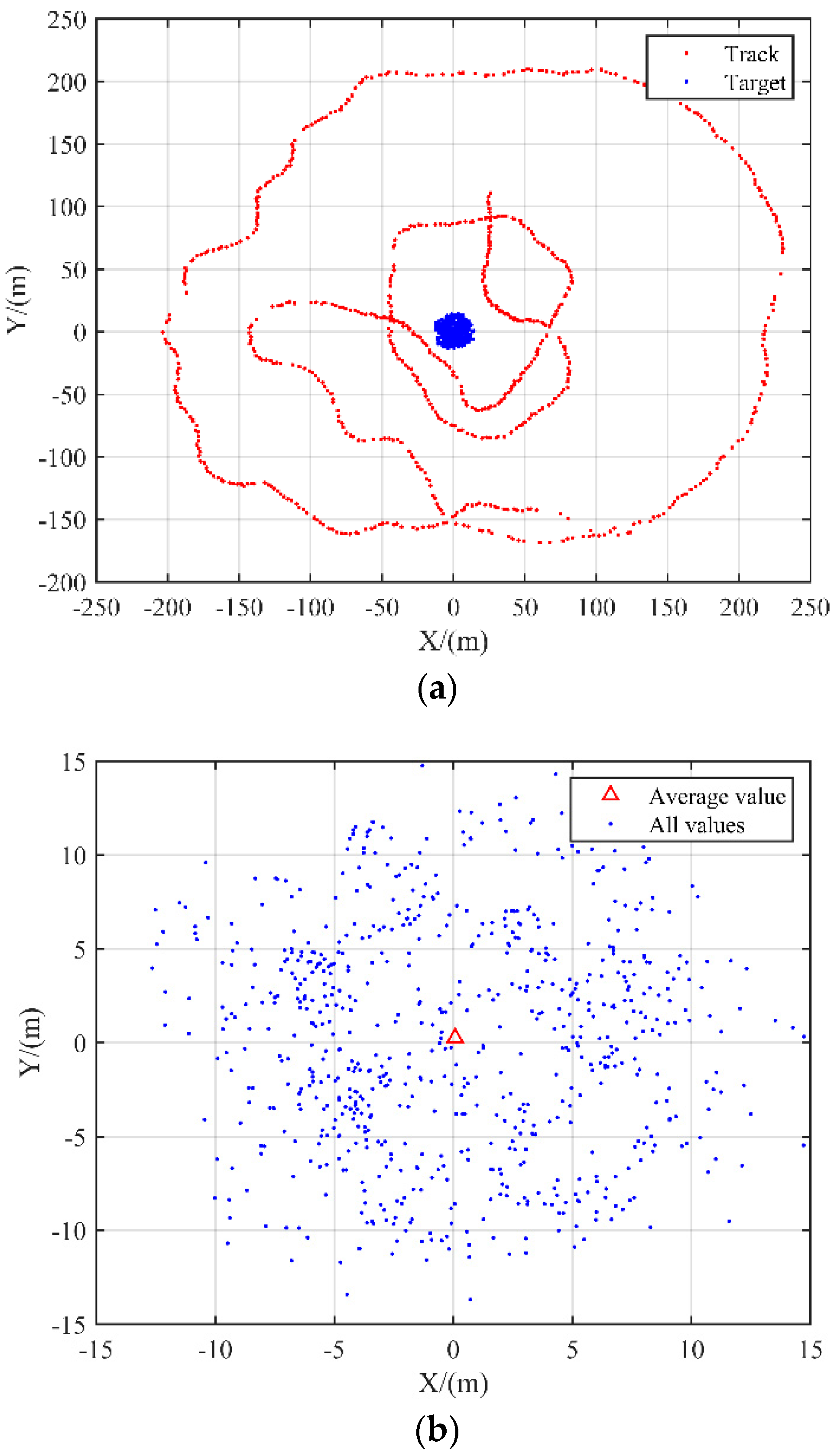
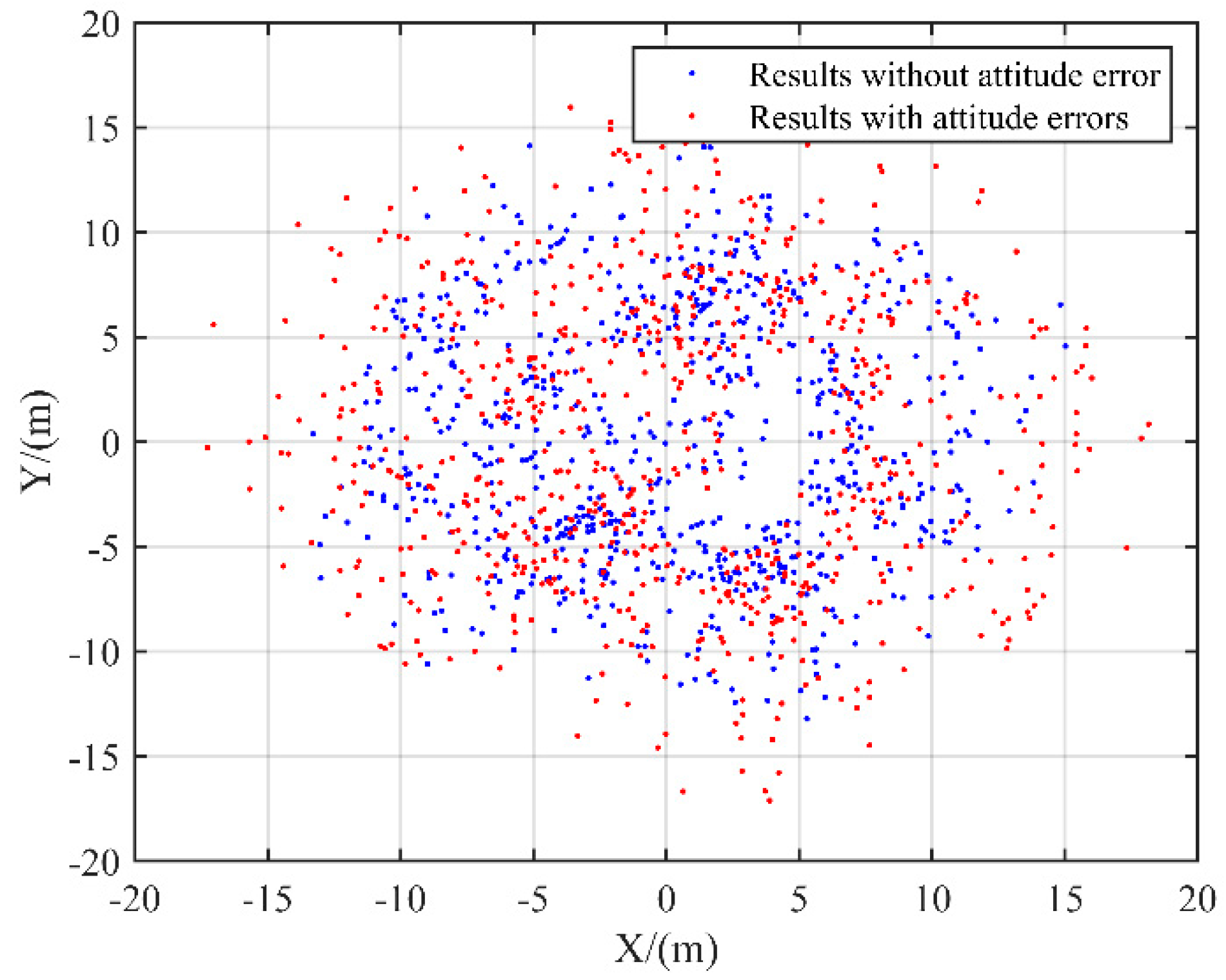
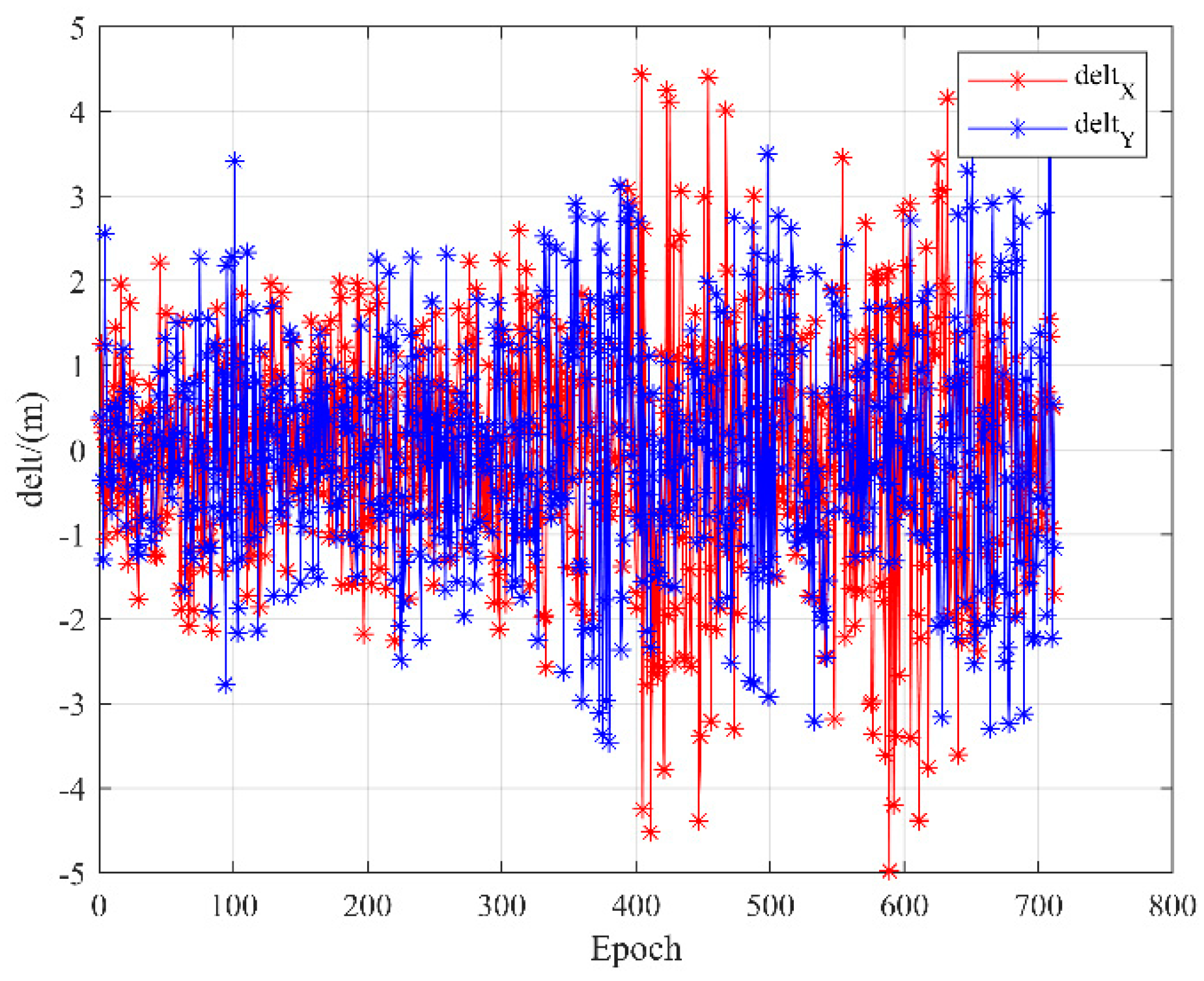
3.1. Influence of Attitude Angle Error on USBL
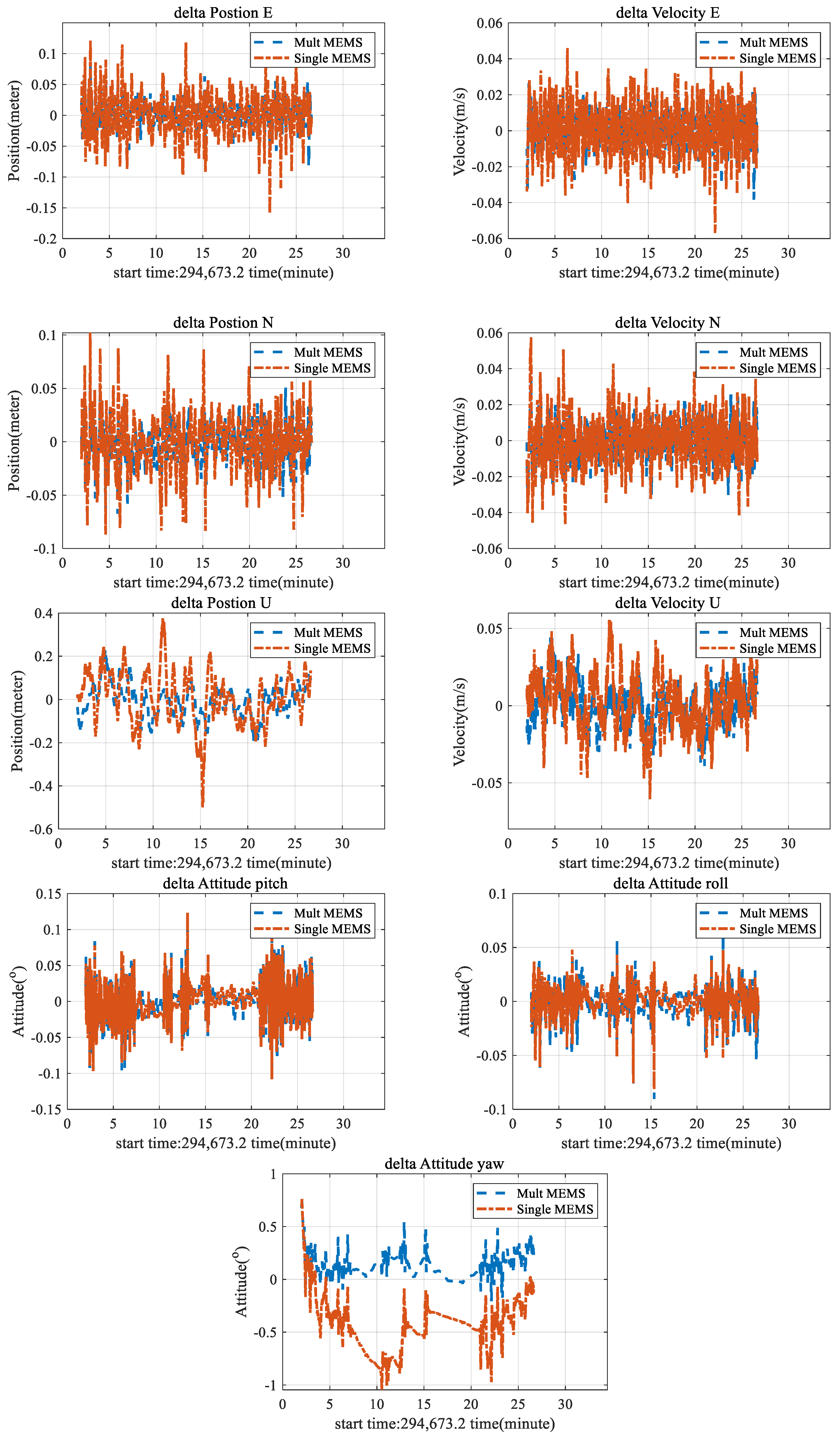
3.2. Multi-Antenna GNSS/INS Attitude Measurement Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Yang, Y.; Liu, Y.; Sun, D.; Xu, T.; Xue, S.; Han, Y.; Zeng, A. Seafloor geodetic network establishment and key technologies. Sci. China Earth Sci. 2020, 63, 1188–1198. [Google Scholar] [CrossRef]
- Yang, Y. Concepts of comprehensive PNT and Related Key Technologies. Acta Geod. Cartogr. Sin. 2016, 45, 505–510. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Lu, X.; Xue, S.; Wang, S. A new underwater positioning model based on average sound speed. J. Navig. 2021, 74, 1009–1025. [Google Scholar] [CrossRef]
- Fujita, M.; Ishikawa, T.; Mochizuki, M.; Sato, M.; Toyama, S.; Katayama, M.; Kawai, K.; Matsumoto, Y.; Yabuki, T.; Asada, A.; et al. GPS/Acoustic seafloor geodetic observation: Method of data analysis and its application. Earth Planet Space 2006, 58, 265–275. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Wang, Z.; He, K.; Ding, N. Investigation on Underwater Positioning Stochastic Model Based on Acoustic Ray Incidence Angle. Appl. Ocean Res. 2018, 77, 69–77. [Google Scholar] [CrossRef]
- Liu, Y.; Xue, S.; Qu, G.; Lu, X.; Qi, K. Influence of the ray elevation angle on seafloor positioning precision in the context of acoustic ray tracing algorithm. Appl. Ocean Res. 2020, 105, 102403. [Google Scholar] [CrossRef]
- Kussat, N.H.; Chadwell, C.D.; Zimmerman, R. Absolute positioning of an autonomous underwater vehicle using GPS and acoustic measurements. IEEE J. Ocean. Eng. 2005, 30, 153–164. [Google Scholar] [CrossRef]
- Jin, S.; Liu, G.; Sun, W.; Bian, G.; Cui, Y. The Research on Depth Reduction Model of Multibeam Echosounding Considering Ship Attitude and Sound Ray Bending. Hydrogr. Surv. Charting 2019, 39, 5. [Google Scholar] [CrossRef]
- Fund, F.; Perosanz, F.; Testut, L.; Loyer, S. An Integer Precise Point Positioning technique for sea surface observations using a GPS buoy. Adv. Space Res. 2013, 51, 1311–1322. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuuh, H. Tightly coupled integration of multi-GNSS PPP and MEMS inertial measurement unit data. GPS Solut. 2017, 21, 377–391. [Google Scholar] [CrossRef]
- Eling, C.; Zeimetz, P.; Kuhlmann, H. Development of an instantaneous GNSS/MEMS attitude determination system. GPS Solut. 2013, 17, 129–138. [Google Scholar] [CrossRef]
- Chai, Y.; Hu, F.; Zhong, S. Analysis on Results of Multi-antenna GNSS/INS. In Proceedings of the 12th China Satellite Navigation Annual Conference—S09, User Terminal Technology, Nanchang, China, 26–28 May 2021; pp. 146–150. [Google Scholar] [CrossRef]
- Yang, W.; Xue, S.; Liu, Y. P-Order Secant Method for Rapidly Solving the Ray Inverse Problem of Underwater Acoustic Positioning. Mar. Geod. 2021, 1–13. [Google Scholar] [CrossRef]
- Chen, G.; Liu, Y.; Liu, Y.; Liu, J. Improving GNSS-acoustic positioning by optimizing the ship’s track lines and observation combinations. J. Geod. 2020, 94, 61. [Google Scholar] [CrossRef]
- Zheng, C. Application of USBL Positioning Technology on Underwater Submersible InterCall; Harbin Engineering University: Harbin, China, 2008. [Google Scholar]
- Zheng, C.; Li, Z.; Sun, D. Study on the calibration method of USBL system based on ray tracing. Oceans IEEE 2013, 1–4. [Google Scholar] [CrossRef]
- Wu, Y. Study on Theory and Method of Precise LBL Positioning and Development of Positioning Software System; Wuhan University: Wuhan, China, 2013. [Google Scholar]
- Zhao, J.; Liu, J.; Zhang, H. The Analysis of Vessel Attitude and the Effect for Multibeam Echo Sounding. Geomat. Inf. Sci. Wuhan Univ. 2001, 26, 144–149. [Google Scholar] [CrossRef]
- Zhao, Y.; Zou, J.; Zhang, P.; Guo, J.; Wang, X.; Huang, G. An Optimization Method of Ambiguity Function Based on Multi-Antenna Constrained and Application in Vehicle Attitude Determination. Micromachines 2022, 13, 64. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Hsu, H.; Chai, H.; Ding, L.; Wang, Y. Multi-antenna GNSS and INS Integrated Position and Attitude Determination without Base Station for Land Vehicles. J. Navig. 2019, 72, 342–358. [Google Scholar] [CrossRef]
- Zhang, B.; Hou, P.; Zha, J.; Liu, T. Integer-estimable FDMA model as an enabler of GLONASS PPP-RTK. J. Geod. 2019, 95, 91. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Y.; Yuan, Y. PPP-RTK based on undifferenced and uncombined observations: Theoretical and practical aspects. J. Geod. 2019, 93, 1011–1024. [Google Scholar] [CrossRef]


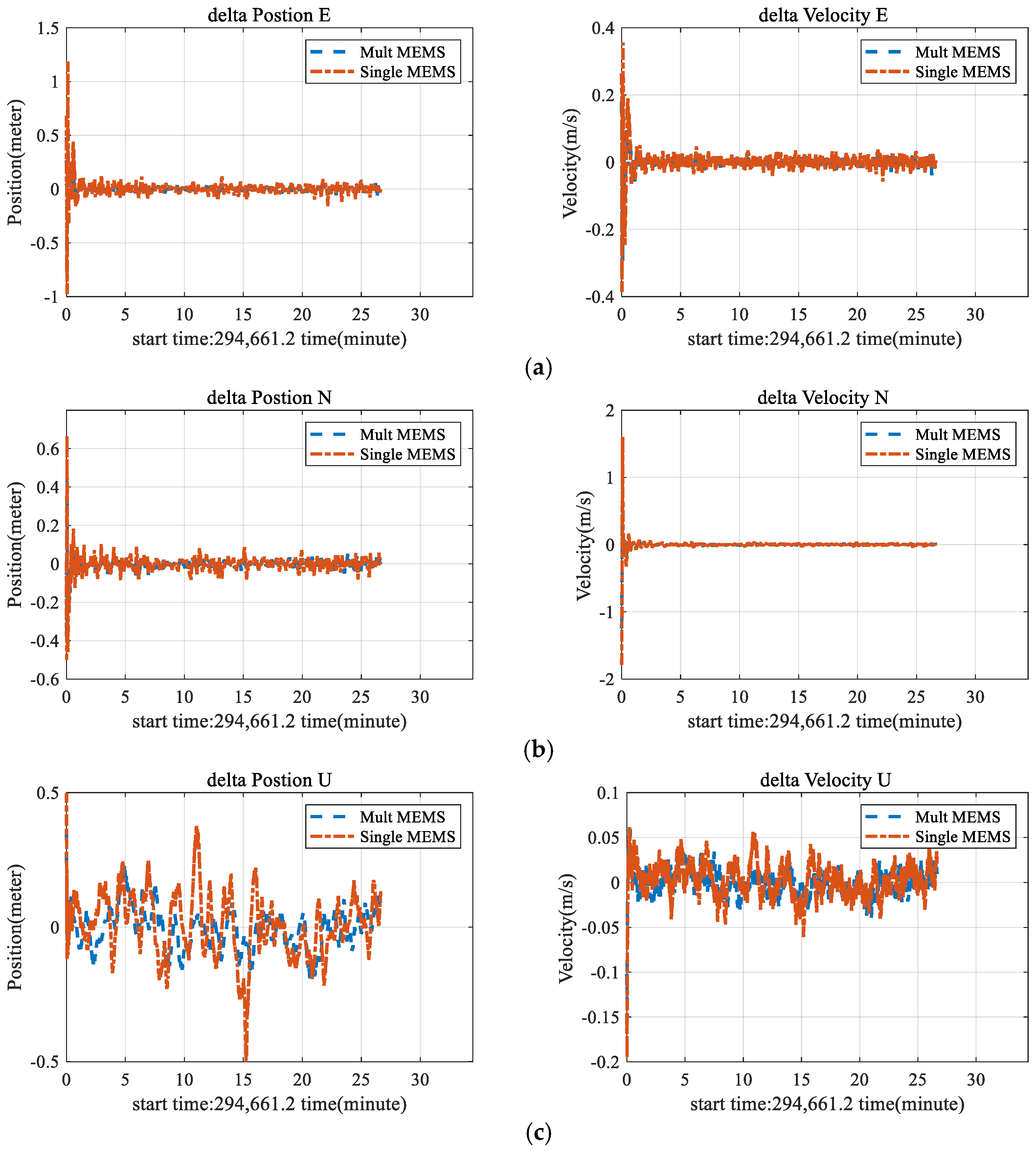
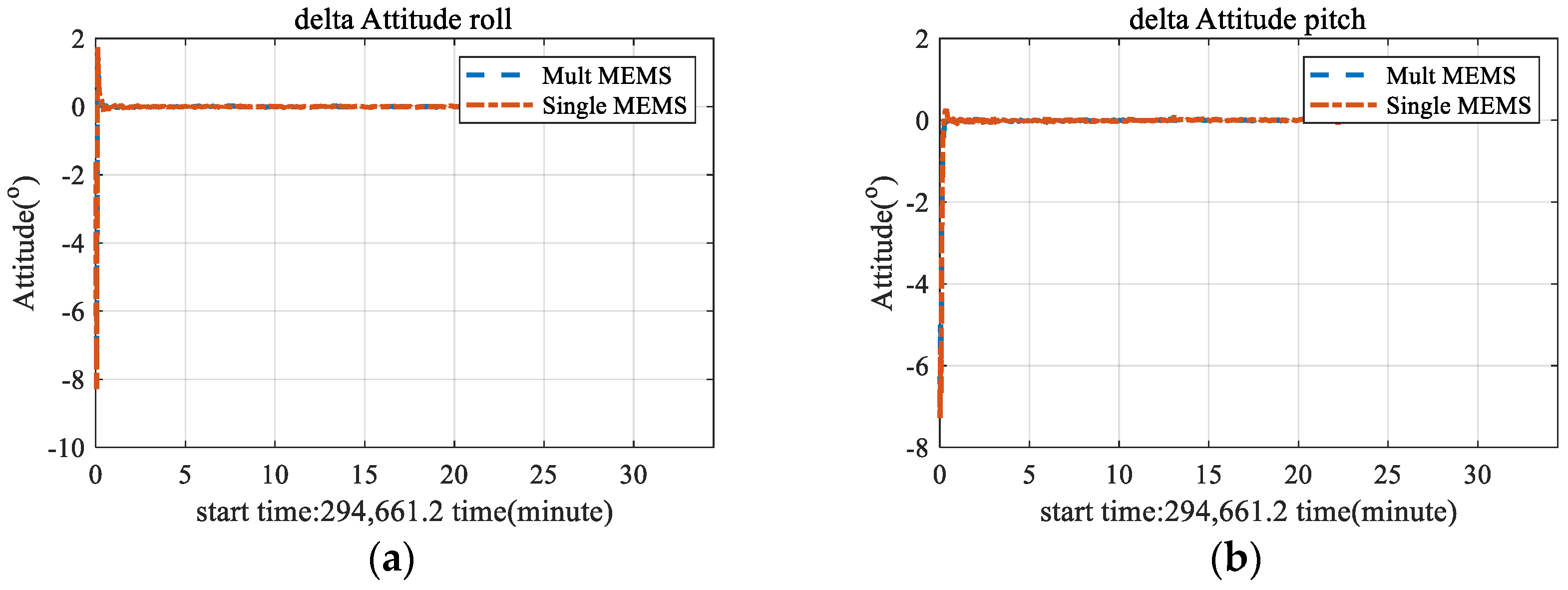
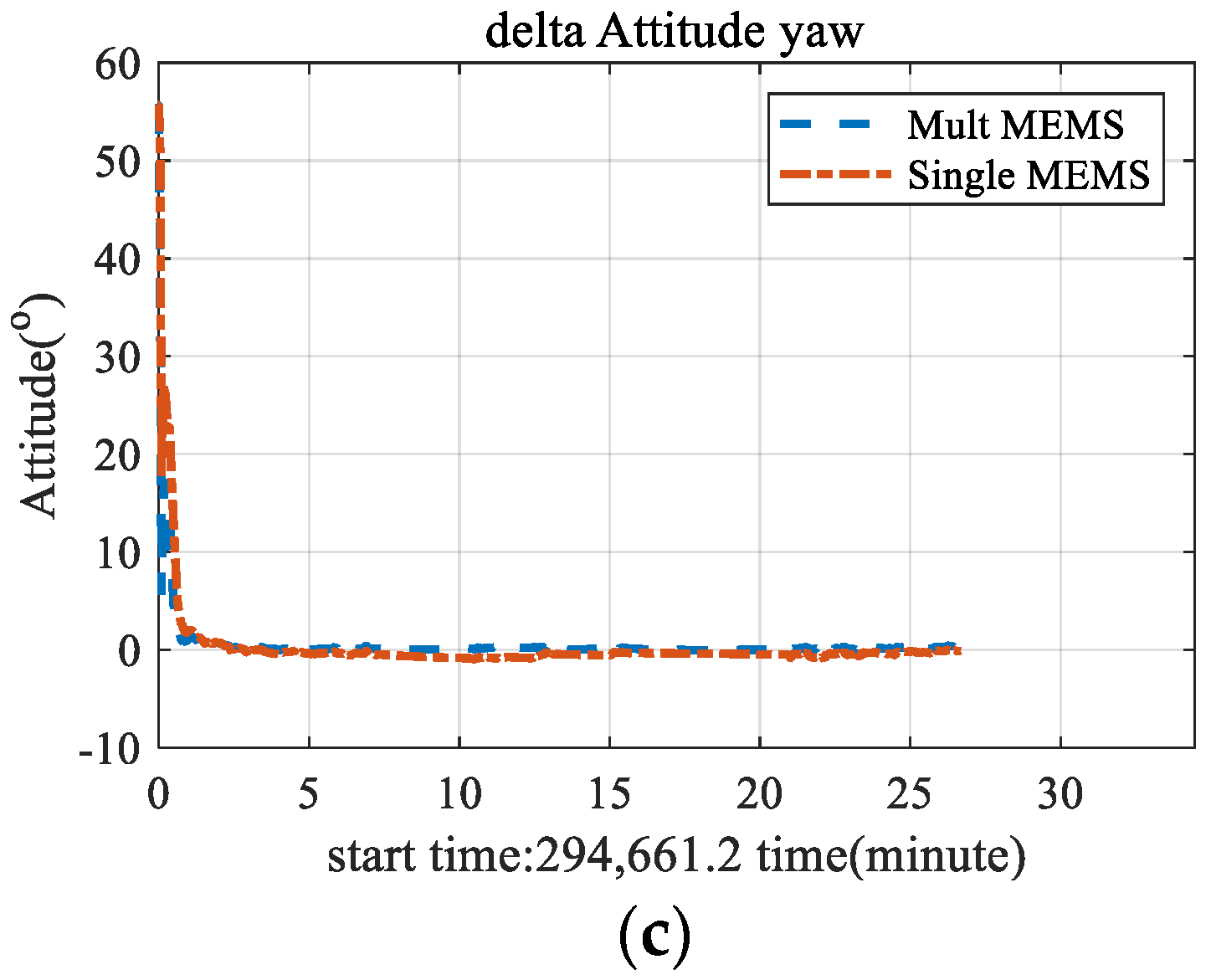
| Multi Antenna | Single Antenna | ||
|---|---|---|---|
| E | 0.0423 | 0.0377 | |
| Position (m) | N | 0.0524 | 0.0558 |
| U | 0.1225 | 0.1084 | |
| E | 0.0746 | 0.0709 | |
| Velocity (m/s) | N | 0.0243 | 0.0238 |
| U | 0.0195 | 0.0182 | |
| Roll | 0.2705 | 0.3008 | |
| Attitude (°) | Pitch | 0.2833 | 0.3100 |
| Yaw | 2.5639 | 3.6273 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wang, L.; Hu, L.; Cui, H.; Wang, S. Analysis of the Influence of Attitude Error on Underwater Positioning and Its High-Precision Realization Algorithm. Remote Sens. 2022, 14, 3878. https://doi.org/10.3390/rs14163878
Liu Y, Wang L, Hu L, Cui H, Wang S. Analysis of the Influence of Attitude Error on Underwater Positioning and Its High-Precision Realization Algorithm. Remote Sensing. 2022; 14(16):3878. https://doi.org/10.3390/rs14163878
Chicago/Turabian StyleLiu, Yixu, Lei Wang, Liangliang Hu, Haonan Cui, and Shengli Wang. 2022. "Analysis of the Influence of Attitude Error on Underwater Positioning and Its High-Precision Realization Algorithm" Remote Sensing 14, no. 16: 3878. https://doi.org/10.3390/rs14163878
APA StyleLiu, Y., Wang, L., Hu, L., Cui, H., & Wang, S. (2022). Analysis of the Influence of Attitude Error on Underwater Positioning and Its High-Precision Realization Algorithm. Remote Sensing, 14(16), 3878. https://doi.org/10.3390/rs14163878







