Multimodal Satellite Image Time Series Analysis Using GAN-Based Domain Translation and Matrix Profile
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Areas
2.1.1. First Use-Case Scenario: Flood Detection and Monitoring
2.1.2. Second Use-Case Scenario: Landslides
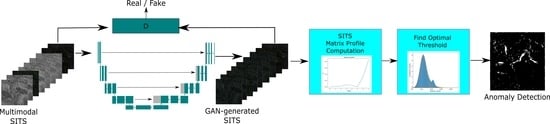
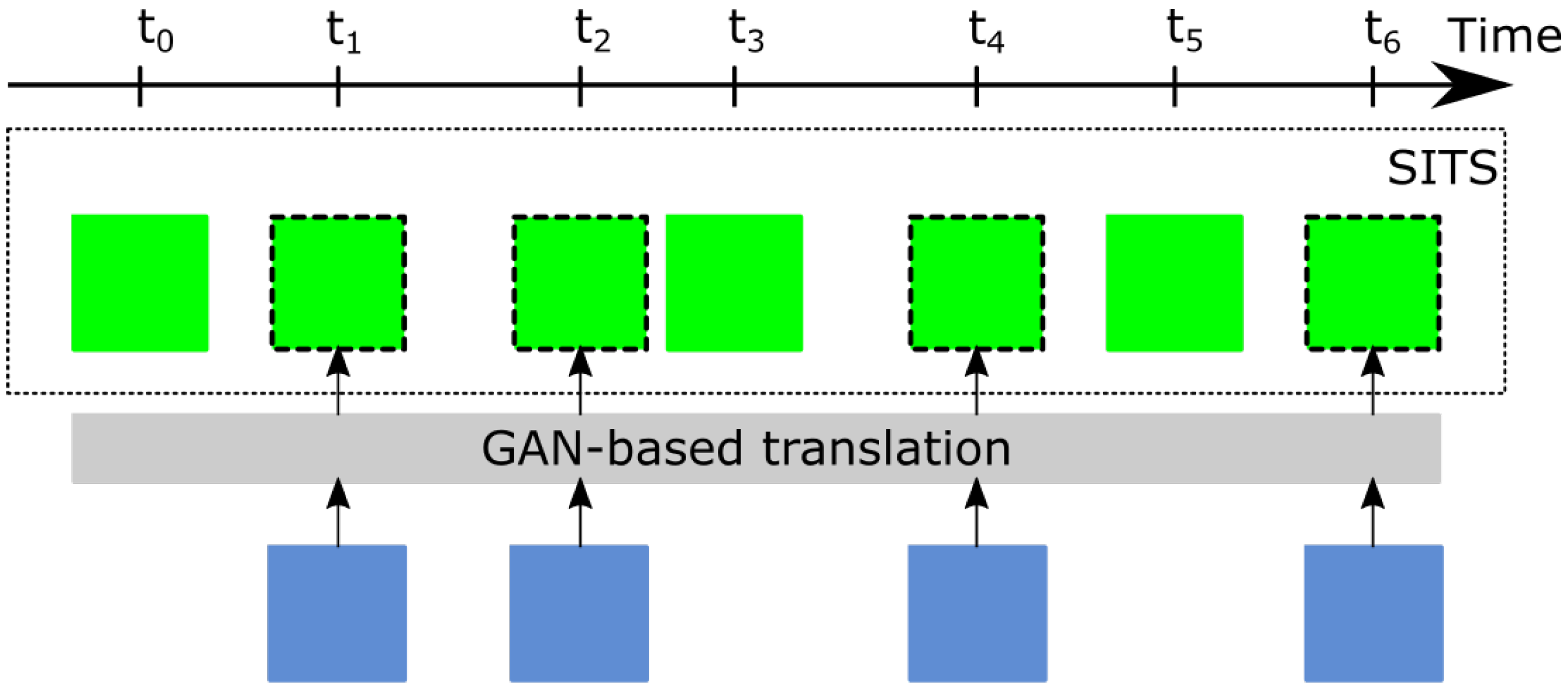
2.2. Methodology Overview
2.3. GAN-Based Modality-to-Modality Translation
2.3.1. Translation Loss
2.3.2. Cycle-Consistency Loss
2.3.3. Adversarial Loss
2.3.4. U-Net-Based Inter-Modality Image Translation
2.4. Identification of Anomalies in a Change Detection Framework for Multimodal SITS
2.4.1. Detection of Abnormal Events in SITS
2.4.2. Unsupervised Change Detection in a Maximum-Likelihood Estimation Framework
3. Experiments
3.1. Inter-Modality Translation
3.2. Performance Evaluation for Multimodal Time-Series Change Detection
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EO | Earth Observation |
| SITS | Satellite Image Time Series |
| SAR | Synthetic Aperture Radar |
| GAN | Generative Adversarial Network |
| CNN | Convolutional Neural Network |
| MLE | Maximum Likelihood Estimation |
| EM | Expectation Maximization |
| DTW | Dynamic Time Warping |
References
- Simoes, R.; Camara, G.; Queiroz, G.; Souza, F.; Andrade, P.R.; Santos, L.; Carvalho, A.; Ferreira, K. Satellite Image Time Series Analysis for Big Earth Observation Data. Remote Sens. 2021, 13, 2428. [Google Scholar] [CrossRef]
- Zhao, C.; Lu, Z. Remote Sensing of Landslides—A Review. Remote Sens. 2018, 10, 279. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Celik, T.; Liu, N.; Li, H.C. A Comparative Analysis of GAN-Based Methods for SAR-to-Optical Image Translation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Barbu, M.; Radoi, A.; Suciu, G. Landslide Monitoring using Convolutional Autoencoders. In Proceedings of the 2020 12th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Bucharest, Romania, 25–27 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Petitjean, F.; Inglada, J.; Gancarski, P. Satellite Image Time Series Analysis Under Time Warping. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3081–3095. [Google Scholar] [CrossRef]
- Prendes, J.; Chabert, M.; Pascal, F.; Giros, A.; Tourneret, J.Y. Performance assessment of a recent change detection method for homogeneous and heterogeneous images. Rev. Française Photogrammétrie Télédétection 2015, 209, 23–29. [Google Scholar] [CrossRef]
- Petitjean, F.; Forestier, G.; Webb, G.I.; Nicholson, A.E.; Chen, Y.; Keogh, E. Dynamic Time Warping Averaging of Time Series Allows Faster and More Accurate Classification. In Proceedings of the 2014 IEEE International Conference on Data Mining, Shenzhen, China, 14–17 December 2014; pp. 470–479. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Wang, L.; He, H.; Liang, D.; Song, W.; Han, W. Large-Area Land-Cover Changes Monitoring With Time-Series Remote Sensing Images Using Transferable Deep Models. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Liu, X.; Hong, D.; Chanussot, J.; Zhao, B.; Ghamisi, P. Modality Translation in Remote Sensing Time Series. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Luppino, L.T.; Kampffmeyer, M.; Bianchi, F.M.; Moser, G.; Serpico, S.B.; Jenssen, R.; Anfinsen, S.N. Deep Image Translation With an Affinity-Based Change Prior for Unsupervised Multimodal Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–22. [Google Scholar] [CrossRef]
- Luppino, L.T.; Hansen, M.A.; Kampffmeyer, M.; Bianchi, F.M.; Moser, G.; Jenssen, R.; Anfinsen, S.N. Code-Aligned Autoencoders for Unsupervised Change Detection in Multimodal Remote Sensing Images. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–13. [Google Scholar] [CrossRef]
- Maggiolo, L.; Solarna, D.; Moser, G.; Serpico, S.B. Registration of Multisensor Images through a Conditional Generative Adversarial Network and a Correlation-Type Similarity Measure. Remote Sens. 2022, 14, 2811. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef] [Green Version]
- Radoi, A.; Datcu, M. Automatic Change Analysis in Satellite Images Using Binary Descriptors and Lloyd-Max Quantization. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1223–1227. [Google Scholar] [CrossRef] [Green Version]
- Touati, R.; Mignotte, M.; Dahmane, M. Change Detection in Heterogeneous Remote Sensing Images Based on an Imaging Modality-Invariant MDS Representation. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 3998–4002. [Google Scholar] [CrossRef]
- Liu, Z.; Li, G.; Mercier, G.; He, Y.; Pan, Q. Change Detection in Heterogenous Remote Sensing Images via Homogeneous Pixel Transformation. IEEE Trans. Image Process. 2018, 27, 1822–1834. [Google Scholar] [CrossRef] [PubMed]
- Luppino, L.T.; Bianchi, F.M.; Moser, G.; Anfinsen, S.N. Unsupervised Image Regression for Heterogeneous Change Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9960–9975. [Google Scholar] [CrossRef] [Green Version]
- Mignotte, M. A Fractal Projection and Markovian Segmentation-Based Approach for Multimodal Change Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8046–8058. [Google Scholar] [CrossRef]
- Liu, J.; Gong, M.; Qin, K.; Zhang, P. A Deep Convolutional Coupling Network for Change Detection Based on Heterogeneous Optical and Radar Images. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 545–559. [Google Scholar] [CrossRef]
- Zhang, P.; Gong, M.; Su, L.; Liu, J.; Li, Z. Change detection based on deep feature representation and mapping transformation for multi-spatial-resolution remote sensing images. ISPRS J. Photogramm. Remote Sens. 2016, 116, 24–41. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks. In Proceedings of the IEEE International Conf. on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar] [CrossRef] [Green Version]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar] [CrossRef] [Green Version]
- Benedetti, P.; Ienco, D.; Gaetano, R.; Ose, K.; Pensa, R.G.; Dupuy, S. M3Fusion: A Deep Learning Architecture for Multiscale Multimodal Multitemporal Satellite Data Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4939–4949. [Google Scholar] [CrossRef] [Green Version]
- Yeh, C.C.M.; Zhu, Y.; Ulanova, L.; Begum, N.; Ding, Y.; Dau, H.A.; Silva, D.F.; Mueen, A.; Keogh, E. Matrix Profile I: All Pairs Similarity Joins for Time Series: A Unifying View That Includes Motifs, Discords and Shapelets. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 1317–1322. [Google Scholar] [CrossRef]
- Copernicus Open Access Hub. Available online: https://scihub.copernicus.eu/ (accessed on 1 September 2020).
- Rambour, C.; Audebert, N.; Koeniguer, E.; Le Saux, B.; Crucianu, M.; Datcu, M. Flood Detection in the Time Series of Optical and SAR Images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B2-2020, 1343–1346. [Google Scholar] [CrossRef]
- SNAP-ESA Sentinel Application Platform. Available online: http://step.esa.int/ (accessed on 1 September 2020).
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N., Weinberger, K., Eds.; Curran Associates, Inc.: Montreal, QC, Canada, 2014; Volume 27. [Google Scholar]
- Pathak, D.; Krähenbühl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context Encoders: Feature Learning by Inpainting. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2536–2544. [Google Scholar] [CrossRef] [Green Version]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.; Wang, Z.; Smolley, S.P. Least Squares Generative Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2813–2821. [Google Scholar] [CrossRef] [Green Version]
- Kurach, K.; Lučić, M.; Zhai, X.; Michalski, M.; Gelly, S. A Large-Scale Study on Regularization and Normalization in GANs. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Yun, S.; Han, D.; Oh, S.J.; Chun, S.; Choe, J.; Yoo, Y.J. CutMix: Regularization Strategy to Train Strong Classifiers With Localizable Features. IEEE/CVF Int. Conf. Comput. Vis. (ICCV) 2019, 6022–6031. [Google Scholar] [CrossRef] [Green Version]
- Karras, T.; Aittala, M.; Hellsten, J.; Laine, S.; Lehtinen, J.; Aila, T. Training Generative Adversarial Networks with Limited Data. Proc. Adv. Neural Inf. Process. Syst. 2020, 33, 12104–12114. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Chandola, V.; Cheboli, D.; Kumar, V. Detecting Anomalies in a Time Series Database; Technical Report; University of Minnesota Digital Conservancy: Minneapolis, MN, USA, 2009; Volume UMN TR 09-004. [Google Scholar]
- Radoi, A.; Burileanu, C. Retrieval of Similar Evolution Patterns from Satellite Image Time Series. Appl. Sci. 2018, 8, 2435. [Google Scholar] [CrossRef] [Green Version]
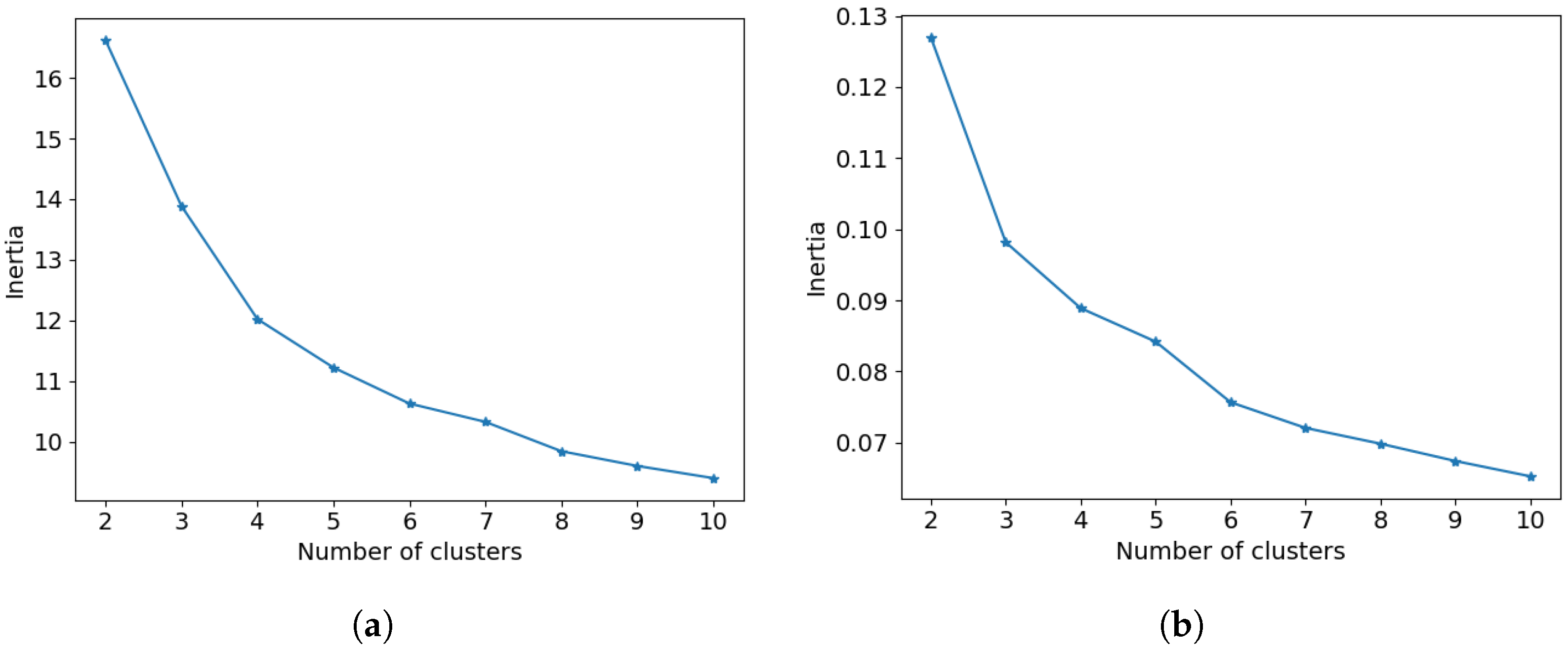
- Liu, F.; Deng, Y. Determine the Number of Unknown Targets in Open World Based on Elbow Method. IEEE Trans. Fuzzy Syst. 2021, 29, 986–995. [Google Scholar] [CrossRef]









| Event | Location | Monitoring Period | Number of Images in SITS | Image Dimensions |
|---|---|---|---|---|
| Flooding | BuheraZimbabwe | 1 February 2019–17 April 2019 | 9 Sentinel-12 Sentinel-2 | |
| Landslide | AlunuRomania | 18 December 2016–6 October 2017 | 6 Sentinel-13 Sentinel-2 |
| Event | Method | Overall Accuracy | True Positive Rate | True Negative Rate | F-Score |
|---|---|---|---|---|---|
| Flooding | Proposed GAN-MP | 96.59% | 92.29% | 96.93% | 0.79 |
| DTW-EM [36] | 95.26% | 56.21% | 98.37% | 0.64 | |
| ACE-Net [10] | 61.64% | 65.38% | 61.34% | 0.20 | |
| Landslide | Proposed GAN-MP | 97.18% | 80.68% | 97.46% | 0.49 |
| DTW-EM [36] | 93.05% | 85.75% | 93.18% | 0.29 | |
| ACE-Net [10] | 80.66% | 87.67% | 80.53% | 0.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radoi, A. Multimodal Satellite Image Time Series Analysis Using GAN-Based Domain Translation and Matrix Profile. Remote Sens. 2022, 14, 3734. https://doi.org/10.3390/rs14153734
Radoi A. Multimodal Satellite Image Time Series Analysis Using GAN-Based Domain Translation and Matrix Profile. Remote Sensing. 2022; 14(15):3734. https://doi.org/10.3390/rs14153734
Chicago/Turabian StyleRadoi, Anamaria. 2022. "Multimodal Satellite Image Time Series Analysis Using GAN-Based Domain Translation and Matrix Profile" Remote Sensing 14, no. 15: 3734. https://doi.org/10.3390/rs14153734
APA StyleRadoi, A. (2022). Multimodal Satellite Image Time Series Analysis Using GAN-Based Domain Translation and Matrix Profile. Remote Sensing, 14(15), 3734. https://doi.org/10.3390/rs14153734