Framework to Extract Extreme Phytoplankton Bloom Events with Remote Sensing Datasets: A Case Study
Abstract
:1. Introduction
2. Data and Methods
2.1. Datasets
2.1.1. Remote Sensing Reconstruction: SCSDCT
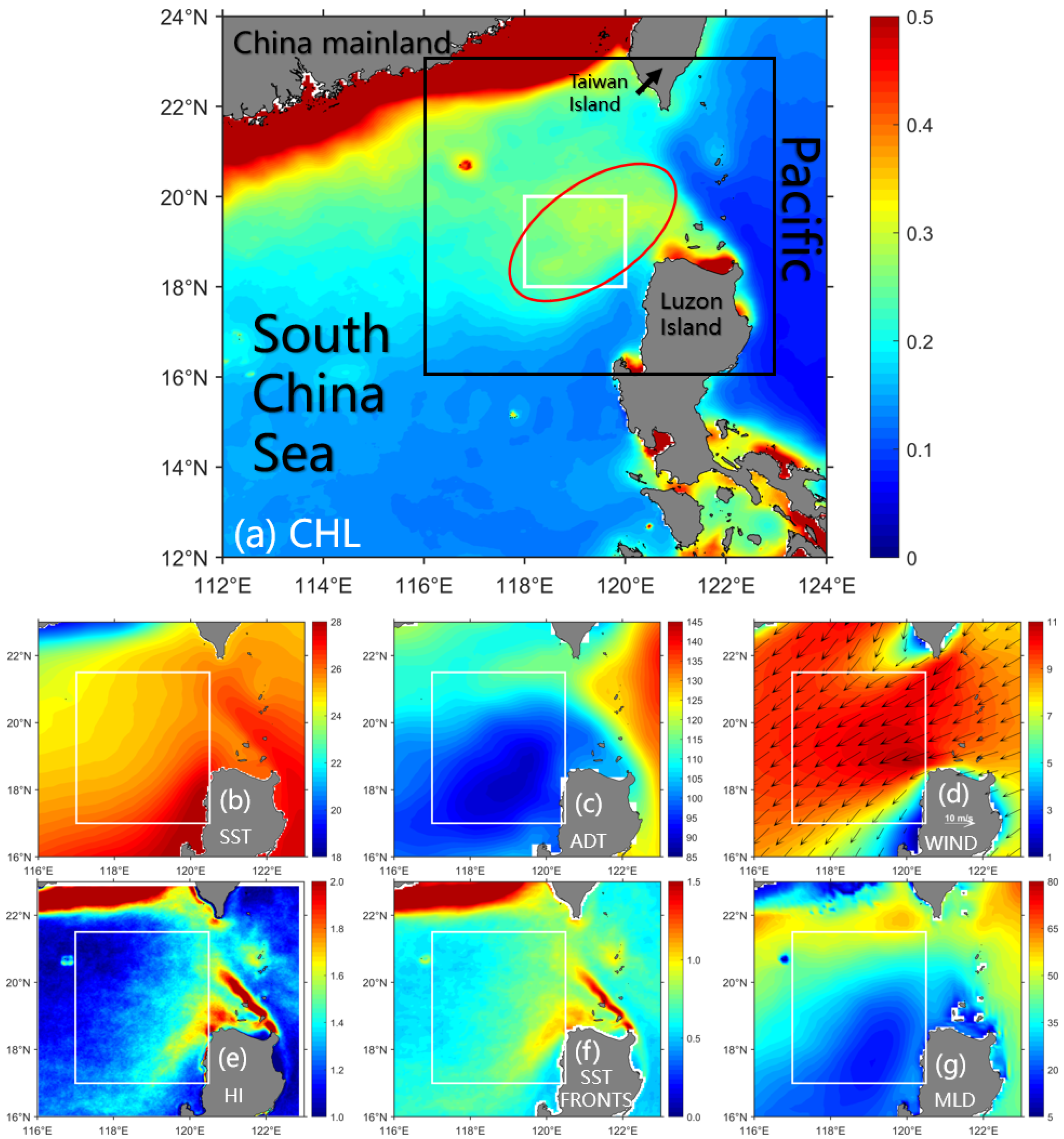
2.1.2. Other Products: Controlling Factors
2.2. Method: H16 Framework for Marine Heat Waves
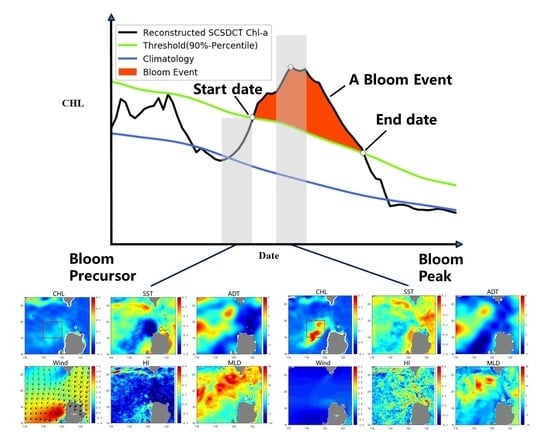
2.3. Method: Bloom Composite
3. Results
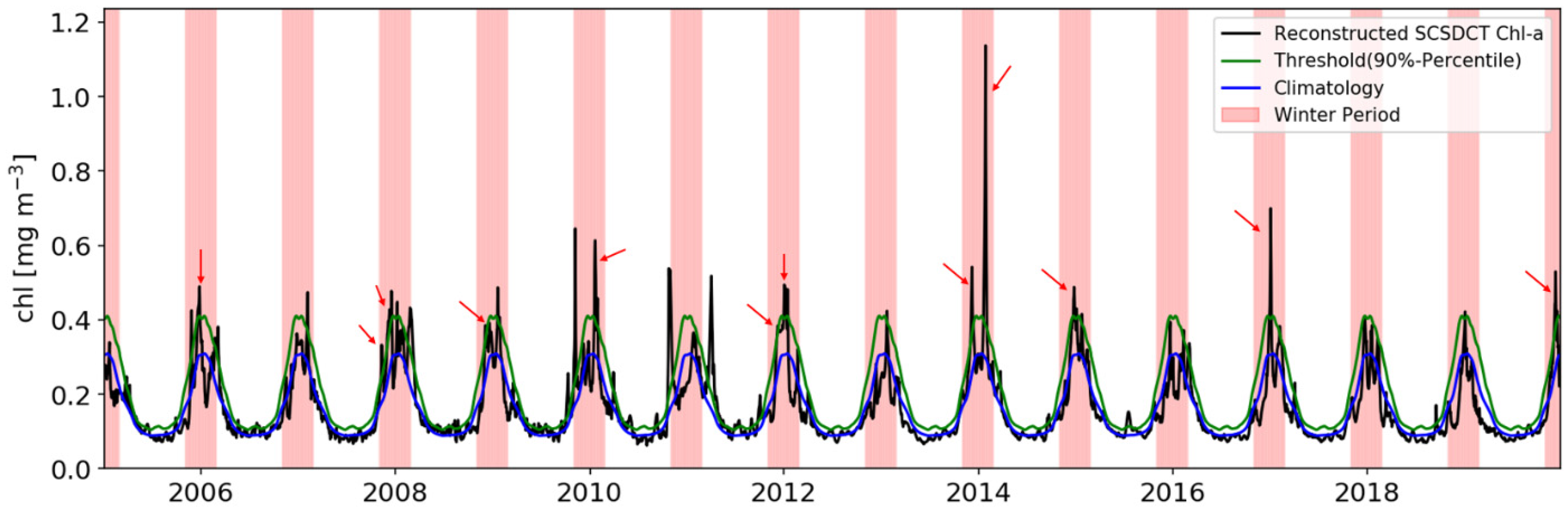
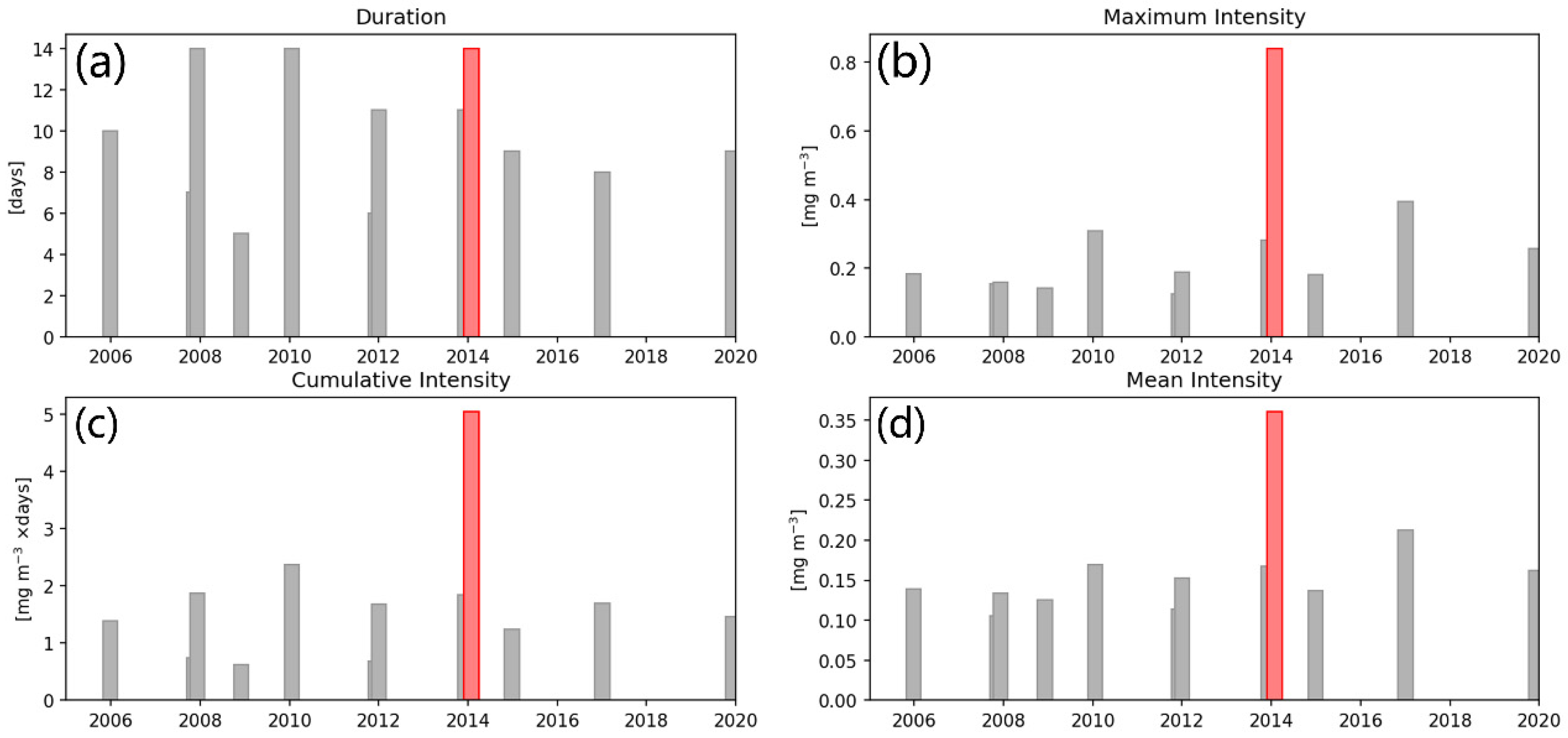
3.1. Bloom Events Defined via H16
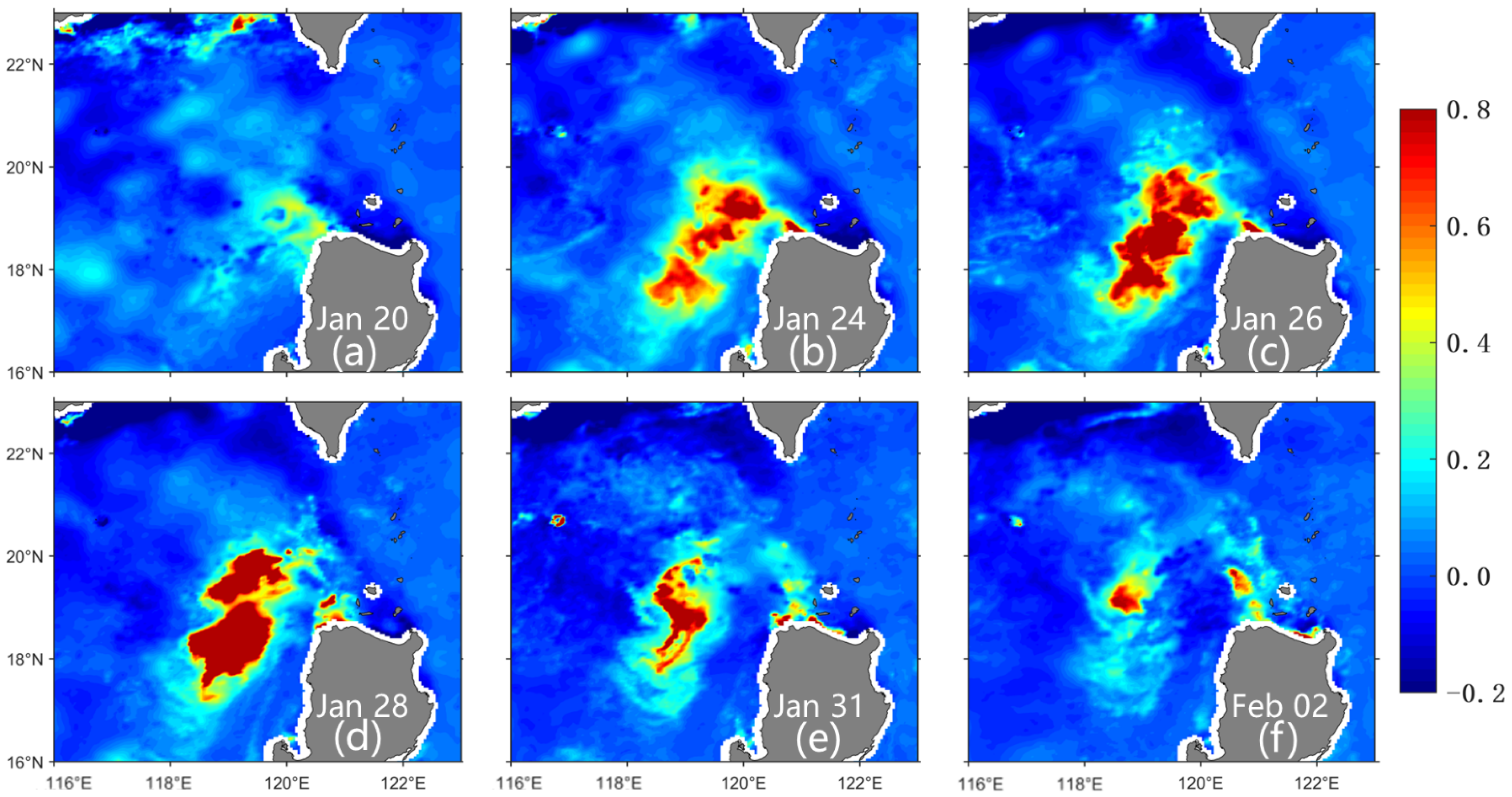
3.2. Event of 2014 Winter
3.3. Trends
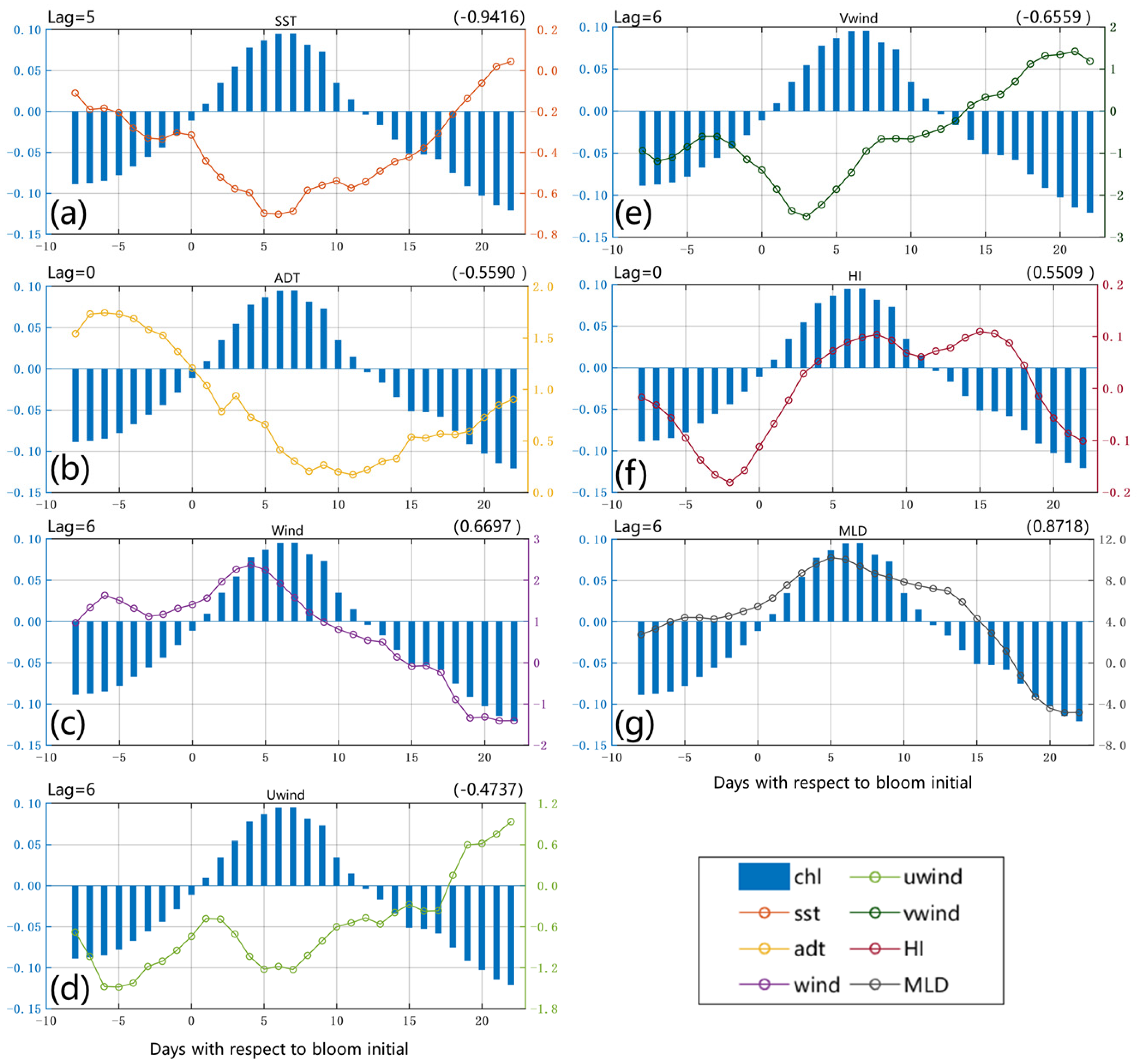
4. Controlling Factors
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wong, G.T.F.; Ku, T.L.; Mulholland, M.; Tseng, C.M.; Wang, D.P. The SouthEast Asian time-series study (SEATS) and the biogeochemistry of the South China Sea—An overview. Deep Sea Res. Part II Top. Stud. Oceanogr. 2007, 54, 1434–1447. [Google Scholar] [CrossRef]
- Lu, W.; Yan, X.-H.; Han, L.; Jiang, Y. One-dimensional ocean model with three types of vertical velocities: A case study in the South China Sea. Ocean. Dyn. 2017, 67, 253–262. [Google Scholar] [CrossRef]
- Tang, D.; Ni, I.-H.; Kester, D.R.; Muller-Karger, F.E. Remote sensing observations of winter phytoplankton blooms southwest of the Luzon Strait in the South China Sea. Mar. Ecol. Prog. Ser. 1999, 191, 43–51. [Google Scholar] [CrossRef] [Green Version]
- Shang, S.; Li, L.; Li, J.; Li, Y.; Lin, G.; Sun, J. Phytoplankton bloom during the northeast monsoon in the Luzon Strait bordering the Kuroshio. Remote Sens. Environ. 2012, 124, 38–48. [Google Scholar] [CrossRef]
- Lu, W.; Yan, X.-H.; Jiang, Y. Winter bloom and associated upwelling northwest of the Luzon Island: A coupled physical-biological modeling approach. J. Geophys. Res. Ocean. 2015, 120, 533–546. [Google Scholar] [CrossRef]
- Wang, J.; Tang, D.; Sui, Y. Winter phytoplankton bloom induced by subsurface upwelling and mixed layer entrainment southwest of Luzon Strait. J. Mar. Syst. 2010, 83, 141–149. [Google Scholar] [CrossRef]
- Xing, X.; Qiu, G.; Boss, E.; Wang, H. Temporal and Vertical Variations of Particulate and Dissolved Optical Properties in the South China Sea. J. Geophys. Res. Ocean. 2019, 124, 3779–3795. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Liu, X.; Xiao, W.; Laws, E.A.; Huang, B. Spatial and temporal variations of satellite-derived phytoplankton size classes using a three-component model bridged with temperature in Marginal Seas of the Western Pacific Ocean. Prog. Oceanogr. 2021, 191, 102511. [Google Scholar] [CrossRef]
- Guo, L.; Xiu, P.; Chai, F.; Xue, H.; Wang, D.; Sun, J. Enhanced chlorophyll concentrations induced by Kuroshio intrusion fronts in the northern South China Sea. Geophys. Res. Lett. 2017, 44, 11565–11572. [Google Scholar] [CrossRef] [Green Version]
- Shuai, Y.; Li, Q.P.; Wu, Z. Biogeochemical Responses to Nutrient Fluxes in the Open South China Sea: A 3-D Modeling Study. J. Geophys. Res. Ocean. 2021, 126, e2020JC016895. [Google Scholar] [CrossRef]
- Gao, H.; Zhao, H.; Han, G.; Dong, C. Spatio-Temporal Variations of Winter Phytoplankton Blooms Northwest of the Luzon Island in the South China Sea. Front. Mar. Sci. 2021, 8, 637499. [Google Scholar] [CrossRef]
- Du, C.; Liu, Z.; Kao, S.J.; Dai, M. Diapycnal Fluxes of Nutrients in an Oligotrophic Oceanic Regime: The South China Sea. Geophys. Res. Lett. 2017, 44, 11510–11518. [Google Scholar] [CrossRef]
- Mahadevan, A. The Impact of Submesoscale Physics on Primary Productivity of Plankton. Ann. Rev. Mar. Sci. 2016, 8, 161–184. [Google Scholar] [CrossRef] [Green Version]
- Omand, M.M.; D’Asaro, E.A.; Lee, C.M.; Perry, M.J.; Briggs, N.; Cetinić, I.; Mahadevan, A. Eddy-driven subduction exports particulate organic carbon from the spring bloom. Science 2015, 348, 222–225. [Google Scholar] [CrossRef] [Green Version]
- McWilliams, J.C. Submesoscale, coherent vortices in the ocean. Rev. Geophys. 1985, 23, 165–182. [Google Scholar] [CrossRef]
- Molemaker, M.J.; McWilliams, J.C.; Yavneh, I. Baroclinic instability and loss of balance. J. Phys. Oceanogr. 2005, 35, 1505–1517. [Google Scholar] [CrossRef] [Green Version]
- Mahadevan, A.; D’Asaro, E.; Lee, C.; Perry, M.J. Eddy-driven stratification initiates North Atlantic spring phytoplankton blooms. Science 2012, 337, 54–58. [Google Scholar] [CrossRef]
- Dong, J.; Zhong, Y. The spatiotemporal features of submesoscale processes in the northeastern South China Sea. Acta Oceanol. Sin. 2018, 37, 8–18. [Google Scholar] [CrossRef]
- Lin, H.; Liu, Z.; Hu, J.; Menemenlis, D.; Huang, Y. Characterizing meso-to submesoscale features in the South China Sea. Prog. Oceanogr. 2020, 188, 102420. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, X.; Qiu, B.; Zhao, W.; Zhou, C.; Huang, X.; Tian, J. Submesoscale Currents in the Subtropical Upper Ocean Observed by Long-Term High-Resolution Mooring Arrays. J. Phys. Oceanogr. 2021, 51, 187–206. [Google Scholar] [CrossRef]
- Zhong, Y.; Bracco, A.; Tian, J.; Dong, J.; Zhao, W.; Zhang, Z. Observed and simulated submesoscale vertical pump of an anticyclonic eddy in the South China Sea. Sci. Rep. 2017, 7, 44011. [Google Scholar] [CrossRef] [PubMed]
- Bagniewski, W.; Fennel, K.; Perry, M.J.; D’Asaro, E.A. Optimizing models of the North Atlantic spring bloom using physical, chemical and bio-optical observations from a Lagrangian float. Biogeosciences 2011, 8, 1291–1307. [Google Scholar] [CrossRef] [Green Version]
- Kuroda, H.; Takasuka, A.; Hirota, Y.; Kodama, T.; Ichikawa, T.; Takahashi, D.; Aoki, K.; Setou, T. Numerical experiments based on a coupled physical–biochemical ocean model to study the Kuroshio-induced nutrient supply on the shelf-slope region off the southwestern coast of Japan. J. Mar. Syst. 2018, 179, 38–54. [Google Scholar] [CrossRef]
- Lévy, M.; Iovino, D.; Resplandy, L.; Klein, P.; Madec, G.; Tréguier, A.M.; Masson, S.; Takahashi, K. Large-scale impacts of submesoscale dynamics on phytoplankton: Local and remote effects. Ocean. Model. 2012, 43, 77–93. [Google Scholar] [CrossRef]
- Lévy, M.; Klein, P.; Treguier, A.-M. Impact of sub-mesoscale physics on production and subduction of phytoplankton in an oligotrophic regime. J. Mar. Res. 2001, 59, 535–565. [Google Scholar] [CrossRef] [Green Version]
- Lévy, M.; Resplandy, L.; Lengaigne, M. Oceanic mesoscale turbulence drives large biogeochemical interannual variability at middle and high latitudes. Geophys. Res. Lett. 2014, 41, 2467–2474. [Google Scholar] [CrossRef]
- Mahadevan, A.; Archer, D. Modeling the impact of fronts and mesoscale circulation on the nutrient supply and biogeochemistry of the upper ocean. J. Geophys. Res. Ocean. 2000, 105, 1209–1225. [Google Scholar] [CrossRef] [Green Version]
- Castro, S.L.; Emery, W.J.; Wick, G.A.; Tandy, W. Submesoscale Sea Surface Temperature Variability from UAV and Satellite Measurements. Remote Sens. 2017, 9, 1089. [Google Scholar] [CrossRef] [Green Version]
- Gaube, P.; Chickadel, C.C.; Branch, R.; Jessup, A. Satellite Observations of SST-Induced Wind Speed Perturbation at the Oceanic Submesoscale. Geophys. Res. Lett. 2019, 46, 2690–2695. [Google Scholar] [CrossRef]
- Hosegood, P.J.; Nightingale, P.D.; Rees, A.P.; Widdicombe, C.E.; Woodward, E.M.S.; Clark, D.R.; Torres, R.J. Nutrient pumping by submesoscale circulations in the mauritanian upwelling system. Prog. Oceanogr. 2017, 159, 223–236. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Levine, N.M. Enhancement of phytoplankton chlorophyll by submesoscale frontal dynamics in the North Pacific Subtropical Gyre. Geophys. Res. Lett. 2016, 43, 1651–1659. [Google Scholar] [CrossRef] [PubMed]
- Ni, Q.; Zhai, X.; Wilson, C.; Chen, C.; Chen, D. Submesoscale Eddies in the South China Sea. Geophys. Res. Lett. 2021, 48, e2020GL091555. [Google Scholar] [CrossRef]
- Xu, G.; Yang, J.; Dong, C.; Chen, D.; Wang, J. Statistical study of submesoscale eddies identified from synthetic aperture radar images in the Luzon Strait and adjacent seas. Int. J. Remote Sens. 2015, 36, 4621–4631. [Google Scholar] [CrossRef]
- Hobday, A.J.; Alexander, L.V.; Perkins, S.E.; Smale, D.A.; Straub, S.C.; Oliver, E.C.J.; Benthuysen, J.A.; Burrows, M.T.; Donat, M.G.; Feng, M.; et al. A hierarchical approach to defining marine heatwaves. Prog. Oceanogr. 2016, 141, 227–238. [Google Scholar] [CrossRef] [Green Version]
- Oliver, E.C.J. Mean warming not variability drives marine heatwave trends. Clim. Dyn. 2019, 53, 1653–1659. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Donat, M.G.; Burrows, M.T.; Moore, P.J.; Smale, D.A.; Alexander, L.V.; Benthuysen, J.A.; Feng, M.; Sen Gupta, A.; Hobday, A.J.; et al. Longer and more frequent marine heatwaves over the past century. Nat. Commun. 2018, 9, 1324. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Benthuysen, J.A.; Darmaraki, S.; Donat, M.G.; Hobday, A.J.; Holbrook, N.J.; Schlegel, R.W.; Sen Gupta, A. Marine Heatwaves. Ann. Rev. Mar. Sci. 2021, 13, 313–342. [Google Scholar] [CrossRef]
- Lindstrom, E.; Gunn, J.; Fischer, A.; McCurdy, A.; Glover, L.K. A Framework for Ocean Observing. By the Task Team for an Integrated Framework for Sustained Ocean Observing; Unesco: Paris, France, 2012. [Google Scholar]
- Gruber, N.; Boyd, P.W.; Frolicher, T.L.; Vogt, M. Biogeochemical extremes and compound events in the ocean. Nature 2021, 600, 395–407. [Google Scholar] [CrossRef]
- Boyce, D.G.; Lewis, M.R.; Worm, B. Global phytoplankton decline over the past century. Nature 2010, 466, 591–596. [Google Scholar] [CrossRef]
- Oey, L.Y.; Chang, M.C.; Huang, S.M.; Lin, Y.C.; Lee, M.A. The influence of shelf-sea fronts on winter monsoon over East China Sea. Clim. Dyn. 2015, 45, 2047–2068. [Google Scholar] [CrossRef]
- Wang, T.; Yu, P.; Wu, Z.; Lu, W.; Liu, X.; Li, Q.P.; Huang, B. Revisiting the Intraseasonal Variability of Chlorophyll-a in the Adjacent Luzon Strait With a New Gap-Filled Remote Sensing Data Set. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–11. [Google Scholar] [CrossRef]
- Xiao, W.; Wang, L.; Laws, E.; Xie, Y.; Chen, J.; Liu, X.; Chen, B.; Huang, B. Realized niches explain spatial gradients in seasonal abundance of phytoplankton groups in the South China Sea. Prog. Oceanogr. 2018, 162, 223–239. [Google Scholar] [CrossRef]
- Belkin, I.M.; O’Reilly, J.E. An algorithm for oceanic front detection in chlorophyll and SST satellite imagery. J. Mar. Syst. 2009, 78, 319–326. [Google Scholar] [CrossRef]
- Chin, T.M.; Vazquez-Cuervo, J.; Armstrong, E.M. A multi-scale high-resolution analysis of global sea surface temperature. Remote Sens. Environ. 2017, 200, 154–169. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Thomson, R.E.; Emery, W.J. Data Analysis Methods in Physical Oceanography; Newnes: Oxford, UK, 2014. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Chen, Y.-L.L.; Chen, H.-Y.; Lin, I.-I.; Lee, M.-A.; Chang, J. Effects of cold eddy on phytoplankton production and assemblages in Luzon Strait bordering the South China Sea. J. Oceanogr. 2007, 63, 671–683. [Google Scholar] [CrossRef]
- Sverdrup, H.U. On conditions for the vernal blooming of phytoplankton. ICES J. Mar. Sci. 1953, 18, 287–295. [Google Scholar] [CrossRef]
- Boccaletti, G.; Ferrari, R.; Fox-Kemper, B. Mixed Layer Instabilities and Restratification. J. Phys. Oceanogr. 2007, 37, 2228–2250. [Google Scholar] [CrossRef]
- Fox-Kemper, B.; Ferrari, R.; Hallberg, R. Parameterization of Mixed Layer Eddies. Part I: Theory and Diagnosis. J. Phys. Oceanogr. 2008, 38, 1145–1165. [Google Scholar] [CrossRef]
- Taylor, J.R.; Ferrari, R. Ocean fronts trigger high latitude phytoplankton blooms. Geophys. Res. Lett. 2011, 38, L23601. [Google Scholar] [CrossRef]
- Bondur, V.G.; Zamshin, V.V.; Chvertkova, O.I. Space Study of a Red Tide-Related Environmental Disaster near Kamchatka Peninsula in September–October 2020. Dokl. Earth Sci. 2021, 497, 255–260. [Google Scholar] [CrossRef]
- Yagci, A.L.; Colkesen, I.; Kavzoglu, T.; Sefercik, U.G. Daily monitoring of marine mucilage using the MODIS products: A case study of 2021 mucilage bloom in the Sea of Marmara, Turkey. Environ. Monit. Assess. 2022, 194, 170. [Google Scholar] [CrossRef] [PubMed]
- Wei, G.; Tang, D.; Wang, S. Distribution of chlorophyll and harmful algal blooms (HABs): A review on space based studies in the coastal environments of Chinese marginal seas. Adv. Space Res. 2008, 41, 12–19. [Google Scholar] [CrossRef]
- Aumont, O.; Éthé, C.; Tagliabue, A.; Bopp, L.; Gehlen, M. PISCES-v2: An ocean biogeochemical model for carbon and ecosystem studies. Geosci. Model Dev. 2015, 8, 2465–2513. [Google Scholar] [CrossRef] [Green Version]
- Lu, W.; Wang, J.; Jiang, Y.; Chen, Z.; Wu, W.; Yang, L.; Liu, Y. Data-Driven Method with Numerical Model: A Combining Framework for Predicting Subtropical River Plumes. J. Geophys. Res. Ocean. 2022, 127, e2021JC017925. [Google Scholar] [CrossRef]
- Lu, W.; Oey, L.-Y.; Liao, E.; Zhuang, W.; Yan, X.-H.; Jiang, Y. Physical modulation to the biological productivity in the summer Vietnam upwelling system. Ocean. Sci. 2018, 14, 1303–1320. [Google Scholar] [CrossRef] [Green Version]
- Lu, W.; Luo, Y.; Yan, X.; Jiang, Y. Modeling the Contribution of the Microbial Carbon Pump to Carbon Sequestration in the South China Sea. Sci. China Earth Sci. 2018, 61, 1594–1604. [Google Scholar] [CrossRef]



| Data Abbreviation | Variable | Full Name | Source * | References | Resolution |
|---|---|---|---|---|---|
| SCSDCT | CHL | South China Sea Full-coverage Daily 4 km Surface Chlorophyll-a Remote Sensing Reconstruction Dataset from Discrete Cosine Transform 2005–2019 | https://www.scidb.cn/detail?dataSetId=1387ffe83af54f0fb574d60e97b206b2 | [42] | 4 km × 4 km |
| MUR | SST and HI and frontal intensity derived from SST | Multi-scale Ultra-high Resolution (MUR) Sea Surface Temperature | https://podaac.jpl.nasa.gov/MEaSUREs-MUR?sections=data | [31,44,45] | 0.01° × 0.01° |
| ERA5 | Meridional and zonal wind | Fifth generation of the European Center for Medium-Range Weather Forecasts atmospheric reanalyses of the global climate | https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview | [46] | 0.1° × 0.1° |
| AVISO | SSH and Absolute Dynamic Topography (ADT) | Archiving, Validation, and Interpretation of Satellite Oceanographic | https://resources.marine.copernicus.eu/?option=com_csw&view=details&product_id=SEALEVELGLO_PHY_L4_REP_OBSERVATIONS_008_047 | / | 0.25° × 0.25° |
| GLORYS | Mixed-Layer Depth (MLD) | Mixed-layer depth from the GLORYSV12 reanalysis product from the Copernicus Marine Service | https://resources.marine.copernicus.eu/product-detail/GLOBAL_MULTIYEAR_PHY_001_030/INFORMATION | / | 0.083° × 0.083° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Gao, X.; Wu, Z.; Wang, T.; Lin, S.; Xiao, C.; Lai, Z. Framework to Extract Extreme Phytoplankton Bloom Events with Remote Sensing Datasets: A Case Study. Remote Sens. 2022, 14, 3557. https://doi.org/10.3390/rs14153557
Lu W, Gao X, Wu Z, Wang T, Lin S, Xiao C, Lai Z. Framework to Extract Extreme Phytoplankton Bloom Events with Remote Sensing Datasets: A Case Study. Remote Sensing. 2022; 14(15):3557. https://doi.org/10.3390/rs14153557
Chicago/Turabian StyleLu, Wenfang, Xinyu Gao, Zelun Wu, Tianhao Wang, Shaowen Lin, Canbo Xiao, and Zhigang Lai. 2022. "Framework to Extract Extreme Phytoplankton Bloom Events with Remote Sensing Datasets: A Case Study" Remote Sensing 14, no. 15: 3557. https://doi.org/10.3390/rs14153557
APA StyleLu, W., Gao, X., Wu, Z., Wang, T., Lin, S., Xiao, C., & Lai, Z. (2022). Framework to Extract Extreme Phytoplankton Bloom Events with Remote Sensing Datasets: A Case Study. Remote Sensing, 14(15), 3557. https://doi.org/10.3390/rs14153557